Théorème de Bell

Le théorème de Bell est un terme englobant un certain nombre de résultats étroitement liés en physique, qui déterminent tous que la mécanique quantique est incompatible avec les théories locales des variables cachées . Le « local » dans ce cas fait référence au principe de localité , l’idée qu’une particule ne peut être influencée que par son environnement immédiat, et que les interactions médiées par des champs physiques ne peuvent se produire qu’à des vitesses ne dépassant pas la vitesse de la lumière . Les « variables cachées » sont des propriétés hypothétiques possédées par des particules quantiques, des propriétés qui sont indétectables mais qui affectent toujours le résultat des expériences. Dans les mots du physicien John Stewart Bell, pour qui cette famille de résultats est nommée, “Si [une Théorie des variables cachées] est locale, elle ne sera pas en accord avec la mécanique quantique, et si elle est en accord avec la mécanique quantique, elle ne sera pas locale.” ^[1]

Le terme est largement appliqué à un certain nombre de dérivations différentes, dont la première a été introduite par Bell dans un article de 1964 intitulé “On the Einstein Podolsky Rosen Paradox “. L’article de Bell était une réponse à une expérience de pensée de 1935 qu’Albert Einstein , Boris Podolsky et Nathan Rosen utilisaient pour affirmer que la physique quantique est une théorie “incomplète”. ^{[2] [3]} En 1935, il était déjà reconnu que les prédictions de la physique quantique sont probabilistes . Einstein, Podolsky et Rosen ont présenté un scénario qui consiste à préparer une paire de particules de sorte que l’ état quantique de la paire soitintriqué , puis séparant les particules à une distance arbitrairement grande. L’expérimentateur a le choix entre les mesures possibles pouvant être effectuées sur l’une des particules. Lorsqu’ils choisissent une mesure et obtiennent un résultat, l’état quantique de l’autre particule s’effondre instantanément dans un nouvel état en fonction de ce résultat, quelle que soit la distance à laquelle se trouve l’autre particule. Cela pourrait seulement signifier que soit la mesure de la première particule a également interagi avec la seconde particule à une vitesse supérieure à la vitesse de la lumière, soitque les particules intriquées avaient une propriété non mesurée qui prédéterminait leurs états quantiques finaux avant qu’elles ne soient séparées. Par conséquent, en supposant la localité, la mécanique quantique doit être incomplète, car elle ne peut pas donner une description complète des véritables caractéristiques physiques de la particule. En d’autres termes, les particules quantiques, comme les électrons et les photons , doivent porter certaines propriétés ou attributs non inclus dans la théorie quantique, et les incertitudes dans les prédictions de la théorie quantique seraient alors dues à l’ignorance ou à l’inconnaissabilité de ces propriétés, appelées plus tard “variables cachées”.

Bell a poussé l’analyse de l’intrication quantique beaucoup plus loin. Il en a déduit que si les mesures sont effectuées indépendamment sur les deux particules séparées d’une paire intriquée, alors l’hypothèse que les résultats dépendent de variables cachées dans chaque moitié implique une contrainte mathématique sur la façon dont les résultats des deux mesures sont corrélés. Cette contrainte sera plus tard nommée l’ inégalité de Bell . Bell a ensuite montré que la physique quantique prédit des corrélations qui violent cette inégalité. Par conséquent, la seule façon dont les variables cachées pourraient expliquer les prédictions de la physique quantique est si elles sont “non locales”, c’est-à-dire que d’une manière ou d’une autre, les deux particules ont pu interagir instantanément, quelle que soit la distance entre les deux particules. ^{[4] [5]}

De multiples variations du théorème de Bell ont été proposées dans les années suivantes, introduisant d’autres conditions étroitement liées généralement connues sous le nom d’inégalités de Bell (ou «de type Bell»). La première expérience rudimentaire conçue pour tester le théorème de Bell a été réalisée en 1972 par John Clauser et Stuart Freedman ; expériences plus avancées, connues collectivement sous le nom de tests de Bell, ont été jouées plusieurs fois depuis. Souvent, ces expériences ont eu pour objectif de “fermer les lacunes”, c’est-à-dire d’améliorer les problèmes de conception ou de configuration expérimentales qui pourraient en principe affecter la validité des résultats des tests de Bell antérieurs. À ce jour, les tests de Bell ont constamment montré que les systèmes physiques obéissent à la mécanique quantique et violent les inégalités de Bell ; c’est-à-dire que les résultats de ces expériences sont incompatibles avec toute Théorie des variables cachées locales. ^{[6] [7]}

La nature exacte des hypothèses requises pour prouver une contrainte de type Bell sur les corrélations a été débattue par des physiciens et des philosophes . Alors que la signification du théorème de Bell ne fait aucun doute, toutes ses implications pour l’ Interprétation de la mécanique quantique restent non résolues.

Théorème

Il existe de nombreuses variantes de l’idée de base, certaines utilisant des hypothèses mathématiques plus fortes que d’autres. ^[8] De manière significative, les théorèmes de type Bell ne se réfèrent à aucune théorie particulière des variables cachées locales, mais montrent plutôt que la physique quantique viole les hypothèses générales derrière les images classiques de la nature. Le théorème original prouvé par Bell en 1964 n’est pas le plus propice à l’expérimentation, et il convient d’introduire le genre des inégalités de type Bell avec un exemple ultérieur. ^[9]

Alice et Bob se tiennent dans des endroits très éloignés. Victor prépare une paire de particules et en envoie une à Alice et l’autre à Bob. Lorsqu’Alice reçoit sa particule, elle choisit d’effectuer l’une des deux mesures possibles (peut-être en lançant une pièce pour décider laquelle). Notons ces mesures par A 0 {displaystyle A_{0}} $A_{0}$ $A_{0}$ et A 1 {displaystyle A_{1}} $A_{1}$ $A_{1}$ . Tous les deux A 0 {displaystyle A_{0}} $A_{0}$ $A_{0}$ et A 1 {displaystyle A_{1}} $A_{1}$ $A_{1}$ sont des mesures binaires : le résultat de A 0 {displaystyle A_{0}} $A_{0}$ $A_{0}$ est soit + 1 {displaystyle +1} ou alors − 1 {displaystyle -1} , et de même pour A 1 {displaystyle A_{1}} $A_{1}$ $A_{1}$ . Lorsque Bob reçoit sa particule, il choisit l’une des deux mesures, B 0 {displaystyle B_{0}} $B_{0}$ $B_{0}$ et B 1 {displaystyle B_{1}} $B_{1}$ $B_{1}$ , qui sont également tous deux binaires.

Supposons que chaque mesure révèle une propriété que la particule possédait déjà. Par exemple, si Alice choisit de mesurer A 0 {displaystyle A_{0}} $A_{0}$ $A_{0}$ et obtient le résultat + 1 {displaystyle +1} , alors la particule qu’elle a reçue portait une valeur de + 1 {displaystyle +1} pour une propriété a 0 {displaystyle a_{0}} $a_{0}$ $un_{0}$ . ^{[note 1]} Considérez la combinaison suivante :

a 0 b 0 + a 0 b 1 + a 1 b 0 − a 1 b 1 = ( a 0 + a 1 ) b 0 + ( a 0 − a 1 ) b 1 . {displaystyle a_{0}b_{0}+a_{0}b_{1}+a_{1}b_{0}-a_{1}b_{1}=(a_{0}+a_{1}) b_{0}+(a_{0}-a_{1})b_{1},.} ${displaystyle a_{0}b_{0}+a_{0}b_{1}+a_{1}b_{0}-a_{1}b_{1}=(a_{0}+a_{1})b_{0}+(a_{0}-a_{1})b_{1},.}$ ${displaystyle a_{0}b_{0}+a_{0}b_{1}+a_{1}b_{0}-a_{1}b_{1}=(a_{0}+a_{1}) b_{0}+(a_{0}-a_{1})b_{1},.}$

Parce que les deux a 0 {displaystyle a_{0}} $a_{0}$ $un_{0}$ et a 1 {displaystyle a_{1}} $a_{1}$ $un_{1}$ prendre les valeurs ± 1 {style d’affichage pm 1} pm 1 , alors soit a 0 = a 1 {displaystyle a_{0}=a_{1}} ${displaystyle a_{0}=a_{1}}$ ${displaystyle a_{0}=a_{1}}$ ou alors a 0 = − a 1 {displaystyle a_{0}=-a_{1}} ${displaystyle a_{0}=-a_{1}}$ ${displaystyle a_{0}=-a_{1}}$ . Dans le cas précédent, ( a 0 − a 1 ) b 1 = 0 {displaystyle (a_{0}-a_{1})b_{1}=0} ${displaystyle (a_{0}-a_{1})b_{1}=0}$ ${displaystyle (a_{0}-a_{1})b_{1}=0}$ , tandis que dans ce dernier cas, ( a 0 + a 1 ) b 0 = 0 {displaystyle (a_{0}+a_{1})b_{0}=0} ${displaystyle (a_{0}+a_{1})b_{0}=0}$ ${displaystyle (a_{0}+a_{1})b_{0}=0}$ . Ainsi, l’un des termes du côté droit de l’expression ci-dessus disparaîtra et l’autre sera égal à ± 2 {style d’affichage pm 2} pm 2 . Par conséquent, si l’expérience est répétée sur de nombreux essais, Victor préparant de nouvelles paires de particules, la valeur moyenne de la combinaison a 0 b 0 + a 0 b 1 + a 1 b 0 − a 1 b 1 {displaystyle a_{0}b_{0}+a_{0}b_{1}+a_{1}b_{0}-a_{1}b_{1}} ${displaystyle a_{0}b_{0}+a_{0}b_{1}+a_{1}b_{0}-a_{1}b_{1}}$ sur tous les essais sera inférieur ou égal à 2. Aucun essai ne peut mesurer cette quantité, car Alice et Bob ne peuvent choisir qu’une seule mesure chacun, mais en supposant que les propriétés sous-jacentes existent, la valeur moyenne de la somme est juste la somme des moyennes pour chaque terme. En utilisant des crochets angulaires pour indiquer les moyennes,

⟨ A 0 B 0 ⟩ + ⟨ A 0 B 1 ⟩ + ⟨ A 1 B 0 ⟩ − ⟨ A 1 B 1 ⟩ ≤ 2 . {displaystyle langle A_{0}B_{0}rangle +langle A_{0}B_{1}rangle +langle A_{1}B_{0}rangle -langle A_{1}B_{ 1}rangle leq 2,.} ${displaystyle langle A_{0}B_{0}rangle +langle A_{0}B_{1}rangle +langle A_{1}B_{0}rangle -langle A_{1}B_{1}rangle leq 2,.}$ ${displaystyle langle A_{0}B_{0}rangle +langle A_{0}B_{1}rangle +langle A_{1}B_{0}rangle -langle A_{1}B_{ 1}rangle leq 2,.}$ Il s’agit d’une inégalité de Bell, plus précisément de l’ inégalité CHSH . ^{[9] : 115} Sa dérivation ici dépend de deux hypothèses : premièrement, que les propriétés physiques sous-jacentes a 0 , a 1 , b 0 , {displaystyle a_{0},a_{1},b_{0},} ${displaystyle a_{0},a_{1},b_{0},}$ ${displaystyle a_{0},a_{1},b_{0},}$ et b 1 {displaystyle b_{1}} $b_{1}$ $b_{1}$ exister indépendamment d’être observé ou mesuré (parfois appelé hypothèse de réalisme ); et deuxièmement, que le choix d’action d’Alice ne peut pas influencer le résultat de Bob ou vice versa (souvent appelé l’hypothèse de localité ). ^{[9] : 117}

La mécanique quantique peut violer l’inégalité CHSH, comme suit. Victor prépare une paire de qubits qu’il décrit par l’ état de Bell

| ψ ⟩ = | 01 ⟩ − | 10 ⟩ 2 . {displaystyle |psi rangle ={frac {|01rangle -|10rangle }{sqrt {2}}}.} ${displaystyle |psi rangle ={frac {|01rangle -|10rangle }{sqrt {2}}}.}$ ${displaystyle |psi rangle ={frac {|01rangle -|10rangle }{sqrt {2}}}.}$ Victor passe ensuite le premier qubit à Alice et le second à Bob. Les choix de mesures possibles d’Alice et Bob sont définis par les matrices de Pauli . Alice mesure l’un ou l’autre des deux observables σ z {displaystyle sigma _{z}} $sigma _{z}$ $sigma _{z}$ et σ x {displaystyle sigma _{x}} $sigma _{x}$ $sigma _{x}$ : A 0 = σ z = ( 1 0 0 − 1 ) , A 1 = σ x = ( 0 1 1 0 ) ; {displaystyle A_{0}=sigma _{z}={begin{pmatrix}1&0\0&-1end{pmatrix}}, A_{1}=sigma _{x}={begin {pmatrix}0&1\1&0end{pmatrix}} ;} ${displaystyle A_{0}=sigma _{z}={begin{pmatrix}1&0\0&-1end{pmatrix}}, A_{1}=sigma _{x}={begin{pmatrix}0&1\1&0end{pmatrix}};}$ ${displaystyle A_{0}=sigma _{z}={begin{pmatrix}1&0\0&-1end{pmatrix}}, A_{1}=sigma _{x}={begin{pmatrix}0&1\1&0end{pmatrix}};}$ et Bob mesure l’une ou l’autre des deux observables B 0 = − σ x + σ z 2 , B 1 = σ x − σ z 2 . {displaystyle B_{0}=-{frac {sigma _{x}+sigma _{z}}{sqrt {2}}}, B_{1}={frac {sigma _{ x}-sigma _{z}}{sqrt {2}}}.} ${displaystyle B_{0}=-{frac {sigma _{x}+sigma _{z}}{sqrt {2}}}, B_{1}={frac {sigma _{x}-sigma _{z}}{sqrt {2}}}.}$ ${displaystyle B_{0}=-{frac {sigma _{x}+sigma _{z}}{sqrt {2}}}, B_{1}={frac {sigma _{x}-sigma _{z}}{sqrt {2}}}.}$ Victor peut calculer les valeurs d’espérance quantique pour des paires de ces observables en utilisant la règle de Born : ⟨ A 0 ⊗ B 0 ⟩ = 1 2 , ⟨ A 0 ⊗ B 1 ⟩ = 1 2 , ⟨ A 1 ⊗ B 0 ⟩ = 1 2 , ⟨ A 1 ⊗ B 1 ⟩ = − 1 2 . {displaystyle langle A_{0}otimes B_{0}rangle ={frac {1}{sqrt {2}}},langle A_{0}otimes B_{1}rangle ={ frac {1}{sqrt {2}}},langle A_{1}otimes B_{0}rangle ={frac {1}{sqrt {2}}},langle A_{1} parfois B_{1}rangle =-{frac {1}{sqrt {2}}},.} ${displaystyle langle A_{0}otimes B_{0}rangle ={frac {1}{sqrt {2}}},langle A_{0}otimes B_{1}rangle ={frac {1}{sqrt {2}}},langle A_{1}otimes B_{0}rangle ={frac {1}{sqrt {2}}},langle A_{1}otimes B_{1}rangle =-{frac {1}{sqrt {2}}},.}$ ${displaystyle langle A_{0}otimes B_{0}rangle ={frac {1}{sqrt {2}}},langle A_{0}otimes B_{1}rangle ={frac {1}{sqrt {2}}},langle A_{1}otimes B_{0}rangle ={frac {1}{sqrt {2}}},langle A_{1}otimes B_{1}rangle =-{frac {1}{sqrt {2}}},.}$ Alors qu’une seule de ces quatre mesures peut être effectuée dans un seul essai de l’expérience, la somme ⟨ A 0 ⊗ B 0 ⟩ + ⟨ A 0 ⊗ B 1 ⟩ + ⟨ A 1 ⊗ B 0 ⟩ − ⟨ A 1 ⊗ B 1 ⟩ = 2 2 {displaystyle langle A_{0}otimes B_{0}rangle +langle A_{0}otimes B_{1}rangle +langle A_{1}otimes B_{0}rangle -langle A_{1}parfois B_{1}rangle =2{sqrt {2}}} ${displaystyle langle A_{0}otimes B_{0}rangle +langle A_{0}otimes B_{1}rangle +langle A_{1}otimes B_{0}rangle -langle A_{1}otimes B_{1}rangle =2{sqrt {2}}}$ ${displaystyle langle A_{0}otimes B_{0}rangle +langle A_{0}otimes B_{1}rangle +langle A_{1}otimes B_{0}rangle -langle A_{1}otimes B_{1}rangle =2{sqrt {2}}}$ donne la somme des valeurs moyennes que Victor s’attend à trouver sur plusieurs essais. Cette valeur dépasse la borne supérieure classique de 2 qui a été déduite de l’hypothèse des variables cachées locales. ^{[9] : 116} La valeur 2 2 {displaystyle 2{sqrt {2}}} est en fait la plus grande que la physique quantique autorise pour cette combinaison de valeurs d’espérance, ce qui en fait une borne de Tsirelson . 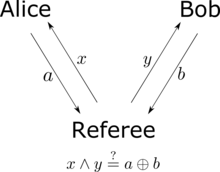^{[12] : 140} Une illustration du Jeu CHSH : l’arbitre, Victor, envoie un peu chacun à Alice et à Bob, et Alice et Bob renvoient chacun un peu à l’arbitre.

L’inégalité CHSH peut également être considérée comme un jeu dans lequel Alice et Bob essaient de coordonner leurs actions . ^{[13] [14]} Victor prépare deux morceaux, x {style d’affichage x} et y {displaystyle y} , indépendamment et au hasard. Il envoie peu x {style d’affichage x} à Alice et peu y {displaystyle y} À bob. Alice et Bob gagnent s’ils retournent des bits de réponse a {displaystyle a} et b {displaystyle b} à Victor, satisfaisant

x y = a + b mod 2 . {displaystyle xy=a+bmod 2,.} Ou, de manière équivalente, Alice et Bob gagnent si le ET logique de x {style d’affichage x} et y {displaystyle y} est le XOR logique de a {displaystyle a} et b {displaystyle b} . Alice et Bob peuvent convenir de la stratégie qu’ils désirent avant le jeu, mais ils ne peuvent pas communiquer une fois que le jeu commence. Dans toute théorie basée sur des variables cachées locales, la probabilité de gagner d’Alice et Bob n’est pas supérieure à 3 / 4 {displaystyle 3/4} 3/4 , quelle que soit la stratégie sur laquelle ils se sont mis d’accord au préalable. Cependant, s’ils partagent un état quantique intriqué, leur probabilité de gagner peut être aussi grande que 2 + 2 4 ≈ 0.85 . {displaystyle {frac {2+{sqrt {2}}}{4}}environ 0,85,.} ${displaystyle {frac {2+{sqrt {2}}}{4}}approx 0.85,.}$ ${displaystyle {frac {2+{sqrt {2}}}{4}}approx 0.85,.}$

Variations et résultats associés

Cloche (1964)

L’article de Bell de 1964 souligne que dans des conditions restreintes, les modèles de variables cachées locales peuvent reproduire les prédictions de la mécanique quantique. Il démontre ensuite que cela ne peut pas être vrai en général. ^[3] Bell considère un raffinement par David Bohm de l’expérience de pensée d’Einstein-Podolsky-Rosen (EPR). Dans ce scénario, une paire de particules sont formées ensemble de telle manière qu’elles sont décrites par un état singulet de spin (qui est un exemple d’état intriqué). Les particules se séparent alors dans des directions opposées. Chaque particule est mesurée par un appareil Stern-Gerlach , un instrument de mesure qui peut être orienté dans différentes directions et qui signale l’un des deux résultats possibles, représentable par + 1 {displaystyle +1} et − 1 {displaystyle -1} . La configuration de chaque instrument de mesure est représentée par un vecteur , et la prédiction de la mécanique quantique pour la corrélation entre deux détecteurs avec des paramètres a → {displaystyle {vec {a}}} et b → {displaystyle {vec {b}}} est

P ( a → , b → ) = − a → ⋅ b → . {displaystyle P({vec {a}},{vec {b}})=-{vec {a}}cdot {vec {b}},.}

En particulier, si l’orientation des deux détecteurs est la même ( a → = b → {displaystyle {vec {a}}={vec {b}}} ), alors le résultat d’une mesure est certain d’être le négatif du résultat de l’autre, ce qui donne P ( a → , a → ) = − 1 {displaystyle P({vec {a}},{vec {a}})=-1} . Et si les orientations des deux détecteurs sont orthogonales ( a → ⋅ b → = 0 {displaystyle {vec {a}}cdot {vec {b}}=0} ), alors les résultats ne sont pas corrélés, et P ( a → , b → ) = 0 {displaystyle P({vec {a}},{vec {b}})=0} . Bell prouve par l’exemple que ces cas particuliers peuvent être expliqués en termes de variables cachées, puis procède à montrer que la gamme complète des possibilités impliquant des angles intermédiaires ne peut pas.

Bell a postulé qu’un modèle de variable cachée locale pour ces corrélations les expliquerait en termes d’intégrale sur les valeurs possibles d’un paramètre caché λ {displaystylelambda} lambda :

P ( a → , b → ) = ∫ d λ ρ ( λ ) A ( a → , λ ) B ( b → , λ ) , {displaystyle P({vec {a}},{vec {b}})=int dlambda ,rho (lambda )A({vec {a}},lambda )B( {vec {b}},lambda ),,} où ρ ( λ ) {displaystyle rho (lambda)} est une fonction de densité de probabilité . Les deux fonctions A ( a → , λ ) {displaystyle A({vec {a}},lambda )} et B ( b → , λ ) {displaystyle B({vec {b}},lambda )} fournir les réponses des deux détecteurs étant donné les vecteurs d’orientation et la variable cachée : A ( a → , λ ) = ± 1 , B ( b → , λ ) = ± 1 . {displaystyle A({vec {a}},lambda )=pm 1,,B({vec {b}},lambda )=pm 1,.} Fondamentalement, le résultat du détecteur A {displaystyle A} ne dépend pas de b → {displaystyle {vec {b}}} , et de même le résultat de B {displaystyle B} ne dépend pas de a → {displaystyle {vec {a}}} , car les deux détecteurs sont physiquement séparés. Supposons maintenant que l’expérimentateur dispose d’un choix de réglages pour le second détecteur : il peut être réglé soit sur b → {displaystyle {vec {b}}} ou pour c → {displaystyle {vec {c}}} vec{c} . Bell prouve que la différence de corrélation entre ces deux choix de réglage du détecteur doit satisfaire l’inégalité | P ( a → , b → ) − P ( a → , c → ) | ≤ 1 + P ( b → , c → ) . {displaystyle |P({vec {a}},{vec {b}})-P({vec {a}},{vec {c}})|leq 1+P({ vec {b}},{vec {c}}),.} Cependant, il est facile de trouver des situations où la mécanique quantique viole l’inégalité de Bell. ^{[15] : 425–426} Par exemple, laissez les vecteurs a → {displaystyle {vec {a}}} et b → {displaystyle {vec {b}}} être orthogonal, et soit c → {displaystyle {vec {c}}} vec{c} reposent dans leur plan à un angle de 45° par rapport aux deux. Puis P ( a → , b → ) = 0 , {displaystyle P({vec {a}},{vec {b}})=0,,} pendant que P ( a → , c → ) = P ( b → , c → ) = − 2 2 , {displaystyle P({vec {a}},{vec {c}})=P({vec {b}},{vec {c}})=-{frac {sqrt {2 }}{2}},,} ${displaystyle P({vec {a}},{vec {c}})=P({vec {b}},{vec {c}})=-{frac {sqrt {2}}{2}},,}$ ${displaystyle P({vec {a}},{vec {c}})=P({vec {b}},{vec {c}})=-{frac {sqrt {2}}{2}},,}$ mais 2 2 ≰ 1 − 2 2 . {displaystyle {frac {sqrt {2}}{2}}nleq 1-{frac {sqrt {2}}{2}},.} ${displaystyle {frac {sqrt {2}}{2}}nleq 1-{frac {sqrt {2}}{2}},.}$ Par conséquent, il n’y a pas de modèle de variables cachées locales qui puisse reproduire les prédictions de la mécanique quantique pour tous les choix de a → {displaystyle {vec {a}}} , b → {displaystyle {vec {b}}} , et c → {displaystyle {vec {c}}} vec{c} . Les résultats expérimentaux contredisent les courbes classiques et correspondent à la courbe prédite par la mécanique quantique tant que les lacunes expérimentales sont prises en compte. ^[8]

Le théorème de Bell de 1964 nécessite la possibilité d’anti-corrélations parfaites : la capacité de faire une prédiction de probabilité 1 sur le résultat du deuxième détecteur, connaissant le résultat du premier. Ceci est lié au «critère EPR de la réalité», un concept introduit dans l’article de 1935 d’Einstein, Podolsky et Rosen. Cet article postule : « Si, sans perturber en aucune façon un système, nous pouvons prédire avec certitude (c’est-à-dire avec une probabilité égale à l’unité) la valeur d’une quantité physique, alors il existe un élément de réalité correspondant à cette quantité. ^[2]

GHZ–Mermin

Greenberger, Horne et Zeilinger ont présenté une expérience de pensée à quatre particules, que Mermin a ensuite simplifiée pour n’utiliser que trois particules. ^{[16] [17]} Dans cette expérience de pensée, Victor génère un ensemble de trois particules de spin-1/2 décrites par l’état quantique

| ψ ⟩ = 1 2 ( | 000 ⟩ − | 111 ⟩ ) , {displaystyle |psi rangle ={frac {1}{sqrt {2}}}(|000rangle -|111rangle ),,} ${displaystyle |psi rangle ={frac {1}{sqrt {2}}}(|000rangle -|111rangle ),,}$ ${displaystyle |psi rangle ={frac {1}{sqrt {2}}}(|000rangle -|111rangle ),,}$ où comme ci-dessus, | 0 ⟩ {displaystyle |0rangle } et | 1 ⟩ {displaystyle |1rangle} sont les vecteurs propres de la matrice de Pauli σ z {displaystyle sigma _{z}} $sigma _{z}$ $sigma _{z}$ . Victor envoie ensuite une particule chacun à Alice, Bob et Charlie, qui attendent à des endroits très éloignés. Alice mesure soit σ x {displaystyle sigma _{x}} $sigma _{x}$ $sigma _{x}$ ou alors σ y {displaystyle sigma _{y}} sigma_y sur sa particule, tout comme Bob et Charlie. Le résultat de chaque mesure est soit + 1 {displaystyle +1} ou alors − 1 {displaystyle -1} . Application de la règle de Born à l’état à trois qubits | ψ ⟩ {displaystyle |psirangle } |psi rangle , Victor prédit que chaque fois que les trois mesures incluent une σ x {displaystyle sigma _{x}} $sigma _{x}$ $sigma _{x}$ et deux σ y {displaystyle sigma _{y}} sigma_y ‘s, le produit des résultats sera toujours + 1 {displaystyle +1} . Cela suit parce que | ψ ⟩ {displaystyle |psirangle } |psi rangle est un vecteur propre de σ x ⊗ σ y ⊗ σ y {displaystyle sigma _{x}otimes sigma _{y}otimes sigma _{y}} ${displaystyle sigma _{x}otimes sigma _{y}otimes sigma _{y}}$ ${displaystyle sigma _{x}otimes sigma _{y}otimes sigma _{y}}$ avec valeur propre + 1 {displaystyle +1} , et de même pour σ y ⊗ σ x ⊗ σ y {displaystyle sigma _{y}otimes sigma _{x}otimes sigma _{y}} ${displaystyle sigma _{y}otimes sigma _{x}otimes sigma _{y}}$ ${displaystyle sigma _{y}otimes sigma _{x}otimes sigma _{y}}$ et σ y ⊗ σ y ⊗ σ x {displaystyle sigma _{y}otimes sigma _{y}otimes sigma _{x}} ${displaystyle sigma _{y}otimes sigma _{y}otimes sigma _{x}}$ ${displaystyle sigma _{y}otimes sigma _{y}otimes sigma _{x}}$ . Par conséquent, connaissant le résultat d’Alice pour un σ x {displaystyle sigma _{x}} $sigma _{x}$ $sigma _{x}$ mesure et le résultat de Bob pour un σ y {displaystyle sigma _{y}} sigma_y mesure, Victor peut prédire avec probabilité 1 quel résultat Charlie retournera pour un σ y {displaystyle sigma _{y}} sigma_y la mesure. Selon le critère de réalité EPR, il y aurait un “élément de réalité” correspondant au résultat d’une σ y {displaystyle sigma _{y}} sigma_y mesure sur le qubit de Charlie. En effet, cette même logique s’applique aux deux mesures et aux trois qubits. Selon le critère de réalité EPR, chaque particule contient un “jeu d’instructions” qui détermine le résultat d’un σ x {displaystyle sigma _{x}} $sigma _{x}$ $sigma _{x}$ ou alors σ y {displaystyle sigma _{y}} sigma_y mesure sur elle. L’ensemble des trois particules serait alors décrit par le jeu d’instructions ( a x , a y , b x , b y , c x , c y ) , {displaystyle (a_{x},a_{y},b_{x},b_{y},c_{x},c_{y}),,} ${displaystyle (a_{x},a_{y},b_{x},b_{y},c_{x},c_{y}),,}$ ${displaystyle (a_{x},a_{y},b_{x},b_{y},c_{x},c_{y}),,}$ chaque entrée étant soit − 1 {displaystyle -1} ou alors + 1 {displaystyle +1} , et chaque σ x {displaystyle sigma _{x}} $sigma _{x}$ $sigma _{x}$ ou alors σ y {displaystyle sigma _{y}} sigma_y mesure renvoyant simplement la valeur appropriée.

Si Alice, Bob et Charlie exécutent tous le σ x {displaystyle sigma _{x}} $sigma _{x}$ $sigma _{x}$ mesure, alors le produit de leurs résultats serait a x b x c x {displaystyle a_{x}b_{x}c_{x}} ${displaystyle a_{x}b_{x}c_{x}}$ ${displaystyle a_{x}b_{x}c_{x}}$ . Cette valeur peut être déduite de

( a x b y c y ) ( a y b x c y ) ( a y b y c x ) = a x b x c x a y 2 b y 2 c y 2 = a x b x c x , {displaystyle (a_{x}b_{y}c_{y})(a_{y}b_{x}c_{y})(a_{y}b_{y}c_{x})=a_{x} b_{x}c_{x}a_{y}^{2}b_{y}^{2}c_{y}^{2}=a_{x}b_{x}c_{x},,} ${displaystyle (a_{x}b_{y}c_{y})(a_{y}b_{x}c_{y})(a_{y}b_{y}c_{x})=a_{x}b_{x}c_{x}a_{y}^{2}b_{y}^{2}c_{y}^{2}=a_{x}b_{x}c_{x},,}$ ${displaystyle (a_{x}b_{y}c_{y})(a_{y}b_{x}c_{y})(a_{y}b_{y}c_{x})=a_{x}b_{x}c_{x}a_{y}^{2}b_{y}^{2}c_{y}^{2}=a_{x}b_{x}c_{x},,}$ parce que le carré de l’un ou l’autre − 1 {displaystyle -1} ou alors + 1 {displaystyle +1} est 1 {displaystyle 1} . Chaque facteur entre parenthèses est égal à + 1 {displaystyle +1} , alors a x b x c x = + 1 , {displaystyle a_{x}b_{x}c_{x}=+1,,} ${displaystyle a_{x}b_{x}c_{x}=+1,,}$ ${displaystyle a_{x}b_{x}c_{x}=+1,,}$ et le produit des résultats d’Alice, Bob et Charlie sera + 1 {displaystyle +1} avec probabilité unité. Mais ceci est incompatible avec la physique quantique : Victor peut prédire en utilisant l’état | ψ ⟩ {displaystyle |psirangle } |psi rangle que la mesure σ x ⊗ σ x ⊗ σ x {displaystyle sigma _{x}otimes sigma _{x}otimes sigma _{x}} ${displaystyle sigma _{x}otimes sigma _{x}otimes sigma _{x}}$ ${displaystyle sigma _{x}otimes sigma _{x}otimes sigma _{x}}$ cédera plutôt − 1 {displaystyle -1} avec probabilité unité.

Cette expérience de pensée peut également être refondue comme une inégalité de Bell traditionnelle ou, de manière équivalente, comme un jeu non local dans le même esprit que le Jeu CHSH. ^[18] Dans ce document, Alice, Bob et Charlie reçoivent des morceaux x , y , z {displaystyle x, y, z} x,y,z de Victor, promis d’en avoir toujours un nombre pair, c’est-à-dire x ⊕ y ⊕ z = 0 {displaystyle xoplus yoplus z=0} , et lui renvoyer des morceaux a , b , c {displaystyle a,b,c} a,b,c . Ils gagnent la partie si a , b , c {displaystyle a,b,c} a,b,c avoir un nombre impair de uns pour toutes les entrées sauf x = y = z = 0 {displaystyle x=y=z=0} x=y=z=0 , lorsqu’ils doivent avoir un nombre pair d’unités. C’est-à-dire qu’ils gagnent le jeu ssi a ⊕ b ⊕ c = x ∨ y ∨ z {displaystyle aoplus boplus c=xlor ylor z} . Avec des variables cachées locales, la probabilité de victoire la plus élevée qu’ils peuvent avoir est de 3/4, alors qu’en utilisant la stratégie quantique ci-dessus, ils la gagnent avec certitude. Ceci est un exemple de pseudo-télépathie quantique .

Théorème de Kochen-Specker

En théorie quantique, les bases orthonormées d’un espace de Hilbert représentent des mesures qui peuvent être effectuées sur un système ayant cet espace de Hilbert. Chaque vecteur dans une base représente un résultat possible de cette mesure. ^{[note 2]} Supposons qu’une variable cachée λ {displaystylelambda} lambda existe, de sorte que connaître la valeur de λ {displaystylelambda} lambda impliquerait une certitude quant au résultat de toute mesure. Étant donné une valeur de λ {displaystylelambda} lambda , chaque résultat de mesure – c’est-à-dire chaque vecteur dans l’espace de Hilbert – est soit impossible , soit garanti. Une configuration de Kochen – Specker est un ensemble fini de vecteurs constitués de plusieurs bases imbriquées, avec la propriété qu’un vecteur dans celle-ci sera toujours impossible lorsqu’il est considéré comme appartenant à une base et garanti lorsqu’il est considéré comme appartenant à une autre. En d’autres termes, une configuration Kochen-Specker est un “ensemble incolorable” qui démontre l’incohérence de supposer une variable cachée λ {displaystylelambda} lambda peut contrôler les résultats de la mesure. ^{[23] : 196–201}

Théorème du libre arbitre

L’argument de type Kochen-Specker, utilisant des configurations de bases imbriquées, peut être combiné avec l’idée de mesurer des paires intriquées qui sous-tend les inégalités de type Bell. Cela a été noté à partir des années 1970 par Kochen, ^[24] Heywood et Redhead, ^[25] Stairs, ^[26] et Brown et Svetlichny. ^[27] Comme l’a souligné EPR, l’obtention d’un résultat de mesure sur une moitié d’une paire intriquée implique la certitude du résultat d’une mesure correspondante sur l’autre moitié. Le “critère de réalité EPR” postule que puisque la seconde moitié de la paire n’a pas été perturbée, cette certitude doit être due à une propriété physique lui appartenant. ^[28] En d’autres termes, selon ce critère, une variable cachée λ {displaystylelambda} lambda doit exister dans la seconde moitié non encore mesurée de la paire. Aucune contradiction n’apparaît si une seule mesure sur la première moitié est considérée. Cependant, si l’observateur a le choix entre plusieurs mesures possibles et que les vecteurs définissant ces mesures forment une configuration Kochen-Specker, alors un résultat sur la seconde moitié sera simultanément impossible et garanti.

Ce type d’argument a attiré l’attention lorsqu’un exemple en a été avancé par John Conway et Simon Kochen sous le nom de théorème du libre arbitre . ^{[29] [30] [31]} Le théorème de Conway–Kochen utilise une paire de qutrits intriqués et une configuration de Kochen–Specker découverte par Asher Peres . ^[32]

Enchevêtrement quasi classique

Comme l’a souligné Bell, certaines prédictions de la mécanique quantique peuvent être reproduites dans des modèles de variables cachées locales, y compris des cas particuliers de corrélations produites à partir de l’intrication. Ce sujet a été étudié systématiquement dans les années depuis le théorème de Bell. En 1989, Reinhard Werner a introduit ce qu’on appelle maintenant les états de Werner , des états quantiques conjoints pour une paire de systèmes qui produisent des corrélations de type EPR mais admettent également un modèle à variable cachée. ^[33] Les états de Werner sont des états quantiques bipartites qui sont invariants sous des unitaires de forme de produit tensoriel symétrique :

ρ A B = ( U ⊗ U ) ρ A B ( U † ⊗ U † ) . {displaystyle rho _{AB}=(Uotimes U)rho _{AB}(U^{dagger }otimes U^{dagger }),.} ${displaystyle rho _{AB}=(Uotimes U)rho _{AB}(U^{dagger }otimes U^{dagger }),.}$ ${displaystyle rho _{AB}=(Uotimes U)rho _{AB}(U^{dagger }otimes U^{dagger }),.}$

Plus récemment, Robert Spekkens a introduit un modèle de jouet qui commence par la prémisse de degrés de liberté discrétisés locaux, puis impose un “principe d’équilibre des connaissances” qui limite ce qu’un observateur peut savoir sur ces degrés de liberté, les transformant ainsi en variables cachées. . Les états de connaissance autorisés (“états épistémiques”) sur les variables sous-jacentes (“états ontiques”) imitent certaines caractéristiques des états quantiques. Les corrélations dans le modèle du jouet peuvent émuler certains aspects de l’intrication, comme la monogamie , mais par construction, le modèle du jouet ne peut jamais violer une inégalité de Bell. ^{[34] [35]}

Histoire

Arrière-plan

La question de savoir si la mécanique quantique peut être « complétée » par des variables cachées remonte aux premières années de la théorie quantique. Dans son manuel de 1932 sur la mécanique quantique , le polymathe d’origine hongroise John von Neumann a présenté ce qu’il prétendait être une preuve qu’il ne pouvait y avoir de “paramètres cachés”. La validité et le caractère définitif de la preuve de von Neumann ont été remis en question par Hans Reichenbach , plus en détail par Grete Hermann , et peut-être en conversation mais pas en version imprimée par Albert Einstein . ^{[note 3]} ( Simon Kochen et Ernst Specker ont rejeté l’hypothèse clé de von Neumann dès 1961, mais n’en ont publié une critique qu’en 1967. ^[41])

Einstein a soutenu avec persistance que la mécanique quantique ne pouvait pas être une théorie complète. Son argument préféré reposait sur un principe de localité :

Considérons un système mécanique constitué de deux systèmes partiels A et B qui n’interagissent l’un avec l’autre que pendant un temps limité. Soit la fonction ψ avant leur interaction soit donnée. Ensuite, l’ équation de Schrödinger fournira la fonction ψ après que leur interaction a eu lieu. Déterminons maintenant l’état physique du système partiel A aussi complètement que possible par des mesures. Ensuite la mécanique quantique permet de déterminer la fonction ψ du système partiel B à partir des mesures effectuées, et à partir de la fonction ψ du système total. Cette détermination donne cependant un résultat qui dépend de laquelle des grandeurs déterminantes spécifiant la condition de A a été mesurée (par exemple les coordonnées ou les impulsions). Puisqu’il ne peut y avoir qu’une seule condition physique de B après l’interaction et qui ne peut raisonnablement pas être considérée comme dépendante de la mesure particulière que nous effectuons sur le système A séparé de B , on peut conclure que la fonction ψ n’est pas coordonnée sans ambiguïté avec la physique état. Cette coordination de plusieurs fonctions ψ avec la même condition physique du système Bmontre à nouveau que la fonction ψ ne peut pas être interprétée comme une description (complète) d’une condition physique d’un système d’unités. ^[42]

L’expérience de pensée EPR est similaire, considérant également deux systèmes séparés A et B décrits par une fonction d’onde conjointe. Cependant, l’article EPR ajoute l’idée connue plus tard sous le nom de critère de réalité EPR, selon laquelle la capacité de prédire avec probabilité 1 le résultat d’une mesure sur B implique l’existence d’un “élément de réalité” dans B . ^[43]

En 1951, David Bohm a proposé une variante de l’expérience de pensée EPR dans laquelle les mesures ont des plages discrètes de résultats possibles, contrairement aux mesures de position et d’impulsion considérées par EPR. ^[44] L’année précédente, Chien-Shiung Wu et Irving Shaknov avaient mesuré avec succès les polarisations de photons produits dans des paires intriquées, rendant ainsi pratiquement réalisable la version Bohm de l’expérience de pensée EPR. ^[45]

À la fin des années 1940, le mathématicien George Mackey s’est intéressé aux fondements de la physique quantique et, en 1957, il a dressé une liste de postulats qu’il considérait comme une définition précise de la mécanique quantique. ^[46] Mackey a conjecturé que l’un des postulats était redondant, et peu de temps après, Andrew M. Gleason a prouvé qu’il était effectivement déductible des autres postulats. ^{[47] [48]} Le théorème de Gleason a fourni un argument selon lequel une large classe de théories de variables cachées est incompatible avec la mécanique quantique. ^{[note 4]}Plus précisément, le théorème de Gleason exclut les modèles à variables cachées qui sont “non contextuels”. Tout modèle à variable cachée pour la mécanique quantique doit, afin d’éviter les implications du théorème de Gleason, impliquer des variables cachées qui ne sont pas des propriétés appartenant au seul système mesuré mais qui dépendent également du contexte externe dans lequel la mesure est effectuée. Ce type de dépendance est souvent considéré comme artificiel ou indésirable ; dans certains contextes, il est incompatible avec la relativité restreinte . ^{[5] [50]} Le théorème de Kochen-Specker affine cette déclaration en construisant un sous-ensemble fini spécifique de rayons sur lesquels aucune telle mesure de probabilité ne peut être définie. ^{[5] [51]}

Tsung-Dao Lee est venu près de dériver le théorème de Bell en 1960. Il a considéré des événements où deux kaons ont été produits voyageant dans des directions opposées, et est arrivé à la conclusion que les variables cachées ne pouvaient pas expliquer les corrélations qui pouvaient être obtenues dans de telles situations. Cependant, des complications surgissent du fait que les kaons se désintègrent, et il n’est pas allé jusqu’à en déduire une inégalité de type Bell. ^{[note 5]}

Les publications de Bell

Learn more.

Isomorphisme

Jul 14, 2022

Premier article sur la théorie des ensembles de Cantor

Jul 12, 2022

Énergie gravitationnelle

Jul 9, 2022

Sphère de Riemann

Jul 8, 2022

Bell a choisi de publier son théorème dans une revue relativement obscure car il n’exigeait pas de Frais de page et, à l’époque, il payait en fait les auteurs qui y publiaient. Cependant, comme la revue ne fournissait pas de réimpressions gratuites d’articles à distribuer aux auteurs, Bell a dû dépenser l’argent qu’il recevait pour acheter des copies qu’il pouvait envoyer à d’autres physiciens. ^[52] Alors que les articles imprimés dans la revue eux-mêmes mentionnaient simplement le nom de la publication comme Physique , les couvertures portaient la version trilingue Physique Physique Физика pour refléter qu’elle imprimerait des articles en anglais, français et russe. ^{[40] : 92–100, 289}

Avant de prouver son résultat de 1964, Bell a également prouvé un résultat équivalent au théorème de Kochen-Specker (d’où la raison pour laquelle ce dernier est parfois également connu sous le nom de théorème de Bell-Kochen-Specker ou Bell-KS). Cependant, la publication de ce théorème a été retardée par inadvertance jusqu’en 1966. ^{[5] [53]} Dans cet article, Bell a soutenu que parce qu’une explication des phénomènes quantiques en termes de variables cachées nécessiterait la non-localité, le paradoxe EPR “est résolu de la manière qui Einstein aurait moins aimé”. ^[53]

Expériences

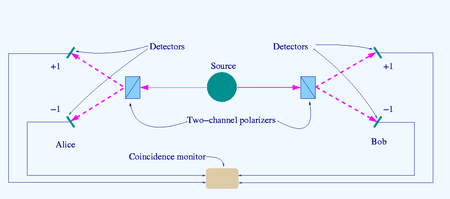
Schéma d’un test de Bell “deux canaux”
La source S produit des paires de “photons”, émis dans des directions opposées. Chaque photon rencontre un polariseur à deux canaux dont l’orientation (a ou b) peut être fixée par l’expérimentateur. Les signaux émergents de chaque canal sont détectés et les coïncidences de quatre types (++, −−, +− et −+) sont comptées par le moniteur de coïncidence.

En 1967, le titre inhabituel Physics Physique Физика a attiré l’attention de John Clauser , qui a alors découvert l’article de Bell et a commencé à réfléchir à la manière d’effectuer un test de Bell en laboratoire. ^[54] Clauser et Stuart Freedman continueraient à effectuer un test de Bell en 1972. ^{[55] [56]} Ce n’était qu’un test limité, car le choix des réglages du détecteur était fait avant que les photons aient quitté la source. En 1982, Alain Aspect et ses collaborateurs ont effectué le premier test Bell pour supprimer cette limitation. ^[57]Cela a commencé une tendance à des tests de Bell de plus en plus stricts. L’expérience de pensée GHZ a été mise en œuvre dans la pratique, en utilisant des triplets de photons intriqués, en 2000. ^[58] En 2002, tester l’inégalité CHSH était faisable dans les cours de laboratoire de premier cycle. ^[59]

Dans les tests de Bell, il peut y avoir des problèmes de conception ou de configuration expérimentale qui affectent la validité des résultats expérimentaux. Ces problèmes sont souvent qualifiés de “lacunes”. Le but de l’expérience est de tester si la nature peut être décrite par la Théorie des variables cachées locales , ce qui contredirait les prédictions de la mécanique quantique.

Les failles les plus répandues dans les expériences réelles sont les failles de détection et de localité . ^[60] La faille de détection est ouverte lorsqu’une petite fraction des particules (généralement des photons) est détectée dans l’expérience, ce qui permet d’expliquer les données avec des variables cachées locales en supposant que les particules détectées sont un échantillon non représentatif. La faille de localité est ouverte lorsque les détections ne se font pas avec une séparation spatiale , permettant au résultat d’une mesure d’influencer l’autre sans contredire la relativité. Dans certaines expériences, il peut y avoir des défauts supplémentaires qui rendent possibles des explications de variables cachées locales des violations du test de Bell. ^[61]

Bien que les failles de localisation et de détection aient été fermées dans différentes expériences, un défi de longue date consistait à fermer les deux simultanément dans la même expérience. Cela a finalement été atteint dans trois expériences en 2015. ^{[62] [63] [64] [65] [66]} Au sujet de ces résultats, Alain Aspect écrit que “… aucune expérience… ne peut être dite totalement échappatoire- libre”, mais il dit que les expériences “lèvent les derniers doutes auxquels nous devrions renoncer” les variables cachées locales, et se réfère à des exemples de lacunes restantes comme étant “farfelues” et “étrangères à la manière habituelle de raisonner en physique”. ^[67]

Faille de détection

Un problème courant dans les tests optiques de Bell est que seule une petite fraction des photons émis est détectée. Il est alors possible que les corrélations des photons détectés ne soient pas représentatives : bien qu’elles montrent une violation d’une inégalité de Bell, si tous les photons étaient détectés l’inégalité de Bell serait en fait respectée. Cela a été noté pour la première fois par Pearle en 1970, ^[68] qui a conçu un modèle de variable cachée locale qui a simulé une violation de Bell en laissant le photon être détecté uniquement si le réglage de mesure était favorable. L’hypothèse selon laquelle cela ne se produit pas, c’est-à-dire que le petit échantillon est en fait représentatif de l’ensemble, est appelée hypothèse d’échantillonnage équitable .

Pour s’affranchir de cette hypothèse, il faut détecter une fraction suffisamment importante des photons. Ceci est généralement caractérisé en termes d’efficacité de détection η {displaystyle eta} eta , défini comme la probabilité qu’un photodétecteur détecte un photon qui lui parvient. Garg et Mermin ont montré qu’en utilisant un état intriqué au maximum et l’inégalité CHSH, une efficacité de η > 2 2 − 2 ≈ 0.83 {displaystyle eta >2{sqrt {2}}-2environ 0,83} est nécessaire pour une violation sans échappatoire. ^[69] Plus tard, Eberhard a montré que lors de l’utilisation d’un état partiellement intriqué, une violation sans échappatoire est possible pour η > 2 / 3 ≈ 0.67 {displaystyle eta >2/3environ 0,67} {displaystyle eta >2/3approx 0.67} , ^[70] qui est la borne optimale pour l’inégalité CHSH. ^[71] D’autres inégalités de Bell permettent des bornes encore plus basses. Par exemple, il existe une inégalité à quatre paramètres qui est violée pour η > ( 5 − 1 ) / 2 ≈ 0.62 {displaystyle eta >({sqrt {5}}-1)/2environ 0,62} . ^[72]

Historiquement, seules les expériences avec des systèmes non optiques ont été en mesure d’atteindre des rendements suffisamment élevés pour combler cette lacune, comme les ions piégés, ^[73] les qubits supraconducteurs, ^[74] et les centres de lacune d’azote . ^[75] Ces expériences n’ont pas été en mesure de combler l’échappatoire de localité, ce qui est facile à faire avec des photons. Plus récemment, cependant, les configurations optiques ont réussi à atteindre des efficacités de détection suffisamment élevées en utilisant des photodétecteurs supraconducteurs, ^{[65] [66]} et les configurations hybrides ont réussi à combiner l’efficacité de détection élevée typique des systèmes de matière avec la facilité de distribution de l’enchevêtrement à distance. typique des systèmes photoniques. ^[64]

Échappatoire de la localité

L’une des hypothèses du théorème de Bell est celle de localité, à savoir que le choix du réglage à un site de mesure n’influence pas le résultat de l’autre. La motivation de cette hypothèse est la théorie de la relativité , qui interdit la communication plus rapide que la lumière. Pour que cette motivation s’applique à une expérience, elle doit avoir une séparation spatiale entre ses événements de mesure. C’est-à-dire que le temps qui s’écoule entre le choix du cadre de mesure et la production d’un résultat doit être plus court que le temps nécessaire à un signal lumineux pour se déplacer entre les sites de mesure. ^[76]

La première expérience qui s’est efforcée de respecter cette condition est l’expérience d’ Alain Aspect en 1982. ^[77] Dans ce document, les paramètres ont été modifiés assez rapidement, mais de manière déterministe. La première expérience à modifier les paramètres de manière aléatoire, avec les choix effectués par un Générateur de nombres aléatoires quantiques , a été l’expérience de 1998 de Weihs et al. ^[78] Scheidl et al. amélioré encore plus en 2010 en menant une expérience entre des emplacements séparés par une distance de 144 km (89 mi). ^[79]

Échappatoire de coïncidence

Dans de nombreuses expériences, en particulier celles basées sur la polarisation des photons, les paires d’événements dans les deux ailes de l’expérience ne sont identifiées comme appartenant à une seule paire qu’après la réalisation de l’expérience, en jugeant si leurs temps de détection sont suffisamment proches l’un de l’autre. . Cela génère une nouvelle possibilité pour une Théorie des variables cachées locales de “fausser” les corrélations quantiques : retarder le temps de détection de chacune des deux particules d’une quantité plus ou moins grande en fonction d’une relation entre les variables cachées portées par les particules et les paramètres du détecteur rencontrés au poste de mesure. ^[80]

L’échappatoire à la coïncidence peut être entièrement éliminée en travaillant avec un réseau préfixé de fenêtres de détection qui sont suffisamment courtes pour que la plupart des paires d’événements se produisant dans la même fenêtre proviennent de la même émission et suffisamment longues pour qu’une vraie paire ne soit pas séparée. par une bordure de fenêtre. ^[80]

Faille de la mémoire

Dans la plupart des expériences, les mesures sont effectuées à plusieurs reprises aux deux mêmes endroits. Une Théorie des variables cachées locales pourrait exploiter la mémoire des paramètres et des résultats de mesure passés afin d’augmenter la violation d’une inégalité de Bell. De plus, les paramètres physiques peuvent varier dans le temps. Il a été démontré que, à condition que chaque nouvelle paire de mesures soit effectuée avec une nouvelle paire aléatoire de paramètres de mesure, ni la mémoire ni l’inhomogénéité temporelle n’ont un effet sérieux sur l’expérience. ^{[81] [82] [83]}

Interprétations du théorème de Bell

L’interprétation de Copenhague

L’ interprétation de Copenhague est un recueil de vues sur la signification de la mécanique quantique principalement attribuées à Niels Bohr et Werner Heisenberg . C’est l’une des plus anciennes des nombreuses interprétations proposées de la mécanique quantique , car ses caractéristiques datent du développement de la mécanique quantique entre 1925 et 1927, et elle reste l’une des plus enseignées. ^[84] Il n’y a aucune déclaration historique définitive de ce qu’est l’ interprétation de Copenhague. En particulier, il y avait des désaccords fondamentaux entre les vues de Bohr et Heisenberg. ^{[85] [86] [87]}Parmi les principes de base généralement acceptés dans le cadre de la collection de Copenhague figurent l’idée que la mécanique quantique est intrinsèquement indéterministe, avec des probabilités calculées à l’aide de la règle de Born ^[88] et le principe de complémentarité : certaines propriétés ne peuvent être définies conjointement pour un même système en même temps. temps. Pour parler d’une propriété spécifique d’un système, ce système doit être considéré dans le contexte d’un arrangement de laboratoire spécifique. Les quantités observables correspondant à des arrangements de laboratoire mutuellement exclusifs ne peuvent pas être prédites ensemble, mais il est nécessaire de considérer plusieurs de ces expériences mutuellement exclusives pour caractériser un système. ^[85]Bohr lui-même a utilisé la complémentarité pour affirmer que le “paradoxe” de l’EPR était fallacieux. Les mesures de position et de quantité de mouvement étant complémentaires, faire le choix de mesurer l’une exclut la possibilité de mesurer l’autre. Par conséquent, a-t-il soutenu, un fait déduit concernant un agencement d’appareils de laboratoire ne pouvait pas être combiné avec un fait déduit au moyen de l’autre, et donc, l’inférence de valeurs de position et d’impulsion prédéterminées pour la deuxième particule n’était pas valide. ^{[37] : 194–197} Bohr a conclu que “les arguments d’EPR ne justifient pas leur conclusion que la description quantique s’avère être essentiellement incomplète”. ^[89]

Les interprétations de type Copenhague prennent généralement la violation des inégalités de Bell comme motif pour rejeter l’hypothèse souvent appelée « réalisme », ce qui n’est pas nécessairement la même chose que d’abandonner le réalisme dans un sens philosophique plus large. ^{[90] [91]} Par exemple, Roland Omnès plaide pour le rejet des variables cachées et conclut que “la mécanique quantique est probablement aussi réaliste que le sera jamais toute théorie de sa portée et de sa maturité”. ^{[92] : 531} C’est aussi la voie empruntée par les interprétations qui descendent de la tradition de Copenhague, telles que les histoires cohérentes (souvent annoncées comme « Copenhague bien fait »), ^[93] ainsi que le QBisme . ^[94]

Interprétation à plusieurs mondes de la mécanique quantique

L’ interprétation à plusieurs mondes , également connue sous le nom d’interprétation d’Everett, est locale et déterministe, car elle consiste en la partie unitaire de la mécanique quantique sans effondrement. Il peut générer des corrélations qui violent une inégalité de Bell car il viole une hypothèse implicite de Bell selon laquelle les mesures ont un résultat unique. En fait, le théorème de Bell peut être prouvé dans le cadre de plusieurs mondes à partir de l’hypothèse qu’une mesure a un résultat unique. Par conséquent, une violation d’une inégalité de Bell peut être interprétée comme une démonstration que les mesures ont des résultats multiples. ^[95]

L’explication qu’il fournit pour les corrélations de Bell est que lorsque Alice et Bob effectuent leurs mesures, ils se divisent en branches locales. Du point de vue de chaque copie d’Alice, plusieurs copies de Bob connaissent des résultats différents, donc Bob ne peut pas avoir de résultat définitif, et il en va de même du point de vue de chaque copie de Bob. Ils n’obtiendront un résultat mutuellement bien défini que lorsque leurs futurs cônes de lumière se chevaucheront. À ce stade, nous pouvons dire que la corrélation de Bell commence à exister, mais elle a été produite par un mécanisme purement local. La violation d’une inégalité de Bell ne peut donc pas être interprétée comme une preuve de non-localité. ^[96]

Variables masquées non locales

La plupart des partisans de l’idée des variables cachées pensent que les expériences ont exclu les variables cachées locales. ^{[note 6]} Ils sont prêts à abandonner la localité, expliquant la violation de l’inégalité de Bell au moyen d’une Théorie des variables cachées non locales , dans laquelle les particules échangent des informations sur leurs états. C’est la base de l’ Interprétation de Bohm de la mécanique quantique, qui exige que toutes les particules de l’univers soient capables d’échanger instantanément des informations avec toutes les autres. Une expérience de 2007 a exclu une grande classe de théories des variables cachées non bohmiennes non locales, mais pas la mécanique bohmienne elle-même. ^[98]

L’ interprétation transactionnelle , qui postule des ondes voyageant à la fois en arrière et en avant dans le temps, est également non locale. ^[99]

Superdéterminisme

Une hypothèse nécessaire pour dériver le théorème de Bell est que les variables cachées ne sont pas corrélées avec les paramètres de mesure. Cette hypothèse a été justifiée au motif que l’expérimentateur a le « libre arbitre » pour choisir les paramètres, et qu’il est nécessaire de faire de la science en premier lieu. Une théorie (hypothétique) où le choix de la mesure est déterminé par le système mesuré est appelée superdéterministe . ^[60]

Quelques partisans des modèles déterministes n’ont pas renoncé aux variables cachées locales. Par exemple, Gerard ‘t Hooft a soutenu que le superdéterminisme ne peut être écarté. ^[100]

Voir également

portail physique

Les expériences de pensée d’Einstein
Lettres épistémologiques
Groupe Fysiks fondamental
Inégalité de Leggett
Inégalité de Leggett-Garg
Problème de mots
Théorème PBR
Contextualité quantique
Non-localité quantique
Expérience de Renninger à résultat négatif

Remarques

^ Nous supposons par commodité que la réponse du détecteur à la propriété sous-jacente est déterministe. Cette hypothèse peut être remplacée ; cela revient à postuler une distribution de probabilité conjointe sur toutes les observables de l’expérience. ^{[10] [11]}
↑ Plus en détail, tel que développé par Paul Dirac ,^[19] David Hilbert ,^[20] John von Neumann ,^[21] et Hermann Weyl ,^[22] l’état d’un système mécanique quantique est un vecteur | ψ ⟩ {displaystyle |psirangle } appartenant à un espace de Hilbert ( séparable ) H {displaystyle {mathcal{H}}} . Les grandeurs physiques d’intérêt – position, quantité de mouvement, énergie, spin – sont représentées par des «observables», qui sont des opérateurs linéaires auto-adjoints agissant sur l’espace de Hilbert. Lorsqu’une observable est mesurée, le résultat sera une de ses valeurs propres avec une probabilité donnée par la règle de Born : dans le cas le plus simple la valeur propre η {displaystyle eta} est non dégénéré et la probabilité est donnée par | ⟨ η | ψ ⟩ | 2 {displaystyle |langle eta |psi rangle |^{2}} ${displaystyle |langle eta |psi rangle |^{2}}$ ${displaystyle |langle eta |psi rangle |^{2}}$ , où | η ⟩ {displaystyle |eta rangle } est son vecteur propre associé. Plus généralement, la valeur propre est dégénérée et la probabilité est donnée par ⟨ ψ | P η ψ ⟩ {displaystyle langle psi |P_{eta }psi rangle } ${displaystyle langle psi |P_{eta }psi rangle }$ ${displaystyle langle psi |P_{eta }psi rangle }$ , où P η {displaystyle P_{eta }} ${displaystyle P_{eta }}$ ${displaystyle P_{eta }}$ est le projecteur sur son espace propre associé. Pour les besoins de cette discussion, nous pouvons considérer les valeurs propres comme non dégénérées.
^ Voir Reichenbach^[36] et Jammer,^{[37] : 276} Mermin et Schack,^[38] et pour les remarques d’Einstein, Clauser et Shimony^[39] et Wick. ^{[40] : 286}
^ Une Théorie des variables cachées qui est déterministe implique que la probabilité d’un résultat donné est toujours de 0 ou de 1. Par exemple, une mesure de Stern-Gerlach sur un atome de spin-1 indiquera que le moment cinétique de l’atome le long de l’axe choisi est l’une des trois valeurs possibles, qui peut être désignée − {displaystyle -} , 0 {displaystyle 0} et + {displaystyle +} . Dans une théorie déterministe des variables cachées, il existe une propriété physique sous-jacente qui fixe le résultat trouvé dans la mesure. Sous réserve de la valeur de la propriété physique sous-jacente, tout résultat donné (par exemple, un résultat de + {displaystyle +} ) doit être impossible ou garanti. Mais le théorème de Gleason implique qu’il ne peut y avoir une telle mesure de probabilité déterministe, car il prouve que toute mesure de probabilité doit prendre la forme d’une application u → ⟨ ρ u , u ⟩ {displaystyle uto langle rho u,urangle } pour un opérateur de densité ρ {style d’affichage rho} . Cette application est continue sur la sphère unitaire de l’espace de Hilbert, et puisque cette sphère unitaire est connexe , aucune mesure de probabilité continue sur celle-ci ne peut être déterministe. ^{[49] : §1.3}
^ Cela a été rapporté par Max Jammer . ^{[37] : 308} Lee est surtout connu pour sa prédiction avec Chen-Ning Yang de la violation de la conservation de la parité, une prédiction qui leur a valu le prix Nobel après avoir été confirmée par Chien-Shiung Wu , qui n’a pas partagé le prix.
^ ET Jaynes était une exception,^[97] mais les arguments de Jaynes n’ont généralement pas été trouvés persuasifs. ^[83]

Références

^ Bell, John S. (1987). Parlable et Indicible en Mécanique Quantique . La presse de l’Universite de Cambridge. p. 65. ISBN 9780521368698. OCLC 15053677 .
^ ^un ^b Einstein, A. ; Podolsky, B. ; Rosen, N. (1935-05-15). « La description mécanique quantique de la réalité physique peut-elle être considérée comme complète ? » . Examen physique . 47 (10): 777–780. Bibcode : 1935PhRv…47..777E . doi : 10.1103/PhysRev.47.777 .
^ ^une cloche ^b , JS (1964). “Sur le Paradoxe d’Einstein Podolsky Rosen” (PDF) . Physique Physique Физика . 1 (3): 195-200. doi : 10.1103/PhysicsPhysiqueFizika.1.195 .
^ Parker, Sybil B. (1994). Encyclopédie McGraw-Hill de physique (2e éd.). McGraw-Hill. p. 542 . ISBN 978-0-07-051400-3.
^ ^un ^bcd ^{Mermin ,} ^N. David (juillet 1993). “Variables cachées et les deux théorèmes de John Bell” (PDF) . Revues de physique moderne . 65 (3): 803–15. arXiv : 1802.10119 . Bibcode : 1993RvMP…65..803M . doi : 10.1103/RevModPhys.65.803 . S2CID 119546199 .
^ La collaboration de test BIG Bell (9 mai 2018). “Défier le réalisme local avec des choix humains”. Nature . 557 (7704): 212–216. arXiv : 1805.04431 . Bibcode : 2018Natur.557..212B . doi : 10.1038/s41586-018-0085-3 . PMID 29743691 . S2CID 13665914 .
^ Wolchover, Natalie (2017-02-07). “L’expérience réaffirme l’étrangeté quantique” . Revue Quanta . Récupéré le 08/02/2020 .
^ ^un ^b Shimony, Abner . “Théorème de Bell” . À Zalta, Edward N. (éd.). Encyclopédie de philosophie de Stanford .
^ ^un ^bcd ^{Nielsen ,} ^Michael A. ; Chuang, Isaac L. (2010). Calcul quantique et information quantique (2e éd.). Cambridge : Cambridge University Press. ISBN 978-1-107-00217-3. OCLC 844974180 .
^ Très bien, Arthur (1982-02-01). “Variables cachées, probabilité conjointe et inégalités de Bell” . Lettres d’examen physique . 48 (5): 291–295. Bibcode : 1982PhRvL..48..291F . doi : 10.1103/PhysRevLett.48.291 . ISSN 0031-9007 .
^ Braunstein, Samuel L.; Caves, Carlton M. (août 1990). « Essorer de meilleures inégalités de Bell ». Annales de Physique . 202 (1): 22–56. Bibcode : 1990AnPhy.202…22B . doi : 10.1016/0003-4916(90)90339-P .
^ Rau, Jochen (2021). Théorie quantique : une approche de traitement de l’information . Presse universitaire d’Oxford. ISBN 978-0-192-65027-6. OCLC 1256446911 .
^ Cleve, R. ; Hoyer, P.; Toner, B. ; En ligneWatrous, J. (2004). “Conséquences et limites des stratégies non locales”. Procédure. 19e conférence annuelle de l’IEEE sur la complexité computationnelle, 2004 . IEEE . p. 236–249. arXiv : quant-ph/0404076 . Bibcode : 2004quant.ph..4076C . doi : 10.1109/CCC.2004.1313847 . ISBN 0-7695-2120-7. OCLC 55954993 . S2CID 8077237 .
^ Barnum, H.; Beigi, S.; Boixo, S.; Elliott, MB; Wehner, S. (2010-04-06). “La mesure quantique locale et l’absence de signalisation impliquent des corrélations quantiques”. Lettres d’examen physique . 104 (14) : 140401. arXiv : 0910.3952 . Bib code : 2010PhRvL.104n0401B . doi : 10.1103/PhysRevLett.104.140401 . ISSN 0031-9007 . PMID 20481921 . S2CID 17298392 .
^ Griffiths, David J. (2005). Introduction à la mécanique quantique (2e éd.). Upper Saddle River, New Jersey : Pearson Prentice Hall. ISBN 0-13-111892-7. OCLC 53926857 .
^ Greenberger, D. ; Horne, M. ; Shimony, A. ; En ligneZeilinger, A. (1990). “Le théorème de Bell sans inégalités”. Journal américain de physique . 58 (12): 1131. Bibcode : 1990AmJPh..58.1131G . doi : 10.1119/1.16243 .
^ Mermin, N. David (1990). “Les mystères quantiques revisités”. Journal américain de physique . 58 (8): 731–734. Bibcode : 1990AmJPh..58..731M . doi : 10.1119/1.16503 .
↑ Brassard, Gilles ; Broadbent, Anne ; Tapp, Alain (2005). “Refonte du jeu multijoueur de Mermin dans le cadre de la pseudo-télépathie”. Information et calcul quantiques . 5 (7): 538–550. arXiv : quant-ph/0408052 . Bibcode : 2004quant.ph..8052B . doi : 10.26421/QIC5.7-2 .
^ Dirac, Paul Adrien Maurice (1930). Les principes de la mécanique quantique . Oxford : Clarendon Press.
^ Hilbert, David (2009). Sauer, Tilman; Majer, Ulrich (dir.). Conférences sur les fondements de la physique 1915-1927 : relativité, théorie quantique et épistémologie . Springer. doi : 10.1007/b12915 . ISBN 978-3-540-20606-4. OCLC 463777694 .
^ von Neumann, John (1932). Mathematische Grundlagen der Quantenmechanik . Berlin : Springer. Traduction anglaise : Fondements mathématiques de la mécanique quantique . Traduit par Beyer, Robert T. Princeton University Press. 1955.
^ Weyl, Hermann (1950) [1931]. La Théorie des Groupes et la Mécanique Quantique . Traduit par Robertson, HP Dover. ISBN 978-0-486-60269-1.Traduit de l’allemand Gruppentheorie und Quantenmechanik (2e éd.). S. Hirzel Verlag [ de ] . 1931.
^ Peres, Asher (1993). Théorie quantique : concepts et méthodes . Kluwer . ISBN 0-7923-2549-4. OCLC 28854083 .
^ Rousse, Michael ; Brown, Harvey (1991-07-01). “Non-localité en mécanique quantique”. Actes de la société aristotélicienne, volumes supplémentaires . 65 (1): 119-160. doi : 10.1093/aristoteliansupp/65.1.119 . ISSN 0309-7013 . JSTOR 4106773 . Une approche similaire a été adoptée indépendamment par Simon Kochen, bien que jamais publiée (communication privée).
^ Heywood, Pierre; Rousse, Michael LG (mai 1983). “La non-localité et le paradoxe Kochen-Specker”. Fondements de la Physique . 13 (5): 481–499. Bibcode : 1983FoPh…13..481H . doi : 10.1007/BF00729511 . ISSN 0015-9018 . S2CID 120340929 .
^ Escaliers, Allen (décembre 1983). “Logique quantique, réalisme et définition de la valeur”. Philosophie des sciences . 50 (4): 578–602. doi : 10.1086/289140 . ISSN 0031-8248 . S2CID 122885859 .
^ Brown, RH ; Svetlichny, G. (novembre 1990). “Non-localité et lemme de Gleason. Partie I. Théories déterministes”. Fondements de la Physique . 20 (11): 1379-1387. Bibcode : 1990FoPh…20.1379B . doi : 10.1007/BF01883492 . ISSN 0015-9018 . S2CID 122868901 .
^ Glick, David; Boge, Florian J. (2019-10-22). “Le critère de réalité est-il analytique?”. Erkenntnis . 86 (6): 1445–1451. arXiv : 1909.11893 . Bibcode : 2019arXiv190911893G . doi : 10.1007/s10670-019-00163-w . ISSN 0165-0106 . S2CID 202889160 .
^ Conway, Jean ; Kochen, Simon (2006). “Le théorème du libre arbitre”. Fondements de la Physique . 36 (10): 1441. arXiv : quant-ph/0604079 . Bibcode : 2006FoPh…36.1441C . doi : 10.1007/s10701-006-9068-6 . S2CID 12999337 .
^ Rehmeyer, Julie (2008-08-15). « Les particules subatomiques ont-elles le libre arbitre ? » . Actualités scientifiques . Récupéré le 23/04/2022 .
^ Thomas, Rachel (2011-12-27). “John Conway – découvrir le libre arbitre (partie I)” . Magazine+ . Récupéré le 23/04/2022 .
^ Conway, John H. ; Kochen, Simon (2009). “Le théorème du libre arbitre fort” (PDF) . Avis de l’AMS . 56 (2): 226–232.
^ Werner, Reinhard F. (1989-10-01). “Etats quantiques avec corrélations d’Einstein-Podolsky-Rosen admettant un modèle à variable cachée”. Examen physique A . 40 (8): 4277–4281. Bibcode : 1989PhRvA..40.4277W . doi : 10.1103/PhysRevA.40.4277 . ISSN 0556-2791 . PMID 9902666 .
^ Spekkens, Robert W. (2007-03-19). “Preuve pour la vision épistémique des états quantiques: une théorie du jouet”. Examen physique A . 75 (3): 032110. arXiv : quant-ph/0401052 . Bibcode : 2007PhRvA..75c2110S . doi : 10.1103/PhysRevA.75.032110 . ISSN 1050-2947 . S2CID 117284016 .
^ Catani, Lorenzo; Browne, Dan E. (2017-07-27). “Le modèle de jouet de Spekkens dans toutes les dimensions et sa relation avec la mécanique quantique du stabilisateur” . Nouveau Journal de Physique . 19 (7) : 073035. Bibcode : 2017NJPh…19g3035C . doi : 10.1088/1367-2630/aa781c . ISSN 1367-2630 . S2CID 119428107 .
^ Reichenbach, Hans (1944). Fondements philosophiques de la mécanique quantique . Presse de l’Université de Californie. p. 14. OCLC 872622725 .
^ ^un ^bc ^Jammer , Max (1974). La philosophie de la mécanique quantique . John Wiley et fils. ISBN 0-471-43958-4.
^ Mermin, N.David ; Schack, Rudiger (2018). “Homer hocha la tête: l’oubli surprenant de von Neumann”. Fondements de la Physique . 48 (9): 1007-1020. arXiv : 1805.10311 . Code Bib : 2018FoPh …48.1007M . doi : 10.1007/s10701-018-0197-5 . S2CID 118951033 .
^ Clauser, JF; En ligneShimony, A. (1978). “Théorème de Bell: tests expérimentaux et implications” (PDF) . Rapports sur les progrès de la physique . 41 (12): 1881–1927. Code Bib : 1978RPPh …41.1881C . CiteSeerX 10.1.1.482.4728 . doi : 10.1088/0034-4885/41/12/002 . Archivé (PDF) de l’original le 2017-09-23 . Récupéré le 28/10/2017 .
^ ^{une mèche} ^b , David (1995). La frontière infâme: sept décennies d’hérésie en physique quantique . New York : Springer. doi : 10.1007/978-1-4612-4030-3_11 . ISBN 978-0-387-94726-6.
^ Conway, Jean ; Kochen, Simon (2002). “La Géométrie des Paradoxes Quantiques”. Dans Bertlmann, Reinhold A. ; Zeilinger, Anton (éd.). Quantum [Un]speakables : de Bell à l’information quantique . Berlin : Springer. p. 257–269. ISBN 3-540-42756-2. OCLC 49404213 .
^ Einstein, Albert (mars 1936). “Physique et réalité”. Journal de l’Institut Franklin . 221 (3): 349–382. Bibcode : 1936FrInJ.221..349E . doi : 10.1016/S0016-0032(36)91047-5 .
^ Harrigan, Nicolas; Spekkens, Robert W. (2010). “Einstein, l’incomplétude et la vision épistémique des états quantiques”. Fondements de la Physique . 40 (2): 125. arXiv : 0706.2661 . Bibcode : 2010FoPh…40..125H . doi : 10.1007/s10701-009-9347-0 . S2CID 32755624 .
^ Bohm, David (1989) [1951]. Théorie quantique (réimpression Dover éd.). Prentice Hall. pages 614–623. ISBN 978-0-486-65969-5. OCLC 1103789975 .
^ Wu, C.-S. ; Shaknov, I. (1950). “La corrélation angulaire du rayonnement d’annihilation dispersé”. Examen physique . 77 (1): 136. Bibcode : 1950PhRv…77..136W . doi : 10.1103/PhysRev.77.136 .
^ Mackey, George W. (1957). “Mécanique quantique et espace de Hilbert”. Le mensuel mathématique américain . 64 (8P2): 45–57. doi : 10.1080/00029890.1957.11989120 . JSTOR 2308516 .
^ Gleason, Andrew M. (1957). “Mesures sur les sous-espaces fermés d’un espace de Hilbert” . Journal de mathématiques de l’Université de l’Indiana . 6 (4): 885–893. doi : 10.1512/iumj.1957.6.56050 . MR 0096113 .
^ Chernoff, Paul R. “Andy Gleason et la mécanique quantique” (PDF) . Avis de l’AMS . 56 (10): 1253–1259.
^ Wilce, A. (2017). « Logique quantique et théorie des probabilités » . Encyclopédie de philosophie de Stanford . Laboratoire de recherche en métaphysique, Université de Stanford.
^ Shimony, Abner (1984). “Théories contextuelles des variables cachées et inégalités de Bell”. Journal britannique pour la philosophie des sciences . 35 (1): 25–45. doi : 10.1093/bjps/35.1.25 .
^ Peres, Asher (1991). “Deux preuves simples du théorème de Kochen-Specker” . Journal of Physics A: Mathematical and General . 24 (4) : L175–L178. Bibcode : 1991JPhA…24L.175P . doi : 10.1088/0305-4470/24/4/003 . ISSN 0305-4470 .
^ Whitaker, Andrew (2016). John Stewart Bell et la physique du vingtième siècle : vision et intégrité . Presse universitaire d’Oxford. ISBN 978-0-19-874299-9.
^ ^{une cloche} ^b , JS (1966). “Sur le problème des variables cachées en mécanique quantique”. Revues de physique moderne . 38 (3): 447–452. Bibcode : 1966RvMP…38..447B . doi : 10.1103/revmodphys.38.447 . OSTI 1444158 .
^ Kaiser, David (2012-01-30). “Comment les hippies ont sauvé la physique: science, contre-culture et renouveau quantique [extrait]” . Scientifique américain . Récupéré le 11/02/2020 .
^ Freedman, SJ ; Clauser, JF (1972). “Test expérimental des théories des variables cachées locales” (PDF) . Lettres d’examen physique . 28 (938): 938–941. Bibcode : 1972PhRvL..28..938F . doi : 10.1103/PhysRevLett.28.938 .
^ Freedman, Stuart Jay (1972-05-05). Test expérimental des théories des variables cachées locales (PDF) (PhD). Université de Californie, Berkeley.
↑ Aspect, Alain ; Dalibard, Jean; Roger, Gérard (1982). “Test expérimental des inégalités de Bell à l’aide d’analyseurs variant dans le temps” . Lettres d’examen physique . 49 (25) : 1804–7. Bibcode : 1982PhRvL..49.1804A . doi : 10.1103/PhysRevLett.49.1804 .
^ Casserole, Jian-Wei; Bouwmeester, D.; Daniell, M.; Weinfurter, H.; En ligneZeilinger, A. (2000). “Test expérimental de non-localité quantique dans l’intrication à trois photons GHZ”. Nature . 403 (6769): 515–519. Bibcode : 2000Natur.403..515P . doi : 10.1038/35000514 . PMID 10676953 . S2CID 4309261 .
^ Dehlinger, Dietrich; Mitchell, MW (2002). “Photons intriqués, non-localité et inégalités de Bell dans le laboratoire de premier cycle”. Journal américain de physique . 70 (9): 903–910. arXiv : quant-ph/0205171 . Bibcode : 2002AmJPh..70..903D . doi : 10.1119/1.1498860 . S2CID 49487096 .
^ ^un ^b Larsson, Jan-Åke (2014). “Échappatoires dans les tests d’inégalité de Bell du réalisme local”. Journal of Physics A: Mathématique et Théorique . 47 (42) : 424003. arXiv : 1407,0363 . Bibcode : 2014JPhA…47P4003L . doi : 10.1088/1751-8113/47/42/424003 . S2CID 40332044 .
^ Gerhardt, I.; Liu, Q. ; Lamas-Linares, A.; Skaar, J.; Scarani, V.; et coll. (2011). “Faire expérimentalement semblant de violer les inégalités de Bell”. Lettres d’examen physique . 107 (17) : 170404. arXiv : 1106.3224 . Bibcode : 2011PhRvL.107q0404G . doi : 10.1103/PhysRevLett.107.170404 . PMID 22107491 . S2CID 16306493 .
^ Merali, Zeeya (27 août 2015). “La “fantaisie” quantique passe le test le plus difficile à ce jour” . Nouvelles de la Nature . 525 (7567): 14–15. Bibcode : 2015Natur.525…14M . doi : 10.1038/nature.2015.18255 . PMID 26333448 . S2CID 4409566 .
^ Markoff, Jack (21 octobre 2015). “Désolé, Einstein. Une étude quantique suggère que ‘l’action effrayante’ est réelle” . New York Times . Récupéré le 21 octobre 2015 .
^ ^un ^b Hensen, B.; et coll. (21 octobre 2015). “Violation de l’inégalité de Bell sans échappatoire utilisant des spins d’électrons séparés de 1,3 kilomètres”. Nature . 526 (7575): 682–686. arXiv : 1508.05949 . Bibcode : 2015Natur.526..682H . doi : 10.1038/nature15759 . PMID 26503041 . S2CID 205246446 .
^ ^un ^b Shalm, LK; et coll. (16 décembre 2015). “Test fort sans échappatoire du réalisme local” . Lettres d’examen physique . 115 (25) : 250402. arXiv : 1511.03189 . Bibcode : 2015PhRvL.115y0402S . doi : 10.1103/PhysRevLett.115.250402 . PMC 5815856 . PMID 26722906 .
^ ^un ^b Giustina, M.; et coll. (16 décembre 2015). “Test significatif sans échappatoire du théorème de Bell avec des photons enchevêtrés”. Lettres d’examen physique . 115 (25): 250401. arXiv : 1511.03190 . Bibcode : 2015PhRvL.115y0401G . doi : 10.1103/PhysRevLett.115.250401 . PMID 26722905 . S2CID 13789503 .
^ Aspect, Alain (16 décembre 2015). “Fermer la porte sur Einstein et le débat quantique de Bohr” . Physique . 8 : 123. Bibcode : 2015PhyOJ…8..123A . doi : 10.1103/Physique.8.123 .
^ Pearle, Philip M. (1970). “Exemple de variable cachée basé sur le rejet de données”. Examen physique D . 2 (8) : 1418–1425. Bibcode : 1970PhRvD…2.1418P . doi : 10.1103/PhysRevD.2.1418 .
^ Garg, Anupam; Mermin, N. David (1987). “Inefficacités de détecteur dans l’expérience d’Einstein-Podolsky-Rosen”. Examen physique D . 25 (12): 3831–5. Bibcode : 1987PhRvD..35.3831G . doi : 10.1103/PhysRevD.35.3831 . PMID 9957644 .
^ Eberhard, PH (1993). “Niveau de fond et contre-efficacité requis pour une expérience Einstein-Podolsky-Rosen sans échappatoire”. Examen physique A . 47 (2): 747–750. Bibcode : 1993PhRvA..47..747E . doi : 10.1103/PhysRevA.47.R747 . PMID 9909100 .
^ Larsson, Jan-Åke; Semitecolos, Jason (2001). “Limites strictes d’efficacité du détecteur pour les inégalités de Clauser-Horne à n sites”. Examen physique A . 63 (2): 022117. arXiv : quant-ph/0006022 . Bibcode : 2001PhRvA..63b2117L . doi : 10.1103/PhysRevA.63.022117 . S2CID 119469607 .
^ Vértesi, Tamas; Pironio, Stefano; Brunner, Nicolas (2010). “Fermer l’échappatoire de détection dans les expériences de Bell en utilisant des qudits”. Lettres d’examen physique . 104 (6) : 060401. arXiv : 0909.3171 . Bib code : 2010PhRvL.104f0401V . doi : 10.1103/PhysRevLett.104.060401 . PMID 20366808 . S2CID 22053479 .
^ Rowe, MA; Kielpinski, D.; Meyer, V.; Sackett, Californie ; Itano, WM; et coll. (2001). “Violation expérimentale de l’inégalité de Bell avec détection efficace” (PDF) . Nature . 409 (6822): 791–94. Bibcode : 2001Natur.409..791K . doi : 10.1038/35057215 . hdl : 2027.42/62731 . PMID 11236986 . S2CID 205014115 .
^ Ansmann, M.; Wang, H.; Bialczak, RC; Hofheinz, M.; Lucero, E.; et coll. (24 septembre 2009). “Violation de l’inégalité de Bell dans les qubits de phase Josephson”. Nature . 461 (7263): 504–506. Bibcode : 2009Natur.461..504A . doi : 10.1038/nature08363 . PMID 19779447 . S2CID 4401494 .
^ Pfaff, W.; Taminiau, TH; Robledo, L.; Bernien, H. ; Markham, M.; et coll. (2013). “Démonstration de l’intrication par mesure de qubits à l’état solide”. Physique naturelle . 9 (1) : 29–33. arXiv : 1206.2031 . Bibcode : 2013NatPh…9…29P . doi : 10.1038/nphys2444 . S2CID 2124119 .
^ Bell, JS (1980). “Photons en cascade atomique et non-localité mécanique quantique”. Commentaires sur la physique atomique et moléculaire . 9 : 121–126. Réimprimé sous le nom de Bell, JS (1987). “Chapitre 13”. Parlable et Indicible en Mécanique Quantique . La presse de l’Universite de Cambridge. p. 109.
↑ Aspect, Alain ; Dalibard, Jean; Roger, Gérard (1982). “Test expérimental des inégalités de Bell à l’aide d’analyseurs variant dans le temps” . Lettres d’examen physique . 49 (25) : 1804–7. Bibcode : 1982PhRvL..49.1804A . doi : 10.1103/PhysRevLett.49.1804 .
^ Weihs, G.; Jennewein, T.; Simon, C.; Weinfurter, H.; En ligneZeilinger, A. (1998). “Violation de l’inégalité de Bell dans des conditions strictes de localité d’Einstein”. Lettres d’examen physique . 81 (23): 5039–5043. arXiv : quant-ph/9810080 . Bibcode : 1998PhRvL..81.5039W . doi : 10.1103/PhysRevLett.81.5039 . S2CID 29855302 .
^ Scheidl, Thomas; Ursin, Rupert; Kofler, Johannes; Ramelow, Sven; Ma, Xiao-Song; Herbst, Thomas; Ratschbacher, Lothar; Fedrizzi, Alessandro; Langford, Nathan K.; Jennewein, Thomas; Zeilinger, Anton; et coll. (2010). “Violation du réalisme local avec la liberté de choix” . PNAS . 107 (46): 19708–19713. arXiv : 0811.3129 . Bibcode : 2010PNAS..10719708S . doi : 10.1073/pnas.1002780107 . PMC 2993398 . PMID 21041665 .
^ ^un ^b Larsson, Jan-Åke; Gill, Richard (2004). “L’inégalité de Bell et l’échappatoire du temps de coïncidence”. Lettres d’Europhysique . 67 (5): 707. arXiv : quant-ph/0312035 . Bibcode : 2004EL…..67..707L . doi : 10.1209/epl/i2004-10124-7 . S2CID 17135877 .
^ Barrett, Jonathan; Collins, Daniel; Hardy, Lucien; Kent, Adrien ; Popescu, Sandu (2002). “La non-localité quantique, les inégalités de Bell et la faille de la mémoire”. Examen physique A . 66 (4). 042111. arXiv : quant-ph/0205016 . Bibcode : 2002PhRvA..66d2111B . doi : 10.1103/PhysRevA.66.042111 . S2CID 6524446 .
^ Gill, Richard D. (2003). “Accardi contra Bell (cum mundi): L’accouplement impossible”. Dans M. Moore; S. Froda ; C. Léger (dir.). Statistiques mathématiques et applications : Festschrift pour Constance van Eeden . Notes de cours IMS — Série de monographies. Vol. 42. Beachwood, Ohio : Institut de statistiques mathématiques. p. 133–154. arXiv : quant-ph/0110137 .
^ ^un ^b Gill, Richard D. (2002). “Le temps, les statistiques finies et la cinquième position de Bell”. Actes de la conférence Foundations of Probability and Physics – 2 : Växjö (Soland), Suède, 2-7 juin 2002 . Vol. 5. Presse universitaire de Växjö. pp. 179–206. arXiv : quant-ph/0301059 . Bibcode : 2003quant.ph..1059G .
^ Siddiqui, Shabnam; Singh, Chandralekha (2017). “Dans quelle mesure les attitudes et les approches des professeurs de physique sont-elles diverses pour enseigner la mécanique quantique au premier cycle?” . Journal européen de physique . 38 (3) : 035703. Bibcode : 2017EJPh…38c5703S . doi : 10.1088/1361-6404/aa6131 .
^ ^un ^b Faye, janvier (2019). “L’interprétation de Copenhague de la mécanique quantique” . À Zalta, Edward N. (éd.). Encyclopédie de philosophie de Stanford . Laboratoire de recherche en métaphysique, Université de Stanford. Archivé de l’original le 2019-04-29 . Récupéré le 16/09/2021 .
^ Camilleri, K.; En ligneSchlosshauer, M. (2015). “Niels Bohr en tant que philosophe de l’expérience: la théorie de la décohérence défie-t-elle la doctrine des concepts classiques de Bohr?”. Études en histoire et philosophie de la physique moderne . 49 : 73–83. arXiv : 1502.06547 . Bibcode : 2015SHPMP..49…73C . doi : 10.1016/j.shpsb.2015.01.005 . S2CID 27697360 .
^ Peres, Asher (2002). “L’expérience de Popper et l’interprétation de Copenhague”. Études en histoire et philosophie de la physique moderne . 33 : 23. arXiv : quant-ph/9910078 . Bibcode : 1999quant.ph.10078P . doi : 10.1016/S1355-2198(01)00034-X .
^ Bohr, N. (1928). “Le postulat quantique et le développement récent de la théorie atomique” . Nature . 121 (3050): 580–590. Bibcode : 1928Natur.121..580B . doi : 10.1038/121580a0 ., p. 586: “A cet égard [Born] a réussi à obtenir une interprétation statistique des fonctions d’onde, permettant un calcul de la probabilité des processus de transition individuels requis par le postulat quantique.”
^ Bohr, N. (1935-10-13). « La description mécanique quantique de la réalité physique peut-elle être considérée comme complète ? » (PDF) . Examen physique . 48 (8): 696–702. Bibcode : 1935PhRv…48..696B . doi : 10.1103/PhysRev.48.696 . Archivé (PDF) de l’original le 2020-01-09 . Récupéré le 16/09/2021 .
^ Werner, Reinhard F. (2014-10-24). “Commentaire sur ‘Ce que Bell a fait’ “. Journal of Physics A: Mathematical and Theoretical . 47 (42): 424011. Bibcode : 2014JPhA…47P4011W . doi : 10.1088/1751-8113/47/42/424011 . ISSN 1751-8113 .
^ Żukowski, Marek (2017), Bertlmann, Reinhold; Zeilinger, Anton (eds.), “Le théorème de Bell ne nous dit pas ce qu’est la mécanique quantique, mais ce que la mécanique quantique n’est pas”, Quantum [Un] Speakables II , The Frontiers Collection, Cham: Springer International Publishing, pp. 175–185, arXiv : 1501.05640 , Bibcode : 2015arXiv150105640Z , doi : 10.1007/978-3-319-38987-5_10 , ISBN 978-3-319-38985-1, S2CID 119214547
↑ Omnes, R. (1994). L’Interprétation de la mécanique quantique . Presse universitaire de Princeton. ISBN 978-0-691-03669-4. OCLC 439453957 .
^ Hohenberg, CP (2010-10-05). “Colloque : Une introduction à la théorie quantique cohérente”. Revues de physique moderne . 82 (4): 2835–2844. arXiv : 0909.2359 . Bibcode : 2010RvMP…82.2835H . doi : 10.1103/RevModPhys.82.2835 . ISSN 0034-6861 . S2CID 20551033 .
^ Healey, Richard (2016). “Vues quantiques-bayésiennes et pragmatistes de la théorie quantique” . À Zalta, Edward N. (éd.). Encyclopédie de philosophie de Stanford . Laboratoire de recherche en métaphysique, Université de Stanford. Archivé de l’original le 2021-08-17 . Récupéré le 16/09/2021 .
^ Deutsch, David ; Hayden, Patrick (2000). “Flux d’informations dans les systèmes quantiques intriqués”. Actes de la Royal Society A . 456 (1999): 1759–1774. arXiv : quant-ph/9906007 . Bibcode : 2000RSPSA.456.1759D . doi : 10.1098/rspa.2000.0585 . S2CID 13998168 .
^ Brown, Harvey R. ; Timpson, Christopher G. (2016). “Bell sur le théorème de Bell: le visage changeant de la non-localité”. Dans Bell, Marie; Gao, Shan (éd.). Non-localité quantique et réalité : 50 ans du théorème de Bell . La presse de l’Universite de Cambridge. p. 91–123. arXiv : 1501.03521 . doi : 10.1017/CBO9781316219393.008 . ISBN 9781316219393. S2CID 118686956 .
^ Jaynes, ET (1989). “Éclaircir les mystères – le but initial”. Éclaircir les mystères—L’objectif initial (PDF) . Entropie maximale et méthodes bayésiennes . p. 1–27. CiteSeerX 10.1.1.46.1264 . doi : 10.1007/978-94-015-7860-8_1 . ISBN 978-90-481-4044-2. Archivé (PDF) de l’original le 2011-10-28 . Récupéré le 18/10/2011 .
^ Gröblacher, Simon; Paterek, Tomasz; Kaltenbaek, Rainer; Brukner, Časlav; Żukowski, Marek; Aspelmeyer, Markus; En ligneZeilinger, Anton (2007). “Un test expérimental de réalisme non local”. Nature . 446 (7138): 871–5. arXiv : 0704.2529 . Bibcode : 2007Natur.446..871G . doi : 10.1038/nature05677 . PMID 17443179 . S2CID 4412358 .
^ Kastner, Ruth E. (mai 2010). “L’expérience du menteur quantique dans l’interprétation transactionnelle de Cramer” . Études en histoire et philosophie des sciences Partie B : Études en histoire et philosophie de la physique moderne . 41 (2): 86–92. arXiv : 0906.1626 . Bibcode : 2010SHPMP..41…86K . doi : 10.1016/j.shpsb.2010.01.001 . S2CID 16242184 . Archivé de l’original le 2018-06-24 . Récupéré le 16/09/2021 .
^ ‘t Hooft, Gérard (2016). L’interprétation des automates cellulaires de la mécanique quantique . Théories fondamentales de la physique. Vol. 185. Springer. doi : 10.1007/978-3-319-41285-6 . ISBN 978-3-319-41284-9. OCLC 951761277 . S2CID 7779840 . Archivé de l’original le 2021-12-29 . Récupéré le 27/08/2020 .

Lectures complémentaires

Les éléments suivants sont destinés à un public général.

En ligneAczel, Amir D. (2001). Intrication : Le plus grand mystère de la physique . New York : quatre murs huit fenêtres.
Afriat, A.; En ligneSelleri, F. (1999). Le paradoxe d’Einstein, Podolsky et Rosen . New York et Londres : Plenum Press.
En ligneBaggott, J. (1992). La signification de la théorie quantique . Presse universitaire d’Oxford.
Gilder, Louisa (2008). L’âge de l’enchevêtrement : quand la physique quantique renaît . New York : Alfred A. Knopf.
Greene, Brian (2004). Le Tissu du Cosmos . Vintage. ISBN 0-375-72720-5.
Mermin, N. David (1981). “Ramener à la maison le monde atomique: les mystères quantiques pour n’importe qui”. Journal américain de physique . 49 (10): 940–943. Bibcode : 1981AmJPh..49..940M . doi : 10.1119/1.12594 . S2CID 122724592 .
Mermin, N. David (avril 1985). “Est-ce que la lune est là quand personne ne regarde? La réalité et la théorie quantique”. La physique aujourd’hui . 38 (4): 38–47. Bibcode : 1985PhT….38d..38M . doi : 10.1063/1.880968 .

Les suivants sont plus orientés techniquement.

Aspect, A.; et coll. (1981). “Tests expérimentaux de théories locales réalistes via le théorème de Bell” . Phys. Rév. Lett . 47 (7): 460–463. Bibcode : 1981PhRvL..47..460A . doi : 10.1103/physrevlett.47.460 .
Aspect, A.; et coll. (1982). “Réalisation expérimentale d’Einstein – Podolsky – Rosen – Bohm Gedankenexperiment: Une nouvelle violation des inégalités de Bell” . Phys. Rév. Lett . 49 (2): 91–94. Bibcode : 1982PhRvL..49…91A . doi : 10.1103/physrevlett.49.91 .
Aspect, A.; En ligneGrangier, P. (1985). “À propos de la diffusion résonnante et d’autres effets hypothétiques dans les tests expérimentaux de cascade atomique d’Orsay des inégalités de Bell: une discussion et quelques nouvelles données expérimentales”. Lettere al Nuovo Cimento . 43 (8): 345–348. doi : 10.1007/bf02746964 . S2CID 120840672 .
Bell, JS (1971). “Introduction à la question de la variable cachée”. Actes de l’École Internationale de Physique ‘Enrico Fermi’, Cours IL, Fondements de la Mécanique Quantique . pp. 171–81.
En ligneBell, JS (2004). “Les chaussettes de Bertlmann et la nature de la réalité”. Parlable et Indicible en Mécanique Quantique . La presse de l’Universite de Cambridge. p. 139–158.
En ligneD’Espagnat, B. (1979). “La théorie quantique et la réalité” (PDF) . Scientifique américain . 241 (5): 158–181. Bib code : 1979SciAm.241e.158D . doi : 10.1038/scientificamerican1179-158 . Archivé (PDF) de l’original le 2009-03-27 . Récupéré le 18/03/2009 .
Frire, ES ; Walther, T.; Li, S. (1995). “Proposition pour un test sans échappatoire des inégalités de Bell” (PDF) . Phys. Rév. A . 52 (6): 4381–4395. Bibcode : 1995PhRvA..52.4381F . doi : 10.1103/physreva.52.4381 . hdl : 1969.1/126533 . PMID 9912775 . Archivé de l’original le 2021-12-29 . Récupéré le 19/03/2018 .
Frire, ES ; En ligneWalther, T. (2002). “Tests basés sur Atom des inégalités de Bell – l’héritage de John Bell continue”. Dans Bertlmann, RA; Zeilinger, A. (éd.). Quantum [In]dicibles . Berlin-Heidelberg-New York : Springer. p. 103–117.
Goldstein, Sheldon; et coll. (2011). “Théorème de Bell” . Scholarpédia . 6 (10): 8378. Bibcode : 2011SchpJ…6.8378G . doi : 10.4249/scholarpedia.8378 .
Griffiths, RB (2001). Théorie quantique cohérente . La presse de l’Universite de Cambridge. ISBN 978-0-521-80349-6. OCLC 1180958776 .
En ligneHardy, L. (1993). “Non localité pour 2 particules sans inégalités pour presque tous les états intriqués”. Lettres d’examen physique . 71 (11): 1665-1668. Bibcode : 1993PhRvL..71.1665H . doi : 10.1103/physrevlett.71.1665 . PMID 10054467 . S2CID 11839894 .
Matsukevitch, DN ; Maunz, P.; Moehring, DL; Olmschenk, S.; En ligneMonroe, C. (2008). “Violation de l’inégalité de Bell avec deux qubits atomiques distants”. Phys. Rév. Lett . 100 (15) : 150404. arXiv : 0801.2184 . Bib code : 2008PhRvL.100o0404M . doi : 10.1103/physrevlett.100.150404 . PMID 18518088 . S2CID 11536757 .
Rieffel, Eleanor G. ; Polak, Wolfgang H. (4 mars 2011). “4.4 Paradoxe EPR et théorème de Bell”. L’informatique quantique : une introduction en douceur . Presse du MIT. p. 60–65. ISBN 978-0-262-01506-6.
Sulcs, S. (2003). “La nature de la lumière et la physique expérimentale du XXe siècle”. Fondements des sciences . 8 (4): 365–391. doi : 10.1023/A:1026323203487 . S2CID 118769677 .
van Fraassen, C.-B. (1991). Mécanique quantique : une vision empiriste . Presse Clarendon. ISBN 978-0-198-24861-3. OCLC 22906474 .

Liens externes

Wikibooks a un livre sur le thème de : Quantum_Mechanics

Wikiversité a des ressources d’apprentissage sur le théorème de Bell

Wikimedia Commons a des médias liés au théorème de Bell .

Mermin : des actions effrayantes à distance ? Conférence Oppenheimer
Intrication quantique, par Andrew H. Thomas .
Théorème de Bell avec Easy Math, par David R. Schneider . Une autre explication simple de l’inégalité de Bell.
Expériences interactives avec des photons uniques : intrication et théorème de Bell
“Théorème de Bell” . Encyclopédie Internet de Philosophie .
“Inégalités de Bell” , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
Action fantasmagorique à distance : une explication du théorème de Bell