Propriété associative

En mathématiques , la propriété associative ^[1] est une propriété de certaines opérations binaires , ce qui signifie que réorganiser les Parenthèses dans une expression ne changera pas le résultat. En Logique propositionnelle , l’ associativité est une règle valide de remplacement des expressions dans les preuves logiques .

Dans une expression contenant deux ou plusieurs occurrences d’affilée du même opérateur associatif, l’ordre dans lequel les opérations sont effectuées n’a pas d’importance tant que la séquence des opérandes n’est pas modifiée. Autrement dit (après avoir réécrit l’expression avec des Parenthèses et en notation infixe si nécessaire), réorganiser les Parenthèses dans une telle expression ne changera pas sa valeur. Considérez les équations suivantes :

( 2 + 3 ) + 4 = 2 + ( 3 + 4 ) = 9 {displaystyle (2+3)+4=2+(3+4)=9,} 2 × ( 3 × 4 ) = ( 2 × 3 ) × 4 = 24. {displaystyle 2times (3times 4)=(2times 3)times 4=24.} 2fois (3fois 4)=(2fois 3)fois 4=24.

Même si les Parenthèses ont été réarrangées sur chaque ligne, les valeurs des expressions n’ont pas été modifiées. Puisque cela est vrai lors de l’exécution d’additions et de multiplications sur des nombres réels , on peut dire que “l’addition et la multiplication de nombres réels sont des opérations associatives”.

L’associativité n’est pas la même chose que la Commutativité , qui détermine si l’ordre de deux opérandes affecte le résultat. Par exemple, l’ordre n’a pas d’importance dans la multiplication des nombres réels, c’est-à-dire a × b = b × a , on dit donc que la multiplication des nombres réels est une opération commutative. Cependant, les opérations telles que la composition de fonctions et la multiplication de matrices sont associatives, mais (généralement) non commutatives.

Les opérations associatives sont abondantes en mathématiques ; en fait, de nombreuses structures algébriques (telles que les semi -groupes et les catégories ) exigent explicitement que leurs opérations binaires soient associatives.

Cependant, de nombreuses opérations importantes et intéressantes sont non associatives ; quelques exemples incluent la soustraction , l ‘ exponentiation et le Produit croisé vectoriel . Contrairement aux propriétés théoriques des nombres réels, l’addition de nombres à virgule flottante en informatique n’est pas associative, et le choix de la manière d’associer une expression peut avoir un effet significatif sur l’erreur d’arrondi.

Définition

Une opération binaire ∗ sur l’ensemble S est associative lorsque ce diagramme commute . Autrement dit, lorsque les deux chemins de S × S × S à S composent la même fonction de S × S × S à S .

Formellement, une opération binaire ∗ sur un ensemble S est dite associative si elle satisfait la loi associative :

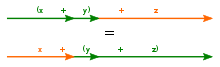
( x ∗ y ) ∗ z = x ∗ ( y ∗ z ) pour tout x , y , z dans S .

Ici, ∗ est utilisé pour remplacer le symbole de l’opération, qui peut être n’importe quel symbole, et même l’absence de symbole ( juxtaposition ) comme pour la multiplication .

( xy ) z = x ( yz ) = xyz pour tout x , y , z dans S .

La loi associative peut également être exprimée en notation fonctionnelle ainsi : f ( f ( x , y ), z ) = f ( x , f ( y , z )) .

Droit associatif généralisé

En l’absence de propriété associative, cinq facteurs a , b , c , d , e donnent un réseau de Tamari d’ordre quatre, éventuellement des produits différents.

Si une opération binaire est associative, l’application répétée de l’opération produit le même résultat, quelle que soit la manière dont les paires de Parenthèses valides sont insérées dans l’expression. ^[2] C’est ce qu’on appelle la loi associative généralisée . Par exemple, un produit de quatre éléments peut s’écrire, sans changer l’ordre des facteurs, de cinq manières possibles :

( ( un b ) c ) ré {displaystyle ((ab)c)d} ( un b ) ( c ré ) {displaystyle (ab)(cd)} ( un ( b c ) ) ré {displaystyle (a(bc))d} un ( ( b c ) ré ) {displaystyle a((bc)d)} un ( b ( c ré ) ) {displaystyle a(b(cd))}

Si l’opération de produit est associative, la loi associative généralisée dit que toutes ces formules donneront le même résultat. Ainsi, à moins que la formule avec des Parenthèses omises ait déjà une signification différente (voir ci-dessous), les Parenthèses peuvent être considérées comme inutiles et “le” produit peut être écrit sans ambiguïté comme

un b c ré . {displaystyle abcd.}

Au fur et à mesure que le nombre d’éléments augmente, le nombre de façons possibles d’insérer des Parenthèses augmente rapidement, mais elles restent inutiles pour la désambiguïsation.

Un exemple où cela ne fonctionne pas est le biconditionnel logique ↔. C’est associatif; ainsi, A ↔ ( B ↔ C ) est équivalent à ( A ↔ B ) ↔ C , mais A ↔ B ↔ C signifie le plus souvent ( A ↔ B et B ↔ C ) , ce qui n’est pas équivalent.

Exemples

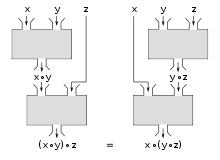
Dans les opérations associatives est ( x ∘ y ) ∘ z = x ∘ ( y ∘ z ) {displaystyle (xcirc y)circ z=xcirc (ycirc z)} . L’addition des nombres réels est associative.

Voici quelques exemples d’opérations associatives.

La concaténation des trois chaînes “hello”, ” “, “world”peut être calculée en concaténant les deux premières chaînes (donnant “hello “) et en ajoutant la troisième chaîne ( “world”), ou en joignant la deuxième et la troisième chaîne (donnant ” world”) et en concaténant la première chaîne ( “hello”) avec le résultat. Les deux méthodes produisent le même résultat ; la Concaténation de chaînes est associative (mais pas commutative).
En arithmétique , l’ addition et la multiplication de nombres réels sont associatives ; c’est à dire,

( x + y ) + z = x + ( y + z ) = x + y + z ( x y ) z = x ( y z ) = x y z } for all x , y , z ∈ R . {displaystyle left.{begin{matrice}(x+y)+z=x+(y+z)=x+y+zquad \(x,y)z=x(y,z )=x,y,zqquad qquad qquad quad ,end{matrice}}right}{mbox{pour tout }}x,y,zin mathbb {R } .} $left.{begin{matrix}(x+y)+z=x+(y+z)=x+y+zquad \(x,y)z=x(y,z)=x,y,zqquad qquad qquad quad ,end{matrix}}right}{mbox{for all }}x,y,zin mathbb {R} .$ $left.{begin{matrice}(x+y)+z=x+(y+z)=x+y+zquad \(x,y)z=x(y,z)=x ,y,zqquad qquad qquad quad ,end{matrice}}right}{mbox{for all }}x,y,zin mathbb {R} .$ En raison de l’associativité, les Parenthèses de regroupement peuvent être omises sans ambiguïté.

L’opération triviale x ∗ y = x (c’est-à-dire que le résultat est le premier argument, quel que soit le second argument) est associative mais pas commutative. De même, l’opération triviale x ∘ y = y (c’est-à-dire que le résultat est le deuxième argument, quel que soit le premier argument) est associative mais pas commutative.
L’addition et la multiplication des nombres complexes et des quaternions sont associatives. L’addition d’ Octonions est également associative, mais la multiplication d’Octonions est non associative.
Le plus grand commun diviseur et les plus petites fonctions multiples communes agissent de manière associative.

gcd ⁡ ( gcd ⁡ ( x , y ) , z ) = gcd ⁡ ( x , gcd ⁡ ( y , z ) ) = gcd ⁡ ( x , y , z ) lcm ⁡ ( lcm ⁡ ( x , y ) , z ) = lcm ⁡ ( x , lcm ⁡ ( y , z ) ) = lcm ⁡ ( x , y , z ) } for all x , y , z ∈ Z . {displaystyle left.{begin{matrice}operatorname {gcd} (operatorname {gcd} (x,y),z)=operatorname {gcd} (x,operatorname {gcd} (y,z) )=operatorname {gcd} (x,y,z) quad \operatorname {lcm} (operatorname {lcm} (x,y),z)=operatorname {lcm} (x,operatorname { lcm} (y,z))=operatorname {lcm} (x,y,z)quad end{matrice}}right}{mbox{ for all }}x,y,zin mathbb {Z} .} $left.{begin{matrix}operatorname {gcd} (operatorname {gcd} (x,y),z)=operatorname {gcd} (x,operatorname {gcd} (y,z))=operatorname {gcd} (x,y,z) quad \operatorname {lcm} (operatorname {lcm} (x,y),z)=operatorname {lcm} (x,operatorname {lcm} (y,z))=operatorname {lcm} (x,y,z)quad end{matrix}}right}{mbox{ for all }}x,y,zin mathbb {Z} .$ $left.{begin{matrix}operatorname {gcd} (operatorname {gcd} (x,y),z)=operatorname {gcd} (x,operatorname {gcd} (y,z))=operatorname {gcd} (x,y,z) quad \operatorname {lcm} (operatorname {lcm} (x,y),z)=operatorname {lcm} (x,operatorname {lcm} (y,z))=operatorname {lcm} (x,y,z)quad end{matrix}}right}{mbox{ for all }}x,y,zin mathbb {Z} .$

En prenant l’ intersection ou l’ union d’ ensembles :

( A ∩ B ) ∩ C = A ∩ ( B ∩ C ) = A ∩ B ∩ C ( A ∪ B ) ∪ C = A ∪ ( B ∪ C ) = A ∪ B ∪ C } for all sets A , B , C . {displaystyle left.{begin{matrice}(Acap B)cap C=Acap (Bcap C)=Acap Bcap Cquad \(Acup B) cup C=Acup (Bcup C)=Acup Bcup Cquad end{matrice}}right}{mbox{for all sets }}A,B,C.} $left.{begin{matrix}(Acap B)cap C=Acap (Bcap C)=Acap Bcap Cquad \(Acup B)cup C=Acup (Bcup C)=Acup Bcup Cquad end{matrix}}right}{mbox{for all sets }}A,B,C.$ $left.{begin{matrix}(Acap B)cap C=Acap (Bcap C)=Acap Bcap Cquad \(Acup B)cup C=Acup (Bcup C)=Acup Bcup Cquad end{matrix}}right}{mbox{for all sets }}A,B,C.$

Si M est un ensemble et S désigne l’ensemble de toutes les fonctions de M à M , alors l’opération de composition de fonctions sur S est associative :

( f ∘ g ) ∘ h = f ∘ ( g ∘ h ) = f ∘ g ∘ h for all f , g , h ∈ S . {displaystyle (fcirc g)circ h=fcirc (gcirc h)=fcirc gcirc hqquad {mbox{for all}}f,g,hin S.}

Un peu plus généralement, étant donné quatre ensembles M , N , P et Q , avec h : M à N , g : N à P , et f : P à Q , alors

( f ∘ g ) ∘ h = f ∘ ( g ∘ h ) = f ∘ g ∘ h {displaystyle (fcirc g)circ h=fcirc (gcirc h)=fcirc gcirc h} comme avant. Bref, la composition des cartes est toujours associative.

Considérons un ensemble de trois éléments, A, B et C. L’opération suivante :

×	UN	B	C
UN	UN	UN	UN
B	UN	B	C
C	UN	UN	UN

est associatif. Ainsi, par exemple, A(BC)=(AB)C = A. Cette opération n’est pas commutative.

Étant donné que les matrices représentent des fonctions linéaires et que la multiplication matricielle représente la composition de fonctions, on peut immédiatement conclure que la multiplication matricielle est associative. ^[3]

Logique propositionnelle

Règle de remplacement

Dans la Logique propositionnelle vérifonctionnelle standard, l’ association , ^{[4] [5]} ou l’ associativité ^[6] sont deux règles valides de remplacement . Les règles permettent de déplacer les Parenthèses dans les expressions logiques des preuves logiques . Les règles (utilisant la notation des connecteurs logiques ) sont :

( P ∨ ( Q ∨ R ) ) ⇔ ( ( P ∨ Q ) ∨ R ) {displaystyle (Plor (Qlor R))Leftrightarrow ((Plor Q)lor R)}

( P ∧ ( Q ∧ R ) ) ⇔ ( ( P ∧ Q ) ∧ R ) , {displaystyle (Pland (Qland R))Leftrightarrow ((Pland Q)land R),}

où ” ⇔ {displaystyle Leftrightarrow } ” est un symbole métalogique représentant “peut être remplacé dans une preuve par”.

Connecteurs fonctionnels de vérité

L’associativité est une propriété de certains connecteurs logiques de la Logique propositionnelle vérifonctionnelle . Les équivalences logiques suivantes démontrent que l’associativité est une propriété de connecteurs particuliers. Ce qui suit sont des tautologies vérifonctionnelles . ^[7]

Associativité de la disjonction :

( ( P ∨ Q ) ∨ R ) ↔ ( P ∨ ( Q ∨ R ) ) {displaystyle ((Plor Q)lor R)leftrightarrow (Plor (Qlor R))} ( P ∨ ( Q ∨ R ) ) ↔ ( ( P ∨ Q ) ∨ R ) {displaystyle (Plor (Qlor R))leftrightarrow ((Plor Q)lor R)}

Associativité de conjonction :

( ( P ∧ Q ) ∧ R ) ↔ ( P ∧ ( Q ∧ R ) ) {displaystyle ((Pland Q)land R)leftrightarrow (Pland (Qland R))} ( P ∧ ( Q ∧ R ) ) ↔ ( ( P ∧ Q ) ∧ R ) {displaystyle (Pland (Qland R))leftrightarrow ((Pland Q)land R)}

Associativité d’équivalence :

( ( P ↔ Q ) ↔ R ) ↔ ( P ↔ ( Q ↔ R ) ) {displaystyle ((Pleftrightarrow Q)leftrightarrow R)leftrightarrow (Pleftrightarrow (Qleftrightarrow R))} ( P ↔ ( Q ↔ R ) ) ↔ ( ( P ↔ Q ) ↔ R ) {displaystyle (Pleftrightarrow (Qleftrightarrow R))leftrightarrow ((Pleftrightarrow Q)leftrightarrow R)}

Le déni conjoint est un exemple de connecteur fonctionnel de vérité qui n’est pas associatif.

Learn more.

Isomorphisme

Jul 14, 2022

Premier article sur la théorie des ensembles de Cantor

Jul 12, 2022

Énergie gravitationnelle

Jul 9, 2022

Sphère de Riemann

Jul 8, 2022

Fonctionnement non associatif

Une opération binaire ∗ {displaystyle *} sur un ensemble S qui ne satisfait pas la loi associative est dit non associatif . Symboliquement,

( x ∗ y ) ∗ z ≠ x ∗ ( y ∗ z ) for some x , y , z ∈ S . {displaystyle (x*y)*zneq x*(y*z)qquad {mbox{pour certains}}x,y,zin S.}

Pour une telle opération, l’ordre d’évaluation importe . Par example:

Soustraction

( 5 − 3 ) − 2 ≠ 5 − ( 3 − 2 ) {displaystyle (5-3)-2,neq ,5-(3-2)}

Division

( 4 / 2 ) / 2 ≠ 4 / ( 2 / 2 ) {displaystyle (4/2)/2,neq ,4/(2/2)}

Exponentation

2 ( 1 2 ) ≠ ( 2 1 ) 2 {displaystyle 2^{(1^{2})},neq ,(2^{1})^{2}} $2^{(1^{2})},neq ,(2^{1})^{2}$ $2^{(1^{2})},neq ,(2^{1})^{2}$

Produit croisé vectoriel

i × ( i × j ) = i × k = − j ( i × i ) × j = 0 × j = 0 {displaystyle {begin{aligné}mathbf {i} times (mathbf {i} times mathbf {j} )&=mathbf {i} times mathbf {k} =-mathbf {j } \(mathbf {i} times mathbf {i} )times mathbf {j} &=mathbf {0} times mathbf {j} =mathbf {0} end{aligné}} } ${displaystyle {begin{aligned}mathbf {i} times (mathbf {i} times mathbf {j} )&=mathbf {i} times mathbf {k} =-mathbf {j} \(mathbf {i} times mathbf {i} )times mathbf {j} &=mathbf {0} times mathbf {j} =mathbf {0} end{aligned}}}$ ${displaystyle {begin{aligned}mathbf {i} times (mathbf {i} times mathbf {j} )&=mathbf {i} times mathbf {k} =-mathbf {j} \(mathbf {i} times mathbf {i} )times mathbf {j} &=mathbf {0} times mathbf {j} =mathbf {0} end{aligned}}}$

De plus, bien que l’addition soit associative pour des sommes finies, elle n’est pas associative à l’intérieur de sommes infinies ( séries ). Par example,

( 1 + − 1 ) + ( 1 + − 1 ) + ( 1 + − 1 ) + ( 1 + − 1 ) + ( 1 + − 1 ) + ( 1 + − 1 ) + ⋯ = 0 {displaystyle (1+-1)+(1+-1)+(1+-1)+(1+-1)+(1+-1)+(1+-1)+dots =0}

tandis que

1 + ( − 1 + 1 ) + ( − 1 + 1 ) + ( − 1 + 1 ) + ( − 1 + 1 ) + ( − 1 + 1 ) + ( − 1 + 1 ) + ⋯ = 1. {displaystyle 1+(-1+1)+(-1+1)+(-1+1)+(-1+1)+(-1+1)+(-1+1)+dots = 1.}

Certaines opérations non associatives sont fondamentales en mathématiques. Ils apparaissent souvent comme la multiplication dans des structures appelées algèbres non associatives , qui ont aussi une addition et une multiplication scalaire . Des exemples sont les Octonions et les algèbres de Lie . Dans les algèbres de Lie, la multiplication satisfait l’ identité de Jacobi au lieu de la loi associative ; cela permet d’abstraire la nature algébrique des transformations infinitésimales .

D’autres exemples sont le quasigroupe , le quasichamp , l’Anneau non associatif et les magmas non associatifs commutatifs .

Non associativité du calcul en virgule flottante

En mathématiques, l’addition et la multiplication de nombres réels sont associatives. En revanche, en informatique, l’addition et la multiplication de nombres à virgule flottante ne sont pas associatives, car des erreurs d’arrondi sont introduites lorsque des valeurs de tailles différentes sont jointes. ^[8]

Pour illustrer cela, considérons une représentation en virgule flottante avec une mantisse de 4 bits :
(1.000 ₂ ×2 ⁰ + 1.000 ₂ ×2 ⁰ ) + 1.000 ₂ ×2 ⁴ = 1.000 ₂ ×2 ¹ + 1.000 ₂ ×2 ⁴ = 1.00 1 ₂ ×2 ⁴
1,000 ₂ ×2 ⁰ + (1,000 ₂ ×2 ⁰ + 1,000 ₂ ×2 ⁴ ) = 1,000 ₂ ×2 ⁰ + 1,000 ₂ ×2 ⁴ = 1,000 ₂ ×2 ⁴

Même si la plupart des ordinateurs calculent avec une mantisse de 24 ou 53 bits, ^[9] c’est une source importante d’erreur d’arrondi, et des approches telles que l’ algorithme de sommation de Kahan sont des moyens de minimiser les erreurs. Cela peut être particulièrement problématique dans le calcul parallèle. ^{[10] [11]}

Notation pour les opérations non associatives

En général, les Parenthèses doivent être utilisées pour indiquer l’ ordre d’évaluation si une opération non associative apparaît plus d’une fois dans une expression (à moins que la notation ne spécifie l’ordre d’une autre manière, comme 2 3 / 4 {displaystyle {dfrac {2}{3/4}}} ${displaystyle {dfrac {2}{3/4}}}$ ${displaystyle {dfrac {2}{3/4}}}$ ). Cependant, les mathématiciens s’accordent sur un ordre particulier d’évaluation pour plusieurs opérations communes non associatives. Il s’agit simplement d’une convention de notation pour éviter les Parenthèses.

Une opération associative à gauche est une opération non associative qui est classiquement évaluée de gauche à droite, c’est-à-dire,

x ∗ y ∗ z = ( x ∗ y ) ∗ z w ∗ x ∗ y ∗ z = ( ( w ∗ x ) ∗ y ) ∗ z etc. } for all w , x , y , z ∈ S {displaystyle left.{begin{matrice}x*y*z=(x*y)*zqquad qquad quad ,\w*x*y*z=((w*x)* y)*zquad \{mbox{etc.}}qquad qquad qquad qquad qquad qquad ,end{matrice}}right}{mbox{pour tous }} w,x,y,zdans S} $left.{begin{matrix}x*y*z=(x*y)*zqquad qquad quad ,\w*x*y*z=((w*x)*y)*zquad \{mbox{etc.}}qquad qquad qquad qquad qquad qquad ,end{matrix}}right}{mbox{for all }}w,x,y,zin S$ $left.{begin{matrix}x*y*z=(x*y)*zqquad qquad quad ,\w*x*y*z=((w*x)*y)*zquad \{mbox{etc.}}qquad qquad qquad qquad qquad qquad ,end{matrix}}right}{mbox{for all }}w,x,y,zin S$

tandis qu’une opération associative à droite est classiquement évaluée de droite à gauche :

x ∗ y ∗ z = x ∗ ( y ∗ z ) w ∗ x ∗ y ∗ z = w ∗ ( x ∗ ( y ∗ z ) ) etc. } for all w , x , y , z ∈ S {displaystyle left.{begin{matrice}x*y*z=x*(y*z)qquad qquad quad ,\w*x*y*z=w*(x*(y *z))quad \{mbox{etc.}}qquad qquad qquad qquad qquad qquad ,end{matrice}}right}{mbox{pour tous }} w,x,y,zdans S} $left.{begin{matrix}x*y*z=x*(y*z)qquad qquad quad ,\w*x*y*z=w*(x*(y*z))quad \{mbox{etc.}}qquad qquad qquad qquad qquad qquad ,end{matrix}}right}{mbox{for all }}w,x,y,zin S$ $left.{begin{matrix}x*y*z=x*(y*z)qquad qquad quad ,\w*x*y*z=w*(x*(y*z))quad \{mbox{etc.}}qquad qquad qquad qquad qquad qquad ,end{matrix}}right}{mbox{for all }}w,x,y,zin S$

Des opérations associatives à gauche et à droite se produisent. Les opérations associatives à gauche incluent les éléments suivants :

Soustraction et division de nombres réels : ^{[12] [13] [14] [15] [16]}

x − y − z = ( x − y ) − z {displaystyle xyz=(xy)-z} {displaystyle x-y-z=(x-y)-z} x / y / z = ( x / y ) / z {displaystyle x/y/z=(x/y)/z}

Application de la fonction :

( f x y ) = ( ( f x ) y ) {displaystyle (f,x,y)=((f,x),y)} Cette notation peut être motivée par l’ isomorphisme currying .

Les opérations associatives à droite incluent les éléments suivants :

Exponentiation des nombres réels en notation en exposant :

x y z = x ( y z ) {displaystyle x^{y^{z}}=x^{(y^{z})}} ${displaystyle x^{y^{z}}=x^{(y^{z})}}$ ${displaystyle x^{y^{z}}=x^{(y^{z})}}$ L’exponentiation est couramment utilisée avec des Parenthèses ou de manière associative à droite car une opération répétée d’exponentiation associative à gauche est peu utile. Les puissances répétées seraient principalement réécrites avec multiplication: ( x y ) z = x ( y z ) {displaystyle (x^{y})^{z}=x^{(yz)}} ${displaystyle (x^{y})^{z}=x^{(yz)}}$ ${displaystyle (x^{y})^{z}=x^{(yz)}}$ Formaté correctement, l’exposant se comporte intrinsèquement comme un ensemble de Parenthèses ; par exemple dans l’expression 2 x + 3 {displaystyle 2^{x+3}} ${displaystyle 2^{x+3}}$ ${displaystyle 2^{x+3}}$ l’addition est effectuée avant l’exponentiation malgré l’absence de Parenthèses explicites 2 ( x + 3 ) {displaystyle 2^{(x+3)}} ${displaystyle 2^{(x+3)}}$ ${displaystyle 2^{(x+3)}}$ enroulé autour de lui. Ainsi étant donnée une expression telle que x y z {displaystyle x^{y^{z}}} $x^{y^z}$ , l’exposant complet y z {displaystyle y^{z}} ${displaystyle y^{z}}$ ${displaystyle y^{z}}$ de la base x {style d’affichage x} est évalué en premier. Cependant, dans certains contextes, notamment en écriture manuscrite, la différence entre x y z = ( x y ) z {displaystyle {x^{y}}^{z}=(x^{y})^{z}} ${displaystyle {x^{y}}^{z}=(x^{y})^{z}}$ ${displaystyle {x^{y}}^{z}=(x^{y})^{z}}$ , x y z = X ( y z ) {displaystyle x^{yz}=x^{(yz)}} ${displaystyle x^{yz}=x^{(yz)}}$ ${displaystyle x^{yz}=x^{(yz)}}$ et x y z = x ( y z ) {displaystyle x^{y^{z}}=x^{(y^{z})}} ${displaystyle x^{y^{z}}=x^{(y^{z})}}$ ${displaystyle x^{y^{z}}=x^{(y^{z})}}$ peut être difficile à voir. Dans un tel cas, l’associativité à droite est généralement implicite.

Définition de la fonction

Z → Z → Z = Z → ( Z → Z ) {displaystyle mathbb {Z} rightarrow mathbb {Z} rightarrow mathbb {Z} =mathbb {Z} rightarrow (mathbb {Z} rightarrow mathbb {Z} )} x ↦ y ↦ x − y = x ↦ ( y ↦ x − y ) {displaystyle xmapsto ymapsto xy=xmapsto (ymapsto xy)} xmapsto ymapsto x-y=xmapsto (ymapsto x-y) L’utilisation de la notation associative à droite pour ces opérations peut être motivée par la correspondance Curry-Howard et par l’ isomorphisme de curry .

Les opérations non associatives pour lesquelles aucun ordre d’évaluation conventionnel n’est défini comprennent les opérations suivantes.

Exponentiation des nombres réels en notation infixe : ^[17]

( x ∧ y ) ∧ z ≠ x ∧ ( y ∧ z ) {displaystyle (x^{coin }y)^{coin }zneq x^{coin }(y^{coin }z)} ${displaystyle (x^{wedge }y)^{wedge }zneq x^{wedge }(y^{wedge }z)}$ ${displaystyle (x^{coin }y)^{coin }zneq x^{coin }(y^{coin }z)}$

Les opérateurs flèche vers le haut de Knuth :

a ↑ ↑ ( b ↑ ↑ c ) ≠ ( a ↑ ↑ b ) ↑ ↑ c {displaystyle auparrow uparrow (buparrow uparrow c)neq (auparrow uparrow b)uparrow uparrow c} a ↑ ↑ ↑ ( b ↑ ↑ ↑ c ) ≠ ( a ↑ ↑ ↑ b ) ↑ ↑ ↑ c {displaystyle auparrow uparrow uparrow (buparrow uparrow uparrow c)neq (auparrow uparrow uparrow b)uparrow uparrow uparrow c}

En prenant le produit croisé de trois vecteurs :

a → × ( b → × c → ) ≠ ( a → × b → ) × c → for some a → , b → , c → ∈ R 3 {displaystyle {vec {a}}times ({vec {b}}times {vec {c}})neq ({vec {a}}times {vec {b}}) times {vec {c}}qquad {mbox{ for some }}{vec {a}},{vec {b}},{vec {c}}in mathbb {R} ^ {3}} ${vec {a}}times ({vec {b}}times {vec {c}})neq ({vec {a}}times {vec {b}})times {vec {c}}qquad {mbox{ for some }}{vec {a}},{vec {b}},{vec {c}}in mathbb {R} ^{3}$ ${vec {a}}times ({vec {b}}times {vec {c}})neq ({vec {a}}times {vec {b}})times { vec {c}}qquad {mbox{ pour certains }}{vec {a}},{vec {b}},{vec {c}}in mathbb {R} ^{3}$

En prenant la moyenne par paires des nombres réels :

( x + y ) / 2 + z 2 ≠ x + ( y + z ) / 2 2 for all x , y , z ∈ R with x ≠ z . {displaystyle {(x+y)/2+z over 2}neq {x+(y+z)/2 over 2}qquad {mbox{for all}}x,y,zin mathbb {R} {mbox{ avec }}xneq z.}

Prendre le complément relatif des ensembles ( A ∖ B ) ∖ C {displaystyle (Aantislash B)antislash C} n’est pas le même que A ∖ ( B ∖ C ) {displaystyle Abarre oblique inverse (Bbarre oblique inverse C)} . (Comparez la non- implication matérielle dans la logique.)

Histoire

William Rowan Hamilton semble avoir inventé le terme “propriété associative” ^[18] vers 1844, une époque où il envisageait l’algèbre non associative des Octonions qu’il avait apprise de John T. Graves ^[19]

Voir également

Recherchez la propriété associative dans Wiktionary, le dictionnaire gratuit.

Test d’associativité de la lumière
Série télescopique , l’utilisation de l’associativité d’addition pour annuler les termes d’une série infinie
Un semi -groupe est un ensemble avec une opération binaire associative.
La Commutativité et la Distributivité sont deux autres propriétés fréquemment discutées des opérations binaires.
L’associativité de puissance , l’alternativité , la flexibilité et l’associativité N-aire sont des formes faibles d’associativité.
Les identités moufang fournissent également une forme faible d’associativité.

Références

^ Hungerford, Thomas W. (1974). Algèbre (1ère éd.). Springer . p. 24. ISBN 978-0387905181. Définition 1.1 (i) a(bc) = (ab)c pour tout a, b, c dans G.
^ Durbin, John R. (1992). Algèbre moderne: une introduction (3e éd.). New York : Wiley. p. 78. ISBN 978-0-471-51001-7. Si a 1 , a 2 , … , a n ( n ≥ 2 ) {displaystyle a_{1},a_{2},dots ,a_{n},,(ngeq 2)} $a_{1},a_{2},dots ,a_{n},,(ngeq 2)$ $a_{1},a_{2},dots ,a_{n},,(ngeq 2)$ sont des éléments d’un ensemble avec une opération associative, alors le produit a 1 a 2 ⋯ a n {displaystyle a_{1}a_{2}cdots a_{n}} ${displaystyle a_{1}a_{2}cdots a_{n}}$ ${displaystyle a_{1}a_{2}cdots a_{n}}$ est sans ambiguïté ; c’est-à-dire que le même élément sera obtenu quelle que soit la façon dont les Parenthèses sont insérées dans le produit.
^ “Associativité des produits matriciels” . Académie Khan . Récupéré le 5 juin 2016 .
^ Moore, Brooke Noel; Parker, Richard (2017). Pensée critique (12e éd.). New York : Éducation McGraw-Hill. p. 321.ISBN _ 9781259690877.
^ Copi, Irving M.; Cohen, Carl; McMahon, Kenneth (2014). Introduction à la logique (14e éd.). Essex : Éducation Pearson. p. 387. ISBN 9781292024820.
^ Hurley, Patrick J.; Watson, Lori (2016). Une introduction concise à la logique (13e éd.). Boston : Apprentissage Cengage. p. 427.ISBN _ 9781305958098.
^ “Preuve logique symbolique de l’associativité” . Math.stackexchange.com . 22 mars 2017.
^ Knuth, Donald, L’art de la programmation informatique , Volume 3, section 4.2.2
^ IEEE Computer Society (29 août 2008). Norme IEEE pour l’arithmétique à virgule flottante . doi : 10.1109/IEEESTD.2008.4610935 . ISBN 978-0-7381-5753-5. Norme IEEE 754-2008.
↑ Villa, Oreste ; Chavarria-mir, Daniel; Gurumoorthi, Vidhya ; Marquez, Andrés; Krishnamoorthy, Sriram, Effects of Floating-Point non-Associativity on Numerical Computations on Massively Multithreaded Systems (PDF) , archivé de l’original (PDF) le 15 février 2013 , récupéré le 8 avril 2014
^ Goldberg, David (mars 1991). “Ce que tout informaticien devrait savoir sur l’arithmétique à virgule flottante” (PDF) . Enquêtes informatiques ACM . 23 (1): 5–48. doi : 10.1145/103162.103163 . S2CID 222008826 . Récupéré le 20 janvier 2016 . ( [1] , [2] Archivé le 06/04/2016 sur la Wayback Machine )
^ George Mark Bergman: Ordre des opérations arithmétiques
^ Education Place: L’ordre des opérations
^ Khan Academy : L’ordre des opérations , horodatage 5m40s
^ Virginia Department of Education: Utilisation de l’ordre des opérations et exploration des propriétés , section 9
^ Bronstein: de:Taschenbuch der Mathematik , pages 115-120, chapitre : 2.4.1.1, ISBN 978-3-8085-5673-3
^ Associativité d’exponentiation et Codeplea de notation mathématique standard. 23 août 2016. Récupéré le 20 septembre 2016.
^ Hamilton, WR (1844–1850). “Sur les quaternions ou un nouveau système d’imaginaires en algèbre” . Collection David R. Wilkins. Revue Philosophique . Trinity College de Dublin .
^ Baez, John C. (2002). “Les Octonions” . Bulletin de l’American Mathematical Society . 39 (2): 145-205. arXiv : math/0105155 . doi : 10.1090/S0273-0979-01-00934-X . ISSN 0273-0979 . M. 1886087 . S2CID 586512 .