Moment angulaire

Apprendre encore plus Cet article peut être trop technique pour que la plupart des lecteurs le comprennent . ( Février 2021 )Aidez -nous à l’améliorer pour le rendre compréhensible aux non-experts , sans supprimer les détails techniques. (Découvrez comment et quand supprimer ce modèle de message)

En physique , le moment cinétique (rarement, moment d’impulsion ou moment de rotation ) est l’analogue de rotation du Moment linéaire . C’est une quantité importante en physique car c’est une quantité conservée – le moment cinétique total d’un système fermé reste constant. Le moment cinétique a à la fois une direction et une amplitude, et les deux sont conservées. Les motos , les Frisbees ^[1] et les balles rayées doivent tous leurs propriétés utiles à la conservation du moment cinétique. La conservation du moment cinétique est aussi la raison pour laquelle les ouragans ^[2] ont des spirales et des étoiles à neutronsont des taux de rotation élevés. En général, la conservation limite le mouvement possible d’un système mais ne le détermine pas de manière unique.

Moment angulaire
Ce gyroscope reste droit tout en tournant grâce à la conservation de son moment cinétique.
Symboles communs	L
En unités de base SI	kg m ² s ⁻¹
Conservé ?	oui
Dérivations à partir d’ autres grandeurs	L = je ω = r × p
Dimension	M L ²T ⁻¹

Le moment angulaire tridimensionnel d’une particule ponctuelle est classiquement représenté par un pseudovecteur r × p , le produit croisé du vecteur de position de la particule r (par rapport à une origine) et de son vecteur de moment ; ce dernier est p = m v en mécanique newtonienne. Contrairement au moment, le moment cinétique dépend de l’endroit où cette origine est choisie, puisque la position de la particule est mesurée à partir de celle-ci.

Le moment cinétique est une grandeur extensive ; c’est-à-dire que le moment cinétique total de tout système composite est la somme des moments cinétiques de ses éléments constitutifs. Pour un corps rigide continu ou un fluide, le moment cinétique total est l’intégrale volumique de la densité de moment cinétique (c’est-à-dire le moment cinétique par unité de volume dans la limite lorsque le volume se réduit à zéro) sur tout le corps.

Semblable à la conservation du Moment linéaire où il est conservé s’il n’y a pas de force externe, le moment cinétique est conservé s’il n’y a pas de couple externe. Le couple peut être défini comme le taux de variation du moment cinétique, analogue à la force . Le couple externe net sur tout système est toujours égal au couple total sur le système ; en d’autres termes, la somme de tous les couples internes de tout système est toujours 0 (c’est l’analogue de rotation de la Troisième loi du mouvement de Newton ). Par conséquent, pour un système fermé (où il n’y a pas de couple externe net), le totalle couple sur le système doit être égal à 0, ce qui signifie que le moment cinétique total du système est constant. Le changement de moment cinétique pour une interaction particulière est parfois appelé twirl , ^[3] mais c’est assez rare. Twirl est l’analogue angulaire de l’impulsion.

Définition en mécanique classique

Tout comme pour la vitesse angulaire , il existe deux types particuliers de moment cinétique d’un objet : le moment cinétique de spin est le moment cinétique autour du Centre de masse de l’objet , tandis que le moment cinétique orbital est le moment cinétique autour d’un centre de rotation choisi. La Terre a un moment cinétique orbital par nature de tourner autour du Soleil, et un moment cinétique de spin par la nature de sa rotation journalière autour de l’axe polaire. Le moment cinétique total est la somme des moments cinétiques de spin et d’orbite. Dans le cas de la Terre, la quantité primaire conservée est le moment cinétique total du système solaire car le moment cinétique est échangé dans une mesure faible mais importante entre les planètes et le Soleil. Le vecteur de moment angulaire orbital d’une particule ponctuelle est toujours parallèle et directement proportionnel à son vecteur de vitesse angulaire orbitale ω , où la constante de proportionnalité dépend à la fois de la masse de la particule et de sa distance à l’origine. Le vecteur moment angulaire de spin d’un corps rigide est proportionnel mais pas toujours parallèle au vecteur vitesse angulaire de spin Ω, faisant de la constante de proportionnalité un tenseur de second rang plutôt qu’un scalaire.

Moment cinétique orbital en deux dimensions

La vitesse de la particule m par rapport à l’origine O peut être résolue en composantes parallèles à ( v _∥ ) et perpendiculaires à ( v _⊥ ) le rayon vecteur r . Le moment cinétique de m est proportionnel à la Composante perpendiculaire v _⊥ de la vitesse, ou de manière équivalente, à la distance perpendiculaire r _⊥ de l’origine.

Le moment cinétique est une quantité vectorielle (plus précisément, un pseudovecteur ) qui représente le produit de l’ inertie de rotation et de la vitesse de rotation d’un corps (en radians/sec) autour d’un axe particulier. Cependant, si la trajectoire de la particule se situe dans un seul plan , il suffit d’écarter la nature vectorielle du moment cinétique et de le traiter comme un scalaire (plus précisément, un pseudoscalaire ). ^[4] Le moment angulaire peut être considéré comme un analogue de rotation du Moment linéaire. Ainsi, où le Moment linéaire p est proportionnel à la masse m et à la vitesse linéaire v ,

p = m v , {displaystyle p=mv,} p=mv,

le moment cinétique L est proportionnel au moment d’inertie I et à la vitesse angulaire ω mesurée en radians par seconde. ^[5]

L = je ω . {displaystyle L=Iomega .}

Contrairement à la masse, qui ne dépend que de la quantité de matière, le moment d’inertie dépend également de la position de l’axe de rotation et de la forme de la matière. Contrairement à la vitesse linéaire, qui ne dépend pas du choix de l’origine, la vitesse angulaire orbitale est toujours mesurée par rapport à une origine fixe. Par conséquent, à proprement parler, L devrait être appelé le moment cinétique par rapport à ce centre . ^[6]

Car je = r 2 m {displaystyle I=r^{2}m} ${displaystyle I=r^{2}m}$ ${displaystyle I=r^{2}m}$ pour une seule particule et ω = v r {displaystyle omega ={frac {v}{r}}} $omega ={frac {v}{r}}$ $oméga ={frac {v}{r}}$ pour un mouvement circulaire, le moment cinétique peut être étendu, L = r 2 m ⋅ v r , {displaystyle L=r^{2}mcdot {frac {v}{r}},} ${displaystyle L=r^{2}mcdot {frac {v}{r}},}$ ${displaystyle L=r^{2}mcdot {frac {v}{r}},}$ et réduit à,

L = r m v , {displaystyle L=rmv,}

le produit du rayon de rotation r et de la quantité de mouvement linéaire de la particule p = m v {displaystyle p=mv} p = mv , où v {style d’affichage v} dans ce cas est la vitesse linéaire (tangentielle) équivalente au rayon ( = r ω {displaystyle =romega } ).

Cette analyse simple peut également s’appliquer au mouvement non circulaire si seule la composante du mouvement qui est perpendiculaire au rayon vecteur est considérée. Dans ce cas,

L = r m v ⊥ , {displaystyle L=rmv_{perp },} ${displaystyle L=rmv_{perp },}$ ${displaystyle L=rmv_{perp },}$

où v ⊥ = v sin ⁡ ( θ ) {displaystyle v_{perp }=vsin(theta )} ${displaystyle v_{perp }=vsin(theta )}$ ${displaystyle v_{perp }=vsin(theta )}$ est la Composante perpendiculaire du mouvement. Expansion, L = r m v sin ⁡ ( θ ) , {displaystyle L=rmvsin(theta ),} réorganiser, L = r sin ⁡ ( θ ) m v , {displaystyle L=rsin(theta )mv,} et en réduisant, le moment cinétique peut également être exprimé,

L = r ⊥ m v , {displaystyle L=r_{perp}mv,} ${displaystyle L=r_{perp }mv,}$ ${displaystyle L=r_{perp}mv,}$

où r ⊥ = r sin ⁡ ( θ ) {displaystyle r_{perp }=rsin(theta )} ${displaystyle r_{perp }=rsin(theta )}$ ${displaystyle r_{perp }=rsin(theta )}$ est la longueur du bras de moment , une ligne tombant perpendiculairement de l’origine sur la trajectoire de la particule. C’est à cette définition, (longueur du bras de moment) × (Moment linéaire) à laquelle se réfère le terme moment de moment . ^[7]

Scalaire – moment angulaire de la mécanique lagrangienne

Une autre approche consiste à définir le moment cinétique comme le Moment conjugué (également appelé moment canonique ) de la coordonnée angulaire φ {displaystylephi} phi exprimé dans le lagrangien du système mécanique. Considérons un système mécanique avec une masse m {displaystyle m} contraint de se déplacer dans un cercle de rayon a {displaystyle a} en l’absence de tout champ de force extérieur. L’énergie cinétique du système est

T = 1 2 m a 2 ω 2 = 1 2 m a 2 φ ̇ 2 . {displaystyle T={frac {1}{2}}ma^{2}omega ^{2}={frac {1}{2}}ma^{2}{dot {phi }} ^{2}.} ${displaystyle T={frac {1}{2}}ma^{2}omega ^{2}={frac {1}{2}}ma^{2}{dot {phi }}^{2}.}$ ${displaystyle T={frac {1}{2}}ma^{2}omega ^{2}={frac {1}{2}}ma^{2}{dot {phi }} ^{2}.}$

Et l’énergie potentielle est

U = 0. {displaystyle U=0.}

Alors le lagrangien est

L ( φ , φ ̇ ) = T − U = 1 2 m a 2 φ ̇ 2 . {displaystyle {mathcal {L}}left(phi ,{dot {phi }}right)=TU={frac {1}{2}}ma^{2}{dot { phi }}^{2}.} ${displaystyle {mathcal {L}}left(phi ,{dot {phi }}right)=T-U={frac {1}{2}}ma^{2}{dot {phi }}^{2}.}$ ${displaystyle {mathcal {L}}left(phi ,{dot {phi }}right)=TU={frac {1}{2}}ma^{2}{dot { phi }}^{2}.}$

La quantité de mouvement généralisée “canoniquement conjuguée à” la coordonnée φ {displaystylephi} phi est défini par

p φ = ∂ L ∂ φ ̇ = m a 2 φ ̇ = I ω = L . {displaystyle p_{phi }={frac {partial {mathcal {L}}}{partial {dot {phi }}}}=ma^{2}{dot {phi }} =Ioméga =L.} ${displaystyle p_{phi }={frac {partial {mathcal {L}}}{partial {dot {phi }}}}=ma^{2}{dot {phi }}=Iomega =L.}$ ${displaystyle p_{phi }={frac {partial {mathcal {L}}}{partial {dot {phi }}}}=ma^{2}{dot {phi }}=Iomega =L.}$

Moment cinétique orbital en trois dimensions

Relation entre les vecteurs force ( F ), couple ( τ ), moment ( p ) et moment cinétique ( L ) dans un système en rotation. r est le vecteur position .

Pour définir complètement le moment cinétique orbital en trois dimensions , il est nécessaire de connaître la vitesse à laquelle le vecteur position balaie l’angle, la direction perpendiculaire au plan instantané de déplacement angulaire et la masse impliquée, ainsi que la façon dont cette masse est répartie. dans l’espace. ^[8] En conservant cette nature vectorielle du moment cinétique, la nature générale des équations est également conservée et peut décrire toute sorte de mouvement tridimensionnel autour du centre de rotation – circulaire , linéaire ou autre. En notation vectorielle , le moment cinétique orbital d’une particule ponctuelleen mouvement autour de l’origine peut s’exprimer par :

L = I ω , {displaystyle mathbf {L} =je{boldsymbol {omega }},} mathbf {L} =I{boldsymbol {omega }},

où

I = r 2 m {displaystyle I=r^{2}m} ${displaystyle I=r^{2}m}$ ${displaystyle I=r^{2}m}$ est le moment d’inertie d’une masse ponctuelle ,
ω = r × v r 2 {displaystyle {boldsymbol {omega }}={frac {mathbf {r} times mathbf {v} }{r^{2}}}} ${boldsymbol {omega }}={frac {mathbf {r} times mathbf {v} }{r^{2}}}$ ${boldsymbol {omega }}={frac {mathbf {r} times mathbf {v} }{r^{2}}}$ est la vitesse angulaire orbitale en radians/sec (unités 1/sec) de la particule autour de l’origine,
r {displaystyle mathbf {r}} est le Vecteur de position de la particule par rapport à l’origine, r = | r | {displaystyle r=leftvert mathbf {r} rightvert } ,
v {displaystyle mathbf {v} } est la vitesse linéaire de la particule par rapport à l’origine, et
m {displaystyle m} est la masse de la particule.

Cela peut être étendu, réduit et, selon les règles de l’ algèbre vectorielle , réorganisé :

L = ( r 2 m ) ( r × v r 2 ) = m ( r × v ) = r × m v = r × p , {displaystyle {begin{aligned}mathbf {L} &=left(r^{2}mright)left({frac {mathbf {r} times mathbf {v} }{r ^{2}}}right)\&=mleft(mathbf {r} times mathbf {v} right)\&=mathbf {r} times mmathbf {v} &=mathbf {r} times mathbf {p} ,end{aligné}}} ${displaystyle {begin{aligned}mathbf {L} &=left(r^{2}mright)left({frac {mathbf {r} times mathbf {v} }{r^{2}}}right)\&=mleft(mathbf {r} times mathbf {v} right)\&=mathbf {r} times mmathbf {v} \&=mathbf {r} times mathbf {p} ,end{aligned}}}$ ${displaystyle {begin{aligned}mathbf {L} &=left(r^{2}mright)left({frac {mathbf {r} times mathbf {v} }{r^{2}}}right)\&=mleft(mathbf {r} times mathbf {v} right)\&=mathbf {r} times mmathbf {v} \&=mathbf {r} times mathbf {p} ,end{aligned}}}$

qui est le produit vectoriel du vecteur position r {displaystyle mathbf {r}} et la quantité de mouvement linéaire p = m v {displaystyle mathbf {p} =mmathbf {v} } {mathbf {p}}=m{mathbf {v}} de la particule. Par la définition du produit vectoriel, le L {displaystyle mathbf {L} } le vecteur est perpendiculaire aux deux r {displaystyle mathbf {r}} et p {displaystyle mathbf {p}} . Il est dirigé perpendiculairement au plan de déplacement angulaire, comme indiqué par la règle de la main droite – de sorte que la vitesse angulaire est vue dans le sens antihoraire à partir de la tête du vecteur. A l’inverse, la L {displaystyle mathbf {L} } vecteur définit le plan dans lequel r {displaystyle mathbf {r}} et p {displaystyle mathbf {p}} mensonge.

En définissant un vecteur unitaire u ^ {displaystyle mathbf {hat {u}} } perpendiculairement au plan de déplacement angulaire, une vitesse angulaire scalaire ω {displaystyle oméga} omega résultats, où

ω u ^ = ω , {displaystyle omega mathbf {hat {u}} ={boldsymbol {omega }},} et ω = v ⊥ r , {displaystyle omega ={frac {v_{perp}}{r}},} ${displaystyle omega ={frac {v_{perp }}{r}},}$ ${displaystyle omega ={frac {v_{perp }}{r}},}$ où v ⊥ {displaystyle v_{perp}} v_perp est la Composante perpendiculaire du mouvement, comme ci-dessus.

Les équations scalaires bidimensionnelles de la section précédente peuvent ainsi être orientées :

L = I ω = I ω u ^ = ( r 2 m ) ω u ^ = r m v ⊥ u ^ = r ⊥ m v u ^ , {displaystyle {begin{aligned}mathbf {L} &=I{boldsymbol {omega }}\&=Iomega mathbf {hat {u}} \&=left(r^ {2}mright)omega mathbf {hat {u}} \&=rmv_{perp }mathbf {hat {u}} \&=r_{perp}mvmathbf { chapeau {u}} ,end{aligned}}} ${displaystyle {begin{aligned}mathbf {L} &=I{boldsymbol {omega }}\&=Iomega mathbf {hat {u}} \&=left(r^{2}mright)omega mathbf {hat {u}} \&=rmv_{perp }mathbf {hat {u}} \&=r_{perp }mvmathbf {hat {u}} ,end{aligned}}}$ ${displaystyle {begin{aligned}mathbf {L} &=I{boldsymbol {omega }}\&=Iomega mathbf {hat {u}} \&=left(r^{2}mright)omega mathbf {hat {u}} \&=rmv_{perp }mathbf {hat {u}} \&=r_{perp }mvmathbf {hat {u}} ,end{aligned}}}$

et L = r m v u ^ {displaystyle mathbf {L} =rmvmathbf {hat {u}} } pour un mouvement circulaire, où tout le mouvement est perpendiculaire au rayon r {displaystyle r} .

Dans le système de coordonnées sphériques, le vecteur de moment cinétique s’exprime par

L = m r × v = m r 2 ( θ ̇ φ ^ − φ ̇ sin ⁡ θ θ ^ ) . {displaystyle mathbf {L} =mmathbf {r} times mathbf {v} =mr^{2}left({dot {theta }},{hat {boldsymbol {varphi }}}-{dot {varphi }}sin theta ,mathbf {hat {boldsymbol {theta }}} right).} ${displaystyle mathbf {L} =mmathbf {r} times mathbf {v} =mr^{2}left({dot {theta }},{hat {boldsymbol {varphi }}}-{dot {varphi }}sin theta ,mathbf {hat {boldsymbol {theta }}} right).}$ ${displaystyle mathbf {L} =mmathbf {r} times mathbf {v} =mr^{2}left({dot {theta }},{hat {boldsymbol {varphi }}}-{dot {varphi }}sin theta ,mathbf {hat {boldsymbol {theta }}} right).}$

Moment angulaire dans n’importe quel nombre de dimensions

Apprendre encore plus Cette section a besoin d’être agrandie . Vous pouvez aider en y ajoutant . ( juin 2021 )

La définition du moment cinétique à l’aide du produit croisé ne s’applique qu’en trois dimensions. Le définir comme le bivecteur L = r ∧ p , où ∧ est le Produit extérieur , est valable dans n’importe quel nombre de dimensions.

Analogie à la quantité de mouvement linéaire

Le moment angulaire peut être décrit comme l’analogue de rotation du Moment linéaire . Comme le Moment linéaire, il implique des éléments de masse et de déplacement . Contrairement à l’élan linéaire, il implique également des éléments de position et de forme .

De nombreux problèmes de physique impliquent de la matière en mouvement autour d’un certain point de l’espace, que ce soit en rotation réelle autour de lui, ou simplement en le dépassant, où l’on souhaite savoir quel effet la matière en mouvement a sur le point – peut-elle exercer de l’énergie sur ou effectuer des travaux à ce sujet? L’énergie , la capacité de faire un travail , peut être stockée dans la matière en la mettant en mouvement, une combinaison de son inertie et de son déplacement. L’inertie est mesurée par sa masse et le déplacement par sa vitesse . Leur produit,

( amount of inertia ) × ( amount of displacement ) = amount of (inertia⋅displacement) mass × velocity = momentum m × v = p {displaystyle {begin{aligned}({text{amount of inertia}})times ({text{amount of displacement}})&={text{amount of (inertia⋅displacement)}}\{text{mass}}times {text{velocity}}&={text{momentum}}\mtimes v&=p\end{aligned}}} ${displaystyle {begin{aligned}({text{amount of inertia}})times ({text{amount of displacement}})&={text{amount of (inertia⋅displacement)}}\{text{mass}}times {text{velocity}}&={text{momentum}}\mtimes v&=p\end{aligned}}}$ ${displaystyle {begin{aligned}({text{amount of inertia}})times ({text{amount of displacement}})&={text{amount of (inertia⋅displacement)}}\{text{mass}}times {text{velocity}}&={text{momentum}}\mtimes v&=p\end{aligned}}}$

est l’ élan de la matière . ^[9] Faire référence à cet élan à un point central introduit une complication : l’élan n’est pas appliqué directement au point. Par exemple, une particule de matière au bord extérieur d’une roue est, en effet, à l’extrémité d’un levier de la même longueur que le rayon de la roue, son élan faisant tourner le levier autour du point central. Ce levier imaginaire est connu sous le nom de bras de moment . Il a pour effet de multiplier l’effort de l’élan proportionnellement à sa longueur, effet connu sous le nom de moment . Par conséquent, la quantité de mouvement de la particule se réfère à un point particulier,

( moment arm ) × ( amount of inertia ) × ( amount of displacement ) = moment of (inertia⋅displacement) length × mass × velocity = moment of momentum r × m × v = L {displaystyle {begin{aligned}({text{moment arm}})times ({text{quantité d’inertie}})times ({text{quantité de déplacement}})&={text {moment de (inertie⋅déplacement)}}\{text{longueur}}times {text{masse}}times {text{vitesse}}&={text{moment d’impulsion}}\ rfois mfois v&=L\end{aligné}}} ${displaystyle {begin{aligned}({text{moment arm}})times ({text{amount of inertia}})times ({text{amount of displacement}})&={text{moment of (inertia⋅displacement)}}\{text{length}}times {text{mass}}times {text{velocity}}&={text{moment of momentum}}\rtimes mtimes v&=L\end{aligned}}}$ ${displaystyle {begin{aligned}({text{moment arm}})times ({text{amount of inertia}})times ({text{amount of displacement}})&={text{moment of (inertia⋅displacement)}}\{text{length}}times {text{mass}}times {text{velocity}}&={text{moment of momentum}}\rtimes mtimes v&=L\end{aligned}}}$

est le moment cinétique , parfois appelé, comme ici, le moment du moment de la particule par rapport à ce point central particulier. L’équation L = r m v {displaystyle L=rmv} L=rmv combine un moment (une masse m {displaystyle m} bras tournant r {displaystyle r} ) avec une vitesse linéaire (équivalent en ligne droite) v {style d’affichage v} . La vitesse linéaire rapportée au point central est simplement le produit de la distance r {displaystyle r} et la vitesse angulaire ω {displaystyle oméga} omega contre le point: v = r ω , {displaystyle v=romega ,} un autre instant. Ainsi, le moment cinétique contient un moment double : L = r m r ω . {displaystyle L=rmroméga .} L=rmromega . En simplifiant un peu, L = r 2 m ω , {displaystyle L=r^{2}momega ,} $L=r^{2}momega ,$ $L=r^{2}momega ,$ la quantité r 2 m {displaystyle r^{2}m} $r^{2}m$ $r^{2}m$ est le moment d’inertie de la particule , parfois appelé deuxième moment de masse. C’est une mesure de l’inertie de rotation. ^[dix]

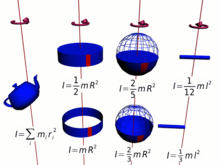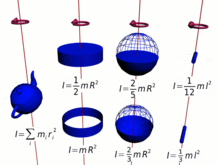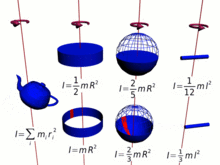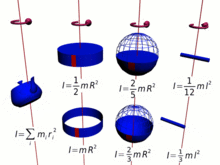
Le moment d’inertie (illustré ici), et donc le moment cinétique, est différent pour chaque configuration possible de masse et d’axe de rotation .

Parce que le moment d’inertie est une partie cruciale du moment cinétique de spin, ce dernier comprend nécessairement toutes les complications du premier, qui est calculé en multipliant les bits élémentaires de la masse par les carrés de leurs Distances au centre de rotation. ^[11] Par conséquent, le moment d’inertie total, et le moment cinétique, est une fonction complexe de la configuration de la matière autour du centre de rotation et de l’orientation de la rotation pour les différents bits.

Pour un corps rigide , par exemple une roue ou un astéroïde, l’orientation de la rotation est simplement la position de l’ axe de rotation par rapport à la matière du corps. Il peut ou non passer par le Centre de masse , ou il peut se trouver complètement à l’extérieur du corps. Pour le même corps, le moment cinétique peut prendre une valeur différente pour chaque axe possible autour duquel la rotation peut avoir lieu. ^[12] Il atteint un minimum lorsque l’axe passe par le Centre de masse. ^[13]

Pour une collection d’objets tournant autour d’un centre, par exemple tous les corps du système solaire , les orientations peuvent être quelque peu organisées, comme c’est le cas du système solaire, la plupart des axes des corps étant proches de l’axe du système. Leurs orientations peuvent aussi être totalement aléatoires.

En bref, plus la masse est importante et plus elle est éloignée du centre de rotation (plus le bras de moment est long ), plus le moment d’inertie est important, et donc plus le moment cinétique est important pour une vitesse angulaire donnée . Dans de nombreux cas, le moment d’inertie , et donc le moment cinétique, peut être simplifié par, ^[14]

I = k 2 m , {displaystyle I=k^{2}m,} $I=k^{2}m,$ $I=k^{2}m,$ où k {displaystyle k} est le rayon de giration , la distance de l’axe à laquelle la masse entière m {displaystyle m} peut être considéré comme concentré.

De même, pour une masse ponctuelle m {displaystyle m} le moment d’inertie est défini comme,

I = r 2 m {displaystyle I=r^{2}m} $I=r^{2}m$ $I=r^{2}m$ où r {displaystyle r} est le rayon de la masse ponctuelle à partir du centre de rotation,

et pour toute collection de particules m i {displaystyle m_{i}} $m_{i}$ $m_{i}$ comme la somme,

∑ i I i = ∑ i r i 2 m i {displaystyle sum _{i}I_{i}=sum _{i}r_{i}^{2}m_{i}} $sum _{i}I_{i}=sum _{i}r_{i}^{2}m_{i}$ $sum _{i}I_{i}=sum _{i}r_{i}^{2}m_{i}$

La dépendance du moment cinétique à la position et à la forme se reflète dans ses unités par rapport au Moment linéaire : kg⋅m ² /s, N⋅m⋅s ou J⋅s pour le moment cinétique contre kg⋅m/s ou N⋅s pour le Moment linéaire. Lors du calcul du moment cinétique comme le produit du moment d’inertie par la vitesse angulaire, la vitesse angulaire doit être exprimée en radians par seconde, où le radian prend la valeur sans dimension de l’unité. (Lors de l’exécution d’une analyse dimensionnelle, il peut être productif d’utiliser une analyse d’orientation qui traite les radians comme une unité de base, mais cela sort du cadre du Système international d’unités ). Les unités du moment cinétique peuvent être interprétées comme un couple⋅temps ou en énergie⋅temps par angle. Un objet avec un moment cinétique de L N⋅m⋅s peut être réduit à une rotation nulle (toute l’énergie de rotation peut en être transférée) par une impulsion angulaire de L N⋅m⋅s ^[15] ou de manière équivalente, par un couple ou travail de L N⋅m pendant une seconde, ou énergie de L J pendant une seconde. ^[16]

Le plan perpendiculaire à l’axe du moment cinétique et passant par le Centre de masse ^[17] est parfois appelé le plan invariable , car la direction de l’axe reste fixe si seulement les interactions des corps au sein du système, libres des influences extérieures, sont considérés. ^[18] Un de ces plans est le plan invariable du système solaire .

Moment angulaire et couple

La deuxième loi du mouvement de Newton peut être exprimée mathématiquement,

F = m a , {displaystyle mathbf {F} =mmathbf {a} ,}

ou force = masse × accélération . L’équivalent rotationnel des particules ponctuelles peut être dérivé comme suit :

L = I ω {displaystyle mathbf {L} =I{boldsymbol {omega}}}

ce qui signifie que le couple (c’est-à-dire la dérivée temporelle du moment cinétique) est

τ = d I d t ω + I d ω d t . {displaystyle {boldsymbol {tau }}={frac {dI}{dt}}{boldsymbol {omega }}+I{frac {d{boldsymbol {omega }}}{dt}} .} ${displaystyle {boldsymbol {tau }}={frac {dI}{dt}}{boldsymbol {omega }}+I{frac {d{boldsymbol {omega }}}{dt}}.}$ ${displaystyle {boldsymbol {tau }}={frac {dI}{dt}}{boldsymbol {omega }}+I{frac {d{boldsymbol {omega }}}{dt}}.}$

Parce que le moment d’inertie est m r 2 {displaystyle monsieur^{2}} $mr^{2}$ $mr^{2}$ , il s’ensuit que d I d t = 2 m r d r d t = 2 r p | | {displaystyle {frac {dI}{dt}}=2mr{frac {dr}{dt}}=2rp_{||}} ${displaystyle {frac {dI}{dt}}=2mr{frac {dr}{dt}}=2rp_{||}}$ ${displaystyle {frac {dI}{dt}}=2mr{frac {dr}{dt}}=2rp_{||}}$ , et d L d t = I d ω d t + 2 r p | | ω , {displaystyle {frac {dmathbf {L} }{dt}}=I{frac {d{boldsymbol {omega }}}{dt}}+2rp_{||}{boldsymbol {omega }},} ${displaystyle {frac {dmathbf {L} }{dt}}=I{frac {d{boldsymbol {omega }}}{dt}}+2rp_{||}{boldsymbol {omega }},}$ ${displaystyle {frac {dmathbf {L} }{dt}}=I{frac {d{boldsymbol {omega }}}{dt}}+2rp_{||}{boldsymbol {omega }},}$ qui, réduit à

τ = I α + 2 r p | | ω . {displaystyle {boldsymbol {tau }}=Je{boldsymbol {alpha }}+2rp_{||}{boldsymbol {omega }}.} ${displaystyle {boldsymbol {tau }}=I{boldsymbol {alpha }}+2rp_{||}{boldsymbol {omega }}.}$ ${displaystyle {boldsymbol {tau }}=I{boldsymbol {alpha }}+2rp_{||}{boldsymbol {omega }}.}$

C’est l’analogue rotationnel de la deuxième loi de Newton. Notez que le couple n’est pas nécessairement proportionnel ou parallèle à l’accélération angulaire (comme on pourrait s’y attendre). La raison en est que le moment d’inertie d’une particule peut changer avec le temps, ce qui ne peut pas se produire pour une masse ordinaire.

Conservation du moment cinétique

Une patineuse artistique en pirouette utilise la conservation du moment cinétique – la diminution de son moment d’inertie en rentrant ses bras et ses jambes augmente sa vitesse de rotation .

Considérations générales

Un analogue rotationnel de la Troisième loi du mouvement de Newton pourrait s’écrire : “Dans un système fermé , aucun couple ne peut être exercé sur une matière sans l’effort sur une autre matière d’un couple égal et opposé.” ^[19] Par conséquent, le moment cinétique peut être échangé entre des objets dans un système fermé, mais le moment cinétique total avant et après un échange reste constant (est conservé). ^[20]

Vu d’une autre manière, un analogue rotationnel de la première loi du mouvement de Newton pourrait s’écrire : “Un corps rigide continue dans un état de rotation uniforme à moins qu’il ne soit agi par une influence extérieure.” ^[19] Ainsi , sans influence externe pour agir sur lui, le moment cinétique d’origine du système reste constant . ^[21]

La conservation du moment cinétique est utilisée dans l’analyse du mouvement de la force centrale . Si la force nette sur un corps est toujours dirigée vers un point, le centre , alors il n’y a pas de couple sur le corps par rapport au centre, car toute la force est dirigée le long du rayon vecteur , et aucune n’est perpendiculaire au rayon . Mathématiquement, le couple τ = r × F = 0 , {displaystyle {boldsymbol {tau }}=mathbf {r} times mathbf {F} =mathbf {0} ,} car dans ce cas r {displaystyle mathbf {r}} et F {displaystyle mathbf {F} } sont des vecteurs parallèles. Par conséquent, le moment cinétique du corps autour du centre est constant. C’est le cas de l’attraction gravitationnelle dans les orbites des planètes et des satellites , où la force gravitationnelle est toujours dirigée vers le corps primaire et les corps en orbite conservent le moment cinétique en échangeant la distance et la vitesse lorsqu’ils se déplacent autour du primaire. Le mouvement de la force centrale est également utilisé dans l’analyse du modèle de Bohr de l’ atome .

Pour une planète, le moment cinétique est réparti entre le spin de la planète et sa révolution sur son orbite, et ceux-ci sont souvent échangés par divers mécanismes. La conservation du moment cinétique dans le système Terre-Lune entraîne le transfert du moment cinétique de la Terre à la Lune, en raison du couple de marée que la Lune exerce sur la Terre. Cela entraîne à son tour un ralentissement du taux de rotation de la Terre, à environ 65,7 nanosecondes par jour, ^[22] et une augmentation progressive du rayon de l’orbite de la Lune, à environ 3,82 centimètres par an. ^[23]

Le couple provoqué par les deux forces opposées F _g et – F _g provoque une modification du moment cinétique L dans la direction de ce couple (puisque le couple est la dérivée temporelle du moment cinétique). Cela provoque la précession du sommet .

La conservation du moment cinétique explique l’accélération angulaire d’une patineuse à glace lorsqu’elle rapproche ses bras et ses jambes de l’axe vertical de rotation. En rapprochant une partie de la masse de son corps de l’axe, elle diminue le moment d’inertie de son corps. Parce que le moment cinétique est le produit du moment d’inertie et de la vitesse angulaire , si le moment cinétique reste constant (est conservé), alors la vitesse angulaire (vitesse de rotation) du patineur doit augmenter.

Le même phénomène entraîne une rotation extrêmement rapide des étoiles compactes (comme les naines blanches , les étoiles à neutrons et les trous noirs ) lorsqu’elles sont formées d’étoiles en rotation beaucoup plus grandes et plus lentes. La diminution de la taille d’un objet n fois entraîne une augmentation de sa vitesse angulaire d’un facteur n ² .

La conservation n’est pas toujours une explication complète de la dynamique d’un système, mais c’est une contrainte clé. Par exemple, une toupie est soumise à un couple gravitationnel qui la fait pencher et modifier le moment cinétique autour de l’ axe de nutation , mais en négligeant le frottement au point de contact en rotation, elle a un moment cinétique conservé autour de son axe de rotation, et un autre autour de son axe de précession . De plus, dans n’importe quel système planétaire , les planètes, les étoiles, les comètes et les astéroïdes peuvent tous se déplacer de nombreuses manières compliquées, mais uniquement pour que le moment cinétique du système soit conservé.

Le théorème de Noether stipule que chaque loi de conservation est associée à une symétrie (invariant) de la physique sous-jacente. La symétrie associée à la conservation du moment cinétique est l’invariance rotationnelle . Le fait que la physique d’un système est inchangée s’il est tourné d’un angle quelconque autour d’un axe implique que le moment cinétique est conservé. ^[24]

Relation avec la deuxième loi du mouvement de Newton

Alors que la conservation totale du moment cinétique peut être comprise séparément des lois du mouvement de Newton comme découlant du théorème de Noether dans les systèmes symétriques sous rotations, elle peut également être comprise simplement comme une méthode efficace de calcul des résultats qui peuvent également être obtenus directement à partir de la seconde de Newton. loi, ainsi que les lois régissant les forces de la nature (telles que la troisième loi de Newton, les équations de Maxwell et la force de Lorentz ). En effet, étant donné les conditions initiales de position et de vitesse pour chaque point, et les forces à une telle condition, on peut utiliser la deuxième loi de Newton pour calculer la dérivée seconde de la position, et la résolution de cela donne des informations complètes sur le développement du système physique avec temps.^[25] Notez, cependant, que ce n’est plus vrai en mécanique quantique , en raison de l’existence du spin des particules , qui est un moment cinétique qui ne peut pas être décrit par l’effet cumulatif des mouvements ponctuels dans l’espace.

Par exemple, considérez la diminution du moment d’inertie , par exemple lorsqu’un patineur artistique tire dans ses mains, accélérant le mouvement circulaire. En termes de conservation du moment cinétique, nous avons, pour le moment cinétique L , le moment d’inertie I et la vitesse angulaire ω :

0 = d L = d ( I ⋅ ω ) = d I ⋅ ω + I ⋅ d ω {displaystyle 0=dL=d(Icdot omega )=dIcdot omega +Icdot domega }

En utilisant cela, nous voyons que le changement nécessite une énergie de :

d E = d ( 1 2 I ⋅ ω 2 ) = 1 2 d I ⋅ ω 2 + I ⋅ ω ⋅ d ω = − 1 2 d I ⋅ ω 2 {displaystyle dE=dleft({frac {1}{2}}Icdot omega ^{2}right)={frac {1}{2}}dIcdot omega ^{2 }+Icdot omega cdot domega =-{frac {1}{2}}dIcdot omega ^{2}} ${displaystyle dE=dleft({frac {1}{2}}Icdot omega ^{2}right)={frac {1}{2}}dIcdot omega ^{2}+Icdot omega cdot domega =-{frac {1}{2}}dIcdot omega ^{2}}$ ${displaystyle dE=dleft({frac {1}{2}}Icdot omega ^{2}right)={frac {1}{2}}dIcdot omega ^{2}+Icdot omega cdot domega =-{frac {1}{2}}dIcdot omega ^{2}}$

de sorte qu’une diminution du moment d’inertie nécessite d’investir de l’énergie.

Cela peut être comparé au travail effectué tel que calculé à l’aide des lois de Newton. Chaque point du corps en rotation accélère, à chaque instant, avec une accélération radiale de :

− r ⋅ ω 2 {displaystyle -rcdot omega ^{2}} ${displaystyle -rcdot omega ^{2}}$ ${displaystyle -rcdot omega ^{2}}$

Observons un point de masse m , dont le vecteur position par rapport au centre du mouvement est parallèle à l’axe z à un instant donné, et est à une distance z . La force centripète sur ce point, gardant le mouvement circulaire, est :

− m ⋅ z ⋅ ω 2 {displaystyle -mcdot zcdot omega ^{2}} ${displaystyle -mcdot zcdot omega ^{2}}$ ${displaystyle -mcdot zcdot omega ^{2}}$

Ainsi le travail nécessaire pour déplacer ce point à une distance dz plus éloignée du centre du mouvement est :

d W = − m ⋅ z ⋅ ω 2 ⋅ d z = − m ⋅ ω 2 ⋅ d ( 1 2 z 2 ) {displaystyle dW=-mcdot zcdot omega ^{2}cdot dz=-mcdot omega ^{2}cdot dleft({frac {1}{2}}z^ {2}droite)} ${displaystyle dW=-mcdot zcdot omega ^{2}cdot dz=-mcdot omega ^{2}cdot dleft({frac {1}{2}}z^{2}right)}$ ${displaystyle dW=-mcdot zcdot omega ^{2}cdot dz=-mcdot omega ^{2}cdot dleft({frac {1}{2}}z^{2}right)}$

Pour un corps non ponctuel, il faut intégrer par-dessus cela, avec m remplacé par la densité de masse par unité z . Cela donne:

d W = − 1 2 d I ⋅ ω 2 {displaystyle dW=-{frac {1}{2}}dIcdot omega ^{2}} ${displaystyle dW=-{frac {1}{2}}dIcdot omega ^{2}}$ ${displaystyle dW=-{frac {1}{2}}dIcdot omega ^{2}}$

qui est exactement l’énergie nécessaire pour conserver le moment cinétique conservé.

Notez que le calcul ci-dessus peut également être effectué par masse, en utilisant uniquement la cinématique . Ainsi, les phénomènes du patineur artistique accélérant la vitesse tangentielle tout en rentrant ses mains peuvent être compris comme suit en langage profane : les paumes du patineur ne se déplacent pas en ligne droite, elles accélèrent donc constamment vers l’intérieur, mais ne gagnent pas de vitesse supplémentaire car l’accélération se fait toujours lorsque leur mouvement vers l’intérieur est nul. Cependant, c’est différent en rapprochant les paumes du corps : l’accélération due à la rotation augmente maintenant la vitesse ; mais du fait de la rotation, l’augmentation de vitesse ne se traduit pas par une vitesse significative vers l’intérieur, mais par une augmentation de la vitesse de rotation.

Dans le formalisme lagrangien

En mécanique lagrangienne , le moment cinétique de rotation autour d’un axe donné est le Moment conjugué de la Coordonnée généralisée de l’angle autour du même axe. Par example, L z {displaystyle L_{z}} $L_{z}$ $L_{z}$ , le moment cinétique autour de l’axe z, est :

L z = ∂ L ∂ θ ̇ z {displaystyle L_{z}={frac {partial {cal {L}}}{partial {dot {theta}}_{z}}}} ${displaystyle L_{z}={frac {partial {cal {L}}}{partial {dot {theta }}_{z}}}}$ ${displaystyle L_{z}={frac {partial {cal {L}}}{partial {dot {theta }}_{z}}}}$

où L {displaystyle {cal {L}}} est le lagrangien et θ z {displaystyle thêta _{z}} ${displaystyle theta _{z}}$ ${displaystyle theta _{z}}$ est l’angle autour de l’axe z.

Noter que θ ̇ z {displaystyle {point {thêta}}_{z}} ${displaystyle {dot {theta }}_{z}}$ ${displaystyle {dot {theta }}_{z}}$ , la dérivée temporelle de l’angle, est la vitesse angulaire ω z {displaystyle oméga _{z}} $omega _{z}$ $omega _{z}$ . Ordinairement, le lagrangien dépend de la vitesse angulaire passant par l’énergie cinétique : cette dernière s’écrit en séparant la vitesse de sa partie radiale et tangentielle, la partie tangentielle au plan xy, autour de l’axe z, étant égale à :

∑ i 1 2 m i v T i 2 = ∑ i 1 2 m i ( x i 2 + y i 2 ) ω z i 2 {displaystyle sum _{i}{frac {1}{2}}m_{i}{v_{T}}_{i}^{2}=sum _{i}{frac {1} {2}}m_{i}(x_{i}^{2}+y_{i}^{2}){{omega _{z}}_{i}}^{2}} ${displaystyle sum _{i}{frac {1}{2}}m_{i}{v_{T}}_{i}^{2}=sum _{i}{frac {1}{2}}m_{i}(x_{i}^{2}+y_{i}^{2}){{omega _{z}}_{i}}^{2}}$ ${displaystyle sum _{i}{frac {1}{2}}m_{i}{v_{T}}_{i}^{2}=sum _{i}{frac {1}{2}}m_{i}(x_{i}^{2}+y_{i}^{2}){{omega _{z}}_{i}}^{2}}$

où l’indice i représente le i-ème corps, et m , v _T et ω _z représentent respectivement la masse, la vitesse tangentielle autour de l’axe z et la vitesse angulaire autour de cet axe.

Pour un corps non ponctuel, de densité ρ , on a plutôt :

1 2 ∫ ρ ( x , y , z ) ( x i 2 + y i 2 ) ω z i 2 d x d y = 1 2 I z i ω z i 2 {displaystyle {frac {1}{2}}int rho (x,y,z)(x_{i}^{2}+y_{i}^{2}){{omega _{z }}_{i}}^{2},dx,dy={frac {1}{2}}{I_{z}}_{i}{{omega _{z}}_{i }}^{2}} ${displaystyle {frac {1}{2}}int rho (x,y,z)(x_{i}^{2}+y_{i}^{2}){{omega _{z}}_{i}}^{2},dx,dy={frac {1}{2}}{I_{z}}_{i}{{omega _{z}}_{i}}^{2}}$ ${displaystyle {frac {1}{2}}int rho (x,y,z)(x_{i}^{2}+y_{i}^{2}){{omega _{z}}_{i}}^{2},dx,dy={frac {1}{2}}{I_{z}}_{i}{{omega _{z}}_{i}}^{2}}$

où l’intégration s’étend sur la surface du corps, ^[26] et I _z est le moment d’inertie autour de l’axe z.

Ainsi, en supposant que l’énergie potentielle ne dépend pas de ω _z (cette hypothèse peut échouer pour les systèmes électromagnétiques), nous avons le moment cinétique du i-ème objet :

L z i = ∂ L ∂ ω z i = ∂ E k ∂ ω z i = I z i ⋅ ω z i {displaystyle {begin{aligned}{L_{z}}_{i}&={frac {partial {cal {L}}}{partial {{omega _{z}}_{i }}}}={frac {partial E_{k}}{partial {{omega _{z}}_{i}}}}\&={I_{z}}_{i} cdot {omega _{z}}_{i}end{aligned}}} ${displaystyle {begin{aligned}{L_{z}}_{i}&={frac {partial {cal {L}}}{partial {{omega _{z}}_{i}}}}={frac {partial E_{k}}{partial {{omega _{z}}_{i}}}}\&={I_{z}}_{i}cdot {omega _{z}}_{i}end{aligned}}}$ ${displaystyle {begin{aligned}{L_{z}}_{i}&={frac {partial {cal {L}}}{partial {{omega _{z}}_{i}}}}={frac {partial E_{k}}{partial {{omega _{z}}_{i}}}}\&={I_{z}}_{i}cdot {omega _{z}}_{i}end{aligned}}}$

Nous avons jusqu’ici fait pivoter chaque objet d’un angle distinct ; nous pouvons également définir un angle global θ _z par lequel nous faisons tourner l’ensemble du système, faisant ainsi tourner également chaque objet autour de l’axe z, et avoir le moment cinétique global :

L z = ∑ i I z i ⋅ ω z i {displaystyle L_{z}=sum _{i}{I_{z}}_{i}cdot {omega _{z}}_{i}} ${displaystyle L_{z}=sum _{i}{I_{z}}_{i}cdot {omega _{z}}_{i}}$ ${displaystyle L_{z}=sum _{i}{I_{z}}_{i}cdot {omega _{z}}_{i}}$

Des Équations d’Euler-Lagrange, il s’ensuit alors que :

0 = ∂ L ∂ θ z i − d d t ( ∂ L ∂ θ ̇ z i ) = ∂ L ∂ θ z i − d L z i d t {displaystyle 0={frac {partial {cal {L}}}{partial {{theta _{z}}_{i}}}}-{frac {d}{dt}} left({frac {partial {cal {L}}}{partial {{{dot {theta }}_{z}}_{i}}}}right)={frac { partiel {cal {L}}}{partial {{theta _{z}}_{i}}}}-{frac {d{L_{z}}_{i}}{dt}}} ${displaystyle 0={frac {partial {cal {L}}}{partial {{theta _{z}}_{i}}}}-{frac {d}{dt}}left({frac {partial {cal {L}}}{partial {{{dot {theta }}_{z}}_{i}}}}right)={frac {partial {cal {L}}}{partial {{theta _{z}}_{i}}}}-{frac {d{L_{z}}_{i}}{dt}}}$ ${displaystyle 0={frac {partial {cal {L}}}{partial {{theta _{z}}_{i}}}}-{frac {d}{dt}}left({frac {partial {cal {L}}}{partial {{{dot {theta }}_{z}}_{i}}}}right)={frac {partial {cal {L}}}{partial {{theta _{z}}_{i}}}}-{frac {d{L_{z}}_{i}}{dt}}}$

Puisque le lagrangien ne dépend des angles de l’objet que par le potentiel, nous avons :

d L z i d t = ∂ L ∂ θ z i = − ∂ V ∂ θ z je {displaystyle {frac {d{L_{z}}_{i}}{dt}}={frac {partial {cal {L}}}{partial {{theta _{z}} _{i}}}}=-{frac {partial V}{partial {{theta _{z}}_{i}}}}} ${displaystyle {frac {d{L_{z}}_{i}}{dt}}={frac {partial {cal {L}}}{partial {{theta _{z}}_{i}}}}=-{frac {partial V}{partial {{theta _{z}}_{i}}}}}$ ${displaystyle {frac {d{L_{z}}_{i}}{dt}}={frac {partial {cal {L}}}{partial {{theta _{z}}_{i}}}}=-{frac {partial V}{partial {{theta _{z}}_{i}}}}}$

qui est le couple sur le i-ème objet.

Supposons que le système soit invariant aux rotations, de sorte que le potentiel soit indépendant d’une rotation globale d’angle θ _z (il ne peut donc dépendre des angles des objets que par leurs différences, sous la forme V ( θ z i , θ z j ) = V ( θ z je − θ z j ) {displaystyle V({theta _{z}}_{i},{theta _{z}}_{j})=V({theta _{z}}_{i}-{theta _{z}}_{j})} ${displaystyle V({theta _{z}}_{i},{theta _{z}}_{j})=V({theta _{z}}_{i}-{theta _{z}}_{j})}$ ${displaystyle V({theta _{z}}_{i},{theta _{z}}_{j})=V({theta _{z}}_{i}-{theta _{z}}_{j})}$ ). On obtient donc pour le moment cinétique total :

ré L z d t = − ∂ V ∂ θ z = 0 {displaystyle {frac {dL_{z}}{dt}}=-{frac {partial V}{partial {theta _{z}}}}=0} ${displaystyle {frac {dL_{z}}{dt}}=-{frac {partial V}{partial {theta _{z}}}}=0}$ ${displaystyle {frac {dL_{z}}{dt}}=-{frac {partial V}{partial {theta _{z}}}}=0}$

Et ainsi le moment cinétique autour de l’axe z est conservé.

Cette analyse peut être répétée séparément pour chaque axe, donnant la conversation du vecteur de moment cinétique. Cependant, les angles autour des trois axes ne peuvent pas être traités simultanément comme des coordonnées généralisées, car ils ne sont pas indépendants ; en particulier, deux angles par point suffisent pour déterminer sa position. S’il est vrai que dans le cas d’un corps rigide, sa description complète nécessite, en plus de trois degrés de liberté en translation , également la spécification de trois degrés de liberté en rotation ; cependant ceux-ci ne peuvent pas être définis comme des rotations autour des axes cartésiens (voir angles d’Euler ). Cette mise en garde se reflète en mécanique quantique dans les relations de commutation non triviales des différents composants duopérateur moment cinétique .

Dans le formalisme hamiltonien

De manière équivalente, en mécanique hamiltonienne, l’hamiltonien peut être décrit en fonction du moment cinétique. Comme précédemment, la partie de l’énergie cinétique liée à la rotation autour de l’axe z pour le i-ème objet est :

1 2 I z i ω z i 2 = L z i 2 2 I z i {displaystyle {frac {1}{2}}{I_{z}}_{i}{{omega _{z}}_{i}}^{2}={frac {{{L_{ z}}_{i}}^{2}}{2{I_{z}}_{i}}}} ${displaystyle {frac {1}{2}}{I_{z}}_{i}{{omega _{z}}_{i}}^{2}={frac {{{L_{z}}_{i}}^{2}}{2{I_{z}}_{i}}}}$ ${displaystyle {frac {1}{2}}{I_{z}}_{i}{{omega _{z}}_{i}}^{2}={frac {{{L_{z}}_{i}}^{2}}{2{I_{z}}_{i}}}}$

qui est analogue à la dépendance énergétique de la quantité de mouvement le long de l’axe z, p z i 2 2 m i {displaystyle {frac {{{p_{z}}_{i}}^{2}}{{2m}_{i}}}} ${displaystyle {frac {{{p_{z}}_{i}}^{2}}{{2m}_{i}}}}$ ${displaystyle {frac {{{p_{z}}_{i}}^{2}}{{2m}_{i}}}}$ .

Les équations de Hamilton relient l’angle autour de l’axe z à son Moment conjugué, le moment cinétique autour du même axe :

d θ z i d t = ∂ H ∂ L z i = L z i I z i d L z i d t = − ∂ H ∂ θ z i = − ∂ V ∂ θ z i {displaystyle {begin{aligned}{frac {d{theta _{z}}_{i}}{dt}}&={frac {partial {cal {H}}}{partial {L_{z}}_{i}}}={frac {{L_{z}}_{i}}{{I_{z}}_{i}}}\{frac {d{L_ {z}}_{i}}{dt}}&=-{frac {partial {cal {H}}}{partial {theta _{z}}_{i}}}=-{ frac {partial V}{partial {theta _{z}}_{i}}}end{aligned}}} ${displaystyle {begin{aligned}{frac {d{theta _{z}}_{i}}{dt}}&={frac {partial {cal {H}}}{partial {L_{z}}_{i}}}={frac {{L_{z}}_{i}}{{I_{z}}_{i}}}\{frac {d{L_{z}}_{i}}{dt}}&=-{frac {partial {cal {H}}}{partial {theta _{z}}_{i}}}=-{frac {partial V}{partial {theta _{z}}_{i}}}end{aligned}}}$ ${displaystyle {begin{aligned}{frac {d{theta _{z}}_{i}}{dt}}&={frac {partial {cal {H}}}{partial {L_{z}}_{i}}}={frac {{L_{z}}_{i}}{{I_{z}}_{i}}}\{frac {d{L_{z}}_{i}}{dt}}&=-{frac {partial {cal {H}}}{partial {theta _{z}}_{i}}}=-{frac {partial V}{partial {theta _{z}}_{i}}}end{aligned}}}$

La première équation donne

L z i = I z i ⋅ θ ̇ z i = I z i ⋅ ω z i {displaystyle {L_{z}}_{i}={I_{z}}_{i}cdot {{{dot {theta}}_{z}}_{i}}={I_{ z}}_{i}cdot {omega _{z}}_{i}} ${displaystyle {L_{z}}_{i}={I_{z}}_{i}cdot {{{dot {theta }}_{z}}_{i}}={I_{z}}_{i}cdot {omega _{z}}_{i}}$ ${displaystyle {L_{z}}_{i}={I_{z}}_{i}cdot {{{dot {theta }}_{z}}_{i}}={I_{z}}_{i}cdot {omega _{z}}_{i}}$

On obtient ainsi les mêmes résultats que dans le formalisme lagrangien.

Notez que pour combiner tous les axes ensemble, nous écrivons l’énergie cinétique comme suit :

E k = 1 2 ∑ i | p i | 2 2 m i = ∑ i ( p r i 2 2 m i + 1 2 L i T I i − 1 L i ) {displaystyle E_{k}={frac {1}{2}}sum _{i}{frac {|{bf {{p}_{i}|^{2}}}}{2m_ {i}}}=sum _{i}left({frac {{{p_{r}}_{i}}^{2}}{2m_{i}}}+{frac {1} {2}}{bf {{L}_{i}}}^{textsf {T}}{I_{i}}^{-1}{bf {{L}_{i}}} à droite)} ${displaystyle E_{k}={frac {1}{2}}sum _{i}{frac {|{bf {{p}_{i}|^{2}}}}{2m_{i}}}=sum _{i}left({frac {{{p_{r}}_{i}}^{2}}{2m_{i}}}+{frac {1}{2}}{bf {{L}_{i}}}^{textsf {T}}{I_{i}}^{-1}{bf {{L}_{i}}}right)}$ ${displaystyle E_{k}={frac {1}{2}}sum _{i}{frac {|{bf {{p}_{i}|^{2}}}}{2m_{i}}}=sum _{i}left({frac {{{p_{r}}_{i}}^{2}}{2m_{i}}}+{frac {1}{2}}{bf {{L}_{i}}}^{textsf {T}}{I_{i}}^{-1}{bf {{L}_{i}}}right)}$

où p _r est la quantité de mouvement dans la direction radiale et le moment d’inertie est une matrice tridimensionnelle ; les lettres en gras représentent des vecteurs tridimensionnels.

Learn more.

Accélération

Jul 6, 2022

Potentiel électrique

Jun 28, 2022

Dipôle

Jun 22, 2022

Quaternion

May 25, 2022

Pour les corps ponctuels, nous avons :

E k = ∑ i ( p r i 2 2 m i + | L i | 2 2 m i r i 2 ) {displaystyle E_{k}=sum _{i}left({frac {{{p_{r}}_{i}}^{2}}{2m_{i}}}+{frac { |{bf {{L}_{i}}}|^{2}}{2m_{i}{r_{i}}^{2}}}right)} ${displaystyle E_{k}=sum _{i}left({frac {{{p_{r}}_{i}}^{2}}{2m_{i}}}+{frac {|{bf {{L}_{i}}}|^{2}}{2m_{i}{r_{i}}^{2}}}right)}$ ${displaystyle E_{k}=sum _{i}left({frac {{{p_{r}}_{i}}^{2}}{2m_{i}}}+{frac {|{bf {{L}_{i}}}|^{2}}{2m_{i}{r_{i}}^{2}}}right)}$

Cette forme de la partie énergie cinétique de l’hamiltonien est utile pour analyser les problèmes de potentiel central et est facilement transformée en un cadre de travail mécanique quantique (par exemple dans le problème de l’ atome d’hydrogène ).

Moment angulaire en mécanique orbitale

Alors qu’en mécanique classique, le langage du moment cinétique peut être remplacé par les lois du mouvement de Newton, il est particulièrement utile pour le mouvement au potentiel central tel que le mouvement planétaire dans le système solaire. Ainsi, l’orbite d’une planète dans le système solaire est définie par son énergie, son moment cinétique et les angles du grand axe de l’orbite par rapport à un cadre de coordonnées.

En astrodynamique et en mécanique céleste , une quantité étroitement liée au moment cinétique est définie comme ^[27]

h = r × v , {displaystyle mathbf {h} =mathbf {r} times mathbf {v} ,}

appelé moment cinétique spécifique . Noter que L = m h . {displaystyle mathbf {L} =mmathbf {h} .} La masse est souvent sans importance dans les calculs de mécanique orbitale, car le mouvement d’un corps est déterminé par la gravité . Le corps principal du système est souvent tellement plus grand que tous les corps en mouvement autour de lui que l’effet gravitationnel des corps plus petits sur lui peut être négligé; il maintient, en effet, une vitesse constante. Le mouvement de tous les corps est affecté par sa gravité de la même manière, quelle que soit la masse, et donc tous se déplacent approximativement de la même manière dans les mêmes conditions.

Corps solides

Le moment cinétique est également un concept extrêmement utile pour décrire des corps rigides en rotation tels qu’un gyroscope ou une planète rocheuse. Pour une distribution de masse continue avec une fonction de densité ρ ( r ), un élément de volume différentiel dV avec un Vecteur de position r dans la masse a un élément de masse dm = ρ ( r ) dV . Par conséquent, le moment cinétique infinitésimal de cet élément est :

d L = r × d m v = r × ρ ( r ) d V v = d V r × ρ ( r ) v {displaystyle dmathbf {L} =mathbf {r} times dmmathbf {v} =mathbf {r} times rho (mathbf {r} )dVmathbf {v} =dVmathbf {r} times rho (mathbf {r} )mathbf {v} }

et l’ intégration de ce différentiel sur le volume de la masse entière donne son moment cinétique total :

L = ∫ V d V r × ρ ( r ) v {displaystyle mathbf {L} =int _{V}dVmathbf {r} times rho (mathbf {r} )mathbf {v} } $mathbf {L} =int _{V}dVmathbf {r} times rho (mathbf {r} )mathbf {v}$ $mathbf {L} =int _{V}dVmathbf {r} times rho (mathbf {r} )mathbf {v}$

Dans la dérivation qui suit, des intégrales similaires à celle-ci peuvent remplacer les sommes pour le cas de la masse continue.

Collecte de particules

Le moment cinétique des particules i est la somme des produits croisés R × M V + Σ r _i × m _i v _i .

Pour une collection de particules en mouvement autour d’une origine arbitraire, il est instructif de développer l’équation du moment cinétique en résolvant leur mouvement en composants autour de leur propre Centre de masse et autour de l’origine. Donné,

m i {displaystyle m_{i}} $m_{i}$ $m_{i}$ est la masse de la particule i {displaystyle i} ,
R i {displaystyle mathbf {R} _{i}} $mathbf {R} _{i}$ $mathbf {R} _{i}$ est le vecteur position de la particule i {displaystyle i} contre l’origine,
V i {displaystyle mathbf {V} _{i}} $mathbf {V} _{i}$ $mathbf {V} _{i}$ est la vitesse de la particule i {displaystyle i} contre l’origine,
R {displaystyle mathbf {R} } est le Vecteur de position du Centre de masse par rapport à l’origine,
V {displaystyle mathbf {V} } est la vitesse du Centre de masse par rapport à l’origine,
r i {displaystyle mathbf {r} _{i}} $mathbf {r} _{i}$ $mathbf {r} _{i}$ est le vecteur position de la particule i {displaystyle i} vs le Centre de masse,
v i {displaystyle mathbf {v} _{i}} $mathbf {v} _{i}$ $mathbf {v} _{i}$ est la vitesse de la particule i {displaystyle i} vs le Centre de masse,

La masse totale des particules est simplement leur somme,

M = ∑ i m i . {displaystyle M=sum _{i}m_{i}.} $M=sum _{i}m_{i}.$ $M=sum _{i}m_{i}.$

Le vecteur position du Centre de masse est défini par, ^[28]

M R = ∑ i m i R i . {displaystyle Mmathbf {R} =sum _{i}m_{i}mathbf {R} _{i}.} $Mmathbf {R} =sum _{i}m_{i}mathbf {R} _{i}.$ $Mmathbf {R} =sum _{i}m_{i}mathbf {R} _{i}.$

Par inspection,

R i = R + r i {displaystyle mathbf {R} _{i}=mathbf {R} +mathbf {r} _{i}} $mathbf {R} _{i}=mathbf {R} +mathbf {r} _{i}$ $mathbf {R} _{i}=mathbf {R} +mathbf {r} _{i}$ et V i = V + v i . {displaystyle mathbf {V} _{i}=mathbf {V} +mathbf {v} _{i}.} $mathbf {V} _{i}=mathbf {V} +mathbf {v} _{i}.$ $mathbf {V} _{i}=mathbf {V} +mathbf {v} _{i}.$

Le moment cinétique total de la collection de particules est la somme du moment cinétique de chaque particule,

L = ∑ i ( R i × m i V i ) {displaystyle mathbf {L} =sum _{i}left(mathbf {R} _{i}times m_{i}mathbf {V} _{i}right)} ${displaystyle mathbf {L} =sum _{i}left(mathbf {R} _{i}times m_{i}mathbf {V} _{i}right)}$ ${displaystyle mathbf {L} =sum _{i}left(mathbf {R} _{i}times m_{i}mathbf {V} _{i}right)}$ ( 1 )

Expansion R i {displaystyle mathbf {R} _{i}} $mathbf {R} _{i}$ $mathbf {R} _{i}$ ,

L = ∑ i [ ( R + r i ) × m i V i ] = ∑ i [ R × m i V i + r i × m i V i ] {displaystyle {begin{aligned}mathbf {L} &=sum _{i}left[left(mathbf {R} +mathbf {r} _{i}right)times m_{ i}mathbf {V} _{i}right]\&=sum _{i}left[mathbf {R} times m_{i}mathbf {V} _{i}+mathbf {r} _{i}times m_{i}mathbf {V} _{i}right]end{aligned}}} ${displaystyle {begin{aligned}mathbf {L} &=sum _{i}left[left(mathbf {R} +mathbf {r} _{i}right)times m_{i}mathbf {V} _{i}right]\&=sum _{i}left[mathbf {R} times m_{i}mathbf {V} _{i}+mathbf {r} _{i}times m_{i}mathbf {V} _{i}right]end{aligned}}}$ ${displaystyle {begin{aligned}mathbf {L} &=sum _{i}left[left(mathbf {R} +mathbf {r} _{i}right)times m_{i}mathbf {V} _{i}right]\&=sum _{i}left[mathbf {R} times m_{i}mathbf {V} _{i}+mathbf {r} _{i}times m_{i}mathbf {V} _{i}right]end{aligned}}}$

Expansion V i {displaystyle mathbf {V} _{i}} $mathbf {V} _{i}$ $mathbf {V} _{i}$ ,

L = ∑ i [ R × m i ( V + v i ) + r i × m i ( V + v i ) ] = ∑ i [ R × m je V + R × m je v je + r je × m je V + r i × m i v i ] = ∑ i R × m i V + ∑ i R × m i v i + ∑ i r i × m i V + ∑ i r i × m i v i {displaystyle {begin{aligned}mathbf {L} &=sum _{i}left[mathbf {R} times m_{i}left(mathbf {V} +mathbf {v} _{i}right)+mathbf {r} _{i}times m_{i}(mathbf {V} +mathbf {v} _{i})right]\&=sum _ {i}left[mathbf {R} times m_{i}mathbf {V} +mathbf {R} times m_{i}mathbf {v} _{i}+mathbf {r} _ {i}times m_{i}mathbf {V} +mathbf {r} _{i}times m_{i}mathbf {v} _{i}right]\&=sum _{ je}mathbf {R} times m_{i}mathbf {V} +sum _{i}mathbf {R} times m_{i}mathbf {v} _{i}+sum _{ je}mathbf {r} _{i}times m_{i}mathbf {V} +sum _{i}mathbf {r} _{i}times m_{i}mathbf {v} _ {i}end{aligné}}} ${displaystyle {begin{aligned}mathbf {L} &=sum _{i}left[mathbf {R} times m_{i}left(mathbf {V} +mathbf {v} _{i}right)+mathbf {r} _{i}times m_{i}(mathbf {V} +mathbf {v} _{i})right]\&=sum _{i}left[mathbf {R} times m_{i}mathbf {V} +mathbf {R} times m_{i}mathbf {v} _{i}+mathbf {r} _{i}times m_{i}mathbf {V} +mathbf {r} _{i}times m_{i}mathbf {v} _{i}right]\&=sum _{i}mathbf {R} times m_{i}mathbf {V} +sum _{i}mathbf {R} times m_{i}mathbf {v} _{i}+sum _{i}mathbf {r} _{i}times m_{i}mathbf {V} +sum _{i}mathbf {r} _{i}times m_{i}mathbf {v} _{i}end{aligned}}}$ ${displaystyle {begin{aligned}mathbf {L} &=sum _{i}left[mathbf {R} times m_{i}left(mathbf {V} +mathbf {v} _{i}right)+mathbf {r} _{i}times m_{i}(mathbf {V} +mathbf {v} _{i})right]\&=sum _{i}left[mathbf {R} times m_{i}mathbf {V} +mathbf {R} times m_{i}mathbf {v} _{i}+mathbf {r} _{i}times m_{i}mathbf {V} +mathbf {r} _{i}times m_{i}mathbf {v} _{i}right]\&=sum _{i}mathbf {R} times m_{i}mathbf {V} +sum _{i}mathbf {R} times m_{i}mathbf {v} _{i}+sum _{i}mathbf {r} _{i}times m_{i}mathbf {V} +sum _{i}mathbf {r} _{i}times m_{i}mathbf {v} _{i}end{aligned}}}$

On peut montrer que (voir encadré),

Prouve-le ∑ i m i r i = 0 {displaystyle sum _{i}m_{i}mathbf {r} _{i}=mathbf {0} } $sum _{i}m_{i}mathbf {r} _{i}=mathbf {0}$ $sum _{i}m_{i}mathbf {r} _{i}=mathbf {0}$

r i = R i − R m i r i = m i ( R i − R ) ∑ i m i r i = ∑ i m i ( R i − R ) = ∑ i ( m i R i − m i R ) = ∑ i m i R i − ∑ i m i R = ∑ i m i R i − ( ∑ i m i ) R = ∑ i m i R i − M R {displaystyle {begin{aligned}mathbf {r} _{i}&=mathbf {R} _{i}-mathbf {R} \m_{i}mathbf {r} _{i} &=m_{i}left(mathbf {R} _{i}-mathbf {R} right)\sum _{i}m_{i}mathbf {r} _{i}&= sum _{i}m_{i}left(mathbf {R} _{i}-mathbf {R} right)\&=sum _{i}(m_{i}mathbf {R } _{i}-m_{i}mathbf {R} )\&=sum _{i}m_{i}mathbf {R} _{i}-sum _{i}m_{i} mathbf {R} \&=sum _{i}m_{i}mathbf {R} _{i}-left(sum _{i}m_{i}right)mathbf {R} \&=sum _{i}m_{i}mathbf {R} _{i}-Mmathbf {R} end{aligné}}} ${displaystyle {begin{aligned}mathbf {r} _{i}&=mathbf {R} _{i}-mathbf {R} \m_{i}mathbf {r} _{i}&=m_{i}left(mathbf {R} _{i}-mathbf {R} right)\sum _{i}m_{i}mathbf {r} _{i}&=sum _{i}m_{i}left(mathbf {R} _{i}-mathbf {R} right)\&=sum _{i}(m_{i}mathbf {R} _{i}-m_{i}mathbf {R} )\&=sum _{i}m_{i}mathbf {R} _{i}-sum _{i}m_{i}mathbf {R} \&=sum _{i}m_{i}mathbf {R} _{i}-left(sum _{i}m_{i}right)mathbf {R} \&=sum _{i}m_{i}mathbf {R} _{i}-Mmathbf {R} end{aligned}}}$ ${displaystyle {begin{aligned}mathbf {r} _{i}&=mathbf {R} _{i}-mathbf {R} \m_{i}mathbf {r} _{i}&=m_{i}left(mathbf {R} _{i}-mathbf {R} right)\sum _{i}m_{i}mathbf {r} _{i}&=sum _{i}m_{i}left(mathbf {R} _{i}-mathbf {R} right)\&=sum _{i}(m_{i}mathbf {R} _{i}-m_{i}mathbf {R} )\&=sum _{i}m_{i}mathbf {R} _{i}-sum _{i}m_{i}mathbf {R} \&=sum _{i}m_{i}mathbf {R} _{i}-left(sum _{i}m_{i}right)mathbf {R} \&=sum _{i}m_{i}mathbf {R} _{i}-Mmathbf {R} end{aligned}}}$

qui, par définition du Centre de masse, est 0 , {displaystyle mathbf {0} ,} et de même pour ∑ i m i v i . {displaystyle sum _{i}m_{i}mathbf {v} _{i}.} $sum _{i}m_{i}mathbf {v} _{i}.$ $sum _{i}m_{i}mathbf {v} _{i}.$

∑ i m i r i = 0 {displaystyle sum _{i}m_{i}mathbf {r} _{i}=mathbf {0} } $sum _{i}m_{i}mathbf {r} _{i}=mathbf {0}$ $sum _{i}m_{i}mathbf {r} _{i}=mathbf {0}$ et ∑ i m i v i = 0 , {displaystyle sum _{i}m_{i}mathbf {v} _{i}=mathbf {0} ,} ${displaystyle sum _{i}m_{i}mathbf {v} _{i}=mathbf {0} ,}$ ${displaystyle sum _{i}m_{i}mathbf {v} _{i}=mathbf {0} ,}$

donc les deuxième et troisième termes disparaissent,

L = ∑ i R × m i V + ∑ i r i × m i v i . {displaystyle mathbf {L} =sum _{i}mathbf {R} times m_{i}mathbf {V} +sum _{i}mathbf {r} _{i}times m_ {i}mathbf {v} _{i}.} $mathbf {L} =sum _{i}mathbf {R} times m_{i}mathbf {V} +sum _{i}mathbf {r} _{i}times m_{i}mathbf {v} _{i}.$ $mathbf {L} =sum _{i}mathbf {R} times m_{i}mathbf {V} +sum _{i}mathbf {r} _{i}times m_{i}mathbf {v} _{i}.$

Le premier terme peut être réorganisé,

∑ i R × m i V = R × ∑ i m i V = R × M V , {displaystyle sum _{i}mathbf {R} times m_{i}mathbf {V} =mathbf {R} times sum _{i}m_{i}mathbf {V} = mathbf {R} times Mmathbf {V} ,} $sum _{i}mathbf {R} times m_{i}mathbf {V} =mathbf {R} times sum _{i}m_{i}mathbf {V} =mathbf {R} times Mmathbf {V} ,$ $sum _{i}mathbf {R} times m_{i}mathbf {V} =mathbf {R} times sum _{i}m_{i}mathbf {V} =mathbf {R} times Mmathbf {V} ,$

et le moment cinétique total pour la collection de particules est finalement, ^[29]

L = R × M V + ∑ i r i × m i v i {displaystyle mathbf {L} =mathbf {R} times Mmathbf {V} +sum _{i}mathbf {r} _{i}times m_{i}mathbf {v} _ {je}} ${displaystyle mathbf {L} =mathbf {R} times Mmathbf {V} +sum _{i}mathbf {r} _{i}times m_{i}mathbf {v} _{i}}$ ${displaystyle mathbf {L} =mathbf {R} times Mmathbf {V} +sum _{i}mathbf {r} _{i}times m_{i}mathbf {v} _{i}}$ ( 2 )

Le premier terme est le moment cinétique du Centre de masse par rapport à l’origine. Semblable à Particule unique , ci-dessous, il s’agit du moment cinétique d’une particule de masse M au Centre de masse se déplaçant à la vitesse V . Le deuxième terme est le moment cinétique des particules se déplaçant par rapport au Centre de masse, similaire au Centre de masse fixe , ci-dessous. Le résultat est général – le mouvement des particules n’est pas limité à la rotation ou à la révolution autour de l’origine ou du Centre de masse. Les particules n’ont pas besoin d’être des masses individuelles, mais peuvent être des éléments d’une distribution continue, comme un corps solide.

En réorganisant l’équation ( 2 ) par des identités vectorielles, en multipliant les deux termes par “un”, et en regroupant de manière appropriée,

L = M ( R × V ) + ∑ i [ m i ( r i × v i ) ] , = R 2 R 2 M ( R × V ) + ∑ i [ r i 2 r i 2 m i ( r i × v i ) ] , = R 2 M ( R × V R 2 ) + ∑ i [ r i 2 m i ( r i × v i r i 2 ) ] , {displaystyle {begin{aligned}mathbf {L} &=M(mathbf {R} times mathbf {V} )+sum _{i}left[m_{i}left(mathbf {r} _{i}times mathbf {v} _{i}right)right],\&={frac {R^{2}}{R^{2}}}Mleft (mathbf {R} times mathbf {V} right)+sum _{i}left[{frac {r_{i}^{2}}{r_{i}^{2}}} m_{i}left(mathbf {r} _{i}times mathbf {v} _{i}right)right],\&=R^{2}Mleft({frac {mathbf {R} times mathbf {V} }{R^{2}}}right)+sum _{i}left[r_{i}^{2}m_{i}left( {frac {mathbf {r} _{i}times mathbf {v} _{i}}{r_{i}^{2}}}right)right],\end{aligned} }} ${displaystyle {begin{aligned}mathbf {L} &=M(mathbf {R} times mathbf {V} )+sum _{i}left[m_{i}left(mathbf {r} _{i}times mathbf {v} _{i}right)right],\&={frac {R^{2}}{R^{2}}}Mleft(mathbf {R} times mathbf {V} right)+sum _{i}left[{frac {r_{i}^{2}}{r_{i}^{2}}}m_{i}left(mathbf {r} _{i}times mathbf {v} _{i}right)right],\&=R^{2}Mleft({frac {mathbf {R} times mathbf {V} }{R^{2}}}right)+sum _{i}left[r_{i}^{2}m_{i}left({frac {mathbf {r} _{i}times mathbf {v} _{i}}{r_{i}^{2}}}right)right],\end{aligned}}}$ ${displaystyle {begin{aligned}mathbf {L} &=M(mathbf {R} times mathbf {V} )+sum _{i}left[m_{i}left(mathbf {r} _{i}times mathbf {v} _{i}right)right],\&={frac {R^{2}}{R^{2}}}Mleft(mathbf {R} times mathbf {V} right)+sum _{i}left[{frac {r_{i}^{2}}{r_{i}^{2}}}m_{i}left(mathbf {r} _{i}times mathbf {v} _{i}right)right],\&=R^{2}Mleft({frac {mathbf {R} times mathbf {V} }{R^{2}}}right)+sum _{i}left[r_{i}^{2}m_{i}left({frac {mathbf {r} _{i}times mathbf {v} _{i}}{r_{i}^{2}}}right)right],\end{aligned}}}$

donne le moment cinétique total du système de particules en termes de moment d’inertie I {displaystyle I} et vitesse angulaire ω {displaystyle {boldsymbol {omega}}} {boldsymbol {omega }} ,

L = I R ω R + ∑ i I i ω i . {displaystyle mathbf {L} =I_{R}{boldsymbol {omega }}_{R}+sum _{i}I_{i}{boldsymbol {omega }}_{i}.} $mathbf {L} =I_{R}{boldsymbol {omega }}_{R}+sum _{i}I_{i}{boldsymbol {omega }}_{i}.$ $mathbf {L} =I_{R}{boldsymbol {omega }}_{R}+sum _{i}I_{i}{boldsymbol {omega }}_{i}.$ ( 3 )

Cas d’une seule particule

Dans le cas d’une seule particule se déplaçant autour de l’origine arbitraire,

r i = v i = 0 , r = R , v = V , m = M , {displaystyle {begin{aligned}mathbf {r} _{i}&=mathbf {v} _{i}=mathbf {0} ,\mathbf {r} &=mathbf {R} ,\mathbf {v} &=mathbf {V} ,\m&=M,end{aligné}}} ${displaystyle {begin{aligned}mathbf {r} _{i}&=mathbf {v} _{i}=mathbf {0} ,\mathbf {r} &=mathbf {R} ,\mathbf {v} &=mathbf {V} ,\m&=M,end{aligned}}}$ ${displaystyle {begin{aligned}mathbf {r} _{i}&=mathbf {v} _{i}=mathbf {0} ,\mathbf {r} &=mathbf {R} ,\mathbf {v} &=mathbf {V} ,\m&=M,end{aligned}}}$ ∑ i r i × m i v i = 0 , {displaystyle sum _{i}mathbf {r} _{i}times m_{i}mathbf {v} _{i}=mathbf {0} ,} $sum _{i}mathbf {r} _{i}times m_{i}mathbf {v} _{i}=mathbf {0} ,$ $sum _{i}mathbf {r} _{i}times m_{i}mathbf {v} _{i}=mathbf {0} ,$ ∑ i I i ω i = 0 , {displaystyle sum _{i}I_{i}{boldsymbol {omega }}_{i}=mathbf {0} ,} $sum _{i}I_{i}{boldsymbol {omega }}_{i}=mathbf {0} ,$ $sum _{i}I_{i}{boldsymbol {omega }}_{i}=mathbf {0} ,$ et les équations ( 2 ) et ( 3 ) pour le moment cinétique total se réduisent à, L = R × m V = I R ω R . {displaystyle mathbf {L} =mathbf {R} times mmathbf {V} =I_{R}{boldsymbol {omega }}_{R}.} $mathbf {L} =mathbf {R} times mmathbf {V} =I_{R}{boldsymbol {omega }}_{R}.$ $mathbf {L} =mathbf {R} times mmathbf {V} =I_{R}{boldsymbol {omega }}_{R}.$ Cas d’un Centre de masse fixe

Pour le cas du Centre de masse fixé dans l’espace par rapport à l’origine,

V = 0 , {displaystyle mathbf {V} =mathbf {0} ,} R × M V = 0 , {displaystyle mathbf {R} times Mmathbf {V} =mathbf {0} ,} I R ω R = 0 , {displaystyle I_{R}{boldsymbol {omega }}_{R}=mathbf {0} ,} $I_{R}{boldsymbol {omega }}_{R}=mathbf {0} ,$ $I_{R}{boldsymbol {omega }}_{R}=mathbf {0} ,$ et les équations ( 2 ) et ( 3 ) pour le moment cinétique total se réduisent à, L = ∑ i r i × m i v i = ∑ i I i ω i . {displaystyle mathbf {L} =sum _{i}mathbf {r} _{i}times m_{i}mathbf {v} _{i}=sum _{i}I_{i} {boldsymbol {omega}}_{i}.} $mathbf {L} =sum _{i}mathbf {r} _{i}times m_{i}mathbf {v} _{i}=sum _{i}I_{i}{boldsymbol {omega }}_{i}.$ $mathbf {L} =sum _{i}mathbf {r} _{i}times m_{i}mathbf {v} _{i}=sum _{i}I_{i}{boldsymbol {omega }}_{i}.$

Moment angulaire en relativité générale

Le moment angulaire 3 en tant que bivecteur (élément plan) et vecteur axial , d’une particule de masse m avec 3 positions instantanées x et 3 impulsions p .

Dans la physique théorique moderne (XXe siècle), le moment cinétique (n’incluant aucun moment cinétique intrinsèque – voir ci- dessous ) est décrit en utilisant un formalisme différent, au lieu d’un pseudovecteur classique . Dans ce formalisme, le moment cinétique est la charge de Noether de forme 2 associée à l’invariance rotationnelle. En conséquence, le moment cinétique n’est pas conservé pour les espaces- temps courbes généraux , à moins qu’il ne soit asymptotiquement invariant en rotation. ^{[ citation nécessaire ]}

En mécanique classique, le moment cinétique d’une particule peut être réinterprété comme un élément plan :

L = r ∧ p , {displaystyle mathbf {L} =mathbf {r} wedge mathbf {p} ,,}

dans laquelle le Produit extérieur ∧ remplace le produit croisé × (ces produits ont des caractéristiques similaires mais ne sont pas équivalents). Cela a l’avantage d’une interprétation géométrique plus claire en tant qu’élément plan, défini à partir des vecteurs x et p , et l’expression est vraie dans n’importe quel nombre de dimensions (deux ou plus). En coordonnées cartésiennes :

L = ( x p y − y p x ) e x ∧ e y + ( y p z − z p y ) e y ∧ e z + ( z p x − x p z ) e z ∧ e x = L x y e x ∧ e y + L y z e y ∧ e z + L z x e z ∧ e x , {displaystyle {begin{aligned}mathbf {L} &=left(xp_{y}-yp_{x}right)mathbf {e} _{x}wedge mathbf {e} _{y }+left(yp_{z}-zp_{y}right)mathbf {e} _{y}wedge mathbf {e} _{z}+left(zp_{x}-xp_{z} right)mathbf {e} _{z}wedge mathbf {e} _{x}\&=L_{xy}mathbf {e} _{x}wedge mathbf {e} _{y }+L_{yz}mathbf {e} _{y}coin mathbf {e} _{z}+L_{zx}mathbf {e} _{z}coin mathbf {e} _{x },,end{aligné}}} ${displaystyle {begin{aligned}mathbf {L} &=left(xp_{y}-yp_{x}right)mathbf {e} _{x}wedge mathbf {e} _{y}+left(yp_{z}-zp_{y}right)mathbf {e} _{y}wedge mathbf {e} _{z}+left(zp_{x}-xp_{z}right)mathbf {e} _{z}wedge mathbf {e} _{x}\&=L_{xy}mathbf {e} _{x}wedge mathbf {e} _{y}+L_{yz}mathbf {e} _{y}wedge mathbf {e} _{z}+L_{zx}mathbf {e} _{z}wedge mathbf {e} _{x},,end{aligned}}}$ ${displaystyle {begin{aligned}mathbf {L} &=left(xp_{y}-yp_{x}right)mathbf {e} _{x}wedge mathbf {e} _{y}+left(yp_{z}-zp_{y}right)mathbf {e} _{y}wedge mathbf {e} _{z}+left(zp_{x}-xp_{z}right)mathbf {e} _{z}wedge mathbf {e} _{x}\&=L_{xy}mathbf {e} _{x}wedge mathbf {e} _{y}+L_{yz}mathbf {e} _{y}wedge mathbf {e} _{z}+L_{zx}mathbf {e} _{z}wedge mathbf {e} _{x},,end{aligned}}}$

ou plus compact en notation d’index :

L i j = x i p j − x j p i . {displaystyle L_{ij}=x_{i}p_{j}-x_{j}p_{i},.} ${displaystyle L_{ij}=x_{i}p_{j}-x_{j}p_{i},.}$ ${displaystyle L_{ij}=x_{i}p_{j}-x_{j}p_{i},.}$

La vitesse angulaire peut également être définie comme un tenseur antisymétrique du second ordre, avec des composantes ω _ij . La relation entre les deux tenseurs antisymétriques est donnée par le moment d’inertie qui doit maintenant être un tenseur du quatrième ordre : ^[30]

L i j = I i j k l ω k l . {displaystyle L_{ij}=I_{ijkell }omega _{kell },.} $L_{ij}=I_{ijkell }omega _{kell },.$ $L_{ij}=I_{ijkell }omega _{kell },.$

Encore une fois, cette équation dans L et ω en tant que tenseurs est vraie dans n’importe quel nombre de dimensions. Cette équation apparaît également dans le formalisme de l’algèbre géométrique , dans lequel L et ω sont des bivecteurs, et le moment d’inertie est une application entre eux.

En mécanique relativiste , le moment cinétique relativiste d’une particule s’exprime comme un tenseur antisymétrique du second ordre :

M α β = X α P β − X β P α {displaystyle M_{alpha beta }=X_{alpha }P_{beta }-X_{beta }P_{alpha }} ${displaystyle M_{alpha beta }=X_{alpha }P_{beta }-X_{beta }P_{alpha }}$ ${displaystyle M_{alpha beta }=X_{alpha }P_{beta }-X_{beta }P_{alpha }}$

dans le langage des quatre vecteurs , à savoir les quatre positions X et les quatre impulsions P , et absorbe le L ci-dessus avec le mouvement du Centre de masse de la particule.

Dans chacun des cas ci-dessus, pour un système de particules, le moment cinétique total n’est que la somme des moments cinétiques individuels des particules, et le Centre de masse est pour le système.

Moment angulaire en mécanique quantique

En mécanique quantique , le moment cinétique (comme d’autres grandeurs) est exprimé sous la forme d’un opérateur , et ses projections unidimensionnelles ont des valeurs propres quantifiées . Le moment cinétique est soumis au principe d’ incertitude de Heisenberg , ce qui implique qu’à tout moment, une seule projection (également appelée «composante») peut être mesurée avec une précision définie; les deux autres restent alors incertains. De ce fait, l’axe de rotation d’une particule quantique n’est pas défini. Les particules quantiques possèdent un type de moment cinétique non orbital appelé “spin”, mais ce moment cinétique ne correspond pas à un mouvement de rotation. ^[31] En mécanique quantique relativistela définition relativiste ci-dessus devient un opérateur tensoriel.

Rotation, orbite et moment cinétique total

Moment angulaire d’un objet classique .

A gauche : le moment cinétique de “spin” S est vraiment le moment cinétique orbital de l’objet en chaque point.
A droite : moment cinétique orbital extrinsèque L autour d’un axe.
En haut : le tenseur du moment d’inertie I et la vitesse angulaire ω ( L n’est pas toujours parallèle à ω ). ^[32]
En bas : la quantité de mouvement p et sa position radiale r par rapport à l’axe. Le moment cinétique total (spin plus orbital) est J . Pour une particule quantique les interprétations sont différentes ; le spin des particules n’a pas l’interprétation ci-dessus.

La définition classique du moment cinétique comme L = r × p {displaystyle mathbf {L} =mathbf {r} times mathbf {p} } peut être transposée à la mécanique quantique, en réinterprétant r comme l’ opérateur de position quantique et p comme l’ opérateur de moment quantique . L est alors un opérateur , plus précisément appelé opérateur de moment cinétique orbital . Les composantes de l’opérateur moment cinétique satisfont les relations de commutation de l’algèbre de Lie so(3). En effet, ces opérateurs sont précisément l’action infinitésimale du groupe de rotation sur l’espace quantique de Hilbert. ^[33] (Voir aussi la discussion ci-dessous sur les opérateurs de moment cinétique en tant que générateurs de rotations.)

Cependant, en physique quantique, il existe un autre type de moment cinétique, appelé moment cinétique de spin , représenté par l’opérateur de spin S . Le spin est souvent décrit comme une particule tournant littéralement autour d’un axe, mais c’est une image trompeuse et inexacte : le spin est une propriété intrinsèque d’une particule, sans rapport avec tout type de mouvement dans l’espace et fondamentalement différent du moment cinétique orbital. Toutes les particules élémentaires ont un spin caractéristique (éventuellement nul), ^[34] et presque toutes les particules élémentaires ont un spin non nul. ^[35] Par exemple , les électrons ont “spin 1/2” (cela signifie en fait “spin ħ /2”), les photonsont “spin 1” (cela signifie en fait “spin ħ”), et les mésons pi ont un spin 0. ^[36]

Enfin, il y a le moment cinétique total J , qui combine à la fois le spin et le moment cinétique orbital de toutes les particules et de tous les champs. (Pour une particule, J = L + S .) La conservation du moment cinétique s’applique à J , mais pas à L ou S ; par exemple, l’ interaction spin-orbite permet au moment cinétique de se transférer dans les deux sens entre L et S , le total restant constant. Les électrons et les photons n’ont pas besoin d’avoir des valeurs entières pour le moment cinétique total, mais peuvent également avoir des valeurs demi-entières. ^[37]

Dans les molécules, le moment cinétique total F est la somme du moment cinétique rovibronique (orbital) N , du moment cinétique de spin électronique S et du moment cinétique de spin nucléaire I . Pour les états singulets électroniques, le moment cinétique rovibronique est noté J plutôt que N . Comme l’explique Van Vleck ^[38] , les composantes du moment cinétique rovibronique moléculaire référées à des axes fixes à la molécule ont des relations de commutation différentes de celles des composantes autour d’axes fixes à l’espace.

Quantification

En mécanique quantique , le moment cinétique est quantifié , c’est-à-dire qu’il ne peut pas varier de manière continue, mais uniquement par ” sauts quantiques ” entre certaines valeurs autorisées. Pour tout système, les restrictions suivantes sur les résultats de mesure s’appliquent, où ħ {displaystylehbar} hbar est la constante de Planck réduite et n ^ {displaystyle {chapeau {n}}} {hat {n}} est un vecteur euclidien tel que x, y ou z :

Si vous mesurez …	Le résultat peut être…
L n ^ {displaystyle L_{chapeau {n}}} ${displaystyle L_{hat {n}}}$ ${displaystyle L_{hat {n}}}$	… , − 2 ħ , − ħ , 0 , ħ , 2 ħ , … {displaystyle ldots ,-2hbar ,-hbar ,0,hbar ,2hbar ,ldots }
S n ^ {displaystyle S_{chapeau {n}}} ${displaystyle S_{hat {n}}}$ ${displaystyle S_{hat {n}}}$ ou alors J n ^ {displaystyle J_{chapeau {n}}} ${displaystyle J_{hat {n}}}$ ${displaystyle J_{hat {n}}}$	… , − 3 2 ħ , − ħ , − 1 2 ħ , 0 , 1 2 ħ , ħ , 3 2 ħ , … {displaystyle ldots ,-{frac {3}{2}}hbar ,-hbar ,-{frac {1}{2}}hbar ,0,{frac {1}{2}} hbar ,hbar ,{frac {3}{2}}hbar ,ldots } $ldots ,-{frac {3}{2}}hbar ,-hbar ,-{frac {1}{2}}hbar ,0,{frac {1}{2}}hbar ,hbar ,{frac {3}{2}}hbar ,ldots$ $ldots ,-{frac {3}{2}}hbar ,-hbar ,-{frac {1}{2}}hbar ,0,{frac {1}{2}}hbar ,hbar ,{frac {3}{2}}hbar ,ldots$
L 2 = L x 2 + L y 2 + L z 2 {displaystyle {begin{aligned}&L^{2}\={}&L_{x}^{2}+L_{y}^{2}+L_{z}^{2}end{aligned} }} ${displaystyle {begin{aligned}&L^{2}\={}&L_{x}^{2}+L_{y}^{2}+L_{z}^{2}end{aligned}}}$ ${displaystyle {begin{aligned}&L^{2}\={}&L_{x}^{2}+L_{y}^{2}+L_{z}^{2}end{aligned}}}$	[ ħ 2 n ( n + 1 ) ] {displaystyle left[hbar ^{2}n(n+1)right]} ${displaystyle left[hbar ^{2}n(n+1)right]}$ ${displaystyle left[hbar ^{2}n(n+1)right]}$ , où n = 0 , 1 , 2 , … {displaystyle n=0,1,2,ldots}
S 2 {displaystyle S^{2}} $S^{2}$ $S^{2}$ ou alors J 2 {displaystyle J^{2}} $J^{2}$ $J^{2}$	[ ħ 2 n ( n + 1 ) ] {displaystyle left[hbar ^{2}n(n+1)right]} ${displaystyle left[hbar ^{2}n(n+1)right]}$ ${displaystyle left[hbar ^{2}n(n+1)right]}$ , où n = 0 , 1 2 , 1 , 3 2 , … {displaystyle n=0,{frac {1}{2}},1,{frac {3}{2}},ldots } ${displaystyle n=0,{frac {1}{2}},1,{frac {3}{2}},ldots }$ ${displaystyle n=0,{frac {1}{2}},1,{frac {3}{2}},ldots }$

Dans cette onde stationnaire sur une corde circulaire, le cercle est divisé en exactement 8 longueurs d’onde . Une onde stationnaire comme celle-ci peut avoir 0, 1, 2 ou n’importe quel nombre entier de longueurs d’onde autour du cercle, mais elle ne peut pas avoir un nombre non entier de longueurs d’onde comme 8,3. En mécanique quantique, le moment cinétique est quantifié pour une raison similaire.

La constante de Planck réduite ħ {displaystylehbar} hbar est minuscule selon les normes de tous les jours, environ 10 ⁻³⁴ J s , et donc cette quantification n’affecte pas sensiblement le moment cinétique des objets macroscopiques. Cependant, il est très important dans le monde microscopique. Par exemple, la structure des couches et sous-couches d’ électrons en chimie est considérablement affectée par la quantification du moment cinétique.

La quantification du moment cinétique a d’abord été postulée par Niels Bohr dans son modèle de l’atome et a ensuite été prédite par Erwin Schrödinger dans son équation de Schrödinger .

Incertitude

Dans la définition L = r × p {displaystyle mathbf {L} =mathbf {r} times mathbf {p} } , six opérateurs interviennent : Les opérateurs de position r x {displaystyle r_{x}} $r_{x}$ $r_{x}$ , r y {displaystyle r_{y}} $r_{y}$ $r_{y}$ , r z {displaystyle r_{z}} $r_{z}$ $r_{z}$ , et les opérateurs momentum p x {displaystyle p_{x}} $p_{x}$ $p_{x}$ , p y {displaystyle p_{y}} $p_{y}$ $p_{y}$ , p z {displaystyle p_{z}} $p_{z}$ $p_{z}$ . Cependant, le principe d’incertitude de Heisenberg nous dit qu’il n’est pas possible que ces six quantités soient connues simultanément avec une précision arbitraire. Par conséquent, il y a des limites à ce qui peut être connu ou mesuré sur le moment cinétique d’une particule. Il s’avère que le mieux que l’on puisse faire est de mesurer simultanément à la fois l’ amplitude du vecteur de moment cinétique et sa composante le long d’un axe.

L’incertitude est étroitement liée au fait que les différentes composantes d’un opérateur de moment cinétique ne commutent pas , par exemple L x L y ≠ L y L x {displaystyle L_{x}L_{y}neq L_{y}L_{x}} $L_{x}L_{y}neq L_{y}L_{x}$ $L_{x}L_{y}neq L_{y}L_{x}$ . (Pour les relations de commutation précises , voir opérateur de moment cinétique .)

Moment cinétique total comme générateur de rotations

Comme mentionné ci-dessus, le moment cinétique orbital L est défini comme en mécanique classique : L = r × p {displaystyle mathbf {L} =mathbf {r} times mathbf {p} } , mais le moment cinétique total J est défini d’une manière différente, plus basique : J est défini comme le “générateur de rotations”. ^[39] Plus précisément, J est défini de sorte que l’opérateur

R ( n ^ , φ ) ≡ exp ⁡ ( − i ħ φ J ⋅ n ^ ) {displaystyle R({hat {n}},phi )equiv exp left(-{frac {i}{hbar }}phi ,mathbf {J} cdot {hat { mathbf {n} }}right)} $R({hat {n}},phi )equiv exp left(-{frac {i}{hbar }}phi ,mathbf {J} cdot {hat {mathbf {n} }}right)$ $R({hat {n}},phi )equiv exp left(-{frac {i}{hbar }}phi ,mathbf {J} cdot {hat {mathbf {n} }}right)$

est l’ opérateur de rotation qui prend n’importe quel système et le fait tourner d’un angle φ {displaystylephi} phi autour de l’axe n ^ {displaystyle {hat {mathbf {n} }}} . (Le “exp” dans la formule fait référence à l’ opérateur exponentiel ) Pour l’inverse, quel que soit notre espace de Hilbert quantique, nous nous attendons à ce que le groupe de rotation SO(3) agisse dessus. Il y a alors une action associée de l’algèbre de Lie so(3) de SO(3) ; les opérateurs décrivant l’action de so(3) sur notre espace de Hilbert sont les opérateurs de moment cinétique (total).

La relation entre l’opérateur de moment cinétique et les opérateurs de rotation est la même que la relation entre les algèbres de Lie et les groupes de Lie en mathématiques. La relation étroite entre le moment cinétique et les rotations se reflète dans le théorème de Noether qui prouve que le moment cinétique est conservé chaque fois que les lois de la physique sont invariantes en rotation.

Moment angulaire en électrodynamique

Lors de la description du mouvement d’une particule chargée dans un champ électromagnétique , la quantité de mouvement canonique P (dérivée du lagrangien pour ce système) n’est pas invariante de jauge . En conséquence, le moment cinétique canonique L = r × P n’est pas non plus invariant de jauge. Au lieu de cela, la quantité de mouvement qui est physique, la soi-disant quantité de mouvement cinétique (utilisée tout au long de cet article), est (en unités SI )

p = m v = P − e A {displaystyle mathbf {p} =mmathbf {v} =mathbf {P} -emathbf {A} }

où e est la charge électrique de la particule et A le potentiel vecteur magnétique du champ électromagnétique. Le moment cinétique invariant de jauge, c’est-à-dire le moment cinétique , est donné par

K = r × ( P − e A ) {displaystyle mathbf {K} =mathbf {r} times (mathbf {P} -emathbf {A} )}

L’interaction avec la mécanique quantique est discutée plus loin dans l’article sur les relations de commutation canoniques .

Moment angulaire en optique

En électrodynamique Maxwell classique, le vecteur de Poynting est une densité d’impulsion linéaire du champ électromagnétique. ^[40]

S ( r , t ) = ε 0 c 2 E ( r , t ) × B ( r , t ) . {displaystyle mathbf {S} (mathbf {r} ,t)=epsilon _{0}c^{2}mathbf {E} (mathbf {r} ,t)times mathbf {B} (mathbf {r} ,t).} ${displaystyle mathbf {S} (mathbf {r} ,t)=epsilon _{0}c^{2}mathbf {E} (mathbf {r} ,t)times mathbf {B} (mathbf {r} ,t).}$ ${displaystyle mathbf {S} (mathbf {r} ,t)=epsilon _{0}c^{2}mathbf {E} (mathbf {r} ,t)times mathbf {B} (mathbf {r} ,t).}$

Le vecteur de densité de moment cinétique L ( r , t ) {displaystyle mathbf {L} (mathbf {r} ,t)} est donnée par un produit vectoriel comme en mécanique classique : ^[41]

L ( r , t ) = r × S ( r , t ) . {displaystyle mathbf {L} (mathbf {r} ,t)=mathbf {r} times mathbf {S} (mathbf {r} ,t).}

Les identités ci-dessus sont valides localement , c’est-à-dire en chaque point de l’espace r {displaystyle mathbf {r}} à un instant donné t {displaystyle t} .

Moment angulaire dans la nature et le cosmos

Les cyclones tropicaux et autres phénomènes météorologiques connexes impliquent la conservation du moment cinétique afin d’expliquer la dynamique. Les vents tournent lentement autour des systèmes de basse pression, principalement en raison de l’ effet de coriolis . Si la basse pression s’intensifie et que l’air circulant lentement est attiré vers le centre, les molécules doivent accélérer afin de conserver le moment cinétique. Au moment où ils atteignent le centre, les vitesses deviennent destructrices. ^[42]

Johannes Kepler a déterminé les lois du mouvement planétaire sans connaître la conservation de la quantité de mouvement. Cependant, peu de temps après sa découverte, leur dérivation a été déterminée à partir de la conservation du moment cinétique. Les planètes se déplacent d’autant plus lentement qu’elles sont éloignées de leurs orbites elliptiques, ce qui s’explique intuitivement par le fait que le moment cinétique orbital est proportionnel au rayon de l’orbite. Comme la masse ne change pas et que le moment cinétique est conservé, la vitesse chute.

L’accélération des marées est un effet des forces de marée entre un satellite naturel en orbite (par exemple la Lune ) et la planète primaire sur laquelle il orbite (par exemple la Terre). Le couple gravitationnel entre la Lune et le renflement de marée de la Terre fait que la Lune est constamment promue sur une orbite légèrement plus élevée et que la Terre est ralentie dans sa rotation. La Terre perd du moment cinétique qui est transféré à la Lune de sorte que le moment cinétique global est conservé.

Moment angulaire en ingénierie et technologie

Les exemples d’utilisation de la conservation du moment cinétique pour un avantage pratique sont nombreux. Dans les moteurs tels que les moteurs à vapeur ou les moteurs à combustion interne , un volant d’inertie est nécessaire pour convertir efficacement le mouvement latéral des pistons en mouvement de rotation.

Les systèmes de navigation inertielle utilisent explicitement le fait que le moment cinétique est conservé par rapport au référentiel inertiel de l’espace. La navigation inertielle est ce qui permet les voyages sous-marins sous la calotte glaciaire polaire, mais elle est également cruciale pour toutes les formes de navigation moderne.

Les balles rayées utilisent la stabilité fournie par la conservation du moment cinétique pour être plus fidèles à leur trajectoire. L’invention des armes à feu rayées et des canons a donné à leurs utilisateurs un avantage stratégique significatif au combat, et a donc constitué un tournant technologique dans l’histoire.

Histoire

Isaac Newton , dans les Principia , a fait allusion au moment cinétique dans ses exemples de la première loi du mouvement ,

Une toupie, dont les parties par leur cohésion sont perpétuellement écartées des mouvements rectilignes, ne cesse sa rotation qu’en étant retardée par l’air. Les corps plus grands des planètes et des comètes, rencontrant moins de résistance dans des espaces plus libres, conservent leurs mouvements à la fois progressifs et circulaires pendant un temps beaucoup plus long. ^[43]

Il n’a pas étudié plus avant le moment cinétique directement dans les Principia , en disant :

De telles sortes de réflexions naissent aussi parfois les mouvements circulaires des corps autour de leurs propres centres. Mais ce sont des cas que je ne considère pas dans ce qui suit ; et il serait trop fastidieux de démontrer tout ce qui se rapporte à ce sujet. ^[44]

Cependant, sa preuve géométrique de la loi des aires est un exemple remarquable du génie de Newton, et prouve indirectement la conservation du moment cinétique dans le cas d’une force centrale .

La loi des aires

Dérivation de Newton 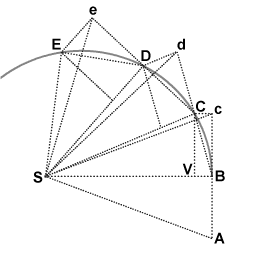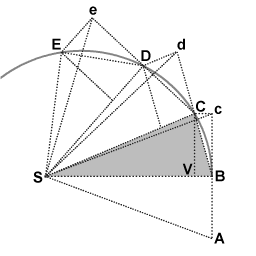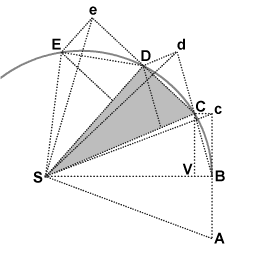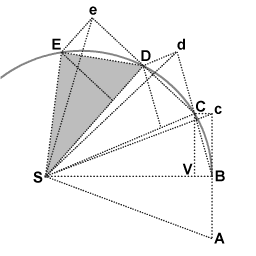Dérivation de Newton de la loi d’aire à l’aide de moyens géométriques.

Lorsqu’une planète orbite autour du Soleil , la ligne entre le Soleil et la planète balaie des zones égales dans des intervalles de temps égaux. Cela était connu depuis que Kepler avait exposé sa deuxième loi du mouvement planétaire . Newton a dérivé une preuve géométrique unique et a ensuite montré que la force d’attraction de la gravité du Soleil était la cause de toutes les lois de Kepler.

Pendant le premier intervalle de temps, un objet est en mouvement du point A au point B . Non perturbé, il continuerait au point c pendant le deuxième intervalle. Lorsque l’objet arrive en B , il reçoit une impulsion dirigée vers le point S . L’impulsion lui donne une petite vitesse supplémentaire vers S , telle que si c’était sa seule vitesse, elle se déplacerait de B à V pendant le deuxième intervalle. Par les règles de composition des vitesses , ces deux vitesses s’additionnent, et le point C se trouve par construction du parallélogramme BcCV. Ainsi la trajectoire de l’objet est déviée par l’impulsion pour qu’il arrive au point C à la fin du deuxième intervalle. Comme les triangles SBc et SBC ont la même base SB et la même hauteur Bc ou VC , ils ont la même aire. Par symétrie, le triangle SBc a aussi la même aire que le triangle SAB , donc l’objet a balayé des aires égales SAB et SBC en des temps égaux.

Au point C , l’objet reçoit une autre impulsion vers S , déviant à nouveau sa trajectoire pendant le troisième intervalle de d à D . Il continue ainsi jusqu’en E et au-delà, les triangles SAB , SBc , SBC , SCd , SCD , SDe , SDE ayant tous la même aire. En laissant les intervalles de temps devenir de plus en plus petits, le chemin ABCDE se rapproche indéfiniment d’une courbe continue.

Notez que parce que cette dérivation est géométrique et qu’aucune force spécifique n’est appliquée, elle prouve une loi plus générale que la deuxième loi de Kepler sur le mouvement planétaire. Elle montre que la loi des aires s’applique à toute force centrale, attractive ou répulsive, continue ou non continue, ou nulle.

Conservation du moment cinétique dans la loi des aires

La proportionnalité du moment cinétique à la zone balayée par un objet en mouvement peut être comprise en réalisant que les bases des triangles, c’est-à-dire les lignes de S à l’objet, sont équivalentes au rayon r , et que les hauteurs des les triangles sont proportionnels à la Composante perpendiculaire de la vitesse v _⊥ . Par conséquent, si la zone balayée par unité de temps est constante, alors par la formule de la zone triangulaire1/2(base)(hauteur) , le produit (base)(hauteur) et donc le produit rv _⊥ sont constants : si r et la longueur de la base sont diminués, v _⊥ et la hauteur doivent augmenter proportionnellement. La masse est constante, donc le moment cinétique rmv _⊥ est conservé par cet échange de distance et de vitesse.

Dans le cas du triangle SBC , l’aire est égale à 1/2( SB )( VC ). Partout où C est finalement localisé en raison de l’impulsion appliquée à B , le produit ( SB )( VC ), et donc rmv _⊥ restent constants. De même pour chacun des triangles.

Après Newton

Leonhard Euler , Daniel Bernoulli et Patrick d’Arcy ont tous compris le moment cinétique en termes de conservation de la vitesse surfacique , résultat de leur analyse de la deuxième loi de Kepler sur le mouvement planétaire. Il est peu probable qu’ils aient réalisé les implications pour la matière en rotation ordinaire. ^[45]

En 1736, Euler, comme Newton, a abordé certaines des équations du moment cinétique dans son Mechanica sans les développer davantage. ^[46]

Bernoulli a écrit dans une lettre de 1744 un “moment de mouvement de rotation”, peut-être la première conception du moment cinétique tel que nous le comprenons maintenant. ^[47]

En 1799, Pierre-Simon Laplace s’est rendu compte pour la première fois qu’un plan fixe était associé à la rotation – son plan invariable .

Louis Poinsot en 1803 a commencé à représenter les rotations comme un segment de ligne perpendiculaire à la rotation, et a élaboré sur la “conservation des moments”.

En 1852 , Léon Foucault a utilisé un gyroscope dans une expérience pour afficher la rotation de la Terre.

Le Manuel de mécanique appliquée de 1858 de William JM Rankine a défini pour la première fois le moment cinétique au sens moderne :

…une ligne dont la longueur est proportionnelle à la grandeur du moment cinétique, et dont la direction est perpendiculaire au plan de mouvement du corps et du point fixe, et telle que, lorsque le mouvement du corps est vu depuis le extrémité de la droite, le rayon vecteur du corps semble avoir une rotation à droite.

Dans une édition de 1872 du même livre, Rankine a déclaré que “Le terme moment cinétique a été introduit par M. Hayward,” ^[48] se référant probablement à l’article de RB Hayward Sur une méthode directe d’estimation des vitesses, des accélérations et de toutes les quantités similaires en ce qui concerne à Axes mobiles de quelque manière que ce soit dans Space with Applications, ^[49] qui a été introduit en 1856 et publié en 1864. Rankine s’est trompé, car de nombreuses publications présentent le terme commençant à la fin du 18e au début du 19e siècle. ^[50] Cependant, l’article de Hayward était apparemment la première utilisation du terme et du concept vu par une grande partie du monde anglophone. Avant cela, le moment cinétique était généralement appelé “momentum of rotation” en anglais.^[51]

Voir également

Moment cinétique absolu
Couplage moment angulaire
Moment angulaire de la lumière
Diagrammes de moment cinétique (mécanique quantique)
Rotation chaotique
Coefficients de Clebsch-Gordan
Analogues linéaires-rotatifs
Ordres de grandeur (moment angulaire)
Pseudovecteur de Pauli – Lubanski
Moment angulaire relatif
Moment cinétique relativiste
Rotor rigide
Énergie de rotation
Moment angulaire relatif spécifique
Yrast

Notes de bas de page

^ “Soaring Science: L’aérodynamique du vol d’un frisbee” . Scientifique américain. 9 août 2012 . Consulté le 4 janvier 2022 .
^ “Structure des cyclones tropicaux” . Service météorologique national . Consulté le 4 janvier 2022 .
^ Moore, Thomas (2016). Six idées qui ont façonné la physique, unité C : les lois de conservation contraignent les interactions (troisième éd.). McGraw Hill Education. p. 91. ISBN 978-0-07-351394-2.
^ Wilson, EB (1915). Moment linéaire, énergie cinétique et moment angulaire . Le mensuel mathématique américain . Vol. XXIII. Ginn and Co., Boston, en coopération avec l’Université de Chicago, et al. p. 190 – via Google livres.
^ Worthington, Arthur M. (1906). Dynamique de Rotation . Longmans, Green and Co., Londres. p. 21 – via Google livres.
^ Taylor, John R. (2005). Mécanique classique . Livres scientifiques universitaires, Mill Valley, Californie. p. 90 . ISBN 978-1-891389-22-1.
^ Dadourian, HM (1913). Mécanique analytique pour les étudiants en physique et en génie . D. Van Nostrand Company, New York. p. 266 – via Google livres.
^ Watson, W. (1912). Physique générale . Longmans, Green and Co., New York. p. 33 – via Google livres.
^ Barker, George F. (1893). Physique: cours avancé (4e éd.). Henry Holt et compagnie, New York. p. 66 – via Google Livres.
^ Barker, George F. (1893). Physique: cours avancé (4e éd.). Henry Holt et compagnie, New York. pp. 67-68 – via Google Livres.
^ Oberg, Erik; et coll. (2000). Manuel des machines (26e éd.). Industrial Press, Inc., New York. p. 143. ISBN 978-0-8311-2625-4.
^ Watson, W. (1912). Physique générale . Longmans, Green and Co., New York. p. 34 – via Google livres.
^ Kent, Guillaume (1916). Le livre de poche des ingénieurs mécaniques (9e éd.). John Wiley and Sons, Inc., New York. p. 517 – via Google livres.
^ Oberg, Erik; et coll. (2000). Manuel des machines (26e éd.). Industrial Press, Inc., New York. p. 146. ISBN 978-0-8311-2625-4.
^ Oberg, Erik; et coll. (2000). Manuel des machines (26e éd.). Industrial Press, Inc., New York. p. 161–162. ISBN 978-0-8311-2625-4.
^ Kent, Guillaume (1916). Le livre de poche des ingénieurs mécaniques (9e éd.). John Wiley and Sons, Inc., New York. p. 527 – via Google livres.
^ Battin, Richard H. (1999). Une introduction aux mathématiques et aux méthodes de l’astrodynamique, édition révisée . Institut américain d’aéronautique et d’astronautique, Inc. ISBN 978-1-56347-342-5., p. 97
^ Rankine, WJM (1872). Un manuel de mécanique appliquée (6e éd.). Charles Griffin and Company, Londres. p. 507 – via Google livres.
^ ^un Équipage ^{b , Henry (1908).}Les principes de la mécanique : pour les étudiants en physique et en génie . Longmans, Green et Company, New York. p. 88 – via Google livres.
^ Worthington, Arthur M. (1906). Dynamique de Rotation . Longmans, Green and Co., Londres. p. 82 – via Google livres.
^ Worthington, Arthur M. (1906). Dynamique de Rotation . Longmans, Green and Co., Londres. p. 11 – via Google livres.
^ Stephenson, FR; Morrison, LV ; Whitrow, GJ (1984). “Les changements à long terme dans la rotation de la terre – 700 avant JC à 1980 après JC”. Transactions philosophiques de la Royal Society . 313 (1524): 47–70. Bibcode : 1984RSPTA.313…47S . doi : 10.1098/rsta.1984.0082 . S2CID 120566848 . +2,40 ms/siècle divisé par 36525 jours.
^ Dickey, JO; et coll. (1994). “Télémétrie laser lunaire: un héritage continu du programme Apollo” (PDF) . Sciences . 265 (5171) : 482–90, voir 486. Bibcode : 1994Sci…265..482D . doi : 10.1126/science.265.5171.482 . PMID 17781305 . S2CID 10157934 .
^ Landau, LD; Lifshitz, EM (1995). La théorie classique des champs . Cours de physique théorique. Oxford, Butterworth-Heinemann. ISBN 978-0-7506-2768-9.
^ Tenenbaum, M., & Pollard, H. (1985). Équations différentielles ordinaires en manuel élémentaire pour les étudiants en mathématiques. Ingénierie et Sciences.
^ David Morin (2008). Introduction à la mécanique classique : avec problèmes et solutions . La presse de l’Universite de Cambridge. p. 311.ISBN _ 978-1-139-46837-4. Extrait de la page 311
^ Battin, Richard H. (1999). Une introduction aux mathématiques et aux méthodes de l’astrodynamique, édition révisée . Institut américain d’aéronautique et d’astronautique, Inc. p. 115. ISBN 978-1-56347-342-5.
^ Wilson, EB (1915). Moment linéaire, énergie cinétique et moment angulaire . Le mensuel mathématique américain . Vol. XXIII. Ginn and Co., Boston, en coopération avec l’Université de Chicago, et al. p. 188, équation (3) – via Google Books.
^ Wilson, EB (1915). Moment linéaire, énergie cinétique et moment angulaire . Le mensuel mathématique américain . Vol. XXIII. Ginn and Co., Boston, en coopération avec l’Université de Chicago, et al. p. 191, Théorème 8 – via Google livres.
^ Synge et Schild, Calcul tenseur, publications de Douvres, édition 1978, p. 161. ISBN 978-0-486-63612-2 .
^ de Podesta, Michael (2002). Comprendre les propriétés de la matière (2e édition illustrée et révisée). Presse CRC. p. 29 . ISBN 978-0-415-25788-6.
^ RP Feynman; RB Leighton; M. Sands (1964). Conférences de Feynman sur la physique (volume 2) . Addison–Wesley. p. 31–7. ISBN 978-0-201-02117-2.
^ Salle 2013 Section 17.3
^ Veltman, Martinus JG (2018). Faits et mystères de la physique des particules élémentaires (édition révisée). Scientifique mondial. ISBN 978-981-323-707-0.
^ Thaller, Bernd (2005). Advanced Visual Quantum Mechanics (éd. illustrée). Springer Science et médias d’affaires. p. 114 . ISBN 978-0-387-27127-9.
^ Étrange, Paul (1998). Mécanique quantique relativiste: avec des applications dans la matière condensée et la physique atomique (éd. illustré). La presse de l’Universite de Cambridge. p. 64 . ISBN 978-0-521-56583-7.
^ Ballantine, KE; Donegan, JF; Eastham, PR (2016). “Il y a plusieurs façons de faire tourner un photon : Demi-quantification d’un moment cinétique optique total” . Les avancées scientifiques . 2 (4) : e1501748. Bibcode : 2016SciA….2E1748B . doi : 10.1126/sciadv.1501748 . PMC 5565928 . PMID 28861467 .
^ JH Van Vleck (1951). “Le couplage des vecteurs de moment angulaire dans les molécules”. Rév. Mod. Phys . 23 (3): 213. Bibcode : 1951RvMP…23..213V . doi : 10.1103/RevModPhys.23.213 .
^ Littlejohn, Robert (2011). “Notes de cours sur les rotations en mécanique quantique” (PDF) . Physique 221B Printemps 2011 . Récupéré le 13 janvier 2012 .
^ Okulov, A Yu (2008). “Moment angulaire des photons et conjugaison de phase”. Journal of Physics B: physique atomique, moléculaire et optique . 41 (10) : 101001. arXiv : 0801.2675 . Bibcode : 2008JPhB…41j1001O . doi : 10.1088/0953-4075/41/10/101001 .
^ Okulov, AY (2008). “Structures hélicoïdales optiques et sonores dans un miroir de Mandelstam – Brillouin” . Lettres JETP (en russe). 88 (8): 561–566. Bibcode : 2008JETPL..88..487O . doi : 10.1134/s0021364008200046 . S2CID 120371573 . Archivé de l’original le 2015-12-22 . Récupéré le 31/10/2015 .
^ “Structure des cyclones tropicaux” . Service météorologique national . Consulté le 4 janvier 2022 .
^ Newton, Isaac (1803). “Axiomes ; ou lois du mouvement, loi I” . Les principes mathématiques de la philosophie naturelle . Andrew Motte, traducteur. HD Symonds, Londres. p. 322 – via Google livres.
^ Newton, Axiomes; ou lois du mouvement, corollaire III
^ voir Borrelli, Arianna (2011). “Moment angulaire entre physique et mathématiques” (PDF) . pour un excellent résumé détaillé du concept de moment cinétique à travers l’histoire.
^ Bruce, Ian (2008). “Euler : Mechanica Vol. 1” .
^ “Correspondance d’Euler avec Daniel Bernoulli, Bernoulli à Euler, 04 février 1744” (PDF) . Les archives Euler .
^ Rankine, WJM (1872). Un manuel de mécanique appliquée (6e éd.). Charles Griffin and Company, Londres. p. 506 – via Google livres.
^ Hayward, Robert B. (1864). “Sur une méthode directe d’estimation des vitesses, des accélérations et de toutes les quantités similaires par rapport aux axes mobiles de quelque manière que ce soit dans l’espace avec des applications” . Transactions de la Cambridge Philosophical Society . 10 : 1. Bibcode : 1864TCaPS..10….1H .
^ voir, par exemple, Gompertz, Benjamin (1818). “Sur les pendules vibrant entre les joues” . Le Journal des sciences et des arts . III (V): 17 – via Google livres.; Herapath, Jean (1847). Physique Mathématique . Whittaker and Co., Londres. p. 56 – via Google livres.
^ voir, par exemple, Landen, John (1785). « Du mouvement de rotation d’un corps de n’importe quelle forme ». Transactions philosophiques . LXXV (I): 311–332. doi : 10.1098/rstl.1785.0016 . S2CID 186212814 .

Références

Cohen-Tannoudji, Claude; Diu, Bernard; Laloe, Franck (2006). Mécanique quantique (édition de 2 volumes). John Wiley et fils. ISBN 978-0-471-56952-7.
Condon, UE ; Shortley, GH (1935). “Surtout le chapitre 3” . La théorie des spectres atomiques . La presse de l’Universite de Cambridge. ISBN 978-0-521-09209-8.
Edmonds, AR (1957). Moment angulaire en mécanique quantique . Presse universitaire de Princeton. ISBN 978-0-691-07912-7.
Hall, Brian C. (2013), Théorie quantique pour les mathématiciens , Graduate Texts in Mathematics, vol. 267, Springer, ISBN 978-0-387-40122-5.
Jackson, John David (1998). Électrodynamique classique (3e éd.). John Wiley et fils. ISBN 978-0-471-30932-1.
Serway, Raymond A.; En ligneJewett, John W. (2004). Physique pour les scientifiques et les ingénieurs (6e éd.). Brooks/Cole. ISBN 978-0-534-40842-8.
Thompson, William J. (1994). Moment angulaire : un guide illustré des symétries de rotation pour les systèmes physiques . Wiley. ISBN 978-0-471-55264-2.
Tipler, Paul (2004). Physique pour les scientifiques et les ingénieurs: mécanique, oscillations et ondes, thermodynamique (5e éd.). WH Freeman. ISBN 978-0-7167-0809-4.
Feynman R , Leighton R et Sands M. (septembre 2013). “19–4 Énergie cinétique de rotation” . Les conférences Feynman sur la physique . Le site Web des conférences Feynman (éd. En ligne).{{cite book}}: CS1 maint: uses authors parameter (link)

Liens externes

Moment angulairedans les projets frères de Wikipédia

Définitions du Wiktionnaire
Médias de Commons
Manuels de Wikibooks
Ressources de Wikiversité
Données de Wikidata

“Qu’est-ce qu’un sous-marin, une fusée et un ballon de football ont en commun ? Pourquoi le sphéroïde allongé est la forme du succès” ( Scientific American , 8 novembre 2010)
Conservation of Angular Momentum – un chapitre d’un manuel en ligne
Moment angulaire dans un processus de collision – dérivation du cas tridimensionnel
Moment angulaire et mouvement de roulement – plus de théorie de l’élan