Accélération

En mécanique , l’ accélération est le taux de variation de la vitesse d’un objet par rapport au temps. Les accélérations sont des quantités vectorielles (en ce sens qu’elles ont une amplitude et une direction ). ^{[1] [2]} L’orientation de l’accélération d’un objet est donnée par l’orientation de la force nette agissant sur cet objet. L’amplitude de l’accélération d’un objet, telle que décrite par la Deuxième loi de Newton [ ^3] , est l’effet combiné de deux causes :

le solde net de toutes les forces externes agissant sur cet objet – la magnitude est directement proportionnelle à cette force résultante nette;
la masse de cet objet , selon les matériaux dont il est fait – la magnitude est inversement proportionnelle à la masse de l’objet.

Accélération
Dans le vide (pas de résistance de l’air ), les objets attirés par la Terre gagnent en vitesse à un rythme régulier.
Symboles communs	un
Unité SI	m/s ² , m·s ⁻² , m s ⁻²
Dérivations à partir d’ autres grandeurs	un = ré v ré t = ré 2 X ré t 2 {displaystyle mathbf {a} ={frac {dmathbf {v} }{dt}}={frac {d^{2}mathbf {x} }{dt^{2}}}} $mathbf {a} ={frac {dmathbf {v} }{dt}}={frac {d^{2}mathbf {x} }{dt^{2}}}$
Dimension	L J − 2 {displaystyle {mathsf {L}}{mathsf {T}}^{-2}} ${displaystyle {mathsf {L}}{mathsf {T}}^{-2}}$

L’ Unité SI de l’accélération est le mètre par seconde au carré ( m⋅s ⁻² , m s 2 {displaystyle {tfrac {operatorname {m} }{operatorname {s} ^{2}}}} ${displaystyle {tfrac {operatorname {m} }{operatorname {s} ^{2}}}}$ ).

Par exemple, lorsqu’un véhicule part d’un arrêt (vitesse nulle, dans un référentiel inertiel ) et roule en ligne droite à des vitesses croissantes, il accélère dans le sens de la marche. Si le véhicule tourne, une accélération se produit vers la nouvelle direction et modifie son vecteur de mouvement. L’accélération du véhicule dans sa direction de mouvement actuelle est appelée accélération linéaire (ou tangentielle lors de mouvements circulaires ), la réaction à laquelle les passagers à bord subissent une force les repoussant dans leurs sièges. Lors d’un changement de direction, l’accélération effectuée est appelée accélération radiale (ou orthogonale lors de mouvements circulaires), la réaction à laquelle les passagers subissent uneforce centrifuge . Si la vitesse du véhicule diminue, il s’agit d’une accélération dans la direction opposée et mathématiquement négative , parfois appelée décélération ou ralentissement , et les passagers ressentent la réaction à la décélération comme une force d’ inertie les poussant vers l’avant. De telles accélérations négatives sont souvent obtenues par la combustion de rétrofusées dans des engins spatiaux . ^[4] L’accélération et la décélération sont traitées de la même manière, car ce sont toutes deux des changements de vitesse. Chacune de ces accélérations (tangentielle, radiale, décélération) est ressentie par les passagers jusqu’à neutralisation de leur vitesse relative (différentielle) par rapport au véhicule.

Définition et propriétés

Grandeurs cinématiques d’une particule classique : masse m , position r , vitesse v , accélération a .

Accélération moyenne

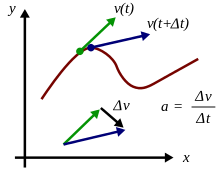
L’accélération est le taux de changement de vitesse. En tout point d’une trajectoire, l’amplitude de l’accélération est donnée par le taux de changement de vitesse à la fois en amplitude et en direction à ce point. La véritable accélération au temps t se trouve dans la limite comme Intervalle de temps Δ t → 0 de Δ v /Δ t

L’accélération moyenne d’un objet sur une période de temps est son changement de vitesse , Δ v {displaystyle Delta mathbf {v}} , divisé par la durée de la période, Δ t {displaystyle Delta t} Delta t . Mathématiquement,

un ̄ = Δ v Δ t . {displaystyle {bar {mathbf {a} }}={frac {Delta mathbf {v} }{Delta t}}.} ${displaystyle {bar {mathbf {a} }}={frac {Delta mathbf {v} }{Delta t}}.}$

Accélération instantanée

De bas en haut :

une fonction d’accélération a ( t ) ;
l’intégrale de l’accélération est la fonction de vitesse v ( t ) ;
et l’intégrale de la vitesse est la fonction de distance s ( t ) .

L’accélération instantanée, quant à elle, est la limite de l’accélération moyenne sur un Intervalle de temps infinitésimal . En termes de calcul , l’accélération instantanée est la dérivée du vecteur vitesse par rapport au temps :

un = lim Δ t → 0 Δ v Δ t = ré v ré t {displaystyle mathbf {a} =lim _{{Delta t}to 0}{frac {Delta mathbf {v} }{Delta t}}={frac {dmathbf {v } }{dt}}} ${displaystyle mathbf {a} =lim _{{Delta t}to 0}{frac {Delta mathbf {v} }{Delta t}}={frac {dmathbf {v} }{dt}}}$ ${displaystyle mathbf {a} =lim _{{Delta t}to 0}{frac {Delta mathbf {v} }{Delta t}}={frac {dmathbf {v} }{dt}}}$ Comme l’accélération est définie comme la dérivée de la vitesse, v , par rapport au temps t et que la vitesse est définie comme la dérivée de la position, x , par rapport au temps, l’accélération peut être considérée comme la dérivée seconde de x par rapport à t : un = ré v ré t = ré 2 x d t 2 {displaystyle mathbf {a} ={frac {dmathbf {v} }{dt}}={frac {d^{2}mathbf {x} }{dt^{2}}}} ${displaystyle mathbf {a} ={frac {dmathbf {v} }{dt}}={frac {d^{2}mathbf {x} }{dt^{2}}}}$ ${displaystyle mathbf {a} ={frac {dmathbf {v} }{dt}}={frac {d^{2}mathbf {x} }{dt^{2}}}}$

(Ici et ailleurs, si le mouvement est en ligne droite , les quantités vectorielles peuvent être remplacées par des scalaires dans les équations.)

Par le théorème fondamental du calcul , on peut voir que l’ intégrale de la fonction d’accélération a ( t ) est la fonction de vitesse v ( t ) ; c’est-à-dire que l’aire sous la courbe d’un graphique d’accélération en fonction du temps ( a vs t ) correspond au changement de vitesse.

Δ v = ∫ a d t {displaystyle mathbf {Delta v} =int mathbf {a} ,dt}

De même, l’intégrale de la fonction jerk j ( t ) , la dérivée de la fonction d’accélération, peut être utilisée pour trouver le changement d’accélération à un certain instant :

Δ a = ∫ j d t {displaystyle mathbf {Delta a} =int mathbf {j} ,dt}

Unités

L’accélération a pour dimension la vitesse (L/T) divisée par le temps, soit L T ^-2 . L’ Unité SI d’accélération est le mètre par seconde au carré (ms ⁻² ); ou “mètre par seconde par seconde”, car la vitesse en mètres par seconde change de la valeur d’accélération, chaque seconde.

Autres formes

Un objet se déplaçant dans un mouvement circulaire, tel qu’un satellite en orbite autour de la Terre, accélère en raison du changement de direction du mouvement, bien que sa vitesse puisse être constante. Dans ce cas, on dit qu’il subit une accélération centripète (dirigée vers le centre).

L’accélération propre , l’accélération d’un corps par rapport à une condition de chute libre, est mesurée par un instrument appelé accéléromètre .

En mécanique classique , pour un corps de masse constante, l’accélération (vectorielle) du centre de masse du corps est proportionnelle au vecteur de force net (c’est-à-dire la somme de toutes les forces) agissant sur lui ( Deuxième loi de Newton ) :

F = m a ⟹ a = F m { displaystyle mathbf {F} = m mathbf {a} quad implique quad mathbf {a} = { frac { mathbf {F} }{ m}}} ${displaystyle mathbf {F} =mmathbf {a} quad implies quad mathbf {a} ={frac {mathbf {F} }{m}}}$ ${displaystyle mathbf {F} =mmathbf {a} quad implies quad mathbf {a} ={frac {mathbf {F} }{m}}}$ où F est la force nette agissant sur le corps, m est la masse du corps et a est l’accélération du centre de masse. À mesure que les vitesses se rapprochent de la vitesse de la lumière , les effets relativistes deviennent de plus en plus importants.

Accélération tangentielle et centripète

Un pendule oscillant, avec une vitesse et une accélération marquées. Il subit à la fois une Accélération tangentielle et centripète. Composantes d’accélération pour un mouvement courbe. La composante tangentielle a _t est due au changement de vitesse de déplacement et pointe le long de la courbe dans la direction du vecteur vitesse (ou dans la direction opposée). La composante normale (également appelée composante centripète pour le mouvement circulaire) a _c est due au changement de direction du vecteur vitesse et est normale à la trajectoire, pointant vers le centre de courbure de la trajectoire.

La vitesse d’une particule se déplaçant sur une trajectoire courbe en fonction du temps peut s’écrire :

v ( t ) = v ( t ) v ( t ) v ( t ) = v ( t ) u t ( t ) , {displaystyle mathbf {v} (t)=v(t){frac {mathbf {v} (t)}{v(t)}}=v(t)mathbf {u} _{mathrm {t} }(t),} ${displaystyle mathbf {v} (t)=v(t){frac {mathbf {v} (t)}{v(t)}}=v(t)mathbf {u} _{mathrm {t} }(t),}$ ${displaystyle mathbf {v} (t)=v(t){frac {mathbf {v} (t)}{v(t)}}=v(t)mathbf {u} _{mathrm {t} }(t),}$

avec v ( t ) égal à la vitesse de déplacement le long du chemin, et

u t = v ( t ) v ( t ) , {displaystyle mathbf {u} _{mathrm {t} }={frac {mathbf {v} (t)}{v(t)}} ,} ${displaystyle mathbf {u} _{mathrm {t} }={frac {mathbf {v} (t)}{v(t)}} ,}$ ${displaystyle mathbf {u} _{mathrm {t} }={frac {mathbf {v} (t)}{v(t)}} ,}$

un vecteur unitaire tangent à la trajectoire pointant dans la direction du mouvement à l’instant choisi. En tenant compte à la fois de la vitesse changeante v ( t ) et de la direction changeante de u _t , l’accélération d’une particule se déplaçant sur une trajectoire courbe peut être écrite en utilisant la règle de différenciation en chaîne ^[5] pour le produit de deux fonctions du temps comme :

a = d v d t = d v d t u t + v ( t ) d u t d t = d v d t u t + v 2 r u n , {displaystyle {begin{alignedat}{3}mathbf {a} &={frac {dmathbf {v} }{dt}}\&={frac {dv}{dt}}mathbf {u} _{mathrm {t} }+v(t){frac {dmathbf {u} _{mathrm {t} }}{dt}}\&={frac {dv}{dt}}mathbf {u} _{mathrm {t} }+{frac {v^{2}}{r}}mathbf {u} _{mathrm {n} } ,end{alignedat}}} ${displaystyle {begin{alignedat}{3}mathbf {a} &={frac {dmathbf {v} }{dt}}\&={frac {dv}{dt}}mathbf {u} _{mathrm {t} }+v(t){frac {dmathbf {u} _{mathrm {t} }}{dt}}\&={frac {dv}{dt}}mathbf {u} _{mathrm {t} }+{frac {v^{2}}{r}}mathbf {u} _{mathrm {n} } ,end{alignedat}}}$ ${displaystyle {begin{alignedat}{3}mathbf {a} &={frac {dmathbf {v} }{dt}}\&={frac {dv}{dt}}mathbf {u} _{mathrm {t} }+v(t){frac {dmathbf {u} _{mathrm {t} }}{dt}}\&={frac {dv}{dt}}mathbf {u} _{mathrm {t} }+{frac {v^{2}}{r}}mathbf {u} _{mathrm {n} } ,end{alignedat}}}$

où u _n est le vecteur normal unitaire (vers l’intérieur) à la trajectoire de la particule (également appelée normale principale ), et r est son rayon de courbure instantané basé sur le cercle osculateur au temps t . Ces composantes sont appelées l’ Accélération tangentielle et l’accélération normale ou radiale (ou accélération centripète en mouvement circulaire, voir aussi mouvement circulaire et force centripète ).

L’analyse géométrique des courbes spatiales tridimensionnelles, qui explique la tangente, la normale (principale) et la binormale, est décrite par les formules de Frenet-Serret . ^{[6] [7]}

Cas spéciaux

Learn more.

Isomorphisme

Jul 14, 2022

Premier article sur la théorie des ensembles de Cantor

Jul 12, 2022

Énergie gravitationnelle

Jul 9, 2022

Sphère de Riemann

Jul 8, 2022

Accélération uniforme

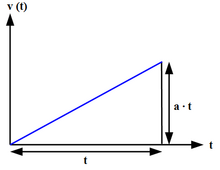
Calcul de la différence de vitesse pour une accélération uniforme

L’accélération uniforme ou constante est un type de mouvement dans lequel la vitesse d’un objet change d’une quantité égale à chaque période de temps égale.

Un exemple fréquemment cité d’accélération uniforme est celui d’un objet en chute libre dans un champ gravitationnel uniforme. L’accélération d’un corps qui tombe en l’absence de résistances au mouvement ne dépend que de l’ intensité du champ gravitationnel g (également appelée accélération due à la gravité ). D’ après la Deuxième loi de Newton, la force F g {displaystyle mathbf {F_{g}} } ${displaystyle mathbf {F_{g}} }$ ${displaystyle mathbf {F_{g}} }$ agir sur un corps est donné par :

F g = m g {displaystyle mathbf {F_{g}} =mmathbf {g} } ${displaystyle mathbf {F_{g}} =mmathbf {g} }$ ${displaystyle mathbf {F_{g}} =mmathbf {g} }$

En raison des propriétés analytiques simples du cas de l’accélération constante, il existe des formules simples reliant le déplacement , les vitesses initiales et dépendant du temps , et l’accélération au temps écoulé : ^[8]

s ( t ) = s 0 + v 0 t + 1 2 a t 2 = s 0 + v 0 + v ( t ) 2 t {displaystyle mathbf {s} (t)=mathbf {s} _{0}+mathbf {v} _{0}t+{tfrac {1}{2}}mathbf {a} t^{ 2}=mathbf {s} _{0}+{frac {mathbf {v} _{0}+mathbf {v} (t)}{2}}t} ${displaystyle mathbf {s} (t)=mathbf {s} _{0}+mathbf {v} _{0}t+{tfrac {1}{2}}mathbf {a} t^{2}=mathbf {s} _{0}+{frac {mathbf {v} _{0}+mathbf {v} (t)}{2}}t}$ ${displaystyle mathbf {s} (t)=mathbf {s} _{0}+mathbf {v} _{0}t+{tfrac {1}{2}}mathbf {a} t^{2}=mathbf {s} _{0}+{frac {mathbf {v} _{0}+mathbf {v} (t)}{2}}t}$ v ( t ) = v 0 + a t {displaystyle mathbf {v} (t)=mathbf {v} _{0}+mathbf {a} t} ${displaystyle mathbf {v} (t)=mathbf {v} _{0}+mathbf {a} t}$ ${displaystyle mathbf {v} (t)=mathbf {v} _{0}+mathbf {a} t}$ v 2 ( t ) = v 0 2 + 2 a ⋅ [ s ( t ) − s 0 ] {displaystyle {v^{2}}(t)={v_{0}}^{2}+2mathbf {acdot } [mathbf {s} (t)-mathbf {s} _{ 0}]} ${displaystyle {v^{2}}(t)={v_{0}}^{2}+2mathbf {acdot } [mathbf {s} (t)-mathbf {s} _{0}]}$ ${displaystyle {v^{2}}(t)={v_{0}}^{2}+2mathbf {acdot } [mathbf {s} (t)-mathbf {s} _{0}]}$

où

t {displaystyle t} est le temps écoulé,
s 0 {displaystyle mathbf {s} _{0}} $mathbf {s} _{0}$ $mathbf {s} _{0}$ est le déplacement initial depuis l’origine,
s ( t ) {displaystyle mathbf {s} (t)} est le déplacement depuis l’origine au temps t {displaystyle t} ,
v 0 {displaystyle mathbf {v} _{0}} $mathbf {v} _{0}$ $mathbf {v} _{0}$ est la vitesse initiale,
v ( t ) {displaystyle mathbf {v} (t)} est la vitesse au temps t {displaystyle t} , et
a {displaystyle mathbf {a} } est le taux d’accélération uniforme.

En particulier, le mouvement peut être résolu en deux parties orthogonales, l’une de vitesse constante et l’autre selon les équations ci-dessus. Comme l’a montré Galileo , le résultat net est un mouvement parabolique, qui décrit, par ex. ex., la trajectoire d’un projectile dans le vide près de la surface de la Terre. ^[9]

Mouvement circulaire

Le vecteur de position r , pointe toujours radialement à partir de l’origine. Vecteur vitesse v , toujours tangent à la trajectoire du mouvement. Vecteur d’accélération a , non parallèle au mouvement radial mais compensé par les accélérations angulaire et de Coriolis, ni tangent à la trajectoire mais compensé par les accélérations centripète et radiale. Vecteurs cinématiques en Coordonnées polaires planes . Notez que la configuration n’est pas limitée à l’espace 2d, mais peut représenter le plan du plan osculateur en un point d’une courbe arbitraire dans n’importe quelle dimension supérieure.

En mouvement circulaire uniforme , c’est-à-dire se déplaçant à vitesse constante le long d’une trajectoire circulaire, une particule subit une accélération résultant du changement de direction du vecteur vitesse, tandis que sa magnitude reste constante. La dérivée de la position d’un point sur une courbe par rapport au temps, c’est-à-dire sa vitesse, s’avère être toujours exactement tangente à la courbe, respectivement orthogonale au rayon en ce point. Étant donné que dans un mouvement uniforme, la vitesse dans la direction tangentielle ne change pas, l’accélération doit être dans la direction radiale, pointant vers le centre du cercle. Cette accélération change constamment la direction de la vitesse pour qu’elle soit tangente au point voisin, faisant ainsi tourner le vecteur vitesse le long du cercle.

Pour une vitesse donnée v {style d’affichage v} , l’amplitude de cette accélération d’origine géométrique (accélération centripète) est inversement proportionnelle au rayon r {displaystyle r} du cercle, et augmente comme le carré de cette vitesse : a c = v 2 r . {displaystyle a_{c}={frac {v^{2}}{r}};.} ${displaystyle a_{c}={frac {v^{2}}{r}};.}$ ${displaystyle a_{c}={frac {v^{2}}{r}};.}$
Notez que, pour une vitesse angulaire donnée ω {displaystyle oméga} , l’accélération centripète est directement proportionnelle au rayon r {displaystyle r} . Ceci est dû à la dépendance de la vitesse v {style d’affichage v} sur le rayon r {displaystyle r} . v = ω r . {displaystyle v=omega r.}

Expression du vecteur d’accélération centripète en composantes polaires, où r {displaystyle mathbf {r}} est un vecteur du centre du cercle à la particule de magnitude égale à cette distance, et compte tenu de l’orientation de l’accélération vers le centre, donne

a c = − v 2 | r | ⋅ r | r | . {displaystyle mathbf {a_{c}} =-{frac {v^{2}}{|mathbf {r} |}}cdot {frac {mathbf {r} }{|mathbf { r} |}};.} ${displaystyle mathbf {a_{c}} =-{frac {v^{2}}{|mathbf {r} |}}cdot {frac {mathbf {r} }{|mathbf {r} |}};.}$ ${displaystyle mathbf {a_{c}} =-{frac {v^{2}}{|mathbf {r} |}}cdot {frac {mathbf {r} }{|mathbf {r} |}};.}$

Comme d’habitude dans les rotations, la vitesse v {style d’affichage v} d’une particule peut être exprimée comme une vitesse angulaire par rapport à un point à la distance r {displaystyle r} comme

ω = v r . {displaystyle omega ={frac {v}{r}}.} ${displaystyle omega ={frac {v}{r}}.}$ ${displaystyle omega ={frac {v}{r}}.}$

Ainsi a c = − ω 2 r . {displaystyle mathbf {a_{c}} =-omega ^{2}mathbf {r} ;.} ${displaystyle mathbf {a_{c}} =-omega ^{2}mathbf {r} ;.}$ ${displaystyle mathbf {a_{c}} =-omega ^{2}mathbf {r} ;.}$

Cette accélération et la masse de la particule déterminent la force centripète nécessaire , dirigée vers le centre du cercle, comme la force nette agissant sur cette particule pour la maintenir dans ce mouvement circulaire uniforme. La soi-disant « force centrifuge », semblant agir vers l’extérieur sur le corps, est une soi-disant Pseudo-force ressentie dans le cadre de référence du corps en mouvement circulaire, en raison de l’ élan linéaire du corps , un vecteur tangent au cercle de mouvement.

Dans un mouvement circulaire non uniforme, c’est-à-dire que la vitesse le long de la trajectoire courbe change, l’accélération a une composante non nulle tangentielle à la courbe et n’est pas confinée à la normale principale , qui se dirige vers le centre du cercle osculateur, que détermine le rayon r {displaystyle r} pour l’accélération centripète. La composante tangentielle est donnée par l’accélération angulaire α {displaystylealpha} alpha , c’est-à-dire le taux de variation α = ω ̇ {displaystyle alpha ={point {omega}}} {displaystyle alpha ={dot {omega }}} de la vitesse angulaire ω {displaystyle oméga} omega fois le rayon r {displaystyle r} . C’est,

a t = r α . {displaystyle a_{t}=ralpha .} ${displaystyle a_{t}=ralpha .}$ ${displaystyle a_{t}=ralpha .}$

Le signe de la composante tangentielle de l’accélération est déterminé par le signe de l’ accélération angulaire ( α {displaystylealpha} alpha ), et la tangente est toujours dirigée perpendiculairement au rayon vecteur.

Relation à la relativité

Relativité restreinte

La théorie spéciale de la relativité décrit le comportement d’objets se déplaçant par rapport à d’autres objets à des vitesses proches de celle de la lumière dans le vide. La Mécanique newtonienne se révèle exactement être une approximation de la réalité, valable avec une grande précision à des vitesses inférieures. Lorsque les vitesses pertinentes augmentent vers la vitesse de la lumière, l’accélération ne suit plus les équations classiques.

Lorsque les vitesses se rapprochent de celle de la lumière, l’accélération produite par une force donnée diminue, devenant infiniment petite à mesure que l’on se rapproche de la vitesse de la lumière ; un objet avec une masse peut s’approcher asymptotiquement de cette vitesse , mais ne l’atteint jamais.

Relativité générale

À moins que l’état de mouvement d’un objet ne soit connu, il est impossible de distinguer si une force observée est due à la gravité ou à l’accélération – la gravité et l’accélération inertielle ont des effets identiques. Albert Einstein a appelé cela le principe d’équivalence et a déclaré que seuls les observateurs qui ne ressentent aucune force – y compris la force de gravité – sont justifiés de conclure qu’ils n’accélèrent pas. ^[dix]

Conversions

Conversions entre unités communes d’accélération

Valeur de base	( Gal , ou cm/s ² )	( pi/s ² )	( m/s ² )	( gravité standard , g ₀ )
1 Gal, ou cm/s ²	1	0,032 8084	0,01	1,019 72 × 10−3
1 pied/s ²	30.4800	1	0,304 800	0,031 0810
1 m/s ²	100	3.280 84	1	0,101 972
1 g ₀	980.665	32.1740	9.806 65	1

Voir également

Accélération (géométrie différentielle)
Quadrivecteur : rendre explicite le lien entre l’espace et le temps
Accélération gravitationnelle
Inertie
Ordres de grandeur (accélération)
Choc (mécanique)
Enregistreur de données de chocs et de vibrations
mesurant l’accélération sur 3 axes
Voyage dans l’espace en utilisant une accélération constante
Force spécifique

Références

^ Bondi, Hermann (1980). Relativité et bon sens . Courrier Douvres Publications. p. 3 . ISBN 978-0-486-24021-3.
^ Lehrman, Robert L. (1998). La physique en toute simplicité . Série éducative de Barron. p. 27 . ISBN 978-0-7641-0236-3.
^ Équipage, Henry (2008). Les principes de la mécanique . BiblioBazaar, LLC. p. 43. ISBN 978-0-559-36871-4.
^ Raymond A. Serway; Chris Vuille; Jerry S. Faughn (2008). Physique universitaire, volume 10 . Cengage. p. 32. ISBN 9780495386933.
^ Weisstein, Eric W. “Règle de chaîne” . Wolfram MathWorld . Recherche Wolfram . Récupéré le 2 août 2016 .
^ Larry C. Andrews; Ronald L. Phillips (2003). Techniques mathématiques pour ingénieurs et scientifiques . Presse SPIE. p. 164. ISBN 978-0-8194-4506-3.
^ ChV Ramana Murthy; NC Srinivas (2001). Mathématiques Appliquées . New Delhi : S. Chand & Co. p. 337. ISBN 978-81-219-2082-7.
^ Keith Johnson (2001). Physique pour vous: édition révisée du programme national pour GCSE (4e éd.). Nelson Thornes. p. 135. ISBN 978-0-7487-6236-1.
^ David C. Cassidy; Gérald James Holton; F.James Rutherford (2002). Comprendre la physique . Birkhauser. p. 146. ISBN 978-0-387-98756-9.
^ Brian Greene, The Fabric of the Cosmos: Space, Time, and the Texture of Reality , page 67. Vintage ISBN 0-375-72720-5

Liens externes

Wikimedia Commons a des médias liés à l’ accélération .

Calculateur d’ accélération Convertisseur d’unité d’accélération simple
Calculatrice d’ accélération Calculatrice de conversion d’accélération convertit les unités sous forme de mètre par seconde carrée, kilomètre par seconde carrée, millimètre par seconde carrée et plus avec conversion métrique.