Distribution normale

En statistique , une distribution normale (également appelée distribution gaussienne , gauss ou distribution de Laplace-Gauss ) est un type de Distribution de probabilité continue pour une variable aléatoire à valeur réelle . La forme générale de sa fonction de densité de probabilité est

Distribution normale

Fonction de densité de probabilité 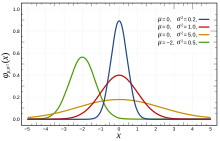La courbe rouge est la distribution normale standard
Fonction de distribution cumulative
Notation	N ( μ , σ 2 ) {displaystyle {mathcal {N}}(mu ,sigma ^{2})}
Paramètres	μ ∈ R {displaystyle mu in mathbb {R}} = moyenne ( emplacement ) σ 2 ∈ R > 0 {displaystyle sigma ^{2}in mathbb {R} _{>0}} = variance ( échelle au carré )
Soutien	x ∈ R {displaystyle xin mathbb {R}}
PDF	1 σ 2 π e − 1 2 ( x − μ σ ) 2 {displaystyle {frac {1}{sigma {sqrt {2pi }}}}e^{-{frac {1}{2}}left({frac {x-mu }{ sigma }}right)^{2}}}
CDF	1 2 [ 1 + erf ⁡ ( x − μ σ 2 ) ] {displaystyle {frac {1}{2}}left[1+operatorname {erf} left({frac {x-mu }{sigma {sqrt {2}}}}right) à droite]}
quantile	μ + σ 2 erf − 1 ⁡ ( 2 p − 1 ) {displaystyle mu +sigma {sqrt {2}}operatorname {erf} ^{-1}(2p-1)}
Moyenne	μ {displaystylemu}
Médian	μ {displaystylemu}
Mode	μ {displaystylemu}
Variance	σ 2 {displaystyle sigma ^{2}}
FURIEUX	σ 2 / π {displaystyle sigma {sqrt {2/pi }}}
Asymétrie	0 {displaystyle 0}
Ex. aplatissement	0 {displaystyle 0}
Entropie	1 2 log ⁡ ( 2 π σ 2 ) + 1 2 {displaystyle {frac {1}{2}}log(2pi sigma ^{2})+{frac {1}{2}}}
FMG	exp ⁡ ( μ t + σ 2 t 2 / 2 ) {displaystyle exp(mu t+sigma ^{2}t^{2}/2)}
FC	exp ⁡ ( i μ t − σ 2 t 2 / 2 ) {displaystyle exp(imu t-sigma ^{2}t^{2}/2)}
Informations sur les pêcheurs	I ( μ , σ ) = ( 1 / σ 2 0 0 2 / σ 2 ) {displaystyle {mathcal {I}}(mu ,sigma )={begin{pmatrix}1/sigma ^{2}&0\0&2/sigma ^{2}end{pmatrix}}} I ( μ , σ 2 ) = ( 1 / σ 2 0 0 1 / ( 2 σ 4 ) ) {displaystyle {mathcal {I}}(mu ,sigma ^{2})={begin{pmatrix}1/sigma ^{2}&0\0&1/(2sigma ^{4}) end{pmatrice}}}
Divergence de Kullback-Leibler	1 2 { ( σ 0 σ 1 ) 2 + ( μ 1 − μ 0 ) 2 σ 1 2 − 1 + ln ⁡ σ 1 σ 0 } {displaystyle {1 over 2}left{left({frac {sigma _{0}}{sigma _{1}}}right)^{2}+{frac {( mu _{1}-mu _{0})^{2}}{sigma _{1}^{2}}}-1+ln {sigma _{1} over sigma _{0 }}à droite}}

f ( x ) = 1 σ 2 π e − 1 2 ( x − μ σ ) 2 {displaystyle f(x)={frac {1}{sigma {sqrt {2pi }}}}e^{-{frac {1}{2}}left({frac {x -mu }{sigma }}right)^{2}}}

Le paramètre μ {displaystylemu} est la moyenne ou l’ espérance de la distribution (ainsi que sa médiane et son mode ), tandis que le paramètre σ {displaystylesigma} est son écart-type . La variance de la distribution est σ 2 {displaystyle sigma ^{2}} . ^[1] Une variable aléatoire avec une distribution gaussienne est dite normalement distribuée , et est appelée écart normal .

Les distributions normales sont importantes en statistique et sont souvent utilisées dans les sciences naturelles et sociales pour représenter des variables aléatoires à valeurs réelles dont les distributions ne sont pas connues. ^{[2] [3]} Leur importance est due en partie au théorème central limite . Il stipule que, sous certaines conditions, la moyenne de nombreux échantillons (observations) d’une variable aléatoire avec une moyenne et une variance finies est elle-même une variable aléatoire – dont la distribution converge vers une distribution normale à mesure que le nombre d’échantillons augmente. Par conséquent, les grandeurs physiques censées être la somme de nombreux processus indépendants, tels que les erreurs de mesure, ont souvent des distributions presque normales. ^[4]

De plus, les distributions gaussiennes ont des propriétés uniques qui sont précieuses dans les études analytiques. Par exemple, toute combinaison linéaire d’une collection fixe d’écarts normaux est un écart normal. De nombreux résultats et méthodes, tels que la propagation de l’incertitude et l’ajustement des paramètres des moindres carrés , peuvent être dérivés analytiquement sous une forme explicite lorsque les variables pertinentes sont normalement distribuées.

Une distribution normale est parfois appelée officieusement une courbe en cloche . ^[5] Cependant , de nombreuses autres distributions sont en forme de cloche (telles que les distributions de Cauchy , de Student et logistiques ).

La distribution de probabilité univariée est généralisée pour les vecteurs dans la distribution normale multivariée et pour les matrices dans la distribution normale matricielle .

Définitions

Distribution normale standard

Le cas le plus simple d’une distribution normale est connu sous le nom de distribution normale standard ou distribution normale unitaire . Il s’agit d’un cas particulier lorsque μ = 0 {displaystylemu =0} et σ = 1 {displaystylesigma =1} , et il est décrit par cette fonction de densité de probabilité (ou densité) :

φ ( z ) = e − z 2 2 2 π {displaystyle varphi (z)={frac {e^{-{frac {z^{2}}{2}}}}{sqrt {2pi }}}}

La variable z {displaystyle z} a une moyenne de 0 et une variance et un écart-type de 1. La densité φ ( z ) {displaystyle varphi (z)} a son apogée 1 / 2 π {displaystyle 1/{sqrt {2pi }}} à z = 0 {style d’affichage z=0} et des points d’inflexion à z = + 1 {displaystyle z=+1} et z = − 1 {displaystyle z=-1} .

Bien que la densité ci-dessus soit plus communément connue sous le nom de normale standard, quelques auteurs ont utilisé ce terme pour décrire d’autres versions de la distribution normale. Carl Friedrich Gauss , par exemple, a un jour défini la normale standard comme

φ ( z ) = e − z 2 π {displaystyle varphi (z)={frac {e^{-z^{2}}}{sqrt {pi }}}}

qui a une variance de 1/2, et Stephen Stigler ^[6] a défini une fois la normale standard comme

φ ( z ) = e − π z 2 {displaystyle varphi (z)=e^{-pi z^{2}}}

qui a une forme fonctionnelle simple et une variance de σ 2 = 1 / ( 2 π ) {displaystyle sigma ^{2}=1/(2pi)} :

Distribution normale générale

Chaque distribution normale est une version de la distribution normale standard, dont le domaine a été étiré d’un facteur σ {displaystylesigma} (l’écart type) puis traduit par μ {displaystylemu} (la valeur moyenne):

f ( x ∣ μ , σ 2 ) = 1 σ φ ( x − μ σ ) {displaystyle f(xmid mu ,sigma ^{2})={frac {1}{sigma }}varphi left({frac {x-mu }{sigma }} à droite)}

La densité de probabilité doit être mise à l’échelle par 1 / σ {displaystyle 1/sigma} de sorte que l’intégrale vaut toujours 1.

Si Z {displaystyle Z} est un écart normal standard , alors X = σ Z + μ {displaystyle X=sigma Z+mu } aura une distribution normale avec une valeur attendue μ {displaystylemu} et écart-type σ {displaystylesigma} . Cela revient à dire que la distribution normale “standard” Z {displaystyle Z} peut être mis à l’échelle/étiré d’un facteur de σ {displaystylesigma} et déplacé de μ {displaystylemu} pour produire une distribution normale différente, appelée X {displaystyle X} . A l’inverse, si X {displaystyle X} est un écart normal avec des paramètres μ {displaystylemu} et σ 2 {displaystyle sigma ^{2}} , ensuite ceci X {displaystyle X} la distribution peut être redimensionnée et décalée via la formule Z = ( X − μ ) / σ {displaystyle Z=(X-mu )/sigma} pour le convertir en distribution normale “standard”. Cette variable est aussi appelée la forme standardisée de X {displaystyle X} .

Notation

La densité de probabilité de la distribution gaussienne standard (distribution normale standard, avec une moyenne nulle et une variance unitaire) est souvent désignée par la lettre grecque φ {displaystylephi} ( phi ). ^[7] La ​​forme alternative de la lettre grecque phi, φ {displaystylevarphi } , est également utilisé assez souvent.

La distribution normale est souvent appelée N ( μ , σ 2 ) {displaystyle N(mu ,sigma ^{2})} ou alors N ( μ , σ 2 ) {displaystyle {mathcal {N}}(mu ,sigma ^{2})} . ^[8] Ainsi lorsqu’une variable aléatoire X {displaystyle X} est normalement distribué avec une moyenne μ {displaystylemu} et écart-type σ {displaystylesigma} , on peut écrire

X ∼ N ( μ , σ 2 ) . {displaystyle Xsim {mathcal {N}}(mu ,sigma ^{2}).}

Paramétrages alternatifs

Certains auteurs préconisent d’utiliser la précision τ {displaystyletau} comme paramètre définissant la largeur de la distribution, au lieu de l’écart σ {displaystylesigma} ou la variance σ 2 {displaystyle sigma ^{2}} . La précision est normalement définie comme l’inverse de la variance, 1 / σ 2 {displaystyle 1/sigma ^{2}} . ^[9] La formule de la distribution devient alors

f ( x ) = τ 2 π e − τ ( x − μ ) 2 / 2 . {displaystyle f(x)={sqrt {frac {tau }{2pi }}}e^{-tau (x-mu )^{2}/2}.}

Ce choix est revendiqué comme ayant des avantages dans les calculs numériques lorsque σ {displaystylesigma} est très proche de zéro et simplifie les formules dans certains contextes, comme dans l’ inférence bayésienne de variables avec une distribution normale multivariée .

Alternativement, l’inverse de l’écart type τ ′ = 1 / σ {displaystyle tau ^{prime}=1/sigma} peut être définie comme la précision , auquel cas l’expression de la distribution normale devient

f ( x ) = τ ′ 2 π e − ( τ ′ ) 2 ( x − μ ) 2 / 2 . {displaystyle f(x)={frac {tau ^{prime }}{sqrt {2pi }}}e^{-(tau ^{prime })^{2}(x- mu )^{2}/2}.}

Selon Stigler, cette formulation est avantageuse en raison d’une formule beaucoup plus simple et plus facile à retenir, et de formules approchées simples pour les quantiles de la distribution.

Les distributions normales forment une famille exponentielle avec des paramètres naturels θ 1 = μ σ 2 {displaystyle textstyle theta _{1}={frac {mu }{sigma ^{2}}}} et θ 2 = − 1 2 σ 2 {displaystyle textstyle theta _{2}={frac {-1}{2sigma ^{2}}}} , et statistiques naturelles x et x ² . Les paramètres d’espérance double pour la distribution normale sont η ₁ = μ et η ₂ = μ ² + σ ² .

Fonctions de distribution cumulées

La fonction de distribution cumulative (CDF) de la distribution normale standard, généralement désignée par la lettre grecque majuscule Φ {displaystyle Phi} ( phi ), est l’intégrale

Φ ( x ) = 1 2 π ∫ − ∞ x e − t 2 / 2 d t {displaystyle Phi (x)={frac {1}{sqrt {2pi }}}int _{-infty}^{x}e^{-t^{2}/2} ,dt}

La fonction d’erreur associée erf ⁡ ( x ) {displaystyle operatorname {erf} (x)} donne la probabilité d’une variable aléatoire, avec une distribution normale de moyenne 0 et de variance 1/2 tombant dans la plage [ − x , x ] {displaystyle [-x,x]} . C’est:

erf ⁡ ( x ) = 2 π ∫ 0 x e − t 2 d t {displaystyle operatorname {erf} (x)={frac {2}{sqrt {pi }}}int _{0}^{x}e^{-t^{2}},dt }

Ces intégrales ne peuvent pas être exprimées en termes de fonctions élémentaires et sont souvent qualifiées de fonctions spéciales . Cependant, de nombreuses approximations numériques sont connues ; voir ci- dessous pour plus.

Les deux fonctions sont étroitement liées, à savoir

Φ ( x ) = 1 2 [ 1 + erf ⁡ ( x 2 ) ] {displaystyle Phi (x)={frac {1}{2}}left[1+operatorname {erf} left({frac {x}{sqrt {2}}}right) à droite]}

Pour une distribution normale générique avec densité f {displaystyle f} , moyenne μ {displaystylemu} et déviation σ {displaystylesigma} , la fonction de distribution cumulative est

F ( x ) = Φ ( x − μ σ ) = 1 2 [ 1 + erf ⁡ ( x − μ σ 2 ) ] {displaystyle F(x)=Phi left({frac {x-mu }{sigma }}right)={frac {1}{2}}left[1+operatorname {erf } left({frac {x-mu }{sigma {sqrt {2}}}}right)right]}

Le complément du CDF normal standard, Q ( x ) = 1 − Φ ( x ) {displaystyle Q(x)=1-Phi (x)} , est souvent appelée la fonction Q , en particulier dans les textes d’ingénierie. ^{[10] [11]} Il donne la probabilité que la valeur d’une variable aléatoire normale standard X {displaystyle X} dépassera x {style d’affichage x} : P ( X > x ) {displaystyle P(X>x)} . D’autres définitions du Q {displaystyle Q} -fonction, qui sont toutes de simples transformations de Φ {displaystyle Phi} , sont également utilisés occasionnellement. ^[12]

Le graphique du CDF normal standard Φ {displaystyle Phi} a une symétrie de rotation double autour du point (0,1/2); C’est, Φ ( − x ) = 1 − Φ ( x ) {displaystyle Phi (-x)=1-Phi (x)} . Sa primitive (intégrale indéfinie) peut être exprimée comme suit :

∫ Φ ( x ) d x = x Φ ( x ) + φ ( x ) + C . {displaystyle int Phi (x),dx=xPhi (x)+varphi (x)+C.}

La CDF de la distribution normale standard peut être étendue par intégration par parties dans une série :

Φ ( x ) = 1 2 + 1 2 π ⋅ e − x 2 / 2 [ x + x 3 3 + x 5 3 ⋅ 5 + ⋯ + x 2 n + 1 ( 2 n + 1 ) ! ! + ⋯ ] {displaystyle Phi (x)={frac {1}{2}}+{frac {1}{sqrt {2pi }}}cdot e^{-x^{2}/2} left[x+{frac {x^{3}}{3}}+{frac {x^{5}}{3cdot 5}}+cdots +{frac {x^{2n+1 }}{(2n+1)!!}}+cdots right]}

où ! ! {displaystyle !!} désigne la factorielle double .

Une expansion asymptotique de la CDF pour un grand x peut également être dérivée en utilisant l’intégration par parties. Pour plus d’informations, voir Error function#Asymptotic expansion . ^[13]

Une approximation rapide du CDF de la distribution normale standard peut être trouvée en utilisant une approximation en série de Taylor :

Φ ( x ) ≈ 1 2 + 1 2 π ∑ k = 0 n ( − 1 ) k x ( 2 k + 1 ) 2 k k ! ( 2 k + 1 ) {displaystyle Phi (x)approx {frac {1}{2}}+{frac {1}{sqrt {2pi }}}sum _{k=0}^{n}{ frac {left(-1right)^{k}x^{left(2k+1right)}}{2^{k}k!left(2k+1right)}}}

Écart-type et couverture Pour la distribution normale, les valeurs à moins d’un écart type de la moyenne représentent 68,27 % de l’ensemble ; tandis que deux écarts types par rapport à la moyenne représentent 95,45 % ; et trois écarts-types représentent 99,73 %.

Environ 68 % des valeurs tirées d’une distribution normale se situent à moins d’un écart type σ de la moyenne ; environ 95 % des valeurs se situent à moins de deux écarts-types ; et environ 99,7 % se situent à moins de trois écarts-types. ^[5] Ce fait est connu sous le nom de règle 68-95-99.7 (empirique) ou règle des 3 sigma .

Plus précisément, la probabilité qu’un écart normal soit compris entre μ − n σ {displaystyle mu -nsigma } et μ + n σ {displaystyle mu +nsigma } est donné par

F ( μ + n σ ) − F ( μ − n σ ) = Φ ( n ) − Φ ( − n ) = erf ⁡ ( n 2 ) . {displaystyle F(mu +nsigma )-F(mu -nsigma )=Phi (n)-Phi (-n)=operatorname {erf} left({frac {n} {sqrt {2}}}right).}

A 12 chiffres significatifs, les valeurs de n = 1 , 2 , … , 6 {displaystyle n=1,2,ldots,6} sont : ^[14]

n {displaystyle n}	p = F ( μ + n σ ) − F ( μ − n σ ) {displaystyle p=F(mu +nsigma )-F(mu -nsigma )}	i.e. 1 − p {displaystyle {text{c’est-à-dire}}1-p}	or 1 in p {displaystyle {text{ou }}1{text{ dans }}p}	OEIS
1	0,682 689 492 137	0,317 310 507 863	3 .151 487 187 53	OEIS : A178647
2	0,954 499 736 104	0,045 500 263 896	21 .977 894 5080	OEIS : A110894
3	0,997 300 203 937	0,002 699 796 063	370 .398 347 345	OEIS : A270712
4	0,999 936 657 516	0,000 063 342 484	15 787 .192 7673
5	0,999 999 426 697	0,000 000 573 303	1 744 277 .893 62
6	0,999 999 998 027	0,000 000 001 973	506 797 345 .897

Pour les grands n {displaystyle n} , on peut utiliser l’approximation 1 − p ≈ e − n 2 / 2 n π / 2 {displaystyle 1-papprox {frac {e^{-n^{2}/2}}{n{sqrt {pi /2}}}}} .

Fonction quantile

La fonction quantile d’une distribution est l’inverse de la fonction de distribution cumulative. La fonction quantile de la distribution normale standard est appelée fonction probit et peut être exprimée en fonction de la fonction d’ erreur inverse :

Φ − 1 ( p ) = 2 erf − 1 ⁡ ( 2 p − 1 ) , p ∈ ( 0 , 1 ) . {displaystyle Phi ^{-1}(p)={sqrt {2}}operatorname {erf} ^{-1}(2p-1),quad pin (0,1).}

Pour une variable aléatoire normale de moyenne μ {displaystylemu} et variance σ 2 {displaystyle sigma ^{2}} , la fonction quantile est

F − 1 ( p ) = μ + σ Φ − 1 ( p ) = μ + σ 2 erf − 1 ⁡ ( 2 p − 1 ) , p ∈ ( 0 , 1 ) . {displaystyle F^{-1}(p)=mu +sigma Phi ^{-1}(p)=mu +sigma {sqrt {2}}operatorname {erf} ^{-1 }(2p-1),quad pin (0,1).}

Le quantile Φ − 1 ( p ) {displaystyle Phi ^{-1}(p)} de la distribution normale standard est communément notée z p {displaystyle z_{p}} . Ces valeurs sont utilisées dans les tests d’hypothèses , la construction d’ intervalles de confiance et les diagrammes Q–Q . Une variable aléatoire normale X {displaystyle X} dépassera μ + z p σ {displaystyle mu +z_{p}sigma } avec probabilité 1 − p {displaystyle 1-p} , et se trouvera en dehors de l’intervalle μ ± z p σ {displaystyle mu pm z_{p}sigma } avec probabilité 2 ( 1 − p ) {displaystyle 2(1-p)} . En particulier, le quantile z 0.975 {displaystyle z_{0.975}} est de 1,96 ; donc une variable aléatoire normale se trouvera en dehors de l’intervalle μ ± 1.96 σ {displaystyle mu pm 1.96sigma } dans seulement 5% des cas.

Le tableau suivant donne le quantile z p {displaystyle z_{p}} tel que X {displaystyle X} se situera dans la gamme μ ± z p σ {displaystyle mu pm z_{p}sigma } avec une probabilité spécifiée p {displaystyle p} . Ces valeurs sont utiles pour déterminer l’ intervalle de tolérance pour les moyennes d’échantillons et d’autres estimateurs statistiques avec des distributions normales (ou asymptotiquement normales). ^{[15] [16]} Notez que le tableau suivant montre 2 erf − 1 ⁡ ( p ) = Φ − 1 ( p + 1 2 ) {displaystyle {sqrt {2}}operatorname {erf} ^{-1}(p)=Phi ^{-1}left({frac {p+1}{2}}right)} , ne pas Φ − 1 ( p ) {displaystyle Phi ^{-1}(p)} tel que défini ci-dessus.

p {displaystyle p}	z p {displaystyle z_{p}}	p {displaystyle p}	z p {displaystyle z_{p}}
0,80	1.281 551 565 545	0,999	3.290 526 731 492
0,90	1.644 853 626 951	0,9999	3.890 591 886 413
0,95	1.959 963 984 540	0,99999	4.417 173 413 469
0,98	2.326 347 874 041	0,999999	4.891 638 475 699
0,99	2.575 829 303 549	0,9999999	5.326 723 886 384
0,995	2.807 033 768 344	0,99999999	5.730 728 868 236
0,998	3.090 232 306 168	0,999999999	6.109 410 204 869

Pour les petits p {displaystyle p} , la fonction quantile a le développement asymptotique utile Φ − 1 ( p ) = − ln ⁡ 1 p 2 − ln ⁡ ln ⁡ 1 p 2 − ln ⁡ ( 2 π ) + o ( 1 ) . {displaystyle Phi ^{-1}(p)=-{sqrt {ln {frac {1}{p^{2}}}-ln ln {frac {1}{p^{ 2}}}-ln(2pi )}}+{mathcal {o}}(1).}

Propriétés

La distribution normale est la seule distribution dont les cumulants au-delà des deux premiers (c’est-à-dire autres que la moyenne et la variance ) sont nuls. C’est aussi la distribution continue avec l’ entropie maximale pour une moyenne et une variance spécifiées. ^{[17] [18]} Geary a montré, en supposant que la moyenne et la variance sont finies, que la distribution normale est la seule distribution où la moyenne et la variance calculées à partir d’un ensemble de tirages indépendants sont indépendantes l’une de l’autre. ^{[19] [20]}

La distribution normale est une sous-classe des distributions elliptiques . La distribution normale est symétrique par rapport à sa moyenne et est non nulle sur toute la ligne réelle. En tant que tel, il peut ne pas être un modèle approprié pour des variables intrinsèquement positives ou fortement biaisées, telles que le poids d’une personne ou le prix d’une action . Ces variables peuvent être mieux décrites par d’autres distributions, telles que la distribution log-normale ou la distribution de Pareto .

La valeur de la distribution normale est pratiquement nulle lorsque la valeur x {style d’affichage x} se situe à plus de quelques écarts-types de la moyenne (par exemple, un écart de trois écarts-types couvre tout sauf 0,27 % de la distribution totale). Par conséquent, ce n’est peut-être pas un modèle approprié lorsque l’on s’attend à une fraction significative de valeurs aberrantes – des valeurs qui se situent à de nombreux écarts-types de la moyenne – et les moindres carrés et autres méthodes d’ inférence statistique qui sont optimales pour les variables normalement distribuées deviennent souvent très peu fiables lorsqu’elles sont appliquées . à de telles données. Dans ces cas, une distribution à queue plus lourde doit être supposée et les méthodes d’ inférence statistique robustes appropriées doivent être appliquées.

La distribution gaussienne appartient à la famille des distributions stables qui sont les attracteurs de sommes de distributions indépendantes et identiquement distribuées , que la moyenne ou la variance soit finie ou non. À l’exception de la gaussienne qui est un cas limite, toutes les distributions stables ont des queues lourdes et une variance infinie. C’est l’une des rares distributions qui soient stables et qui aient des fonctions de densité de probabilité exprimables analytiquement, les autres étant la distribution de Cauchy et la distribution de Lévy .

Symétries et dérivées

La distribution normale avec densité f ( x ) {displaystyle f(x)} (moyenne μ {displaystylemu} et écart-type σ > 0 {displaystylesigma >0} ) a les propriétés suivantes :

• Il est symétrique autour du point x = μ , {displaystyle x=mu ,} qui est à la fois le mode , la médiane et la moyenne de la distribution. ^[21]
• Elle est unimodale : sa dérivée première est positive pour x < μ , {displaystyle x<mu ,} négatif pour x > μ , {displaystyle x>mu ,} et zéro seulement à x = μ . {displaystyle x=mu .}
• La zone délimitée par la courbe et la x {style d’affichage x} -axe est l’unité (c’est-à-dire égal à un).
• Sa dérivée première est f ′ ( x ) = − x − μ σ 2 f ( x ) . {displaystyle f^{prime}(x)=-{frac {x-mu }{sigma ^{2}}}f(x).}
• Sa densité a deux points d’inflexion (où la dérivée seconde de f {displaystyle f} est nul et change de signe), situé à un écart type de la moyenne, à savoir à x = μ − σ {displaystyle x=mu -sigma } et x = μ + σ . {displaystyle x=mu +sigma .} ^[21]
• Sa densité est log-concave . ^[21]
• Sa densité est infiniment dérivable , voire superlisse d’ordre 2. ^[22]

De plus, la densité φ {displaystylevarphi } de la distribution normale standard (c’est-à-dire μ = 0 {displaystylemu =0} et σ = 1 {displaystylesigma =1} ) possède également les propriétés suivantes :

• Sa dérivée première est φ ′ ( x ) = − x φ ( x ) . {displaystyle varphi ^{prime}(x)=-xvarphi (x).}
• Sa dérivée seconde est φ ′ ′ ( x ) = ( x 2 − 1 ) φ ( x ) {displaystyle varphi ^{prime prime}(x)=(x^{2}-1)varphi (x)}
• Plus généralement, sa n ième dérivée est φ ( n ) ( x ) = ( − 1 ) n He n ⁡ ( x ) φ ( x ) , {displaystyle varphi ^{(n)}(x)=(-1)^{n}operatorname {He} _{n}(x)varphi (x),} où He n ⁡ ( x ) {displaystyle operatorname {Il} _{n}(x)} est le n ième polynôme d’Hermite (probabiliste) . ^[23]
• La probabilité qu’une variable distribuée normalement X {displaystyle X} avec connu μ {displaystylemu} et σ {displaystylesigma} est dans un ensemble particulier, peut être calculé en utilisant le fait que la fraction Z = ( X − μ ) / σ {displaystyle Z=(X-mu )/sigma} a une distribution normale standard.

Des moments

Les moments simples et absolus d’une variable X {displaystyle X} sont les valeurs attendues de X p {displaystyle X^{p}} et | X | p {displaystyle |X|^{p}} , respectivement. Si la valeur attendue μ {displaystylemu} de X {displaystyle X} est nul, ces paramètres sont appelés moments centraux ; sinon, ces paramètres sont appelés moments non centraux. Habituellement, nous ne nous intéressons qu’aux moments d’ordre entier p {displaystylep} .

Si X {displaystyle X} a une distribution normale, les moments non centraux existent et sont finis pour tout p {displaystyle p} dont la partie réelle est supérieure à −1. Pour tout entier non négatif p {displaystyle p} , les moments centraux simples sont : ^[24]

E ⁡ [ ( X − μ ) p ] = { 0 if p is odd, σ p ( p − 1 ) ! ! if p is even. {displaystyle operatorname {E} left[(X-mu )^{p}right]={begin{cases}0&{text{if}}p{text{ est impair,}} \sigma ^{p}(p-1) !!&{text{if }}p{text{ est pair.}}end{cases}}}

Ici n ! ! {displaystyle n !!} désigne la factorielle double , c’est-à-dire le produit de tous les nombres de n {displaystyle n} à 1 qui ont la même parité que n . {displaystyle n.}

Les moments centraux absolus coïncident avec les moments simples pour tous les ordres pairs, mais sont différents de zéro pour les ordres impairs. Pour tout entier non négatif p , {displaystyle p,}

E ⁡ [ | X − μ | p ] = σ p ( p − 1 ) ! ! ⋅ { 2 π if p is odd 1 if p is even = σ p ⋅ 2 p / 2 Γ ( p + 1 2 ) π . {displaystyle {begin{aligned}operatorname {E} left[|X-mu |^{p}right]&=sigma ^{p}(p-1) !!cdot {begin {cases}{sqrt {frac {2}{pi }}}&{text{if }}p{text{ est impair}}\1&{text{if }}p{text{ est pair}}end{cases}}\&=sigma ^{p}cdot {frac {2^{p/2}Gamma left({frac {p+1}{2}} right)}{sqrt {pi }}}.end{aligned}}}

La dernière formule est également valable pour tout non entier p > − 1. {displaystyle p>-1.} Quand la moyenne μ ≠ 0 , {displaystyle mu neq 0,} les moments simples et absolus peuvent être exprimés en termes de fonctions hypergéométriques confluentes 1 F 1 {style d’affichage {}_{1}F_{1}} et U . {displaystyle U.} ^{[ citation nécessaire ]}

E ⁡ [ X p ] = σ p ⋅ ( − i 2 ) p U ( − p 2 , 1 2 , − 1 2 ( μ σ ) 2 ) , E ⁡ [ | X | p ] = σ p ⋅ 2 p / 2 Γ ( 1 + p 2 ) π 1 F 1 ( − p 2 , 1 2 , − 1 2 ( μ σ ) 2 ) . {displaystyle {begin{aligned}operatorname {E} left[X^{p}right]&=sigma ^{p}cdot (-i{sqrt {2}})^{p} Uleft(-{frac {p}{2}},{frac {1}{2}},-{frac {1}{2}}left({frac {mu }{ sigma }}right)^{2}right),\nomopérateur{E} left[|X|^{p}right]&=sigma ^{p}cdot 2^{p/2 }{frac {Gamma left({frac {1+p}{2}}right)}{sqrt {pi }}}{}_{1}F_{1}left(-{ frac {p}{2}},{frac {1}{2}},-{frac {1}{2}}left({frac {mu }{sigma }}right) ^{2}right).end{aligned}}}

Ces expressions restent valables même si p {displaystyle p} n’est pas un entier. Voir aussi polynômes d’Hermite généralisés .

Commande	Moment non central	Moment central
1	μ {displaystylemu}	0 {displaystyle 0}
2	μ 2 + σ 2 {displaystyle mu ^{2}+sigma ^{2}}	σ 2 {displaystyle sigma ^{2}}
3	μ 3 + 3 μ σ 2 {displaystyle mu ^{3}+3mu sigma ^{2}}	0 {displaystyle 0}
4	μ 4 + 6 μ 2 σ 2 + 3 σ 4 {displaystyle mu ^{4}+6mu ^{2}sigma ^{2}+3sigma ^{4}}	3 σ 4 {displaystyle 3sigma ^{4}}
5	μ 5 + 10 μ 3 σ 2 + 15 μ σ 4 {displaystyle mu ^{5}+10mu ^{3}sigma ^{2}+15mu sigma ^{4}}	0 {displaystyle 0}
6	μ 6 + 15 μ 4 σ 2 + 45 μ 2 σ 4 + 15 σ 6 {displaystyle mu ^{6}+15mu ^{4}sigma ^{2}+45mu ^{2}sigma ^{4}+15sigma ^{6}}	15 σ 6 {displaystyle 15sigma ^{6}}
7	μ 7 + 21 μ 5 σ 2 + 105 μ 3 σ 4 + 105 μ σ 6 {displaystyle mu ^{7}+21mu ^{5}sigma ^{2}+105mu ^{3}sigma ^{4}+105mu sigma ^{6}}	0 {displaystyle 0}
8	μ 8 + 28 μ 6 σ 2 + 210 μ 4 σ 4 + 420 μ 2 σ 6 + 105 σ 8 {displaystyle mu ^{8}+28mu ^{6}sigma ^{2}+210mu ^{4}sigma ^{4}+420mu ^{2}sigma ^{6 }+105sigma ^{8}}	105 σ 8 {displaystyle 105sigma ^{8}}

Si la variable aléatoire X {displaystyle X} est normalement distribué avec une moyenne μ {displaystylemu} et variance finie non nulle σ 2 {displaystyle sigma ^{2}} , Puis pour 0 < δ < 1 {displaystyle 0<delta <1} la valeur attendue de l’inverse de la valeur absolue de X {displaystyle X} est

E ⁡ [ 1 | X | δ ] ≤ 2 ( 1 − δ ) 2 Γ ( 1 − δ 2 ) σ δ 2 π . {displaystyle {begin{aligned}operatorname {E} left[{frac {1}{vert Xvert ^{delta }}}right]&leq 2^{frac {(1 -delta )}{2}}{frac {Gamma left({frac {1-delta }{2}}right)}{sigma ^{delta }{sqrt {2pi }}}}.end{aligné}}} ^[25]

L’attente de X {displaystyle X} conditionnée à l’événement que X {displaystyle X} se situe dans un intervalle [ a , b ] {displaystyle [a,b]} est donné par

E ⁡ [ X ∣ a < X < b ] = μ − σ 2 f ( b ) − f ( a ) F ( b ) − F ( a ) {displaystyle operatorname {E} left[Xmid a<X<bright]=mu -sigma ^{2}{frac {f(b)-f(a)}{F(b )-FA)}}}

où f {displaystyle f} et F {displaystyle F} sont respectivement la densité et la fonction de distribution cumulative de X {displaystyle X} . Pour b = ∞ {displaystyle b=infty} c’est ce qu’on appelle le rapport de Mills inverse . Notez que ci-dessus, la densité f {displaystyle f} de X {displaystyle X} est utilisé à la place de la densité normale standard comme dans le rapport de Mills inverse, nous avons donc ici σ 2 {displaystyle sigma ^{2}} à la place de σ {displaystylesigma} .

Transformée de Fourier et fonction caractéristique

La transformée de Fourier d’une densité normale f {displaystyle f} avec moyenne μ {displaystylemu} et écart-type σ {displaystylesigma} est ^[26]

f ^ ( t ) = ∫ − ∞ ∞ f ( x ) e − i t x d x = e − i μ t e − 1 2 ( σ t ) 2 {displaystyle {hat {f}}(t)=int _{-infty }^{infty}f(x)e^{-itx},dx=e^{-imu t} e^{-{frac {1}{2}}(sigma t)^{2}}}

où i {displaystyle i} est l’ unité imaginaire . Si la moyenne μ = 0 {displaystylemu =0} , le premier facteur vaut 1, et la transformée de Fourier est, à un facteur constant près, une densité normale sur le domaine fréquentiel , de moyenne 0 et d’écart type 1 / σ {displaystyle 1/sigma} . En particulier, la distribution normale standard φ {displaystylevarphi } est une fonction propre de la transformée de Fourier.

En théorie des probabilités , la transformée de Fourier de la distribution de probabilité d’une variable aléatoire à valeur réelle X {displaystyle X} est étroitement liée à la fonction caractéristique φ X ( t ) {displaystyle varphi _{X}(t)} de cette variable, qui est définie comme la valeur attendue de e i t X {displaystyle e^{itX}} , en fonction de la variable réelle t {displaystyle t} (le paramètre de fréquence de la transformée de Fourier). Cette définition peut être étendue analytiquement à une variable à valeur complexe t {displaystyle t} . ^[27] La ​​relation entre les deux est :

φ X ( t ) = f ^ ( − t ) {displaystyle varphi _{X}(t)={hat {f}}(-t)}

Fonctions génératrices de moment et de cumulant

La fonction génératrice de moment d’une variable aléatoire réelle X {displaystyle X} est la valeur attendue de e t X {displaystyle e^{tX}} , en fonction du paramètre réel t {displaystyle t} . Pour une distribution normale de densité f {displaystyle f} , moyenne μ {displaystylemu} et déviation σ {displaystylesigma} , la fonction génératrice des moments existe et est égale à

M ( t ) = E ⁡ [ e t X ] = f ^ ( i t ) = e μ t e 1 2 σ 2 t 2 {displaystyle M(t)=operatorname {E} [e^{tX}]={hat {f}}(it)=e^{mu t}e^{{tfrac {1}{2 }}sigma ^{2}t^{2}}}

La fonction génératrice cumulante est le logarithme de la fonction génératrice du moment, à savoir

g ( t ) = ln ⁡ M ( t ) = μ t + 1 2 σ 2 t 2 {displaystyle g(t)=ln M(t)=mu t+{tfrac {1}{2}}sigma ^{2}t^{2}}

Comme il s’agit d’un polynôme quadratique en t {displaystyle t} , seuls les deux premiers cumulants sont non nuls, à savoir la moyenne μ {displaystylemu} et la variance σ 2 {displaystyle sigma ^{2}} .

Opérateur et classe de Stein

Dans la méthode de Stein, l’opérateur et la classe de Stein d’une variable aléatoire X ∼ N ( μ , σ 2 ) {displaystyle Xsim {mathcal {N}}(mu ,sigma ^{2})} sont A f ( x ) = σ 2 f ′ ( x ) − ( x − μ ) f ( x ) {displaystyle {mathcal {A}}f(x)=sigma ^{2}f'(x)-(x-mu )f(x)} et F {displaystyle {mathcal {F}}} la classe de toutes les fonctions absolument continues f : R → R such that E [ | f ′ ( X ) | ] < ∞ {displaystyle f:mathbb {R} to mathbb {R} {mbox{ tel que }}mathbb {E} [|f'(X)|]<infty } .

Limite de variance nulle

A la limite quand σ {displaystylesigma} tend vers zéro, la densité de probabilité f ( x ) {displaystyle f(x)} tend finalement vers zéro à tout moment x ≠ μ {displaystyle xneq mu } , mais croît sans limite si x = μ {displaystyle x=mu } , tandis que son intégrale reste égale à 1. Par conséquent, la distribution normale ne peut pas être définie comme une fonction ordinaire lorsque σ = 0 {displaystylesigma =0} .

Cependant, on peut définir la distribution normale à variance nulle comme une fonction généralisée ; spécifiquement, comme la “fonction delta” de Dirac δ {displaystyledelta} traduit par le moyen μ {displaystylemu} , C’est f ( x ) = δ ( x − μ ) . {displaystyle f(x)=delta (x-mu ).} Sa CDF est alors la fonction échelon de Heaviside traduite par la moyenne μ {displaystylemu} , à savoir

F ( x ) = { 0 if x < μ 1 if x ≥ μ {displaystyle F(x)={begin{cases}0&{text{if }}x<mu \1&{text{if }}xgeq mu end{cases}}}

Entropie maximale

De toutes les distributions de probabilité sur les réels avec une moyenne spécifiée μ {displaystylemu} et variance σ 2 {displaystyle sigma ^{2}} , la distribution normale N ( μ , σ 2 ) {displaystyle N(mu ,sigma ^{2})} est celui qui a le maximum d’entropie . ^[28] Si X {displaystyle X} est une variable aléatoire continue de densité de probabilité f ( x ) {displaystyle f(x)} , alors l’entropie de X {displaystyle X} est défini comme ^{[29] [30] [31]}

H ( X ) = − ∫ − ∞ ∞ f ( x ) log ⁡ f ( x ) d x {displaystyle H(X)=-int _{-infty}^{infty}f(x)log f(x),dx}

où f ( x ) log ⁡ f ( x ) {displaystyle f(x)log f(x)} est compris comme nul chaque fois que f ( x ) = 0 {displaystyle f(x)=0} . Cette fonctionnelle peut être maximisée, sous réserve que la distribution soit correctement normalisée et ait une variance spécifiée, en utilisant le calcul variationnel . Une fonction à deux multiplicateurs de Lagrange est définie :

L = ∫ − ∞ ∞ f ( x ) ln ⁡ ( f ( x ) ) d x − λ 0 ( 1 − ∫ − ∞ ∞ f ( x ) d x ) − λ ( σ 2 − ∫ − ∞ ∞ f ( x ) ( x − μ ) 2 d x ) {displaystyle L=int _{-infty}^{infty}f(x)ln(f(x)),dx-lambda _{0}left(1-int _{- infty }^{infty }f(x),dxright)-lambda left(sigma ^{2}-int _{-infty }^{infty }f(x)(x -mu )^{2},dxright)}

où f ( x ) {displaystyle f(x)} est, pour l’instant, considérée comme une fonction de densité de moyenne μ {displaystylemu} et écart-type σ {displaystylesigma} .

A l’entropie maximale, une petite variation δ f ( x ) {displaystyle delta f(x)} à propos f ( x ) {displaystyle f(x)} produira une variation δ L {displaystyledelta L} à propos L {displaystyle L} qui est égal à 0 :

0 = δ L = ∫ − ∞ ∞ δ f ( x ) ( ln ⁡ ( f ( x ) ) + 1 + λ 0 + λ ( x − μ ) 2 ) d x {displaystyle 0=delta L=int _{-infty}^{infty}delta f(x)left(ln(f(x))+1+lambda _{0}+ lambda (x-mu )^{2}right),dx}

Comme cela doit être vrai pour tout petit δ f ( x ) {displaystyle delta f(x)} , le terme entre parenthèses doit être zéro, et résoudre pour f ( x ) {displaystyle f(x)} donne :

f ( x ) = e − λ 0 − 1 − λ ( x − μ ) 2 {displaystyle f(x)=e^{-lambda _{0}-1-lambda (x-mu )^{2}}}

Utilisation des équations de contrainte pour résoudre λ 0 {style d’affichage lambda _{0}} et λ {displaystylelambda} donne la densité de la distribution normale :

f ( x , μ , σ ) = 1 2 π σ 2 e − ( x − μ ) 2 2 σ 2 {displaystyle f(x,mu ,sigma )={frac {1}{sqrt {2pi sigma ^{2}}}}e^{-{frac {(x-mu ) ^{2}}{2sigma ^{2}}}}}

L’entropie d’une distribution normale est égale à

H ( X ) = 1 2 ( 1 + log ⁡ ( 2 σ 2 π ) ) {displaystyle H(X)={tfrac {1}{2}}(1+log(2sigma ^{2}pi ))}

Autres propriétés

1. Si la fonction caractéristique φ X {displaystyle phi _{X}} d’une variable aléatoire X {displaystyle X} est de la forme φ X ( t ) = exp Q ( t ) {displaystyle phi _{X}(t)=exp ^{Q(t)}} , où Q ( t ) {displaystyle Q(t)} est un polynôme , alors le théorème de Marcinkiewicz (du nom de Józef Marcinkiewicz ) affirme que Q {displaystyle Q} peut être au plus un polynôme quadratique, et donc X {displaystyle X} est une variable aléatoire normale. ^[32] La conséquence de ce résultat est que la distribution normale est la seule distribution avec un nombre fini (deux) de cumulants non nuls .
2. Si X {displaystyle X} et Y {displaystyle Y} sont conjointement normaux et non corrélés , alors ils sont indépendants . L’exigence que X {displaystyle X} et Y {displaystyle Y} devrait être conjointement normal est essentiel ; sans elle la propriété ne tient pas. ^{[33] [34] [preuve]} Pour les variables aléatoires non normales, la non-corrélation n’implique pas l’indépendance.
3. La divergence Kullback – Leibler d’une distribution normale X 1 ∼ N ( μ 1 , σ 1 2 ) {displaystyle X_{1}sim N(mu _{1},sigma _{1}^{2})} D’un autre X 2 ∼ N ( μ 2 , σ 2 2 ) {displaystyle X_{2}sim N(mu _{2},sigma _{2}^{2})} est donné par : ^[35] D K L ( X 1 ‖ X 2 ) = ( μ 1 − μ 2 ) 2 2 σ 2 2 + 1 2 ( σ 1 2 σ 2 2 − 1 − ln ⁡ σ 1 2 σ 2 2 ) {displaystyle D_{mathrm {KL}}(X_{1},|,X_{2})={frac {(mu _{1}-mu _{2})^{2 }}{2sigma _{2}^{2}}}+{frac {1}{2}}left({frac {sigma _{1}^{2}}{sigma _{ 2}^{2}}}-1-ln {frac {sigma _{1}^{2}}{sigma _{2}^{2}}}right)} La distance Hellinger entre les mêmes distributions est égale à H 2 ( X 1 , X 2 ) = 1 − 2 σ 1 σ 2 σ 1 2 + σ 2 2 e − 1 4 ( μ 1 − μ 2 ) 2 σ 1 2 + σ 2 2 {displaystyle H^{2}(X_{1},X_{2})=1-{sqrt {frac {2sigma _{1}sigma _{2}}{sigma _{1} ^{2}+sigma _{2}^{2}}}}e^{-{frac {1}{4}}{frac {(mu _{1}-mu _{2} )^{2}}{sigma _{1}^{2}+sigma _{2}^{2}}}}}
4. La matrice d’information de Fisher pour une distribution normale est diagonale et prend la forme I = ( 1 σ 2 0 0 1 2 σ 4 ) {displaystyle {mathcal {I}}={begin{pmatrix}{frac {1}{sigma ^{2}}}&0\0&{frac {1}{2sigma ^{4} }}end{pmatrix}}}
5. L’ a priori conjugué de la moyenne d’une distribution normale est une autre distribution normale. ^[36] Plus précisément, si x 1 , … , x n {displaystyle x_{1},ldots ,x_{n}} sont iid ∼ N ( μ , σ 2 ) {displaystyle sim N(mu ,sigma ^{2})} et le prior est μ ∼ N ( μ 0 , σ 0 2 ) {displaystyle mu sim N(mu _{0},sigma _{0}^{2})} , alors la distribution a posteriori pour l’estimateur de μ {displaystylemu} sera μ ∣ x 1 , … , x n ∼ N ( σ 2 n μ 0 + σ 0 2 x ̄ σ 2 n + σ 0 2 , ( n σ 2 + 1 σ 0 2 ) − 1 ) {displaystyle mu mid x_{1},ldots ,x_{n}sim {mathcal {N}}left({frac {{frac {sigma ^{2}}{n}} mu _{0}+sigma _{0}^{2}{bar {x}}}{{frac {sigma ^{2}}{n}}+sigma _{0}^{ 2}}},left({frac {n}{sigma ^{2}}}+{frac {1}{sigma _{0}^{2}}}right)^{-1 }à droite)}
6. La famille des distributions normales forme non seulement une famille exponentielle (EF), mais forme en fait une famille exponentielle naturelle (NEF) avec quadratique fonction de variance quadratique ( NEF-QVF ). De nombreuses propriétés des distributions normales se généralisent aux propriétés des distributions NEF-QVF, des distributions NEF ou des distributions EF en général. Les distributions NEF-QVF comprennent 6 familles, y compris les distributions de Poisson, Gamma, binomiales et binomiales négatives, tandis que de nombreuses familles courantes étudiées en probabilités et statistiques sont NEF ou EF.
7. En géométrie de l’information , la famille des distributions normales forme une variété statistique à courbure constante − 1 {displaystyle -1} . La même famille est plate par rapport aux (±1)-connexions ∇ ( e ) {displaystyle nabla ^{(e)}} et ∇ ( m ) {displaystyle nabla ^{(m)}} . ^[37]

Distributions associées

Théorème central limite

À mesure que le nombre d’événements discrets augmente, la fonction commence à ressembler à une distribution normale Comparaison des fonctions de densité de probabilité, p ( k ) {displaystyle p(k)} pour la somme de n {displaystyle n} dés à 6 faces justes pour montrer leur convergence vers une distribution normale avec n a {displaystyle na} , conformément au théorème central limite. Dans le graphique en bas à droite, les profils lissés des graphiques précédents sont redimensionnés, superposés et comparés à une distribution normale (courbe noire).

Le théorème central limite stipule que sous certaines conditions (assez courantes), la somme de nombreuses variables aléatoires aura une distribution approximativement normale. Plus précisément, où X 1 , … , X n {displaystyle X_{1},ldots ,X_{n}} sont des variables aléatoires indépendantes et distribuées de manière identique avec la même distribution arbitraire, la même moyenne nulle et la même variance σ 2 {displaystyle sigma ^{2}} et Z {displaystyle Z} est leur moyenne mise à l’échelle par n {displaystyle {sqrt {n}}}

Z = n ( 1 n ∑ i = 1 n X i ) {displaystyle Z={sqrt {n}}left({frac {1}{n}}sum _{i=1}^{n}X_{i}right)}

Ensuite, comme n {displaystyle n} augmente, la distribution de probabilité de Z {displaystyle Z} tendra vers la distribution normale avec une moyenne et une variance nulles σ 2 {displaystyle sigma ^{2}} .

Le théorème peut être étendu aux variables ( X i ) {displaystyle (X_{i})} qui ne sont pas indépendants et/ou pas identiquement distribués si certaines contraintes sont posées sur le degré de dépendance et les moments des distributions.

De nombreuses statistiques de test , scores et estimateurs rencontrés dans la pratique contiennent des sommes de certaines variables aléatoires, et encore plus d’estimateurs peuvent être représentés comme des sommes de variables aléatoires grâce à l’utilisation de fonctions d’influence . Le théorème central limite implique que ces paramètres statistiques auront des distributions asymptotiquement normales.

Le théorème central limite implique également que certaines distributions peuvent être approchées par la distribution normale, par exemple :

• La distribution binomiale B ( n , p ) {displaystyle B(n,p)} est approximativement normal avec une moyenne n p {displaystyle np} et variance n p ( 1 − p ) {displaystyle np(1-p)} pour les grands n {displaystyle n} et pour p {displaystyle p} pas trop proche de 0 ou 1.
• La distribution de Poisson de paramètre λ {displaystylelambda} est approximativement normal avec une moyenne λ {displaystylelambda} et variance λ {displaystylelambda} , pour les grandes valeurs de λ {displaystylelambda} . ^[38]
• La distribution du chi carré χ 2 ( k ) {displaystyle chi ^{2}(k)} est approximativement normal avec une moyenne k {displaystyle k} et variance 2 k {displaystyle 2k} , pour les grands k {displaystyle k} .
• La distribution t de Student t ( ν ) {displaystyle t(nu )} est approximativement normal avec une moyenne de 0 et une variance de 1 lorsque ν {displaystylenu } est large.

La précision de ces approximations dépend de l’objectif pour lequel elles sont nécessaires et du taux de convergence vers la distribution normale. Il arrive généralement que de telles approximations soient moins précises dans les queues de la distribution.

Une limite supérieure générale pour l’erreur d’approximation dans le théorème central limite est donnée par le théorème de Berry-Esseen , des améliorations de l’approximation sont données par les développements d’Edgeworth .

Ce théorème peut également être utilisé pour justifier la modélisation de la somme de nombreuses sources de bruit uniformes sous forme de bruit gaussien . Voir AWGN .

Opérations et fonctions des variables normales

a : Densité de probabilité d’une fonction cos ⁡ x 2 { style d’affichage cos x ^ {2}} d’une variable normale x {style d’affichage x} avec μ = − 2 {displaystylemu =-2} et σ = 3 {displaystylesigma =3} . b : Densité de probabilité d’une fonction x y {displaystyle x^{y}} de deux variables normales x {style d’affichage x} et y {displaystyle y} , où μ x = 1 {displaystylemu _{x}=1} , μ y = 2 {displaystylemu _{y}=2} , σ x = 0.1 {displaystylesigma _{x}=0.1} , σ y = 0.2 {displaystylesigma _{y}=0.2} , et ρ x y = 0.8 {displaystyle rho _{xy}=0.8} . c : carte thermique de la densité de probabilité conjointe de deux fonctions de deux variables normales corrélées x {style d’affichage x} et y {displaystyle y} , où μ x = − 2 {displaystylemu _{x}=-2} , μ y = 5 {displaystylemu _{y}=5} , σ x 2 = 10 {displaystylesigma _{x}^{2}=10} , σ y 2 = 20 {displaystylesigma _{y}^{2}=20} , et ρ x y = 0.495 {displaystyle rho _{xy}=0,495} . d : Densité de probabilité d’une fonction ∑ i = 1 4 | x i | {textstyle sum _{i=1}^{4}vert x_{i}vert } de 4 iid variables normales standard. Celles-ci sont calculées par la méthode numérique du lancer de rayons. ^[39]

La densité de probabilité , la distribution cumulative et la distribution cumulative inverse de toute fonction d’une ou plusieurs variables normales indépendantes ou corrélées peuvent être calculées avec la méthode numérique du lancer de rayons ^[39] ( code Matlab ). Dans les sections suivantes, nous examinons quelques cas particuliers.

Opérations sur une seule variable normale

Si X {displaystyle X} est distribué normalement avec une moyenne μ {displaystylemu} et variance σ 2 {displaystyle sigma ^{2}} , alors

• a X + b {displaystyle aX+b} , pour tout nombre réel a {displaystyle a} et b {displaystyle b} , est également distribué normalement, avec une moyenne a μ + b {displaystyle amu +b} et écart-type | a | σ {displaystyle |a|sigma } . Autrement dit, la famille des distributions normales est fermée sous les transformations linéaires.
• L’exponentielle de X {displaystyle X} est distribué log-normalement : e ^X ~ ln( N ( μ , σ ² )) .
• La valeur absolue de X {displaystyle X} a une distribution normale pliée : | X | ~ N _f ( μ , σ ² ) . Si μ = 0 {displaystylemu =0} c’est ce qu’on appelle la distribution semi-normale .
• La valeur absolue des résidus normalisés, | X − μ |/ σ , a une distribution chi à un degré de liberté : | X − μ | / σ ∼ χ 1 {displaystyle |X-mu |/sigma sim chi _{1}} .
• Le carré de X / σ a la distribution chi carré non centrale avec un degré de liberté : X 2 / σ 2 ∼ χ 1 2 ( μ 2 / σ 2 ) {textstyle X^{2}/sigma ^{2}sim chi _{1}^{2}(mu ^{2}/sigma ^{2})} . Si μ = 0 {displaystylemu =0} , la distribution est appelée simplement chi carré .
• Le log de vraisemblance d’une variable normale x {style d’affichage x} est simplement le logarithme de sa fonction de densité de probabilité : ln ⁡ p ( x ) = − 1 2 ( x − μ σ ) 2 − ln ⁡ ( σ 2 π ) = − 1 2 z 2 − ln ⁡ ( σ 2 π ) . {displaystyle ln p(x)=-{frac {1}{2}}left({frac {x-mu }{sigma }}right)^{2}-ln left (sigma {sqrt {2pi }}right)=-{frac {1}{2}}z^{2}-ln left(sigma {sqrt {2pi }} à droite).} Puisqu’il s’agit d’un carré mis à l’échelle et décalé d’une variable normale standard, il est distribué comme une variable chi carré mise à l’échelle et décalée .
• La distribution de la variable X restreinte à un intervalle [ a , b ] est appelée distribution normale tronquée .
• ( X − μ ) ⁻² a une distribution de Lévy de position 0 et d’échelle σ ⁻² .

Opérations sur deux variables normales indépendantes

• Si X 1 {displaystyle X_{1}} et X 2 {displaystyle X_{2}} sont deux variables aléatoires normales indépendantes , avec des moyennes μ 1 {displaystylemu _{1}} , μ 2 {displaystylemu _{2}} et écarts types σ 1 {displaystyle sigma _{1}} , σ 2 {displaystyle sigma _{2}} , alors leur somme X 1 + X 2 {displaystyle X_{1}+X_{2}} sera également distribué normalement, ^[preuve] avec une moyenne μ 1 + μ 2 {displaystyle mu _{1}+mu _{2}} et variance σ 1 2 + σ 2 2 {displaystyle sigma _{1}^{2}+sigma _{2}^{2}} .
• En particulier, si X {displaystyle X} et Y {displaystyle Y} sont des écarts normaux indépendants avec une moyenne et une variance nulles σ 2 {displaystyle sigma ^{2}} , alors X + Y {displaystyle X+Y} et X − Y {style d’affichage XY} sont également indépendants et normalement distribués, avec une moyenne et une variance nulles 2 σ 2 {displaystyle 2sigma ^{2}} . C’est un cas particulier de l’ identité de polarisation . ^[40]
• Si X 1 {displaystyle X_{1}} , X 2 {displaystyle X_{2}} sont deux écarts normaux indépendants de moyenne μ {displaystylemu} et déviation σ {displaystylesigma} , et a {displaystyle a} , b {displaystyle b} sont des nombres réels arbitraires, alors la variable X 3 = a X 1 + b X 2 − ( a + b ) μ a 2 + b 2 + μ {displaystyle X_{3}={frac {aX_{1}+bX_{2}-(a+b)mu }{sqrt {a^{2}+b^{2}}}}+ mu } est aussi normalement distribué avec une moyenne μ {displaystylemu} et déviation σ {displaystylesigma} . Il s’ensuit que la distribution normale est stable (d’exposant α = 2 {displaystylealpha =2} ).

Opérations sur deux variables normales standard indépendantes

Si X 1 {displaystyle X_{1}} et X 2 {displaystyle X_{2}} sont deux variables aléatoires normales standard indépendantes de moyenne 0 et de variance 1, alors

• Leur somme et leur différence sont distribuées normalement avec une moyenne nulle et une variance deux : X 1 ± X 2 ∼ N ( 0 , 2 ) {displaystyle X_{1}pm X_{2}sim N(0,2)} .
• Leur produit Z = X 1 X 2 {displaystyle Z=X_{1}X_{2}} suit la distribution du produit ^[41] avec la fonction de densité f Z ( z ) = π − 1 K 0 ( | z | ) {displaystyle f_{Z}(z)=pi ^{-1}K_{0}(|z|)} où K 0 {displaystyle K_{0}} est la fonction de Bessel modifiée de seconde espèce . Cette distribution est symétrique autour de zéro, illimitée en z = 0 {style d’affichage z=0} , et a la fonction caractéristique φ Z ( t ) = ( 1 + t 2 ) − 1 / 2 {displaystyle phi _{Z}(t)=(1+t^{2})^{-1/2}} .
• Leur rapport suit la distribution standard de Cauchy : X 1 / X 2 ∼ Cauchy ⁡ ( 0 , 1 ) {displaystyle X_{1}/X_{2}sim operatorname {Cauchy} (0,1)} .
• Leur norme euclidienne X 1 2 + X 2 2 {displaystyle {sqrt {X_{1}^{2}+X_{2}^{2}}}} a la distribution de Rayleigh .

Opérations sur plusieurs variables normales indépendantes

• Toute combinaison linéaire d’écarts normaux indépendants est un écart normal.
• Si X 1 , X 2 , … , X n {displaystyle X_{1},X_{2},ldots ,X_{n}} sont des variables aléatoires normales standard indépendantes, alors la somme de leurs carrés a la distribution du chi carré avec n {displaystyle n} degrés de liberté X 1 2 + ⋯ + X n 2 ∼ χ n 2 . {displaystyle X_{1}^{2}+cdots +X_{n}^{2}sim chi _{n}^{2}.}
• Si X 1 , X 2 , … , X n {displaystyle X_{1},X_{2},ldots ,X_{n}} sont des variables aléatoires indépendantes normalement distribuées avec des moyennes μ {displaystylemu} et écarts σ 2 {displaystyle sigma ^{2}} , alors leur moyenne d’échantillon est indépendante de l’ écart type d’échantillon , ^[42] qui peut être démontré en utilisant le théorème de Basu ou le théorème de Cochran . ^[43] Le rapport de ces deux quantités aura la distribution t de Student avec n − 1 {displaystyle n-1} degrés de liberté: t = X ̄ − μ S / n = 1 n ( X 1 + ⋯ + X n ) − μ 1 n ( n − 1 ) [ ( X 1 − X ̄ ) 2 + ⋯ + ( X n − X ̄ ) 2 ] ∼ t n − 1 . {displaystyle t={frac {{overline {X}}-mu }{S/{sqrt {n}}}}={frac {{frac {1}{n}}(X_{ 1}+cdots +X_{n})-mu }{sqrt {{frac {1}{n(n-1)}}left[(X_{1}-{overline {X}} )^{2}+cdots +(X_{n}-{overline {X}})^{2}right]}}}sim t_{n-1}.}
• Si X 1 , X 2 , … , X n {displaystyle X_{1},X_{2},ldots ,X_{n}} , Y 1 , Y 2 , … , Y m {displaystyle Y_{1},Y_{2},ldots ,Y_{m}} sont des variables aléatoires normales standard indépendantes, alors le rapport de leurs sommes de carrés normalisées aura la distribution F avec ( n , m ) degrés de liberté : ^[44] F = ( X 1 2 + X 2 2 + ⋯ + X n 2 ) / n ( Y 1 2 + Y 2 2 + ⋯ + Y m 2 ) / m ∼ F n , m . {displaystyle F={frac {left(X_{1}^{2}+X_{2}^{2}+cdots +X_{n}^{2}right)/n}{left (Y_{1}^{2}+Y_{2}^{2}+cdots +Y_{m}^{2}right)/m}}sim F_{n,m}.}

Opérations sur plusieurs variables normales corrélées

• Une forme quadratique d’un vecteur normal, c’est-à-dire une fonction quadratique q = ∑ x i 2 + ∑ x j + c {textstyle q=sum x_{i}^{2}+sum x_{j}+c} de plusieurs variables normales indépendantes ou corrélées, est une variable chi carré généralisée .

Opérations sur la fonction de densité

La distribution normale divisée est définie le plus directement en termes de jonction de sections mises à l’échelle des fonctions de densité de différentes distributions normales et de remise à l’échelle de la densité pour l’intégrer à une. La distribution normale tronquée résulte de la remise à l’échelle d’une section d’une fonction de densité unique.

Divisibilité infinie et théorème de Cramér

Pour tout entier positif n {displaystyle {text{n}}} , toute distribution normale de moyenne μ {displaystylemu} et variance σ 2 {displaystyle sigma ^{2}} est la distribution de la somme de n {displaystyle {text{n}}} écarts normaux indépendants, chacun avec une moyenne μ n {displaystyle {frac {mu }{n}}} et variance σ 2 n {displaystyle {frac {sigma ^{2}}{n}}} . Cette propriété est appelée divisibilité infinie . ^[45]

A l’inverse, si X 1 {displaystyle X_{1}} et X 2 {displaystyle X_{2}} sont des variables aléatoires indépendantes et leur somme X 1 + X 2 {displaystyle X_{1}+X_{2}} a une distribution normale, alors les deux X 1 {displaystyle X_{1}} et X 2 {displaystyle X_{2}} doit être des déviations normales. ^[46]

Ce résultat est connu sous le nom de théorème de décomposition de Cramér et équivaut à dire que la convolution de deux distributions est normale si et seulement si les deux sont normales. Le théorème de Cramér implique qu’une combinaison linéaire de variables non gaussiennes indépendantes n’aura jamais une distribution exactement normale, bien qu’elle puisse s’en approcher arbitrairement de près. ^[32]

Théorème de Bernstein

Le théorème de Bernstein stipule que si X {displaystyle X} et Y {displaystyle Y} sont indépendants et X + Y {displaystyle X+Y} et X − Y {style d’affichage XY} sont également indépendants, alors X et Y doivent nécessairement avoir des distributions normales. ^{[47] [48]}

Plus généralement, si X 1 , … , X n {displaystyle X_{1},ldots ,X_{n}} sont des variables aléatoires indépendantes, alors deux combinaisons linéaires distinctes ∑ a k X k {textstyle sum {a_{k}X_{k}}} et ∑ b k X k {textstyle sum {b_{k}X_{k}}} seront indépendants si et seulement si tous X k {displaystyle X_{k}} sont normaux et ∑ a k b k σ k 2 = 0 {textstyle sum {a_{k}b_{k}sigma _{k}^{2}=0}} , où σ k 2 {displaystyle sigma _{k}^{2}} désigne la variance de X k {displaystyle X_{k}} . ^[47]

Rallonges

La notion de distribution normale, étant l’une des distributions les plus importantes de la théorie des probabilités, a été étendue bien au-delà du cadre standard du cas univarié (c’est-à-dire unidimensionnel) (cas 1). Toutes ces extensions sont également appelées lois normales ou gaussiennes , il existe donc une certaine ambiguïté dans les noms.

• La distribution normale multivariée décrit la loi gaussienne dans l’ espace euclidien de dimension k . Un vecteur X ∈ R ^k est multivarié-normalement distribué si toute combinaison linéaire de ses composantes Σ^k
  _{j =1}a _j X _j a une distribution normale (univariée). La variance de X est unematrice définie positive symétrique k×k V . La distribution normale multivariée est un cas particulier des distributions elliptiques . En tant que tel, ses lieux d’iso-densité dans le cas k = 2 sont des ellipses et dans le cas de k arbitrairesont des ellipsoïdes .
• Distribution gaussienne rectifiée une version rectifiée de la distribution normale avec tous les éléments négatifs remis à 0
• La distribution normale complexe traite des vecteurs normaux complexes. Un vecteur complexe X ∈ C ^k est dit normal si ses composantes réelles et imaginaires possèdent conjointement une distribution normale multivariée à 2 k dimensions. La structure de variance-covariance de X est décrite par deux matrices : la matrice de variance Γ et la matrice de relation C .
• La distribution normale matricielle décrit le cas des matrices normalement distribuées.
• Les processus gaussiens sont les processus stochastiques normalement distribués . Ceux-ci peuvent être considérés comme des éléments d’un espace de Hilbert de dimension infinie H , et sont donc les analogues de vecteurs normaux multivariés pour le cas k = ∞ . Un élément aléatoire h ∈ H est dit normal si pour toute constante a ∈ H le produit scalaire ( a , h ) a une distribution normale (univariée). La structure de variance d’un tel élément aléatoire gaussien peut être décrite en termes d’opérateur de covariance linéaire K : H → H. Plusieurs processus gaussiens sont devenus suffisamment populaires pour avoir leur propre nom :
  • mouvement brownien ,
  • Pont brownien ,
  • Processus d’Ornstein-Uhlenbeck .
• La distribution q gaussienne est une construction mathématique abstraite qui représente un ” q-analogue » de la distribution normale.
• la q-gaussienne est un analogue de la distribution gaussienne, en ce sens qu’elle maximise l’ entropie de Tsallis , et est un type de distribution de Tsallis . Notez que cette distribution est différente de la distribution q gaussienne ci- dessus.

Une variable aléatoire X a une distribution normale en deux parties si elle a une distribution

f X ( x ) = N ( μ , σ 1 2 ) if x ≤ μ {displaystyle f_{X}(x)=N(mu ,sigma _{1}^{2}){text{ if }}xleq mu } f X ( x ) = N ( μ , σ 2 2 ) if x ≥ μ {displaystyle f_{X}(x)=N(mu ,sigma _{2}^{2}){text{ if }}xgeq mu }

où μ est la moyenne et σ ₁ et σ ₂ sont les écarts-types de la distribution à gauche et à droite de la moyenne respectivement.

La moyenne, la variance et le troisième moment central de cette distribution ont été déterminés ^[49]

E ⁡ ( X ) = μ + 2 π ( σ 2 − σ 1 ) {displaystyle operatorname {E} (X)=mu +{sqrt {frac {2}{pi }}}(sigma _{2}-sigma _{1})} V ⁡ ( X ) = ( 1 − 2 π ) ( σ 2 − σ 1 ) 2 + σ 1 σ 2 {displaystyle operatorname {V} (X)=left(1-{frac {2}{pi }}right)(sigma _{2}-sigma _{1})^{2} +sigma _{1}sigma _{2}} T ⁡ ( X ) = 2 π ( σ 2 − σ 1 ) [ ( 4 π − 1 ) ( σ 2 − σ 1 ) 2 + σ 1 σ 2 ] {displaystyle operatorname {T} (X)={sqrt {frac {2}{pi }}}(sigma _{2}-sigma _{1})left[left({ frac {4}{pi }}-1right)(sigma _{2}-sigma _{1})^{2}+sigma _{1}sigma _{2}right]}

où E( X ), V( X ) et T( X ) sont respectivement la moyenne, la variance et le troisième moment central.

L’une des principales utilisations pratiques de la loi gaussienne est de modéliser les distributions empiriques de nombreuses variables aléatoires différentes rencontrées dans la pratique. Dans ce cas, une extension possible serait une famille de distributions plus riche, ayant plus de deux paramètres et pouvant donc s’adapter plus précisément à la distribution empirique. Les exemples de telles extensions sont :

• Répartition de Pearson – une famille à quatre paramètres de distributions de probabilité qui étendent la loi normale pour inclure différentes valeurs d’asymétrie et d’aplatissement.
• La distribution normale généralisée , également connue sous le nom de distribution de puissance exponentielle, permet des queues de distribution avec des comportements asymptotiques plus épais ou plus fins.

Inférence statistique

Estimation des paramètres

Il arrive souvent que nous ne connaissions pas les paramètres de la distribution normale, mais que nous souhaitions plutôt les estimer . c’est-à-dire avoir un échantillon ( x 1 , … , x n ) {displaystyle (x_{1},ldots ,x_{n})} d’une normale N ( μ , σ 2 ) {displaystyle N(mu ,sigma ^{2})} population, nous aimerions connaître les valeurs approximatives des paramètres μ {displaystylemu} et σ 2 {displaystyle sigma ^{2}} . L’approche standard de ce problème est la méthode du maximum de vraisemblance , qui nécessite la maximisation de la fonction log-vraisemblance :

ln ⁡ L ( μ , σ 2 ) = ∑ i = 1 n ln ⁡ f ( x i ∣ μ , σ 2 ) = − n 2 ln ⁡ ( 2 π ) − n 2 ln ⁡ σ 2 − 1 2 σ 2 ∑ i = 1 n ( x i − μ ) 2 . {displaystyle ln {mathcal {L}}(mu ,sigma ^{2})=sum _{i=1}^{n}ln f(x_{i}mid mu , sigma ^{2})=-{frac {n}{2}}ln(2pi )-{frac {n}{2}}ln sigma ^{2}-{frac {1 }{2sigma ^{2}}}sum _{i=1}^{n}(x_{i}-mu )^{2}.}

Prendre des dérivées par rapport à μ {displaystylemu} et σ 2 {displaystyle sigma ^{2}} et la résolution du système résultant de conditions de premier ordre donne les estimations du maximum de vraisemblance :

μ ^ = x ̄ ≡ 1 n ∑ i = 1 n x i , σ ^ 2 = 1 n ∑ i = 1 n ( x i − x ̄ ) 2 . {displaystyle {hat {mu }}={overline {x}}equiv {frac {1}{n}}sum _{i=1}^{n}x_{i},qquad {hat {sigma }}^{2}={frac {1}{n}}sum _{i=1}^{n}(x_{i}-{overline {x}})^ {2}.} Moyenne de l’échantillon

Estimateur μ ^ {displaystyle textstyle {hat {mu }}} s’appelle la moyenne de l’échantillon , puisqu’il s’agit de la moyenne arithmétique de toutes les observations. La statistique x ̄ {displaystyle textstyle {overline {x}}} est complet et suffisant pour μ {displaystylemu} , et donc par le théorème de Lehmann–Scheffé , μ ^ {displaystyle textstyle {hat {mu }}} est l’ estimateur uniforme sans biais de la variance minimale (UMVU). ^[50] Dans les échantillons finis, il est distribué normalement :

μ ^ ∼ N ( μ , σ 2 / n ) . {displaystyle {hat {mu }}sim {mathcal {N}}(mu ,sigma ^{2}/n).}

La variance de cet estimateur est égale à l’ élément μμ de la matrice d’information inverse de Fisher I − 1 {displaystyle textstyle {mathcal {I}}^{-1}} . Cela implique que l’estimateur est efficace en échantillon fini . D’une importance pratique est le fait que l’ erreur type de μ ^ {displaystyle textstyle {hat {mu }}} est proportionnel à 1 / n {displaystyle textstyle 1/{sqrt {n}}} , c’est-à-dire que si l’on souhaite diminuer l’erreur type d’un facteur 10, il faut augmenter le nombre de points dans l’échantillon d’un facteur 100. Ce fait est largement utilisé pour déterminer la taille des échantillons pour les sondages d’opinion et le nombre de essais dans des simulations de Monte Carlo .

Du point de vue de la théorie asymptotique , μ ^ {displaystyle textstyle {hat {mu }}} est cohérent , c’est-à-dire qu’il converge en probabilité vers μ {displaystylemu} comme n → ∞ {displaystyle nrightarrow infty} . L’estimateur est aussi asymptotiquement normal , ce qui est un simple corollaire du fait qu’il est normal en échantillons finis :

n ( μ ^ − μ ) → d N ( 0 , σ 2 ) . {displaystyle {sqrt {n}}({hat {mu}}-mu ),{xrightarrow {d}},{mathcal {N}}(0,sigma ^{2} ).} Écart d’échantillon

L’estimateur σ ^ 2 {displaystyle textstyle {chapeau {sigma}}^{2}} s’appelle la variance de l’échantillon , puisqu’il s’agit de la variance de l’échantillon ( ( x 1 , … , x n ) {displaystyle (x_{1},ldots ,x_{n})} ). En pratique, un autre estimateur est souvent utilisé à la place du σ ^ 2 {displaystyle textstyle {chapeau {sigma}}^{2}} . Cet autre estimateur est noté s 2 {displaystyle s^{2}} , et est également appelée la variance de l’échantillon , ce qui représente une certaine ambiguïté dans la terminologie ; sa racine carrée s {displaystyle s} s’appelle l’ écart-type de l’échantillon . L’estimateur s 2 {displaystyle s^{2}} diffère de σ ^ 2 {displaystyle textstyle {chapeau {sigma}}^{2}} en ayant ( n − 1) au lieu de n au dénominateur (la soi-disant correction de Bessel ):

s 2 = n n − 1 σ ^ 2 = 1 n − 1 ∑ i = 1 n ( x i − x ̄ ) 2 . {displaystyle s^{2}={frac {n}{n-1}}{hat {sigma}}^{2}={frac {1}{n-1}}sum _{ i=1}^{n}(x_{i}-{overline {x}})^{2}.}

La différence entre s 2 {displaystyle s^{2}} et σ ^ 2 {displaystyle textstyle {chapeau {sigma}}^{2}} devient négligeable pour les grands n ‘s . Dans des échantillons finis cependant, la motivation derrière l’utilisation de s 2 {displaystyle s^{2}} est qu’il s’agit d’un estimateur sans biais du paramètre sous-jacent σ 2 {displaystyle sigma ^{2}} , tandis que σ ^ 2 {displaystyle textstyle {chapeau {sigma}}^{2}} est biaisé. De plus, par le théorème de Lehmann – Scheffé, l’estimateur s 2 {displaystyle s^{2}} est uniformément minimum variance sans biais (UMVU), ^[50] ce qui en fait le “meilleur” estimateur parmi tous les estimateurs sans biais. Cependant, on peut montrer que l’estimateur biaisé σ ^ 2 {displaystyle textstyle {chapeau {sigma}}^{2}} est “meilleur” que le s 2 {displaystyle s^{2}} en termes de critère d’erreur quadratique moyenne (MSE). Dans les échantillons finis, les deux s 2 {displaystyle s^{2}} et σ ^ 2 {displaystyle textstyle {chapeau {sigma}}^{2}} ont une distribution du chi carré à l’échelle avec ( n – 1) degrés de liberté :

s 2 ∼ σ 2 n − 1 ⋅ χ n − 1 2 , σ ^ 2 ∼ σ 2 n ⋅ χ n − 1 2 . {displaystyle s^{2}sim {frac {sigma ^{2}}{n-1}}cdot chi _{n-1}^{2},qquad {hat {sigma }}^{2}sim {frac {sigma ^{2}}{n}}cdot chi _{n-1}^{2}.}

La première de ces expressions montre que la variance de s 2 {displaystyle s^{2}} est égal à 2 σ 4 / ( n − 1 ) {displaystyle 2sigma ^{4}/(n-1)} , qui est légèrement supérieur à l’ élément σσ de la matrice d’information inverse de Fisher I − 1 {displaystyle textstyle {mathcal {I}}^{-1}} . Ainsi, s 2 {displaystyle s^{2}} n’est pas un estimateur efficace pour σ 2 {displaystyle sigma ^{2}} , et de plus, puisque s 2 {displaystyle s^{2}} est UMVU, nous pouvons conclure que l’estimateur efficace à échantillon fini pour σ 2 {displaystyle sigma ^{2}} n’existe pas.

En appliquant la théorie asymptotique, les deux estimateurs s 2 {displaystyle s^{2}} et σ ^ 2 {displaystyle textstyle {chapeau {sigma}}^{2}} sont cohérents, c’est-à-dire qu’ils convergent en probabilité vers σ 2 {displaystyle sigma ^{2}} que la taille de l’échantillon n → ∞ {displaystyle nrightarrow infty} . Les deux estimateurs sont également asymptotiquement normaux :

n ( σ ^ 2 − σ 2 ) ≃ n ( s 2 − σ 2 ) → d N ( 0 , 2 σ 4 ) . {displaystyle {sqrt {n}}({hat {sigma }}^{2}-sigma ^{2})simeq {sqrt {n}}(s^{2}-sigma ^ {2}),{xrightarrow {d}},{mathcal {N}}(0,2sigma ^{4}).}

En particulier, les deux estimateurs sont asymptotiquement efficaces pour σ 2 {displaystyle sigma ^{2}} .

Intervalles de confiance

D’ après le théorème de Cochran , pour les distributions normales, la moyenne de l’échantillon μ ^ {displaystyle textstyle {hat {mu }}} et les variances d’échantillon s ² sont indépendantes , ce qui signifie qu’il ne peut y avoir aucun gain à considérer leur distribution conjointe . Il existe également un théorème inverse : si dans un échantillon la moyenne et la variance de l’échantillon sont indépendantes, alors l’échantillon doit provenir de la distribution normale. L’indépendance entre μ ^ {displaystyle textstyle {hat {mu }}} et s peuvent être utilisés pour construire la soi-disant statistique t :

t = μ ^ − μ s / n = x ̄ − μ 1 n ( n − 1 ) ∑ ( x i − x ̄ ) 2 ∼ t n − 1 {displaystyle t={frac {{hat {mu }}-mu }{s/{sqrt {n}}}}={frac {{overline {x}}-mu }{ sqrt {{frac {1}{n(n-1)}}sum (x_{i}-{overline {x}})^{2}}}}sim t_{n-1}}

Cette quantité t a la distribution t de Student avec ( n − 1) degrés de liberté, et c’est une statistique auxiliaire (indépendante de la valeur des paramètres). L’inversion de la distribution de cette statistique t nous permettra de construire l’ intervalle de confiance pour μ ; ^[51] de même, l’inversion de la distribution χ ² de la statistique s ² nous donnera l’intervalle de confiance pour σ ² : ^[52]

μ ∈ [ μ ^ − t n − 1 , 1 − α / 2 1 n s , μ ^ + t n − 1 , 1 − α / 2 1 n s ] , {displaystyle mu in left[{hat {mu }}-t_{n-1,1-alpha /2}{frac {1}{sqrt {n}}}s,{ chapeau {mu }}+t_{n-1,1-alpha /2}{frac {1}{sqrt {n}}}sright],} σ 2 ∈ [ ( n − 1 ) s 2 χ n − 1 , 1 − α / 2 2 , ( n − 1 ) s 2 χ n − 1 , α / 2 2 ] , {displaystyle sigma ^{2}in left[{frac {(n-1)s^{2}}{chi _{n-1,1-alpha /2}^{2}} },{frac {(n-1)s^{2}}{chi _{n-1,alpha /2}^{2}}}right],}

où t _k,p et χ 2
k,p sont les p ièmes quantiles des distributions t – et χ ² respectivement. Ces intervalles de confiance sont du niveau de confiance 1 − α , ce qui signifie que les vraies valeurs μ et σ ² se situent en dehors de ces intervalles avec probabilité (ou niveau de signification ) α . En pratique, les gens prennent généralement α = 5 % , ce qui donne des intervalles de confiance à 95%.

Des formules approximatives peuvent être dérivées des distributions asymptotiques de μ ^ {displaystyle textstyle {hat {mu }}} et s ² :

μ ∈ [ μ ^ − | z α / 2 | 1 n s , μ ^ + | z α / 2 | 1 n s ] , {displaystyle mu in left[{hat {mu }}-|z_{alpha /2}|{frac {1}{sqrt {n}}}s,{hat {mu }}+|z_{alpha /2}|{frac {1}{sqrt {n}}}sright],} σ 2 ∈ [ s 2 − | z α / 2 | 2 n s 2 , s 2 + | z α / 2 | 2 n s 2 ] , {displaystyle sigma ^{2}in left[s^{2}-|z_{alpha /2}|{frac {sqrt {2}}{sqrt {n}}}s^{ 2},s^{2}+|z_{alpha /2}|{frac {sqrt {2}}{sqrt {n}}}s^{2}right],}

Les formules approchées deviennent valides pour les grandes valeurs de n , et sont plus pratiques pour le calcul manuel puisque les quantiles normaux standard z _{α /2} ne dépendent pas de n . En particulier, la valeur la plus populaire de α = 5% , donne | z _0,025 | = 1,96 .

Tests de normalité

Les tests de normalité évaluent la probabilité que l’ensemble de données donné { x ₁ , …, x _n } provienne d’une distribution normale. Typiquement, l’ hypothèse nulle H ₀ est que les observations sont distribuées normalement avec une moyenne μ et une variance σ ² non spécifiées , contre l’alternative H _a que la distribution est arbitraire. De nombreux tests (plus de 40) ont été conçus pour ce problème. Les plus importants d’entre eux sont décrits ci-dessous:

Les diagrammes de diagnostic sont plus attrayants intuitivement mais subjectifs en même temps, car ils reposent sur un jugement humain informel pour accepter ou rejeter l’hypothèse nulle.

• Diagramme Q–Q , également appelé diagramme de probabilité normale ou diagramme de classement , est un diagramme des valeurs triées de l’ensemble de données par rapport aux valeurs attendues des quantiles correspondants de la distribution normale standard. C’est-à-dire qu’il s’agit d’un tracé de points de la forme (Φ ⁻¹ ( p _k ), x _{( k )} ), où les points de traçage p _k sont égaux à p _k = ( k − α )/( n + 1 − 2 α ) et αest une constante d’ajustement, qui peut être comprise entre 0 et 1. Si l’hypothèse nulle est vraie, les points tracés doivent se trouver approximativement sur une ligne droite.
• Graphique P – P – similaire au graphique Q – Q, mais utilisé beaucoup moins fréquemment. Cette méthode consiste à tracer les points (Φ( z _{( k )} ), p _k ), où z ( k ) = ( x ( k ) − μ ^ ) / σ ^ {displaystyle textstyle z_{(k)}=(x_{(k)}-{hat {mu }})/{hat {sigma }}} . Pour des données normalement distribuées, ce tracé doit se trouver sur une ligne à 45° entre (0, 0) et (1, 1).

Tests d’adéquation :

Tests basés sur les moments :

• Test du K au carré de D’Agostino
• Essai de Jarque-Bera
• Test de Shapiro-Wilk : Ceci est basé sur le fait que la ligne dans le graphique Q–Q a la pente de σ . Le test compare l’estimation des moindres carrés de cette pente avec la valeur de la variance de l’échantillon et rejette l’hypothèse nulle si ces deux quantités diffèrent de manière significative.

Tests basés sur la fonction de distribution empirique :

• Test d’Anderson-Darling
• Test de Lilliefors (une adaptation du test de Kolmogorov-Smirnov )

Analyse bayésienne de la distribution normale

L’analyse bayésienne de données normalement distribuées est compliquée par les nombreuses possibilités différentes qui peuvent être envisagées :

• Soit la moyenne, soit la variance, soit ni l’une ni l’autre, peut être considérée comme une quantité fixe.
• Lorsque la variance est inconnue, l’analyse peut être effectuée directement en termes de variance, ou en termes de précision , l’inverse de la variance. La raison d’exprimer les formules en termes de précision est que l’analyse de la plupart des cas est simplifiée.
• Les cas univariés et multivariés doivent être pris en compte.
• Des distributions a priori conjuguées ou impropres peuvent être placées sur les variables inconnues.
• Un ensemble supplémentaire de cas se produit dans la régression linéaire bayésienne , où, dans le modèle de base, les données sont supposées être normalement distribuées et des priors normaux sont placés sur les coefficients de régression . L’analyse qui en résulte est similaire aux cas de base de données indépendantes identiquement distribuées .

Les formules pour les cas de régression non linéaire sont résumées dans l’ article antérieur conjugué .

Somme de deux quadratiques Forme scalaire

La formule auxiliaire suivante est utile pour simplifier les équations de mise à jour postérieure , qui autrement deviennent assez fastidieuses.

a ( x − y ) 2 + b ( x − z ) 2 = ( a + b ) ( x − a y + b z a + b ) 2 + a b a + b ( y − z ) 2 {displaystyle a(xy)^{2}+b(xz)^{2}=(a+b)left(x-{frac {ay+bz}{a+b}}right)^{ 2}+{frac {ab}{a+b}}(yz)^{2}}

Cette équation réécrit la somme de deux quadratiques en x en développant les carrés, en regroupant les termes en x et en complétant le carré . Notez ce qui suit au sujet des facteurs constants complexes attachés à certains des termes :

1. Le facteur a y + b z a + b {displaystyle {frac {ay+bz}{a+b}}} a la forme d’une moyenne pondérée de y et z .
2. a b a + b = 1 1 a + 1 b = ( a − 1 + b − 1 ) − 1 . {displaystyle {frac {ab}{a+b}}={frac {1}{{frac {1}{a}}+{frac {1}{b}}}}=(a^ {-1}+b^{-1})^{-1}.} Cela montre que ce facteur peut être considéré comme résultant d’une situation où les inverses des quantités a et b s’additionnent directement, donc pour combiner a et b eux-mêmes, il est nécessaire d’échanger, d’ajouter et d’échanger à nouveau le résultat pour revenir dans le unités d’origine. C’est exactement le genre d’opération effectuée par la moyenne harmonique , il n’est donc pas surprenant que a b a + b {displaystyle {frac {ab}{a+b}}} est la moitié de la moyenne harmonique de a et b .

Forme vectorielle

Une formule similaire peut être écrite pour la somme de deux vecteurs quadratiques : Si x , y , z sont des vecteurs de longueur k , et A et B sont des matrices symétriques et inversibles de taille k × k {displaystyle kfois k} , alors

( y − x ) ′ A ( y − x ) + ( x − z ) ′ B ( x − z ) = ( x − c ) ′ ( A + B ) ( x − c ) + ( y − z ) ′ ( A − 1 + B − 1 ) − 1 ( y − z ) {displaystyle {begin{aligned}&(mathbf {y} -mathbf {x} )’mathbf {A} (mathbf {y} -mathbf {x} )+(mathbf {x} – mathbf {z} )’mathbf {B} (mathbf {x} -mathbf {z} )\={}&(mathbf {x} -mathbf {c} )'(mathbf {A } +mathbf {B} )(mathbf {x} -mathbf {c} )+(mathbf {y} -mathbf {z} )'(mathbf {A} ^{-1}+mathbf {B} ^{-1})^{-1}(mathbf {y} -mathbf {z} )end{aligné}}}

où

c = ( A + B ) − 1 ( A y + B z ) {displaystyle mathbf {c} =(mathbf {A} +mathbf {B} )^{-1}(mathbf {A} mathbf {y} +mathbf {B} mathbf {z}) }

Notez que la forme x ′ A x est appelée une forme quadratique et est un scalaire :

x ′ A x = ∑ i , j a i j x i x j {displaystyle mathbf {x} ‘mathbf {A} mathbf {x} =sum _{i,j}a_{ij}x_{i}x_{j}}

En d’autres termes, il résume toutes les combinaisons possibles de produits de paires d’éléments de x , avec un coefficient séparé pour chacun. De plus, depuis x i x j = x j x i {displaystyle x_{i}x_{j}=x_{j}x_{i}} , seule la somme a i j + a j i {displaystyle a_{ij}+a_{ji}} importe pour tous les éléments hors diagonale de A , et il n’y a pas de perte de généralité en supposant que A est symétrique . De plus, si A est symétrique, alors la forme x ′ A y = y ′ A x . {displaystyle mathbf {x} ‘mathbf {A} mathbf {y} =mathbf {y} ‘mathbf {A} mathbf {x} .}

Somme des différences par rapport à la moyenne

Une autre formule utile est la suivante :

∑ i = 1 n ( x i − μ ) 2 = ∑ i = 1 n ( x i − x ̄ ) 2 + n ( x ̄ − μ ) 2 {displaystyle sum _{i=1}^{n}(x_{i}-mu )^{2}=sum _{i=1}^{n}(x_{i}-{bar {x}})^{2}+n({bar {x}}-mu )^{2}} où x ̄ = 1 n ∑ i = 1 n x i . {textstyle {bar {x}}={frac {1}{n}}sum _{i=1}^{n}x_{i}.}

Avec variance connue

Pour un ensemble de points de données iid normalement distribués X de taille n où chaque point individuel x suit x ∼ N ( μ , σ 2 ) {displaystyle xsim {mathcal {N}}(mu ,sigma ^{2})} avec une variance connue σ ² , la distribution a priori conjuguée est également normalement distribuée.

Cela peut être montré plus facilement en réécrivant la variance comme précision , c’est – à – dire en utilisant τ = 1/σ ² . Puis si x ∼ N ( μ , 1 / τ ) {displaystyle xsim {mathcal {N}}(mu ,1/tau )} et μ ∼ N ( μ 0 , 1 / τ 0 ) , {displaystyle mu sim {mathcal {N}}(mu _{0},1/tau _{0}),} nous procédons comme suit.

Premièrement, la fonction de vraisemblance est (en utilisant la formule ci-dessus pour la somme des différences par rapport à la moyenne) :

p ( X ∣ μ , τ ) = ∏ i = 1 n τ 2 π exp ⁡ ( − 1 2 τ ( x i − μ ) 2 ) = ( τ 2 π ) n / 2 exp ⁡ ( − 1 2 τ ∑ i = 1 n ( x i − μ ) 2 ) = ( τ 2 π ) n / 2 exp ⁡ [ − 1 2 τ ( ∑ i = 1 n ( x i − x ̄ ) 2 + n ( x ̄ − μ ) 2 ) ] . {displaystyle {begin{aligned}p(mathbf {X} mid mu ,tau )&=prod _{i=1}^{n}{sqrt {frac {tau }{2 pi }}}exp left(-{frac {1}{2}}tau (x_{i}-mu )^{2}right)\&=left({frac { tau }{2pi }}right)^{n/2}exp left(-{frac {1}{2}}tau sum _{i=1}^{n}(x_ {i}-mu )^{2}right)\&=left({frac {tau }{2pi }}right)^{n/2}exp left[-{ frac {1}{2}}tau left(sum _{i=1}^{n}(x_{i}-{bar {x}})^{2}+n({bar {x}}-mu )^{2}right)right].end{aligned}}}

Ensuite, nous procédons comme suit :

p ( μ ∣ X ) ∝ p ( X ∣ μ ) p ( μ ) = ( τ 2 π ) n / 2 exp ⁡ [ − 1 2 τ ( ∑ i = 1 n ( x i − x ̄ ) 2 + n ( x ̄ − μ ) 2 ) ] τ 0 2 π exp ⁡ ( − 1 2 τ 0 ( μ − μ 0 ) 2 ) ∝ exp ⁡ ( − 1 2 ( τ ( ∑ i = 1 n ( x i − x ̄ ) 2 + n ( x ̄ − μ ) 2 ) + τ 0 ( μ − μ 0 ) 2 ) ) ∝ exp ⁡ ( − 1 2 ( n τ ( x ̄ − μ ) 2 + τ 0 ( μ − μ 0 ) 2 ) ) = exp ⁡ ( − 1 2 ( n τ + τ 0 ) ( μ − n τ x ̄ + τ 0 μ 0 n τ + τ 0 ) 2 + n τ τ 0 n τ + τ 0 ( x ̄ − μ 0 ) 2 ) ∝ exp ⁡ ( − 1 2 ( n τ + τ 0 ) ( μ − n τ x ̄ + τ 0 μ 0 n τ + τ 0 ) 2 ) {displaystyle {begin{aligned}p(mu mid mathbf {X} )&propto p(mathbf {X} mid mu )p(mu )\&=left({frac {tau }{2pi }}right)^{n/2}exp left[-{frac {1}{2}}tau left(sum _{i=1}^{n}(x_{i}-{bar {x}})^{2}+n({bar {x}}-mu )^{2}right)right]{sqrt {frac {tau _{0}}{2pi }}}exp left(-{frac {1}{2}}tau _{0}(mu -mu _{0})^{2}right)\&propto exp left(-{frac {1}{2}}left(tau left(sum _{i=1}^{n}(x_{i}-{bar {x}})^{2}+n({bar {x}}-mu )^{2}right)+tau _{0}(mu -mu _{0})^{2}right)right)\&propto exp left(-{frac {1}{2}}left(ntau ({bar {x}}-mu )^{2}+tau _{0}(mu -mu _{0})^{2}right)right)\&=exp left(-{frac {1}{2}}(ntau +tau _{0})left(mu -{dfrac {ntau {bar {x}}+tau _{0}mu _{0}}{ntau +tau _{0}}}right)^{2}+{frac {ntau tau _{0}}{ntau +tau _{0}}}({bar {x}}-mu _{0})^{2}right)\&propto exp left(-{frac {1}{2}}(ntau +tau _{0})left(mu -{dfrac {ntau {bar {x}}+tau _{0}mu _{0}}{ntau +tau _{0}}}right)^{2}right)end{aligned}}}

Dans la dérivation ci-dessus, nous avons utilisé la formule ci-dessus pour la somme de deux quadratiques et éliminé tous les facteurs constants n’impliquant pas μ . Le résultat est le noyau d’une distribution normale, de moyenne n τ x ̄ + τ 0 μ 0 n τ + τ 0 {displaystyle {frac {ntau {bar {x}}+tau _{0}mu _{0}}{ntau +tau _{0}}}} et précision n τ + τ 0 {displaystyle ntau +tau _{0}} , c’est à dire

p ( μ ∣ X ) ∼ N ( n τ x ̄ + τ 0 μ 0 n τ + τ 0 , 1 n τ + τ 0 ) {displaystyle p(mu mid mathbf {X} )sim {mathcal {N}}left({frac {ntau {bar {x}}+tau _{0}mu _{0}}{ntau +tau _{0}}},{frac {1}{ntau +tau _{0}}}right)}

Cela peut être écrit comme un ensemble d’équations de mise à jour bayésiennes pour les paramètres postérieurs en termes de paramètres antérieurs :

τ 0 ′ = τ 0 + n τ μ 0 ′ = n τ x ̄ + τ 0 μ 0 n τ + τ 0 x ̄ = 1 n ∑ i = 1 n x i {displaystyle {begin{aligned}tau _{0}’&=tau _{0}+ntau \mu _{0}’&={frac {ntau {bar { x}}+tau _{0}mu _{0}}{ntau +tau _{0}}}\{bar {x}}&={frac {1}{n} }somme _{i=1}^{n}x_{i}end{aligné}}}

Autrement dit, pour combiner n points de données avec une précision totale de nτ (ou de manière équivalente, une variance totale de n / σ ² ) et une moyenne des valeurs x ̄ {displaystyle {bar {x}}} , dérivez une nouvelle précision totale simplement en ajoutant la précision totale des données à la précision totale précédente, et formez une nouvelle moyenne à l’aide d’une moyenne pondérée en précision , c’est-à-dire un moyenne pondéréede la moyenne des données et de la moyenne a priori, chacune pondérée par la précision totale associée. Cela a un sens logique si la précision est considérée comme indiquant la certitude des observations : dans la distribution de la moyenne a posteriori, chacune des composantes d’entrée est pondérée par sa certitude, et la certitude de cette distribution est la somme des certitudes individuelles. . (Pour l’intuition de ceci, comparez l’expression “le tout est (ou n’est pas) plus grand que la somme de ses parties”. De plus, considérez que la connaissance du postérieur provient d’une combinaison de la connaissance du prior et de la vraisemblance , il est donc logique que nous en soyons plus certains que de l’un ou l’autre de ses composants.)

La formule ci-dessus révèle pourquoi il est plus pratique de faire une analyse bayésienne des priors conjugués pour la distribution normale en termes de précision. La précision a posteriori est simplement la somme des précisions a priori et de vraisemblance, et la moyenne a posteriori est calculée à l’aide d’une moyenne pondérée en précision, comme décrit ci-dessus. Les mêmes formules peuvent être écrites en termes de variance en échangeant toutes les précisions, ce qui donne les formules les plus laides

σ 0 2 ′ = 1 n σ 2 + 1 σ 0 2 μ 0 ′ = n x ̄ σ 2 + μ 0 σ 0 2 n σ 2 + 1 σ 0 2 x ̄ = 1 n ∑ i = 1 n x i {displaystyle {begin{aligned}{sigma _{0}^{2}}’&={frac {1}{{frac {n}{sigma ^{2}}}+{frac {1}{sigma _{0}^{2}}}}\mu _{0}’&={frac {{frac {n{bar {x}}}{sigma ^ {2}}}+{frac {mu _{0}}{sigma _{0}^{2}}}}{{frac {n}{sigma ^{2}}}+{ frac {1}{sigma _{0}^{2}}}}}\{bar {x}}&={frac {1}{n}}sum _{i=1}^{ n}x_{i}end{aligné}}} Avec une moyenne connue

Pour un ensemble de points de données iid normalement distribués X de taille n où chaque point individuel x suit x ∼ N ( μ , σ 2 ) {displaystyle xsim {mathcal {N}}(mu ,sigma ^{2})} avec une moyenne μ connue, la distribution a priori conjuguée de la variance a une distribution gamma inverse ou une distribution chi carré inverse mise à l’échelle . Les deux sont équivalents sauf qu’ils ont des paramétrisations différentes . Bien que le gamma inverse soit plus couramment utilisé, nous utilisons le chi carré inverse mis à l’échelle pour des raisons de commodité. Le prior pour σ ² est le suivant :

p ( σ 2 ∣ ν 0 , σ 0 2 ) = ( σ 0 2 ν 0 2 ) ν 0 / 2 Γ ( ν 0 2 ) exp ⁡ [ − ν 0 σ 0 2 2 σ 2 ] ( σ 2 ) 1 + ν 0 2 ∝ exp ⁡ [ − ν 0 σ 0 2 2 σ 2 ] ( σ 2 ) 1 + ν 0 2 {displaystyle p(sigma ^{2}mid nu _{0},sigma _{0}^{2})={frac {(sigma _{0}^{2}{frac {nu _{0}}{2}})^{nu _{0}/2}}{Gamma left({frac {nu _{0}}{2}}right)} }~{frac {exp left[{frac {-nu _{0}sigma _{0}^{2}}{2sigma ^{2}}}right]}{( sigma ^{2})^{1+{frac {nu _{0}}{2}}}}}propto {frac {exp left[{frac {-nu _{0} sigma _{0}^{2}}{2sigma ^{2}}}right]}{(sigma ^{2})^{1+{frac {nu _{0}}{ 2}}}}}}

La fonction de vraisemblance ci-dessus, écrite en termes de variance, est :

p ( X ∣ μ , σ 2 ) = ( 1 2 π σ 2 ) n / 2 exp ⁡ [ − 1 2 σ 2 ∑ i = 1 n ( x i − μ ) 2 ] = ( 1 2 π σ 2 ) n / 2 exp ⁡ [ − S 2 σ 2 ] {displaystyle {begin{aligned}p(mathbf {X} mid mu ,sigma ^{2})&=left({frac {1}{2pi sigma ^{2}} }right)^{n/2}exp left[-{frac {1}{2sigma ^{2}}}sum _{i=1}^{n}(x_{i}- mu )^{2}right]\&=left({frac {1}{2pi sigma ^{2}}}right)^{n/2}exp left[- {frac {S}{2sigma ^{2}}}right]end{aligned}}}

où

S = ∑ i = 1 n ( x i − μ ) 2 . {displaystyle S=sum _{i=1}^{n}(x_{i}-mu )^{2}.}

Puis:

p ( σ 2 ∣ X ) ∝ p ( X ∣ σ 2 ) p ( σ 2 ) = ( 1 2 π σ 2 ) n / 2 exp ⁡ [ − S 2 σ 2 ] ( σ 0 2 ν 0 2 ) ν 0 2 Γ ( ν 0 2 ) exp ⁡ [ − ν 0 σ 0 2 2 σ 2 ] ( σ 2 ) 1 + ν 0 2 ∝ ( 1 σ 2 ) n / 2 1 ( σ 2 ) 1 + ν 0 2 exp ⁡ [ − S 2 σ 2 + − ν 0 σ 0 2 2 σ 2 ] = 1 ( σ 2 ) 1 + ν 0 + n 2 exp ⁡ [ − ν 0 σ 0 2 + S 2 σ 2 ] {displaystyle {begin{aligned}p(sigma ^{2}mid mathbf {X} )&propto p(mathbf {X} mid sigma ^{2})p(sigma ^{2})\&=left({frac {1}{2pi sigma ^{2}}}right)^{n/2}exp left[-{frac {S}{2sigma ^{2}}}right]{frac {(sigma _{0}^{2}{frac {nu _{0}}{2}})^{frac {nu _{0}}{2}}}{Gamma left({frac {nu _{0}}{2}}right)}}~{frac {exp left[{frac {-nu _{0}sigma _{0}^{2}}{2sigma ^{2}}}right]}{(sigma ^{2})^{1+{frac {nu _{0}}{2}}}}}\&propto left({frac {1}{sigma ^{2}}}right)^{n/2}{frac {1}{(sigma ^{2})^{1+{frac {nu _{0}}{2}}}}}exp left[-{frac {S}{2sigma ^{2}}}+{frac {-nu _{0}sigma _{0}^{2}}{2sigma ^{2}}}right]\&={frac {1}{(sigma ^{2})^{1+{frac {nu _{0}+n}{2}}}}}exp left[-{frac {nu _{0}sigma _{0}^{2}+S}{2sigma ^{2}}}right]end{aligned}}}

Ce qui précède est également une distribution chi carré inverse à l’échelle où

ν 0 ′ = ν 0 + n ν 0 ′ σ 0 2 ′ = ν 0 σ 0 2 + ∑ i = 1 n ( x i − μ ) 2 {displaystyle {begin{aligned}nu _{0}’&=nu _{0}+n\nu _{0}'{sigma _{0}^{2}}’&= nu _{0}sigma _{0}^{2}+sum _{i=1}^{n}(x_{i}-mu )^{2}end{aligned}}}

ou équivalent

ν 0 ′ = ν 0 + n σ 0 2 ′ = ν 0 σ 0 2 + ∑ i = 1 n ( x i − μ ) 2 ν 0 + n {displaystyle {begin{aligned}nu _{0}’&=nu _{0}+n\{sigma _{0}^{2}}’&={frac {nu _ {0}sigma _{0}^{2}+sum _{i=1}^{n}(x_{i}-mu )^{2}}{nu _{0}+n} }end{aligné}}}

En reparamétrant en termes de distribution gamma inverse , le résultat est :

α ′ = α + n 2 β ′ = β + ∑ i = 1 n ( x i − μ ) 2 2 {displaystyle {begin{aligned}alpha ‘&=alpha +{frac {n}{2}}\beta ‘&=beta +{frac {sum _{i=1}^ {n}(x_{i}-mu )^{2}}{2}}end{aligned}}} Avec moyenne inconnue et variance inconnue

Pour un ensemble de points de données iid normalement distribués X de taille n où chaque point individuel x suit x ∼ N ( μ , σ 2 ) {displaystyle xsim {mathcal {N}}(mu ,sigma ^{2})} avec une moyenne inconnue μ et une variance inconnue σ ^{2 , un a} priori conjugué combiné (multivarié) est placé sur la moyenne et la variance, consistant en une distribution normale-inverse-gamma . Logiquement, cela provient de la manière suivante :

1. De l’analyse du cas avec une moyenne inconnue mais une variance connue, nous voyons que les équations de mise à jour impliquent des statistiques suffisantes calculées à partir des données constituées de la moyenne des points de données et de la variance totale des points de données, calculées à leur tour à partir de la variance connue divisé par le nombre de points de données.
2. À partir de l’analyse du cas avec une variance inconnue mais une moyenne connue, nous voyons que les équations de mise à jour impliquent des statistiques suffisantes sur les données consistant en le nombre de points de données et la somme des écarts au carré .
3. Gardez à l’esprit que les valeurs de mise à jour postérieures servent de distribution antérieure lorsque d’autres données sont traitées. Ainsi, nous devrions logiquement penser à nos priors en termes de statistiques suffisantes que nous venons de décrire, avec la même sémantique gardée à l’esprit autant que possible.
4. Pour gérer le cas où la moyenne et la variance sont inconnues, nous pourrions placer des a priori indépendants sur la moyenne et la variance, avec des estimations fixes de la moyenne moyenne, de la variance totale, du nombre de points de données utilisés pour calculer la variance avant et de la somme des écarts au carré. . Notez cependant qu’en réalité, la variance totale de la moyenne dépend de la variance inconnue, et la somme des écarts au carré qui entre dans la variance antérieure (semble) dépendre de la moyenne inconnue. En pratique, cette dernière dépendance est relativement peu importante : le décalage de la moyenne réelle décale les points générés d’une quantité égale, et en moyenne les écarts au carré resteront les mêmes. Ce n’est pas le cas, cependant, avec la variance totale de la moyenne : à mesure que la variance inconnue augmente, la variance totale de la moyenne augmente proportionnellement,
5. Cela suggère que nous créons un a priori conditionnel de la moyenne sur la variance inconnue, avec un hyperparamètre spécifiant la moyenne des pseudo-observationsassocié à l’a priori, et un autre paramètre précisant le nombre de pseudo-observations. Ce nombre sert de paramètre d’échelle sur la variance, permettant de contrôler la variance globale de la moyenne par rapport au paramètre de variance réel. L’a priori de la variance possède également deux hyperparamètres, l’un spécifiant la somme des écarts au carré des pseudo-observations associées à l’a priori, et l’autre spécifiant à nouveau le nombre de pseudo-observations. Notez que chacun des priors a un hyperparamètre spécifiant le nombre de pseudo-observations, et dans chaque cas, cela contrôle la variance relative de ce prior. Ceux-ci sont donnés sous forme de deux hyperparamètres distincts afin que la variance (c’est-à-dire la confiance) des deux a priori puisse être contrôlée séparément.
6. Cela conduit immédiatement à la distribution normale-inverse-gamma , qui est le produit des deux distributions que nous venons de définir, avec des priors conjugués utilisés (une distribution gamma inverse sur la variance et une distribution normale sur la moyenne, conditionnelle à la variance) et avec les mêmes quatre paramètres juste définis.

Les priors sont normalement définis comme suit :

p ( μ ∣ σ 2 ; μ 0 , n 0 ) ∼ N ( μ 0 , σ 2 / n 0 ) p ( σ 2 ; ν 0 , σ 0 2 ) ∼ I χ 2 ( ν 0 , σ 0 2 ) = I G ( ν 0 / 2 , ν 0 σ 0 2 / 2 ) {displaystyle {begin{aligned}p(mu mid sigma ^{2};mu _{0},n_{0})&sim {mathcal {N}}(mu _{0 },sigma ^{2}/n_{0})\p(sigma ^{2};nu _{0},sigma _{0}^{2})&sim Ichi ^ {2}(nu _{0},sigma _{0}^{2})=IG(nu _{0}/2,nu _{0}sigma _{0}^{2} /2)end{aligné}}}

Les équations de mise à jour peuvent être dérivées et se présentent comme suit :

x ̄ = 1 n ∑ i = 1 n x i μ 0 ′ = n 0 μ 0 + n x ̄ n 0 + n n 0 ′ = n 0 + n ν 0 ′ = ν 0 + n ν 0 ′ σ 0 2 ′ = ν 0 σ 0 2 + ∑ i = 1 n ( x i − x ̄ ) 2 + n 0 n n 0 + n ( μ 0 − x ̄ ) 2 {displaystyle {begin{aligned}{bar {x}}&={frac {1}{n}}sum _{i=1}^{n}x_{i}\mu _{ 0}’&={frac {n_{0}mu _{0}+n{bar {x}}}{n_{0}+n}}\n_{0}’&=n_{0 }+n\nu _{0}’&=nu _{0}+n\nu _{0}'{sigma _{0}^{2}}’&=nu _{ 0}sigma _{0}^{2}+sum _{i=1}^{n}(x_{i}-{bar {x}})^{2}+{frac {n_{ 0}n}{n_{0}+n}}(mu _{0}-{bar {x}})^{2}end{aligned}}}

Aux nombres respectifs de pseudo-observations s’ajoutent les nombres d’observations réelles. Le nouvel hyperparamètre moyen est à nouveau une moyenne pondérée, cette fois pondérée par les nombres relatifs d’observations. Enfin, la mise à jour de ν 0 ′ σ 0 2 ′ {displaystyle nu _{0}'{sigma _{0}^{2}}’} est similaire au cas avec une moyenne connue, mais dans ce cas, la somme des écarts au carré est prise par rapport à la moyenne des données observées plutôt qu’à la vraie moyenne, et par conséquent un nouveau “terme d’interaction” doit être ajouté pour prendre soin de la source d’erreur supplémentaire provenant de l’écart entre l’a priori et la moyenne des données.

Preuve

Les distributions antérieures sont

p ( μ ∣ σ 2 ; μ 0 , n 0 ) ∼ N ( μ 0 , σ 2 / n 0 ) = 1 2 π σ 2 n 0 exp ⁡ ( − n 0 2 σ 2 ( μ − μ 0 ) 2 ) ∝ ( σ 2 ) − 1 / 2 exp ⁡ ( − n 0 2 σ 2 ( μ − μ 0 ) 2 ) p ( σ 2 ; ν 0 , σ 0 2 ) ∼ I χ 2 ( ν 0 , σ 0 2 ) = I G ( ν 0 / 2 , ν 0 σ 0 2 / 2 ) = ( σ 0 2 ν 0 / 2 ) ν 0 / 2 Γ ( ν 0 / 2 ) exp ⁡ [ − ν 0 σ 0 2 2 σ 2 ] ( σ 2 ) 1 + ν 0 / 2 ∝ ( σ 2 ) − ( 1 + ν 0 / 2 ) exp ⁡ [ − ν 0 σ 0 2 2 σ 2 ] . {displaystyle {begin{aligned}p(mu mid sigma ^{2};mu _{0},n_{0})&sim {mathcal {N}}(mu _{0},sigma ^{2}/n_{0})={frac {1}{sqrt {2pi {frac {sigma ^{2}}{n_{0}}}}}}exp left(-{frac {n_{0}}{2sigma ^{2}}}(mu -mu _{0})^{2}right)\&propto (sigma ^{2})^{-1/2}exp left(-{frac {n_{0}}{2sigma ^{2}}}(mu -mu _{0})^{2}right)\p(sigma ^{2};nu _{0},sigma _{0}^{2})&sim Ichi ^{2}(nu _{0},sigma _{0}^{2})=IG(nu _{0}/2,nu _{0}sigma _{0}^{2}/2)\&={frac {(sigma _{0}^{2}nu _{0}/2)^{nu _{0}/2}}{Gamma (nu _{0}/2)}}~{frac {exp left[{frac {-nu _{0}sigma _{0}^{2}}{2sigma ^{2}}}right]}{(sigma ^{2})^{1+nu _{0}/2}}}\&propto {(sigma ^{2})^{-(1+nu _{0}/2)}}exp left[{frac {-nu _{0}sigma _{0}^{2}}{2sigma ^{2}}}right].end{aligned}}}

Therefore, the joint prior is

p ( μ , σ 2 ; μ 0 , n 0 , ν 0 , σ 0 2 ) = p ( μ ∣ σ 2 ; μ 0 , n 0 ) p ( σ 2 ; ν 0 , σ 0 2 ) ∝ ( σ 2 ) − ( ν 0 + 3 ) / 2 exp ⁡ [ − 1 2 σ 2 ( ν 0 σ 0 2 + n 0 ( μ − μ 0 ) 2 ) ] . {displaystyle {begin{aligned}p(mu ,sigma ^{2};mu _{0},n_{0},nu _{0},sigma _{0}^{2} )&=p(mu mid sigma ^{2};mu _{0},n_{0}),p(sigma ^{2};nu _{0},sigma _{ 0}^{2})\&propto (sigma ^{2})^{-(nu _{0}+3)/2}exp left[-{frac {1}{2 sigma ^{2}}}left(nu _{0}sigma _{0}^{2}+n_{0}(mu -mu _{0})^{2}right) right].end{aligné}}}

La fonction de vraisemblance de la section ci-dessus avec une variance connue est :

p ( X ∣ μ , σ 2 ) = ( 1 2 π σ 2 ) n / 2 exp ⁡ [ − 1 2 σ 2 ( ∑ i = 1 n ( x i − μ ) 2 ) ] {displaystyle {begin{aligned}p(mathbf {X} mid mu ,sigma ^{2})&=left({frac {1}{2pi sigma ^{2}} }right)^{n/2}exp left[-{frac {1}{2sigma ^{2}}}left(sum _{i=1}^{n}(x_{ i}-mu )^{2}right)right]end{aligné}}}

En l’écrivant en termes de variance plutôt que de précision, nous obtenons :

p ( X ∣ μ , σ 2 ) = ( 1 2 π σ 2 ) n / 2 exp ⁡ [ − 1 2 σ 2 ( ∑ i = 1 n ( x i − x ̄ ) 2 + n ( x ̄ − μ ) 2 ) ] ∝ σ 2 − n / 2 exp ⁡ [ − 1 2 σ 2 ( S + n ( x ̄ − μ ) 2 ) ] {displaystyle {begin{aligned}p(mathbf {X} mid mu ,sigma ^{2})&=left({frac {1}{2pi sigma ^{2}} }right)^{n/2}exp left[-{frac {1}{2sigma ^{2}}}left(sum _{i=1}^{n}(x_{ je}-{bar {x}})^{2}+n({bar {x}}-mu )^{2}right)right]\&propto {sigma ^{2 }}^{-n/2}exp left[-{frac {1}{2sigma ^{2}}}left(S+n({bar {x}}-mu )^ {2}right)right]end{aligné}}}

où S = ∑ i = 1 n ( x i − x ̄ ) 2 . {textstyle S=sum _{i=1}^{n}(x_{i}-{bar {x}})^{2}.}

Par conséquent, le postérieur est (en supprimant les hyperparamètres comme facteurs de conditionnement):

p ( μ , σ 2 ∣ X ) ∝ p ( μ , σ 2 ) p ( X ∣ μ , σ 2 ) ∝ ( σ 2 ) − ( ν 0 + 3 ) / 2 exp ⁡ [ − 1 2 σ 2 ( ν 0 σ 0 2 + n 0 ( μ − μ 0 ) 2 ) ] σ 2 − n / 2 exp ⁡ [ − 1 2 σ 2 ( S + n ( x ̄ − μ ) 2 ) ] = ( σ 2 ) − ( ν 0 + n + 3 ) / 2 exp ⁡ [ − 1 2 σ 2 ( ν 0 σ 0 2 + S + n 0 ( μ − μ 0 ) 2 + n ( x ̄ − μ ) 2 ) ] = ( σ 2 ) − ( ν 0 + n + 3 ) / 2 exp ⁡ [ − 1 2 σ 2 ( ν 0 σ 0 2 + S + n 0 n n 0 + n ( μ 0 − x ̄ ) 2 + ( n 0 + n ) ( μ − n 0 μ 0 + n x ̄ n 0 + n ) 2 ) ] ∝ ( σ 2 ) − 1 / 2 exp ⁡ [ − n 0 + n 2 σ 2 ( μ − n 0 μ 0 + n x ̄ n 0 + n ) 2 ] × ( σ 2 ) − ( ν 0 / 2 + n / 2 + 1 ) exp ⁡ [ − 1 2 σ 2 ( ν 0 σ 0 2 + S + n 0 n n 0 + n ( μ 0 − x ̄ ) 2 ) ] = N μ ∣ σ 2 ( n 0 μ 0 + n x ̄ n 0 + n , σ 2 n 0 + n ) ⋅ I G σ 2 ( 1 2 ( ν 0 + n ) , 1 2 ( ν 0 σ 0 2 + S + n 0 n n 0 + n ( μ 0 − x ̄ ) 2 ) ) . {displaystyle {begin{aligned}p(mu ,sigma ^{2}mid mathbf {X} )&propto p(mu ,sigma ^{2}),p(mathbf {X} mid mu ,sigma ^{2})\&propto (sigma ^{2})^{-(nu _{0}+3)/2}exp left[-{frac {1}{2sigma ^{2}}}left(nu _{0}sigma _{0}^{2}+n_{0}(mu -mu _{0})^{2}right)right]{sigma ^{2}}^{-n/2}exp left[-{frac {1}{2sigma ^{2}}}left(S+n({bar {x}}-mu )^{2}right)right]\&=(sigma ^{2})^{-(nu _{0}+n+3)/2}exp left[-{frac {1}{2sigma ^{2}}}left(nu _{0}sigma _{0}^{2}+S+n_{0}(mu -mu _{0})^{2}+n({bar {x}}-mu )^{2}right)right]\&=(sigma ^{2})^{-(nu _{0}+n+3)/2}exp left[-{frac {1}{2sigma ^{2}}}left(nu _{0}sigma _{0}^{2}+S+{frac {n_{0}n}{n_{0}+n}}(mu _{0}-{bar {x}})^{2}+(n_{0}+n)left(mu -{frac {n_{0}mu _{0}+n{bar {x}}}{n_{0}+n}}right)^{2}right)right]\&propto (sigma ^{2})^{-1/2}exp left[-{frac {n_{0}+n}{2sigma ^{2}}}left(mu -{frac {n_{0}mu _{0}+n{bar {x}}}{n_{0}+n}}right)^{2}right]\&quad times (sigma ^{2})^{-(nu _{0}/2+n/2+1)}exp left[-{frac {1}{2sigma ^{2}}}left(nu _{0}sigma _{0}^{2}+S+{frac {n_{0}n}{n_{0}+n}}(mu _{0}-{bar {x}})^{2}right)right]\&={mathcal {N}}_{mu mid sigma ^{2}}left({frac {n_{0}mu _{0}+n{bar {x}}}{n_{0}+n}},{frac {sigma ^{2}}{n_{0}+n}}right)cdot {rm {IG}}_{sigma ^{2}}left({frac {1}{2}}(nu _{0}+n),{frac {1}{2}}left(nu _{0}sigma _{0}^{2}+S+{frac {n_{0}n}{n_{0}+n}}(mu _{0}-{bar {x}})^{2}right)right).end{aligned}}}

En d’autres termes, la distribution postérieure a la forme d’un produit d’une distribution normale sur p ( μ | σ ² ) fois une distribution gamma inverse sur p (σ ² ), avec des paramètres qui sont les mêmes que les équations de mise à jour ci-dessus.

Occurrence et applications

L’occurrence de la distribution normale dans les problèmes pratiques peut être grossièrement classée en quatre catégories :

1. Distributions exactement normales ;
2. Lois approximativement normales, par exemple lorsqu’une telle approximation est justifiée par le théorème central limite ; et
3. Distributions modélisées comme normales – la distribution normale étant la distribution avec une entropie maximale pour une moyenne et une variance données.
4. Problèmes de régression – la distribution normale étant trouvée après que les effets systématiques ont été suffisamment bien modélisés.

Normalité exacte

L’état fondamental d’un oscillateur harmonique quantique a la distribution gaussienne .

Certaines quantités en physique sont distribuées normalement, comme l’a d’abord démontré James Clerk Maxwell . Des exemples de telles quantités sont :

• Fonction de densité de probabilité d’un état fondamental dans un oscillateur harmonique quantique .
• La position d’une particule qui subit la diffusion . Si initialement la particule est située à un point spécifique (c’est-à-dire que sa distribution de probabilité est la fonction delta de Dirac ), alors après le temps t son emplacement est décrit par une distribution normale de variance t , qui satisfait l’ équation de diffusion ∂ ∂ t f ( x , t ) = 1 2 ∂ 2 ∂ x 2 f ( x , t ) {displaystyle {frac {partial }{partial t}}f(x,t)={frac {1}{2}}{frac {partial ^{2}}{partial x^{ 2}}}f(x,t)} . Si l’emplacement initial est donné par une certaine fonction de densité g ( x ) {displaystyle g(x)} , alors la densité au temps t est la convolution de g et la PDF normale.

Normalité approximative

Des distributions approximativement normales se produisent dans de nombreuses situations, comme l’explique le théorème central limite . Lorsque le résultat est produit par de nombreux petits effets agissant de manière additive et indépendante , sa distribution sera proche de la normale. L’approximation normale ne sera pas valide si les effets agissent de manière multiplicative (au lieu de s’additionner), ou s’il existe une seule influence externe qui a une ampleur considérablement plus grande que le reste des effets.

• Dans les problèmes de comptage, où le théorème central limite comprend une approximation discrète à continue et où des distributions infiniment divisibles et décomposables sont impliquées, telles que
  • Variables aléatoires binomiales , associées à des variables de réponse binaires ;
  • Variables aléatoires de Poisson , associées à des événements rares ;
• Le rayonnement thermique a une distribution de Bose-Einstein sur des échelles de temps très courtes et une distribution normale sur des échelles de temps plus longues en raison du théorème central limite.

Normalité supposée

Histogramme des largeurs de sépales pour Iris versicolor à partir de l’ensemble de données sur les fleurs d’Iris de Fisher , avec une distribution normale superposée la mieux ajustée.

Je ne peux reconnaître l’apparition de la courbe normale – la courbe laplacienne des erreurs – que comme un phénomène très anormal. Il est approximativement approximé dans certaines distributions; pour cette raison, et à cause de sa belle simplicité, on peut peut-être s’en servir comme première approximation, notamment dans les investigations théoriques.

—Pearson (1901)

Il existe des méthodes statistiques pour tester empiriquement cette hypothèse; voir la section Tests de normalité ci-dessus .

• En biologie , le logarithme de diverses variables a tendance à avoir une distribution normale, c’est-à-dire qu’ils ont tendance à avoir une distribution log-normale (après séparation sur les sous-populations hommes/femmes), avec des exemples comprenant :
  • Mesures de la taille des tissus vivants (longueur, taille, surface cutanée, poids) ; ^[53]
  • La longueur des appendices inertes (poils, griffes, ongles, dents) des spécimens biologiques, dans le sens de la croissance ; vraisemblablement l’épaisseur de l’écorce des arbres entre également dans cette catégorie;
  • Certaines mesures physiologiques, telles que la pression artérielle des humains adultes.
• En finance, en particulier dans le modèle Black-Scholes , les variations du logarithme des taux de change, des indices de prix et des indices boursiers sont supposées normales (ces variables se comportent comme des intérêts composés , et non comme des intérêts simples, et sont donc multiplicatives). Certains mathématiciens comme Benoit Mandelbrot ont soutenu que les distributions log-Levy , qui possèdent des queues lourdes , seraient un modèle plus approprié, en particulier pour l’analyse des krachs boursiers . L’utilisation de l’hypothèse de distribution normale survenant dans les modèles financiers a également été critiquée par Nassim Nicholas Taleb dans ses travaux.
• Les erreurs de mesure dans les expériences physiques sont souvent modélisées par une distribution normale. Cette utilisation d’une distribution normale n’implique pas que l’on suppose que les erreurs de mesure sont distribuées normalement, mais l’utilisation de la distribution normale produit les prédictions les plus conservatrices possibles étant donné uniquement la connaissance de la moyenne et de la variance des erreurs. ^[54]
• Dans les tests standardisés , les résultats peuvent être amenés à avoir une distribution normale en sélectionnant le nombre et la difficulté des questions (comme dans le test de QI ) ou en transformant les résultats bruts des tests en scores de “sortie” en les ajustant à la distribution normale. Par exemple, la plage traditionnelle de 200 à 800 du SAT est basée sur une distribution normale avec une moyenne de 500 et un écart type de 100.

Ajustement de la distribution normale cumulative aux précipitations d’octobre, voir l’ajustement de la distribution

• De nombreux scores sont dérivés de la distribution normale, y compris les rangs centiles (“centiles” ou “quantiles”), les équivalents de courbe normale , les stanines , les scores z et les scores T. De plus, certaines procédures statistiques comportementales supposent que les scores sont normalement distribués ; par exemple, les tests t et les ANOVA . La notation de la courbe en cloche attribue des notes relatives sur la base d’une distribution normale des scores.
• En hydrologie , la distribution du débit fluvial ou des précipitations de longue durée, par exemple les totaux mensuels et annuels, est souvent considérée comme pratiquement normale selon le théorème central limite . ^[55] L’image bleue, réalisée avec CumFreq , illustre un exemple d’ajustement de la distribution normale aux précipitations d’octobre classées montrant la ceinture de confiance à 90% basée sur la distribution binomiale . Les données pluviométriques sont représentées en traçant les positions dans le cadre de l’ analyse des fréquences cumulées .

Problèmes méthodologiques et examen par les pairs

John Ioannidis soutient que l’utilisation d’écarts-types normalement distribués comme normes pour valider les résultats de la recherche laisse des prédictions falsifiablessur des phénomènes qui ne sont pas normalement distribués non testés. Cela inclut, par exemple, les phénomènes qui n’apparaissent que lorsque toutes les conditions nécessaires sont réunies et qu’on ne peut pas se substituer à un autre d’une manière semblable à une addition et les phénomènes qui ne sont pas distribués au hasard. Ioannidis soutient que la validation centrée sur l’écart type donne une fausse apparence de validité aux hypothèses et aux théories où certaines prédictions falsifiables, mais pas toutes, sont normalement distribuées puisque la partie des prédictions falsifiables contre lesquelles il existe des preuves peut et dans certains cas se trouve dans le non-normalement parties distribuées de la gamme de prédictions falsifiables, ainsi que rejeter sans fondement des hypothèses pour lesquelles aucune des prédictions falsifiables n’est normalement distribuée comme si elles étaient infalsifiables alors qu’en fait elles font des prédictions falsifiables.^[56]

Méthodes de calcul

Génération de valeurs à partir d’une distribution normale

La machine à haricots , un dispositif inventé par Francis Galton , peut être appelée le premier générateur de variables aléatoires normales. Cette machine se compose d’une planche verticale avec des rangées de broches entrelacées. Les petites balles sont lâchées par le haut, puis rebondissent au hasard à gauche ou à droite lorsqu’elles frappent les quilles. Les balles sont collectées dans des bacs en bas et se déposent dans un motif ressemblant à la courbe gaussienne.

Dans les simulations informatiques, en particulier dans les applications de la méthode de Monte-Carlo , il est souvent souhaitable de générer des valeurs normalement distribuées. Les algorithmes répertoriés ci-dessous génèrent tous les écarts normaux standard, car a N ( μ , σ ² ) peut être généré comme X = μ + σZ , où Z est la normale standard. Tous ces algorithmes reposent sur la disponibilité d’un générateur de nombres aléatoires U capable de produire des variables aléatoires uniformes .

• La méthode la plus simple est basée sur la propriété de transformation intégrale de probabilité : si U est distribué uniformément sur (0,1), alors Φ ⁻¹ ( U ) aura la distribution normale standard. L’inconvénient de cette méthode est qu’elle repose sur le calcul de la fonction probit Φ ^-1 , ce qui ne peut être fait analytiquement. Certaines méthodes approximatives sont décrites dans Hart (1968) et dans l’ article erf . Wichura donne un algorithme rapide pour calculer cette fonction à 16 décimales, ^[57] qui est utilisé par R pour calculer des variables aléatoires de la distribution normale.
• Une approche approximative facile à programmer qui repose sur le théorème central limite est la suivante : générez 12 écarts U (0,1) uniformes, additionnez-les tous et soustrayez 6 – la variable aléatoire résultante aura une distribution normale approximativement standard. En vérité, la distribution sera Irwin-Hall , qui est une approximation polynomiale d’ordre 11 à 12 sections de la distribution normale. Cet écart aléatoire aura une plage limitée de (−6, 6). ^[58] Notez que dans une vraie distribution normale, seulement 0,00034 % de tous les échantillons tomberont en dehors de ±6σ.
• La méthode de Box-Muller utilise deux nombres aléatoires indépendants U et V répartis uniformément sur (0,1). Alors les deux variables aléatoires X et Y X = − 2 ln ⁡ U cos ⁡ ( 2 π V ) , Y = − 2 ln ⁡ U sin ⁡ ( 2 π V ) . {displaystyle X={sqrt {-2ln U}},cos(2pi V),qquad Y={sqrt {-2ln U}},sin(2pi V).} auront tous deux la distribution normale standard et seront indépendants . Cette formulation survient parce que pour un vecteur aléatoire normal bivarié ( X , Y ) la norme au carré X ² + Y ² aura la distribution du chi carré à deux degrés de liberté, qui est une variable aléatoire exponentielle facilement générée correspondant à la quantité −2ln ( U ) dans ces équations ; et l’angle est réparti uniformément autour du cercle, choisi par la variable aléatoire V .
• La méthode polaire de Marsaglia est une modification de la méthode de Box-Muller qui ne nécessite pas le calcul des fonctions sinus et cosinus. Dans cette méthode, U et V sont tirés de la distribution uniforme (−1,1), puis S = U ² + V ² est calculé. Si S est supérieur ou égal à 1, alors la méthode recommence, sinon les deux quantités X = U − 2 ln ⁡ S S , Y = V − 2 ln ⁡ S S {displaystyle X=U{sqrt {frac {-2ln S}{S}}},qquad Y=V{sqrt {frac {-2ln S}{S}}}} sont retournés. Encore une fois, X et Y sont des variables aléatoires normales standard indépendantes.
• La méthode Ratio ^[59] est une méthode de rejet. L’algorithme procède comme suit :
  • Génère deux déviations uniformes indépendantes U et V ;
  • Calculer X = √ 8/ e ( V − 0.5)/ U ;
  • Facultatif : si X ² ≤ 5 − 4 e ^1/4 U alors accepter X et terminer l’algorithme ;
  • Facultatif : si X ² ≥ 4 e ^−1,35 / U + 1,4 alors rejeter X et recommencer depuis l’étape 1 ;
  • Si X ² ≤ −4 ln U alors accepter X , sinon recommencer l’algorithme.

  Les deux étapes optionnelles permettent d’éviter dans la plupart des cas l’évaluation du logarithme à la dernière étape. Ces étapes peuvent être grandement améliorées ^[60] de sorte que le logarithme est rarement évalué.

• L’ algorithme de ziggourat ^[61] est plus rapide que la transformée de Box-Muller et toujours exact. Dans environ 97% de tous les cas, il n’utilise que deux nombres aléatoires, un entier aléatoire et un uniforme aléatoire, une multiplication et un test if. Ce n’est que dans 3% des cas, où la combinaison de ces deux tombe en dehors du “noyau de la ziggourat” (une sorte d’échantillonnage de rejet utilisant des logarithmes), que des exponentielles et des nombres aléatoires plus uniformes doivent être employés.
• L’arithmétique des nombres entiers peut être utilisée pour échantillonner à partir de la distribution normale standard. ^[62] Cette méthode est exacte en ce sens qu’elle satisfait aux conditions d’ approximation idéale ; ^[63] c’est-à-dire que cela équivaut à échantillonner un nombre réel à partir de la distribution normale standard et à l’arrondir au nombre à virgule flottante représentable le plus proche.
• Il y a aussi une enquête ^[64] sur le lien entre la transformée rapide de Hadamard et la distribution normale, puisque la transformée utilise juste l’addition et la soustraction et par le théorème de la limite centrale, des nombres aléatoires de presque n’importe quelle distribution seront transformés en distribution normale. À cet égard, une série de transformées de Hadamard peut être combinée avec des permutations aléatoires pour transformer des ensembles de données arbitraires en données normalement distribuées.

Approximations numériques pour le CDF normal et la fonction quantile normale

Le CDF normal standard est largement utilisé dans le calcul scientifique et statistique.

Les valeurs Φ( x ) peuvent être approchées très précisément par une variété de méthodes, telles que l’intégration numérique , la série de Taylor , la série asymptotique et les fractions continues . Différentes approximations sont utilisées en fonction du niveau de précision souhaité.

• Zelen & Severo (1964) donnent l’approximation de Φ( x ) pour x > 0 avec l’erreur absolue | ε ( x ) | < 7.5·10 ⁻⁸ (algorithme 26.2.17 ) : Φ ( x ) = 1 − φ ( x ) ( b 1 t + b 2 t 2 + b 3 t 3 + b 4 t 4 + b 5 t 5 ) + ε ( x ) , t = 1 1 + b 0 x , {displaystyle Phi (x)=1-varphi (x)left(b_{1}t+b_{2}t^{2}+b_{3}t^{3}+b_{4}t ^{4}+b_{5}t^{5}right)+varepsilon (x),qquad t={frac {1}{1+b_{0}x}},} où φ ( x ) est la PDF normale standard, et b ₀ = 0,2316419, b ₁ = 0,319381530, b ₂ = −0,356563782, b ₃ = 1,781477937, b ₄ = −1,821255978, b ₅ = 1,330274429.
• Hart (1968) liste quelques dizaines d’approximations – au moyen de fonctions rationnelles, avec ou sans exponentielles – pour la fonction erfc() . Ses algorithmes varient dans le degré de complexité et la précision qui en résulte, avec une précision absolue maximale de 24 chiffres. Un algorithme de West (2009) combine l’algorithme de Hart 5666 avec une approximation de fraction continue dans la queue pour fournir un algorithme de calcul rapide avec une précision à 16 chiffres.
• Cody (1969) après avoir rappelé que la solution de Hart68 n’est pas adaptée à erf, donne une solution à la fois pour erf et erfc, avec une erreur relative maximale liée, via l’approximation rationnelle de Chebyshev .
• Marsaglia (2004) a proposé un algorithme simple ^{[note 1]} basé sur le développement en série de Taylor Φ ( x ) = 1 2 + φ ( x ) ( x + x 3 3 + x 5 3 ⋅ 5 + x 7 3 ⋅ 5 ⋅ 7 + x 9 3 ⋅ 5 ⋅ 7 ⋅ 9 + ⋯ ) {displaystyle Phi (x)={frac {1}{2}}+varphi (x)left(x+{frac {x^{3}}{3}}+{frac {x^ {5}}{3cdot 5}}+{frac {x^{7}}{3cdot 5cdot 7}}+{frac {x^{9}}{3cdot 5cdot 7cdot 9}}+cdots right)} pour calculer Φ( x ) avec une précision arbitraire. L’inconvénient de cet algorithme est un temps de calcul relativement lent (par exemple, il faut plus de 300 itérations pour calculer la fonction avec 16 chiffres de précision lorsque x = 10 ).
• La bibliothèque scientifique GNU calcule les valeurs du CDF normal standard à l’aide des algorithmes de Hart et des approximations avec les polynômes de Chebyshev .

Shore (1982) a introduit des approximations simples qui peuvent être incorporées dans les modèles d’optimisation stochastique de l’ingénierie et de la recherche opérationnelle, comme l’ingénierie de la fiabilité et l’analyse des stocks. En notant p = Φ( z ) , l’approximation la plus simple pour la fonction quantile est :

z = Φ − 1 ( p ) = 5.5556 [ 1 − ( 1 − p p ) 0.1186 ] , p ≥ 1 / 2 {displaystyle z=Phi ^{-1}(p)=5.5556left[1-left({frac {1-p}{p}}right)^{0.1186}right],qquad pgeq 1/2}

Cette approximation délivre pour z une erreur absolue maximale de 0,026 (pour 0,5 ≤ p ≤ 0,9999 , correspondant à 0 ≤ z ≤ 3,719 ). Pour p < 1/2 remplacer p par 1 − p et changer de signe. Une autre approximation, un peu moins précise, est l’approximation à paramètre unique :

z = − 0.4115 { 1 − p p + log ⁡ [ 1 − p p ] − 1 } , p ≥ 1 / 2 {displaystyle z=-0.4115left{{frac {1-p}{p}}+log left[{frac {1-p}{p}}right]-1right} ,qquad pgeq 1/2}

Ce dernier avait servi à dériver une approximation simple de l’intégrale de perte de la distribution normale, définie par

L ( z ) = ∫ z ∞ ( u − z ) φ ( u ) d u = ∫ z ∞ [ 1 − Φ ( u ) ] d u L ( z ) ≈ { 0.4115 ( p 1 − p ) − z , p < 1 / 2 , 0.4115 ( 1 − p p ) , p ≥ 1 / 2. or, equivalently, L ( z ) ≈ { 0.4115 { 1 − log ⁡ [ p 1 − p ] } , p < 1 / 2 , 0.4115 1 − p p , p ≥ 1 / 2. {displaystyle {begin{aligned}L(z)&=int _{z}^{infty }(uz)varphi (u),du=int _{z}^{infty }[ 1-Phi (u)],du\[5pt]L(z)&approx {begin{cases}0.4115left({dfrac {p}{1-p}}right)-z ,&p<1/2,\\0.4115left({dfrac {1-p}{p}}right),&pgeq 1/2.end{cases}}\[5pt]{ text{ou, de manière équivalente,}}\L(z)&approx {begin{cases}0.4115left{1-log left[{frac {p}{1-p}}right ]right},&p<1/2,\\0.4115{dfrac {1-p}{p}},&pgeq 1/2.end{cases}}end{aligned}}}

Cette approximation est particulièrement précise pour la queue droite (erreur maximale de 10 ^-3 pour z≥1,4). Des approximations très précises pour le CDF, basées sur la méthodologie de modélisation de la réponse (RMM, Shore, 2011, 2012), sont présentées dans Shore (2005).

D’autres approximations peuvent être trouvées sur : Error function#Approximation with basic functions . En particulier, petite erreur relative sur tout le domaine pour la CDF Φ {displaystyle Phi} et la fonction quantile Φ − 1 {displaystyle Phi ^{-1}} ainsi, est réalisé via une formule explicitement inversible par Sergei Winitzki en 2008.

Histoire

Développement

Certains auteurs ^{[65] [66]} attribuent le mérite de la découverte de la distribution normale à de Moivre , qui en 1738 ^{[note 2]} publia dans la deuxième édition de sa « Doctrine des hasards » l’étude des coefficients dans le binôme développement de ( a + b ) ⁿ . De Moivre a prouvé que le moyen terme de cette expansion a la magnitude approximative de 2 n / 2 π n {textstyle 2^{n}/{sqrt {2pi n}}} , et que “Si m ou1/2n soit une Quantité infiniment grande, alors le Logarithme du Rapport, qu’un Terme éloigné du milieu par l’Intervalle l , a au Terme moyen, est − 2 l l n {textstyle -{frac {2ell ell }{n}}} .” ^[67] Bien que ce théorème puisse être interprété comme la première expression obscure de la loi de probabilité normale, Stigler souligne que de Moivre lui-même n’a interprété ses résultats que comme la règle approchée des coefficients binomiaux, et en particulier de Moivre n’avait pas le concept de la fonction de densité de probabilité ^[68].

Carl Friedrich Gauss a découvert la distribution normale en 1809 comme un moyen de rationaliser la méthode des moindres carrés .

En 1823 , Gauss publie sa monographie ” Theoria combinationis observationum erroribus minimis obnoxiae ” où, entre autres choses, il introduit plusieurs concepts statistiques importants, tels que la méthode des moindres carrés , la méthode du maximum de vraisemblance et la distribution normale . Gauss a utilisé M , M ′ , M ′′, … pour dénoter les mesures d’une quantité inconnue V , et a cherché l’estimateur « le plus probable » de cette quantité : celui qui maximise la probabilité φ ( M − V ) ·φ( M′ − V ) · φ ( M ′′ − V ) · … d’obtenir les résultats expérimentaux observés. Dans sa notation φΔ est la fonction de densité de probabilité des erreurs de mesure d’amplitude Δ. Ne sachant pas quelle est la fonction φ , Gauss exige que sa méthode se réduise à la réponse bien connue : la moyenne arithmétique des valeurs mesurées. ^{[note 3]} Partant de ces principes, Gauss démontre que la seule loi qui rationalise le choix de la moyenne arithmétique comme estimateur du paramètre de localisation, est la loi normale des erreurs : ^[69]

φ Δ = h √ π e − h h Δ Δ , {displaystyle varphi {mathit {Delta }}={frac {h}{surd pi }},e^{-mathrm {hh} Delta Delta },} où h est “la mesure de la précision des observations”. En utilisant cette loi normale comme modèle générique pour les erreurs dans les expériences, Gauss formule ce qui est maintenant connu sous le nom de méthode des moindres carrés pondérés non linéaires . ^[70] Pierre-Simon Laplace a prouvé le théorème central limite en 1810, consolidant l’importance de la distribution normale dans les statistiques.

Bien que Gauss ait été le premier à suggérer la loi de distribution normale, Laplace a apporté des contributions significatives. ^{[note 4]} C’était Laplace qui a posé le premier le problème d’agréger plusieurs observations en 1774, ^[71] bien que sa propre solution ait mené à la distribution Laplacian . C’est Laplace qui a calculé le premier la valeur de l’ intégrale ∫ e ^{− t 2} dt = √ π en 1782, fournissant la constante de normalisation pour la distribution normale. ^[72] Enfin, c’est Laplace qui, en 1810, a prouvé et présenté à l’Académie les principes fondamentaux théorème fondamental limite central, qui a souligné l’importance théorique de la distribution normale. ^[73]

Il est intéressant de noter qu’en 1809, un mathématicien irlandais Adrain a publié deux dérivations de la loi de probabilité normale, simultanément et indépendamment de Gauss. ^[74] Ses travaux sont restés en grande partie inaperçus par la communauté scientifique, jusqu’à ce qu’en 1871 ils aient été ” redécouverts ” par Abbe . ^[75]

Au milieu du XIXe siècle , Maxwell a démontré que la distribution normale n’est pas seulement un outil mathématique pratique, mais peut également se produire dans des phénomènes naturels : ^[76] “Le nombre de particules dont la vitesse, résolue dans une certaine direction, se situe entre x et x + dx est

N ⁡ 1 α π e − x 2 α 2 d x {displaystyle operatorname {N} {frac {1}{alpha ;{sqrt {pi }}}};e^{-{frac {x^{2}}{alpha ^{ 2}}}},dx}

Appellation

Depuis son introduction, la distribution normale a été connue sous de nombreux noms différents : la loi de l’erreur, la loi de la facilité des erreurs, la deuxième loi de Laplace, la loi gaussienne, etc. Gauss lui-même a apparemment inventé le terme en référence aux “équations normales” impliqués dans ses applications, la normale ayant son sens technique d’orthogonal plutôt que “d’habitude”. ^[77] Cependant, à la fin du 19e siècle, certains auteurs ^{[note 5]} avaient commencé à utiliser le nom de distribution normale , où le mot “normal” était utilisé comme adjectif – le terme étant désormais considéré comme le reflet du fait que cette distribution était perçue comme typique, courante – et donc « normale ». Peirce(l’un de ces auteurs) a un jour défini la “normale” ainsi : “… la “normale” n’est pas la moyenne (ou toute autre sorte de moyenne) de ce qui se produit réellement, mais de ce qui se produirait , à long terme, sous certaines circonstances.” ^[78] Au tournant du 20e siècle , Pearson a popularisé le terme normal comme une désignation pour cette distribution. ^[79]

Il y a de nombreuses années, j’ai appelé la courbe de Laplace-Gaussien la courbe normale , ce nom, s’il évite une question internationale de priorité, a l’inconvénient de faire croire que toutes les autres distributions de fréquence sont dans un sens ou dans un autre « anormales ».

—Pearson (1920)

De plus, c’est Pearson qui a écrit pour la première fois la distribution en termes d’écart type σ comme dans la notation moderne. Peu de temps après, en 1915, Fisher a ajouté le paramètre de localisation à la formule de distribution normale, l’exprimant de la manière dont il est écrit de nos jours :

d f = 1 2 σ 2 π e − ( x − m ) 2 / ( 2 σ 2 ) d x . {displaystyle df={frac {1}{sqrt {2sigma ^{2}pi }}}e^{-(xm)^{2}/(2sigma ^{2})} ,dx.}

Le terme “normale standard”, qui désigne la distribution normale avec une moyenne nulle et une variance unitaire, s’est généralisé vers les années 1950, apparaissant dans les manuels populaires de P. G. Hoel (1947) “ Introduction aux statistiques mathématiques ” et A. M. Mood (1950) ” Introduction à la théorie des statistiques “. ^[80]

Voir également

• Portail des mathématiques

• Distribution de Bates – similaire à la distribution Irwin – Hall, mais remise à l’échelle dans la plage de 0 à 1
• Problème de Behrens – Fisher – le problème de longue date consistant à tester si deux échantillons normaux avec des variances différentes ont les mêmes moyennes;
• Distance de Bhattacharyya – méthode utilisée pour séparer les mélanges de distributions normales
• Théorème d’ Erdős – Kac – sur l’occurrence de la distribution normale en théorie des nombres
• Pleine largeur à mi-hauteur
• Flou gaussien – convolution , qui utilise la distribution normale comme noyau
• Distribution semi-normale modifiée
• Normalement distribué et non corrélé n’implique pas indépendant
• Rapport distribution normale
• Distribution normale réciproque
• Table normale standard
• Lemme de Stein
• Distribution sous-gaussienne
• Somme des variables aléatoires normalement distribuées
• Distribution de Tweedie – La distribution normale fait partie de la famille des modèles de dispersion exponentielle de Tweedie .
• Distribution normale enveloppée – la distribution normale appliquée à un domaine circulaire
• Test Z – en utilisant la distribution normale

Remarques

1. ↑ Par exemple, cet algorithme est donné dans l’article Langage de programmation Bc .
2. ↑ De Moivre a publié ses découvertes pour la première fois en 1733, dans un pamphlet “Approximatio ad Summam Terminorum Binomii ( a + b ) ⁿ in Seriem Expansi” qui était réservé à la circulation privée. Mais ce n’est qu’en 1738 qu’il rendit ses résultats accessibles au public. La brochure originale a été réimprimée plusieurs fois, voir par exemple Walker (1985) .
3. ↑ “Il est d’usage de considérer certainement comme un axiome l’hypothèse que si une quantité quelconque a été déterminée par plusieurs observations directes, faites dans les mêmes circonstances et avec un soin égal, la moyenne arithmétique des valeurs observées donne la valeur la plus probable, si pas rigoureusement, mais du moins de très près, de sorte qu’il est toujours plus sûr d’y adhérer. » — Gauss (1809 , article 177)
4. ^ “Ma coutume d’appeler la courbe la courbe de Gauss-Laplacienne ou normale nous évite de répartir le mérite de la découverte entre les deux grands mathématiciens astronomes.” citation de Pearson (1905 , p. 189)
5. ↑ Outre ceux spécifiquement référencés ici, un tel usage est rencontré dans les travaux de Peirce , Galton ( Galton (1889 , chapitre V)) et Lexis ( Lexis (1878) , Rohrbasser & Véron (2003) ) c. 1875. ^{[ citation nécessaire ]}

Références

Citations

1. ^ Weisstein, Eric W. ” Distribution normale ” . mathworld.wolfram.com . Consulté le 15 août 2020 .
2. ^ Distribution normale , Gale Encyclopedia of Psychology
3. ^ Casella & Berger (2001 , p. 102)
4. ^ Lyon, A. (2014). Pourquoi les distributions normales sont-elles normales ? , Le British Journal pour la philosophie des sciences.
5. ^ ^{un b} “Distribution Normale” . www.mathsisfun.com . Consulté le 15 août 2020 .
6. ^ Stigler (1982)
7. ^ Halperin, Hartley & Hoel (1965 , point 7)
8. ^ Mc Pherson (1990 , p. 110)
9. ^ Bernardo & Smith (2000 , p. 121)
10. ^ Scott, Clayton; Nowak, Robert (7 août 2003). “La fonction Q” . Connexions .
11. ^ Barak, Ohad (6 avril 2006). “Fonction Q et fonction d’erreur” (PDF) . Université de Tel-Aviv. Archivé de l’original (PDF) le 25 mars 2009.
12. ^ Weisstein, Eric W. “Fonction de distribution normale” . MathWorld .
13. ^ Abramowitz, Milton ; Stegun, Irene Ann , éd. (1983) [juin 1964]. “Chapitre 26, eqn 26.2.12” . Manuel des fonctions mathématiques avec formules, graphiques et tableaux mathématiques . Série Mathématiques Appliquées. Vol. 55 (Neuvième réimpression avec corrections supplémentaires de la dixième impression originale avec corrections (décembre 1972); première éd.). Washington DC; New York : Département du commerce des États-Unis, Bureau national des normes ; Publications de Douvres. p. 932. ISBN 978-0-486-61272-0. RCAC 64-60036 . MR 0167642 . RCAC 65-12253 .
14. ^ “Wolfram | Alpha : Moteur de connaissances informatiques” . Wolframalpha.com . Consulté le 3 mars 2017 .
15. ^ “Wolfram | Alpha : Moteur de connaissances informatiques” . Wolframalpha.com .
16. ^ “Wolfram | Alpha : Moteur de connaissances informatiques” . Wolframalpha.com . Consulté le 3 mars 2017 .
17. ^ Couverture, Thomas M.; Thomas, Joy A. (2006). Éléments de théorie de l’information . John Wiley et fils. p. 254 . ISBN 9780471748816.
18. ^ Park, Sung Y.; Bera, Anil K. (2009). “Maximum Entropy Autoregressive Conditional Heteroskedasticity Model” (PDF). Journal of Econometrics. 150 (2): 219–230. CiteSeerX 10.1.1.511.9750. doi:10.1016/j.jeconom.2008.12.014. Archived from the original (PDF) on March 7, 2016. Retrieved June 2, 2011.
19. ^ Geary RC(1936) The distribution of the “Student’s” ratio for the non-normal samples”. Supplement to the Journal of the Royal Statistical Society 3 (2): 178–184
20. ^ Lukacs, Eugene (March 1942). “A Characterization of the Normal Distribution”. Annals of Mathematical Statistics. 13 (1): 91–93. doi:10.1214/AOMS/1177731647. ISSN 0003-4851. JSTOR 2236166. MR 0006626. Zbl 0060.28509. Wikidata Q55897617.
21. ^ ^{a b c} Patel & Read (1996, [2.1.4])
22. ^ Fan (1991, p. 1258)
23. ^ Patel & Read (1996, [2.1.8])
24. ^ Papoulis, Athanasios. Probabilité, variables aléatoires et processus stochastiques (4e éd.). p. 148.
25. ^ Pal, Subhadip; Khare, Kshitij (2014). “Ergodicité géométrique pour les modèles de retrait bayésiens” . Journal électronique de statistiques . 8 (1): 604–645. doi : 10.1214/14-EJS896 . ISSN 1935-7524 .
26. ^ Bryc (1995 , p. 23)
27. ^ Bryc (1995 , p. 24)
28. ^ Couverture & Thomas (2006 , p. 254)
29. ^ Williams, David (2001). Weighing the odds : a course in probability and statistics (Reprinted. ed.). Cambridge [u.a.]: Cambridge Univ. Press. pp. 197–199. ISBN 978-0-521-00618-7.
30. ^ Smith, José M. Bernardo; Adrian F. M. (2000). Bayesian theory (Reprint ed.). Chichester [u.a.]: Wiley. pp. 209, 366. ISBN 978-0-471-49464-5.
31. ^ O’Hagan, A. (1994) Kendall’s Advanced Theory of statistics, Vol 2B, Bayesian Inference, Edward Arnold. ISBN 0-340-52922-9 (Section 5.40)
32. ^ ^{a b} Bryc (1995, p. 35)
33. ^ UIUC, Lecture 21. The Multivariate Normal Distribution, 21.6:”Individually Gaussian Versus Jointly Gaussian”.
34. ^ Edward L. Melnick and Aaron Tenenbein, “Misspecifications of the Normal Distribution”, The American Statistician, volume 36, number 4 November 1982, pages 372–373
35. ^ “Kullback Leibler (KL) Distance of Two Normal (Gaussian) Probability Distributions”. Allisons.org. December 5, 2007. Retrieved March 3, 2017.
36. ^ Jordan, Michael I. (February 8, 2010). “Stat260: Bayesian Modeling and Inference: The Conjugate Prior for the Normal Distribution” (PDF).
37. ^ Amari & Nagaoka (2000)
38. ^ “Normal Approximation to Poisson Distribution”. Stat.ucla.edu. Retrieved March 3, 2017.
39. ^ ^{a b} Das, Abhranil (2020). “A method to integrate and classify normal distributions”. arXiv:2012.14331 [stat.ML].
40. ^ Bryc (1995, p. 27)
41. ^ Weisstein, Eric W. “Normal Product Distribution”. MathWorld. wolfram.com.
42. ^ Lukacs, Eugene (1942). “A Characterization of the Normal Distribution”. The Annals of Mathematical Statistics. 13 (1): 91–3. doi:10.1214/aoms/1177731647. ISSN 0003-4851. JSTOR 2236166.
43. ^ Basu, D.; Laha, R. G. (1954). “On Some Characterizations of the Normal Distribution”. Sankhyā. 13 (4): 359–62. ISSN 0036-4452. JSTOR 25048183.
44. ^ Lehmann, E. L. (1997). Testing Statistical Hypotheses (2nd ed.). Springer. p. 199. ISBN 978-0-387-94919-2.
45. ^ Patel & Read (1996, [2.3.6])
46. ^ Galambos & Simonelli (2004, Theorem 3.5)
47. ^ ^{a b} Lukacs & King (1954)
48. ^ Quine, M.P. (1993). “On three characterisations of the normal distribution”. Probability and Mathematical Statistics. 14 (2): 257–263.
49. ^ John, S (1982). “The three parameter two-piece normal family of distributions and its fitting”. Communications in Statistics – Theory and Methods. 11 (8): 879–885. doi:10.1080/03610928208828279.
50. ^ ^{a b} Krishnamoorthy (2006, p. 127)
51. ^ Krishnamoorthy (2006, p. 130)
52. ^ Krishnamoorthy (2006, p. 133)
53. ^ Huxley (1932)
54. ^ Jaynes, Edwin T. (2003). Probability Theory: The Logic of Science. Cambridge University Press. pp. 592–593. ISBN 9780521592710.
55. ^ Oosterbaan, Roland J. (1994). “Chapter 6: Frequency and Regression Analysis of Hydrologic Data” (PDF). In Ritzema, Henk P. (ed.). Drainage Principles and Applications, Publication 16 (second revised ed.). Wageningen, The Netherlands: International Institute for Land Reclamation and Improvement (ILRI). pp. 175–224. ISBN 978-90-70754-33-4.
56. ^ Why Most Published Research Findings Are False, John P. A. Ioannidis, 2005
57. ^ Wichura, Michael J. (1988). “Algorithm AS241: The Percentage Points of the Normal Distribution”. Applied Statistics. 37 (3): 477–84. doi:10.2307/2347330. JSTOR 2347330.
58. ^ Johnson, Kotz & Balakrishnan (1995, Equation (26.48))
59. ^ Kinderman & Monahan (1977)
60. ^ Leva (1992)
61. ^ Marsaglia & Tsang (2000)
62. ^ Karney (2016)
63. ^ Monahan (1985, section 2)
64. ^ Wallace (1996)
65. ^ Johnson, Kotz & Balakrishnan (1994, p. 85)
66. ^ Le Cam & Lo Yang (2000, p. 74)
67. ^ De Moivre, Abraham (1733), Corollary I – see Walker (1985, p. 77)
68. ^ Stigler (1986, p. 76)
69. ^ Gauss (1809, section 177)
70. ^ Gauss (1809, section 179)
71. ^ Laplace (1774, Problem III)
72. ^ Pearson (1905, p. 189)
73. ^ Stigler (1986, p. 144)
74. ^ Stigler (1978, p. 243)
75. ^ Stigler (1978, p. 244)
76. ^ Maxwell (1860, p. 23)
77. ^ Jaynes, Edwin J.; Probability Theory: The Logic of Science, Ch. 7.
78. ^ Peirce, Charles S. (c. 1909 MS), Collected Papers v. 6, paragraph 327.
79. ^ Kruskal & Stigler (1997).
80. ^ “Earliest uses… (entry STANDARD NORMAL CURVE)”.

Sources

• Aldrich, John; Miller, Jeff. “Earliest Uses of Symbols in Probability and Statistics”.
• Aldrich, John; Miller, Jeff. “Earliest Known Uses of Some of the Words of Mathematics”. In particular, the entries for “bell-shaped and bell curve”, “normal (distribution)”, “Gaussian”, and “Error, law of error, theory of errors, etc.”.
• Amari, Shun-ichi; Nagaoka, Hiroshi (2000). Methods of Information Geometry. Oxford University Press. ISBN 978-0-8218-0531-2.
• Bernardo, José M.; Smith, Adrian F. M. (2000). Bayesian Theory. Wiley. ISBN 978-0-471-49464-5.
• Bryc, Wlodzimierz (1995). The Normal Distribution: Characterizations with Applications. Springer-Verlag. ISBN 978-0-387-97990-8.
• Casella, George; Berger, Roger L. (2001). Statistical Inference (2nd ed.). Duxbury. ISBN 978-0-534-24312-8.
• Cody, William J. (1969). “Rational Chebyshev Approximations for the Error Function”. Mathematics of Computation. 23 (107): 631–638. doi:10.1090/S0025-5718-1969-0247736-4.
• Cover, Thomas M.; Thomas, Joy A. (2006). Elements of Information Theory. John Wiley and Sons.
• de Moivre, Abraham (1738). The Doctrine of Chances. ISBN 978-0-8218-2103-9.
• Fan, Jianqing (1991). “On the optimal rates of convergence for nonparametric deconvolution problems”. The Annals of Statistics. 19 (3): 1257–1272. doi:10.1214/aos/1176348248. JSTOR 2241949.
• Galton, Francis (1889). Natural Inheritance (PDF). London, UK: Richard Clay and Sons.
• Galambos, Janos; Simonelli, Italo (2004). Products of Random Variables: Applications to Problems of Physics and to Arithmetical Functions. Marcel Dekker, Inc. ISBN 978-0-8247-5402-0.
• Gauss, Carolo Friderico (1809). Theoria motvs corporvm coelestivm in sectionibvs conicis Solem ambientivm [Theory of the Motion of the Heavenly Bodies Moving about the Sun in Conic Sections] (in Latin). English translation.
• Gould, Stephen Jay (1981). The Mismeasure of Man (first ed.). W. W. Norton. ISBN 978-0-393-01489-1.
• Halperin, Max; Hartley, Herman O.; Hoel, Paul G. (1965). “Recommended Standards for Statistical Symbols and Notation. COPSS Committee on Symbols and Notation”. The American Statistician. 19 (3): 12–14. doi:10.2307/2681417. JSTOR 2681417.
• Hart, John F.; et al. (1968). Computer Approximations. New York, NY: John Wiley & Sons, Inc. ISBN 978-0-88275-642-4.
• “Normal Distribution”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Herrnstein, Richard J.; Murray, Charles (1994). The Bell Curve: Intelligence and Class Structure in American Life. Free Press. ISBN 978-0-02-914673-6.
• Huxley, Julian S. (1932). Problems of Relative Growth. London. ISBN 978-0-486-61114-3. OCLC 476909537.
• Johnson, Norman L.; Kotz, Samuel; Balakrishnan, Narayanaswamy (1994). Continuous Univariate Distributions, Volume 1. Wiley. ISBN 978-0-471-58495-7.
• Johnson, Norman L.; Kotz, Samuel; Balakrishnan, Narayanaswamy (1995). Continuous Univariate Distributions, Volume 2. Wiley. ISBN 978-0-471-58494-0.
• Karney, C. F. F. (2016). “Sampling exactly from the normal distribution”. ACM Transactions on Mathematical Software. 42 (1): 3:1–14. arXiv:1303.6257. doi:10.1145/2710016. S2CID 14252035.
• Kinderman, Albert J.; Monahan, John F. (1977). “Computer Generation of Random Variables Using the Ratio of Uniform Deviates”. ACM Transactions on Mathematical Software. 3 (3): 257–260. doi:10.1145/355744.355750. S2CID 12884505.
• Krishnamoorthy, Kalimuthu (2006). Handbook of Statistical Distributions with Applications. Chapman & Hall/CRC. ISBN 978-1-58488-635-8.
• Kruskal, William H.; Stigler, Stephen M. (1997). Spencer, Bruce D. (ed.). Normative Terminology: ‘Normal’ in Statistics and Elsewhere. Statistics and Public Policy. Oxford University Press. ISBN 978-0-19-852341-3.
• Laplace, Pierre-Simon de (1774). “Mémoire sur la probabilité des causes par les événements”. Mémoires de l’Académie Royale des Sciences de Paris (Savants étrangers), Tome 6: 621–656. Translated by Stephen M. Stigler in Statistical Science 1 (3), 1986: JSTOR 2245476.
• Laplace, Pierre-Simon (1812). Théorie analytique des probabilités [Analytical theory of probabilities]. Paris, Ve. Courcier.
• Le Cam, Lucien; Lo Yang, Grace (2000). Asymptotics in Statistics: Some Basic Concepts (second ed.). Springer. ISBN 978-0-387-95036-5.
• Leva, Joseph L. (1992). “A fast normal random number generator” (PDF). ACM Transactions on Mathematical Software. 18 (4): 449–453. CiteSeerX 10.1.1.544.5806. doi:10.1145/138351.138364. S2CID 15802663. Archived from the original (PDF) on July 16, 2010.
• Lexis, Wilhelm (1878). “Sur la durée normale de la vie humaine et sur la théorie de la stabilité des rapports statistiques”. Annales de Démographie Internationale. Paris. II: 447–462.
• Lukacs, Eugene; King, Edgar P. (1954). “A Property of Normal Distribution”. The Annals of Mathematical Statistics. 25 (2): 389–394. doi:10.1214/aoms/1177728796. JSTOR 2236741.
• McPherson, Glen (1990). Statistics in Scientific Investigation: Its Basis, Application and Interpretation. Springer-Verlag. ISBN 978-0-387-97137-7.
• Marsaglia, George; Tsang, Wai Wan (2000). “The Ziggurat Method for Generating Random Variables”. Journal of Statistical Software. 5 (8). doi:10.18637/jss.v005.i08.
• Marsaglia, George (2004). “Evaluating the Normal Distribution”. Journal of Statistical Software. 11 (4). doi:10.18637/jss.v011.i04.
• Maxwell, James Clerk (1860). “V. Illustrations of the dynamical theory of gases. — Part I: On the motions and collisions of perfectly elastic spheres”. Philosophical Magazine. Series 4. 19 (124): 19–32. doi:10.1080/14786446008642818.
• Monahan, J. F. (1985). “Accuracy in random number generation”. Mathematics of Computation. 45 (172): 559–568. doi:10.1090/S0025-5718-1985-0804945-X.
• Patel, Jagdish K.; Read, Campbell B. (1996). Handbook of the Normal Distribution (2nd ed.). CRC Press. ISBN 978-0-8247-9342-5.
• Pearson, Karl (1901). “On Lines and Planes of Closest Fit to Systems of Points in Space” (PDF). Philosophical Magazine. 6. 2 (11): 559–572. doi:10.1080/14786440109462720.
• Pearson, Karl (1905). “‘Das Fehlergesetz und seine Verallgemeinerungen durch Fechner und Pearson’. A rejoinder”. Biometrika. 4 (1): 169–212. doi:10.2307/2331536. JSTOR 2331536.
• Pearson, Karl (1920). “Notes on the History of Correlation”. Biometrika. 13 (1): 25–45. doi:10.1093/biomet/13.1.25. JSTOR 2331722.
• Rohrbasser, Jean-Marc; Véron, Jacques (2003). “Wilhelm Lexis: The Normal Length of Life as an Expression of the “Nature of Things””. Population. 58 (3): 303–322. doi:10.3917/pope.303.0303.
• Shore, H (1982). “Simple Approximations for the Inverse Cumulative Function, the Density Function and the Loss Integral of the Normal Distribution”. Journal of the Royal Statistical Society. Series C (Applied Statistics). 31 (2): 108–114. doi:10.2307/2347972. JSTOR 2347972.
• Shore, H (2005). “Accurate RMM-Based Approximations for the CDF of the Normal Distribution”. Communications in Statistics – Theory and Methods. 34 (3): 507–513. doi:10.1081/sta-200052102. S2CID 122148043.
• Shore, H (2011). “Response Modeling Methodology”. WIREs Comput Stat. 3 (4): 357–372. doi:10.1002/wics.151. S2CID 62021374.
• Shore, H (2012). “Estimating Response Modeling Methodology Models”. WIREs Comput Stat. 4 (3): 323–333. doi:10.1002/wics.1199. S2CID 122366147.
• Stigler, Stephen M. (1978). “Mathematical Statistics in the Early States”. The Annals of Statistics. 6 (2): 239–265. doi:10.1214/aos/1176344123. JSTOR 2958876.
• Stigler, Stephen M. (1982). “A Modest Proposal: A New Standard for the Normal”. The American Statistician. 36 (2): 137–138. doi:10.2307/2684031. JSTOR 2684031.
• Stigler, Stephen M. (1986). The History of Statistics: The Measurement of Uncertainty before 1900. Harvard University Press. ISBN 978-0-674-40340-6.
• Stigler, Stephen M. (1999). Statistics on the Table. Harvard University Press. ISBN 978-0-674-83601-3.
• Walker, Helen M. (1985). “De Moivre on the Law of Normal Probability” (PDF). In Smith, David Eugene (ed.). A Source Book in Mathematics. Dover. ISBN 978-0-486-64690-9.
• Wallace, C. S. (1996). “Fast pseudo-random generators for normal and exponential variates”. ACM Transactions on Mathematical Software. 22 (1): 119–127. doi:10.1145/225545.225554. S2CID 18514848.
• Weisstein, Eric W. “Normal Distribution”. MathWorld.
• West, Graeme (2009). “Better Approximations to Cumulative Normal Functions” (PDF). Wilmott Magazine: 70–76.
• Zelen, Marvin; Severo, Norman C. (1964). Probability Functions (chapter 26). Handbook of mathematical functions with formulas, graphs, and mathematical tables, by Abramowitz, M.; and Stegun, I. A.: National Bureau of Standards. New York, NY: Dover. ISBN 978-0-486-61272-0.

External links

Wikimedia Commons has media related to Normal distribution.

• “Normal distribution”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Calculatrice de distribution normale , Calculatrice plus puissante