Dipôle
En électromagnétisme , il existe deux sortes de dipôles :
- Un Dipôle électrique traite de la séparation des charges positives et négatives présentes dans tout système Électromagnétique . Un exemple simple de ce système est une paire de charges électriques d’amplitude égale mais de signe opposé séparées par une distance généralement faible. (Un Dipôle électrique permanent est appelé un électret .)
- Un dipôle magnétique est la circulation fermée d’un système de courant électrique . Un exemple simple est une seule boucle de fil parcourue par un courant constant. Un barreau magnétique est un exemple d’aimant à Moment dipolaire magnétique permanent . [1] [2]
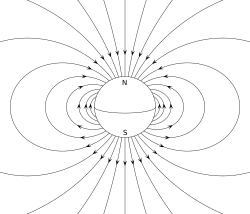 Le champ magnétique d’une sphère avec un pôle magnétique nord en haut et un pôle magnétique sud en bas. Par comparaison, la Terre a un pôle magnétique sud près de son pôle géographique nord et un pôle magnétique nord près de son Pôle Sud.
Le champ magnétique d’une sphère avec un pôle magnétique nord en haut et un pôle magnétique sud en bas. Par comparaison, la Terre a un pôle magnétique sud près de son pôle géographique nord et un pôle magnétique nord près de son Pôle Sud.
Les dipôles, qu’ils soient électriques ou magnétiques, peuvent être caractérisés par leur moment dipolaire, une grandeur vectorielle. Pour le Dipôle électrique simple, le Moment dipolaire électrique pointe de la charge négative vers la charge positive et a une amplitude égale à la force de chaque charge multipliée par la séparation entre les charges. (Pour être précis : pour la définition du moment dipolaire, il faut toujours considérer la “limite dipolaire”, où, par exemple, la distance des charges génératrices doit converger vers 0 tandis que simultanément, l’intensité de la charge doit diverger à l’infini dans un tel de manière à ce que le produit reste une constante positive.)
Pour la boucle de courant magnétique (dipôle), le Moment dipolaire magnétique pointe à travers la boucle (selon la règle de la poignée droite ), avec une amplitude égale au courant dans la boucle multiplié par l’aire de la boucle.
Semblable aux boucles de courant magnétique, la particule électronique et certaines autres particules fondamentales ont des moments dipolaires magnétiques, car un électron génère un champ magnétique identique à celui généré par une très petite boucle de courant. Cependant, le Moment dipolaire magnétique d’un électron n’est pas dû à une boucle de courant, mais à une propriété intrinsèque de l’électron. [3] L’électron peut également avoir un moment dipolaire électrique bien que celui-ci n’ait pas encore été observé (voir Moment dipolaire électrique de l’électron ).
 Tracé de contour du Potentiel électrostatique d’un Dipôle électrique orienté horizontalement de taille infinitésimale. Les couleurs fortes indiquent le potentiel le plus élevé et le plus bas (où se trouvent les charges opposées du dipôle).
Tracé de contour du Potentiel électrostatique d’un Dipôle électrique orienté horizontalement de taille infinitésimale. Les couleurs fortes indiquent le potentiel le plus élevé et le plus bas (où se trouvent les charges opposées du dipôle).
Un aimant permanent, tel qu’un barreau aimanté, doit son magnétisme au Moment dipolaire magnétique intrinsèque de l’électron. Les deux extrémités d’un barreau magnétique sont appelées pôles – à ne pas confondre avec les monopôles , voir la classification ci-dessous) – et peuvent être étiquetées “nord” et “sud”. En termes de champ magnétique terrestre, ce sont respectivement des pôles “nord” et “sud”: si l’aimant était librement suspendu dans le champ magnétique terrestre, le Pôle Nord pointerait vers le nord et le sud. pôle de recherche pointerait vers le sud. Le moment dipolaire de la Barre aimantée pointe de son sud magnétique vers son Pôle Nord magnétique . Dans un compas magnétique, le Pôle Nord d’un barreau magnétique pointe vers le nord. Cependant, cela signifie que le Pôle Nord géomagnétique de la Terre est le pôle sud (Pôle Sud) de son moment dipolaire et vice versa.
Les seuls mécanismes connus de création de dipôles magnétiques sont les boucles de courant ou le spin mécanique quantique puisque l’existence de monopôles magnétiques n’a jamais été démontrée expérimentalement.
Le terme vient du grec δίς ( dis ), « deux fois » [4] et πόλος ( polos ), « axe ». [5] [6]
Classification

 Lignes de champ électrique de deux charges opposées séparées par une distance finie.
Lignes de champ électrique de deux charges opposées séparées par une distance finie. 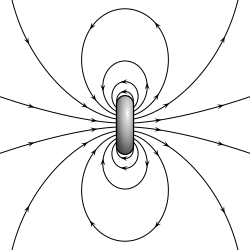
 Lignes de champ magnétique d’un courant annulaire de diamètre fini.
Lignes de champ magnétique d’un courant annulaire de diamètre fini. 
 Lignes de champ d’un dipôle ponctuel de tout type, électrique, magnétique, acoustique, etc.
Lignes de champ d’un dipôle ponctuel de tout type, électrique, magnétique, acoustique, etc.
Un dipôle physique est constitué de deux charges ponctuelles égales et opposées : au sens littéral, deux pôles. Son champ à de grandes distances (c’est-à-dire des distances importantes par rapport à la séparation des pôles) dépend presque entièrement du moment dipolaire tel que défini ci-dessus. Un dipôle ponctuel (électrique) est la limite obtenue en laissant la séparation tendre vers 0 tout en gardant le moment dipolaire fixe. Le champ d’un dipôle ponctuel a une forme particulièrement simple, et le terme d’ordre 1 dans l’ expansion multipolaire est précisément le champ dipolaire ponctuel.
Bien qu’il n’y ait pas de monopôles magnétiques connus dans la nature, il existe des dipôles magnétiques sous la forme du spin mécanique quantique associé à des particules telles que les électrons (bien que la description précise de ces effets ne relève pas de l’électromagnétisme classique). Un dipôle ponctuel magnétique théorique a un champ magnétique ayant exactement la même forme que le champ électrique d’un dipôle ponctuel électrique. Une très petite boucle conductrice de courant est approximativement un dipôle ponctuel magnétique; le Moment dipolaire magnétique d’une telle boucle est le produit du courant circulant dans la boucle et de l’aire (vectorielle) de la boucle.
Toute configuration de charges ou de courants a un «moment dipolaire», qui décrit le dipôle dont le champ est la meilleure approximation, à de grandes distances, de celui de la configuration donnée. Il s’agit simplement d’un terme dans l’expansion multipolaire lorsque la charge totale (“moment monopolaire”) est de 0 – comme c’est toujours le cas pour le cas magnétique, car il n’y a pas de monopôles magnétiques. Le terme dipolaire est le terme dominant aux grandes distances : son champ diminue proportionnellement à1/r 3, par rapport à 1/r 4pour le terme suivant ( quadripolaire ) et les puissances supérieures de 1/rpour des termes plus élevés, ou 1/r 2pour le terme de monopole.
Dipôles moléculaires
De nombreuses molécules ont de tels moments dipolaires en raison de distributions non uniformes de charges positives et négatives sur les différents atomes. C’est le cas des composés polaires comme le fluorure d’hydrogène (HF), où la densité électronique est partagée de manière inégale entre les atomes. Par conséquent, le dipôle d’une molécule est un Dipôle électrique avec un champ électrique inhérent qui ne doit pas être confondu avec un dipôle magnétique qui génère un champ magnétique.
Le physicien chimiste Peter JW Debye a été le premier scientifique à étudier de manière approfondie les dipôles moléculaires et, par conséquent, les moments dipolaires sont mesurés en unités nommées debye en son honneur.
Pour les molécules, il existe trois types de dipôles :
Dipôles permanents Celles-ci se produisent lorsque deux atomes d’une molécule ont une électronégativité sensiblement différente : un atome attire les électrons plus qu’un autre, devenant plus négatif, tandis que l’autre atome devient plus positif. Une molécule à moment dipolaire permanent est appelée molécule polaire . Voir les attractions dipôle-dipôle . Dipôles instantanés Celles-ci se produisent par hasard lorsque les électrons se trouvent être plus concentrés à un endroit qu’à un autre dans une molécule , créant un dipôle temporaire. Ces dipôles sont plus petits que les dipôles permanents, mais jouent toujours un rôle important dans la chimie et la biochimie en raison de leur prévalence. Voir dipôle instantané . Dipôles induits Ceux-ci peuvent se produire lorsqu’une molécule avec un dipôle permanent repousse les électrons d’une autre molécule, induisant un moment dipolaire dans cette molécule. Une molécule est polarisée lorsqu’elle porte un dipôle induit. Voir attraction dipôle induite .
Plus généralement, un dipôle induit de toute distribution de charge polarisable ρ (rappelons qu’une molécule a une distribution de charge) est provoqué par un champ électrique extérieur à ρ . Ce champ peut, par exemple, provenir d’un ion ou d’une molécule polaire au voisinage de ρ ou peut être macroscopique (par exemple, une molécule entre les plaques d’un condensateur chargé ). La taille du moment dipolaire induit est égale au produit de l’intensité du champ externe et de la polarisabilité dipolaire de ρ .
Les valeurs du moment dipolaire peuvent être obtenues à partir de la mesure de la Constante diélectrique . Certaines valeurs de phase gazeuse typiques dans les unités debye sont : [7]
- dioxyde de carbone : 0
- monoxyde de carbone : 0,112 D
- ozone : 0,53 D
- phosgène : 1,17 D
- vapeur d’eau : 1.85 D
- acide cyanhydrique : 2,98 D
- cyanamide : 4.27 D
- bromure de potassium : 10.41 D

 La molécule linéaire CO 2 a un dipôle nul car les deux dipôles de liaison s’annulent.
La molécule linéaire CO 2 a un dipôle nul car les deux dipôles de liaison s’annulent.
Le bromure de potassium (KBr) possède l’un des moments dipolaires les plus élevés car il s’agit d’un composé ionique qui existe sous forme de molécule en phase gazeuse.

 La molécule courbée H 2 O a un dipôle net. Les deux dipôles de liaison ne s’annulent pas.
La molécule courbée H 2 O a un dipôle net. Les deux dipôles de liaison ne s’annulent pas.
Le moment dipolaire global d’une molécule peut être approché comme une somme vectorielle des moments dipolaires de liaison . En tant que somme vectorielle, il dépend de l’orientation relative des liaisons, de sorte qu’à partir du moment dipolaire, des informations peuvent être déduites sur la géométrie moléculaire .
Par exemple, le dipôle nul du CO 2 implique que les deux moments dipolaires de la liaison C=O s’annulent de sorte que la molécule doit être linéaire. Pour H 2 O, les moments de la liaison O−H ne s’annulent pas car la molécule est courbée. Pour l’ozone (O 3 ) qui est également une molécule coudée, les moments dipolaires de liaison ne sont pas nuls même si les liaisons O−O sont entre des atomes similaires. Cela concorde avec les structures de Lewis pour les formes de résonance de l’ozone qui montrent une charge positive sur l’atome d’oxygène central.


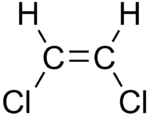
 Isomère Cis , moment dipolaire 1,90 D
Isomère Cis , moment dipolaire 1,90 D 
 Isomère trans , moment dipolaire zéro
Isomère trans , moment dipolaire zéro
Un exemple en chimie organique du rôle de la géométrie dans la détermination du moment dipolaire est les isomères cis et trans du 1,2-dichloroéthène . Dans l’ isomère cis , les deux liaisons polaires C−Cl sont du même côté de la double liaison C=C et le moment dipolaire moléculaire est de 1,90 D. Dans l’ isomère trans , le moment dipolaire est nul car les deux liaisons C−Cl sont sur les côtés opposés du C = C et s’annulent (et les deux moments de liaison pour les liaisons C-H beaucoup moins polaires s’annulent également).
Un autre exemple du rôle de la géométrie moléculaire est le trifluorure de bore , qui possède trois liaisons polaires avec une différence d’ électronégativité supérieure au seuil de 1,7 traditionnellement cité pour la liaison ionique . Cependant, en raison de la distribution triangulaire équilatérale des ions fluorure autour du centre du cation bore, la molécule dans son ensemble ne présente aucun pôle identifiable : on ne peut pas construire un plan qui divise la molécule en une partie négative nette et une partie positive nette.
Opérateur dipôle mécanique quantique
Considérons une collection de N particules avec des charges q i et des vecteurs de position r i . Par exemple, cet ensemble peut être une molécule constituée d’électrons, tous de charge − e , et de noyaux de charge eZ i , où Z i est le numéro atomique du i ème noyau. Le dipôle observable (quantité physique) a l’ opérateur dipôle mécanique quantique : [ citation nécessaire ]
p = ∑ i = 1 N q i r i . {displaystyle {mathfrak {p}}=sum _{i=1}^{N},q_{i},mathbf {r} _{i},.} 
Notez que cette définition n’est valable que pour des atomes ou des molécules neutres, c’est-à-dire une charge totale égale à zéro. Dans le cas ionisé, on a
p = ∑ i = 1 N q i ( r i − r c ) , {displaystyle {mathfrak {p}}=sum _{i=1}^{N},q_{i},(mathbf {r} _{i}-mathbf {r} _{c }),} 
où r c {displaystyle mathbf {r} _{c}} 
est le centre de masse de la molécule/du groupe de particules. [8]
Dipôles atomiques
Un atome non dégénéré (état S ) ne peut avoir qu’un dipôle permanent nul. Ce fait découle mécaniquement quantique de la symétrie d’inversion des atomes. Les 3 composantes de l’opérateur dipolaire sont antisymétriques en inversion par rapport au noyau,
I p I − 1 = − p , {displaystyle {mathfrak {I}};{mathfrak {p}};{mathfrak {I}}^{-1}=-{mathfrak {p}},} 
où p {displaystyle {mathfrak {p}}} 
est l’opérateur dipôle et I {displaystyle {mathfrak {je}}}

est l’opérateur d’inversion.
Le moment dipolaire permanent d’un atome dans un état non dégénéré (voir Niveau d’énergie dégénéré ) est donné comme la valeur attendue (moyenne) de l’opérateur dipolaire,
⟨ p ⟩ = ⟨ S | p | S ⟩ , {displaystyle leftlangle {mathfrak {p}}rightrangle =leftlangle ,S,|{mathfrak {p}}|,S,rightrangle ,} 
où | S ⟩ {displaystyle |,S,rangle } 
est une fonction d’onde à l’état S , non dégénérée, qui est symétrique ou antisymétrique par inversion : I | S ⟩ = ± | S ⟩ {displaystyle {mathfrak {I}},|,S,rangle =pm |,S,rangle }

. Puisque le produit de la fonction d’onde (dans le ket) et son conjugué complexe (dans le soutien-gorge) est toujours symétrique sous inversion et son inverse,
⟨ p ⟩ = ⟨ I − 1 S | p | I − 1 S ⟩ = ⟨ S | I p I − 1 | S ⟩ = − ⟨ p ⟩ {displaystyle leftlangle {mathfrak {p}}rightrangle =leftlangle ,{mathfrak {I}}^{-1},S,|{mathfrak {p}} |,{mathfrak {I}}^{-1},S,rightrangle =leftlangle ,S,|{mathfrak {I}},{mathfrak {p} },{mathfrak {I}}^{-1}|,S,rightrangle =-leftlangle {mathfrak {p}}rightrangle } 
il s’ensuit que la valeur moyenne change de signe sous inversion. Nous avons utilisé ici le fait que I {displaystyle {mathfrak {je}}} 
, étant un opérateur de symétrie, est unitaire : I − 1 = I ∗ {displaystyle {mathfrak {I}}^{-1}={mathfrak {I}}^{*},}

et par définition l’adjoint hermitien I ∗ {displaystyle {mathfrak {I}}^{*},}

peut être déplacé du soutien-gorge au ket et devient alors I ∗ ∗ = I {displaystyle {mathfrak {I}}^{**}={mathfrak {I}},}

. Puisque la seule quantité qui est égale à moins elle-même est le zéro, la valeur d’espérance s’annule,
⟨ p ⟩ = 0. {displaystyle leftlangle {mathfrak {p}}rightrangle =0.} 
Dans le cas d’atomes à couche ouverte avec des niveaux d’énergie dégénérés, on pourrait définir un moment dipolaire à l’aide de l’ effet Stark du premier ordre . Cela donne un dipôle non nul (par définition proportionnel à un décalage de Stark du premier ordre non nul) seulement si certaines des fonctions d’onde appartenant aux énergies dégénérées ont des parités opposées ; c’est-à-dire qu’ils ont un comportement différent sous inversion. Ceci est un événement rare, mais se produit pour l’atome H excité, où les états 2s et 2p sont “accidentellement” dégénérés (voir l’article vecteur Laplace – Runge – Lenz pour l’origine de cette dégénérescence) et ont une parité opposée (2s est pair et 2p est impair).
Champ d’un dipôle magnétique statique
Ordre de grandeur
L’intensité du champ lointain, B , d’un champ magnétique dipolaire est donnée par
B ( m , r , λ ) = μ 0 4 π m r 3 1 + 3 sin 2 ( λ ) , {displaystyle B(m,r,lambda )={frac {mu _{0}}{4pi }}{frac {m}{r^{3}}}{sqrt {1+ 3sin ^{2}(lambda )}},,} 
où
B est la force du champ, mesurée en teslas r est la distance du centre, mesurée en mètres λ est la latitude magnétique (égale à 90° − θ ) où θ est la colatitude magnétique, mesurée en radians ou degrés à partir de l’axe du dipôle [note 1] m est le moment dipolaire, mesuré en ampère -mètres carrés ou joules par tesla μ 0 est la perméabilité de l’espace libre , mesurée en henrys par mètre.
La conversion en coordonnées cylindriques est obtenue en utilisant r 2 = z 2 + ρ 2 et
λ = arcsin ( z z 2 + ρ 2 ) {displaystyle lambda =arcsin left({frac {z}{sqrt {z^{2}+rho ^{2}}}}right)} 
où ρ est la distance perpendiculaire à l’ axe z . Puis,
B ( ρ , z ) = μ 0 m 4 π ( z 2 + ρ 2 ) 3 2 1 + 3 z 2 z 2 + ρ 2 {displaystyle B(rho ,z)={frac {mu _{0}m}{4pi left(z^{2}+rho ^{2}right)^{frac { 3}{2}}}}{sqrt {1+{frac {3z^{2}}{z^{2}+rho ^{2}}}}}} 
Forme vectorielle
Le champ lui-même est une quantité vectorielle :
B ( m , r ) = μ 0 4 π 3 ( m ⋅ r ^ ) r ^ − m r 3 {displaystyle mathbf {B} (mathbf {m} ,mathbf {r} )={frac {mu _{0}}{4pi }} {frac {3(mathbf {m } cdot {hat {mathbf {r} }}){hat {mathbf {r} }}-mathbf {m} }{r^{3}}}} 
où
B est le champ r est le vecteur de la position du dipôle à la position où le champ est mesuré r est la valeur absolue de r : la distance au dipôle r = r/rest le vecteur unitaire parallèle à r ; m est le moment dipolaire (vecteur) μ 0 est la perméabilité de l’espace libre
C’est exactement le champ d’un dipôle ponctuel, exactement le terme dipolaire dans l’expansion multipolaire d’un champ arbitraire, et approximativement le champ de toute configuration de type dipôle à de grandes distances.
Potentiel de vecteur magnétique
Le potentiel vecteur A d’un dipôle magnétique est
A ( r ) = μ 0 4 π m × r ^ r 2 {displaystyle mathbf {A} (mathbf {r} )={frac {mu _{0}}{4pi }}{frac {mathbf {m} times {hat {mathbf {r} }}}{r^{2}}}} 
avec les mêmes définitions que ci-dessus.
Champ d’un Dipôle électrique
Le Potentiel électrostatique à la position r dû à un Dipôle électrique à l’origine est donné par :
Φ ( r ) = 1 4 π ε 0 p ⋅ r ^ r 2 {displaystyle Phi (mathbf {r} )={frac {1}{4pi epsilon _{0}}},{frac {mathbf {p} cdot {hat {mathbf {r} }}}{r^{2}}}} 
où p est le moment dipolaire (vecteur) et є 0 est la Permittivité de l’espace libre .
Ce terme apparaît comme le second terme dans le développement multipolaire d’un Potentiel électrostatique arbitraire Φ( r ). Si la source de Φ( r ) est un dipôle, comme on le suppose ici, ce terme est le seul terme non nul dans le développement multipolaire de Φ( r ). Le champ électrique d’un dipôle peut être trouvé à partir du gradient de ce potentiel :
E = − ∇ Φ = 1 4 π ε 0 3 ( p ⋅ r ^ ) r ^ − p r 3 − δ 3 ( r ) p 3 ε 0 . {displaystyle mathbf {E} =-nabla Phi ={frac {1}{4pi epsilon _{0}}} {frac {3(mathbf {p} cdot {hat {mathbf {r} }}){hat {mathbf {r} }}-mathbf {p}}{r^{3}}}-delta ^{3}(mathbf {r}){ frac {mathbf {p} }{3epsilon _{0}}}.} 
Ceci est de la même forme que l’expression du champ magnétique d’un dipôle magnétique ponctuel, en ignorant la fonction delta. Dans un véritable Dipôle électrique, cependant, les charges sont physiquement séparées et le champ électrique diverge ou converge aux charges ponctuelles. Ceci est différent du champ magnétique d’un véritable dipôle magnétique qui est continu partout. La fonction delta représente le champ fort pointant dans la direction opposée entre les charges ponctuelles, qui est souvent omise car on s’intéresse rarement au champ à la position du dipôle. Pour plus de discussions sur le champ interne des dipôles, voir [2] [9] ou Moment magnétique#Champ magnétique interne d’un dipôle .
Couple sur un dipôle
Étant donné que la direction d’un champ électrique est définie comme la direction de la force sur une charge positive, les lignes de champ électrique s’éloignent d’une charge positive et se dirigent vers une charge négative.
Lorsqu’il est placé dans un champ électrique ou magnétique homogène , des forces égales mais opposées apparaissent de chaque côté du dipôle créant un couple τ } :
τ = p × E {displaystyle {boldsymbol {tau }}=mathbf {p} times mathbf {E} } 
pour un Moment dipolaire électrique p (en coulomb-mètres), ou
τ = m × B {displaystyle {boldsymbol {tau}}=mathbf {m} times mathbf {B} } 
pour un Moment dipolaire magnétique m (en ampère-mètre carré).
Le couple résultant aura tendance à aligner le dipôle avec le champ appliqué, ce qui dans le cas d’un Dipôle électrique, donne une énergie potentielle de
U = − p ⋅ E {displaystyle U=-mathbf {p} cdot mathbf {E} } 
.
L’énergie d’un dipôle magnétique est similaire
U = − m ⋅ B {displaystyle U=-mathbf {m} cdot mathbf {B} } 
.
Rayonnement dipolaire

 Module du vecteur de Poynting pour un Dipôle électrique oscillant (solution exacte). Les deux charges sont représentées par deux petits points noirs.
Module du vecteur de Poynting pour un Dipôle électrique oscillant (solution exacte). Les deux charges sont représentées par deux petits points noirs.
En plus des dipôles en électrostatique, il est également courant de considérer un Dipôle électrique ou magnétique qui oscille dans le temps. Il s’agit d’une extension, ou d’une étape suivante plus physique, du rayonnement d’ ondes sphériques .
En particulier, considérons un Dipôle électrique oscillant harmoniquement, avec une fréquence angulaire ω et un moment dipolaire p 0 le long de la direction ẑ de la forme
p ( r , t ) = p ( r ) e − i ω t = p 0 z ^ e − i ω t . {displaystyle mathbf {p} (mathbf {r} ,t)=mathbf {p} (mathbf {r} )e^{-iomega t}=p_{0}{hat {mathbf {z} }}e^{-iomega t}.} 
Dans le vide, le champ exact produit par ce dipôle oscillant peut être dérivé en utilisant la formulation potentielle retardée comme suit :
E = 1 4 π ε 0 { ω 2 c 2 r ( r ^ × p ) × r ^ + ( 1 r 3 − i ω c r 2 ) ( 3 r ^ [ r ^ ⋅ p ] − p ) } e i ω r c e − i ω t B = ω 2 4 π ε 0 c 3 ( r ^ × p ) ( 1 − c i ω r ) e i ω r / c r e − i ω t . {displaystyle {begin{aligned}mathbf {E} &={frac {1}{4pi varepsilon _{0}}}left{{frac {omega ^{2}}{ c^{2}r}}left({hat {mathbf {r} }}times mathbf {p} right)times {hat {mathbf {r} }}+left({ frac {1}{r^{3}}}-{frac {iomega }{cr^{2}}}right)left(3{hat {mathbf {r} }}left [{hat {mathbf {r} }}cdot mathbf {p} right]-mathbf {p} right)right}e^{frac {iomega r}{c}} e^{-iomega t}\mathbf {B} &={frac {omega ^{2}}{4pi varepsilon _{0}c^{3}}}({hat {mathbf {r} }}times mathbf {p} )left(1-{frac {c}{iomega r}}right){frac {e^{iomega r/c }}{r}}e^{-iomega t}.end{aligned}}} ![{displaystyle {begin{aligned}mathbf {E} &={frac {1}{4pi varepsilon _{0}}}left{{frac {omega ^{2}}{c^{2}r}}left({hat {mathbf {r} }}times mathbf {p} right)times {hat {mathbf {r} }}+left({frac {1}{r^{3}}}-{frac {iomega }{cr^{2}}}right)left(3{hat {mathbf {r} }}left[{hat {mathbf {r} }}cdot mathbf {p} right]-mathbf {p} right)right}e^{frac {iomega r}{c}}e^{-iomega t}\mathbf {B} &={frac {omega ^{2}}{4pi varepsilon _{0}c^{3}}}({hat {mathbf {r} }}times mathbf {p} )left(1-{frac {c}{iomega r}}right){frac {e^{iomega r/c}}{r}}e^{-iomega t}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a84ead8e373689b51cea6ced6348616d2201bd6)
Pour rω/c ≫ 1, le champ lointain prend la forme plus simple d’une onde “sphérique” rayonnante, mais avec une dépendance angulaire intégrée dans le produit vectoriel : [10]
B = ω 2 4 π ε 0 c 3 ( r ^ × p ) e i ω ( r / c − t ) r = ω 2 μ 0 p 0 4 π c ( r ^ × z ^ ) e i ω ( r / c − t ) r = − ω 2 μ 0 p 0 4 π c sin ( θ ) e i ω ( r / c − t ) r φ ^ E = c B × r ^ = − ω 2 μ 0 p 0 4 π sin ( θ ) ( φ ^ × r ^ ) e i ω ( r / c − t ) r = − ω 2 μ 0 p 0 4 π sin ( θ ) e i ω ( r / c − t ) r θ ^ . {displaystyle {begin{aligned}mathbf {B} &={frac {omega ^{2}}{4pi varepsilon _{0}c^{3}}}({hat { mathbf {r} }}times mathbf {p} ){frac {e^{iomega (r/ct)}}{r}}={frac {omega ^{2}mu _{ 0}p_{0}}{4pi c}}({hat {mathbf {r} }}times {hat {mathbf {z} }}){frac {e^{iomega (r/ct)}}{r}}=-{frac {omega ^{2}mu _{0}p_{0}}{4pi c}}sin(theta ){frac {e^{iomega (r/ct)}}{r}}mathbf {hat {phi }} \mathbf {E} &=cmathbf {B} times {hat { mathbf {r} }}=-{frac {omega ^{2}mu _{0}p_{0}}{4pi }}sin(theta )left({hat {phi }}times mathbf {hat {r}} right){frac {e^{iomega (r/ct)}}{r}}=-{frac {omega ^{2} mu _{0}p_{0}}{4pi }}sin(theta ){frac {e^{iomega (r/ct)}}{r}}{hat {theta } }.end{aligné}}} 
Le vecteur de Poynting moyenné dans le temps
⟨ S ⟩ = ( μ 0 p 0 2 ω 4 32 π 2 c ) sin 2 ( θ ) r 2 r ^ {displaystyle langle mathbf {S} rangle =left({frac {mu _{0}p_{0}^{2}omega ^{4}}{32pi ^{2}c }}right){frac {sin ^{2}(theta )}{r^{2}}}mathbf {hat {r}} } 
n’est pas distribué de manière isotrope, mais concentré autour des directions perpendiculaires au moment dipolaire, en raison des ondes électriques et magnétiques non sphériques. En fait, la fonction Harmonique sphérique (sin θ ) responsable d’une telle distribution angulaire toroïdale est précisément l’onde l = 1 “p”.
La puissance totale moyenne dans le temps rayonnée par le champ peut alors être dérivée du vecteur de Poynting comme
P = μ 0 ω 4 p 0 2 12 π c . {displaystyle P={frac {mu _{0}omega ^{4}p_{0}^{2}}{12pi c}}.} 
Notez que la dépendance de la puissance à la quatrième puissance de la fréquence du rayonnement est conforme à la diffusion de Rayleigh et aux effets sous-jacents pour lesquels le ciel est principalement composé de bleu.
Un dipôle polarisé circulaire est décrit comme une superposition de deux dipôles linéaires.
Voir également
- Densité de polarisation
- Modèles de dipôles magnétiques
- Modèle dipôle du champ magnétique terrestre
- Électret
- Dipôle de l’océan Indien et Dipôle subtropical de l’océan Indien , deux phénomènes océanographiques
- Interaction magnétique dipôle-dipôle
- Moment magnétique de spin
- Monopole
- Harmoniques solides
- Moments multipolaires axiaux
- Moments multipolaires cylindriques
- Moments multipolaires sphériques
- Agrandissement de Laplace
- Solide moléculaire
- Moment magnétique # Champ magnétique interne d’un dipôle
Remarques
- ^ La colatitude magnétique est de 0 le long de l’axe du dipôle et de 90° dans le plan perpendiculaire à son axe.
Références
- ^ Brau, Charles A. (2004). Problèmes modernes en électrodynamique classique . Presse universitaire d’Oxford. ISBN 0-19-514665-4.
- ^ un b Griffiths, David J. (1999). Introduction à l’électrodynamique (3e éd.). Prentice Hall. ISBN 0-13-805326-X.
- ^ Griffiths, David J. (1994). Introduction à la mécanique quantique . Prentice Hall. ISBN 978-0-13-124405-4.
- ^ δίς , Henry George Liddell, Robert Scott, Un lexique grec-anglais , sur Persée
- ^ πόλος , Henry George Liddell, Robert Scott, Un lexique grec-anglais , sur Persée
- ^ “dipôle, n.”. Oxford English Dictionary (deuxième éd.). Presse universitaire d’Oxford . 1989.
- ^ West, Robert C. (1984). CRC Handbook of Chemistry and Physics (65e éd.). Presse CRC. ISBN 0-8493-0465-2.
- ^ “Le Vecteur de Moment dipolaire électrique – Direction, Magnitude, Signification, et cetera” .
- ^ Jackson, John D. (1999). Électrodynamique classique, 3e éd . Wiley. p. 148–150. ISBN 978-0-471-30932-1.
- ^ David J. Griffiths , Introduction à l’électrodynamique, Prentice Hall, 1999, page 447
Liens externes
- Programme de géomagnétisme de l’USGS
- Fields of Force : un chapitre d’un manuel en ligne
- Potentiel dipolaire électrique de Stephen Wolfram et densité d’énergie d’un dipôle magnétique de Franz Krafft. Projet de démonstration Wolfram .
