Produit scalaire

En mathématiques , le produit scalaire ou produit scalaire ^{[note 1]} est une opération algébrique qui prend deux séquences de nombres de longueur égale (généralement des vecteurs de coordonnées ) et renvoie un seul nombre. En géométrie euclidienne , le produit scalaire des Coordonnées cartésiennes de deux vecteurs est largement utilisé. Il est souvent appelé produit interne (ou rarement produit de projection ) de l’espace euclidien, même si ce n’est pas le seul produit interne qui peut être défini sur l’espace euclidien (voir Espace produit interne pour en savoir plus).

Algébriquement, le produit scalaire est la somme des produits des entrées correspondantes des deux séquences de nombres. Géométriquement, c’est le produit des grandeurs euclidiennes des deux vecteurs et du Cosinus de l’angle entre eux. Ces définitions sont équivalentes lors de l’utilisation de Coordonnées cartésiennes. Dans la géométrie moderne , les espaces euclidiens sont souvent définis en utilisant des espaces vectoriels . Dans ce cas, le produit scalaire est utilisé pour définir des longueurs (la longueur d’un vecteur est la racine carrée du produit scalaire du vecteur par lui-même) et des angles (le Cosinus de l’angle de deux vecteurs est le quotientde leur produit scalaire par le produit de leurs longueurs).

Le nom « produit scalaire » est dérivé du point centré « · » qui est souvent utilisé pour désigner cette opération ; ^[1] le nom alternatif “produit scalaire” souligne que le résultat est un scalaire , plutôt qu’un vecteur , comme c’est le cas pour le Produit vectoriel dans un espace tridimensionnel.

Définition

Le produit scalaire peut être défini algébriquement ou géométriquement. La définition géométrique est basée sur les notions d’angle et de distance (grandeur des vecteurs). L’équivalence de ces deux définitions repose sur le fait d’avoir un système de coordonnées cartésien pour l’espace euclidien.

Dans les présentations modernes de la géométrie euclidienne , les points de l’espace sont définis en fonction de leurs Coordonnées cartésiennes , et l’espace euclidien lui-même est communément identifié avec l’ espace de coordonnées réel R ⁿ . Dans une telle présentation, les notions de longueur et d’angles sont définies au moyen du produit scalaire. La longueur d’un vecteur est définie comme la racine carrée du produit scalaire du vecteur par lui-même, et le Cosinus de l’angle (non orienté) de deux vecteurs de longueur un est défini comme leur produit scalaire. Ainsi, l’équivalence des deux définitions du produit scalaire fait partie de l’équivalence des formulations classique et moderne de la géométrie euclidienne.

Définition algébrique

Le produit scalaire de deux vecteurs a = [ a ₁ , a ₂ , …, a _n ] et b = [ b ₁ , b ₂ , …, b _n ] est défini comme : ^[2]

un ⋅ b = ∑ je = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {displaystyle mathbf {color {red}a} cdot mathbf {color {blue}b} =sum _{i=1}^{n}{color {red}a}_{i} {color {blue}b}_{i}={color {red}a}_{1}{color {blue}b}_{1}+{color {red}a}_{2} {color {blue}b}_{2}+cdots +{color {red}a}_{n}{color {blue}b}_{n}} ${displaystyle mathbf {color {red}a} cdot mathbf {color {blue}b} =sum _{i=1}^{n}{color {red}a}_{i}{color {blue}b}_{i}={color {red}a}_{1}{color {blue}b}_{1}+{color {red}a}_{2}{color {blue}b}_{2}+cdots +{color {red}a}_{n}{color {blue}b}_{n}}$ ${displaystyle mathbf {color {red}a} cdot mathbf {color {blue}b} =sum _{i=1}^{n}{color {red}a}_{i}{color {blue}b}_{i}={color {red}a}_{1}{color {blue}b}_{1}+{color {red}a}_{2}{color {blue}b}_{2}+cdots +{color {red}a}_{n}{color {blue}b}_{n}}$

où Σ désigne la sommation et n est la dimension de l’ espace vectoriel . Par exemple, dans l’espace tridimensionnel , le produit scalaire des vecteurs [1, 3, −5] et [4, −2, −1] est :

[ 1 , 3 , − 5 ] ⋅ [ 4 , − 2 , − 1 ] = ( 1 × 4 ) + ( 3 × − 2 ) + ( − 5 × − 1 ) = 4 − 6 + 5 = 3 {displaystyle {begin{aligned} [{color {red}1,3,-5}]cdot [{color {blue}4,-2,-1}]&=({color { rouge}1}times {color {blue}4})+({color {red}3}times {color {blue}-2})+({color {red}-5}times {color {blue}-1})\&=4-6+5\&=3end{aligned}}} ${displaystyle {begin{aligned} [{color {red}1,3,-5}]cdot [{color {blue}4,-2,-1}]&=({color {red}1}times {color {blue}4})+({color {red}3}times {color {blue}-2})+({color {red}-5}times {color {blue}-1})\&=4-6+5\&=3end{aligned}}}$ ${displaystyle {begin{aligned} [{color {red}1,3,-5}]cdot [{color {blue}4,-2,-1}]&=({color {red}1}times {color {blue}4})+({color {red}3}times {color {blue}-2})+({color {red}-5}times {color {blue}-1})\&=4-6+5\&=3end{aligned}}}$

Si les vecteurs sont identifiés avec des matrices de lignes , le produit scalaire peut également être écrit comme un Produit matriciel

a ⋅ b = a b T , {displaystyle mathbf {color {rouge}a} cdot mathbf {color {bleu}b} =mathbf {color {rouge}a} mathbf {color {bleu}b} ^{mathsf {T}},} ${displaystyle mathbf {color {red}a} cdot mathbf {color {blue}b} =mathbf {color {red}a} mathbf {color {blue}b} ^{mathsf {T}},}$

où b T {displaystyle mathbf {color {bleu}b} ^{mathsf {T}}} ${displaystyle mathbf {color {blue}b} ^{mathsf {T}}}$ désigne la transposition de b {displaystyle mathbf {color {bleu}b} } .

En exprimant l’exemple ci-dessus de cette manière, une matrice 1 × 3 ( Vecteur ligne ) est multipliée par une matrice 3 × 1 ( Vecteur colonne ) pour obtenir une matrice 1 × 1 identifiée par son entrée unique :

[ 1 3 − 5 ] [ 4 − 2 − 1 ] = 3 {displaystyle {begin{bmatrix}color {red}1&color {red}3&color {red}-5end{bmatrix}}{begin{bmatrix}color {blue}4\color {bleu}-2\color {bleu}-1end{bmatrix}}=color {violet}3} ${displaystyle {begin{bmatrix}color {red}1&color {red}3&color {red}-5end{bmatrix}}{begin{bmatrix}color {blue}4\color {blue}-2\color {blue}-1end{bmatrix}}=color {purple}3}$ ${displaystyle {begin{bmatrix}color {red}1&color {red}3&color {red}-5end{bmatrix}}{begin{bmatrix}color {blue}4\color {blue}-2\color {blue}-1end{bmatrix}}=color {purple}3}$ .

Définition géométrique

Illustration montrant comment trouver l’angle entre les vecteurs à l’aide du produit scalaire Calcul des angles de liaison d’une géométrie moléculaire tétraédrique symétrique à l’ aide d’un produit scalaire

Dans l’espace euclidien , un vecteur euclidien est un objet géométrique qui possède à la fois une grandeur et une direction. Un vecteur peut être représenté par une flèche. Sa grandeur est sa longueur et sa direction est la direction vers laquelle pointe la flèche. La grandeur d’un vecteur a est notée ‖ a ‖ {displaystyle left|mathbf {a} right|} . Le produit scalaire de deux vecteurs euclidiens a et b est défini par ^{[3] [4] [1]}

a ⋅ b = ‖ a ‖ ‖ b ‖ cos ⁡ θ , {displaystyle mathbf {a} cdot mathbf {b} =|mathbf {a} | |mathbf {b} |cos theta ,}

où θ est l’ angle entre a et b .

En particulier, si les vecteurs a et b sont orthogonaux (c’est-à-dire que leur angle est π / 2 ou 90°), alors cos ⁡ π 2 = 0 {displaystyle cos {frac {pi }{2}}=0} ${displaystyle cos {frac {pi }{2}}=0}$ ${displaystyle cos {frac {pi }{2}}=0}$ , ce qui implique que

a ⋅ b = 0. {displaystyle mathbf {a} cdot mathbf {b} =0.}

A l’autre extrême, s’ils sont codirectionnels, alors l’angle entre eux est nul avec cos ⁡ 0 = 1 {displaystylecos 0=1} {displaystyle cos 0=1} et

a ⋅ b = ‖ a ‖ ‖ b ‖ {displaystyle mathbf {a} cdot mathbf {b} =left|mathbf {a} right|,left|mathbf {b} right|}

Cela implique que le produit scalaire d’un vecteur a avec lui-même est

a ⋅ a = ‖ a ‖ 2 , {displaystyle mathbf {a} cdot mathbf {a} =left|mathbf {a} right|^{2},} ${displaystyle mathbf {a} cdot mathbf {a} =left|mathbf {a} right|^{2},}$ ${displaystyle mathbf {a} cdot mathbf {a} =left|mathbf {a} right|^{2},}$

qui donne

‖ a ‖ = a ⋅ a , {displaystyle left|mathbf {a} right|={sqrt {mathbf {a} cdot mathbf {a} }},}

la formule de la Longueur euclidienne du vecteur.

Projection scalaire et premières propriétés

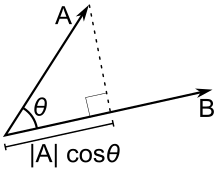
Projection scalaire

La projection scalaire (ou composante scalaire) d’un vecteur euclidien a dans la direction d’un vecteur euclidien b est donnée par

a b = ‖ a ‖ cos ⁡ θ , {displaystyle a_{b}=left|mathbf {a} right|cos theta ,} ${displaystyle a_{b}=left|mathbf {a} right|cos theta ,}$ ${displaystyle a_{b}=left|mathbf {a} right|cos theta ,}$

où θ est l’angle entre a et b .

En termes de définition géométrique du produit scalaire, cela peut être réécrit

a b = a ⋅ b ^ , {displaystyle a_{b}=mathbf {a} cdot {widehat {mathbf {b} }},} ${displaystyle a_{b}=mathbf {a} cdot {widehat {mathbf {b} }},}$ ${displaystyle a_{b}=mathbf {a} cdot {widehat {mathbf {b} }},}$

où b ^ = b / ‖ b ‖ {displaystyle {widehat {mathbf {b} }}=mathbf {b} /left|mathbf {b} right|} est le vecteur unitaire dans la direction de b .

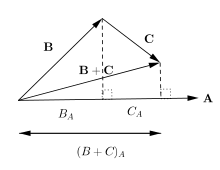
Loi distributive pour le produit scalaire

Le produit scalaire est donc caractérisé géométriquement par ^[5]

a ⋅ b = a b ‖ b ‖ = b a ‖ a ‖ . {displaystyle mathbf {a} cdot mathbf {b} =a_{b}left|mathbf {b} right|=b_{a}left|mathbf {a} right |.} ${displaystyle mathbf {a} cdot mathbf {b} =a_{b}left|mathbf {b} right|=b_{a}left|mathbf {a} right|.}$ ${displaystyle mathbf {a} cdot mathbf {b} =a_{b}left|mathbf {b} right|=b_{a}left|mathbf {a} right|.}$

Le produit scalaire, défini de cette manière, est homogène sous mise à l’échelle dans chaque variable, ce qui signifie que pour tout scalaire α ,

( α a ) ⋅ b = α ( a ⋅ b ) = a ⋅ ( α b ) . {displaystyle (alpha mathbf {a} )cdot mathbf {b} =alpha (mathbf {a} cdot mathbf {b} )=mathbf {a} cdot (alpha mathbf { b} ).}

Il satisfait également une loi distributive , ce qui signifie que

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {displaystyle mathbf {a} cdot (mathbf {b} +mathbf {c} )=mathbf {a} cdot mathbf {b} +mathbf {a} cdot mathbf {c} . }

Ces propriétés peuvent être résumées en disant que le produit scalaire est une forme bilinéaire . De plus, cette forme bilinéaire est définie positive , ce qui signifie que a ⋅ a {displaystyle mathbf {a} cdot mathbf {a} } n’est jamais négatif et vaut zéro si et seulement si a = 0 {displaystyle mathbf {a} =mathbf {0} } —le vecteur zéro.

Le produit scalaire revient donc à multiplier la norme (longueur) de b par la norme de la projection de a sur b .

Équivalence des définitions

Si e ₁ , …, e _n sont les vecteurs de base standard dans R ⁿ , alors on peut écrire

a = [ a 1 , … , a n ] = ∑ i a i e i b = [ b 1 , … , b n ] = ∑ i b i e i . {displaystyle {begin{aligned}mathbf {a} &=[a_{1},dots ,a_{n}]=sum _{i}a_{i}mathbf {e} _{i} \mathbf {b} &=[b_{1},dots ,b_{n}]=sum _{i}b_{i}mathbf {e} _{i}.end{aligned}} } ${displaystyle {begin{aligned}mathbf {a} &=[a_{1},dots ,a_{n}]=sum _{i}a_{i}mathbf {e} _{i}\mathbf {b} &=[b_{1},dots ,b_{n}]=sum _{i}b_{i}mathbf {e} _{i}.end{aligned}}}$ ${displaystyle {begin{aligned}mathbf {a} &=[a_{1},dots ,a_{n}]=sum _{i}a_{i}mathbf {e} _{i}\mathbf {b} &=[b_{1},dots ,b_{n}]=sum _{i}b_{i}mathbf {e} _{i}.end{aligned}}}$

Les vecteurs e _i sont une base orthonormée , ce qui signifie qu’ils ont une longueur unitaire et qu’ils sont perpendiculaires les uns aux autres. Donc puisque ces vecteurs ont une longueur unitaire

e i ⋅ e i = 1 {displaystyle mathbf {e} _{i}cdot mathbf {e} _{i}=1} $mathbf {e} _{i}cdot mathbf {e} _{i}=1$ $mathbf {e} _{i}cdot mathbf {e} _{i}=1$

et comme ils forment des angles droits entre eux, si i ≠ j ,

e i ⋅ e j = 0. {displaystyle mathbf {e} _{i}cdot mathbf {e} _{j}=0.} $mathbf {e} _{i}cdot mathbf {e} _{j}=0.$ $mathbf {e} _{i}cdot mathbf {e} _{j}=0.$

Ainsi en général, on peut dire que :

e i ⋅ e j = δ i j . {displaystyle mathbf {e} _{i}cdot mathbf {e} _{j}=delta _{ij}.} $mathbf {e} _{i}cdot mathbf {e} _{j}=delta _{ij}.$ $mathbf {e} _{i}cdot mathbf {e} _{j}=delta _{ij}.$

Où δ _ij est le delta de Kronecker .

Composantes vectorielles dans une base orthonormée

Aussi, par la définition géométrique, pour tout vecteur e _i et un vecteur a , on note

a ⋅ e i = ‖ a ‖ ‖ e i ‖ cos ⁡ θ i = ‖ a ‖ cos ⁡ θ i = a i , {displaystyle mathbf {a} cdot mathbf {e} _{i}=left|mathbf {a} right|,left|mathbf {e} _{i}right |cos theta _{i}=left|mathbf {a} right|cos theta _{i}=a_{i},} ${displaystyle mathbf {a} cdot mathbf {e} _{i}=left|mathbf {a} right|,left|mathbf {e} _{i}right|cos theta _{i}=left|mathbf {a} right|cos theta _{i}=a_{i},}$ ${displaystyle mathbf {a} cdot mathbf {e} _{i}=left|mathbf {a} right|,left|mathbf {e} _{i}right|cos theta _{i}=left|mathbf {a} right|cos theta _{i}=a_{i},}$

où a _i est la composante du vecteur a dans la direction de e _i . La dernière étape de l’égalité peut être vue sur la figure.

Maintenant, l’application de la distributivité de la version géométrique du produit scalaire donne

a ⋅ b = a ⋅ ∑ i b i e i = ∑ i b i ( a ⋅ e i ) = ∑ i b i a i = ∑ i a i b i , {displaystyle mathbf {a} cdot mathbf {b} =mathbf {a} cdot sum _{i}b_{i}mathbf {e} _{i}=sum _{i}b_ {i}(mathbf {a} cdot mathbf {e} _{i})=sum _{i}b_{i}a_{i}=sum _{i}a_{i}b_{i },} ${displaystyle mathbf {a} cdot mathbf {b} =mathbf {a} cdot sum _{i}b_{i}mathbf {e} _{i}=sum _{i}b_{i}(mathbf {a} cdot mathbf {e} _{i})=sum _{i}b_{i}a_{i}=sum _{i}a_{i}b_{i},}$ ${displaystyle mathbf {a} cdot mathbf {b} =mathbf {a} cdot sum _{i}b_{i}mathbf {e} _{i}=sum _{i}b_{i}(mathbf {a} cdot mathbf {e} _{i})=sum _{i}b_{i}a_{i}=sum _{i}a_{i}b_{i},}$

qui est précisément la définition algébrique du produit scalaire. Ainsi, le produit scalaire géométrique est égal au produit scalaire algébrique.

Learn more.

Accélération

Jul 6, 2022

Potentiel électrique

Jun 28, 2022

Dipôle

Jun 22, 2022

Indications géographiques et spécialités traditionnelles dans…

Jun 22, 2022

Propriétés

Le produit scalaire remplit les propriétés suivantes si a , b et c sont des vecteurs réels et r est un scalaire . ^{[2] [3]}

Commutatif : a ⋅ b = b ⋅ a , {displaystyle mathbf {a} cdot mathbf {b} =mathbf {b} cdot mathbf {a} ,} qui découle de la définition ( θ est l’angle entre a et b ) : ^[6] a ⋅ b = ‖ a ‖ ‖ b ‖ cos ⁡ θ = ‖ b ‖ ‖ a ‖ cos ⁡ θ = b ⋅ a . {displaystyle mathbf {a} cdot mathbf {b} =left|mathbf {a} right|left|mathbf {b} right|cos theta =left |mathbf {b} right|left|mathbf {a} right|cos theta =mathbf {b} cdot mathbf {a} .}
Distributif sur l’addition vectorielle : a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {displaystyle mathbf {a} cdot (mathbf {b} +mathbf {c} )=mathbf {a} cdot mathbf {b} +mathbf {a} cdot mathbf {c} . }
Bilinéaire : a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {displaystyle mathbf {a} cdot (rmathbf {b} +mathbf {c} )=r(mathbf {a} cdot mathbf {b} )+(mathbf {a} cdot mathbf {c} ).}
Multiplication scalaire : ( c 1 a ) ⋅ ( c 2 b ) = c 1 c 2 ( a ⋅ b ) . {displaystyle (c_{1}mathbf {a} )cdot (c_{2}mathbf {b} )=c_{1}c_{2}(mathbf {a} cdot mathbf {b}) .} $(c_{1}mathbf {a} )cdot (c_{2}mathbf {b} )=c_{1}c_{2}(mathbf {a} cdot mathbf {b} ).$ $(c_{1}mathbf {a} )cdot (c_{2}mathbf {b} )=c_{1}c_{2}(mathbf {a} cdot mathbf {b} ).$
Non Associatif car le produit scalaire entre un scalaire ( a ⋅ b ) et un vecteur ( c ) n’est pas défini, ce qui signifie que les expressions impliquées dans la propriété associative, ( a ⋅ b ) ⋅ c ou a ⋅ ( b ⋅ c ) sont tous deux mal définis. ^[7] Notez cependant que la propriété de multiplication scalaire mentionnée précédemment est parfois appelée “loi associative pour scalaire et produit scalaire” ^[8] ou on peut dire que “le produit scalaire est Associatif par rapport à la multiplication scalaire” car c ( a ⋅ b ) = ( c une ) ⋅b = une ⋅ ( c b ). ^[9]
Orthogonale : Deux vecteurs non nuls a et b sont orthogonaux si et seulement si a ⋅ b = 0 .
Pas d’annulation : Contrairement à la multiplication de nombres ordinaires, où si ab = ac , alors b est toujours égal à c sauf si a vaut zéro, le produit scalaire n’obéit pas à la loi d’annulation : Si a ⋅ b = a ⋅ c et a ≠ 0 , alors on peut écrire : a ⋅ ( b − c ) = 0 par la loi distributive ; le résultat ci-dessus indique que cela signifie simplement que a est perpendiculaire à ( b – c ) , ce qui permet toujours ( b – c ) ≠ 0 , et donc permet b ≠c .
Règle de produit : Si a et b sont des fonctions différentiables (à valeurs vectorielles) , alors la dérivée ( notée par un nombre premier ′ ) de a ⋅ b est donnée par la règle ( a ⋅ b ) ′ = a ′ ⋅ b + a ⋅ b ′ .

Application à la loi des Cosinus

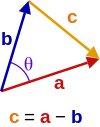
Triangle avec des arêtes vectorielles a et b , séparées par un angle θ .

Étant donné deux vecteurs a et b séparés par un angle θ (voir image de droite), ils forment un triangle avec un troisième côté c = a − b . Le produit scalaire de ceci avec lui-même est :

c ⋅ c = ( a − b ) ⋅ ( a − b ) = a ⋅ a − a ⋅ b − b ⋅ a + b ⋅ b = a 2 − a ⋅ b − a ⋅ b + b 2 = a 2 − 2 a ⋅ b + b 2 c 2 = a 2 + b 2 − 2 a b cos ⁡ θ {displaystyle {begin{aligned}mathbf {color {orange}c} cdot mathbf {color {orange}c} &=(mathbf {color {red}a} -mathbf {color {blue}b} )cdot (mathbf {color {red}a} -mathbf {color {blue}b} )\&=mathbf {color {red}a} cdot mathbf {color {red}a} -mathbf {color {red}a} cdot mathbf {color {blue}b} -mathbf {color {blue}b} cdot mathbf {color {red}a} +mathbf {color {blue}b} cdot mathbf {color {blue}b} \&=mathbf {color {red}a} ^{2}-mathbf {color {red}a} cdot mathbf {color {blue}b} -mathbf {color {red}a} cdot mathbf {color {blue}b} +mathbf {color {blue}b} ^{2}\&=mathbf {color {red}a} ^{2}-2mathbf {color {red}a} cdot mathbf {color {blue}b} +mathbf {color {blue}b} ^{2}\mathbf {color {orange}c} ^{2}&=mathbf {color {red}a} ^{2}+mathbf {color {blue}b} ^{2}-2mathbf {color {red}a} mathbf {color {blue}b} cos mathbf {color {purple}theta } \end{aligned}}} ${displaystyle {begin{aligned}mathbf {color {orange}c} cdot mathbf {color {orange}c} &=(mathbf {color {red}a} -mathbf {color {blue}b} )cdot (mathbf {color {red}a} -mathbf {color {blue}b} )\&=mathbf {color {red}a} cdot mathbf {color {red}a} -mathbf {color {red}a} cdot mathbf {color {blue}b} -mathbf {color {blue}b} cdot mathbf {color {red}a} +mathbf {color {blue}b} cdot mathbf {color {blue}b} \&=mathbf {color {red}a} ^{2}-mathbf {color {red}a} cdot mathbf {color {blue}b} -mathbf {color {red}a} cdot mathbf {color {blue}b} +mathbf {color {blue}b} ^{2}\&=mathbf {color {red}a} ^{2}-2mathbf {color {red}a} cdot mathbf {color {blue}b} +mathbf {color {blue}b} ^{2}\mathbf {color {orange}c} ^{2}&=mathbf {color {red}a} ^{2}+mathbf {color {blue}b} ^{2}-2mathbf {color {red}a} mathbf {color {blue}b} cos mathbf {color {purple}theta } \end{aligned}}}$ ${displaystyle {begin{aligned}mathbf {color {orange}c} cdot mathbf {color {orange}c} &=(mathbf {color {red}a} -mathbf {color {blue}b} )cdot (mathbf {color {red}a} -mathbf {color {blue}b} )\&=mathbf {color {red}a} cdot mathbf {color {red}a} -mathbf {color {red}a} cdot mathbf {color {blue}b} -mathbf {color {blue}b} cdot mathbf {color {red}a} +mathbf {color {blue}b} cdot mathbf {color {blue}b} \&=mathbf {color {red}a} ^{2}-mathbf {color {red}a} cdot mathbf {color {blue}b} -mathbf {color {red}a} cdot mathbf {color {blue}b} +mathbf {color {blue}b} ^{2}\&=mathbf {color {red}a} ^{2}-2mathbf {color {red}a} cdot mathbf {color {blue}b} +mathbf {color {blue}b} ^{2}\mathbf {color {orange}c} ^{2}&=mathbf {color {red}a} ^{2}+mathbf {color {blue}b} ^{2}-2mathbf {color {red}a} mathbf {color {blue}b} cos mathbf {color {purple}theta } \end{aligned}}}$

qui est la loi des Cosinus .

Triple produit

Il existe deux opérations ternaires impliquant le produit scalaire et le produit croisé .

Le triple produit scalaire de trois vecteurs est défini comme

a ⋅ ( b × c ) = b ⋅ ( c × a ) = c ⋅ ( a × b ) . {displaystyle mathbf {a} cdot (mathbf {b} times mathbf {c} )=mathbf {b} cdot (mathbf {c} times mathbf {a} )=mathbf { c} cdot (mathbf {a} times mathbf {b} ).}

Sa valeur est le déterminant de la matrice dont les colonnes sont les Coordonnées cartésiennes des trois vecteurs. C’est le volume signé du parallélépipède défini par les trois vecteurs, et isomorphe au cas particulier tridimensionnel du Produit extérieur de trois vecteurs.

Le triple Produit vectoriel est défini par ^{[2] [3]}

a × ( b × c ) = ( a ⋅ c ) b − ( a ⋅ b ) c . {displaystyle mathbf {a} times (mathbf {b} times mathbf {c} )=(mathbf {a} cdot mathbf {c} ),mathbf {b} -(mathbf {a} cdot mathbf {b} ),mathbf {c} .}

Cette identité, également connue sous le nom de formule de Lagrange , peut être rappelée comme “ACB moins ABC”, en gardant à l’esprit les vecteurs qui sont pointillés ensemble. Cette formule a des applications dans la simplification des calculs vectoriels en physique .

La physique

En physique , la magnitude vectorielle est un scalaire au sens physique (c’est-à-dire une quantité physique indépendante du système de coordonnées), exprimée comme le produit d’une valeur numérique et d’une Unité physique , pas seulement un nombre. Le produit scalaire est également un scalaire dans ce sens, donné par la formule, indépendant du système de coordonnées. Par exemple : ^{[10] [11]}

Le Travail mécanique est le produit scalaire des vecteurs de force et de déplacement ,
La puissance est le produit scalaire de la force et de la vitesse .

Généralisations

Vecteurs complexes

Pour les vecteurs avec des entrées complexes , l’utilisation de la définition donnée du produit scalaire conduirait à des propriétés assez différentes. Par exemple, le produit scalaire d’un vecteur avec lui-même pourrait être nul sans que le vecteur soit le vecteur nul (par exemple, cela se produirait avec le vecteur a = [1 i]). Cela aurait à son tour des conséquences sur des notions telles que la longueur et l’angle. Des propriétés telles que la norme définie positive peuvent être récupérées au prix de l’abandon des propriétés symétriques et bilinéaires du produit scalaire, grâce à la définition alternative ^{[12] [2]}

a ⋅ b = ∑ i a i b i ̄ , {displaystyle mathbf {a} cdot mathbf {b} =sum _{i}{{a_{i}},{overline {b_{i}}}},} ${displaystyle mathbf {a} cdot mathbf {b} =sum _{i}{{a_{i}},{overline {b_{i}}}},}$ ${displaystyle mathbf {a} cdot mathbf {b} =sum _{i}{{a_{i}},{overline {b_{i}}}},}$

où b i ̄ {displaystyle {overline {b_{i}}}} ${displaystyle {overline {b_{i}}}}$ ${displaystyle {overline {b_{i}}}}$ est le conjugué complexe de b i {displaystyle b_{i}} $b_{i}$ $b_{i}$ . Lorsque les vecteurs sont représentés par des vecteurs ligne , le produit scalaire peut être exprimé sous la forme d’un Produit matriciel impliquant une transposée conjuguée , désignée par l’exposant H :

a ⋅ b = b H a . {displaystyle mathbf {a} cdot mathbf {b} =mathbf {b} ^{mathsf {H}}mathbf {a} .} ${displaystyle mathbf {a} cdot mathbf {b} =mathbf {b} ^{mathsf {H}}mathbf {a} .}$ ${displaystyle mathbf {a} cdot mathbf {b} =mathbf {b} ^{mathsf {H}}mathbf {a} .}$

Dans le cas de vecteurs à composantes réelles, cette définition est la même que dans le cas réel. Le produit scalaire de tout vecteur avec lui-même est un nombre réel non négatif, et il est différent de zéro sauf pour le vecteur zéro. Cependant, le produit scalaire complexe est sesquilinéaire plutôt que bilinéaire, car il est conjugué linéaire et non linéaire dans a . Le produit scalaire n’est pas symétrique, puisque

a ⋅ b = b ⋅ a ̄ . {displaystyle mathbf {a} cdot mathbf {b} ={overline {mathbf {b} cdot mathbf {a} }}.}

L’angle entre deux vecteurs complexes est alors donné par

cos ⁡ θ = Re ⁡ ( a ⋅ b ) ‖ a ‖ ‖ b ‖ . {displaystyle cos theta ={frac {operatorname {Re} (mathbf {a} cdot mathbf {b})}{left|mathbf {a} right|,left |mathbf {b} right|}}.} $cos theta ={frac {operatorname {Re} (mathbf {a} cdot mathbf {b} )}{left|mathbf {a} right|,left|mathbf {b} right|}}.$ $cos theta ={frac {operatorname {Re} (mathbf {a} cdot mathbf {b} )}{left|mathbf {a} right|,left|mathbf {b} right|}}.$

Le produit scalaire complexe conduit aux notions de formes hermitiennes et d’ espaces généraux de produits scalaires , largement utilisés en mathématiques et en physique .

Le produit scalaire d’un vecteur complexe a ⋅ a = a H a {displaystyle mathbf {a} cdot mathbf {a} =mathbf {a} ^{mathsf {H}}mathbf {a} } ${displaystyle mathbf {a} cdot mathbf {a} =mathbf {a} ^{mathsf {H}}mathbf {a} }$ ${displaystyle mathbf {a} cdot mathbf {a} =mathbf {a} ^{mathsf {H}}mathbf {a} }$ , impliquant la transposée conjuguée d’un Vecteur ligne, est également connue sous le nom de norme au carré , a ⋅ a = ‖ a ‖ 2 {textstyle mathbf {a} cdot mathbf {a} =|mathbf {a} |^{2}} ${textstyle mathbf {a} cdot mathbf {a} =|mathbf {a} |^{2}}$ ${textstyle mathbf {a} cdot mathbf {a} =|mathbf {a} |^{2}}$ , après la norme euclidienne ; c’est une généralisation vectorielle du carré absolu d’un scalaire complexe (voir aussi : distance euclidienne au carré ).

Produit intérieur

Le produit scalaire généralise le produit scalaire aux espaces vectoriels abstraits sur un champ de scalaires , soit le champ de nombres réels R {displaystyle mathbb {R} } ou le corps des nombres complexes C {displaystyle mathbb {C} } . Il est généralement indiqué à l’aide de parenthèses angulaires par ⟨ a , b ⟩ {displaystyle leftlangle mathbf {a} ,,mathbf {b} rightrangle } .

Le produit interne de deux vecteurs sur le champ des nombres complexes est, en général, un nombre complexe et est sesquilinéaire au lieu de bilinéaire. Un espace de produit scalaire est un espace vectoriel normé , et le produit scalaire d’un vecteur avec lui-même est réel et défini positivement.

Les fonctions

Le produit scalaire est défini pour les vecteurs qui ont un nombre fini d’ entrées . Ainsi ces vecteurs peuvent être considérés comme des fonctions discrètes : un vecteur de longueur n u est alors une fonction de domaine { k ∈ N {displaystyle mathbb {N} } ∣ 1 ≤ k ≤ n } , et u _i est une notation pour l’image de i par la fonction/vecteur u .

Cette notion peut être généralisée aux fonctions continues : tout comme le produit scalaire sur les vecteurs utilise une somme sur les composants correspondants, le produit scalaire sur les fonctions est défini comme une intégrale sur un intervalle a ≤ x ≤ b (également noté [ a , b ] ) : ^[2]

⟨ u , v ⟩ = ∫ a b u ( x ) v ( x ) d x {displaystyle leftlangle u,vrightrangle =int _{a}^{b}u(x)v(x)dx} $leftlangle u,vrightrangle =int _{a}^{b}u(x)v(x)dx$ $leftlangle u,vrightrangle =int _{a}^{b}u(x)v(x)dx$

Généralisé plus loin aux fonctions complexes ψ ( x ) et χ ( x ) , par analogie avec le produit scalaire complexe ci-dessus, donne ^[2]

⟨ ψ , χ ⟩ = ∫ a b ψ ( x ) χ ( x ) ̄ d x . {displaystyle leftlangle psi ,chi rightrangle =int _{a}^{b}psi (x){overline {chi (x)}}dx.} $leftlangle psi ,chi rightrangle =int _{a}^{b}psi (x){overline {chi (x)}}dx.$ $leftlangle psi ,chi rightrangle =int _{a}^{b}psi (x){overline {chi (x)}}dx.$

Fonction poids

Les produits internes peuvent avoir une fonction de pondération (c’est-à-dire une fonction qui pondère chaque terme du produit interne avec une valeur). Explicitement, le produit interne des fonctions u ( x ) {displaystyle u(x)} u(x) et v ( x ) {displaystyle v(x)} v(x) par rapport à la fonction de poids r ( x ) > 0 {displaystyle r(x)>0} est

⟨ u , v ⟩ = ∫ a b r ( x ) u ( x ) v ( x ) d x . {displaystyle leftlangle u,vrightrangle =int _{a}^{b}r(x)u(x)v(x)dx.} ${displaystyle leftlangle u,vrightrangle =int _{a}^{b}r(x)u(x)v(x)dx.}$ ${displaystyle leftlangle u,vrightrangle =int _{a}^{b}r(x)u(x)v(x)dx.}$

Dyadiques et matrices

Un produit à deux points pour les matrices est le produit interne de Frobenius , qui est analogue au produit scalaire sur les vecteurs. Elle est définie comme la somme des produits des composantes correspondantes de deux matrices A et B de même taille :

A : B = ∑ i ∑ j A i j B i j ̄ = tr ⁡ ( B H A ) = tr ⁡ ( A B H ) . {displaystyle mathbf {A} :mathbf {B} =sum _{i}sum _{j}A_{ij}{overline {B_{ij}}}=operatorname {tr} (mathbf {B} ^{mathsf {H}}mathbf {A} )=operatorname {tr} (mathbf {A} mathbf {B} ^{mathsf {H}}).} ${displaystyle mathbf {A} :mathbf {B} =sum _{i}sum _{j}A_{ij}{overline {B_{ij}}}=operatorname {tr} (mathbf {B} ^{mathsf {H}}mathbf {A} )=operatorname {tr} (mathbf {A} mathbf {B} ^{mathsf {H}}).}$ ${displaystyle mathbf {A} :mathbf {B} =sum _{i}sum _{j}A_{ij}{overline {B_{ij}}}=operatorname {tr} (mathbf {B} ^{mathsf {H}}mathbf {A} )=operatorname {tr} (mathbf {A} mathbf {B} ^{mathsf {H}}).}$ A : B = ∑ i ∑ j A i j B i j = tr ⁡ ( B T A ) = tr ⁡ ( A B T ) = tr ⁡ ( A T B ) = tr ⁡ ( B A T ) . {displaystyle mathbf {A} :mathbf {B} =sum _{i}sum _{j}A_{ij}B_{ij}=operatorname {tr} (mathbf {B} ^{ mathsf {T}}mathbf {A} )=nomopérateur {tr} (mathbf {A} mathbf {B} ^{mathsf {T}})=nomopérateur {tr} (mathbf {A} ^ {mathsf {T}}mathbf {B} )=nomopérateur {tr} (mathbf {B} mathbf {A} ^{mathsf {T}}).} ${displaystyle mathbf {A} :mathbf {B} =sum _{i}sum _{j}A_{ij}B_{ij}=operatorname {tr} (mathbf {B} ^{mathsf {T}}mathbf {A} )=operatorname {tr} (mathbf {A} mathbf {B} ^{mathsf {T}})=operatorname {tr} (mathbf {A} ^{mathsf {T}}mathbf {B} )=operatorname {tr} (mathbf {B} mathbf {A} ^{mathsf {T}}).}$ ${displaystyle mathbf {A} :mathbf {B} =sum _{i}sum _{j}A_{ij}B_{ij}=operatorname {tr} (mathbf {B} ^{mathsf {T}}mathbf {A} )=operatorname {tr} (mathbf {A} mathbf {B} ^{mathsf {T}})=operatorname {tr} (mathbf {A} ^{mathsf {T}}mathbf {B} )=operatorname {tr} (mathbf {B} mathbf {A} ^{mathsf {T}}).}$ (Pour les matrices réelles)

En écrivant une matrice sous forme de dyadique , nous pouvons définir un produit à deux points différent (voir Dyadiques § Produit de dyadique et dyadique ), mais ce n’est pas un produit interne.

Tenseurs

Le produit interne entre un tenseur d’ordre n et un tenseur d’ordre m est un tenseur d’ordre n + m – 2 , voir Contraction du tenseur pour plus de détails.

Calcul

Algorithmes

L’algorithme simple pour calculer un produit scalaire à virgule flottante de vecteurs peut souffrir d’ une annulation catastrophique . Pour éviter cela, des approches telles que l’ algorithme de sommation de Kahan sont utilisées.

Bibliothèques

Une fonction de produit scalaire est incluse dans :

BLAS niveau 1 réel SDOT, DDOT ; CDOTU complexe, ZDOTU = X^T * Y, CDOTC ZDOTC = X^H * Y
Matlab as A’ * B or conj(transpose(A)) * B or sum( conj(A) .* B)
GNU Octave comme somme (conj (X) .* Y, dim)
Intel oneAPI Math Kernel Library real p?dot dot = sub(x)’*sub(y); complexe p?dotc dotc = conjg(sub(x)’)*sub(y)

Voir également

Inégalité de Cauchy-Schwarz
Produit croisé
Représentation du produit scalaire d’un graphique
Norme euclidienne , la racine carrée du produit scalaire propre
Multiplication matricielle
Tenseur métrique
Multiplication de vecteurs
Produit extérieur

Remarques

^ Le terme produit scalaire signifie littéralement “produit avec un scalaire comme résultat”. Il est aussi parfois utilisé pour d’autres formes bilinéaires symétriques , par exemple dans un espace pseudo-euclidien .

Références

^ ^un ^b “Produit scalaire” . www.mathsisfun.com . Récupéré le 06/09/2020 .
^ ^un ^bcdef ^S.^Lipschutz ; ^_^_M. Lipson (2009). Algèbre linéaire (contours de Schaum) (4e éd.). McGraw Hill. ISBN 978-0-07-154352-1.
^ ^un ^bc ^MR Spiegel; S. Lipschutz; D. Spellman (2009). Analyse vectorielle (Contours de Schaum) (2e éd.). McGraw Hill. ISBN 978-0-07-161545-7.
^ AIBorisenko; IE Taparov (1968). Analyse vectorielle et tensorielle avec applications . Traduit par Richard Silverman. Douvres. p. 14.
^ Arfken, GB; Weber, HJ (2000). Méthodes mathématiques pour les physiciens (5e éd.). Boston, MA : presse académique . p. 14–15. ISBN 978-0-12-059825-0..
^ Nykamp, Duan. “Le produit scalaire” . Aperçu mathématique . Consulté le 6 septembre 2020 .
^ Weisstein, Eric W. “Produit scalaire.” De MathWorld – Une ressource Web Wolfram. http://mathworld.wolfram.com/DotProduct.html
^ T. Banchoff; J. Wermer (1983). Algèbre linéaire à travers la géométrie . Springer Science et médias d’affaires. p. 12. ISBN 978-1-4684-0161-5.
^ A. Bedford; Wallace L. Fowler (2008). Engineering Mechanics: Static (5e éd.). Prentice Hall. p. 60. ISBN 978-0-13-612915-8.
^ KF Riley; le député Hobson ; SJ Bence (2010). Méthodes mathématiques pour la physique et l’ingénierie (3e éd.). La presse de l’Universite de Cambridge. ISBN 978-0-521-86153-3.
^ M. Mansfield; C. O’Sullivan (2011). Comprendre la physique (4e éd.). John Wiley et fils. ISBN 978-0-47-0746370.
^ Berberian, Sterling K. (2014) [1992], Algèbre linéaire , Douvres, p. 287, ISBN 978-0-486-78055-9

Liens externes

Wikimedia Commons a des médias liés au produit Scalar .

“Produit interne” , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
Explication du produit scalaire y compris avec des vecteurs complexes
“Dot Product” par Bruce Torrence, Wolfram Demonstrations Project , 2007.