Multiplication matricielle

En mathématiques , en particulier en algèbre linéaire , la multiplication matricielle est une opération binaire qui produit une matrice à partir de deux matrices. Pour la multiplication matricielle, le nombre de colonnes dans la première matrice doit être égal au nombre de lignes dans la seconde matrice. La matrice résultante, appelée produit matriciel , a le nombre de lignes de la première et le nombre de colonnes de la seconde matrice. Le produit des matrices A et B est noté AB . ^[1]

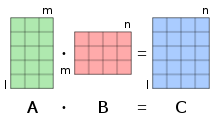Pour la multiplication matricielle, le nombre de colonnes dans la première matrice doit être égal au nombre de lignes dans la seconde matrice. La matrice résultat a le nombre de lignes de la première et le nombre de colonnes de la seconde matrice.

La multiplication matricielle a été décrite pour la première fois par le mathématicien français Jacques Philippe Marie Binet en 1812, ^[2] pour représenter la composition de cartes linéaires représentées par des matrices. La multiplication matricielle est donc un outil de base de l’algèbre linéaire et, en tant que tel, a de nombreuses applications dans de nombreux domaines des mathématiques, ainsi que dans les mathématiques appliquées , les statistiques , la physique , l’économie et l’ingénierie . ^{[3] [4]} Le calcul des produits matriciels est une opération centrale dans toutes les applications informatiques de l’algèbre linéaire.

Notation

Cet article utilisera les conventions de notation suivantes : les matrices sont représentées par des majuscules en gras, par exemple A ; vecteurs en minuscules gras, par exemple a ; et les entrées de vecteurs et de matrices sont en italique (ce sont des nombres d’un champ), par exemple A et a . La notation d’index est souvent le moyen le plus clair d’exprimer des définitions et est utilisée comme norme dans la littérature. L’entrée à la ligne i , colonne j de la matrice A est indiquée par ( A ) _ij , A _ij ou a _ij. En revanche, un seul indice, par exemple A ₁ , A ₂ , est utilisé pour sélectionner une matrice (pas une entrée de matrice) à partir d’une collection de matrices.

Définition

Si A est une matrice m × n et B est une matrice n × p ,

UN = ( un 11 un 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ) , B = ( b 11 b 12 ⋯ b 1 p b 21 b 22 ⋯ b 2 p ⋮ ⋮ ⋱ ⋮ b n 1 b n 2 ⋯ b n p ) {displaystyle mathbf {A} ={begin{pmatrix}a_{11}&a_{12}&cdots &a_{1n}\a_{21}&a_{22}&cdots &a_{2n}\ vdots &vdots &ddots &vdots \a_{m1}&a_{m2}&cdots &a_{mn}\end{pmatrix}},quad mathbf {B} ={begin{pmatrix} b_{11}&b_{12}&cdots &b_{1p}\b_{21}&b_{22}&cdots &b_{2p}\vdots &vdots &ddots &vdots \b_{n1 }&b_{n2}&cdots &b_{np}\end{pmatrix}}}

le produit matriciel C = AB (noté sans signes ni points de multiplication) est défini comme étant la matrice m × p ^{[5] [6] [7] [8]}

C = ( c 11 c 12 ⋯ c 1 p c 21 c 22 ⋯ c 2 p ⋮ ⋮ ⋱ ⋮ c m 1 c m 2 ⋯ c m p ) {displaystyle mathbf {C} ={begin{pmatrix}c_{11}&c_{12}&cdots &c_{1p}\c_{21}&c_{22}&cdots &c_{2p}\ vdots &vdots &ddots &vdots \c_{m1}&c_{m2}&cdots &c_{mp}\end{pmatrix}}}

tel que

c i j = a i 1 b 1 j + a i 2 b 2 j + ⋯ + a i n b n j = ∑ k = 1 n a i k b k j , {displaystyle c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+cdots +a_{in}b_{nj}=sum _{k=1}^{n} a_{ik}b_{kj},}

pour i = 1, …, m et j = 1, …, p .

c’est-à-dire l’entrée c i j {displaystyle c_{ij}} du produit s’obtient en multipliant terme à terme les entrées de la i ème ligne de A et de la j ème colonne de B , et en sommant ces n produits. En d’autres termes, c i j {displaystyle c_{ij}} est le produit scalaire de la i ème ligne de A et de la j ème colonne de B .

Par conséquent, AB peut aussi s’écrire

C = ( a 11 b 11 + ⋯ + a 1 n b n 1 a 11 b 12 + ⋯ + a 1 n b n 2 ⋯ a 11 b 1 p + ⋯ + a 1 n b n p a 21 b 11 + ⋯ + a 2 n b n 1 a 21 b 12 + ⋯ + a 2 n b n 2 ⋯ a 21 b 1 p + ⋯ + a 2 n b n p ⋮ ⋮ ⋱ ⋮ a m 1 b 11 + ⋯ + a m n b n 1 a m 1 b 12 + ⋯ + a m n b n 2 ⋯ a m 1 b 1 p + ⋯ + a m n b n p ) {displaystyle mathbf {C} ={begin{pmatrix}a_{11}b_{11}+cdots +a_{1n}b_{n1}&a_{11}b_{12}+cdots +a_{1n }b_{n2}&cdots &a_{11}b_{1p}+cdots +a_{1n}b_{np}\a_{21}b_{11}+cdots +a_{2n}b_{n1} &a_{21}b_{12}+cdots +a_{2n}b_{n2}&cdots &a_{21}b_{1p}+cdots +a_{2n}b_{np}\vdots &vdots &ddots &vdots \a_{m1}b_{11}+cdots +a_{mn}b_{n1}&a_{m1}b_{12}+cdots +a_{mn}b_{n2}& cdots &a_{m1}b_{1p}+cdots +a_{mn}b_{np}\end{pmatrix}}}

Ainsi le produit AB est défini si et seulement si le nombre de colonnes dans A est égal au nombre de lignes dans B , ^[1] dans ce cas n .

Dans la plupart des scénarios, les entrées sont des nombres, mais il peut s’agir de n’importe quel type d’ objets mathématiques pour lesquels une addition et une multiplication sont définies, qui sont associatifs et tels que l’addition est commutative et la multiplication est distributive par rapport à l’addition . En particulier, les entrées peuvent être elles-mêmes des matrices (voir bloc matrix ).

Illustration

La figure de droite illustre schématiquement le produit de deux matrices A et B , montrant comment chaque intersection dans la matrice produit correspond à une ligne de A et une colonne de B .

[ a 11 a 12 ⋅ ⋅ a 31 a 32 ⋅ ⋅ ] 4 × 2 matrix [ ⋅ b 12 b 13 ⋅ b 22 b 23 ] 2 × 3 matrix = [ ⋅ c 12 c 13 ⋅ ⋅ ⋅ ⋅ c 32 c 33 ⋅ ⋅ ⋅ ] 4 × 3 matrix {displaystyle {overset {4times 2{text{ matrix}}}{begin{bmatrix}{a_{11}}&{a_{12}}\cdot &cdot \{a_{ 31}}&{a_{32}}\cdot &cdot \end{bmatrix}}}{overset {2times 3{text{matrice}}}{begin{bmatrix}cdot &{b_{12}}&{b_{13}}\cdot &{b_{22}}&{b_{23}}\end{bmatrix}}}={overset {4times 3 {text{matrice}}}{begin{bmatrix}cdot &c_{12}&c_{13}\cdot &cdot &cdot \cdot &c_{32}&c_{33}\cdot &cdot &cdot \end{bmatrice}}}}

Les valeurs aux intersections marquées de cercles sont :

c 12 = a 11 b 12 + a 12 b 22 c 33 = a 31 b 13 + a 32 b 23 {displaystyle {begin{aligned}c_{12}&={a_{11}}{b_{12}}+{a_{12}}{b_{22}}\c_{33}&={a_ {31}}{b_{13}}+{a_{32}}{b_{23}}end{aligned}}}

Applications fondamentales

Historiquement, la multiplication matricielle a été introduite pour faciliter et clarifier les calculs en algèbre linéaire . Cette forte relation entre multiplication matricielle et algèbre linéaire reste fondamentale dans toutes les mathématiques, ainsi qu’en physique , chimie , ingénierie et informatique .

Cartes linéaires

Si un espace vectoriel a une base finie , ses vecteurs sont représentés chacun de manière unique par une séquence finie de scalaires, appelée vecteur de Coordonnées , dont les éléments sont les Coordonnées du vecteur sur la base. Ces vecteurs de Coordonnées forment un autre espace vectoriel, qui est isomorphe à l’espace vectoriel d’origine. Un vecteur de Coordonnées est généralement organisé sous la forme d’une Matrice de colonnes (également appelée vecteur de colonnes ), qui est une matrice à une seule colonne. Ainsi, un vecteur colonne représente à la fois un vecteur de Coordonnées et un vecteur de l’espace vectoriel d’origine.

Une application linéaire A d’un espace vectoriel de dimension n dans un espace vectoriel de dimension m applique un vecteur colonne

x = ( x 1 x 2 ⋮ x n ) {displaystyle mathbf {x} ={begin{pmatrix}x_{1}\x_{2}\vdots \x_{n}end{pmatrix}}}

sur le vecteur colonne

y = A ( x ) = ( a 11 x 1 + ⋯ + a 1 n x n a 21 x 1 + ⋯ + a 2 n x n ⋮ a m 1 x 1 + ⋯ + a m n x n ) . {displaystyle mathbf {y} =A(mathbf {x} )={begin{pmatrix}a_{11}x_{1}+cdots +a_{1n}x_{n}\a_{21} x_{1}+cdots +a_{2n}x_{n}\vdots \a_{m1}x_{1}+cdots +a_{mn}x_{n}end{pmatrix}}.}

L’application linéaire A est donc définie par la matrice

A = ( a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ) , {displaystyle mathbf {A} ={begin{pmatrix}a_{11}&a_{12}&cdots &a_{1n}\a_{21}&a_{22}&cdots &a_{2n}\ vdots &vdots &ddots &vdots \a_{m1}&a_{m2}&cdots &a_{mn}\end{pmatrix}},}

et mappe le vecteur colonne x {displaystyle mathbf {x} } au produit matriciel

y = A x . {displaystyle mathbf {y} =mathbf {Axe} .}

Si B est une autre application linéaire de l’espace vectoriel précédent de dimension m , dans un espace vectoriel de dimension p , il est représenté par un p × m {displaystyle pfois m} matrice B . {displaystyle mathbf {B} .} Un calcul simple montre que la matrice de la carte composite B ∘ A {displaystyle Bcirc A} est le produit matriciel B A . {displaystyle mathbf {BA} .} La formule générale ( B ∘ A ) ( x ) = B ( A ( x ) ) {displaystyle (Bcirc A)(mathbf {x} )=B(A(mathbf {x} ))} ) qui définit la composition de la fonction est instancié ici comme un cas particulier d’associativité de produit matriciel (voir § Associativité ci-dessous) :

( B A ) x = B ( A x ) = B A x . {displaystyle (mathbf {BA} )mathbf {x} =mathbf {B} (mathbf {Ax} )=mathbf {BAx} .} Rotations géométriques

En utilisant un système de Coordonnées cartésien dans un plan euclidien, la rotation d’un angle α {displaystylealpha} autour de l’ origine se trouve une carte linéaire. Plus précisément,

[ x ′ y ′ ] = [ cos ⁡ α − sin ⁡ α sin ⁡ α cos ⁡ α ] [ x y ] {displaystyle {begin{bmatrix}x’\y’end{bmatrix}}={begin{bmatrix}cos alpha &-sin alpha \sin alpha &cos alpha end{bmatrix}}{begin{bmatrix}x\yend{bmatrix}}} ,

où le point source ( x , y ) {displaystyle (x,y)} et son image ( x ′ , y ′ ) {displaystyle (x’,y’)} sont écrits sous forme de vecteurs colonnes.

La composition de la rotation par α {displaystylealpha} et que par β {displaystyle bêta} correspond alors au produit matriciel

[ cos ⁡ β − sin ⁡ β sin ⁡ β cos ⁡ β ] [ cos ⁡ α − sin ⁡ α sin ⁡ α cos ⁡ α ] = [ cos ⁡ β cos ⁡ α − sin ⁡ β sin ⁡ α − cos ⁡ β sin ⁡ α − sin ⁡ b cos ⁡ α sin ⁡ β cos ⁡ α + cos ⁡ β sin ⁡ α − sin ⁡ β sin ⁡ α + cos ⁡ β cos ⁡ α ] = [ cos ⁡ ( α + β ) − sin ⁡ ( α + β ) sin ⁡ ( α + β ) cos ⁡ ( α + β ) ] {displaystyle {begin{bmatrix}cos beta &-sin beta \sin beta &cos beta end{bmatrix}}{begin{bmatrix}cos alpha &-sin alpha \sin alpha &cos alpha end{bmatrix}}={begin{bmatrix}cos beta cos alpha -sin beta sin alpha &-cos beta sin alpha -sin bcos alpha \sin beta cos alpha +cos beta sin alpha &-sin beta sin alpha +cos beta cos alpha end{bmatrix}}={begin{bmatrix}cos(alpha +beta )&-sin(alpha +beta )\sin(alpha +beta )&cos(alpha + beta )end{bmatrice}}} ,

où des identités trigonométriques appropriées sont employées pour la deuxième égalité. C’est-à-dire que la composition correspond à la rotation d’angle α + β {displaystyle alpha +bêta} , comme prévu.

Allocation des ressources en économie Le calcul de l’entrée en bas à gauche de A B {displaystyle mathbf {AB} } correspond à la prise en compte de tous les chemins (en surbrillance) depuis le produit de base b 4 {displaystyle b_{4}} au produit final f 1 {displaystyle f_{1}} dans le graphique de flux de production.

Une usine utilise 4 types de produits de base [ de ] , b 1 , b 2 , b 3 , b 4 {style d’affichage b_{1},b_{2},b_{3},b_{4}} produire 3 sortes de biens intermédiaires , m 1 , m 2 , m 3 {displaystyle m_{1},m_{2},m_{3}} , qui à leur tour sont utilisés pour produire 3 types de produits finaux , f 1 , f 2 , f 3 {displaystyle f_{1},f_{2},f_{3}} . Les matrices

A = ( 1 0 1 2 1 1 0 1 1 1 1 2 ) {displaystyle mathbf {A} =left({begin{tableau}{ccc}1&0&1\2&1&1\0&1&1\1&1&2\end{tableau}}right)} et B = ( 1 2 1 2 3 1 4 2 2 ) {displaystyle mathbf {B} =left({begin{tableau}{ccc}1&2&1\2&3&1\4&2&2\end{tableau}}right)}

fournissent la quantité de produits de base nécessaires pour une quantité donnée de biens intermédiaires, et la quantité de biens intermédiaires nécessaires pour une quantité donnée de produits finaux, respectivement. Par exemple, pour produire une unité de bien intermédiaire m 1 {displaystyle m_{1}} , une unité de produit de base b 1 {displaystyle b_{1}} , deux unités de b 2 {displaystyle b_{2}} , aucune unité de b 3 {displaystyle b_{3}} , et une unité de b 4 {displaystyle b_{4}} sont nécessaires, correspondant à la première colonne de A {displaystyle mathbf {A}} .

En utilisant la multiplication matricielle, calculez

A B = ( 5 4 3 8 9 5 6 5 3 11 9 6 ) {displaystyle mathbf {AB} =left({begin{array}{ccc}5&4&3\8&9&5\ 6&5&3\11&9&6\end{array}}right)} ;

cette matrice fournit directement les quantités de produits de base nécessaires pour des quantités données de biens finaux. Par exemple, l’entrée en bas à gauche de A B {displaystyle mathbf {AB} } est calculé comme 1 ⋅ 1 + 1 ⋅ 2 + 2 ⋅ 4 = 11 {displaystyle 1cdot 1+1cdot 2+2cdot 4=11} , reflétant que 11 {displaystyle 11} unités de b 4 {displaystyle b_{4}} sont nécessaires pour produire une unité de f 1 {displaystyle f_{1}} . En effet, un b 4 {displaystyle b_{4}} l’unité est nécessaire pour m 1 {displaystyle m_{1}} , 2 pour m 2 {displaystyle m_{2}} , et 4 {displaystyle 4} pour chacun des deux m 3 {displaystyle m_{3}} unités qui entrent dans le f 1 {displaystyle f_{1}} unité, voir photo.

Afin de produire par exemple 100 unités du produit final f 1 {displaystyle f_{1}} , 80 unités de f 2 {displaystyle f_{2}} , et 60 unités de f 3 {displaystyle f_{3}} , les quantités nécessaires de biens de base peuvent être calculées comme

( A B ) ( 100 80 60 ) = ( 1000 1820 1180 2180 ) {displaystyle (mathbf {AB})left({begin{array}{c}100\80\60\end{array}}right)=left({begin{array} {c}1000\1820\1180\2180\end{tableau}}right)} ,

C’est, 1000 {displaystyle 1000} unités de b 1 {displaystyle b_{1}} , 1820 {displaystyle 1820} unités de b 2 {displaystyle b_{2}} , 1180 {displaystyle 1180} unités de b 3 {displaystyle b_{3}} , 2180 {displaystyle 2180} unités de b 4 {displaystyle b_{4}} sont nécessaires. De même, la matrice produit A B {displaystyle mathbf {AB} } peut être utilisé pour calculer les quantités nécessaires de biens de base pour d’autres données sur les quantités de biens finaux. ^[9]

Système d’équations linéaires

La forme générale d’un système d’équations linéaires est

a 11 x 1 + ⋯ + a 1 n x n = b 1 a 21 x 1 + ⋯ + a 2 n x n = b 2 ⋮ a m 1 x 1 + ⋯ + a m n x n = b m . {displaystyle {begin{matrice}a_{11}x_{1}+cdots +a_{1n}x_{n}=b_{1}\a_{21}x_{1}+cdots +a_{ 2n}x_{n}=b_{2}\vdots \a_{m1}x_{1}+cdots +a_{mn}x_{n}=b_{m}end{matrice}}.}

En utilisant la même notation que ci-dessus, un tel système est équivalent à l’ équation matricielle unique

A x = b . {displaystyle mathbf {Axe} =mathbf {b} .}

Produit scalaire, forme bilinéaire et produit interne

Le produit scalaire de deux vecteurs colonnes est le produit matriciel

x T y , {displaystyle mathbf {x} ^{mathsf {T}}mathbf {y} ,}

où x T {displaystyle mathbf {x} ^{mathsf {T}}} est le Vecteur ligne obtenu en transposant x {displaystyle mathbf {x} } et la matrice 1 × 1 résultante est identifiée par son entrée unique.

Plus généralement, toute forme bilinéaire sur un espace vectoriel de dimension finie peut être exprimée sous la forme d’un produit matriciel

x T A y , {displaystyle mathbf {x} ^{mathsf {T}}mathbf {Ay} ,}

et tout Produit intérieur peut être exprimé comme

x † A y , {displaystyle mathbf {x} ^{poignard}mathbf {Ay} ,}

où x † {displaystyle mathbf {x} ^{poignard}} désigne la transposée conjuguée de x {displaystyle mathbf {x} } (conjugué de la transposée, ou de manière équivalente transposée du conjugué).

Les propriétés générales

La multiplication matricielle partage certaines propriétés avec la multiplication habituelle . Cependant, la multiplication matricielle n’est pas définie si le nombre de colonnes du premier facteur diffère du nombre de lignes du second facteur, et elle est non commutative , ^[10] même lorsque le produit reste défini après changement de l’ordre des facteurs . ^{[11] [12]}

Non-commutativité

Une opération est commutative si, étant donnés deux éléments A et B tels que le produit A B {displaystyle mathbf {A} mathbf {B} } est défini, alors B A {displaystyle mathbf {B} mathbf {A} } est également défini, et A B = B A . {displaystyle mathbf {A} mathbf {B} =mathbf {B} mathbf {A} .}

Si A et B sont des matrices de tailles respectives m × n {displaystyle mfois n} et p × q {displaystyle pfois q} , alors A B {displaystyle mathbf {A} mathbf {B} } est défini si n = p {displaystyle n=p} , et B A {displaystyle mathbf {B} mathbf {A} } est défini si m = q {displaystyle m=q} . Ainsi, si l’un des produits est défini, l’autre n’est pas défini en général. Si m = q ≠ n = p {displaystyle m=qneq n=p} , les deux produits sont définis, mais ont des tailles différentes ; ils ne peuvent donc pas être égaux. Seulement si m = q = n = p {displaystyle m=q=n=p} , c’est-à-dire si A et B sont des Matrices carrées de même taille, sont tous deux des produits définis et de même taille. Même dans ce cas, on a en général

A B ≠ B A . {displaystyle mathbf {A} mathbf {B} neq mathbf {B} mathbf {A} .}

Par example

( 0 1 0 0 ) ( 0 0 1 0 ) = ( 1 0 0 0 ) , {displaystyle {begin{pmatrix}0&1\0&0end{pmatrix}}{begin{pmatrix}0&0\1&0end{pmatrix}}={begin{pmatrix}1&0\0&0end{pmatrix }},}

mais

( 0 0 1 0 ) ( 0 1 0 0 ) = ( 0 0 0 1 ) . {displaystyle {begin{pmatrix}0&0\1&0end{pmatrix}}{begin{pmatrix}0&1\0&0end{pmatrix}}={begin{pmatrix}0&0\0&1end{pmatrix }}.}

Cet exemple peut être développé pour montrer que, si A est un n × n {displaystyle nfois n} matrice avec des entrées dans un champ F , alors A B = B A {displaystyle mathbf {A} mathbf {B} =mathbf {B} mathbf {A} } pour chaque n × n {displaystyle nfois n} matrice B à entrées dans F , si et seulement si A = c I {displaystyle mathbf {A} =c,mathbf {Je} } où c ∈ F {displaystyle cin F} , et je est le n × n {displaystyle nfois n} matrice d’identité . Si, au lieu d’un champ, les entrées sont supposées appartenir à un anneau , alors il faut ajouter la condition que c appartient au centre de l’anneau.

Un cas particulier où la commutativité se produit est lorsque D et E sont deux Matrices diagonales (carrées) (de même taille); alors DE = ED . ^[10] Encore une fois, si les matrices sont sur un anneau général plutôt qu’un champ, les entrées correspondantes dans chacune doivent également commuter les unes avec les autres pour que cela soit valable.

Distributivité

Le produit matriciel est distributif par rapport à l’ addition matricielle . Autrement dit, si A , B , C , D sont des matrices de tailles respectives m × n , n × p , n × p et p × q , on a (distributivité à gauche)

A ( B + C ) = A B + A C , {displaystyle mathbf {A} (mathbf {B} +mathbf {C} )=mathbf {AB} +mathbf {AC} ,}

et (distributivité à droite)

( B + C ) D = B D + C D . {displaystyle (mathbf {B} +mathbf {C} )mathbf {D} =mathbf {BD} +mathbf {CD} .} ^[dix]

Cela résulte de la distributivité des coefficients par

∑ k a i k ( b k j + c k j ) = ∑ k a i k b k j + ∑ k a i k c k j {displaystyle sum _{k}a_{ik}(b_{kj}+c_{kj})=sum _{k}a_{ik}b_{kj}+sum _{k}a_{ik} c_{kj}} ∑ k ( b i k + c i k ) d k j = ∑ k b i k d k j + ∑ k c i k d k j . {displaystyle sum _{k}(b_{ik}+c_{ik})d_{kj}=sum _{k}b_{ik}d_{kj}+sum _{k}c_{ik} d_{kj}.}

Produit avec un scalaire

Si A est une matrice et c un scalaire, alors les matrices c A {displaystyle cmathbf {A}} et A c {displaystyle mathbf {A} c} sont obtenus en multipliant à gauche ou à droite toutes les entrées de A par c . Si les scalaires ont la propriété commutative , alors c A = A c . {displaystyle cmathbf {A} =mathbf {A} c.}

Si le produit A B {displaystyle mathbf {AB} } est défini (c’est-à-dire que le nombre de colonnes de A est égal au nombre de lignes de B ), alors

c ( A B ) = ( c A ) B {displaystyle c(mathbf {AB} )=(cmathbf {A} )mathbf {B} } et ( A B ) c = A ( B c ) . {displaystyle (mathbf {A} mathbf {B} )c=mathbf {A} (mathbf {B} c).}

Si les scalaires ont la propriété commutative, alors les quatre matrices sont égales. Plus généralement, tous les quatre sont égaux si c appartient au centre d’un anneau contenant les entrées des matrices, car dans ce cas, c X = X c pour toutes les matrices X .

Ces propriétés résultent de la Bilinéarité du produit des scalaires :

c ( ∑ k a i k b k j ) = ∑ k ( c a i k ) b k j {displaystyle cleft(sum _{k}a_{ik}b_{kj}right)=sum _{k}(ca_{ik})b_{kj}} ( ∑ k a i k b k j ) c = ∑ k a i k ( b k j c ) . {displaystyle left(sum _{k}a_{ik}b_{kj}right)c=sum _{k}a_{ik}(b_{kj}c).}

Transposer

Si les scalaires ont la propriété commutative , la transposée d’un produit de matrices est le produit, dans l’ordre inverse, des transposées des facteurs. C’est

( A B ) T = B T A T {displaystyle (mathbf {AB} )^{mathsf {T}}=mathbf {B} ^{mathsf {T}}mathbf {A} ^{mathsf {T}}}

où ^T désigne la transposition, c’est-à-dire l’échange de lignes et de colonnes.

Cette identité ne tient pas pour les entrées non commutatives, puisque l’ordre entre les entrées de A et B est inversé, lorsqu’on élargit la définition du produit matriciel.

Conjugaison compliquée

Si A et B ont des entrées complexes , alors

( A B ) ∗ = A ∗ B ∗ {displaystyle (mathbf {AB} )^{*}=mathbf {A} ^{*}mathbf {B} ^{*}}

où ^* désigne le conjugué complexe d’entrée d’une matrice.

Ceci résulte de l’application à la définition de produit matriciel du fait que le conjugué d’une somme est la somme des conjugués des sommes et le conjugué d’un produit est le produit des conjugués des facteurs.

La transposition agit sur les indices des entrées, tandis que la conjugaison agit indépendamment sur les entrées elles-mêmes. Il en résulte que, si A et B ont des entrées complexes, on a

( A B ) † = B † A † , {displaystyle (mathbf {AB} )^{dague }=mathbf {B} ^{dague}mathbf {A} ^{dague },}

où ^† désigne la transposée conjuguée (conjuguée de la transposée, ou de manière équivalente transposée du conjugué).

Associativité

Étant donné trois matrices A , B et C , les produits ( AB ) C et A ( BC ) sont définis si et seulement si le nombre de colonnes de A est égal au nombre de lignes de B , et le nombre de colonnes de B est égal au nombre de lignes de C (en particulier, si l’un des produits est défini, alors l’autre est également défini). Dans ce cas, on a la propriété associative

( A B ) C = A ( B C ) . {displaystyle (mathbf {AB} )mathbf {C} =mathbf {A} (mathbf {BC}).}

Comme pour toute opération associative, cela permet d’omettre les parenthèses et d’écrire les produits ci-dessus sous la forme A B C . {displaystyle mathbf {ABC} .}

Cela s’étend naturellement au produit de n’importe quel nombre de matrices à condition que les dimensions correspondent. Autrement dit, si A ₁ , A ₂ , …, A _n sont des matrices telles que le nombre de colonnes de A _i est égal au nombre de lignes de A _{i + 1} pour i = 1, …, n – 1 , alors le produit

∏ i = 1 n A i = A 1 A 2 ⋯ A n {displaystyle prod _{i=1}^{n}mathbf {A} _{i}=mathbf {A} _{1}mathbf {A} _{2}cdots mathbf {A} _{n}}

est défini et ne dépend pas de l’ ordre des multiplications , si l’ordre des matrices est maintenu fixe.

Ces propriétés peuvent être prouvées par des manipulations de sommation simples mais compliquées . Ce résultat découle également du fait que les matrices représentent des applications linéaires . Par conséquent, la propriété associative des matrices est simplement un cas particulier de la propriété associative de composition de fonction .

La complexité n’est pas associative

Bien que le résultat d’une séquence de produits matriciels ne dépende pas de l’ Ordre d’opération (à condition que l’ordre des matrices ne soit pas modifié), la complexité de calcul peut dépendre considérablement de cet ordre.

Par exemple, si A , B et C sont des matrices de tailles respectives 10×30, 30×5, 5×60 , le calcul de ( AB ) C nécessite 10×30×5 + 10×5×60 = 4 500 multiplications, tandis que le calcul de A ( BC ) nécessite 30×5×60 + 10×30×60 = 27 000 multiplications.

Des algorithmes ont été conçus pour choisir le meilleur ordre de produits, voir Matrix chain multiplication . Lorsque le nombre n de matrices augmente, il a été montré que le choix du meilleur ordre a une complexité de O ( n log ⁡ n ) . {displaystyle O(nlog n).}

Application à la similitude

Toute matrice inversible P {displaystyle mathbf {P} } définit une transformation de similarité (sur des Matrices carrées de même taille que P {displaystyle mathbf {P} } )

S P ( A ) = P − 1 A P . {displaystyle S_{mathbf {P} }(mathbf {A})=mathbf {P} ^{-1}mathbf {A} mathbf {P} .}

Les transformations de similarité mappent les produits aux produits, c’est-à-dire

S P ( A B ) = S P ( A ) S P ( B ) . {displaystyle S_{mathbf {P} }(mathbf {AB} )=S_{mathbf {P} }(mathbf {A} )S_{mathbf {P} }(mathbf {B} ). }

En fait, on a

P − 1 ( A B ) P = P − 1 A ( P P − 1 ) B P = ( P − 1 A P ) ( P − 1 B P ) . {displaystyle mathbf {P} ^{-1}(mathbf {AB} )mathbf {P} =mathbf {P} ^{-1}mathbf {A} (mathbf {P} mathbf { P} ^{-1})mathbf {B} mathbf {P} =(mathbf {P} ^{-1}mathbf {A} mathbf {P} )(mathbf {P} ^{- 1}mathbf {B} mathbf {P} ).}

Matrices carrées

Dénotons M n ( R ) {displaystyle {mathcal {M}}_{n}(R)} l’ensemble des Matrices carrées n × n avec des entrées dans un anneau R , qui, en pratique, est souvent un champ .

Dans M n ( R ) {displaystyle {mathcal {M}}_{n}(R)} , le produit est défini pour chaque couple de matrices. Cela fait M n ( R ) {displaystyle {mathcal {M}}_{n}(R)} un anneau , qui a la matrice d’identité I comme élément d’identité (la matrice dont les entrées diagonales sont égales à 1 et toutes les autres entrées sont 0). Cet anneau est aussi une R – algèbre associative .

Si n > 1 , de nombreuses matrices n’ont pas d’ inverse multiplicatif . Par exemple, une matrice telle que toutes les entrées d’une ligne (ou d’une colonne) sont 0 n’a pas d’inverse. S’il existe, l’inverse d’une matrice A est noté A ⁻¹ , et, vérifie donc

A A − 1 = A − 1 A = I . {displaystyle mathbf {A} mathbf {A} ^{-1}=mathbf {A} ^{-1}mathbf {A} =mathbf {I} .}

Une matrice qui a un inverse est une matrice inversible . Sinon, c’est une Matrice singulière .

Un produit de matrices est inversible si et seulement si chaque facteur est inversible. Dans ce cas, on a

( A B ) − 1 = B − 1 A − 1 . {displaystyle (mathbf {A} mathbf {B} )^{-1}=mathbf {B} ^{-1}mathbf {A} ^{-1}.}

Lorsque R est commutatif , et, en particulier, lorsqu’il s’agit d’un corps, le déterminant d’un produit est le produit des déterminants. Comme les déterminants sont des scalaires et que les scalaires commutent, on a donc

det ( A B ) = det ( B A ) = det ( A ) det ( B ) . {displaystyle det(mathbf {AB} )=det(mathbf {BA} )=det(mathbf {A} )det(mathbf {B} ).}

Les autres invariants de la matrice se comportent moins bien avec les produits. Néanmoins, si R est commutatif, AB et BA ont la même trace , le même polynôme caractéristique , et les mêmes Valeurs propres avec les mêmes multiplicités. Cependant, les vecteurs propres sont généralement différents si AB ≠ BA .

Puissances d’une matrice

On peut élever une matrice carrée à n’importe quelle puissance entière non négative en la multipliant par elle-même à plusieurs reprises de la même manière que pour les nombres ordinaires. C’est,

A 0 = I , {displaystyle mathbf {UNE} ^{0}=mathbf {Je} ,} A 1 = A , {displaystyle mathbf {UNE} ^{1}=mathbf {UNE} ,} A k = A A ⋯ A ⏟ k times . {displaystyle mathbf {A} ^{k}=underbrace {mathbf {A} mathbf {A} cdots mathbf {A} } _{k{text{ fois}}}.}

Le calcul de la k ième puissance d’une matrice nécessite k – 1 fois le temps d’une multiplication matricielle unique, si cela est fait avec l’algorithme trivial (multiplication répétée). Comme cela peut prendre beaucoup de temps, on préfère généralement utiliser l’exponentiation par élévation au carré , qui nécessite moins de 2 log ₂ k multiplications matricielles, et est donc beaucoup plus efficace.

Un cas simple d’exponentiation est celui d’une matrice diagonale . Comme le produit de Matrices diagonales revient simplement à multiplier entre eux des éléments diagonaux correspondants, la k ième puissance d’une matrice diagonale s’obtient en élevant les entrées à la puissance k :

[ a 11 0 ⋯ 0 0 a 22 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ a n n ] k = [ a 11 k 0 ⋯ 0 0 a 22 k ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ a n n k ] . {displaystyle {begin{bmatrix}a_{11}&0&cdots &0\0&a_{22}&cdots &0\vdots &vdots &ddots &vdots \0&0&cdots &a_{nn} end{bmatrix}}^{k}={begin{bmatrix}a_{11}^{k}&0&cdots &0\0&a_{22}^{k}&cdots &0\vdots &vdots & ddots &vdots \0&0&cdots &a_{nn}^{k}end{bmatrice}}.}

Algèbre abstraite

La définition du produit matriciel exige que les entrées appartiennent à un semi-anneau, et n’exige pas que la multiplication des éléments du semi-anneau soit commutative . Dans de nombreuses applications, les éléments de matrice appartiennent à un champ, bien que le semi- anneau tropical soit également un choix courant pour les problèmes de chemin le plus court de graphe . ^[13] Même dans le cas de matrices sur des champs, le produit n’est pas commutatif en général, bien qu’il soit associatif et distributif sur l’ addition matricielle . Les Matrices d’identité (qui sont les Matrices carrées dont les entrées sont nulles en dehors de la diagonale principale et 1 sur la diagonale principale) sontéléments d’identité du produit matriciel. Il s’ensuit que les matrices n × n sur un anneau forment un anneau, qui est Non commutatif sauf si n = 1 et que l’anneau de masse est commutatif.

Une matrice carrée peut avoir un inverse multiplicatif , appelé Matrice inverse . Dans le cas courant où les entrées appartiennent à un anneau commutatif R , une matrice a un inverse si et seulement si son déterminant a un inverse multiplicatif dans R . Le déterminant d’un produit de Matrices carrées est le produit des déterminants des facteurs. Les matrices n × n qui ont un inverse forment un groupe sous multiplication matricielle, dont les sous- groupes sont appelés groupes matriciels . De nombreux groupes classiques (y compris tous les groupes finis ) sont isomorphesaux groupes matriciels ; c’est le point de départ de la théorie des représentations de groupe .

Complexité informatique

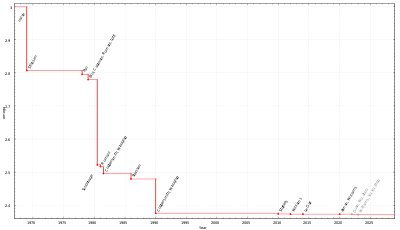
Amélioration des estimations de l’exposant ω au fil du temps pour la complexité de calcul de la multiplication matricielle O ( n ω ) {displaystyle O(n^{omega })} .

L’ algorithme de multiplication matricielle qui résulte de la définition nécessite, dans le pire des cas , n 3 {displaystyle n^{3}} multiplications et ( n − 1 ) n 2 {displaystyle (n-1)n^{2}} additions de scalaires pour calculer le produit de deux Matrices carrées n × n . Sa complexité de calcul est donc O ( n 3 ) {displaystyle O(n^{3})} , dans un modèle de calcul pour lequel les opérations scalaires prennent un temps constant (en pratique, c’est le cas pour les nombres à virgule flottante , mais pas pour les entiers).

De manière assez surprenante, cette complexité n’est pas optimale, comme l’a montré en 1969 Volker Strassen , qui a proposé un algorithme, aujourd’hui appelé algorithme de Strassen , d’une complexité de O ( n log 2 ⁡ 7 ) ≈ O ( n 2.8074 ) . {displaystyle O(n^{log _{2}7})environ O(n^{2.8074}).} ^[14] L’algorithme de Strassen peut être parallélisé pour améliorer encore les performances. ^{[ citation nécessaire ]} En décembre 2020^[update], le meilleur algorithme de multiplication matricielle est de Josh Alman et Virginia Vassilevska Williams et a une complexité O ( n ^2,3728596 ) . ^[15] On ne sait pas si la multiplication matricielle peut être effectuée en O ( n ^{2 + o(1)} ) temps. Ce serait optimal, puisqu’il faut lire le n 2 {displaystyle n^{2}} éléments d’une matrice afin de la multiplier par une autre matrice.

Étant donné que la multiplication matricielle constitue la base de nombreux algorithmes et que de nombreuses opérations sur les matrices ont même la même complexité que la multiplication matricielle (jusqu’à une constante multiplicative), la complexité de calcul de la multiplication matricielle apparaît tout au long de l’algèbre linéaire numérique et de l’informatique théorique .

Généralisations

D’autres types de produits de matrices comprennent:

• Multiplication de matrice de blocs
• Produit Cracovien , défini comme A ∧ B = B ^T A
• Produit intérieur de Frobenius , le produit scalaire des matrices considérées comme des vecteurs, ou, de manière équivalente, la somme des entrées du produit Hadamard
• Produit d’Hadamard de deux matrices de même taille, résultant en une matrice de même taille, qui est le produit entrée par entrée
• Produit de Kronecker ou produit tensoriel , la généralisation à toute taille du précédent
• Produit Khatri-Rao et produit Face-splitting
• Produit extérieur , également appelé produit dyadique ou produit tensoriel de matrices à deux colonnes, qui est a b T {displaystyle mathbf {a} mathbf {b} ^{mathsf {T}}}
• Multiplication scalaire

Voir également

• Calcul matriciel , pour l’interaction de la multiplication matricielle avec des opérations de calcul

Remarques

1. ^ ^{un b} Nykamp, ​​Duane. “Matrices et vecteurs multiplicateurs” . Aperçu mathématique . Consulté le 6 septembre 2020 .
2. ^ O’Connor, John J. ; Robertson, Edmund F. , “Jacques Philippe Marie Binet” , archives MacTutor History of Mathematics , Université de St Andrews
3. ^ Lerner, RG ; Trigg, GL (1991). Encyclopédie de physique (2e éd.). Editeurs VHC. ISBN 978-3-527-26954-9.
4. ^ Parker, CB (1994). McGraw Hill Encyclopaedia of Physics (2e éd.). ISBN 978-0-07-051400-3.
5. ^ Lipschutz, S.; En ligneLipson, M. (2009). Algèbre linéaire . Les contours de Schaum (4e éd.). McGraw Hill (États-Unis). p. 30–31. ISBN 978-0-07-154352-1.
6. ^ Riley, KF; Hobson, député ; En ligneBence, SJ (2010). Méthodes mathématiques pour la physique et l’ingénierie . La presse de l’Universite de Cambridge. ISBN 978-0-521-86153-3.
7. ^ Adams, RA (1995). Calculus, un cours complet (3e éd.). Addison Wesley. p. 627.ISBN _ 0-201-82823-5.
8. ^ Corne, Johnson (2013). Analyse matricielle (2e éd.). La presse de l’Universite de Cambridge. p. 6. ISBN 978-0-521-54823-6.
9. ^ Peter Stingl (1996). Mathematik für Fachhochschulen – Technik und Informatik (en allemand) (5e éd.). Munich : Carl Hanser Verlag . ISBN 3-446-18668-9.Ici : Exm.5.4.10, p.205-206
10. ^ ^{un bc Weisstein} , Eric W. “Multiplication de Matrice” . mathworld.wolfram.com . Récupéré le 06/09/2020 .
11. ^ Lipcshutz, S.; En ligneLipson, M. (2009). “2”. Algèbre linéaire . Les contours de Schaum (4e éd.). McGraw Hill (États-Unis). ISBN 978-0-07-154352-1.
12. ^ Corne, Johnson (2013). “0”. Analyse matricielle (2e éd.). La presse de l’Universite de Cambridge. ISBN 978-0-521-54823-6.
13. ^ Motwani, Rajeev ; Raghavan, Prabhakar (1995). Algorithmes randomisés . La presse de l’Universite de Cambridge. p. 280. ISBN 9780521474658.
14. ^ Volker Strassen (août 1969). “L’élimination gaussienne n’est pas optimale” . Mathématiques numériques . 13 (4): 354–356. doi : 10.1007/BF02165411 . S2CID 121656251 .
15. ^ Alman, Josh; Williams, Virginia Vassilevska (2020), “Une méthode laser raffinée et une multiplication matricielle plus rapide”, 32e symposium annuel ACM-SIAM sur les algorithmes discrets (SODA 2021) , arXiv : 2010.05846

Références

Wikimedia Commons a des médias liés à la multiplication matricielle .

Le Wikibook Linear Algebra a une page sur le thème: Multiplication matricielle

Le Wikibook Applicable Mathematics a une page sur le thème : Multiplier les matrices

• Henry Cohn, Robert Kleinberg , Balázs Szegedy et Chris Umans. Algorithmes de théorie des groupes pour la multiplication matricielle. arXiv : math.GR/0511460 . Actes du 46e Symposium annuel sur les fondements de l’informatique , 23-25 ​​octobre 2005, Pittsburgh, PA, IEEE Computer Society, pp. 379-388.
• Henry Cohn, Chris Umans. Une approche théorique de groupe pour la multiplication matricielle rapide. arXiv : math.GR/0307321 . Actes du 44e symposium annuel de l’IEEE sur les fondements de l’informatique , 11-14 octobre 2003, Cambridge, MA, IEEE Computer Society, pp. 438-449.
• Chaudronnier, D. ; Winograd, S. (1990). “Multiplication matricielle via des progressions arithmétiques” . J. Calcul symbolique . 9 (3): 251–280. doi : 10.1016/s0747-7171(08)80013-2 .
• Horn, Roger A.; Johnson, Charles R. (1991), Sujets en analyse matricielle , Cambridge University Press , ISBN 978-0-521-46713-1
• Knuth, DE , L’art de la programmation informatique Volume 2 : Algorithmes semi-numériques . Addison-Wesley Professionnel ; 3 édition (14 novembre 1997). ISBN 978-0-201-89684-8 . p. 501.
• Presse, William H. ; Flannery, Brian P.; Teukolsky, Saül A. ; Vetterling, William T. (2007), Recettes numériques: L’art du calcul scientifique (3e éd.), Cambridge University Press , ISBN 978-0-521-88068-8.
• Ran Raz . Sur la complexité du produit matriciel. Dans Actes du trente-quatrième symposium annuel de l’ACM sur la théorie de l’informatique. ACM Press, 2002. doi : 10.1145/509907.509932 .
• Robinson, Sara, Vers un algorithme optimal pour la multiplication matricielle, SIAM News 38 (9), novembre 2005. PDF
• Strassen, Volker, L’élimination gaussienne n’est pas optimale , Numer. Math. 13, p. 354-356, 1969.
• Styan, George PH (1973), “Produits Hadamard et analyse statistique multivariée” (PDF) , Algèbre linéaire et ses applications , 6 : 217–240, doi : 10.1016/0024-3795(73)90023-2
• Williams, Virginie Vassilevska (2012-05-19). “Multiplier les matrices plus rapidement que coppersmith-winograd” . Actes du 44e symposium sur la théorie de l’informatique – STOC ’12 . ACM. pp. 887–898. CiteSeerX 10.1.1.297.2680 . doi : 10.1145/2213977.2214056 . ISBN 9781450312455. S2CID 14350287 .