Méthode des différences finies

Apprendre encore plus Cet article a plusieurs problèmes. Aidez -nous à l’améliorer ou discutez de ces problèmes sur la page de discussion . ( Apprenez comment et quand supprimer ces modèles de messages )

This article’s lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (April 2015)

Learn more This article may be too technical for most readers to understand. Please help improve it to make it understandable to non-experts, without removing the technical details. (April 2015) (Learn how and when to remove this template message)

Learn more Le ton ou le style de cet article peut ne pas refléter le ton encyclopédique utilisé sur Wikipédia . Voir le guide de Wikipedia pour écrire de meilleurs articles pour des suggestions. ( juin 2020 ) (Découvrez comment et quand supprimer ce modèle de message)

(Découvrez comment et quand supprimer ce modèle de message)

En analyse numérique , les méthodes de différences finies ( FDM ) sont une classe de techniques numériques pour résoudre des Équations différentielles en rapprochant les dérivées avec des différences finies . Le domaine spatial et l’intervalle de temps (le cas échéant) sont discrétisés ou divisés en un nombre fini d’étapes, et la valeur de la solution à ces points discrets est approchée en résolvant des équations algébriques contenant des différences finies et des valeurs à partir de points proches.

Les méthodes aux différences finies convertissent les Équations différentielles ordinaires (ODE) ou les Équations aux dérivées partielles (PDE), qui peuvent être non linéaires , en un système d’équations linéaires qui peuvent être résolues par des techniques d’algèbre matricielle. Les ordinateurs modernes peuvent effectuer efficacement ces calculs d’algèbre linéaire , ce qui, associé à leur relative facilité de mise en œuvre, a conduit à l’utilisation généralisée de FDM dans l’analyse numérique moderne. ^[1] Aujourd’hui, FDM est l’une des approches les plus courantes de la solution numérique de PDE, avec les méthodes d’ éléments finis . ^[1]

Dérivation du polynôme de Taylor

Tout d’abord, en supposant que la fonction dont les dérivées doivent être approximées se comporte correctement, par le théorème de Taylor , nous pouvons créer un développement en série de Taylor

f ( x 0 + h ) = f ( x 0 ) + f ′ ( x 0 ) 1 ! h + f ( 2 ) ( x 0 ) 2 ! h 2 + ⋯ + f ( n ) ( x 0 ) n ! h n + R n ( x ) , {displaystyle f(x_{0}+h)=f(x_{0})+{frac {f'(x_{0})}{1!}}h+{frac {f^{(2) }(x_{0})}{2!}}h^{2}+cdots +{frac {f^{(n)}(x_{0})}{n!}}h^{n} +R_{n}(x),} $f(x_0 + h) = f(x_0) + frac{f'(x_0)}{1!}h + frac{f^{(2)}(x_0)}{2!}h^2 + cdots + frac{f^{(n)}(x_0)}{n!}h^n + R_n(x),$ $f(x_0 + h) = f(x_0) + frac{f'(x_0)}{1!}h + frac{f^{(2)}(x_0)}{2!}h^2 + cdots + frac{f^{(n)}(x_0)}{n!}h^n + R_n(x),$

où n ! désigne la factorielle de n , et R _n ( x ) est un terme de reste, indiquant la différence entre le polynôme de Taylor de degré n et la fonction d’origine. Nous dériverons une approximation de la dérivée première de la fonction “f” en tronquant d’abord le polynôme de Taylor :

f ( x 0 + h ) = f ( x 0 ) + f ′ ( x 0 ) h + R 1 ( x ) , {displaystyle f(x_{0}+h)=f(x_{0})+f'(x_{0})h+R_{1}(x),} f(x_0 + h) = f(x_0) + f'(x_0)h + R_1(x),

Réglage, x ₀ =a nous avons,

f ( a + h ) = f ( a ) + f ′ ( a ) h + R 1 ( x ) , {displaystyle f(a+h)=f(a)+f'(a)h+R_{1}(x),} f(a+h) = f(a) + f'(a)h + R_1(x),

En divisant par h , on obtient :

f ( a + h ) h = f ( a ) h + f ′ ( a ) + R 1 ( x ) h {displaystyle {f(a+h) over h}={f(a) over h}+f'(a)+{R_{1}(x) over h}} ${f(a+h)over h} = {f(a)over h} + f'(a)+{R_1(x)over h}$ ${f(a+h)over h} = {f(a)over h} + f'(a)+{R_1(x)over h}$

Résolution de f'(a) :

f ′ ( a ) = f ( a + h ) − f ( a ) h − R 1 ( x ) h {displaystyle f'(a)={f(a+h)-f(a) over h}-{R_{1}(x) over h}} $f'(a) = {f(a+h)-f(a)over h} - {R_1(x)over h}$ $f'(a) = {f(a+h)-f(a)over h} - {R_1(x)over h}$

En admettant que R 1 ( x ) {displaystyle R_{1}(x)} R_1(x) est suffisamment petit, l’approximation de la dérivée première de “f” est :

f ′ ( a ) ≈ f ( a + h ) − f ( a ) h . {displaystyle f'(a)approx {f(a+h)-f(a) over h}.} f'(a)approx {f(a+h)-f(a)over h}.

Ce n’est pas par hasard, similaire à la définition de dérivé, qui est donnée comme suit :

f ′ ( a ) = lim h → 0 f ( a + h ) − F ( un ) h . {displaystyle f'(a)=lim _{hto 0}{frac {f(a+h)-f(a)}{h}}.} $f'(a)=lim _{hto 0}{frac {f(a+h)-f(a)}{h}}.$ $f'(a)=lim _{hto 0}{frac {f(a+h)-f(a)}{h}}.$

à l’exception de la limite vers zéro (la méthode porte son nom).

Précision et ordre

L’erreur dans la solution d’une méthode est définie comme la différence entre l’approximation et la solution analytique exacte. Les deux sources d’erreur dans les méthodes aux différences finies sont l’erreur d’arrondi, la perte de précision due à l’arrondi informatique des quantités décimales, et l’erreur de troncature ou l’erreur de discrétisation , la différence entre la solution exacte de l’équation différentielle d’origine et la quantité exacte en supposant arithmétique parfaite (c’est-à-dire sans arrondi).

La méthode des différences finies repose sur la discrétisation d’une fonction sur une grille.

Pour utiliser une méthode des différences finies pour approcher la solution d’un problème, il faut d’abord discrétiser le domaine du problème. Cela se fait généralement en divisant le domaine en une grille uniforme (voir l’image à droite). Cela signifie que les méthodes aux différences finies produisent des ensembles d’approximations numériques discrètes de la dérivée, souvent d’une manière « pas à pas ».

Une expression d’intérêt général est l’ Erreur de troncature locale d’une méthode. Généralement exprimée à l’aide de la Notation Big-O , l’Erreur de troncature locale fait référence à l’erreur d’une seule application d’une méthode. C’est-à-dire que c’est la quantité F ′ ( X i ) − f i ′ {displaystyle f'(x_{i})-f’_{i}} f'(x_i) - f'_i si f ′ ( x i ) {displaystyle f'(x_{i})} f'(x_i) fait référence à la valeur exacte et f i ′ {displaystyle f’_{i}} f'_i à l’approximation numérique. Le terme restant d’un polynôme de Taylor est pratique pour analyser l’Erreur de troncature locale. En utilisant la forme de Lagrange du reste du polynôme de Taylor pour f ( x 0 + h ) {displaystyle f(x_{0}+h)} f(x_0 + h) , lequel est

R n ( x 0 + h ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( h ) n + 1 {displaystyle R_{n}(x_{0}+h)={frac {f^{(n+1)}(xi )}{(n+1) !}}(h)^{n+ 1}} $R_n(x_0 + h) = frac{f^{(n+1)}(xi)}{(n+1)!} (h)^{n+1}$ $R_n(x_0 + h) = frac{f^{(n+1)}(xi)}{(n+1)!} (h)^{n+1}$ , où x 0 < ξ < x 0 + h {displaystyle x_{0}<xi <x_{0}+h} x_0 < xi < x_0 + h ,

le terme dominant de l’Erreur de troncature locale peut être découvert. Par exemple, en utilisant à nouveau la formule de Différence avant pour la première dérivée, sachant que f ( x je ) = F ( X 0 + je h ) {displaystyle f(x_{i})=f(x_{0}+ih)} f(x_i)=f(x_0+i h) ,

F ( X 0 + je h ) = f ( x 0 ) + f ′ ( x 0 ) i h + f ′′ ( ξ ) 2 ! ( i h ) 2 , {displaystyle f(x_{0}+ih)=f(x_{0})+f'(x_{0})ih+{frac {f”(xi )}{2 !}}(ih) ^{2},} $f(x_0 + i h) = f(x_0) + f'(x_0)i h + frac{f''(xi)}{2!} (i h)^{2},$ $f(x_0 + i h) = f(x_0) + f'(x_0)i h + frac{f''(xi)}{2!} (i h)^{2},$

et avec quelques manipulations algébriques, cela conduit à

f ( x 0 + i h ) − f ( x 0 ) i h = f ′ ( x 0 ) + f ′′ ( ξ ) 2 ! i h , {displaystyle {frac {f(x_{0}+ih)-f(x_{0})}{ih}}=f'(x_{0})+{frac {f”(xi ) {2 !}} euh,} $frac{f(x_0 + i h) - f(x_0)}{i h} = f'(x_0) + frac{f''(xi)}{2!} i h,$ $frac{f(x_0 + i h) - f(x_0)}{i h} = f'(x_0) + frac{f''(xi)}{2!} i h,$

et en notant en outre que la quantité de gauche est l’approximation de la méthode des différences finies et que la quantité de droite est la quantité exacte d’intérêt plus un reste, clairement ce reste est l’Erreur de troncature locale. Une expression finale de cet exemple et de son ordre est :

f ( x 0 + i h ) − f ( x 0 ) i h = f ′ ( x 0 ) + O ( h ) . {displaystyle {frac {f(x_{0}+ih)-f(x_{0})}{ih}}=f'(x_{0})+O(h).} $frac{f(x_0 + i h) - f(x_0)}{i h} = f'(x_0) + O(h).$ $frac{f(x_0 + i h) - f(x_0)}{i h} = f'(x_0) + O(h).$

Cela signifie que, dans ce cas, l’Erreur de troncature locale est proportionnelle aux tailles de pas. La qualité et la durée de la solution FDM simulée dépendent de la sélection de l’équation de discrétisation et des tailles de pas (pas de temps et d’espace). La qualité des données et la durée de la simulation augmentent considérablement avec une taille de pas plus petite. ^[2] Par conséquent, un équilibre raisonnable entre la qualité des données et la durée de la simulation est nécessaire pour une utilisation pratique. Les grands pas de temps sont utiles pour augmenter la vitesse de simulation dans la pratique. Cependant, des pas de temps trop grands peuvent créer des instabilités et affecter la qualité des données. ^{[3] [4]}

Les critères de von Neumann et Courant-Friedrichs-Lewy sont souvent évalués pour déterminer la stabilité du modèle numérique. ^{[3] [4] [5] [6]}

Exemple : équation différentielle ordinaire

Par exemple, considérons l’équation différentielle ordinaire

u ′ ( x ) = 3 u ( x ) + 2. {displaystyle u'(x)=3u(x)+2.,} u'(x) = 3u(x) + 2. ,

La méthode d’Euler pour résoudre cette équation utilise le quotient aux différences finies

u ( x + h ) − u ( x ) h ≈ u ′ ( x ) {displaystyle {frac {u(x+h)-u(x)}{h}}approx u'(x)} $frac{u(x+h) - u(x)}{h} approx u'(x)$ $frac{u(x+h) - u(x)}{h} approx u'(x)$

approximer l’équation différentielle en la substituant d’abord à u'(x) puis en appliquant un peu d’algèbre (en multipliant les deux côtés par h, puis en ajoutant u(x) aux deux côtés) pour obtenir

u ( x + h ) = u ( x ) + h ( 3 u ( x ) + 2 ) . {displaystyle u(x+h)=u(x)+h(3u(x)+2).,} u(x+h) = u(x) + h(3u(x)+2). ,

La dernière équation est une équation aux différences finies, et la résolution de cette équation donne une solution approximative à l’équation différentielle.

Exemple : L’équation de la chaleur

Considérons l’ équation de chaleur normalisée à une dimension, avec des conditions aux limites de Dirichlet homogènes

U t = U x x {displaystyle U_{t}=U_{xx},} $U_t=U_{xx} ,$ $U_t=U_{xx} ,$ U ( 0 , t ) = U ( 1 , t ) = 0 {displaystyle U(0,t)=U(1,t)=0,} U(0,t)=U(1,t)=0 , (condition limite) U ( x , 0 ) = U 0 ( x ) {displaystyle U(x,0)=U_{0}(x),} U(x,0) =U_0(x) , (condition initiale)

Une façon de résoudre numériquement cette équation est d’approximer toutes les dérivées par des différences finies. On partitionne le domaine dans l’espace à l’aide d’un maillage x 0 , . . . , x J {displaystyle x_{0},…,x_{J}} x_0, ..., x_J et dans le temps à l’aide d’un maillage t 0 , . . . . , t N {displaystyle t_{0},….,t_{N}} t_0, ...., t_N . Nous supposons une partition uniforme à la fois dans l’espace et dans le temps, donc la différence entre deux points spatiaux consécutifs sera h et entre deux points temporels consécutifs sera k . Les points

u ( x j , t n ) = u j n {displaystyle u(x_{j},t_{n})=u_{j}^{n}} $u(x_j,t_n) = u_{j}^n$ $u(x_j,t_n) = u_{j}^n$

représentera l’approximation numérique de u ( x j , t n ) . {displaystyle u(x_{j},t_{n}).} u(x_j, t_n).

Méthode explicite

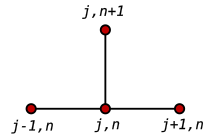
Le gabarit de la Méthode explicite la plus courante pour l’équation de la chaleur.

Utilisation d’une Différence avant à l’heure t n {displaystyle t_{n}} et une Différence centrale du second ordre pour la dérivée spatiale à la position x j {displaystyle x_{j}} $x_{j}$ $x_{j}$ ( FTCS ) on obtient l’équation de récurrence :

u j n + 1 − u j n k = u j + 1 n − 2 u j n + u j − 1 n h 2 . {displaystyle {frac {u_{j}^{n+1}-u_{j}^{n}}{k}}={frac {u_{j+1}^{n}-2u_{j }^{n}+u_{j-1}^{n}}{h^{2}}}.,} $frac{u_{j}^{n+1} - u_{j}^{n}}{k} = frac{u_{j+1}^n - 2u_{j}^n + u_{j-1}^n}{h^2}. ,$ $frac{u_{j}^{n+1} - u_{j}^{n}}{k} = frac{u_{j+1}^n - 2u_{j}^n + u_{j-1}^n}{h^2}. ,$

Il s’agit d’une Méthode explicite pour résoudre l’équation de la chaleur unidimensionnelle .

Nous pouvons obtenir u j n + 1 {displaystyle u_{j}^{n+1}} $u_j^{n+1}$ $u_j^{n+1}$ des autres valeurs de cette façon :

u j n + 1 = ( 1 − 2 r ) u j n + r u j − 1 n + r u j + 1 n {displaystyle u_{j}^{n+1}=(1-2r)u_{j}^{n}+ru_{j-1}^{n}+ru_{j+1}^{n}} $u_{j}^{n+1} = (1-2r)u_{j}^{n} + ru_{j-1}^{n} + ru_{j+1}^{n}$ $u_{j}^{n+1} = (1-2r)u_{j}^{n} + ru_{j-1}^{n} + ru_{j+1}^{n}$

où r = k / h 2 . {displaystyle r=k/h^{2}.} r=k/h^2.

Ainsi, avec cette relation de récurrence, et connaissant les valeurs à l’instant n , on peut obtenir les valeurs correspondantes à l’instant n +1. u 0 n {style d’affichage u_{0}^{n}} u_0^n et u J n {displaystyle u_{J}^{n}} u_J^n doivent être remplacées par les conditions aux limites, dans cet exemple elles sont toutes les deux 0.

Cette Méthode explicite est connue pour être numériquement stable et convergente lorsque r ≤ 1 / 2 {displaystyle rleq 1/2} rle 1/2 . ^[7] Les erreurs numériques sont proportionnelles au pas de temps et au carré du pas d’espace :

Δ u = O ( k ) + O ( h 2 ) {displaystyle Delta u=O(k)+O(h^{2}),} Delta u = O(k)+O(h^2) ,

Méthode implicite

Le gabarit de la Méthode implicite.

Si nous utilisons la différence arrière au temps t n + 1 {displaystyle t_{n+1}} $t_{n+1}$ $t_{n+1}$ et une Différence centrale du second ordre pour la dérivée spatiale à la position x j {displaystyle x_{j}} $x_{j}$ $x_{j}$ (The Backward Time, Centered Space Method “BTCS”) nous obtenons l’équation de récurrence :

u j n + 1 − u j n k = u j + 1 n + 1 − 2 u j n + 1 + u j − 1 n + 1 h 2 . {displaystyle {frac {u_{j}^{n+1}-u_{j}^{n}}{k}}={frac {u_{j+1}^{n+1}-2u_ {j}^{n+1}+u_{j-1}^{n+1}}{h^{2}}}.,} $frac{u_{j}^{n+1} - u_{j}^{n}}{k} =frac{u_{j+1}^{n+1} - 2u_{j}^{n+1} + u_{j-1}^{n+1}}{h^2}. ,$ $frac{u_{j}^{n+1} - u_{j}^{n}}{k} =frac{u_{j+1}^{n+1} - 2u_{j}^{n+1} + u_{j-1}^{n+1}}{h^2}. ,$

Learn more.

Isomorphisme

Jul 14, 2022

Premier article sur la théorie des ensembles de Cantor

Jul 12, 2022

Énergie gravitationnelle

Jul 9, 2022

Sphère de Riemann

Jul 8, 2022

Il s’agit d’une Méthode implicite pour résoudre l’équation de chaleur unidimensionnelle .

Nous pouvons obtenir u j n + 1 {displaystyle u_{j}^{n+1}} $u_j^{n+1}$ $u_j^{n+1}$ à partir de la résolution d’un système d’équations linéaires :

( 1 + 2 r ) u j n + 1 − r u j − 1 n + 1 − r u j + 1 n + 1 = u j n {displaystyle (1+2r)u_{j}^{n+1}-ru_{j-1}^{n+1}-ru_{j+1}^{n+1}=u_{j}^ {n}} $(1+2r)u_j^{n+1} - ru_{j-1}^{n+1} - ru_{j+1}^{n+1}= u_{j}^{n}$ $(1+2r)u_j^{n+1} - ru_{j-1}^{n+1} - ru_{j+1}^{n+1}= u_{j}^{n}$

Le schéma est toujours numériquement stable et convergent mais généralement plus intensif numériquement que la Méthode explicite car il nécessite de résoudre un système d’équations numériques à chaque pas de temps. Les erreurs sont linéaires sur le pas de temps et quadratiques sur le pas d’espace :

Δ u = O ( k ) + O ( h 2 ) . {displaystyle Delta u=O(k)+O(h^{2}).,} Delta u = O(k)+O(h^2). ,

Méthode Crank-Nicolson

Enfin si on utilise la Différence centrale au temps t n + 1 / 2 {displaystyle t_{n+1/2}} $t_{n+1/2}$ $t_{n+1/2}$ et une Différence centrale du second ordre pour la dérivée spatiale à la position x j {displaystyle x_{j}} $x_{j}$ $x_{j}$ (“CTCS”) nous obtenons l’équation de récurrence :

u j n + 1 − u j n k = 1 2 ( u j + 1 n + 1 − 2 u j n + 1 + u j − 1 n + 1 h 2 + u j + 1 n − 2 u j n + u j − 1 n h 2 ) . {displaystyle {frac {u_{j}^{n+1}-u_{j}^{n}}{k}}={frac {1}{2}}left({frac {u_ {j+1}^{n+1}-2u_{j}^{n+1}+u_{j-1}^{n+1}}{h^{2}}}+{frac {u_ {j+1}^{n}-2u_{j}^{n}+u_{j-1}^{n}}{h^{2}}}right).,} $frac{u_j^{n+1} - u_j^{n}}{k} = frac{1}{2} left(frac{u_{j+1}^{n+1} - 2u_j^{n+1} + u_{j-1}^{n+1}}{h^2}+frac{u_{j+1}^{n} - 2u_j^{n} + u_{j-1}^{n}}{h^2}right).,$ $frac{u_j^{n+1} - u_j^{n}}{k} = frac{1}{2} left(frac{u_{j+1}^{n+1} - 2u_j^{n+1} + u_{j-1}^{n+1}}{h^2}+frac{u_{j+1}^{n} - 2u_j^{n} + u_{j-1}^{n}}{h^2}right).,$

Cette formule est connue sous le nom de méthode Crank-Nicolson .

Le pochoir Crank-Nicolson.

Nous pouvons obtenir u j n + 1 {displaystyle u_{j}^{n+1}} $u_j^{n+1}$ $u_j^{n+1}$ à partir de la résolution d’un système d’équations linéaires :

( 2 + 2 r ) u j n + 1 − r u j − 1 n + 1 − r u j + 1 n + 1 = ( 2 − 2 r ) u j n + r u j − 1 n + r u j + 1 n {displaystyle (2+2r)u_{j}^{n+1}-ru_{j-1}^{n+1}-ru_{j+1}^{n+1}=(2-2r) u_{j}^{n}+ru_{j-1}^{n}+ru_{j+1}^{n}} $(2+2r)u_j^{n+1} - ru_{j-1}^{n+1} - ru_{j+1}^{n+1}= (2-2r)u_j^n + ru_{j-1}^n + ru_{j+1}^n$ $(2+2r)u_j^{n+1} - ru_{j-1}^{n+1} - ru_{j+1}^{n+1}= (2-2r)u_j^n + ru_{j-1}^n + ru_{j+1}^n$

Le schéma est toujours numériquement stable et convergent mais généralement plus intensif numériquement car il nécessite de résoudre un système d’équations numériques à chaque pas de temps. Les erreurs sont quadratiques à la fois sur le pas de temps et sur le pas d’espace :

Δ u = O ( k 2 ) + O ( h 2 ) . {displaystyle Delta u=O(k^{2})+O(h^{2}).,} Delta u = O(k^2)+O(h^2). ,

Comparaison

Pour résumer, le schéma Crank-Nicolson est généralement le schéma le plus précis pour les petits pas de temps. Pour des pas de temps plus grands, le schéma implicite fonctionne mieux car il est moins exigeant en termes de calcul. Le schéma explicite est le moins précis et peut être instable, mais c’est aussi le plus simple à mettre en œuvre et le moins intensif numériquement.

Voici un exemple. Les figures ci-dessous présentent les solutions données par les méthodes ci-dessus pour approximer l’équation de la chaleur

U t = α U x x , α = 1 π 2 , {displaystyle U_{t}=alpha U_{xx},quad alpha ={frac {1}{pi ^{2}}},} ${displaystyle U_{t}=alpha U_{xx},quad alpha ={frac {1}{pi ^{2}}},}$ ${displaystyle U_{t}=alpha U_{xx},quad alpha ={frac {1}{pi ^{2}}},}$

avec la condition aux limites

U ( 0 , t ) = U ( 1 , t ) = 0. {displaystyle U(0,t)=U(1,t)=0.}

La solution exacte est

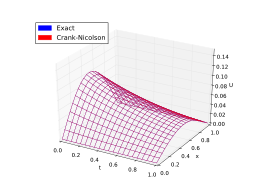
U ( x , t ) = 1 π 2 e − t péché ⁡ ( π X ) . {displaystyle U(x,t)={frac {1}{pi ^{2}}}e^{-t}sin(pi x).} ${displaystyle U(x,t)={frac {1}{pi ^{2}}}e^{-t}sin(pi x).}$ ${displaystyle U(x,t)={frac {1}{pi ^{2}}}e^{-t}sin(pi x).}$ Comparaison des méthodes des différences finies c = 4 c = 4 Méthode explicite ( non stable) c = 6 c = 6 Méthode implicite (stable) c = 8.5 c = 8.5 Méthode de Crank-Nicolson (stable)

Exemple : L’opérateur de Laplace

L’ opérateur de Laplace (continu) dans n {displaystyle n} -dimensions est donnée par Δ tu ( X ) = ∑ je = 1 n ∂ je 2 u ( x ) {displaystyle Delta u(x)=sum _{i=1}^{n}partial _{i}^{2}u(x)} ${displaystyle Delta u(x)=sum _{i=1}^{n}partial _{i}^{2}u(x)}$ ${displaystyle Delta u(x)=sum _{i=1}^{n}partial _{i}^{2}u(x)}$ . L’opérateur de Laplace discret Δ h u {displaystyle Delta _{h}u} ${displaystyle Delta _{h}u}$ ${displaystyle Delta _{h}u}$ dépend de la dimension n {displaystyle n} .

En 1D, l’opérateur de Laplace est approximé comme

Δ u ( x ) = u ′′ ( x ) ≈ u ( x − h ) − 2 u ( x ) + u ( x + h ) h 2 =: Δ h u ( x ) . {displaystyle Delta u(x)=u”(x)approx {frac {u(xh)-2u(x)+u(x+h)}{h^{2}}}=: Delta _{h}u(x),.} ${displaystyle Delta u(x)=u''(x)approx {frac {u(x-h)-2u(x)+u(x+h)}{h^{2}}}=:Delta _{h}u(x),.}$ ${displaystyle Delta u(x)=u''(x)approx {frac {u(x-h)-2u(x)+u(x+h)}{h^{2}}}=:Delta _{h}u(x),.}$

Cette approximation est généralement exprimée via le schéma suivant

Δ h = 1 h 2 [ 1 − 2 1 ] {displaystyle Delta _{h}={frac {1}{h^{2}}}{begin{bmatrix}1&-2&1end{bmatrix}}} ${displaystyle Delta _{h}={frac {1}{h^{2}}}{begin{bmatrix}1&-2&1end{bmatrix}}}$ ${displaystyle Delta _{h}={frac {1}{h^{2}}}{begin{bmatrix}1&-2&1end{bmatrix}}}$

et qui représente une matrice tridiagonale symétrique. Pour une grille équidistante on obtient une matrice de Toeplitz .

Le cas 2D présente toutes les caractéristiques du cas nD plus général. Chaque seconde dérivée partielle doit être approchée comme dans le cas 1D

Δ u ( x , y ) = u x x ( x , y ) + u y y ( x , y ) ≈ u ( x − h , y ) − 2 u ( x , y ) + u ( x + h , y ) h 2 + u ( x , y − h ) − 2 u ( x , y ) + u ( x , y + h ) h 2 = u ( x − h , y ) + u ( x + h , y ) − 4 u ( x , y ) + u ( x , y − h ) + u ( x , y + h ) h 2 =: Δ h u ( x , y ) , {displaystyle {begin{aligned}Delta u(x,y)&=u_{xx}(x,y)+u_{yy}(x,y)\&approx {frac {u(xh ,y)-2u(x,y)+u(x+h,y)}{h^{2}}}+{frac {u(x,yh)-2u(x,y)+u(x ,y+h)}{h^{2}}}\&={frac {u(xh,y)+u(x+h,y)-4u(x,y)+u(x,yh )+u(x,y+h)}{h^{2}}}\&=:Delta _{h}u(x,y),,end{aligned}}} ${displaystyle {begin{aligned}Delta u(x,y)&=u_{xx}(x,y)+u_{yy}(x,y)\&approx {frac {u(x-h,y)-2u(x,y)+u(x+h,y)}{h^{2}}}+{frac {u(x,y-h)-2u(x,y)+u(x,y+h)}{h^{2}}}\&={frac {u(x-h,y)+u(x+h,y)-4u(x,y)+u(x,y-h)+u(x,y+h)}{h^{2}}}\&=:Delta _{h}u(x,y),,end{aligned}}}$ ${displaystyle {begin{aligned}Delta u(x,y)&=u_{xx}(x,y)+u_{yy}(x,y)\&approx {frac {u(x-h,y)-2u(x,y)+u(x+h,y)}{h^{2}}}+{frac {u(x,y-h)-2u(x,y)+u(x,y+h)}{h^{2}}}\&={frac {u(x-h,y)+u(x+h,y)-4u(x,y)+u(x,y-h)+u(x,y+h)}{h^{2}}}\&=:Delta _{h}u(x,y),,end{aligned}}}$

qui est généralement donné par le gabarit suivant

Δ h = 1 h 2 [ 1 1 − 4 1 1 ] . {displaystyle Delta _{h}={frac {1}{h^{2}}}{begin{bmatrix}&1\1&-4&1\&1end{bmatrix}},.} ${displaystyle Delta _{h}={frac {1}{h^{2}}}{begin{bmatrix}&1\1&-4&1\&1end{bmatrix}},.}$ ${displaystyle Delta _{h}={frac {1}{h^{2}}}{begin{bmatrix}&1\1&-4&1\&1end{bmatrix}},.}$

Cohérence

La cohérence de l’approximation mentionnée ci-dessus peut être démontrée pour des fonctions très régulières, telles que u ∈ C 4 ( Ω ) {displaystyle uin C^{4}(Omega )} ${displaystyle uin C^{4}(Omega )}$ ${displaystyle uin C^{4}(Omega )}$ . La déclaration est

Δ u − Δ h u = O ( h 2 ) . {displaystyle Delta u-Delta _{h}u={mathcal {O}}(h^{2}),.} ${displaystyle Delta u-Delta _{h}u={mathcal {O}}(h^{2}),.}$ ${displaystyle Delta u-Delta _{h}u={mathcal {O}}(h^{2}),.}$

Pour le prouver, il faut substituer les développements de la série de Taylor jusqu’à l’ordre 3 dans l’opérateur de Laplace discret.

Propriétés

Sous-harmonique

Semblable aux fonctions sous- harmoniques continues, on peut définir des fonctions sous-harmoniques pour des approximations aux différences finies u h {displaystyle u_{h}} $u_{h}$ $u_{h}$

− Δ h u h ≤ 0 . {displaystyle -Delta _{h}u_{h}leq 0,.} ${displaystyle -Delta _{h}u_{h}leq 0,.}$ ${displaystyle -Delta _{h}u_{h}leq 0,.}$ Valeur moyenne

On peut définir un gabarit général de type positif via

[ α N α W − α C α E α S ] , α i > 0 , α C = ∑ i ∈ { N , E , S , W } α i . {displaystyle {begin{bmatrix}&alpha _{N}\alpha _{W}&-alpha _{C}&alpha _{E}\&alpha _{S}end {bmatrice}},,quad alpha _{i}>0,,quad alpha _{C}=sum _{iin {N,E,S,W}}alpha _{je},.} ${displaystyle {begin{bmatrix}&alpha _{N}\alpha _{W}&-alpha _{C}&alpha _{E}\&alpha _{S}end{bmatrix}},,quad alpha _{i}>0,,quad alpha _{C}=sum _{iin {N,E,S,W}}alpha _{i},.}$ ${displaystyle {begin{bmatrix}&alpha _{N}\alpha _{W}&-alpha _{C}&alpha _{E}\&alpha _{S}end{bmatrix}},,quad alpha _{i}>0,,quad alpha _{C}=sum _{iin {N,E,S,W}}alpha _{i},.}$

Si u h {displaystyle u_{h}} ${displaystyle u_{h}}$ ${displaystyle u_{h}}$ est sous-harmonique (discrète), alors la propriété de valeur moyenne suivante est vérifiée

u h ( x C ) ≤ ∑ i ∈ { N , E , S , W } α i u h ( x i ) ∑ i ∈ { N , E , S , W } α i , {displaystyle u_{h}(x_{C})leq {frac {sum _{iin {N,E,S,W}}alpha _{i}u_{h}(x_ {i})}{sum _{iin {N,E,S,W}}alpha _{i}}},,} ${displaystyle u_{h}(x_{C})leq {frac {sum _{iin {N,E,S,W}}alpha _{i}u_{h}(x_{i})}{sum _{iin {N,E,S,W}}alpha _{i}}},,}$ ${displaystyle u_{h}(x_{C})leq {frac {sum _{iin {N,E,S,W}}alpha _{i}u_{h}(x_{i})}{sum _{iin {N,E,S,W}}alpha _{i}}},,}$

où l’approximation est évaluée sur des points de la grille, et le gabarit est supposé de type positif.

Une propriété de valeur moyenne similaire est également valable pour le cas continu.

Principe maximal

Pour une fonction sous-harmonique (discrète) u h {displaystyle u_{h}} ${displaystyle u_{h}}$ ${displaystyle u_{h}}$ ce qui suit tient

max Ω h u h ≤ max ∂ Ω h u h , {displaystyle max _{Omega _{h}}u_{h}leq max _{partial Omega _{h}}u_{h},,} ${displaystyle max _{Omega _{h}}u_{h}leq max _{partial Omega _{h}}u_{h},,}$ ${displaystyle max _{Omega _{h}}u_{h}leq max _{partial Omega _{h}}u_{h},,}$

où Ω h , ∂ Ω h {displaystyle Omega _{h},partial Omega _{h}} ${displaystyle Omega _{h},partial Omega _{h}}$ ${displaystyle Omega _{h},partial Omega _{h}}$ sont des discrétisations du domaine continu Ω {displaystyle Oméga} Omega , respectivement la frontière ∂ Ω {displaystylepartialOméga} {displaystyle partial Omega } .

Un principe de maximum similaire vaut également pour le cas continu.

La méthode SBP-SAT

La méthode SBP-SAT est une technique stable et précise pour discrétiser et imposer des conditions aux limites d’une équation différentielle partielle bien posée en utilisant des différences finies d’ordre élevé. ^{[8] [9]}La méthode est basée sur des différences finies où les opérateurs de différenciation présentent des propriétés de sommation par parties. En règle générale, ces opérateurs consistent en des matrices de différenciation avec des gabarits de Différence centrale à l’intérieur avec des gabarits de frontière unilatéraux soigneusement choisis conçus pour imiter l’intégration par parties dans le cadre discret. En utilisant la technique SAT, les conditions aux limites de la PDE sont imposées faiblement, où les valeurs aux limites sont “tirées” vers les conditions souhaitées plutôt qu’exactement remplies. Si les paramètres de réglage (inhérents à la technique SAT) sont choisis correctement, le système résultant d’ODE présentera un comportement énergétique similaire à celui de la PDE continue, c’est-à-dire que le système n’a pas de croissance d’énergie non physique. Cela garantit la stabilité si un schéma d’intégration avec une région de stabilité qui comprend des parties de l’axe imaginaire, comme la méthode Runge-Kutta du quatrième ordre, est utilisé. Cela fait de la technique SAT une méthode attrayante pour imposer des conditions aux limites pour les méthodes de différences finies d’ordre supérieur, contrairement par exemple à la méthode d’injection, qui ne sera généralement pas stable si des opérateurs de différenciation d’ordre élevé sont utilisés.

Voir également

Méthode des éléments finis
Différence finie
Domaine temporel des différences finies
Méthode de différence infinie
Stencil (analyse numérique)
Coefficients de différences finies
Pochoir à cinq points
Théorème de Lax-Richtmyer
Méthodes de différences finies pour la tarification des options
Schéma de différenciation au vent pour la convection
Schéma de différenciation centrale
Équation de Poisson discrète
Opérateur de Laplace discret

Références

^ ^un ^b Christian Grossmann; Hans-G. Roos ; Martin Stynes (2007). Traitement numérique des Équations aux dérivées partielles . Springer Science et médias d’affaires. p. 23 . ISBN 978-3-540-71584-9.
^ Arieh Iserles (2008). Un premier cours d’analyse numérique des Équations différentielles . La presse de l’Universite de Cambridge. p. 23 . ISBN 9780521734905.
^ ^un ^b Hoffman JD; Frankel S (2001). Méthodes numériques pour ingénieurs et scientifiques . CRC Press, Boca Raton.
^ ^un ^b Jaluria Y; Atluri S (1994). “Transfert de chaleur informatique”. Mécanique computationnelle . 14 (5): 385–386. Bibcode : 1994CompM..14..385J . doi : 10.1007/BF00377593 .
^ Majumdar P (2005). Méthodes de calcul pour le transfert de chaleur et de masse (1ère éd.). Taylor et Francis, New York.
^ Smith GD (1985). Solution numérique d’Équations aux dérivées partielles: méthodes de différences finies (3e éd.). Presse universitaire d’Oxford.
^ Crank, J. Les mathématiques de la diffusion . 2e édition, Oxford, 1975, p. 143.
^ Bo Strand (1994). “Sommation par parties pour les approximations de différence finie pour d / dx”. Journal de physique computationnelle . 110 (1): 47–67. Code Bib : 1994JCoPh.110 …47S . doi : 10.1006/jcph.1994.1005 .
^ Mark H. Carpenter; David I. Gottlieb; Saul S. Abarbanel (1994). “Conditions aux limites stables dans le temps pour les schémas aux différences finies résolvant les systèmes hyperboliques: méthodologie et application aux schémas compacts d’ordre élevé”. Journal de physique computationnelle . 111 (2): 220–236. Bibcode : 1994JCoPh.111..220C . doi : 10.1006/jcph.1994.1057 .

Lectures complémentaires

KW Morton et DF Mayers, Solution numérique des Équations aux dérivées partielles, une introduction . Cambridge University Press, 2005.
Autar Kaw et E. Eric Kalu, Méthodes numériques avec applications , (2008) [1] . Contient une brève introduction technique à FDM (pour les ODE) au chapitre 08.07 .
John Strikwerda (2004). Schémas aux différences finies et Équations aux dérivées partielles (2e éd.). SIAM. ISBN 978-0-89871-639-9.
Smith, GD (1985), Solution numérique des Équations aux dérivées partielles : Méthodes des différences finies, 3e éd. , Presses universitaires d’Oxford
Peter Olver (2013). Introduction aux Équations aux dérivées partielles . Springer. Chapitre 5 : Différences finies. ISBN 978-3-319-02099-0..
Randall J. LeVeque , Méthodes des différences finies pour les Équations différentielles ordinaires et partielles , SIAM, 2007.
Sergey Lemeshevsky, Piotr Matus, Dmitriy Poliakov (Eds): “Exact Finite-Difference Schemes”, De Gruyter (2016). DOI : https://doi.org/10.1515/9783110491326 .