Le volume

Le volume est une quantité scalaire exprimant la quantité d’ espace tridimensionnel entouré par une Surface fermée . Par exemple, l’espace qu’une substance ( solide , liquide , gaz ou plasma ) ou une Forme 3D occupe ou contient. ^[1] Le volume est souvent quantifié numériquement à l’aide de l’ unité dérivée du SI , le mètre cube . Le volume d’un conteneur s’entend généralement comme étant la capacité du conteneur ; c’est-à-dire la quantité de liquide(gaz ou liquide) que le conteneur pourrait contenir, plutôt que la quantité d’espace que le conteneur lui-même déplace. Des volumes mathématiques sont également attribués à des formes mathématiques tridimensionnelles . Les volumes de certaines formes simples, telles que les formes régulières, droites et circulaires, peuvent être facilement calculés à l’aide de formules arithmétiques . Les volumes de formes compliquées peuvent être calculés avec le Calcul intégral s’il existe une formule pour la limite de la forme. Les figures unidimensionnelles (telles que les lignes ) et les formes bidimensionnelles (telles que les carrés ) se voient attribuer un volume nul dans l’espace tridimensionnel.

Le volume
Une tasse à mesurer peut être utilisée pour mesurer des volumes de liquides . Cette tasse mesure le volume en unités de tasses , onces liquides et millilitres .
Symboles communs	V
Unité SI	Mètre cube [m ³ ]
Autres unités	Litre , once liquide , gallon , pinte , pinte , cuillère à café , dram liquide , in ³ , yd ³ , baril
En unités de base SI	1m3 _ ^_
Dimension	L ³

Le volume d’un solide (qu’il soit de forme régulière ou irrégulière) peut être déterminé par déplacement de fluide . Le déplacement de liquide peut également être utilisé pour déterminer le volume d’un gaz. Le volume combiné de deux substances est généralement supérieur au volume d’une seule des substances. Cependant, parfois une substance se dissout dans l’autre et dans de tels cas, le volume combiné n’est pas additif . ^[2]

En géométrie différentielle , le volume est exprimé au moyen de la forme volumique , et est un invariant riemannien global important . En thermodynamique , le volume est un paramètre fondamental , et est une variable conjuguée à la pression .

Unités

Mesures de volume du 1914 The New Student’s Reference Work .

Conversion approximative en métrique (mL) ^[3]

Lutin.	NOUS
Liquide	Sécher
Gill	142	118	138
Pinte	568	473	551
Litre	1137	946	1101
Gallon	4546	3785	4405

Toute unité de longueur donne une unité de volume correspondante : le volume d’un cube dont les côtés ont la longueur donnée. Par exemple, un centimètre cube (cm ³ ) est le volume d’un cube dont les côtés mesurent un centimètre (1 cm) de longueur.

Dans le Système international d’unités (SI), l’unité standard de volume est le mètre cube (m ³ ). Le système métrique comprend également le litre (L) comme unité de volume, où un litre est le volume d’un cube de 10 centimètres. Ainsi

1 = (10 cm) ³ = 1000 centimètres cubes = 0,001 mètre cube,

alors

1 mètre cube = 1000 litres.

De petites quantités de liquide sont souvent mesurées en millilitres , où

1 Millilitre = 0,001 litre = 1 centimètre cube.

De la même manière, de grandes quantités peuvent être mesurées en mégalitres, où

Learn more.

Isomorphisme

Jul 14, 2022

Premier article sur la théorie des ensembles de Cantor

Jul 12, 2022

Énergie gravitationnelle

Jul 9, 2022

Sphère de Riemann

Jul 8, 2022

1 million de litres = 1000 mètres cubes = 1 mégalitre.

Diverses autres unités de volume traditionnelles sont également utilisées, notamment le pouce cube , le pied cube , le mètre cube , le mile cube , la cuillère à café , la cuillère à soupe , l’ once liquide , le dram liquide , la branchie , la pinte , le quart , le gallon , le minim , le baril , la corde , le peck , le boisseau , le hogshead , l’ acre-foot et le board foot. Ce sont toutes des unités de volume.

Termes connexes

La capacité est définie par l’ Oxford English Dictionary comme “la mesure appliquée au contenu d’un récipient et aux liquides, grains ou similaires, qui prennent la forme de ce qui les contient”. ^[4] (Le mot capacité a d’autres significations sans rapport, comme par exemple la gestion de la capacité .) La capacité n’a pas la même signification que le volume, bien qu’étroitement liée ; la capacité d’un conteneur est toujours le volume de son intérieur. Les unités de capacité sont le litre SI et ses unités dérivées, et les unités impériales telles que gill , pint , gallon et autres. Les unités de volume sont les cubes des Unités de longueur. En SI, les unités de volume et de capacité sont étroitement liées : un litre équivaut exactement à 1 décimètre cube, la capacité d’un cube de 10 cm de côté. Dans d’autres systèmes, la conversion n’est pas triviale ; la capacité du réservoir de carburant d’un véhicule est rarement indiquée en pieds cubes, par exemple, mais en gallons (un gallon impérial remplit un volume de 0,1605 pi3).

La densité d’un objet est définie comme le rapport de la masse au volume. ^[5] L’inverse de la densité est le volume spécifique qui est défini comme le volume divisé par la masse. Le volume spécifique est un concept important en thermodynamique où le volume d’un fluide de travail est souvent un paramètre important d’un système étudié.

Le débit volumique en dynamique des fluides est le volume de fluide qui traverse une surface donnée par unité de temps (par exemple mètres cubes par seconde [m ³ s ^-1 ]).

L’espace volumétrique est une région 3D ayant une forme en plus de la capacité ou du volume.

Calcul

En calcul , une branche des mathématiques , le volume d’ une région D dans R ³ est donné par une triple intégrale de la fonction constante F ( X , y , z ) = 1 {displaystyle f(x,y,z)=1} sur la région et s’écrit généralement :

∫∫∫ ré 1 ré x d y d z . {displaystyle iiint limits _{D}1,dx,dy,dz.} $iiint limits _{D}1,dx,dy,dz.$ $iiint limits _{D}1,dx,dy,dz.$

En coordonnées cylindriques , l’intégrale volumique est

∫∫∫ D r d r d θ d z , {displaystyle iiint limits _{D}r,dr,dtheta ,dz,} $iiint limits _{D}r,dr,dtheta ,dz,$ $iiint limits _{D}r,dr,dtheta ,dz,$

En coordonnées sphériques (en utilisant la convention des angles avec θ {displaystyle thêta} theta que l’azimut et φ {displaystylevarphi } varphi mesuré à partir de l’axe polaire ; voir plus sur les conventions ), l’intégrale de volume est

∫∫∫ D ρ 2 sin ⁡ φ d ρ d θ d φ . {displaystyle iiint limits _{D}rho ^{2}sin varphi ,drho ,dtheta ,dvarphi .} ${displaystyle iiint limits _{D}rho ^{2}sin varphi ,drho ,dtheta ,dvarphi .}$ ${displaystyle iiint limits _{D}rho ^{2}sin varphi ,drho ,dtheta ,dvarphi .}$

Formules

Façonner	Formule volumique	variables
cube	a 3 {displaystyle a^{3}} $a^{3}$ $a^{3}$
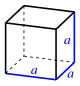Cuboïde	a b c {displaystyle abc}
Prisme ( B : aire de base)	B h {displaystyle Bh}
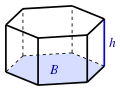Pyramide ( B : aire de base)	1 3 B h {displaystyle {frac {1}{3}}Bh} ${frac {1}{3}}Bh$ ${frac {1}{3}}Bh$
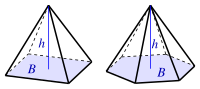Parallélépipède	a b c K {displaystyle abc{sqrt {K}}} K = 1 + 2 cos ⁡ ( α ) cos ⁡ ( β ) cos ⁡ ( γ ) − cos 2 ⁡ ( α ) − cos 2 ⁡ ( β ) − cos 2 ⁡ ( γ ) {displaystyle {begin{aligned}K=1&+2cos(alpha )cos(beta )cos(gamma )\&-cos ^{2}(alpha )-cos ^ {2}(beta )-cos ^{2}(gamma )end{aligné}}} ${displaystyle {begin{aligned}K=1&+2cos(alpha )cos(beta )cos(gamma )\&-cos ^{2}(alpha )-cos ^{2}(beta )-cos ^{2}(gamma )end{aligned}}}$ ${displaystyle {begin{aligned}K=1&+2cos(alpha )cos(beta )cos(gamma )\&-cos ^{2}(alpha )-cos ^{2}(beta )-cos ^{2}(gamma )end{aligned}}}$
Tétraèdre régulier	2 12 a 3 {displaystyle {{sqrt {2}} plus de 12}a^{3},} ${{sqrt {2}} over 12}a^{3},$ ${{sqrt {2}} over 12}a^{3},$
Sphère	4 3 π r 3 {displaystyle {frac {4}{3}}pi r^{3}} ${displaystyle {frac {4}{3}}pi r^{3}}$ ${displaystyle {frac {4}{3}}pi r^{3}}$
Coquille sphérique	4 3 π ( R 3 − r 3 ) {displaystyle {frac {4}{3}}pi (R^{3}-r^{3})} ${displaystyle {frac {4}{3}}pi (R^{3}-r^{3})}$ ${displaystyle {frac {4}{3}}pi (R^{3}-r^{3})}$
Ellipsoïde	4 3 π a b c {displaystyle {frac {4}{3}}pi abc} ${displaystyle {frac {4}{3}}pi abc}$ ${displaystyle {frac {4}{3}}pi abc}$
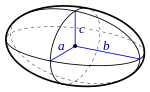Cylindre circulaire	π r 2 h {displaystyle pi r^{2}h} ${displaystyle pi r^{2}h}$ ${displaystyle pi r^{2}h}$
Cône	1 3 π r 2 h {displaystyle {frac {1}{3}}pi r^{2}h} ${displaystyle {frac {1}{3}}pi r^{2}h}$ ${displaystyle {frac {1}{3}}pi r^{2}h}$
Tore solide	2 π 2 R r 2 {displaystyle 2pi ^{2}Rr^{2}} ${displaystyle 2pi ^{2}Rr^{2}}$ ${displaystyle 2pi ^{2}Rr^{2}}$
Solide de révolution	π ⋅ ∫ a b f ( x ) 2 d x {displaystyle pi cdot int _{a}^{b}f(x)^{2}mathrm {d} x} ${displaystyle pi cdot int _{a}^{b}f(x)^{2}mathrm {d} x}$ ${displaystyle pi cdot int _{a}^{b}f(x)^{2}mathrm {d} x}$
Corps solide à surface continue A ( x ) {displaystyle A(x)} de ses sections efficaces (exemple : solide de Steinmetz )	∫ a b A ( x ) d x {displaystyle int _{a}^{b}A(x)mathrm {d} x} ${displaystyle int _{a}^{b}A(x)mathrm {d} x}$ ${displaystyle int _{a}^{b}A(x)mathrm {d} x}$	Pour le solide de révolution ci-dessus : A ( x ) = π f ( x ) 2 {displaystyle A(x)=pi f(x)^{2}} ${displaystyle A(x)=pi f(x)^{2}}$ ${displaystyle A(x)=pi f(x)^{2}}$

Rapports des volumes d’un cône, d’une sphère et d’un cylindre de même rayon et hauteur

Un cône, une sphère et un cylindre de rayon r et de hauteur h

Les formules ci-dessus peuvent être utilisées pour montrer que les volumes d’un cône , d’une sphère et d’un cylindre de même rayon et hauteur sont dans le rapport 1 : 2 : 3 , comme suit.

Supposons que le rayon du cône, du cylindre et de la sphère soit r et que la hauteur soit h (ou 2 r ) pour le cône et le cylindre.

Puis, Volume du cône :

1 3 π r 2 h = 1 3 π r 2 ( 2 r ) = ( 2 3 π r 3 ) × 1 , {displaystyle {frac {1}{3}}pi r^{2}h={frac {1}{3}}pi r^{2}left(2rright)=left( {frac {2}{3}}pi r^{3}right)times 1,} ${displaystyle {frac {1}{3}}pi r^{2}h={frac {1}{3}}pi r^{2}left(2rright)=left({frac {2}{3}}pi r^{3}right)times 1,}$ ${displaystyle {frac {1}{3}}pi r^{2}h={frac {1}{3}}pi r^{2}left(2rright)=left({frac {2}{3}}pi r^{3}right)times 1,}$

Volume de la sphère :

4 3 π r 3 = ( 2 3 π r 3 ) × 2 , {displaystyle {frac {4}{3}}pi r^{3}=left({frac {2}{3}}pi r^{3}right)times 2,} ${displaystyle {frac {4}{3}}pi r^{3}=left({frac {2}{3}}pi r^{3}right)times 2,}$ ${displaystyle {frac {4}{3}}pi r^{3}=left({frac {2}{3}}pi r^{3}right)times 2,}$

Volume du cylindre :

π r 2 h = π r 2 ( 2 r ) = ( 2 3 π r 3 ) × 3. {displaystyle pi r^{2}h=pi r^{2}(2r)=left({frac {2}{3}}pi r^{3}right)times 3. } ${displaystyle pi r^{2}h=pi r^{2}(2r)=left({frac {2}{3}}pi r^{3}right)times 3.}$ ${displaystyle pi r^{2}h=pi r^{2}(2r)=left({frac {2}{3}}pi r^{3}right)times 3.}$

La découverte du rapport 2 : 3 des volumes de la sphère et du cylindre est attribuée à Archimède . ^[6]

Dérivations de formules

Sphère

Le volume d’une sphère est l’ intégrale d’un nombre infini de disques circulaires infiniment petits d’épaisseur dx . Le calcul du volume d’une sphère de centre 0 et de rayon r est le suivant.

La surface du disque circulaire est π r 2 {displaystyle pi r^{2}} $pi r^{2}$ $pi r^{2}$ .

Le rayon des disques circulaires, défini de telle sorte que l’axe des x les coupe perpendiculairement, est

y = r 2 − x 2 {displaystyle y={sqrt {r^{2}-x^{2}}}} ${displaystyle y={sqrt {r^{2}-x^{2}}}}$ ${displaystyle y={sqrt {r^{2}-x^{2}}}}$

ou alors

z = r 2 − x 2 {displaystyle z={sqrt {r^{2}-x^{2}}}} ${displaystyle z={sqrt {r^{2}-x^{2}}}}$ ${displaystyle z={sqrt {r^{2}-x^{2}}}}$

où y ou z peuvent être considérés comme représentant le rayon d’un disque à une valeur x particulière.

En utilisant y comme rayon du disque, le volume de la sphère peut être calculé comme

∫ − r r π y 2 d x = ∫ − r r π ( r 2 − x 2 ) d x . {displaystyle int _{-r}^{r}pi y^{2},dx=int _{-r}^{r}pi left(r^{2}-x^{ 2}right),dx.} ${displaystyle int _{-r}^{r}pi y^{2},dx=int _{-r}^{r}pi left(r^{2}-x^{2}right),dx.}$ ${displaystyle int _{-r}^{r}pi y^{2},dx=int _{-r}^{r}pi left(r^{2}-x^{2}right),dx.}$

À présent

∫ − r r π r 2 d x − ∫ − r r π x 2 d x = π ( r 3 + r 3 ) − π 3 ( r 3 + r 3 ) = 2 π r 3 − 2 π r 3 3 . {displaystyle int _{-r}^{r}pi r^{2},dx-int _{-r}^{r}pi x^{2},dx=pi gauche(r^{3}+r^{3}right)-{frac {pi }{3}}left(r^{3}+r^{3}right)=2pi r ^{3}-{frac {2pi r^{3}}{3}}.} ${displaystyle int _{-r}^{r}pi r^{2},dx-int _{-r}^{r}pi x^{2},dx=pi left(r^{3}+r^{3}right)-{frac {pi }{3}}left(r^{3}+r^{3}right)=2pi r^{3}-{frac {2pi r^{3}}{3}}.}$ ${displaystyle int _{-r}^{r}pi r^{2},dx-int _{-r}^{r}pi x^{2},dx=pi left(r^{3}+r^{3}right)-{frac {pi }{3}}left(r^{3}+r^{3}right)=2pi r^{3}-{frac {2pi r^{3}}{3}}.}$

Combiner les rendements V = 4 3 π r 3 . {displaystyle V={frac {4}{3}}pi r^{3}.} $V={frac {4}{3}}pi r^{3}.$ $V={frac {4}{3}}pi r^{3}.$

Cette formule peut être dérivée plus rapidement en utilisant la formule de la surface de la sphère , qui est 4 π r 2 {displaystyle 4pi r^{2}} $4pi r^{2}$ $4pi r^{2}$ . Le volume de la sphère est constitué de couches de coques sphériques infiniment minces, et le volume de la sphère est égal à

∫ 0 r 4 π r 2 d r = 4 3 π r 3 . {displaystyle int _{0}^{r}4pi r^{2},dr={frac {4}{3}}pi r^{3}.} ${displaystyle int _{0}^{r}4pi r^{2},dr={frac {4}{3}}pi r^{3}.}$ ${displaystyle int _{0}^{r}4pi r^{2},dr={frac {4}{3}}pi r^{3}.}$ Cône

Le cône est un type de forme pyramidale. L’équation fondamentale des pyramides, un tiers fois la base fois l’altitude, s’applique également aux cônes.

Cependant, en utilisant le calcul, le volume d’un cône est l’ intégrale d’un nombre infini de disques circulaires infiniment minces d’épaisseur dx . Le calcul du volume d’un cône de hauteur h , dont la base est centrée en (0, 0, 0) de rayon r , est le suivant.

Le rayon de chaque disque circulaire est r SI x = 0 et 0 SI x = h , et variant linéairement entre les deux, c’est-à-dire

r h − x h . {displaystyle r{frac {hx}{h}}.} ${displaystyle r{frac {h-x}{h}}.}$ ${displaystyle r{frac {h-x}{h}}.}$

La surface du disque circulaire est alors

π ( r h − x h ) 2 = π r 2 ( h − x ) 2 h 2 . {displaystyle pi left(r{frac {hx}{h}}right)^{2}=pi r^{2}{frac {(hx)^{2}}{h^{ 2}}}.} ${displaystyle pi left(r{frac {h-x}{h}}right)^{2}=pi r^{2}{frac {(h-x)^{2}}{h^{2}}}.}$ ${displaystyle pi left(r{frac {h-x}{h}}right)^{2}=pi r^{2}{frac {(h-x)^{2}}{h^{2}}}.}$

Le volume du cône peut alors être calculé comme

∫ 0 h π r 2 ( h − x ) 2 h 2 d x , {displaystyle int _{0}^{h}pi r^{2}{frac {(hx)^{2}}{h^{2}}}dx,} ${displaystyle int _{0}^{h}pi r^{2}{frac {(h-x)^{2}}{h^{2}}}dx,}$ ${displaystyle int _{0}^{h}pi r^{2}{frac {(h-x)^{2}}{h^{2}}}dx,}$

et après extraction des constantes

π r 2 h 2 ∫ 0 h ( h − x ) 2 d x {displaystyle {frac {pi r^{2}}{h^{2}}}int _{0}^{h}(hx)^{2}dx} ${displaystyle {frac {pi r^{2}}{h^{2}}}int _{0}^{h}(h-x)^{2}dx}$ ${displaystyle {frac {pi r^{2}}{h^{2}}}int _{0}^{h}(h-x)^{2}dx}$

L’intégration nous donne

π r 2 h 2 ( h 3 3 ) = 1 3 π r 2 h . {displaystyle {frac {pi r^{2}}{h^{2}}}left({frac {h^{3}}{3}}right)={frac {1} {3}}pi r^{2}h.} ${frac {pi r^{2}}{h^{2}}}left({frac {h^{3}}{3}}right)={frac {1}{3}}pi r^{2}h.$ ${frac {pi r^{2}}{h^{2}}}left({frac {h^{3}}{3}}right)={frac {1}{3}}pi r^{2}h.$ Polyèdre

Géométrie différentielle

En géométrie différentielle , une branche des mathématiques , une forme volumique sur une variété différentiable est une forme différentielle de degré supérieur (c’est-à-dire dont le degré est égal à la dimension de la variété) nulle part égale à zéro. Une variété a une forme volumique SI et seulement SI elle est orientable. Une variété orientable a une infinité de formes volumiques, puisque la multiplication d’une forme volumique par une fonction non nulle donne une autre forme volumique. Sur les variétés non orientables, on peut plutôt définir la notion plus faible de densité . L’intégration de la forme volumique donne le volume de la variété selon cette forme.

Une variété pseudo-riemannienne orientée a une forme volumique naturelle. En coordonnées locales , il peut être exprimé comme

ω = | g | d x 1 ∧ ⋯ ∧ d x n , {displaystyle omega ={sqrt {|g|}},dx^{1}wedge dots wedge dx^{n},} ${displaystyle omega ={sqrt {|g|}},dx^{1}wedge dots wedge dx^{n},}$ ${displaystyle omega ={sqrt {|g|}},dx^{1}wedge dots wedge dx^{n},}$

où le d x i {displaystyle dx^{i}} $dx^{i}$ $dx^{i}$ sont des formes 1 qui forment une base orientée positivement pour le faisceau cotangent de la variété, et g {displaystyle g} est le déterminant de la représentation matricielle du tenseur métrique sur la variété en fonction de la même base.

Thermodynamique

En thermodynamique , le volume d’un système est un paramètre extensif important pour décrire son état thermodynamique . Le volume spécifique , une propriété intensive , est le volume du système par unité de masse. Le volume est une fonction de l’état et est interdépendant d’autres propriétés thermodynamiques telles que la pression et la température . Par exemple, le volume est lié à la pression et à la température d’un gaz parfait par la loi des gaz parfaits .

Calcul

La tâche de calculer numériquement le volume d’objets est étudiée dans le domaine de la géométrie computationnelle en informatique, en étudiant des algorithmes efficaces pour effectuer ce calcul, approximativement ou exactement , pour différents types d’objets. Par exemple, la technique d’approximation du volume convexe montre comment approximer le volume de tout corps convexe à l’ aide d’un oracle d’appartenance .

Voir également

Paradoxe de Banach-Tarski
Conversion d’unités
Poids volumétrique
Dimensionnement
Longueur
Mesure
Périmètre
Volumographie
Masse

Références

^ “Votre entrée de dictionnaire pour” volume ” ” . Récupéré le 01/05/2010 .
^ Un litre de sucre (environ 970 grammes) peut se dissoudre dans 0,6 litre d’eau chaude, produisant un volume total de moins d’un litre. “Solubilité” . Récupéré le 01/05/2010 . Jusqu’à 1800 grammes de saccharose peuvent se dissoudre dans un litre d’eau.
^ “Tableaux généraux des unités de mesure” . Division des poids et mesures du NIST. Archivé de l’original le 2011-12-10 . Récupéré le 12/01/2011 .
^ “capacité” . Dictionnaire anglais Oxford (éd. En ligne). Presse universitaire d’Oxford . (Abonnement ou adhésion à une institution participante requise.)
^ “densité” . Dictionnaire anglais Oxford (éd. En ligne). Presse universitaire d’Oxford . (Abonnement ou adhésion à une institution participante requise.)
^ Rorres, Chris. “Tombe d’Archimède : Sources” . Institut Courant des Sciences Mathématiques . Récupéré le 02/01/2007 .

Liens externes

Wikimedia Commons a des médias liés aux volumes .

Périmètres, zones, volumes sur Wikibooks
Volume sur Wikibooks