Lasso (statistiques)

Dans les statistiques et l’apprentissage automatique , le lasso ( moins absolu de retrait et opérateur de sélection ; également Lasso ou LASSO ) est une méthode d’ analyse de régression qui effectue à la fois la sélection et la régularisation des variables afin d’améliorer la précision de la prédiction et l’interprétabilité du modèle statistique résultant . Il a été initialement introduit en géophysique , ^[1] et plus tard par Robert Tibshirani , ^[2] qui a inventé le terme.

Lasso a été formulé à l’origine pour les modèles de régression linéaire . Ce cas simple en dit long sur l’estimateur. Il s’agit notamment de sa relation avec la régression de crête et la meilleure sélection de sous-ensembles et les liens entre les estimations de coefficients au lasso et ce que l’on appelle le seuillage souple. Il révèle également que (comme la régression linéaire standard) les estimations des coefficients n’ont pas besoin d’être uniques si les covariables sont colinéaires .

Bien qu’initialement définie pour la régression linéaire, la régularisation au lasso est facilement étendue à d’autres modèles statistiques, notamment les modèles linéaires généralisés , les équations d’estimation généralisées , les modèles à risques proportionnels et les estimateurs M . ^{[2] [3]} La capacité de Lasso à effectuer une sélection de sous-ensembles repose sur la forme de la contrainte et a une variété d’interprétations, notamment en termes de géométrie , de statistiques bayésiennes et d’ analyse convexe .

Le LASSO est étroitement lié au débruitage de poursuite de base .

Motivation

Lasso a été introduit afin d’améliorer la précision des prédictions et l’interprétabilité des modèles de régression. Il sélectionne un ensemble réduit de covariables connues à utiliser dans un modèle. ^{[2] [1]}

Histoire

Lasso a été développé indépendamment dans la littérature géophysique en 1986, sur la base de travaux antérieurs qui utilisaient le l 1 {displaystyle ell ^{1}} pénalité pour l’ajustement et la pénalisation des coefficients. Le statisticien Robert Tibshirani l’a indépendamment redécouvert et popularisé en 1996, sur la base du garrot non négatif de Breiman . ^{[1] [4]}

Avant le lasso, la méthode la plus largement utilisée pour choisir les covariables était la sélection par étapes . Cette approche n’améliore la précision de la prédiction que dans certains cas, par exemple lorsque seules quelques covariables ont une forte relation avec le résultat. Cependant, dans d’autres cas, cela peut augmenter l’erreur de prédiction.

À l’époque, la régression de crête était la technique la plus populaire pour améliorer la précision des prévisions. La régression Ridge améliore l’erreur de prédiction en réduisant la somme des carrés des Coefficients de régression pour qu’elle soit inférieure à une valeur fixe afin de réduire le surajustement , mais elle n’effectue pas de sélection de covariables et n’aide donc pas à rendre le modèle plus interprétable.

Lasso atteint ces deux objectifs en forçant la somme de la valeur absolue des Coefficients de régression à être inférieure à une valeur fixe, ce qui force certains coefficients à zéro, les excluant de l’impact sur la prédiction. Cette idée est similaire à la régression de crête, qui réduit également la taille des coefficients, mais la régression de crête a tendance à définir beaucoup moins de coefficients sur zéro.

Forme basique

Moindres carrés

Considérons un échantillon composé de N cas, chacun composé de p covariables et d’un résultat unique. Laisser y je {displaystyle y_{i}} être le résultat et X je := ( X 1 , X 2 , … , X p ) je J {displaystyle x_{i} :=(x_{1},x_{2},ldots ,x_{p})_{i}^{T}} Soit le vecteur Covariable pour le i ^ème cas. Alors l’objectif du lasso est de résoudre

min β 0 , β { ∑ i = 1 N ( y i − β 0 − x i T β ) 2 } subject to ∑ j = 1 p | β j | ≤ t . {displaystyle min _{beta _{0},beta }left{sum _{i=1}^{N}(y_{i}-beta _{0}-x_{i} ^{T}beta )^{2}right}{text{ sujet à }}sum _{j=1}^{p}|beta _{j}|leq t.} ^[2]

Ici β 0 {displaystyle bêta _{0}} est le coefficient constant, β := ( β 1 , β 2 , … , β p ) {displaystyle beta :=(beta _{1},beta _{2},ldots ,beta _{p})} est le vecteur de coefficient, et t {displaystyle t} est un paramètre libre prédéfini qui détermine le degré de régularisation.

Location X {displaystyle X} soit la matrice des covariables, de sorte que X i j = ( x i ) j {displaystyle X_{ij}=(x_{i})_{j}} et x i T {displaystyle x_{i}^{T}} est la i ^ème rangée de X {displaystyle X} , l’expression peut être écrite de manière plus compacte comme

min β 0 , β { ‖ y − β 0 − X β ‖ 2 2 } subject to ‖ β ‖ 1 ≤ t , {displaystyle min _{beta _{0},beta }left{left|y-beta _{0}-Xbeta right|_{2}^{2} droite}{text{ sujet à }}|beta |_{1}leq t,}

où ‖ u ‖ p = ( ∑ i = 1 N | u i | p ) 1 / p {displaystyle |u|_{p}=left(sum _{i=1}^{N}|u_{i}|^{p}right)^{1/p}} est la norme l p {displaystyle ell ^{p}} norme .

Dénotant la moyenne scalaire des points de données x i {displaystyle x_{i}} par x ̄ {displaystyle {bar {x}}} et la moyenne des variables de réponse y i {displaystyle y_{i}} par y ̄ {displaystyle {bar {y}}} , l’estimation résultante pour β 0 {displaystyle bêta _{0}} est β ^ 0 = y ̄ − x ̄ T β {displaystyle {hat {beta}}_{0}={bar {y}}-{bar {x}}^{T}beta } , pour que

y i − β ^ 0 − x i T β = y i − ( y ̄ − x ̄ T β ) − x i T β = ( y i − y ̄ ) − ( x i − x ̄ ) T β , {displaystyle y_{i}-{hat {beta}}_{0}-x_{i}^{T}beta =y_{i}-({bar {y}}-{bar { x}}^{T}beta )-x_{i}^{T}beta =(y_{i}-{bar {y}})-(x_{i}-{bar {x}} )^{T}bêta ,}

et par conséquent, il est courant de travailler avec des variables dont la moyenne est nulle. De plus, les covariables sont généralement standardisées ( ∑ i = 1 N x i 2 = 1 ) {displaystyle textstyle left(sum _{i=1}^{N}x_{i}^{2}=1right)} de sorte que la solution ne dépende pas de l’échelle de mesure.

Il peut être utile de réécrire

min β ∈ R p { 1 N ‖ y − X β ‖ 2 2 } subject to ‖ β ‖ 1 ≤ t . {displaystyle min _{beta in mathbb {R} ^{p}}left{{frac {1}{N}}left|yXbeta right|_{2} ^{2}right}{text{ sujet à }}|beta |_{1}leq t.}

sous la forme dite lagrangienne

min β ∈ R p { 1 N ‖ y − X β ‖ 2 2 + λ ‖ β ‖ 1 } {displaystyle min _{beta in mathbb {R} ^{p}}left{{frac {1}{N}}left|yXbeta right|_{2} ^{2}+lambda |beta |_{1}right}}

où la relation exacte entre t {displaystyle t} et λ {displaystylelambda} dépend des données.

Covariables orthonormées

Certaines propriétés de base de l’estimateur lasso peuvent maintenant être considérées.

En supposant d’abord que les covariables sont orthonormées de sorte que ( x i ∣ x j ) = δ i j {displaystyle (x_{i}mid x_{j})=delta _{ij}} , où ( ⋅ ∣ ⋅ ) {displaystyle (cdot mid cdot )} est le produit scalaire et δ i j {displaystyle delta _{ij}} est le delta de Kronecker , ou, de manière équivalente, X T X = I {displaystyle X^{T}X=I} , puis en utilisant des Méthodes de sous-gradient, on peut montrer que

β ^ j = S N λ ( β ^ j OLS ) = β ^ j OLS max ( 0 , 1 − N λ | β ^ j OLS | ) where β ^ OLS = ( X T X ) − 1 X T y {displaystyle {begin{aligned}{hat {beta }}_{j}={}&S_{Nlambda }({hat {beta }}_{j}^{text{OLS} })={hat {beta }}_{j}^{text{OLS}}max left(0,1-{frac {Nlambda }{|{hat {beta }} _{j}^{text{OLS}}|}}right)\&{text{ où }}{hat {beta }}^{text{OLS}}=(X^{T }X)^{-1}X^{T}yend{aligné}}} ^[2]

S α {displaystyle S_{alpha}} est appelé opérateur de seuillage souple, car il traduit les valeurs vers zéro (les rendant exactement nulles si elles sont suffisamment petites) au lieu de définir des valeurs plus petites à zéro et de laisser les plus grandes intactes comme opérateur de seuillage dur, souvent noté H α {displaystyle H_{alpha}} , voudrais.

Dans la régression ridge, l’objectif est de minimiser

min β ∈ R p { 1 N ‖ y − X β ‖ 2 2 + λ ‖ β ‖ 2 2 } {displaystyle min _{beta in mathbb {R} ^{p}}left{{frac {1}{N}}|yXbeta |_{2}^{2} +lambda |beta |_{2}^{2}right}}

cédant

β ^ j = ( 1 + N λ ) − 1 β ^ j OLS . {displaystyle {hat {beta}}_{j}=(1+Nlambda )^{-1}{hat {beta}}_{j}^{text{OLS}}.}

La régression Ridge réduit tous les coefficients d’un facteur uniforme de ( 1 + N λ ) − 1 {displaystyle (1+Nlambda)^{-1}} et ne met aucun coefficient à zéro.

Elle peut également être comparée à la régression avec sélection du meilleur sous-ensemble , dans laquelle le but est de minimiser

min β ∈ R p { 1 N ‖ y − X β ‖ 2 2 + λ ‖ β ‖ 0 } {displaystyle min _{beta in mathbb {R} ^{p}}left{{frac {1}{N}}left|yXbeta right|_{2} ^{2}+lambda |beta |_{0}right}}

où ‖ ⋅ ‖ 0 {displaystyle |cdot |_{0}} est le ” l 0 {displaystyle ell ^{0}} norme », qui est définie comme ‖ z ‖ = m {displaystyle |z|=m} si exactement m composantes de z sont non nulles. Dans ce cas, on peut montrer que

β ^ j = H N λ ( β ^ j OLS ) = β ^ j OLS I ( | β ^ j OLS | ≥ N λ ) {displaystyle {hat {beta}}_{j}=H_{sqrt {Nlambda}}left({hat {beta}}_{j}^{text{OLS}} right)={hat {beta }}_{j}^{text{OLS}}mathrm {I} left(left|{hat {beta }}_{j}^{text {OLS}}right|geq {sqrt {Nlambda}}right)}

où H α {displaystyle H_{alpha}} est la fonction dite de seuillage dur et I {displaystyle mathrm {je}} est une fonction indicatrice (elle vaut 1 si son argument est vrai et 0 sinon).

Par conséquent, les estimations au lasso partagent les caractéristiques de la régression de sélection de crête et du meilleur sous-ensemble, car elles réduisent toutes deux l’ampleur de tous les coefficients, comme la régression de crête et en fixent certains à zéro, comme dans le cas de la sélection du meilleur sous-ensemble. De plus, alors que la régression de crête met à l’échelle tous les coefficients par un facteur constant, le lasso traduit à la place les coefficients vers zéro par une valeur constante et les met à zéro s’ils l’atteignent.

Covariables corrélées

Dans un cas particulier, deux covariables, disons j et k , sont identiques pour chaque observation, de sorte que x ( j ) = x ( k ) {displaystyle x_{(j)}=x_{(k)}} , où x ( j ) , i = x ( k ) , i {displaystyle x_{(j),i}=x_{(k),i}} . Alors les valeurs de β j {displaystyle bêta _{j}} et β k {displaystyle bêta _{k}} qui minimisent la fonction objectif du lasso ne sont pas déterminés de manière unique. En fait, si certains β ^ {displaystyle {chapeau {bêta}}} dans lequel β ^ j β ^ k ≥ 0 {displaystyle {hat {beta}}_{j}{hat {beta}}_{k}geq 0} , puis si s ∈ [ 0 , 1 ] {displaystyle sin [0,1]} remplacer β ^ j {displaystyle {hat {beta}}_{j}} par s ( β ^ j + β ^ k ) {displaystyle s({hat {beta}}_{j}+{hat {beta}}_{k})} et β ^ k {displaystyle {hat {beta}}_{k}} par ( 1 − s ) ( β ^ j + β ^ k ) {displaystyle (1-s)({hat {beta}}_{j}+{hat {beta}}_{k})} , tout en gardant tous les autres β ^ i {displaystyle {hat {beta}}_{i}} fixe, donne une nouvelle solution, donc la fonction objectif du lasso a alors un continuum de minimiseurs valides. ^[5] Plusieurs variantes du lasso, dont la régularisation nette élastique , ont été conçues pour pallier cette lacune.

Forme générale

La régularisation au lasso peut être étendue à d’autres fonctions objectives telles que celles des modèles linéaires généralisés , des équations d’estimation généralisées , des modèles à risques proportionnels et des estimateurs M . ^{[2] [3]} Compte tenu de la fonction objectif

1 N ∑ i = 1 N f ( x i , y i , α , β ) {displaystyle {frac {1}{N}}sum _{i=1}^{N}f(x_{i},y_{i},alpha ,beta )}

la version régularisée au lasso de l’estimateur s la solution de

min α , β 1 N ∑ i = 1 N f ( x i , y i , α , β ) subject to ‖ β ‖ 1 ≤ t {displaystyle min _{alpha ,beta }{frac {1}{N}}sum _{i=1}^{N}f(x_{i},y_{i},alpha , beta ){text{ sujet à }}|beta |_{1}leq t}

où seulement β {displaystyle bêta} est pénalisé alors que α {displaystylealpha} est libre de prendre n’importe quelle valeur autorisée, tout comme β 0 {displaystyle bêta _{0}} n’a pas été pénalisé dans le cas de base.

Interprétations

Interprétation géométrique

Formes des régions de contrainte pour la régression lasso et ridge.

Le lasso peut mettre les coefficients à zéro, alors que la régression de crête superficiellement similaire ne le peut pas. Cela est dû à la différence de forme de leurs limites de contraintes. La régression du lasso et de la crête peut être interprétée comme minimisant la même fonction objectif

min β 0 , β { 1 N ‖ y − β 0 − X β ‖ 2 2 } {displaystyle min _{beta _{0},beta }left{{frac {1}{N}}left|y-beta _{0}-Xbeta right |_{2}^{2}right}}

mais avec des contraintes différentes : ‖ β ‖ 1 ≤ t {displaystyle |bêta |_{1}leq t} pour lasso et ‖ β ‖ 2 2 ≤ t {displaystyle |bêta |_{2}^{2}leq t} pour crête. La figure montre que la région de contrainte définie par la l 1 {displaystyle ell ^{1}} norm est un carré pivoté de sorte que ses coins reposent sur les axes (en général un polytope croisé ), tandis que la région définie par le l 2 {displaystyle ell ^{2}} norm est un cercle (en général une n -sphère ), qui est invariant en rotation et, par conséquent, n’a pas de coins. Comme on le voit sur la figure, un objet convexe tangent à la frontière, comme la ligne illustrée, est susceptible de rencontrer un coin (ou un équivalent de dimension supérieure) d’un hypercube, pour lequel certains composants de β {displaystyle bêta} sont identiquement nuls, alors que dans le cas d’une n -sphère, les points de la frontière pour lesquels certaines des composantes de β {displaystyle bêta} sont nuls ne se distinguent pas des autres et l’objet convexe n’est plus susceptible d’entrer en contact avec un point où certaines composantes de β {displaystyle bêta} sont nuls que un pour lesquels aucun d’entre eux ne l’est.

Rendre λ plus facile à interpréter avec un compromis précision-simplicité

Le lasso peut être redimensionné de sorte qu’il devient facile d’anticiper et d’influencer le degré de retrait associé à une valeur donnée de λ {displaystylelambda} . ^[6] On suppose que X {displaystyle X} est standardisé avec des scores z et que y {displaystyle y} est centré (moyenne nulle). Laisser β 0 {displaystyle bêta _{0}} représenter les Coefficients de régression hypothétiques et laisser b O L S {displaystyle b_{OLS}} se référer aux solutions des moindres carrés ordinaires optimisées pour les données. Nous pouvons alors définir le lagrangien comme un compromis entre la précision dans l’échantillon des solutions optimisées pour les données et la simplicité de s’en tenir aux valeurs hypothétiques. ^[7] Il en résulte

min β ∈ R p { ( y − X β ) ′ ( y − X β ) ( y − X β 0 ) ′ ( y − X β 0 ) + 2 λ ∑ i = 1 p | β i − β 0 , i | q i } {displaystyle min _{beta in mathbb {R} ^{p}}left{{frac {(yXbeta )'(yXbeta )}{(yXbeta _{0} )'(yXbeta _{0})}}+2lambda sum _{i=1}^{p}{frac {|beta _{i}-beta _{0,i}| }{q_{i}}}right}}

où q i {displaystyle q_{i}} est précisé ci-dessous. La première fraction représente la précision relative, la seconde la simplicité relative et λ {displaystylelambda} des équilibres entre les deux.

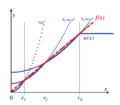
Pistes de solution pour le l 1 {displaystyle ell _{1}} norme et l 2 {displaystyle ell _{2}} norme quand b O L S = 2 {displaystyle b_{OLS}=2} et β 0 = 0 {displaystyle bêta _{0}=0}

Étant donné un seul régresseur, la simplicité relative peut être définie en spécifiant q i {displaystyle q_{i}} comme | b O L S − β 0 | {displaystyle |b_{OLS}-beta _{0}|} , qui est l’écart maximal par rapport à β 0 {displaystyle bêta _{0}} lorsque λ = 0 {displaystylelambda =0} . En admettant que β 0 = 0 {displaystyle bêta _{0}=0} , le chemin de la solution peut être défini en termes de R 2 {displaystyle R^{2}} :

b l 1 = { ( 1 − λ / R 2 ) b O L S if λ ≤ R 2 , 0 if λ > R 2 . {displaystyle b_{ell _{1}}={begin{cases}(1-lambda /R^{2})b_{OLS}&{mbox{if }}lambda leq R^{ 2},\0&{mbox{if}}lambda >R^{2}.end{cases}}}

Si λ = 0 {displaystylelambda =0} , la solution des moindres carrés ordinaires (MCO) est utilisée. La valeur hypothétique de β 0 = 0 {displaystyle bêta _{0}=0} est sélectionné si λ {displaystylelambda} est plus grand que R 2 {displaystyle R^{2}} . De plus, si R 2 = 1 {displaystyle R^{2}=1} , alors λ {displaystylelambda} représente l’influence proportionnelle de β 0 = 0 {displaystyle bêta _{0}=0} . En d’autres termes, λ × 100 % {displaystyle lambdafois 100%} mesure en pourcentage la quantité minimale d’influence de la valeur hypothétique par rapport à la solution OLS optimisée pour les données.

Si un l 2 {displaystyle ell _{2}} -norm est utilisé pour pénaliser les écarts par rapport à zéro étant donné un seul régresseur, le chemin de la solution est donné par

b l 2 = ( 1 + λ R 2 ( 1 − λ ) ) − 1 b O L S {displaystyle b_{ell _{2}}={bigg (}1+{frac {lambda }{R^{2}(1-lambda )}}{bigg )}^{-1 }b_{OLS}} . Aimer b l 1 {displaystyle b_{ell _{1}}} , b l 2 {displaystyle b_{ell _{2}}} se déplace dans la direction du point ( λ = R 2 , b = 0 ) {displaystyle (lambda =R^{2},b=0)} lorsque λ {displaystylelambda} est proche de zéro ; mais contrairement à b l 1 {displaystyle b_{ell _{1}}} , l’influence de R 2 {displaystyle R^{2}} diminue dans b l 2 {displaystyle b_{ell _{2}}} si λ {displaystylelambda} augmente (voir figure).
Étant donné plusieurs régresseurs, le moment où un paramètre est activé (c’est-à-dire autorisé à s’écarter de β 0 {displaystyle bêta _{0}} ) est également déterminé par la contribution d’un régresseur à R 2 {displaystyle R^{2}} précision. Première,

R 2 = 1 − ( y − X b ) ′ ( y − X b ) ( y − X β 0 ) ′ ( y − X β 0 ) . {displaystyle R^{2}=1-{frac {(y-Xb)'(y-Xb)}{(yXbeta _{0})'(yXbeta _{0})}}. }

Un R 2 {displaystyle R^{2}} de 75 % signifie que la précision dans l’échantillon s’améliore de 75 % si les solutions OLS sans restriction sont utilisées au lieu de l’hypothèse β 0 {displaystyle bêta _{0}} valeurs. La contribution individuelle de s’écarter de chaque hypothèse peut être calculée avec la p {displaystyle p} X p {displaystyle p} matrice

R ⊗ = ( X ′ y ~ 0 ) ( X ′ y ~ 0 ) ′ ( X ′ X ) − 1 ( y ~ 0 ′ y ~ 0 ) − 1 , {displaystyle R^{otimes }=(X'{tilde {y}}_{0})(X'{tilde {y}}_{0})'(X’X)^{-1 }({tilde {y}}_{0}'{tilde {y}}_{0})^{-1},}

où y ~ 0 = y − X β 0 {displaystyle {tilde {y}}_{0}=yXbeta _{0}} . Si b = b O L S {displaystyle b=b_{OLS}} lorsque R 2 {displaystyle R^{2}} est calculé, alors les éléments diagonaux de R ⊗ {displaystyle R^{ofois }} somme à R 2 {displaystyle R^{2}} . La diagonale R ⊗ {displaystyle R^{ofois }} les valeurs peuvent être inférieures à 0 ou, moins souvent, supérieures à 1. Si les régresseurs ne sont pas corrélés, alors i t h {displaystyle i^{th}} élément diagonal de R ⊗ {displaystyle R^{ofois }} correspond simplement à la r 2 {displaystyle r^{2}} valeur entre x i {displaystyle x_{i}} et y {displaystyle y} .

Une version remise à l’échelle du lasso adaptatif de peut être obtenue en définissant q adaptive lasso , i = | b O L S , i − β 0 , i | {displaystyle q_{{mbox{lasso adaptatif}},i}=|b_{OLS,i}-beta _{0,i}|} . ^[8] Si les régresseurs ne sont pas corrélés, le moment où le i t h {displaystyle i^{th}} paramètre est activé est donné par la i t h {displaystyle i^{th}} élément diagonal de R ⊗ {displaystyle R^{ofois }} . En supposant par commodité que β 0 {displaystyle bêta _{0}} est un vecteur de zéros,

b i = { ( 1 − λ / R i i ⊗ ) b O L S , i if λ ≤ R i i ⊗ , 0 if λ > R i i ⊗ . {displaystyle b_{i}={begin{cases}(1-lambda /R_{ii}^{otimes})b_{OLS,i}&{mbox{if }}lambda leq R_{ ii}^{otimes },\0&{mbox{if }}lambda >R_{ii}^{otimes }.end{cases}}}

Autrement dit, si les régresseurs ne sont pas corrélés, λ {displaystylelambda} précise à nouveau l’influence minimale de β 0 {displaystyle bêta _{0}} . Même lorsque les régresseurs sont corrélés, la première fois qu’un paramètre de régression est activé se produit lorsque λ {displaystylelambda} est égal à l’élément diagonal le plus élevé de R ⊗ {displaystyle R^{ofois }} .

Ces résultats peuvent être comparés à une version redimensionnée du lasso en définissant q lasso , i = 1 p ∑ l | b O L S , l − β 0 , l | {displaystyle q_{{mbox{lasso}},i}={frac {1}{p}}sum _{l}|b_{OLS,l}-beta _{0,l}|} , qui est l’écart absolu moyen de b O L S {displaystyle b_{OLS}} depuis β 0 {displaystyle bêta _{0}} . En supposant que les régresseurs ne sont pas corrélés, alors le moment d’activation de la i t h {displaystyle i^{th}} régresseur est donné par

λ ~ lasso , i = 1 p R i ⊗ ∑ l = 1 p R l ⊗ . {displaystyle {tilde {lambda}}_{{text{lasso}},i}={frac {1}{p}}{sqrt {R_{i}^{otimes}}} somme _{l=1}^{p}{sqrt {R_{l}^{otimes }}}.}

Pour p = 1 {displaystyle p=1} , le moment d’activation est à nouveau donné par λ ~ lasso , i = R 2 {displaystyle {tilde {lambda}}_{{text{lasso}},i}=R^{2}} . Si β 0 {displaystyle bêta _{0}} est un vecteur de zéros et un sous-ensemble de p B {displaystyle p_{B}} les paramètres pertinents sont également responsables d’un ajustement parfait de R 2 = 1 {displaystyle R^{2}=1} , alors ce sous-ensemble est activé à un λ {displaystylelambda} valeur de 1 p {displaystyle {frac {1}{p}}} . Le moment d’activation d’un régresseur pertinent vaut alors 1 p 1 p B p B 1 p B = 1 p {displaystyle {frac {1}{p}}{frac {1}{sqrt {p_{B}}}}p_{B}{frac {1}{sqrt {p_{B}}} }={frac {1}{p}}} . En d’autres termes, l’inclusion de régresseurs non pertinents retarde le moment où les régresseurs pertinents sont activés par ce lasso redimensionné. Le lasso adaptatif et le lasso sont des cas particuliers d’un estimateur ‘1ASTc’. Ce dernier ne regroupe les paramètres que si la corrélation absolue entre les régresseurs est supérieure à une valeur spécifiée par l’utilisateur. ^[6]

Interprétation bayésienne

Les distributions de Laplace sont fortement culminées à leur moyenne avec plus de densité de probabilité concentrée là-bas par rapport à une distribution normale.

Tout comme la régression de crête peut être interprétée comme une régression linéaire pour laquelle les coefficients ont été attribués à des distributions a priori normales, le lasso peut être interprété comme une régression linéaire pour laquelle les coefficients ont des distributions a priori de Laplace . La distribution de Laplace culmine brusquement à zéro (sa dérivée première est discontinue à zéro) et elle concentre sa masse de probabilité plus près de zéro que ne le fait la distribution normale. Cela fournit une explication alternative de la raison pour laquelle le lasso a tendance à mettre certains coefficients à zéro, contrairement à la régression de crête. ^[2]

Interprétation de la relaxation convexe

Lasso peut également être considéré comme une relaxation convexe du meilleur problème de régression de sélection de sous-ensemble, qui consiste à trouver le sous-ensemble de ≤ k {displaystyle leq k} covariables qui se traduit par la plus petite valeur de la fonction objectif pour un k ≤ n {displaystyle kleq n} , où n est le nombre total de covariables. Le ” l 0 {displaystyle ell ^{0}} norme”, ‖ ⋅ ‖ 0 {displaystyle |cdot |_{0}} , (le nombre d’entrées non nulles d’un vecteur), est le cas limite de ” l p {displaystyle ell ^{p}} normes », de la forme ‖ x ‖ p = ( ∑ i = 1 n | x j | p ) 1 / p {displaystyle textstyle |x|_{p}=left(sum _{i=1}^{n}|x_{j}|^{p}right)^{1/p}} (où les guillemets signifient qu’il ne s’agit pas vraiment de normes pour p < 1 {displaystyle p<1} puisque ‖ ⋅ ‖ p {displaystyle |cdot |_{p}} n’est pas convexe pour p < 1 {displaystyle p<1} , donc l’inégalité triangulaire ne tient pas). Par conséquent, puisque p = 1 est la plus petite valeur pour laquelle le ” l p {displaystyle ell ^{p}} norm” est convexe (et donc en fait une norme), le lasso est, dans un certain sens, la meilleure approximation convexe du meilleur problème de sélection de sous-ensemble, puisque la région définie par ‖ x ‖ 1 ≤ t {displaystyle |x|_{1}leq t} est l’ enveloppe convexe de la région définie par ‖ x ‖ p ≤ t {displaystyle |x|_{p}leq t} pour p < 1 {displaystyle p<1} .

Généralisations

Des variantes de lasso ont été créées afin de remédier aux limitations de la technique originale et de rendre la méthode plus utile pour des problèmes particuliers. Presque tous se concentrent sur le respect ou l’exploitation des dépendances entre les covariables.

La régularisation nette élastique ajoute une pénalité supplémentaire de type régression de crête qui améliore les performances lorsque le nombre de prédicteurs est supérieur à la taille de l’échantillon, permet à la méthode de sélectionner ensemble des variables fortement corrélées et améliore la précision globale de la prédiction. ^[5]

Le lasso de groupe permet de sélectionner des groupes de covariables liées en tant qu’unité unique, ce qui peut être utile dans des contextes où il n’est pas logique d’inclure certaines covariables sans d’autres. ^[9] D’autres extensions du lasso de groupe effectuent une Sélection de variables au sein de groupes individuels (lasso de groupe clairsemé) et permettent un chevauchement entre les groupes (lasso de groupe de chevauchement). ^{[10] [11]}

Le lasso fusionné peut tenir compte des caractéristiques spatiales ou temporelles d’un problème, ce qui donne des estimations qui correspondent mieux à la structure du système. ^[12] Les modèles régularisés au lasso peuvent être ajustés à l’aide de techniques telles que les Méthodes de sous-gradient , la régression des moindres angles (LARS) et les Méthodes de gradient proximal . La détermination de la valeur optimale du paramètre de régularisation est un élément important pour s’assurer que le modèle fonctionne bien ; il est généralement choisi à l’aide de la validation croisée .

Filet élastique

En 2005, Zou et Hastie ont introduit le filet élastique . ^[5] Lorsque p > n (le nombre de covariables est supérieur à la taille de l’échantillon), le lasso ne peut sélectionner que n covariables (même lorsque plusieurs sont associées au résultat) et il a tendance à sélectionner une Covariable dans n’importe quel ensemble de covariables hautement corrélées. De plus, même lorsque n > p , la régression de crête a tendance à mieux fonctionner étant donné les covariables fortement corrélées.

Le filet élastique prolonge le lasso en ajoutant un l 2 {displaystyle ell ^{2}} pénalité terme donner

min β ∈ R p { ‖ y − X β ‖ 2 2 + λ 1 ‖ β ‖ 1 + λ 2 ‖ β ‖ 2 2 } , {displaystyle min _{beta in mathbb {R} ^{p}}left{left|yXbeta right|_{2}^{2}+lambda _{1 }|beta |_{1}+lambda _{2}|beta |_{2}^{2}right},}

ce qui équivaut à résoudre

min β 0 , β { ‖ y − β 0 − X β ‖ 2 2 } subject to ( 1 − α ) ‖ β ‖ 1 + α ‖ β ‖ 2 2 ≤ t , where α = λ 2 λ 1 + λ 2 . {displaystyle {begin{aligned}min _{beta _{0},beta }left{left|y-beta _{0}-Xbeta right|_{2 }^{2}right}&{text{ sujet à }}(1-alpha )|beta |_{1}+alpha |beta |_{2}^{2 }leq t,\&{text{ où }}alpha ={frac {lambda _{2}}{lambda _{1}+lambda _{2}}}.end{aligné }}}

Ce problème peut être écrit sous une forme simple de lasso

min β ∗ ∈ R p { ‖ y ∗ − X ∗ β ∗ ‖ 2 2 + λ ∗ ‖ β ∗ ‖ 1 } {displaystyle min _{beta ^{*}in mathbb {R} ^{p}}left{left|y^{*}-X^{*}beta ^{*} right|_{2}^{2}+lambda ^{*}|beta ^{*}|_{1}right}}

location

X ( n + p ) × p ∗ = ( 1 + λ 2 ) − 1 / 2 ( X λ 2 1 / 2 I p × p ) {displaystyle X_{(n+p)times p}^{*}=(1+lambda _{2})^{-1/2}{binom {X}{lambda _{2}^ {1/2}Je_{pfois p}}}} , y ( n + p ) ∗ = ( y 0 p ) , λ ∗ = λ 1 1 + λ 2 {displaystyle y_{(n+p)}^{*}={binom {y}{0^{p}}},qquad lambda ^{*}={frac {lambda _{1} }{sqrt {1+lambda _{2}}}}} , β ∗ = 1 + λ 2 β . {displaystyle beta ^{*}={sqrt {1+lambda _{2}}}beta .}

Puis β ^ = β ^ ∗ 1 + λ 2 {displaystyle {hat {beta }}={frac {{hat {beta }}^{*}}{sqrt {1+lambda _{2}}}}} , ce qui, lorsque les covariables sont orthogonales entre elles, donne

β ^ j = β ^ j *,OLS 1 + λ 2 max ( 0 , 1 − λ ∗ | β ^ j *,OLS | ) = β ^ j OLS 1 + λ 2 max ( 0 , 1 − λ 1 | β ^ j OLS | ) = ( 1 + λ 2 ) − 1 β ^ j lasso . {displaystyle {hat {beta}}_{j}={frac {{hat {beta}}_{j}^{text{*,OLS}}}{sqrt {1+ lambda _{2}}}}max left(0,1-{frac {lambda ^{*}}{left|{hat {beta}}_{j}^{text{* ,OLS}}right|}}right)={frac {{hat {beta }}_{j}^{text{OLS}}}{1+lambda _{2}}} max left(0,1-{frac {lambda _{1}}{left|{hat {beta }}_{j}^{text{OLS}}right|}}right )=(1+lambda _{2})^{-1}{hat {beta }}_{j}^{text{lasso}}.}

Ainsi, le résultat de la pénalité nette élastique est une combinaison des effets des pénalités de lasso et de crête.

Revenant au cas général, le fait que la fonction de pénalité soit maintenant strictement convexe signifie que si x ( j ) = x ( k ) {displaystyle x_{(j)}=x_{(k)}} , β ^ j = β ^ k {displaystyle {hat {beta}}_{j}={hat {beta}}_{k}} , ce qui change du lasso. ^[5] En général, si β ^ j β k ^ > 0 {displaystyle {hat {beta }}_{j}{hat {beta _{k}}}>0}

| β ^ j − β k ^ | ‖ y ‖ ≤ λ 2 − 1 2 ( 1 − ρ j k ) , where ρ = X t X , {displaystyle {frac {|{hat {beta}}_{j}-{hat {beta _{k}}}|}{|y|}}leq lambda _{2 }^{-1}{sqrt {2(1-rho _{jk})}},{text{ où }}rho =X^{t}X,}

est la matrice de corrélation de l’échantillon car la x {style d’affichage x} ‘s sont normalisés.

Par conséquent, les covariables fortement corrélées ont tendance à avoir des Coefficients de régression similaires, le degré de similarité dépendant à la fois ‖ y ‖ 1 {displaystyle |y|_{1}} et λ 2 {style d’affichage lambda _{2}} , qui est différent du lasso. Ce phénomène, dans lequel des covariables fortement corrélées ont des Coefficients de régression similaires, est appelé effet de regroupement. Le regroupement est souhaitable car, dans des applications telles que lier des gènes à une maladie, il est préférable de trouver toutes les covariables associées, plutôt que d’en sélectionner une dans chaque ensemble de covariables corrélées, comme le fait souvent le lasso. ^[5] De plus, la sélection d’un seul de chaque groupe entraîne généralement une erreur de prédiction accrue, car le modèle est moins robuste (c’est pourquoi la régression de crête surpasse souvent le lasso).

Lasso de groupe

En 2006, Yuan et Lin ont introduit le lasso de groupe pour permettre à des groupes prédéfinis de covariables d’être sélectionnés conjointement dans ou hors d’un modèle. ^[9] Ceci est utile dans de nombreux contextes, peut-être plus évidemment lorsqu’une variable catégorique est codée comme une collection de covariables binaires. Dans ce cas, le lasso de groupe peut garantir que toutes les variables codant la Covariable catégorielle sont incluses ou exclues ensemble. Un autre cadre dans lequel le regroupement est naturel est celui des études biologiques. Étant donné que les gènes et les protéines se trouvent souvent dans des voies connues, quelles voies sont liées à un résultat peuvent être plus importantes que si des gènes individuels le sont. La fonction objectif pour le lasso de groupe est une généralisation naturelle de l’objectif standard du lasso

min β ∈ R p { ‖ y − ∑ j = 1 J X j β j ‖ 2 2 + λ ∑ j = 1 J ‖ β j ‖ K j } , ‖ z ‖ K j = ( z t K j z ) 1 / 2 {displaystyle min _{beta in mathbb {R} ^{p}}left{left|y-sum _{j=1}^{J}X_{j}beta _ {j}right|_{2}^{2}+lambda sum _{j=1}^{J}|beta _{j}|_{K_{j}}right },qquad |z|_{K_{j}}=(z^{t}K_{j}z)^{1/2}}

où la matrice de conception X {displaystyle X} et vecteur Covariable β {displaystyle bêta} ont été remplacés par une collection de matrices de conception X j {displaystyle X_{j}} et vecteurs covariables β j {displaystyle bêta _{j}} , un pour chacun des J groupes. De plus, le terme de pénalité est maintenant une somme supérieure à l 2 {displaystyle ell ^{2}} normes définies par les matrices définies positives K j {displaystyle K_{j}} . Si chaque Covariable est dans son propre groupe et K j = I {displaystyle K_{j}=je} , alors cela se réduit au lasso standard, alors que s’il n’y a qu’un seul groupe et K 1 = I {displaystyle K_{1}=je} , il se réduit à une régression de crête. Étant donné que la peine se réduit à un l 2 {displaystyle ell ^{2}} norme sur les sous-espaces définis par chaque groupe, il ne peut sélectionner que certaines des covariables d’un groupe, tout comme la régression ridge ne le peut pas. Cependant, comme la pénalité est la somme des différentes normes de sous-espace, comme dans le lasso standard, la contrainte a des points non différentiels, qui correspondent à certains sous-espaces identiques à zéro. Par conséquent, il peut mettre à zéro les vecteurs de coefficients correspondant à certains sous-espaces, tout en ne faisant que réduire d’autres. Cependant, il est possible d’étendre le lasso de groupe au soi-disant lasso de groupe clairsemé, qui peut sélectionner des covariables individuelles au sein d’un groupe, en ajoutant un l 1 {displaystyle ell ^{1}} pénalité à chaque sous-espace du groupe. ^[10] Une autre extension, le lasso de groupe avec chevauchement permet aux covariables d’être partagées entre les groupes, par exemple, si un gène devait se produire dans deux voies. ^[11]

Lasso fusionné

Dans certains cas, le phénomène à l’étude peut avoir une structure spatiale ou temporelle importante qui doit être prise en compte lors de l’analyse, comme des séries chronologiques ou des données basées sur des images. En 2005, Tibshirani et ses collègues ont introduit le lasso fusionné pour étendre l’utilisation du lasso à ce type de données. ^[12] La fonction objectif du lasso fusionné est

min β { 1 N ∑ i = 1 N ( y i − x i t β ) 2 } subject to ∑ j = 1 p | β j | ≤ t 1 and ∑ j = 2 p | β j − β j − 1 | ≤ t 2 . {displaystyle {begin{aligned}&min _{beta }left{{frac {1}{N}}sum _{i=1}^{N}left(y_{i}-x_{i}^{t}beta right)^{2}right}\[4pt]&{text{ subject to }}sum _{j=1}^{p}|beta _{j}|leq t_{1}{text{ and }}sum _{j=2}^{p}|beta _{j}-beta _{j-1}|leq t_{2}.end{aligned}}}

La première contrainte est la contrainte du lasso, tandis que la seconde pénalise directement les grands changements par rapport à la structure temporelle ou spatiale, ce qui oblige les coefficients à varier en douceur pour refléter la logique sous-jacente du système. Le lasso groupé ^[13] est une généralisation du lasso fusionné qui identifie et regroupe les covariables pertinentes en fonction de leurs effets (coefficients). L’idée de base est de pénaliser les différences entre les coefficients afin que les uns non nuls se regroupent. Ceci peut être modélisé en utilisant la régularisation suivante :

∑ i < j p | β i − β j | ≤ t 2 . {displaystyle sum _{i<j}^{p}|beta _{i}-beta _{j}|leq t_{2}.}

En revanche, les variables peuvent être regroupées en groupes hautement corrélés, puis une seule Covariable représentative peut être extraite de chaque groupe. ^[14]

Il existe des algorithmes qui résolvent le problème du lasso fusionné et certaines généralisations de celui-ci. Les algorithmes peuvent le résoudre exactement en un nombre fini d’opérations. ^[15]

Quasi-normes et régression de pont

Un exemple de fonction potentielle PQSQ (fonction quadratique par morceaux de croissance sous-quadratique) u ( x ) {displaystyle u(x)} ; ici la fonction majorante est f ( x ) = x {displaystyle f(x)=x} ; le potentiel est défini avec ajustement après r 3 {displaystyle r_{3}} . Un exemple de l’efficacité de la régression régularisée PQSQ l 1 {displaystyle ell ^{1}} -norme lasso. ^[16]

Lasso, filet élastique, groupe et lasso fusionné construisent les fonctions de pénalité à partir des l 1 {displaystyle ell ^{1}} et l 2 {displaystyle ell ^{2}} normes (avec poids, si nécessaire). La régression de pont utilise des l p {displaystyle ell ^{p}} normes ( p ≥ 1 {displaystyle pgeq 1} ) et les quasinormes ( 0 < p < 1 {displaystyle 0<p<1} ). ^[17] Par exemple, pour p =1/2 l’analogue de l’objectif du lasso sous la forme lagrangienne est de résoudre

min β ∈ R p { 1 N ‖ y − X β ‖ 2 2 + λ ‖ β ‖ 1 / 2 } , {displaystyle min _{beta in mathbb {R} ^{p}}left{{frac {1}{N}}left|yXbeta right|_{2} ^{2}+lambda {sqrt {|beta |_{1/2}}}right},}

où

‖ β ‖ 1 / 2 = ( ∑ j = 1 p | β j | ) 2 {displaystyle |beta |_{1/2}=left(sum _{j=1}^{p}{sqrt {|beta _{j}|}}right)^{ 2}}

On prétend que les quasi-normes fractionnaires l p {displaystyle ell ^{p}} ( 0 < p < 1 {displaystyle 0<p<1} ) fournissent des résultats plus significatifs dans l’analyse des données à la fois théoriquement et empiriquement. ^[18] La non-convexité de ces quasi-normes complique le problème d’optimisation. Pour résoudre ce problème, une procédure de minimisation des attentes est développée ^[19] et implémentée ^[16] pour la minimisation de la fonction

min β ∈ R p { 1 N ‖ y − X β ‖ 2 2 + λ ∑ j = 1 p θ ( β j 2 ) } , {displaystyle min _{beta in mathbb {R} ^{p}}left{{frac {1}{N}}left|yXbeta right|_{2} ^{2}+lambda sum _{j=1}^{p}vartheta (beta _{j}^{2})right},}

où θ ( γ ) {displaystyle vartheta (gamma)} est une fonction arbitraire concave monotone croissante (par exemple, θ ( γ ) = γ {displaystyle vartheta (gamma )={sqrt {gamma }}} donne la pénalité du lasso et θ ( γ ) = γ 1 / 4 {displaystyle vartheta (gamma )=gamma ^{1/4}} donne le l 1 / 2 {displaystyle ell ^{1/2}} peine).

L’algorithme efficace de minimisation est basé sur l’ approximation quadratique par morceaux de la croissance sous-quadratique (PQSQ). ^[19]

Lasso adaptatif

Le lasso adaptatif a été introduit par Zou en 2006 pour la régression linéaire ^[20] et par Zhang et Lu en 2007 pour la régression à risques proportionnels. ^[21]

Lasso préalable

Le lasso antérieur a été introduit pour les modèles linéaires généralisés par Jiang et al. en 2016 pour intégrer des informations préalables, telles que l’importance de certaines covariables. ^[22] Dans le lasso préalable, ces informations sont résumées en pseudo-réponses (appelées réponses préalables) y ^ p {displaystyle {hat {y}}^{mathrm {p} }} puis une fonction critère supplémentaire est ajoutée à la fonction objectif habituelle avec une pénalité de lasso. Sans perte de généralité, en régression linéaire, la nouvelle fonction objectif peut s’écrire

min β ∈ R p { 1 N ‖ y − X β ‖ 2 2 + 1 N η ‖ y ^ p − X β ‖ 2 2 + λ ‖ β ‖ 1 } , {displaystyle min _{beta in mathbb {R} ^{p}}left{{frac {1}{N}}left|yXbeta right|_{2} ^{2}+{frac {1}{N}}eta left|{hat {y}}^{mathrm {p} }-Xbeta right|_{2}^{ 2}+lambda |beta |_{1}right},}

qui équivaut à

min β ∈ R p { 1 N ‖ y ~ − X β ‖ 2 2 + λ 1 + η ‖ β ‖ 1 } , {displaystyle min _{beta in mathbb {R} ^{p}}left{{frac {1}{N}}left|{tilde {y}}-Xbeta right|_{2}^{2}+{frac {lambda }{1+eta }}|beta |_{1}right},}

la fonction objectif lasso habituelle avec les réponses y {displaystyle y} étant remplacé par une moyenne pondérée des réponses observées et des réponses antérieures y ~ = ( y + η y ^ p ) / ( 1 + η ) {displaystyle {tilde {y}}=(y+eta {hat {y}}^{mathrm {p} })/(1+eta )} (appelées les valeurs de réponse ajustées par les informations a priori).

Au lasso précédent, le paramètre η {displaystyle eta } est appelé un paramètre d’équilibrage, en ce sens qu’il équilibre l’importance relative des données et de l’information a priori. Dans le cas extrême de η = 0 {displaystyleeta =0} , le lasso précédent est réduit au lasso. Si η = ∞ {displaystyle eta =infty} , le lasso préalable s’appuiera uniquement sur les informations préalables pour s’adapter au modèle. De plus, le paramètre d’équilibrage η {displaystyle eta } a une autre interprétation séduisante : il contrôle la variance de β {displaystyle bêta} dans sa distribution antérieure d’un point de vue bayésien.

Le lasso a priori est plus efficace dans l’estimation et la prédiction des paramètres (avec une erreur d’estimation et une erreur de prédiction plus petites) lorsque l’information a priori est de haute qualité, et est robuste aux informations a priori de faible qualité avec un bon choix du paramètre d’équilibrage η {displaystyle eta } .

Calcul des solutions de lasso

La fonction de perte du lasso n’est pas différentiable, mais une grande variété de techniques issues de l’analyse convexe et de la théorie de l’optimisation ont été développées pour calculer le chemin des solutions du lasso. Celles-ci incluent la descente de coordonnées, ^[23] les Méthodes de sous-gradient, la régression du moindre angle (LARS) et les Méthodes de gradient proximal. ^[24] Les Méthodes de sous-gradient sont la généralisation naturelle des méthodes traditionnelles telles que la descente de gradient et la descente de gradient stochastiqueau cas où la fonction objectif n’est pas dérivable en tout point. LARS est une méthode étroitement liée aux modèles de lasso et, dans de nombreux cas, leur permet d’être ajustés efficacement, bien qu’ils ne fonctionnent pas bien dans toutes les circonstances. LARS génère des chemins de solution complets. ^[24] Les méthodes proximales sont devenues populaires en raison de leur flexibilité et de leurs performances et constituent un domaine de recherche active. Le choix de la méthode dépendra de la variante particulière du lasso, des données et des ressources disponibles. Cependant, les méthodes proximales fonctionnent généralement bien.

Choix du paramètre de régularisation

Choix du paramètre de régularisation ( λ {displaystylelambda} ) est un élément fondamental du lasso. Une bonne valeur est essentielle à la performance du lasso car elle contrôle la force du rétrécissement et la sélection des variables, ce qui, avec modération, peut améliorer à la fois la précision de la prédiction et l’interprétabilité. Cependant, si la régularisation devient trop forte, des variables importantes peuvent être omises et les coefficients peuvent être rétrécis de manière excessive, ce qui peut nuire à la fois à la capacité prédictive et à l’inférence. La validation croisée est souvent utilisée pour trouver le paramètre de régularisation.

Des critères d’information tels que le critère d’information bayésien (BIC) et le critère d’information d’Akaike (AIC) pourraient être préférables à la validation croisée, car ils sont plus rapides à calculer et leurs performances sont moins volatiles dans de petits échantillons. ^[25] Un critère d’information sélectionne le paramètre de régularisation de l’estimateur en maximisant la précision en échantillon d’un modèle tout en pénalisant son nombre effectif de paramètres/degrés de liberté. Zou et al. proposé de mesurer les degrés de liberté effectifs en comptant le nombre de paramètres qui s’écartent de zéro. ^[26] L’approche des degrés de liberté a été considérée comme erronée par Kaufman et Rosset ^[27] et Janson et al., ^[28]car les degrés de liberté d’un modèle peuvent augmenter même lorsqu’il est davantage pénalisé par le paramètre de régularisation. Comme alternative, la mesure de simplicité relative définie ci-dessus peut être utilisée pour compter le nombre effectif de paramètres. ^[25] Pour le lasso, cette mesure est donnée par

P ^ = ∑ i = 1 p | β i − β 0 , i | 1 p ∑ l | b O L S , l − β 0 , l | {displaystyle {hat {mathcal {P}}}=sum _{i=1}^{p}{frac {|beta _{i}-beta _{0,i}|}{ {frac {1}{p}}sum _{l}|b_{OLS,l}-beta _{0,l}|}}} ,

qui augmente de manière monotone de zéro à p {displaystyle p} lorsque le paramètre de régularisation diminue de ∞ {displaystyle infty} à zéro.

Candidatures sélectionnées

LASSO a été appliqué en économie et en finance, et s’est avéré améliorer la prédiction et sélectionner des variables parfois négligées, par exemple dans la littérature sur la prédiction des faillites d’entreprises ^[29] ou la prédiction des entreprises à forte croissance. ^[30]

Voir également

• Sélection du modèle
• Régression non paramétrique
• Régularisation de Tikhonov

Références

1. ^ ^{un bc Santosa} , Fadil; Symes, William W. (1986). “Inversion linéaire des sismogrammes de réflexion à bande limitée”. Journal SIAM sur le calcul scientifique et statistique . SIAM. 7 (4): 1307-1330. doi : 10.1137/0907087 .
2. ^ ^{un bcdefg Tibshirani , Robert ( 1996} ). “Régression retrait et de la sélection via le lasso”. Journal de la Société royale de statistique . Série B (méthodologique). Wiley. 58 (1): 267-288. JSTOR 2346178 .
3. ^ ^{un b} Tibshirani, Robert (1997). “La méthode du lasso pour la Sélection de variables dans le modèle de Cox”. Statistiques en médecine . 16 (4): 385–395. CiteSeerX 10.1.1.411.8024 . doi : 10.1002/(SICI)1097-0258(19970228)16:4<385::AID-SIM380>3.0.CO;2-3 . PMID 9044528 .
4. ^ Breiman, Lion (1995). “Meilleure régression de sous-ensemble en utilisant le garrot non négatif”. Technométrie . 37 (4): 373–384. doi : 10.1080/00401706.1995.10484371 .
5. ^ ^{un bcde Zou , Hui} ; Hastie, Trevor (2005). “Régularisation et Sélection Variable via le Net Élastique”. Journal de la Société royale de statistique . Série B (Méthodologie statistique). Wiley. 67 (2): 301-20. doi : 10.1111/j.1467-9868.2005.00503.x . JSTOR 3647580 .
6. ^ ^{un b} Hoornweg, Victor (2018). “Chapitre 8” . Sciences : En cours de soumission . Presse Hoornweg. ISBN 978-90-829188-0-9.
7. ^ Motamedi, Fahimeh; Sanchez, Horacio; Mehri, Alireza; Ghasemi, Fahimeh (octobre 2021). “Accélérer l’analyse de données volumineuses grâce à l’algorithme de forêt aléatoire LASSO dans les études QSAR”. 37 (19). Bioinformatique : 1–7. doi : 10.1093/bioinformatique/btab659 . ISSN 1367-4803 . {{cite journal}}: Cite journal requires |journal= (help)
8. ^ Zo, Hui (2006). “Le lasso adaptatif et ses propriétés Oracle” (PDF) .
9. ^ ^{un Yuan b} , Ming; Lin, Yi (2006). “Sélection de modèle et estimation dans la régression avec des variables groupées”. Journal de la Société royale de statistique . Série B (Méthodologie statistique). Wiley. 68 (1): 49–67. doi : 10.1111/j.1467-9868.2005.00532.x . JSTOR 3647556 .
10. ^ ^{un b} Puig, Arnau Tibau, Ami Wiesel et Alfred O. Hero III . ” Un opérateur de retrait-seuil multidimensionnel “. Actes du 15e atelier sur le traitement statistique du signal, SSP’09, IEEE, pp. 113–116.
11. ^ ^{un b} Jacob, Laurent, Guillaume Obozinski et Jean-Philippe Vert. ” Groupe Lasso avec chevauchement et graphe LASSO “. Apparu dans les Actes de la 26e Conférence internationale sur l’apprentissage automatique, Montréal, Canada, 2009.
12. ^ ^{un b} Tibshirani, Robert, Michael Saunders, Saharon Rosset, Ji Zhu et Keith Knight. 2005. “Sparsity and Smoothness via the Fused lasso”. Journal de la Société royale de statistique. Série B (Méthodologie statistique) 67 (1). Wiley : 91-108. https://www.jstor.org/stable/3647602 .
13. ^ Elle, Yiyuan (2010). “Régression parcimonieuse avec clustering exact” . Journal électronique de statistiques . 4 : 1055–1096. doi : 10.1214/10-EJS578 .
14. ^ Reid, Stephen (2015). “Régression parcimonieuse et tests marginaux à l’aide de prototypes de cluster” . Biostatistique . 17 (2): 364–376. arXiv : 1503.00334 . Bib code : 2015arXiv150300334R . doi : 10.1093/biostatistics/kxv049 . PMC 5006118 . PMID 26614384 .
15. ^ Bento, José (2018). “Sur la complexité du lasso fondu pondéré”. Lettres IEEE en traitement du signal . 25 (10) : 1595-1599. arXiv : 1801.04987 . Bibcode : 2018ISPL…25.1595B . doi : 10.1109/LSP.2018.2867800 . S2CID 5008891 .
16. ^ ^{a b} Mirkes EM Référentiel de régression PQSQ-régularisé , GitHub.
17. ^ Fu, Wenjiang J. 1998. « Le Pont contre le Lasso ». Journal of Computational and Graphical Statistics 7 (3). Taylor et Francis : 397-416.
18. ^ Aggarwal CC, Hinneburg A., Keim DA (2001) ” Sur le comportement surprenant des métriques de distance dans l’espace de grande dimension .” Dans : Van den Bussche J., Vianu V. (eds) Database Theory — ICDT 2001. ICDT 2001. Lecture Notes in Computer Science, Vol. 1973. Springer, Berlin, Heidelberg, p. 420-434.
19. ^ ^{un b} Gorban, AN; Mirkes, EM ; Zinovyev, A. (2016) « Approximations quadratiques par morceaux de fonctions d’erreur arbitraires pour un apprentissage automatique rapide et robuste. » Neural Networks, 84, 28-38.
20. ^ Zo (2006, JASA)
21. ^ Zhang et Lu (2007, Biometrika)
22. ^ Jiang, Yuan (2016). “Sélection de variables avec information a priori pour les modèles linéaires généralisés via la méthode du lasso a priori” . Journal de l’Association statistique américaine . 111 (513): 355–376. doi : 10.1080/01621459.2015.1008363 . PMC 4874534 . PMID 27217599 .
23. ^ Jérôme Friedman, Trevor Hastie et Robert Tibshirani. 2010. “Chemins de régularisation pour les modèles linéaires généralisés via la descente de coordonnées”. Journal of Statistical Software 33 (1): 1-21. https://www.jstatsoft.org/article/view/v033i01/v33i01.pdf .
24. ^ ^{un b} Efron, Bradley, Trevor Hastie, Iain Johnstone et Robert Tibshirani. 2004. “Régression du moindre angle”. Les Annales de statistiques 32 (2). Institut de statistique mathématique : 407–51. https://www.jstor.org/stable/3448465 .
25. ^ ^{un b} Hoornweg, Victor (2018). “Chapitre 9” . Sciences : En cours de soumission . Presse Hoornweg. ISBN 978-90-829188-0-9.
26. ^ Zo, Hui; Hastie, Trevor ; Tibshirani, Robert (2007). “Sur les ‘Degrés de Liberté’ du Lasso” . Les Annales de la statistique . 35 (5): 2173–2792. doi : 10.1214/009053607000000127 .
27. ^ Kaufman, S.; En ligneRoset, S. (2014). “Quand plus de régularisation implique-t-elle moins de degrés de liberté ? Conditions suffisantes et contre-exemples”. Biométrie . 101 (4): 771–784. doi : 10.1093/biomet/asu034 . ISSN 0006-3444 .
28. ^ Janson, Lucas; Fithian, Guillaume; Hastie, Trevor J. (2015). “Degrés de liberté effectifs: une métaphore erronée” . Biométrie . 102 (2): 479–485. doi : 10.1093/biomet/asv019 . ISSN 0006-3444 . PMC 4787623 . PMID 26977114 .
29. ^ Shaonan, Tian; Yu, Yan; Guo, Hui (2015). “Sélection variable et prévisions de faillite d’entreprise” . Journal de la banque et de la finance . 52 (1): 89-100. doi : 10.1016/j.jbankfin.2014.12.003 .
30. ^ Coad, Alex; Srhoj, Stjepan (2020). “Attraper des gazelles avec un lasso : techniques de données volumineuses pour la prédiction des entreprises à forte croissance” . Économie des petites entreprises . 55 (1): 541–565. doi : 10.1007/s11187-019-00203-3 .