Travail (physique)

En physique , le travail est l’ énergie transférée vers ou depuis un objet via l’application d’une force le long d’un déplacement. Dans sa forme la plus simple, il est souvent représenté comme le produit de la force et du déplacement . On dit qu’une force fait un travail positif si (lorsqu’elle est appliquée) elle a une composante dans la direction du déplacement du point d’application. Une force fait un travail négatif si elle a une composante opposée à la direction du déplacement au point d’application de la force. ^[1]

Travail
Un lanceur de baseball effectue un travail positif sur le ballon en lui appliquant une force sur la distance qu’il parcourt lorsqu’il est dans sa prise.
Symboles communs	O
Unité SI	Joule (J)
Autres unités	Pied-livre , Erg
En unités de base SI	1 kg ⋅ m 2 ⋅ s −2
Dérivations à partir d’ autres grandeurs	W = F ⋅ s W = τ θ
Dimension	M L 2 T −2

Par exemple, lorsqu’une balle est tenue au-dessus du sol puis lâchée, le travail effectué par la force gravitationnelle sur la balle lors de sa chute est égal au poids de la balle (une force) multiplié par la distance au sol (un déplacement ). Lorsque la force F est constante et que l’angle entre la force et le déplacement s est θ , alors le travail effectué est donné par :

O = F s parce que ⁡ θ {displaystyle W=Fscos {thêta}}

Le travail est une quantité scalaire , ^[2] donc il n’a qu’une grandeur et pas de direction. Le travail transfère l’énergie d’un endroit à un autre, ou d’une forme à une autre. L’ Unité SI de travail est le joule (J), la même unité que pour l’énergie.

Histoire

La compréhension grecque antique de la physique se limitait à la statique des machines simples (l’équilibre des forces) et n’incluait pas la dynamique ou le concept de travail. Au cours de la Renaissance, la dynamique des puissances mécaniques , comme on appelait les machines simples , a commencé à être étudiée du point de vue de la distance à laquelle elles pouvaient soulever une charge, en plus de la force qu’elles pouvaient appliquer, conduisant finalement au nouveau concept de mécanique. travail. La théorie dynamique complète des machines simples a été élaborée par le scientifique italien Galileo Galilei en 1600 dans Le Meccaniche ( On Mechanics), dans lequel il a montré la similitude mathématique sous-jacente des machines en tant qu’amplificateurs de force. ^{[3] [4]} Il a été le premier à expliquer que les machines simples ne créent pas d’énergie, seulement la transforment. ^[3]

Selon Jammer, ^[5] le terme travail a été introduit en 1826 par le mathématicien français Gaspard-Gustave Coriolis ^[6] comme “poids soulevé à travers une hauteur”, qui est basé sur l’utilisation des premiers moteurs à vapeur pour soulever des seaux d’eau de mines de minerai inondées. Selon René Dugas, ingénieur et historien français, c’est à Salomon de Caux “que l’on doit le terme travail au sens où il est utilisé en mécanique maintenant”. ^[7] Bien que le travailn’a été formellement utilisé qu’en 1826, des concepts similaires existaient auparavant. En 1759, John Smeaton a décrit une quantité qu’il a appelée “puissance” “pour signifier l’effort de force, de gravitation, d’impulsion ou de pression, pour produire un mouvement”. Smeaton continue que cette quantité peut être calculée si “le poids soulevé est multiplié par la hauteur à laquelle il peut être élevé dans un temps donné”, ce qui rend cette définition remarquablement similaire à celle de Coriolis. ^[8]

Unités

L’ Unité SI de travail est le joule (J), du nom du physicien anglais du XIXe siècle James Prescott Joule , qui est défini comme le travail nécessaire pour exercer une force d’un newton par un déplacement d’un mètre .

Le newton-mètre dimensionnellement équivalent (N⋅m) est parfois utilisé comme unité de mesure pour le travail, mais cela peut être confondu avec l’unité de mesure du couple . L’utilisation de N⋅m est déconseillée par l’ autorité SI , car elle peut prêter à confusion quant à savoir si la quantité exprimée en newtons-mètres est une mesure de couple ou une mesure de travail. ^[9]

Les unités de travail non SI comprennent le newton-mètre, l’ erg , le pied-livre , le pied -livre, le Kilowattheure , le litre-atmosphère et la puissance-heure . En raison du travail ayant la même dimension physique que la chaleur , des unités de mesure généralement réservées à la chaleur ou au contenu énergétique, telles que therm , BTU et calorie , sont utilisées comme unité de mesure.

Travail et énergie

Le travail W effectué par une force constante de magnitude F sur un point qui déplace un déplacement s en ligne droite dans la direction de la force est le produit

O = F s . {displaystyle W=Fs.}

Par exemple, si une force de 10 newtons ( F = 10 N ) agit le long d’un point qui parcourt 2 mètres ( s = 2 m ), alors W = Fs = (10 N) (2 m) = 20 J . C’est approximativement le travail effectué pour soulever un objet de 1 kg du niveau du sol au-dessus de la tête d’une personne contre la force de gravité.

Le travail est doublé soit en soulevant deux fois le poids sur la même distance, soit en soulevant le même poids deux fois sur la distance.

Le travail est étroitement lié à l’énergie . Le principe travail-énergie stipule qu’une augmentation de l’énergie cinétique d’un corps rigide est causée par une quantité égale de travail positif effectué sur le corps par la force résultante agissant sur ce corps. Inversement, une diminution de l’énergie cinétique est causée par une quantité égale de travail négatif effectué par la force résultante. Ainsi, si le travail net est positif, l’énergie cinétique de la particule augmente de la quantité de travail. Si le travail net effectué est négatif, l’énergie cinétique de la particule diminue de la quantité de travail. ^[dix]

À partir de La deuxième loi de Newton , on peut montrer que le travail sur un corps libre (pas de champs), rigide (pas de degrés de liberté internes), est égal à la variation de l’énergie cinétique E _k correspondant à la vitesse linéaire et à la vitesse angulaire de ce corps ,

O = Δ E k . {displaystyle W=Delta E_{k}.}

Le travail des forces générées par une fonction potentielle est appelé énergie potentielle et les forces sont dites conservatrices . Par conséquent, le travail sur un objet qui est simplement déplacé dans un champ de force conservateur , sans changement de vitesse ou de rotation, est égal à moins le changement d’énergie potentielle E _p de l’objet,

O = − Δ E p . {displaystyle W=-Delta E_{p}.}

Ces formules montrent que le travail est l’énergie associée à l’action d’une force, donc le travail possède par la suite les dimensions physiques et les unités de l’énergie. Les principes de travail/énergie discutés ici sont identiques aux principes de travail/énergie électriques.

Forces de contrainte

Les forces de contrainte déterminent le déplacement de l’objet dans le système, le limitant dans une plage. Par exemple, dans le cas d’une pente plus gravité, l’objet est collé à la pente et, lorsqu’il est attaché à une corde tendue, il ne peut pas se déplacer vers l’extérieur pour rendre la corde plus “tendue”. Il élimine tous les déplacements dans cette direction, c’est-à-dire que la vitesse dans la direction de la contrainte est limitée à 0, de sorte que les forces de contrainte n’effectuent pas de travail sur le système.

Pour un Système mécanique , ^[11] les forces de contrainte éliminent le mouvement dans les directions qui caractérisent la contrainte. Ainsi le travail virtuel effectué par les forces de contrainte est nul, résultat qui n’est vrai que si les forces de frottement sont exclues. ^[12]

Les forces de contrainte fixes et sans frottement n’effectuent pas de travail sur le système, ^[13] car l’angle entre le mouvement et les forces de contrainte est toujours de 90° . ^[13] Des exemples de contraintes sans travail sont : les interconnexions rigides entre les particules, le mouvement de glissement sur une surface sans frottement et le contact de roulement sans glissement. ^[14]

Par exemple, dans un système de poulie comme la machine Atwood , les forces internes sur la corde et sur la poulie de support ne travaillent pas sur le système. Par conséquent, le travail n’a besoin d’être calculé que pour les forces gravitationnelles agissant sur les corps. Un autre exemple est la force centripète exercée vers l’ intérieur par une corde sur une balle dans un mouvement circulaire uniforme contraint latéralement la balle à un mouvement circulaire limitant son mouvement loin du centre du cercle. Cette force ne travaille pas parce qu’elle est perpendiculaire à la vitesse de la balle.

La Force magnétique sur une particule chargée est F = q v × B , où q est la charge, v est la vitesse de la particule et B est le champ magnétique . Le résultat d’un produit croisé est toujours perpendiculaire aux deux vecteurs d’origine, donc F ⊥ v . Le Produit scalaire de deux vecteurs perpendiculaires est toujours nul, donc le travail W = F ⋅ v = 0, et la Force magnétique ne fonctionne pas. Il peut changer la direction du mouvement mais jamais changer la vitesse.

Calcul mathématique

Pour les objets en mouvement, la quantité de travail/temps (puissance) est intégrée le long de la trajectoire du point d’application de la force. Ainsi, à tout instant, le taux de travail effectué par une force (mesuré en joules/seconde, ou watts ) est le Produit scalaire de la force (un vecteur), et le vecteur vitesse du point d’application. Ce Produit scalaire de la force et de la vitesse est appelé puissance instantanée . Tout comme les vitesses peuvent être intégrées dans le temps pour obtenir une distance totale, par le théorème fondamental du calcul , le travail total le long d’un chemin est de même l’intégrale temporelle de la puissance instantanée appliquée le long de la trajectoire du point d’application. ^[15]

Le travail est le résultat d’une force sur un point qui suit une courbe X , avec une vitesse v , à chaque instant. La petite quantité de travail δW qui se produit sur un instant de temps dt est calculée comme

δ O = F ⋅ d s = F ⋅ v d t {displaystyle delta W=mathbf {F} cdot dmathbf {s} =mathbf {F} cdot mathbf {v} dt}

où le F ⋅ v est la puissance sur l’instant dt . La somme de ces petites quantités de travail sur la trajectoire du point donne le travail,

W = ∫ t 1 t 2 F ⋅ v d t = ∫ t 1 t 2 F ⋅ d s d t d t = ∫ C F ⋅ d s , {displaystyle W=int _{t_{1}}^{t_{2}}mathbf {F} cdot mathbf {v} dt=int _{t_{1}}^{t_{2} }mathbf {F} cdot {tfrac {dmathbf {s} }{dt}}dt=int _{C}mathbf {F} cdot dmathbf {s} ,}

où C est la trajectoire de x ( t ₁ ) à x ( t ₂ ). Cette intégrale est calculée le long de la trajectoire de la particule, et est donc dite dépendante du chemin .

Si la force est toujours dirigée le long de cette ligne et que l’amplitude de la force est F , alors cette intégrale se simplifie en

W = ∫ C F d s {displaystyle W=int _{C}F,ds}

où s est le déplacement le long de la droite. Si F est constant, en plus d’être dirigé le long de la ligne, alors l’intégrale se simplifie davantage en

W = ∫ C F d s = F ∫ C d s = F s {displaystyle W=int _{C}F,ds=Fint _{C}ds=Fs}

où s est le déplacement du point le long de la droite.

Ce calcul peut être généralisé pour une force constante qui n’est pas dirigée le long de la ligne, suivie de la particule. Dans ce cas, le Produit scalaire F ⋅ d s = F cos θ ds , où θ est l’angle entre le vecteur force et la direction du mouvement, ^[15] c’est-à-dire

W = ∫ C F ⋅ d s = F s cos ⁡ θ . {displaystyle W=int _{C}mathbf {F} cdot dmathbf {s} =Fscos theta .}

Lorsqu’une composante de force est perpendiculaire au déplacement de l’objet (comme lorsqu’un corps se déplace sur une trajectoire circulaire sous une force centrale ), aucun travail n’est effectué, car le cosinus de 90° est égal à zéro. ^[10] Ainsi, aucun travail ne peut être effectué par gravité sur une planète à orbite circulaire (c’est l’idéal, car toutes les orbites sont légèrement elliptiques). De plus, aucun travail n’est effectué sur un corps se déplaçant circulairement à une vitesse constante tout en étant contraint par une force mécanique, comme le déplacement à vitesse constante dans une centrifugeuse idéale sans frottement.

Travail effectué par une force variable

Le calcul du travail en tant que “force multipliée par le segment de trajet rectiligne” ne s’appliquerait que dans les circonstances les plus simples, comme indiqué ci-dessus. Si la force change, ou si le corps se déplace le long d’une trajectoire courbe, éventuellement rotative et pas nécessairement rigide, alors seule la trajectoire du point d’application de la force est pertinente pour le travail effectué, et seule la composante de la force parallèle à la vitesse du point d’application effectue un travail (travail positif lorsqu’il est dans le même sens et négatif lorsqu’il est dans le sens opposé à la vitesse). Cette composante de force peut être décrite par la grandeur scalaire appelée composante tangentielle scalaire ( F cos( θ ) , où θest l’angle entre la force et la vitesse). Et puis la définition la plus générale du travail peut être formulée comme suit :

Le travail d’une force est l’intégrale linéaire de sa composante tangentielle scalaire le long de la trajectoire de son point d’application. Si la force varie (par exemple en comprimant un ressort), nous devons utiliser le calcul pour trouver le travail effectué. Si la force est donnée par F ( x ) (une fonction de x ) alors le travail effectué par la force le long de l’axe des x de a à b est : W = ∫ a b F ( s ) ⋅ d s {displaystyle W=int _{a}^{b}mathbf {F(s)} cdot dmathbf {s} }

Couple et rotation

Un couple de forces résulte de forces égales et opposées, agissant sur deux points différents d’un corps rigide. La somme (résultante) de ces forces peut s’annuler, mais leur effet sur le corps est le couple ou couple T . Le travail du couple est calculé comme

δ W = T ⋅ ω d t , {displaystyle delta W=mathbf {T} cdot {boldsymbol {omega}},dt,}

où T ⋅ ω est la puissance sur l’instant dt . La somme de ces petites quantités de travail sur la trajectoire du corps rigide donne le travail,

W = ∫ t 1 t 2 T ⋅ ω d t . {displaystyle W=int _{t_{1}}^{t_{2}}mathbf {T} cdot {boldsymbol {omega }},dt.}

Cette intégrale est calculée le long de la trajectoire du corps rigide avec une vitesse angulaire ω qui varie avec le temps, et est donc dite dépendante de la trajectoire .

Si le vecteur de vitesse angulaire maintient une direction constante, alors il prend la forme,

ω → = φ ̇ S , {displaystyle {vec {omega }}={dot {phi }}mathbf {S} ,}

où φ est l’angle de rotation autour du vecteur unitaire constant S . Dans ce cas, le travail du couple devient,

W = ∫ t 1 t 2 T ⋅ ω d t = ∫ t 1 t 2 T ⋅ S d φ d t d t = ∫ C T ⋅ S d φ , {displaystyle W=int _{t_{1}}^{t_{2}}mathbf {T} cdot {boldsymbol {omega }},dt=int _{t_{1}}^ {t_{2}}mathbf {T} cdot mathbf {S} {frac {dphi }{dt}}dt=int _{C}mathbf {T} cdot mathbf {S} ,dphi ,}

où C est la trajectoire de φ ( t ₁ ) à φ ( t ₂ ). Cette intégrale dépend de la trajectoire de rotation φ ( t ), et est donc dépendante du chemin.

Si le couple T est aligné avec le vecteur de vitesse angulaire de sorte que,

T = τ S , {displaystyle mathbf {T} =tau mathbf {S} ,}

et le couple et la vitesse angulaire sont constants, alors le travail prend la forme, ^[2]

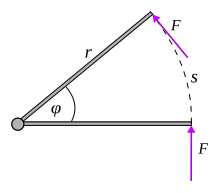
W = ∫ t 1 t 2 τ φ ̇ d t = τ ( φ 2 − φ 1 ) . {displaystyle W=int _{t_{1}}^{t_{2}}tau {dot {phi }}dt=tau (phi _{2}-phi _{1}) .} Une force de grandeur constante et perpendiculaire au bras de levier

Ce résultat peut être compris plus simplement en considérant le couple comme résultant d’une force d’amplitude constante F , appliquée perpendiculairement à un bras de levier à une distance r , comme indiqué sur la figure. Cette force agira sur la distance le long de l’arc de cercle s = rφ , donc le travail effectué est

W = F s = F r φ . {displaystyle W=Fs=Frphi .}

Introduire le couple τ = Fr , pour obtenir

W = F r φ = τ φ , {displaystyle W=Frphi =tau phi ,}

comme présenté ci-dessus.

Notez que seule la composante du couple dans la direction du vecteur vitesse angulaire contribue au travail.

Travail et énergie potentielle

Le Produit scalaire d’une force F et de la vitesse v de son point d’application définit la puissance absorbée par un système à un instant donné. L’intégration de cette puissance sur la trajectoire du point d’application, C = x ( t ) , définit le travail apporté au système par la force.

Dépendance au chemin

Par conséquent, le travail effectué par une force F sur un objet qui se déplace le long d’une courbe C est donné par l’ intégrale linéaire :

W = ∫ C F ⋅ d x = ∫ t 1 t 2 F ⋅ v d t , {displaystyle W=int _{C}mathbf {F} cdot dmathbf {x} =int _{t_{1}}^{t_{2}}mathbf {F} cdot mathbf {v} dt,}

où dx ( t ) définit la trajectoire C et v est la vitesse le long de cette trajectoire. En général, cette intégrale nécessite que le chemin le long duquel la vitesse soit définie, de sorte que l’évaluation du travail est dite dépendante du chemin.

La dérivée temporelle de l’intégrale de travail donne la puissance instantanée,

d W d t = P ( t ) = F ⋅ v . {displaystyle {frac {dW}{dt}}=P(t)=mathbf {F} cdot mathbf {v} .}

Indépendance de chemin

Si le travail pour une force appliquée est indépendant de la trajectoire, alors le travail effectué par la force, par le théorème du gradient , définit une fonction potentielle qui est évaluée au début et à la fin de la trajectoire du point d’application. Cela signifie qu’il existe une fonction potentielle U ( x ), qui peut être évaluée aux deux points x ( t ₁ ) et x ( t ₂ ) pour obtenir le travail sur toute trajectoire entre ces deux points. Il est de tradition de définir cette fonction par un signe négatif afin que le travail positif soit une réduction du potentiel, c’est-à-dire

W = ∫ C F ⋅ d x = ∫ x ( t 1 ) x ( t 2 ) F ⋅ d x = U ( x ( t 1 ) ) − U ( x ( t 2 ) ) . {displaystyle W=int _{C}mathbf {F} cdot mathrm {d} mathbf {x} =int _{mathbf {x} (t_{1})}^{mathbf { x} (t_{2})}mathbf {F} cdot mathrm {d} mathbf {x} =U(mathbf {x} (t_{1}))-U(mathbf {x} ( t_{2})).}

La fonction U ( x ) est appelée l’ énergie potentielle associée à la force appliquée. La force dérivée d’une telle fonction potentielle est dite conservatrice . Des exemples de forces qui ont des énergies potentielles sont les forces de gravité et de ressort.

Dans ce cas, le gradient de travail donne

∇ W = − ∇ U = − ( ∂ U ∂ x , ∂ U ∂ y , ∂ U ∂ z ) = F , {displaystyle nabla W=-nabla U=-left({frac {partial U}{partial x}},{frac {partial U}{partial y}},{frac { partial U}{partial z}}right)=mathbf {F} ,}

et la force F est dite “dérivable d’un potentiel”. ^[16]

Comme le potentiel U définit une force F en chaque point x de l’espace, l’ensemble des forces est appelé champ de force . La puissance appliquée à un corps par un champ de force est obtenue à partir du gradient du travail, ou potentiel, dans la direction de la vitesse V du corps, c’est-à-dire

P ( t ) = − ∇ U ⋅ v = F ⋅ v . {displaystyle P(t)=-nabla Ucdot mathbf {v} =mathbf {F} cdot mathbf {v} .}

Travail par gravité

La gravité F = mg fonctionne W = mgh le long de n’importe quel chemin descendant

En l’absence d’autres forces, la gravité entraîne une accélération constante vers le bas de tout objet en mouvement libre. Près de la surface de la Terre, l’accélération due à la gravité est g = 9,8 m⋅s ⁻² et la force gravitationnelle sur un objet de masse m est F _g = mg . Il convient d’imaginer cette force gravitationnelle concentrée au centre de masse de l’objet.

Si un objet de poids mg est déplacé vers le haut ou vers le bas d’une distance verticale y ₂ − y ₁ , le travail W effectué sur l’objet est :

W = F g ( y 2 − y 1 ) = F g Δ y = m g Δ y {displaystyle W=F_{g}(y_{2}-y_{1})=F_{g}Delta y=mgDelta y}

où F _g est le poids (livres en unités impériales et newtons en unités SI), et Δ y est le changement de hauteur y . Notez que le travail effectué par la gravité ne dépend que du mouvement vertical de l’objet. La présence de frottement n’affecte pas le travail effectué sur l’objet par son poids.

Travail par gravité dans l’espace

La force de gravité exercée par une masse M sur une autre masse m est donnée par

F = − G M m r 3 r , {displaystyle mathbf {F} =-{frac {GMm}{r^{3}}}mathbf {r} ,}

où r est le vecteur position de M à m .

Soit la masse m se déplacer à la vitesse v ; alors le travail de gravité sur cette masse lorsqu’elle se déplace de la position r ( t ₁ ) à r ( t ₂ ) est donné par

W = − ∫ r ( t 1 ) r ( t 2 ) G M m r 3 r ⋅ d r = − ∫ t 1 t 2 G M m r 3 r ⋅ v d t . {displaystyle W=-int _{mathbf {r} (t_{1})}^{mathbf {r} (t_{2})}{frac {GMm}{r^{3}}} mathbf {r} cdot dmathbf {r} =-int _{t_{1}}^{t_{2}}{frac {GMm}{r^{3}}}mathbf {r} cdot mathbf {v} dt.}

Notez que la position et la vitesse de la masse m sont données par

r = r e r , v = d r d t = r ̇ e r + r θ ̇ e t , {displaystyle mathbf {r} =rmathbf {e} _{r},qquad mathbf {v} ={frac {dmathbf {r} }{dt}}={dot {r} }mathbf {e} _{r}+r{dot {theta }}mathbf {e} _{t},}

où e _r et e _t sont les vecteurs unitaires radial et tangentiel orientés par rapport au vecteur de M vers m , et on utilise le fait que d e r / d t = θ ̇ e t . {displaystyle dmathbf {e} _{r}/dt={point {theta}}mathbf {e} _{t}.} Utilisez ceci pour simplifier la formule du travail de gravité à,

W = − ∫ t 1 t 2 G m M r 3 ( r e r ) ⋅ ( r ̇ e r + r θ ̇ e t ) d t = − ∫ t 1 t 2 G m M r 3 r r ̇ d t = G M m r ( t 2 ) − G M m r ( t 1 ) . {displaystyle W=-int _{t_{1}}^{t_{2}}{frac {GmM}{r^{3}}}(rmathbf {e} _{r})cdot ({dot {r}}mathbf {e} _{r}+r{dot {theta }}mathbf {e} _{t})dt=-int _{t_{1}}^ {t_{2}}{frac {GmM}{r^{3}}}r{dot {r}}dt={frac {GMm}{r(t_{2})}}-{frac {GMm}{r(t_{1})}}.}

Ce calcul utilise le fait que

d d t r − 1 = − r − 2 r ̇ = − r ̇ r 2 . {displaystyle {frac {d}{dt}}r^{-1}=-r^{-2}{dot {r}}=-{frac {dot {r}}{r^{ 2}}}.}

La fonction

U = − G M m r , {displaystyle U=-{frac {GMm}{r}},}

est la fonction du potentiel gravitationnel, également appelée Énergie potentielle gravitationnelle . Le signe négatif suit la convention selon laquelle le travail est gagné à partir d’une perte d’énergie potentielle.

Travail par un ressort

Forces dans les ressorts assemblés en parallèle

Considérons un ressort qui exerce une force horizontale F = (− kx , 0, 0) qui est proportionnelle à sa déviation dans la direction x indépendamment de la façon dont un corps se déplace. Le travail de ce ressort sur un corps se déplaçant le long de l’espace avec la courbe X ( t ) = ( x ( t ), y ( t ), z ( t )) , est calculé en utilisant sa vitesse, v = ( v _x , v _y , v _z ) , pour obtenir

W = ∫ 0 t F ⋅ v d t = − ∫ 0 t k x v x d t = − 1 2 k x 2 . {displaystyle W=int _{0}^{t}mathbf {F} cdot mathbf {v} dt=-int _{0}^{t}kxv_{x}dt=-{frac {1}{2}}kx^{2}.}

Pour plus de commodité, considérons que le contact avec le ressort se produit à t = 0 , puis l’intégrale du produit de la distance x et de la vitesse x, xv _x dt , au cours du temps t est (1/2) x ² . Le travail est le produit de la distance par la force du ressort, qui dépend également de la distance ; d’où le résultat x ² .

Travail par un gaz

W = ∫ a b P d V {displaystyle W=int _{a}^{b}{P}dV}

Où P est la pression, V est le volume et a et b sont les volumes initial et final.

Principe travail-énergie

Le principe du travail et de l’énergie cinétique (également connu sous le nom de principe travail-énergie ) stipule que le travail effectué par toutes les forces agissant sur une particule (le travail de la force résultante) est égal à la variation de l’énergie cinétique de la particule. ^[17] Autrement dit, le travail W effectué par la force résultante sur une particule est égal à la variation de l’énergie cinétique de la particule E k {displaystyle E_{k}} , ^[2]

W = Δ E k = 1 2 m v 2 2 − 1 2 m v 1 2 {displaystyle W=Delta E_{k}={frac {1}{2}}mv_{2}^{2}-{frac {1}{2}}mv_{1}^{2}}

où v 1 {style d’affichage v_{1}} et v 2 {style d’affichage v_{2}} sont les vitesses de la particule avant et après le travail, et m est sa masse .

La dérivation du principe travail-énergie commence par la Deuxième loi du mouvement de Newton et la force résultante sur une particule. Le calcul du Produit scalaire des forces avec la vitesse de la particule évalue la puissance instantanée ajoutée au système. ^[18]

Les contraintes définissent la direction du mouvement de la particule en garantissant qu’il n’y a pas de composante de vitesse dans la direction de la force de contrainte. Cela signifie également que les forces de contrainte ne s’ajoutent pas à la puissance instantanée. L’intégrale temporelle de cette équation scalaire donne du travail à partir de la puissance instantanée et de l’énergie cinétique à partir du Produit scalaire de la vitesse et de l’accélération. Le fait que le principe travail-énergie élimine les forces de contrainte sous-tend la mécanique lagrangienne . ^[19]

Cette section se concentre sur le principe travail-énergie tel qu’il s’applique à la dynamique des particules. Dans des systèmes plus généraux, le travail peut modifier l’ énergie potentielle d’un dispositif mécanique, l’énergie thermique dans un système thermique ou l’ énergie électrique dans un dispositif électrique. Le travail transfère l’énergie d’un endroit à un autre ou d’une forme à une autre.

Dérivation pour une particule se déplaçant le long d’une ligne droite

Dans le cas où la force résultante F est constante en amplitude et en direction, et parallèle à la vitesse de la particule, la particule se déplace avec une accélération constante a le long d’une ligne droite. ^[20] La relation entre la force nette et l’accélération est donnée par l’équation F = ma ( deuxième loi de Newton ), et le déplacement des particules s peut être exprimé par l’équation

s = v 2 2 − v 1 2 2 a {displaystyle s={frac {v_{2}^{2}-v_{1}^{2}}{2a}}}

qui découle de v 2 2 = v 1 2 + 2 a s {displaystyle v_{2}^{2}=v_{1}^{2}+2as} (voir Équations du mouvement ).

Le travail de la force nette est calculé comme le produit de sa grandeur et du déplacement des particules. En substituant les équations ci-dessus, on obtient :

W = F s = m a s = m a v 2 2 − v 1 2 2 a = m v 2 2 2 − m v 1 2 2 = Δ E k {displaystyle W=Fs=mas=ma{frac {v_{2}^{2}-v_{1}^{2}}{2a}}={frac {mv_{2}^{2}} {2}}-{frac {mv_{1}^{2}}{2}}=Delta E_{k}}

Autre dérivation :

W = F s = m a s = m v 2 2 − v 1 2 2 s s = 1 2 m v 2 2 − 1 2 m v 1 2 = Δ E k {displaystyle W=Fs=mas=m{frac {v_{2}^{2}-v_{1}^{2}}{2s}}s={frac {1}{2}}mv_{ 2}^{2}-{frac {1}{2}}mv_{1}^{2}=Delta E_{k}}

Dans le cas général du mouvement rectiligne, lorsque la force nette F n’est pas constante en amplitude, mais est constante en direction et parallèle à la vitesse de la particule, le travail doit être intégré le long de la trajectoire de la particule :

W = ∫ t 1 t 2 F ⋅ v d t = ∫ t 1 t 2 F v d t = ∫ t 1 t 2 m a v d t = m ∫ t 1 t 2 v d v d t d t = m ∫ v 1 v 2 v d v = 1 2 m ( v 2 2 − v 1 2 ) . {displaystyle W=int _{t_{1}}^{t_{2}}mathbf {F} cdot mathbf {v} dt=int _{t_{1}}^{t_{2} }F,v,dt=int _{t_{1}}^{t_{2}}ma,v,dt=mint _{t_{1}}^{t_{2}} v,{frac {dv}{dt}},dt=mint _{v_{1}}^{v_{2}}v,dv={tfrac {1}{2}}m gauche(v_{2}^{2}-v_{1}^{2}droite).}

Dérivation générale du principe travail-énergie pour une particule

Pour toute force nette agissant sur une particule se déplaçant le long d’une trajectoire curviligne, on peut démontrer que son travail est égal à la variation de l’énergie cinétique de la particule par une simple dérivation analogue à l’équation ci-dessus. C’est ce qu’on appelle le principe travail-énergie :

W = ∫ t 1 t 2 F ⋅ v d t = m ∫ t 1 t 2 a ⋅ v d t = m 2 ∫ t 1 t 2 d v 2 d t d t = m 2 ∫ v 1 2 v 2 2 d v 2 = m v 2 2 2 − m v 1 2 2 = Δ E k {displaystyle W=int _{t_{1}}^{t_{2}}mathbf {F} cdot mathbf {v} dt=mint _{t_{1}}^{t_{2 }}mathbf {a} cdot mathbf {v} dt={frac {m}{2}}int _{t_{1}}^{t_{2}}{frac {dv^{2 }}{dt}},dt={frac {m}{2}}int _{v_{1}^{2}}^{v_{2}^{2}}dv^{2}= {frac {mv_{2}^{2}}{2}}-{frac {mv_{1}^{2}}{2}}=Delta {E_{k}}}

L’identité a ⋅ v = 1 2 d v 2 d t {textstyle mathbf {a} cdot mathbf {v} ={frac {1}{2}}{frac {dv^{2}}{dt}}} nécessite un peu d’algèbre. De l’identité v 2 = v ⋅ v {textstyle v^{2}=mathbf {v} cdot mathbf {v} } et définition a = d v d t {textstyle mathbf {a} ={frac {dmathbf {v} }{dt}}} ça suit

d v 2 d t = d ( v ⋅ v ) d t = d v d t ⋅ v + v ⋅ d v d t = 2 d v d t ⋅ v = 2 a ⋅ v . {displaystyle {frac {dv^{2}}{dt}}={frac {d(mathbf {v} cdot mathbf {v} )}{dt}}={frac {dmathbf {v} }{dt}}cdot mathbf {v} +mathbf {v} cdot {frac {dmathbf {v} }{dt}}=2{frac {dmathbf {v} }{dt}}cdot mathbf {v} =2mathbf {a} cdot mathbf {v} .}

La partie restante de la dérivation ci-dessus n’est qu’un calcul simple, comme dans le cas rectiligne précédent.

Dérivation pour une particule en mouvement contraint

En dynamique des particules , une formule assimilant le travail appliqué à un système à son changement d’énergie cinétique est obtenue comme première intégrale de la Deuxième loi du mouvement de Newton . Il est utile de noter que la force résultante utilisée dans les lois de Newton peut être séparée en forces appliquées à la particule et en forces imposées par les contraintes sur le mouvement de la particule. Remarquablement, le travail d’une force de contrainte est nul, donc seul le travail des forces appliquées doit être pris en compte dans le principe travail-énergie.

Pour le voir, considérons une particule P qui suit la trajectoire X ( t ) avec une force F agissant sur elle. Isolez la particule de son environnement pour exposer les forces de contrainte R , alors la loi de Newton prend la forme

F + R = m X ̈ , {displaystyle mathbf {F} +mathbf {R} =m{ddot {mathbf {X} }},}

où m est la masse de la particule.

Formule vectorielle

Notez que n points au-dessus d’un vecteur indique sa nième dérivée temporelle . Le Produit scalaire de chaque côté de la loi de Newton avec le vecteur vitesse donne

F ⋅ X ̇ = m X ̈ ⋅ X ̇ , {displaystyle mathbf {F} cdot {dot {mathbf {X} }}=m{ddot {mathbf {X} }}cdot {dot {mathbf {X} }},}

car les forces de contrainte sont perpendiculaires à la vitesse des particules. Intégrez cette équation le long de sa trajectoire du point X ( t ₁ ) au point X ( t ₂ ) pour obtenir

∫ t 1 t 2 F ⋅ X ̇ d t = m ∫ t 1 t 2 X ̈ ⋅ X ̇ d t . {displaystyle int _{t_{1}}^{t_{2}}mathbf {F} cdot {dot {mathbf {X}}}dt=mint _{t_{1}}^ {t_{2}}{ddot {mathbf {X} }}cdot {dot {mathbf {X} }}dt.}

Le côté gauche de cette équation est le travail de la force appliquée lorsqu’elle agit sur la particule le long de la trajectoire du temps t ₁ au temps t ₂ . Cela peut aussi s’écrire comme

W = ∫ t 1 t 2 F ⋅ X ̇ d t = ∫ X ( t 1 ) X ( t 2 ) F ⋅ d X . {displaystyle W=int _{t_{1}}^{t_{2}}mathbf {F} cdot {dot {mathbf {X}}}dt=int _{mathbf {X} (t_{1})}^{mathbf {X} (t_{2})}mathbf {F} cdot dmathbf {X} .}

Cette intégrale est calculée le long de la trajectoire X ( t ) de la particule et est donc dépendante du chemin.

Le côté droit de la première intégrale des équations de Newton peut être simplifié en utilisant l’identité suivante

1 2 d d t ( X ̇ ⋅ X ̇ ) = X ̈ ⋅ X ̇ , {displaystyle {frac {1}{2}}{frac {d}{dt}}({dot {mathbf {X} }}cdot {dot {mathbf {X} }})= {ddot {mathbf {X} }}cdot {dot {mathbf {X} }},}

(voir la règle du produit pour la dérivation). Maintenant, il est intégré explicitement pour obtenir le changement d’énergie cinétique,

Δ K = m ∫ t 1 t 2 X ̈ ⋅ X ̇ d t = m 2 ∫ t 1 t 2 d d t ( X ̇ ⋅ X ̇ ) d t = m 2 X ̇ ⋅ X ̇ ( t 2 ) − m 2 X ̇ ⋅ X ̇ ( t 1 ) = 1 2 m Δ v 2 , {displaystyle Delta K=mint _{t_{1}}^{t_{2}}{ddot {mathbf {X} }}cdot {dot {mathbf {X} }}dt= {frac {m}{2}}int _{t_{1}}^{t_{2}}{frac {d}{dt}}({dot {mathbf {X} }}cdot {dot {mathbf {X} }})dt={frac {m}{2}}{dot {mathbf {X} }}cdot {dot {mathbf {X} }}(t_ {2})-{frac {m}{2}}{dot {mathbf {X} }}cdot {dot {mathbf {X} }}(t_{1})={frac { 1}{2}}mDelta mathbf {v} ^{2},}

où l’énergie cinétique de la particule est définie par la quantité scalaire,

K = m 2 X ̇ ⋅ X ̇ = 1 2 m v 2 {displaystyle K={frac {m}{2}}{dot {mathbf {X} }}cdot {dot {mathbf {X} }}={frac {1}{2}} m{mathbf {v} ^{2}}} Composantes tangentielles et normales

Il est utile de résoudre les vecteurs vitesse et accélération en composantes tangentielles et normales le long de la trajectoire X ( t ), telles que

X ̇ = v T and X ̈ = v ̇ T + v 2 κ N , {displaystyle {dot {mathbf {X} }}=vmathbf {T} quad {mbox{et}}quad {ddot {mathbf {X} }}={dot {v} }mathbf {T} +v^{2}kappa mathbf {N} ,}

où

v = | X ̇ | = X ̇ ⋅ X ̇ . {displaystyle v=|{dot {mathbf {X} }}|={sqrt {{dot {mathbf {X} }}cdot {dot {mathbf {X} }}}}. }

Alors, le Produit scalaire de la vitesse avec l’accélération dans La deuxième loi de Newton prend la forme

Δ K = m ∫ t 1 t 2 v ̇ v d t = m 2 ∫ t 1 t 2 d d t v 2 d t = m 2 v 2 ( t 2 ) − m 2 v 2 ( t 1 ) , {displaystyle Delta K=mint _{t_{1}}^{t_{2}}{dot {v}}v,dt={frac {m}{2}}int _{ t_{1}}^{t_{2}}{frac {d}{dt}}v^{2},dt={frac {m}{2}}v^{2}(t_{2 })-{frac {m}{2}}v^{2}(t_{1}),}

où l’énergie cinétique de la particule est définie par la quantité scalaire,

K = m 2 v 2 = m 2 X ̇ ⋅ X ̇ . {displaystyle K={frac {m}{2}}v^{2}={frac {m}{2}}{dot {mathbf {X} }}cdot {dot {mathbf {X} }}.}

Le résultat est le principe travail-énergie pour la dynamique des particules,

W = Δ K . {displaystyle W=Delta K.}

Cette dérivation peut être généralisée à des systèmes de corps rigides arbitraires.

Se déplacer en ligne droite (déraper jusqu’à l’arrêt)

Considérons le cas d’un véhicule se déplaçant le long d’une trajectoire horizontale rectiligne sous l’action d’une force motrice et d’une pesanteur dont la somme est F . Les forces de contrainte entre le véhicule et la route définissent R , et on a

F + R = m X ̈ . {displaystyle mathbf {F} +mathbf {R} =m{ddot {mathbf {X} }}.}

Pour plus de commodité, supposons que la trajectoire soit le long de l’axe X, donc X = ( d , 0) et la vitesse est V = ( v , 0) , alors R ⋅ V = 0 , et F ⋅ V = F _x v , où F _x est la composante de F le long de l’axe X, donc

F x v = m v ̇ v . {displaystyle F_{x}v=m{point {v}}v.}

L’intégration des rendements des deux côtés

∫ t 1 t 2 F x v d t = m 2 v 2 ( t 2 ) − m 2 v 2 ( t 1 ) . {displaystyle int _{t_{1}}^{t_{2}}F_{x}vdt={frac {m}{2}}v^{2}(t_{2})-{frac {m}{2}}v^{2}(t_{1}).}

Si F _x est constant le long de la trajectoire, alors l’intégrale de la vitesse est la distance, donc

F x ( d ( t 2 ) − d ( t 1 ) ) = m 2 v 2 ( t 2 ) − m 2 v 2 ( t 1 ) . {displaystyle F_{x}(d(t_{2})-d(t_{1}))={frac {m}{2}}v^{2}(t_{2})-{frac {m}{2}}v^{2}(t_{1}).}

À titre d’exemple, considérons une voiture qui dérape jusqu’à un arrêt, où k est le coefficient de frottement et W est le poids de la voiture. Alors la force le long de la trajectoire est F _x = − kW . La vitesse v de la voiture peut être déterminée à partir de la longueur s du patin en utilisant le principe travail-énergie,

k W s = W 2 g v 2 , or v = 2 k s g . {displaystyle kWs={frac {W}{2g}}v^{2},quad {mbox{or}}quad v={sqrt {2ksg}}.}

Notez que cette formule utilise le fait que la masse du véhicule est m = W / g .

Coureur de gravité Lotus type 119B à la célébration du 60e Lotus. Championnat de course de gravité à Campos Novos, Santa Catarina, Brésil, 8 septembre 2010.

Descente en roue libre sur une route de montagne (course gravitationnelle)

Considérons le cas d’un véhicule qui démarre au repos et descend une route de montagne, le principe travail-énergie aide à calculer la distance minimale que le véhicule parcourt pour atteindre une vitesse V , disons 60 mph (88 fps). La résistance au roulement et la traînée aérodynamique ralentiront le véhicule, de sorte que la distance réelle sera plus grande que si ces forces sont négligées.

Soit la trajectoire du véhicule suivant la route X ( t ) qui est une courbe dans l’espace tridimensionnel. La force agissant sur le véhicule qui le pousse sur la route est la force de gravité constante F = (0, 0, W ) , tandis que la force de la route sur le véhicule est la force de contrainte R . La deuxième loi de Newton donne,

F + R = m X ̈ . {displaystyle mathbf {F} +mathbf {R} =m{ddot {mathbf {X} }}.}

Le Produit scalaire de cette équation avec la vitesse, V = ( v _x , v _y , v _z ) , donne

W v z = m V ̇ V , {displaystyle Wv_{z}=m{point {V}}V,}

où V est la grandeur de V . Les forces de contrainte entre le véhicule et la route s’annulent de cette équation car R ⋅ V = 0 , ce qui signifie qu’elles ne font aucun travail. Intégrez les deux côtés pour obtenir

∫ t 1 t 2 W v z d t = m 2 V 2 ( t 2 ) − m 2 V 2 ( t 1 ) . {displaystyle int _{t_{1}}^{t_{2}}Wv_{z}dt={frac {m}{2}}V^{2}(t_{2})-{frac {m}{2}}V^{2}(t_{1}).}

La force de poids W est constante le long de la trajectoire et l’intégrale de la vitesse verticale est la distance verticale, donc,

W Δ z = m 2 V 2 . {displaystyle WDelta z={frac {m}{2}}V^{2}.}

Rappelons que V( t ₁ )=0. Notez que ce résultat ne dépend pas de la forme de la route suivie par le véhicule.

Afin de déterminer la distance le long de la route, supposons que le déclassement est de 6 %, ce qui correspond à une route escarpée. Cela signifie que l’altitude diminue de 6 pieds pour chaque 100 pieds parcourus – pour des angles aussi petits, les fonctions sin et tan sont approximativement égales. Par conséquent, la distance s en pieds sur une pente de 6 % pour atteindre la vitesse V est d’au moins

s = Δ z 0.06 = 8.3 V 2 g , or s = 8.3 88 2 32.2 ≈ 2000 ft . {displaystyle s={frac {Delta z}{0.06}}=8.3{frac {V^{2}}{g}},quad {mbox{or}}quad s=8.3{ frac {88^{2}}{32.2}}approx 2000{mbox{ft}}.}

Cette formule utilise le fait que le poids du véhicule est W = mg .

Travail des forces agissant sur un corps rigide

Le travail des forces agissant en divers points sur un seul corps rigide peut être calculé à partir du travail d’une force et d’un couple résultants . Pour le voir, supposons que les forces F ₁ , F ₂ … F _n agissent sur les points X ₁ , X ₂ … X _n dans un corps rigide.

Les trajectoires de X _i , i = 1, …, n sont définies par le mouvement du corps rigide. Ce mouvement est donné par l’ensemble des rotations [ A ( t )] et la trajectoire d ( t ) d’un point de référence dans le corps. Soient les coordonnées x _i i = 1, …, n définissant ces points dans le repère M du corps rigide en mouvement , de sorte que les trajectoires tracées dans le repère fixe F sont données par

X i ( t ) = [ A ( t ) ] x i + d ( t ) i = 1 , … , n . {displaystyle mathbf {X} _{i}(t)=[A(t)]mathbf {x} _{i}+mathbf {d} (t)quad i=1,ldots ,n .}

La vitesse des points X _i le long de leurs trajectoires est

V i = ω → × ( X i − d ) + d ̇ , {displaystyle mathbf {V} _{i}={vec {omega}}times (mathbf {X} _{i}-mathbf {d})+{dot {mathbf {d} }},}

où ω est le vecteur de vitesse angulaire obtenu à partir de la matrice symétrique asymétrique

[ Ω ] = A ̇ A T , {displaystyle [Omega ]={dot {A}}A^{mathrm {T} },}

connue sous le nom de matrice de vitesse angulaire.

La petite quantité de travail par les forces sur les petits déplacements δ r _i peut être déterminée en approximant le déplacement par δ r = v δt donc

δ W = F 1 ⋅ V 1 δ t + F 2 ⋅ V 2 δ t + … + F n ⋅ V n δ t {displaystyle delta W=mathbf {F} _{1}cdot mathbf {V} _{1}delta t+mathbf {F} _{2}cdot mathbf {V} _{2} delta t+ldots +mathbf {F} _{n}cdot mathbf {V} _{n}delta t}

ou alors

δ W = ∑ i = 1 n F i ⋅ ( ω → × ( X i − d ) + d ̇ ) δ t . {displaystyle delta W=sum _{i=1}^{n}mathbf {F} _{i}cdot ({vec {omega }}times (mathbf {X} _{i }-mathbf {d} )+{point {mathbf {d} }})delta t.}

Cette formule peut être réécrite pour obtenir

δ W = ( ∑ i = 1 n F i ) ⋅ d ̇ δ t + ( ∑ i = 1 n ( X i − d ) × F i ) ⋅ ω → δ t = ( F ⋅ d ̇ + T ⋅ ω → ) δ t , {displaystyle delta W=left(sum _{i=1}^{n}mathbf {F} _{i}right)cdot {dot {mathbf {d} }}delta t+ left(sum _{i=1}^{n}left(mathbf {X} _{i}-mathbf {d} right)times mathbf {F} _{i}right) cdot {vec {omega }}delta t=left(mathbf {F} cdot {dot {mathbf {d} }}+mathbf {T} cdot {vec {omega } }droite)delta t,}

où F et T sont la force et le couple résultants appliqués au point de référence d du cadre mobile M dans le corps rigide.

Références

1. ^ NCERT (2020). “Livre de physique” (PDF) . ncert.nic.in . Récupéré le 24 novembre 2021 .
2. ^ ^{un bc Hugh} D. Young et Roger A. Freedman (2008). Physique universitaire (12e éd.). Addison-Wesley. p. 329.ISBN _ 978-0-321-50130-1.
3. ^ ^{un b} Krebs, Robert E. (2004). Expériences, inventions et découvertes révolutionnaires du Moyen Âge . Groupe d’édition Greenwood. p. 163. ISBN 978-0-313-32433-8. Récupéré le 21/05/2008 .
4. ^ Stephen, Donald; Lowell Cardwell (2001). Roues, horloges et fusées : une histoire de la technologie . États-Unis : WW Norton & Company. p. 85–87. ISBN 978-0-393-32175-3.
5. ^ Brouilleur, Max (1957). Notions de Force . Dover Publications, Inc. p. 167 ; note de bas de page 14. ISBN 0-486-40689-X.
6. ^ Coriolis, Gustave (1829). Calcul de l’effet des machines, ou considérations sur l’utilisation des moteurs et leur évaluation . Carilian-Goeury, Libraire (Paris).
7. ^ Dugas, R. (1955). Une histoire de la mécanique . Suisse : Éditions du Griffon.
8. ^ Smeaton, Jean (1759). “Enquête expérimentale sur les pouvoirs naturels de l’eau et du vent pour faire tourner des moulins et d’autres machines en fonction d’un mouvement circulaire” . Transactions philosophiques de la Royal Society . 51 : 105. doi : 10.1098/rstl.1759.0019 . S2CID 186213498 .
9. ^ “Unités avec des noms et des symboles spéciaux ; unités qui incorporent des noms et des symboles spéciaux” . Le système international d’unités (SI) (8e éd.). Bureau international des poids et mesures . 2006. Archivé de l’original le 20/04/2013 . Récupéré le 27/10/2012 .
10. ^ ^{un marcheur b} , Jerl; Halliday, David; Resnick, Robert (2011). Principes fondamentaux de la physique (9e éd.). Hoboken, New Jersey : Wiley. p. 154. ISBN 9780470469118.
11. ^ Goldstein, Herbert (2002). Mécanique classique (3e éd.). San Fransisco : Addison Wesley. ISBN 978-0-201-65702-9. OCLC 47056311 .
12. ^ Rogalski, Mircea S. (2018). Physique universitaire avancée (2e éd.). Boca Raton : Chapman et Hall/CRC. ISBN 9781351991988.
13. ^ ^{un b} “Les Conférences Feynman sur la Physique Vol. I Ch. 14 : Travail et Énergie Potentielle (conclusion)” . feynmanlectures.caltech.edu .
14. ^ Greenwood, Donald T. (1997). Dynamique classique . Mineola, NY : Publications de Douvres. ISBN 9780486138794.
15. ^ ^{a b} Resnick, Robert, Halliday, David (1966), Physics , Section 1–3 (Vol I et II, édition combinée), Wiley International Edition, Library of Congress Catalog Card No. 66-11527
16. ^ JR Taylor, Mécanique classique, Livres scientifiques universitaires, 2005.
17. ^ Andrew Pytel; Jaan Kiusalaas (2010). Engineering Mechanics: Dynamics – SI Version, Volume 2 (3e éd.). Cengage Apprentissage. p. 654.ISBN _ 9780495295631.
18. ^ Paul, Burton (1979). Cinématique et dynamique des machines planaires . Prentice Hall. ISBN 978-0-13-516062-6.
19. ^ Whittaker, ET (1904). Un traité sur la dynamique analytique des particules et des corps rigides . La presse de l’Universite de Cambridge.
20. ^ “Principe travail-énergie” . wwu.edu . Archivé de l’original le 2012-05-30 . Récupéré le 06/08/2012 .

Bibliographie

• Serway, Raymond A.; En ligneJewett, John W. (2004). Physique pour les scientifiques et les ingénieurs (6e éd.). Brooks/Cole. ISBN 0-534-40842-7.
• Tipler, Paul (1991). Physique pour les scientifiques et les ingénieurs: mécanique (3e éd., version étendue éd.). WH Freeman. ISBN 0-87901-432-6.

Liens externes

• Principe travail-énergie