Potentiel électrique

Le potentiel électrique (également appelé potentiel de champ électrique , chute de potentiel, potentiel électrostatique ) est défini comme la quantité d’ énergie de travail nécessaire pour déplacer une unité de charge électrique d’un point de référence à un point spécifique dans un champ électrique. Plus précisément, c’est l’énergie par unité de charge pour une charge d’essaiqui est si faible que la perturbation du champ considéré est négligeable. De plus, le mouvement à travers le champ est supposé se dérouler avec une accélération négligeable, afin d’éviter que la charge d’essai n’acquière de l’énergie cinétique ou ne produise un rayonnement. Par définition, le potentiel électrique au point de référence est de zéro unité. Typiquement, le point de référence est la terre ou un point à l’ infini , bien que n’importe quel point puisse être utilisé.

Potentiel électrique
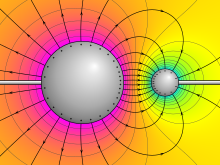Potentiel électrique autour de deux sphères conductrices de charges opposées. Le violet représente le potentiel le plus élevé, le zéro jaune et le cyan le potentiel le plus bas. Les lignes de champ électrique sont représentées partant perpendiculairement à la surface de chaque sphère.
Symboles communs	V , φ
Unité SI	volt
Autres unités	statvolt
En unités de base SI	V = kg⋅m ² ⋅s ⁻³ ⋅A ⁻¹
Vaste ?	oui
Dimension	M L ² T ^-3 je ^-1

En électrostatique classique , le champ électrostatique est une quantité vectorielle exprimée par le gradient du potentiel électrostatique, qui est une quantité scalaire notée V ou parfois φ , ^[1] égale à l’ énergie potentielle électrique de toute particule chargée à n’importe quel endroit (mesurée en joules ) divisée par la charge de cette particule (mesurée en coulombs ). En divisant la charge sur la particule, on obtient un quotient qui est une propriété du champ électrique lui-même. En bref, un potentiel électrique est l’ énergie potentielle électriquepar unité de charge.

Cette valeur peut être calculée dans un champ électrique statique (invariant dans le temps) ou dynamique (variant dans le temps) à un instant précis en unités de joules par coulomb ( J⋅C ⁻¹ ) ou de volts ( V ). Le potentiel électrique à l’infini est supposé nul.

En Électrodynamique , lorsque des champs variant dans le temps sont présents, le champ électrique ne peut pas être exprimé uniquement en termes de potentiel scalaire . Au lieu de cela, le champ électrique peut être exprimé à la fois en termes de potentiel électrique scalaire et de potentiel vectoriel magnétique . ^[2] Le potentiel électrique et le potentiel vectoriel magnétique forment ensemble un quadrivecteur , de sorte que les deux types de potentiel sont mélangés sous les transformations de Lorentz .

Pratiquement, le potentiel électrique est toujours une fonction continue dans l’espace. Sinon, sa dérivée spatiale donnera un champ d’une magnitude infinie, ce qui est pratiquement impossible. Même une charge ponctuelle idéalisée a un potentiel de 1 ⁄ r , qui est continu partout sauf à l’origine. Le champ électrique n’est pas continu à travers une charge de surface idéalisée , mais il n’est infini en aucun point. Par conséquent, le potentiel électrique est continu sur une charge de surface idéalisée. Une charge linéaire idéalisée a un potentiel ln( r ) , qui est continu partout sauf sur la charge linéaire.

Introduction

La mécanique classique explore des concepts tels que la force , l’énergie et le potentiel . ^[3] La force et l’énergie potentielle sont directement liées. Une force nette agissant sur n’importe quel objet le fera accélérer . Lorsqu’un objet se déplace dans la direction de la force qui agit, son énergie potentielle diminue. Par exemple, l’ Énergie potentielle gravitationnelle d’un boulet de canon au sommet d’une colline est plus grande qu’à la base de la colline. Au fur et à mesure qu’il roule vers le bas, son énergie potentielle diminue et est traduite en énergie cinétique de mouvement .

Il est possible de définir le potentiel de certains champs de force de sorte que l’énergie potentielle d’un objet dans ce champ ne dépende que de la position de l’objet par rapport au champ. Deux de ces champs de force sont le champ gravitationnel et un champ électrique (en l’absence de champs magnétiques variant dans le temps). Ces champs doivent affecter les objets en raison des propriétés intrinsèques de l’objet (par exemple, masse ou charge) et de la position de l’objet.

Les objets peuvent posséder une propriété connue sous le nom de charge électrique . Puisqu’un champ électrique exerce une force sur des objets chargés, si l’objet chargé a une charge positive, la force sera dans la direction du vecteur champ électrique à ce point; si la charge est négative, la force sera dans la direction opposée.

L’amplitude de la force est donnée par la quantité de charge multipliée par l’amplitude du vecteur champ électrique :

F = q E {displaystyle F=qE} .

Électrostatique

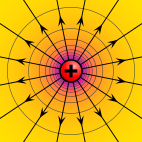
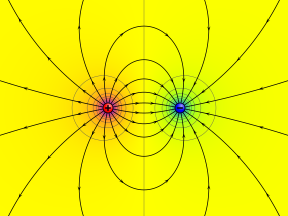
Potentiel électrique de charges ponctuelles positives et négatives séparées représentées par une gamme de couleurs allant du magenta (+), au jaune (0), au cyan (-). Les contours circulaires sont des lignes équipotentielles. Les lignes de champ électrique quittent la charge positive et entrent dans la charge négative. Potentiel électrique au voisinage de deux charges ponctuelles opposées.

Le potentiel électrique en un point r dans un champ électrique statique E est donné par l’ intégrale de ligne

V E = − ∫ C E ⋅ d l {displaystyle V_{mathbf {E} }=-int _{mathcal {C}}mathbf {E} cdot mathrm {d} {boldsymbol {ell }},} ${displaystyle V_{mathbf {E} }=-int _{mathcal {C}}mathbf {E} cdot mathrm {d} {boldsymbol {ell }},}$ ${displaystyle V_{mathbf {E} }=-int _{mathcal {C}}mathbf {E} cdot mathrm {d} {boldsymbol {ell }},}$

où C est un chemin arbitraire d’un point de référence fixe à r {textstyle mathbf {r}} {textstyle mathbf {r} } . En électrostatique, l’ Équation de Maxwell-Faraday révèle que la boucle ∇ × E {textstyle nabla times mathbf {E} } est nul, ce qui rend le champ électrique conservatif . Ainsi, l’intégrale de ligne ci-dessus ne dépend pas du chemin spécifique C choisi mais uniquement de ses extrémités, ce qui rend V E {textstyle V_{mathbf {E} }} ${textstyle V_{mathbf {E} }}$ ${textstyle V_{mathbf {E} }}$ bien défini partout. Le théorème du gradient permet alors d’écrire :

E = − ∇ V E {displaystyle mathbf {E} =-mathbf {nabla} V_{mathbf {E} },} ${displaystyle mathbf {E} =-mathbf {nabla } V_{mathbf {E} },}$ ${displaystyle mathbf {E} =-mathbf {nabla } V_{mathbf {E} },}$

Cela indique que le champ électrique pointe “en descente” vers des tensions plus basses. Par la loi de Gauss , le potentiel peut également être trouvé pour satisfaire l’équation de Poisson :

∇ ⋅ E = ∇ ⋅ ( − ∇ V E ) = − ∇ 2 V E = ρ / ε 0 {displaystyle mathbf {nabla} cdot mathbf {E} =mathbf {nabla} cdot left(-mathbf {nabla} V_{mathbf {E}}right)=-nabla ^{2}V_{mathbf {E} }=rho /varepsilon _{0}} ${displaystyle mathbf {nabla } cdot mathbf {E} =mathbf {nabla } cdot left(-mathbf {nabla } V_{mathbf {E} }right)=-nabla ^{2}V_{mathbf {E} }=rho /varepsilon _{0}}$ ${displaystyle mathbf {nabla } cdot mathbf {E} =mathbf {nabla } cdot left(-mathbf {nabla } V_{mathbf {E} }right)=-nabla ^{2}V_{mathbf {E} }=rho /varepsilon _{0}}$

où ρ est la densité de charge totale et ∇ · désigne la divergence .

Le concept de potentiel électrique est étroitement lié à celui d’énergie potentielle . Une charge d’essai q a une énergie potentielle électrique U _E donnée par

U E = q V . {displaystyle U_{mathbf {E} }=q,V.,} $U_ mathbf{E} = q,V. ,$ $U_ mathbf{E} = q,V. ,$

L’énergie potentielle et donc aussi le potentiel électrique, n’est définie qu’à une constante additive près : il faut choisir arbitrairement une position où l’énergie potentielle et le potentiel électrique sont nuls.

Ces équations ne peuvent pas être utilisées si la boucle ∇ × E ≠ 0 {textstyle nabla times mathbf {E} neq mathbf {0} } , c’est-à-dire dans le cas d’un champ électrique non conservateur (causé par un champ magnétique variable ; voir les équations de Maxwell ). La généralisation du potentiel électrique à ce cas est décrite dans la section § Généralisation à l’Électrodynamique .

Potentiel électrique dû à une charge ponctuelle

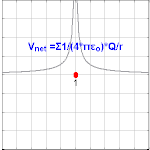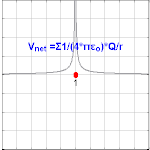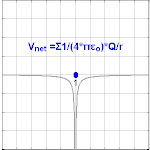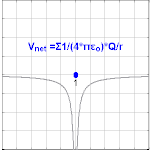
Le potentiel électrique créé par une charge Q est V = Q /(4πε ₀ r ). Différentes valeurs de Q donneront différentes valeurs de potentiel électrique V (indiqué dans l’image).

On observe que le potentiel électrique issu d’une charge ponctuelle Q , à une distance r de la charge est

V E = 1 4 π ε 0 Q r , {displaystyle V_{mathbf {E} }={frac {1}{4pi varepsilon _{0}}}{frac {Q}{r}},} ${displaystyle V_{mathbf {E} }={frac {1}{4pi varepsilon _{0}}}{frac {Q}{r}},}$ ${displaystyle V_{mathbf {E} }={frac {1}{4pi varepsilon _{0}}}{frac {Q}{r}},}$ où ε ₀ est la Permittivité du vide . ^[4] V _E est connu sous le nom de potentiel de Coulomb .

Le potentiel électrique d’un système de charges ponctuelles est égal à la somme des potentiels individuels des charges ponctuelles. Ce fait simplifie considérablement les calculs, car l’addition de champs potentiels (scalaires) est beaucoup plus facile que l’addition de champs électriques (vecteurs). Plus précisément, le potentiel d’un ensemble de charges ponctuelles discrètes q _i aux points r _i devient

V E ( r ) = 1 4 π ε 0 ∑ i q i | r − r i | , {displaystyle V_{mathbf {E} }(mathbf {r} )={frac {1}{4pi varepsilon _{0}}}sum _{i}{frac {q_{i }}{|mathbf {r} -mathbf {r} _{i}|}},} ${displaystyle V_{mathbf {E} }(mathbf {r} )={frac {1}{4pi varepsilon _{0}}}sum _{i}{frac {q_{i}}{|mathbf {r} -mathbf {r} _{i}|}},}$ ${displaystyle V_{mathbf {E} }(mathbf {r} )={frac {1}{4pi varepsilon _{0}}}sum _{i}{frac {q_{i}}{|mathbf {r} -mathbf {r} _{i}|}},}$ où

r {displaystyle mathbf {r}} est un point auquel le potentiel est évalué.
r i {displaystyle mathbf {r} _{i}} ${displaystyle mathbf {r} _{i}}$ ${displaystyle mathbf {r} _{i}}$ est un point où il y a une charge non nulle.
q i {displaystyle q_{i}} ${displaystyle q_{i}}$ ${displaystyle q_{i}}$ est la charge au point r i {displaystyle mathbf {r} _{i}} ${displaystyle mathbf {r} _{i}}$ ${displaystyle mathbf {r} _{i}}$ .

et le potentiel d’une distribution de charge continue ρ ( r ) devient

Learn more.

Accélération

Jul 6, 2022

Résistivité et conductivité électriques

Jun 29, 2022

Salle de musique Franklin

Jun 23, 2022

Dipôle

Jun 22, 2022

V E ( r ) = 1 4 π ε 0 ∫ R ρ ( r ′ ) | r − r ′ | d 3 r ′ . {displaystyle V_{mathbf {E} }(mathbf {r} )={frac {1}{4pi varepsilon _{0}}}int _{R}{frac {rho ( mathbf {r} ‘)}{|mathbf {r} -mathbf {r} ‘|}}d^{3}r’.} ${displaystyle V_{mathbf {E} }(mathbf {r} )={frac {1}{4pi varepsilon _{0}}}int _{R}{frac {rho (mathbf {r} ')}{|mathbf {r} -mathbf {r} '|}}d^{3}r'.}$ ${displaystyle V_{mathbf {E} }(mathbf {r} )={frac {1}{4pi varepsilon _{0}}}int _{R}{frac {rho (mathbf {r} ')}{|mathbf {r} -mathbf {r} '|}}d^{3}r'.}$ Où

r {displaystyle mathbf {r}} est un point auquel le potentiel est évalué.
R {displaystyle R} est une région contenant tous les points où la densité de charge est non nulle.
r ′ {displaystyle mathbf {r} ‘} est un point à l’intérieur R {displaystyle R} .
ρ ( r ′ ) {displaystyle rho (mathbf {r} ‘)} est la densité de charge au point r ′ {displaystyle mathbf {r} ‘} .

Les équations données ci-dessus pour le potentiel électrique (et toutes les équations utilisées ici) sont dans les formes requises par les Unités SI . Dans certains autres systèmes d’unités (moins courants), tels que CGS-Gaussian , bon nombre de ces équations seraient modifiées.

Généralisation à l’Électrodynamique

Lorsque des champs magnétiques variant dans le temps sont présents (ce qui est vrai chaque fois qu’il y a des champs électriques variant dans le temps et vice versa), il n’est pas possible de décrire le champ électrique simplement en termes de potentiel scalaire V car le champ électrique n’est plus conservatif : ∫ C E ⋅ d l {displaystyle textstyle int _{C}mathbf {E} cdot mathrm {d} {boldsymbol {ell }}} $textstyleint_C mathbf{E}cdot mathrm{d}boldsymbol{ell}$ dépend du chemin car ∇ × E ≠ 0 {displaystyle mathbf {nabla } times mathbf {E} neq mathbf {0} } mathbf{nabla} times mathbf{E} neq mathbf{0} (dû à l’ Équation de Maxwell-Faraday ).

Au lieu de cela, on peut toujours définir un potentiel scalaire en incluant également le potentiel vectoriel magnétique A . En particulier, A est défini pour satisfaire :

B = ∇ × A {displaystyle mathbf {B} =mathbf {nabla } times mathbf {A} }

où B est le champ magnétique . Par le Théorème fondamental du calcul vectoriel , un tel A peut toujours être trouvé, puisque la divergence du champ magnétique est toujours nulle en raison de l’absence de monopôles magnétiques . Maintenant, la quantité

F = E + ∂ A ∂ t {displaystyle mathbf {F} =mathbf {E} +{frac {partial mathbf {A} }{partial t}}} $mathbf{F} = mathbf{E} + frac{partialmathbf{A}}{partial t}$ $mathbf{F} = mathbf{E} + frac{partialmathbf{A}}{partial t}$

est un champ conservatif, puisque la boucle de E {displaystyle mathbf {E}} est annulée par la boucle de ∂ A ∂ t {displaystyle {frac {partial mathbf {A} }{partial t}}} ${displaystyle {frac {partial mathbf {A} }{partial t}}}$ ${displaystyle {frac {partial mathbf {A} }{partial t}}}$ selon l’ Équation de Maxwell-Faraday . On peut donc écrire

E = − ∇ V − ∂ A ∂ t {displaystyle mathbf {E} =-mathbf {nabla} V-{frac {partial mathbf {A} }{partial t}}} ${displaystyle mathbf {E} =-mathbf {nabla } V-{frac {partial mathbf {A} }{partial t}}}$ ${displaystyle mathbf {E} =-mathbf {nabla } V-{frac {partial mathbf {A} }{partial t}}}$

où V est le potentiel scalaire défini par le champ conservateur F .

Le potentiel électrostatique est simplement le cas particulier de cette définition où A est invariant dans le temps. En revanche, pour les champs variables dans le temps,

− ∫ a b E ⋅ d l ≠ V ( b ) − V ( a ) {displaystyle -int _{a}^{b}mathbf {E} cdot mathrm {d} {boldsymbol {ell }}neq V_{(b)}-V_{(a)}} ${displaystyle -int _{a}^{b}mathbf {E} cdot mathrm {d} {boldsymbol {ell }}neq V_{(b)}-V_{(a)}}$ ${displaystyle -int _{a}^{b}mathbf {E} cdot mathrm {d} {boldsymbol {ell }}neq V_{(b)}-V_{(a)}}$

contrairement à l’électrostatique.

Liberté de jauge

Le potentiel électrostatique pourrait avoir n’importe quelle constante ajoutée sans affecter le champ électrique. En Électrodynamique, le potentiel électrique a une infinité de degrés de liberté. Pour tout champ scalaire (éventuellement variable dans le temps ou dans l’espace) ψ {displaystylepsi} psi , nous pouvons effectuer la Transformation de jauge suivante pour trouver un nouvel ensemble de potentiels produisant exactement les mêmes champs électriques et magnétiques : ^[5]

V ′ = V − ∂ ψ ∂ t {displaystyle V^{prime}=V-{frac {partial psi }{partial t}}} ${displaystyle V^{prime }=V-{frac {partial psi }{partial t}}}$ ${displaystyle V^{prime }=V-{frac {partial psi }{partial t}}}$ A ′ = A + ∇ ψ {displaystyle mathbf {A} ^{prime}=mathbf {A} +nabla psi} ${displaystyle mathbf {A} ^{prime }=mathbf {A} +nabla psi }$ ${displaystyle mathbf {A} ^{prime }=mathbf {A} +nabla psi }$

Étant donné différents choix de jauge, le potentiel électrique pourrait avoir des propriétés très différentes. Dans la jauge de Coulomb , le potentiel électrique est donné par l’équation de Poisson

∇ 2 V = − ρ ε 0 {displaystyle nabla ^{2}V=-{frac {rho }{varepsilon _{0}}}} ${displaystyle nabla ^{2}V=-{frac {rho }{varepsilon _{0}}}}$ ${displaystyle nabla ^{2}V=-{frac {rho }{varepsilon _{0}}}}$

comme en électrostatique. Or, dans la jauge de Lorenz , le potentiel électrique est un potentiel retardé qui se propage à la vitesse de la lumière, et est la solution d’une équation d’onde inhomogène :

∇ 2 V − 1 c 2 ∂ 2 V ∂ t 2 = − ρ ε 0 {displaystyle nabla ^{2}V-{frac {1}{c^{2}}}{frac {partial ^{2}V}{partial t^{2}}}=-{ frac {rho }{varepsilon _{0}}}} ${displaystyle nabla ^{2}V-{frac {1}{c^{2}}}{frac {partial ^{2}V}{partial t^{2}}}=-{frac {rho }{varepsilon _{0}}}}$ ${displaystyle nabla ^{2}V-{frac {1}{c^{2}}}{frac {partial ^{2}V}{partial t^{2}}}=-{frac {rho }{varepsilon _{0}}}}$

Unités

L’ Unité SI dérivée du potentiel électrique est le volt (en l’honneur d’ Alessandro Volta ), c’est pourquoi une différence de potentiel électrique entre deux points est appelée tension . Les unités plus anciennes sont rarement utilisées aujourd’hui. Les variantes du système d’unités centimètre-gramme-seconde comprenaient un certain nombre d’unités différentes pour le potentiel électrique, y compris l ‘ abvolt et le statvolt .

Potentiel galvani versus potentiel électrochimique

À l’intérieur des métaux (et d’autres solides et liquides), l’énergie d’un électron est affectée non seulement par le potentiel électrique, mais aussi par l’environnement atomique spécifique dans lequel il se trouve. Lorsqu’un voltmètre est connecté entre deux types de métaux différents, il mesure la différence de potentiel corrigée pour les différents environnements atomiques. ^[6] La quantité mesurée par un voltmètre est appelée potentiel électrochimique ou niveau de fermi , tandis que le potentiel électrique pur non ajusté V est parfois appelé potentiel de Galvani φ {displaystylephi } phi . Les termes “tension” et “potentiel électrique” sont un peu ambigus, mais en pratique, ils peuvent se référer à l’un ou l’ autre dans des contextes différents.

Voir également

Potentiel d’électrode absolu
Potentiel électrochimique
Le potentiel de l’électrode

Références

^ Goldstein, Herbert (juin 1959). Mécanique classique . États-Unis : Addison-Wesley. p. 383.ISBN _ 0201025108.
^ Griffiths, David J. (1999). Introduction à l’Électrodynamique . Salle Pearson Prentice. p. 416–417. ISBN 978-81-203-1601-0.
^ Jeune, Hugh A.; Freedman, Roger D. (2012). Sears and Zemansky’s University Physics with Modern Physics (13e éd.). Boston : Addison-Wesley. p. 754.
^ “Valeur CODATA 2018 : permittivité électrique du vide” . La référence NIST sur les constantes, les unités et l’incertitude . NIST . 20 mai 2019 . Récupéré le 20/05/2019 .
^ Griffiths, David J. (1999). Introduction à l’Électrodynamique (3e éd.). Prentice Hall. p. 420.ISBN _ 013805326X.
^ Bagotskii VS (2006). Fondamentaux de l’électrochimie . p. 22. ISBN 978-0-471-70058-6.

Lectures complémentaires

Wikimedia Commons a des médias liés au potentiel électrique .

Politzer P, Truhlar DG (1981). Applications chimiques des potentiels électrostatiques atomiques et moléculaires : réactivité, structure, diffusion et énergétique des systèmes organiques, inorganiques et biologiques . Boston, MA : Springer États-Unis. ISBN 978-1-4757-9634-6.
Sen K, Murray JS (1996). Potentiels électrostatiques moléculaires : concepts et applications . Amsterdam : Elsevier. ISBN 978-0-444-82353-3.
Griffiths DJ (1999). Introduction à l’Électrodynamique (3e éd.). Prentice Hall. ISBN 0-13-805326-X.
Jackson JD (1999). Électrodynamique classique (3e éd.). États-Unis : John Wiley & Sons, Inc. ISBN 978-0-471-30932-1.
En ligneWangsness RK (1986). Champs électromagnétiques (2e édition, révisée, illustrée). Wiley. ISBN 978-0-471-81186-2.