Pi

Le nombre π ( / p aɪ / ; épelé comme ” pi ” ) est une constante mathématique qui est le rapport de la circonférence d’ un cercle à son diamètre , approximativement égal à 3,14159. Le nombre π apparaît dans de nombreuses formules en mathématiques et en physique . C’est un nombre irrationnel , ce qui signifie qu’il ne peut pas être exprimé exactement comme un rapport de deux nombres entiers, bien que des fractions telles que 22/7 soient couramment utilisées pour l’approximer . En conséquence, sonla représentation décimale ne se termine jamais, ni n’entre dans un motif répétitif permanent . C’est un nombre transcendantal , ce qui signifie qu’il ne peut pas être une solution d’une équation impliquant uniquement des sommes, des produits, des puissances et des nombres entiers. La transcendance de π implique qu’il est impossible de résoudre l’ancien défi de la quadrature du cercle avec un compas et une règle . Les chiffres décimaux de π semblent être distribués au hasard , ^[a] mais aucune preuve de cette conjecture n’a été trouvée.

Pendant des milliers d’années, les mathématiciens ont tenté d’étendre leur compréhension de π , parfois en calculant sa valeur avec un haut degré de précision. Les civilisations anciennes, y compris les Égyptiens et les Babyloniens , nécessitaient des approximations assez précises de π pour des calculs pratiques. Vers 250 avant JC, le mathématicien grec Archimède a créé un algorithme pour approximer π avec une précision arbitraire. Au 5ème siècle après JC, les mathématiciens chinois ont approché π à sept chiffres, tandis que les mathématiciens indiensfait une approximation à cinq chiffres, à la fois en utilisant des techniques géométriques. La première formule de calcul pour π , basée sur des séries infinies , a été découverte un millénaire plus tard. ^{[1] [2]} La première utilisation connue de la lettre grecque π pour représenter le rapport de la circonférence d’un cercle à son diamètre était par le mathématicien gallois William Jones en 1706. ^[3]

L’invention du calcul a rapidement conduit au calcul de centaines de chiffres de π , suffisamment pour tous les calculs scientifiques pratiques. Néanmoins, aux 20e et 21e siècles, les mathématiciens et les informaticiens ont poursuivi de nouvelles approches qui, combinées à une puissance de calcul croissante, ont étendu la représentation décimale de π à plusieurs billions de chiffres. ^{[4] [5]} Ces calculs sont motivés par le développement d’algorithmes efficaces pour calculer des séries numériques, ainsi que par la quête humaine pour battre des records. ^{[6] [7]} Les calculs étendus impliqués ont été aussi utilisés pour tester des supercalculateurs .

Parce que sa définition se rapporte au cercle, π se retrouve dans de nombreuses formules en trigonométrie et en géométrie , notamment celles concernant les cercles, les ellipses et les sphères. On le trouve également dans des formules d’autres sujets scientifiques, tels que la cosmologie , les fractales , la thermodynamique , la mécanique et l’électromagnétisme . Dans l’ analyse mathématique moderne , il est souvent plutôt défini sans aucune référence à la géométrie ; par conséquent, il apparaît également dans des domaines ayant peu à voir avec la géométrie, tels que la théorie des nombres et les statistiques . L’ubiquité de πen fait l’une des constantes mathématiques les plus connues à l’intérieur et à l’extérieur de la science. Plusieurs livres consacrés à π ont été publiés et les calculs records des chiffres de π font souvent la une des journaux.

Fondamentaux

Nom

Le symbole utilisé par les mathématiciens pour représenter le rapport de la circonférence d’un cercle à son diamètre est la lettre grecque minuscule π , parfois épelée pi, et dérivée de la première lettre du mot grec perimetros, qui signifie circonférence. ^[8] En anglais, π se prononce comme “pie” ( / p aɪ / PY ). ^[9] En usage mathématique, la lettre minuscule π se distingue de son homologue capitalisé et agrandi Π , qui désigne un produit d’une séquence , analogue à la façon dont Σdésigne la sommation .

Le choix du symbole π est discuté dans la section Adoption du symbole π .

Définition

La circonférence d’un cercle est un peu plus de trois fois plus longue que son diamètre. Le rapport exact est appelé π .

π est communément défini comme le rapport de la circonférence C d’un cercle à son diamètre d : ^{[10] [11]}

π = C d . {displaystyle pi ={frac {C}{d}}.}

Le rapport C / d est constant, quelle que soit la taille du cercle. Par exemple, si un cercle a deux fois le diamètre d’un autre cercle, il aura également deux fois la circonférence, en préservant le rapport C / d . Cette définition de π fait implicitement appel à la géométrie plate (euclidienne) ; bien que la notion de cercle puisse être étendue à toute géométrie courbe (non euclidienne) , ces nouveaux cercles ne satisferont plus la formule π = C / d . ^[dix]

Ici, la circonférence d’un cercle est la longueur de l’arc autour du périmètre du cercle, une quantité qui peut être formellement définie indépendamment de la géométrie à l’aide de limites – un concept en calcul . ^[12] Par exemple, on peut calculer directement la longueur de l’arc de la moitié supérieure du cercle unité, donnée en coordonnées cartésiennes par l’équation x ² + y ² = 1 , comme l’ intégrale : ^[13]

π = ∫ − 1 1 d x 1 − x 2 . {displaystyle pi =int _{-1}^{1}{frac {dx}{sqrt {1-x^{2}}}}.}

Une telle intégrale a été adoptée comme définition de π par Karl Weierstrass , qui l’a définie directement comme une intégrale en 1841. ^[b]

L’intégration n’est plus couramment utilisée dans une première définition analytique car, comme l’ explique Remmert 2012 , le calcul différentiel précède généralement le calcul intégral dans le programme universitaire, il est donc souhaitable d’avoir une définition de π qui ne repose pas sur ce dernier. Une telle définition, due à Richard Baltzer ^[14] et popularisée par Edmund Landau , ^[15] est la suivante : π est deux fois le plus petit nombre positif auquel la fonction cosinus est égale à 0. ^{[10] [13] [16]} π est également le plus petit nombre positif auquel le sinusfonction est égale à zéro, et la différence entre les zéros consécutifs de la fonction sinus. Le cosinus et le sinus peuvent être définis indépendamment de la géométrie comme une série de puissances , ^[17] ou comme la solution d’une équation différentielle . ^[16]

Dans un esprit similaire, π peut être défini en utilisant les propriétés de l’ exponentielle complexe , exp z , d’une variable complexe z . Comme le cosinus, l’exponentielle complexe peut être définie de plusieurs façons. L’ensemble des nombres complexes pour lesquels exp z est égal à un est alors une progression arithmétique (imaginaire) de la forme :

{ … , − 2 π i , 0 , 2 π i , 4 π i , … } = { 2 π k i ∣ k ∈ Z } {displaystyle {dots ,-2pi i,0,2pi i,4pi i,dots }={2pi kimid kin mathbb {Z} }}

et il existe un unique nombre réel positif π avec cette propriété. ^{[13] [18]}

Une variante de la même idée, utilisant des concepts mathématiques sophistiqués de topologie et d’ algèbre , est le théorème suivant : ^[19] il existe un isomorphisme continu unique ( jusqu’à l’ automorphisme ) du groupe R / Z des nombres réels sous l’addition modulo des entiers (le groupe du cercle ), sur le groupe multiplicatif des nombres complexes de valeur absolue un. Le nombre π est alors défini comme la moitié de la grandeur de la dérivée de cet homomorphisme. ^[20]

Irrationalité et normalité

π est un nombre irrationnel , ce qui signifie qu’il ne peut pas être écrit comme le rapport de deux nombres entiers . ^[11] Fractions telles que22/7et 355/113sont couramment utilisés pour approximer π , mais aucune fraction commune (rapport de nombres entiers) ne peut être sa valeur exacte. ^[21] Parce que π est irrationnel, il a un nombre infini de chiffres dans sa représentation décimale et ne s’installe pas dans un motif de chiffres se répétant à l’infini. Il existe plusieurs preuves que π est irrationnel ; ils nécessitent généralement du calcul et reposent sur la technique de la reductio ad absurdum . Le degré auquel π peut être approximé par des nombres rationnels (appelé la mesure d’irrationalité) n’est pas connue avec précision ; des estimations ont établi que la mesure d’irrationalité est plus grande que la mesure de e ou ln 2 mais plus petite que la mesure des nombres de Liouville . ^[22]

Les chiffres de π n’ont pas de motif apparent et ont passé avec succès les tests d’ aléa statistique , y compris les tests de normalité ; un nombre de longueur infinie est dit normal lorsque toutes les séquences possibles de chiffres (de n’importe quelle longueur donnée) apparaissent également souvent. ^[23] La conjecture que π est normal n’a pas été prouvée ou réfutée. ^[23]

Depuis l’avènement des ordinateurs, un grand nombre de chiffres de π sont disponibles pour effectuer des analyses statistiques. Yasumasa Kanada a effectué des analyses statistiques détaillées sur les chiffres décimaux de π et les a trouvés compatibles avec la normalité ; par exemple, les fréquences des dix chiffres de 0 à 9 ont été soumises à des tests de signification statistique et aucune preuve d’un modèle n’a été trouvée. ^[24] Toute séquence aléatoire de chiffres contient des sous-séquences arbitrairement longues qui semblent non aléatoires, par le théorème du singe infini . Ainsi, parce que la suite de π‘s chiffres passent des tests statistiques pour le caractère aléatoire, il contient certaines séquences de chiffres qui peuvent apparaître non aléatoires, comme une séquence de six 9 consécutifs qui commence à la 762e décimale de la représentation décimale de π . ^[25] Ceci est aussi appelé le “point Feynman” dans le folklore mathématique , d’après Richard Feynman , bien qu’aucun lien avec Feynman ne soit connu.

Transcendance

Parce que π est un nombre transcendantal , la quadrature du cercle n’est pas possible en un nombre fini d’étapes en utilisant les outils classiques du compas et de la règle .

En plus d’être irrationnel, π est aussi un nombre transcendantal , ^[11] ce qui signifie qu’il n’est la solution d’aucune équation polynomiale non constante à coefficients rationnels , telle que x5 ^_/120− x3 ^_/6+ x = 0 . ^{[26] [e]}

La transcendance de π a deux conséquences importantes : premièrement, π ne peut pas être exprimé en utilisant une combinaison finie de nombres rationnels et de racines carrées ou n -ièmes racines (telles que ³ √ 31 ou √ 10 ). Deuxièmement, puisqu’aucun nombre transcendantal ne peut être construit avec un compas et une règle , il n’est pas possible de « faire la quadrature du cercle ». En d’autres termes, il est impossible de construire, en utilisant uniquement le compas et la règle, un carré dont l’aire est exactement égale à l’aire d’un cercle donné. ^[27] La ​​quadrature d’un cercle était l’un des problèmes de géométrie importants de lal’antiquité classique . ^[28] Les mathématiciens amateurs des temps modernes ont parfois tenté de quadriller le cercle et de revendiquer le succès, malgré le fait que c’est mathématiquement impossible. ^[29]

Fractions continues

Comme tous les nombres irrationnels, π ne peut pas être représenté comme une fraction commune (également connue sous le nom de fraction simple ou vulgaire ), par la définition même du nombre irrationnel (c’est-à-dire, pas un nombre rationnel). Mais tout nombre irrationnel, y compris π , peut être représenté par une suite infinie de fractions imbriquées, appelée fraction continue :

π = 3 + 1 7 + 1 15 + 1 1 + 1 292 + 1 1 + 1 1 + 1 1 + ⋱ {displaystyle pi =3+textstyle {cfrac {1}{7+textstyle {cfrac {1}{15+textstyle {cfrac {1}{1+textstyle {cfrac {1}{292+textstyle {cfrac {1}{1+textstyle {cfrac {1}{1+textstyle {cfrac {1}{1+ddots }}}}}}}}}}}}}}}

La troncation de la fraction continue en tout point donne une approximation rationnelle de π ; les quatre premiers d’entre eux sont 3, 22/7, 333/106 et 355/113. Ces nombres sont parmi les approximations historiques les plus connues et les plus largement utilisées de la constante. Chaque approximation ainsi générée est une meilleure approximation rationnelle ; c’est-à-dire que chacune est plus proche de π que toute autre fraction avec le même ou un plus petit dénominateur. ^[30] Parce que π est connu pour être transcendantal, il n’est par définition pas algébrique et ne peut donc pas être un irrationnel quadratique . Par conséquent, π ne peut pas avoir de fraction continue périodique . Bien que la fraction continue simple pourπ (illustré ci-dessus) ne présente pas non plus d’autre modèle évident, ^[31] les mathématiciens ont découvert plusieurs fractions continues généralisées qui le font, telles que : ^[32]

π = 4 1 + 1 2 2 + 3 2 2 + 5 2 2 + 7 2 2 + 9 2 2 + ⋱ = 3 + 1 2 6 + 3 2 6 + 5 2 6 + 7 2 6 + 9 2 6 + ⋱ = 4 1 + 1 2 3 + 2 2 5 + 3 2 7 + 4 2 9 + ⋱ {displaystyle {begin{aligned}pi &=textstyle {cfrac {4}{1+textstyle {cfrac {1^{2}}{2+textstyle {cfrac {3^{2} }{2+textstyle {cfrac {5^{2}}{2+textstyle {cfrac {7^{2}}{2+textstyle {cfrac {9^{2}}{2+ ddots }}}}}}}}}}}}=3+textstyle {cfrac {1^{2}}{6+textstyle {cfrac {3^{2}}{6+textstyle { cfrac {5^{2}}{6+textstyle {cfrac {7^{2}}{6+textstyle {cfrac {9^{2}}{6+ddots }}}}}}} }}}\[8pt]&=textstyle {cfrac {4}{1+textstyle {cfrac {1^{2}}{3+textstyle {cfrac {2^{2}}{5 +textstyle {cfrac {3^{2}}{7+textstyle {cfrac {4^{2}}{9+ddots }}}}}}}}}end{aligned}}}

Valeur approximative et chiffres

Certaines approximations de pi incluent :

• Entiers : 3
• Fractions : Les fractions approximatives incluent (par ordre croissant de précision) 22/7, 333/106, 355/113, 52163/16604, 103993/33102, 104348/33215, et 245850922/78256779. ^[30] (La liste est une sélection de termes de OEIS : A063674 et OEIS : A063673 .)
• Chiffres : Les 50 premiers chiffres décimaux sont 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510… ^[33] (voir OEIS : A000796 )

Chiffres dans d’autres systèmes de numération

• Les 48 premiers chiffres binaires ( base 2) (appelés bits ) sont 11.0010 0100 0011 1111 0110 1010 1000 1000 1000 0101 1010 0011… (voir OEIS : A004601 )
• Les 20 premiers chiffres en hexadécimal (base 16) sont 3,243F 6A88 85A3 08D3 1319… ^[34] (voir OEIS : A062964 )
• Les cinq premiers chiffres sexagésimaux (base 60) sont 3;8,29,44,0,47 ^[35] (voir OEIS : A060707 )
• Les 38 premiers chiffres du système numérique ternaire sont 10.010 211 0122 220 102 110 021 111 102 212 222 201… (voir OEIS : A004602 )

Nombres complexes et identité d’Euler

Sine and Cosine functions.” height=”236″ src=”” data-src=”//upload.wikimedia.org/wikipedia/commons/thumb/7/71/Euler%27s_formula.svg/220px-Euler%27s_formula.svg.png” width=”220″> L’association entre les puissances imaginaires du nombre e et les points du cercle unité centrés à l’ origine dans le plan complexe donné par la formule d’Euler

Tout nombre complexe , disons z , peut être exprimé à l’aide d’une paire de nombres réels . Dans le système de coordonnées polaires , un nombre ( rayon ou r ) est utilisé pour représenter la distance de z à partir de l’ origine du plan complexe , et l’autre (angle ou φ ) la rotation dans le sens antihoraire à partir de la ligne réelle positive : ^{[36 ]}

z = r ⋅ ( cos ⁡ φ + i sin ⁡ φ ) , {displaystyle z=rcdot (cos varphi +isin varphi ),}

où i est l’ unité imaginaire vérifiant i ² = −1. L’apparition fréquente de π en analyse complexe peut être liée au comportement de la fonction exponentielle d’une variable complexe, décrite par la formule d’Euler : ^[37]

e i φ = cos ⁡ φ + i sin ⁡ φ , {displaystyle e^{ivarphi }=cos varphi +isin varphi ,}

où la constante e est la base du logarithme naturel . Cette formule établit une correspondance entre les puissances imaginaires de e et les points du cercle unité centrés à l’origine du plan complexe. Définir φ = π dans la formule d’ Euler donne l’identité d’Euler , célébrée en mathématiques car elle contient les cinq constantes mathématiques les plus importantes : ^{[37] [38]}

e i π + 1 = 0. {displaystyle e^{ipi }+1=0.}

Il existe n nombres complexes différents z satisfaisant z ⁿ = 1 , et ceux-ci sont appelés les « n -ièmes racines de l’unité » ^[39] et sont donnés par la formule :

e 2 π i k / n ( k = 0 , 1 , 2 , … , n − 1 ) . {displaystyle e^{2pi ik/n}qquad (k=0,1,2,dots ,n-1).}

Histoire

Antiquité

Les approximations les plus connues de π datant d’ avant l’ère commune étaient précises à deux décimales près; cela a été amélioré dans les mathématiques chinoises en particulier au milieu du premier millénaire, avec une précision de sept décimales. Après cela, aucun autre progrès n’a été réalisé jusqu’à la fin de la période médiévale.

Sur la base des mesures de la Grande Pyramide de Gizeh (vers 2560 avant JC) , ^[d] certains égyptologues ont affirmé que les anciens Égyptiens utilisaient une approximation de π comme 22/7dès l’ Ancien Empire . ^{[40] [41]} Cette affirmation a été accueillie avec scepticisme. ^{[42] [43] [44] [45] [46]} Les premières approximations écrites de π se trouvent à Babylone et en Égypte, toutes deux à moins d’un pour cent de la vraie valeur. À Babylone, une tablette d’argile datée de 1900 à 1600 av. J.-C. contient une déclaration géométrique qui, par implication, traite π comme 25/8 = 3,125. ^[47] En Égypte, le papyrus Rhind , daté d’environ 1650 av. J.-C. mais copié d’un document daté de 1850 av. J.-C., contient une formule pour l’aire d’un cercle qui traite π comme ( 16/9) ² ≈ 3,16. ^[47]

Les calculs astronomiques dans le Shatapatha Brahmana (vers le 4ème siècle avant JC) utilisent une approximation fractionnaire de 339/108 ≈ 3,139 (avec une erreur relative de 9×10 ⁻⁴ ). ^[48] ​​D’autres sources indiennes vers 150 av. J.-C. traitent π comme √ 10 ≈ 3,1622. ^[49]

Ère d’approximation polygonale

π peut être estimé en calculant les périmètres des polygones circonscrits et inscrits. Archimède a développé l’approche polygonale pour approximer π .

Le premier algorithme enregistré pour calculer rigoureusement la valeur de π était une approche géométrique utilisant des polygones, conçue vers 250 avant JC par le mathématicien grec Archimède . ^[50] Cet algorithme polygonal a dominé pendant plus de 1 000 ans et, par conséquent, π est parfois appelé “constante d’Archimède”. ^[51] Archimède a calculé les limites supérieures et inférieures de π en dessinant un hexagone régulier à l’intérieur et à l’extérieur d’un cercle, et en doublant successivement le nombre de côtés jusqu’à ce qu’il atteigne un polygone régulier à 96 côtés. En calculant les périmètres de ces polygones, il a prouvé que 223/71< π < 22/7(c’est-à-dire 3,1408 < π < 3,1429 ). ^[52] Borne supérieure d’Archimède de 22/7peut avoir conduit à une croyance populaire répandue selon laquelle π est égal à 22/7. ^[53] Vers 150 après JC, le scientifique gréco-romain Ptolémée , dans son Almagest , a donné une valeur de π de 3,1416, qu’il a peut-être obtenue d’Archimède ou d’ Apollonios de Perga . ^{[54] [55]} Les mathématiciens utilisant des algorithmes polygonaux ont atteint 39 chiffres de π en 1630, un record seulement battu en 1699 lorsque des séries infinies ont été utilisées pour atteindre 71 chiffres. ^[56]

Dans la Chine ancienne , les valeurs de π comprenaient 3,1547 (environ 1 après JC), √ 10 (100 après JC, environ 3,1623) et 142/45(IIIe siècle, environ 3.1556). ^[57] Vers 265 après JC, le mathématicien du royaume Wei Liu Hui a créé un algorithme itératif basé sur un polygone et l’a utilisé avec un polygone à 3 072 côtés pour obtenir une valeur de π de 3,1416. ^{[58] [59]} Liu inventa plus tard une méthode plus rapide de calcul de π et obtint une valeur de 3,14 avec un polygone à 96 côtés, en profitant du fait que les différences d’aire des polygones successifs forment une série géométrique avec un facteur de 4. ^[58] Le mathématicien chinois Zu Chongzhi , vers 480 après JC, a calculé que 3,1415926 < π < 3,1415927et a suggéré les approximations π ≈ 355/113= 3,14159292035… et π ≈ 22/7= 3,142857142857…, qu’il a nommé respectivement Milü («rapport proche») et Yuelü («rapport approximatif»), en utilisant l’algorithme de Liu Hui appliqué à un polygone de 12 288 côtés. Avec une valeur correcte pour ses sept premières décimales chiffres, cette valeur est restée l’approximation la plus précise de π disponible pour les 800 années suivantes ^[60].

L’astronome indien Aryabhata a utilisé une valeur de 3,1416 dans son Āryabhaṭīya (499 après JC). ^[61] Fibonacci dans c. 1220 calculé 3,1418 en utilisant une méthode polygonale, indépendante d’Archimède. ^[62] L’auteur italien Dante a apparemment employé la valeur 3+ √ 2/dix≈ 3,14142 . ^[62]

L’astronome persan Jamshīd al-Kāshī a produit 9 chiffres sexagésimaux , à peu près l’équivalent de 16 chiffres décimaux, en 1424 en utilisant un polygone de 3 × 2 ²⁸ côtés, ^{[63] [64]} qui a représenté le record du monde pendant environ 180 ans. ^[65] Le mathématicien français François Viète en 1579 a réalisé 9 chiffres avec un polygone de 3×2 ¹⁷ côtés. ^[65] Le mathématicien flamand Adriaan van Roomen est arrivé à 15 décimales en 1593. ^[65] En 1596, le mathématicien néerlandais Ludolph van Ceulen a atteint 20 chiffres, un record qu’il a ensuite augmenté à 35 chiffres (en conséquence, πétait appelé le “nombre de Ludolphian” en Allemagne jusqu’au début du 20ème siècle). ^[66] Le scientifique hollandais Willebrord Snellius a atteint 34 chiffres en 1621, ^[67] et l’astronome autrichien Christoph Grienberger est arrivé à 38 chiffres en 1630 en utilisant 10 ⁴⁰ côtés. ^[68] Christiaan Huygens a pu arriver à 10 décimales en 1654 en utilisant une méthode légèrement différente équivalente à l’ extrapolation de Richardson . ^{[69] [70]}

Série infinie

Comparaison de la convergence de plusieurs séries infinies historiques pour π . S _n est l’approximation après avoir pris n termes. Chaque sous-parcelle suivante agrandit la zone ombrée horizontalement de 10 fois. (cliquez pour le détail)

Le calcul de π a été révolutionné par le développement des techniques des séries infinies aux XVIe et XVIIe siècles. Une série infinie est la somme des termes d’une suite infinie . ^[71] Les séries infinies ont permis aux mathématiciens de calculer π avec une précision beaucoup plus grande qu’Archimède et d’autres qui utilisaient des techniques géométriques. ^[71] Bien que les séries infinies aient été exploitées pour π notamment par des mathématiciens européens tels que James Gregory et Gottfried Wilhelm Leibniz , l’approche a été découverte pour la première fois en Inde entre 1400 et 1500 après JC.^{[72] [73]} La première description écrite d’une série infinie qui pourrait être utilisée pour calculer π a été exposée en vers sanskrit par l’astronome indien Nilakantha Somayaji dans son Tantrasamgraha , vers 1500 après JC. ^[74] Les séries sont présentées sans preuve, mais des preuves sont présentées dans un ouvrage indien ultérieur, Yuktibhāṣā , d’environ 1530 après JC. Nilakantha attribue la série à un ancien mathématicien indien, Madhava de Sangamagrama , qui a vécu c. 1350 – env. 1425. ^[74] Plusieurs séries infinies sont décrites, y compris des séries pour le sinus, la tangente et le cosinus, qui sont maintenant appelées la série Madhava ouSérie Grégory-Leibniz . ^[74] Madhava a utilisé des séries infinies pour estimer π à 11 chiffres vers 1400, mais cette valeur a été améliorée vers 1430 par le mathématicien persan Jamshīd al-Kāshī , en utilisant un algorithme polygonal. ^[75]

Isaac Newton a utilisé des séries infinies pour calculer π à 15 chiffres, écrivant plus tard “J’ai honte de vous dire à combien de chiffres j’ai porté ces calculs”. ^[76]

La première séquence infinie découverte en Europe était un produit infini (plutôt qu’une somme infinie , qui est plus généralement utilisée dans les calculs de π ) trouvé par le mathématicien français François Viète en 1593 : ^{[77] [78] [79]}

2 π = 2 2 ⋅ 2 + 2 2 ⋅ 2 + 2 + 2 2 ⋯ {displaystyle {frac {2}{pi }}={frac {sqrt {2}}{2}}cdot {frac {sqrt {2+{sqrt {2}}}}{ 2}}cdot {frac {sqrt {2+{sqrt {2+{sqrt {2}}}}}}{2}}cdots }

La deuxième séquence infinie trouvée en Europe , par John Wallis en 1655, était aussi un produit infini : ^[77]

π 2 = ( 2 1 ⋅ 2 3 ) ⋅ ( 4 3 ⋅ 4 5 ) ⋅ ( 6 5 ⋅ 6 7 ) ⋅ ( 8 7 ⋅ 8 9 ) ⋯ {displaystyle {frac {pi }{2}}={Big (}{frac {2}{1}}cdot {frac {2}{3}}{Big )}cdot { Big (}{frac {4}{3}}cdot {frac {4}{5}}{Big )}cdot {Big (}{frac {6}{5}}cdot {frac {6}{7}}{Big )}cdot {Big (}{frac {8}{7}}cdot {frac {8}{9}}{Big )} cdots }

La découverte du calcul , par le scientifique anglais Isaac Newton et le mathématicien allemand Gottfried Wilhelm Leibniz dans les années 1660, a conduit au développement de nombreuses séries infinies pour approximer π . Newton lui-même a utilisé une série arcsin pour calculer une approximation à 15 chiffres de π en 1665 ou 1666, en écrivant “J’ai honte de vous dire à combien de chiffres j’ai porté ces calculs, n’ayant pas d’autre affaire à l’époque.” ^[76]

En Europe, la formule de Madhava a été redécouverte par le mathématicien écossais James Gregory en 1671, et par Leibniz en 1674 : ^{[80] [81]}

arctan ⁡ z = z − z 3 3 + z 5 5 − z 7 7 + ⋯ {displaystyle arctan z=z-{frac {z^{3}}{3}}+{frac {z^{5}}{5}}-{frac {z^{7}}{ 7}}+cdots }

Cette formule, la série Gregory-Leibniz, est égale à π/4 lorsqu’elle est évaluée avec z = 1. ^[81] En 1699, le mathématicien anglais Abraham Sharp a utilisé la série Gregory-Leibniz pour z = 1 3 {textstyle z={frac {1}{sqrt {3}}}} pour calculer π à 71 chiffres, battant le record précédent de 39 chiffres, qui a été établi avec un algorithme polygonal. ^[82] Le Grégory-Leibniz pour z = 1 {displaystyle z=1} La série est simple, mais converge très lentement (c’est-à-dire qu’elle s’approche progressivement de la réponse), elle n’est donc pas utilisée dans les calculs π modernes. ^[83]

En 1706 , John Machin a utilisé la série Gregory-Leibniz pour produire un algorithme qui a convergé beaucoup plus rapidement : ^[84]

π 4 = 4 arctan ⁡ 1 5 − arctan ⁡ 1 239 . {displaystyle {frac {pi }{4}}=4arctan {frac {1}{5}}-arctan {frac {1}{239}}.}

Machin a atteint 100 chiffres de π avec cette formule. ^[85] D’autres mathématiciens ont créé des variantes, maintenant connues sous le nom de formules de type Machin , qui ont été utilisées pour établir plusieurs records successifs pour calculer les chiffres de π . ^[85] Les formules de type Machin sont restées la méthode la plus connue pour calculer π jusqu’à l’ère des ordinateurs et ont été utilisées pour établir des records pendant 250 ans, aboutissant à une approximation à 620 chiffres en 1946 par Daniel Ferguson – la meilleure approximation obtenue sans l’aide d’un outil de calcul. ^[86]

Un record a été établi par le prodige calculateur Zacharias Dase , qui en 1844 a utilisé une formule de type Machin pour calculer 200 décimales de π dans sa tête à la demande du mathématicien allemand Carl Friedrich Gauss . ^[87] Le mathématicien britannique William Shanks a calculé π à 607 chiffres en 1853, mais a fait une erreur dans le 528e chiffre, rendant tous les chiffres suivants incorrects. Bien qu’il ait calculé 100 chiffres supplémentaires en 1873, portant le total à 707, son erreur précédente a également rendu tous les nouveaux chiffres incorrects. ^[88]

Taux de convergence

Certaines séries infinies pour π convergent plus rapidement que d’autres. Étant donné le choix de deux séries infinies pour π , les mathématiciens utiliseront généralement celle qui converge plus rapidement car une convergence plus rapide réduit la quantité de calculs nécessaires pour calculer π à une précision donnée. ^[89] Une série infinie simple pour π est la série de Gregory–Leibniz : ^[90]

π = 4 1 − 4 3 + 4 5 − 4 7 + 4 9 − 4 11 + 4 13 − ⋯ {displaystyle pi ={frac {4}{1}}-{frac {4}{3}}+{frac {4}{5}}-{frac {4}{7}}+ {frac {4}{9}}-{frac {4}{11}}+{frac {4}{13}}-cdots }

Au fur et à mesure que les termes individuels de cette série infinie sont ajoutés à la somme, le total se rapproche progressivement de π , et – avec un nombre suffisant de termes – peut se rapprocher de π autant que souhaité. Il converge assez lentement, cependant – après 500 000 termes, il ne produit que cinq chiffres décimaux corrects de π . ^[91]

Une série infinie pour π (publiée par Nilakantha au 15ème siècle) qui converge plus rapidement que la série Gregory-Leibniz est : ^[92] Notez que ( n − 1) n ( n + 1) = n ³ − n . ^[93]

π = 3 + 4 2 × 3 × 4 − 4 4 × 5 × 6 + 4 6 × 7 × 8 − 4 8 × 9 × 10 + ⋯ {displaystyle pi =3+{frac {4}{2times 3times 4}}-{frac {4}{4times 5times 6}}+{frac {4}{6 times 7times 8}}-{frac {4}{8times 9times 10}}+cdots }

Le tableau suivant compare les taux de convergence de ces deux séries :

Série infinie pour π	Après le 1er mandat	Après le 2e mandat	Après le 3e mandat	Après le 4e mandat	Après le 5e mandat	Converge vers :
π = 4 1 − 4 3 + 4 5 − 4 7 + 4 9 − 4 11 + 4 13 + ⋯ {displaystyle pi ={frac {4}{1}}-{frac {4}{3}}+{frac {4}{5}}-{frac {4}{7}}+ {frac {4}{9}}-{frac {4}{11}}+{frac {4}{13}}+cdots }	4.0000	2.6666 …	3.4666 …	2.8952 …	3.3396 …	π = 3,1415 …
π = 3 + 4 2 × 3 × 4 − 4 4 × 5 × 6 + 4 6 × 7 × 8 − ⋯ {displaystyle pi ={3}+{frac {4}{2times 3times 4}}-{frac {4}{4times 5times 6}}+{frac {4} {6fois 7fois 8}}-cdots }	3.0000	3.1666 …	3.1333 …	3.1452 …	3.1396 …

Après cinq termes, la somme de la série Gregory-Leibniz est à moins de 0,2 de la valeur correcte de π , tandis que la somme de la série de Nilakantha est à moins de 0,002 de la valeur correcte de π . La série de Nilakantha converge plus rapidement et est plus utile pour calculer les chiffres de π . Les séries qui convergent encore plus rapidement incluent la série de Machin et la série de Chudnovsky , cette dernière produisant 14 chiffres décimaux corrects par terme. ^[89]

Irrationalité et transcendance

Toutes les avancées mathématiques relatives à π ne visaient pas à augmenter la précision des approximations. Quand Euler résout le problème de Bâle en 1735, trouvant la valeur exacte de la somme des carrés réciproques, il établit une connexion entre π et les nombres premiers qui contribua plus tard au développement et à l’étude de la fonction zêta de Riemann : ^[94]

π 2 6 = 1 1 2 + 1 2 2 + 1 3 2 + 1 4 2 + ⋯ {displaystyle {frac {pi ^{2}}{6}}={frac {1}{1^{2}}}+{frac {1}{2^{2}}}+{ frac {1}{3^{2}}}+{frac {1}{4^{2}}}+cdots }

Le scientifique suisse Johann Heinrich Lambert a prouvé en 1768 que π est irrationnel , ce qui signifie qu’il n’est pas égal au quotient de deux nombres entiers. ^[21] La preuve de Lambert a exploité une représentation en fraction continue de la fonction tangente. ^[95] Le mathématicien français Adrien-Marie Legendre a prouvé en 1794 que π ² est aussi irrationnel. En 1882, le mathématicien allemand Ferdinand von Lindemann a prouvé que π est transcendantal , ^[96] confirmant une conjecture faite par Legendre et Euler. ^{[97] [98]}Hardy et Wright déclarent que “les preuves ont ensuite été modifiées et simplifiées par Hilbert, Hurwitz et d’autres écrivains”. ^[99]

Adoption du symbole π

La première utilisation connue de la lettre grecque π pour représenter le rapport de la circonférence d’un cercle à son diamètre a été faite par le mathématicien gallois William Jones en 1706 . Leonhard Euler a popularisé l’utilisation de la lettre grecque π dans les ouvrages qu’il a publiés en 1736 et 1748.

Dans les premiers usages, la lettre grecque π était une abréviation du mot grec pour périphérie ( περιφέρεια ), ^[100] et était combinée dans des rapports avec δ (pour diamètre ) ou ρ (pour rayon ) pour former des constantes de cercle. ^{[101] [102] [103]} (Auparavant, les mathématiciens utilisaient parfois des lettres telles que c ou p à la place. ^[104] ) La première utilisation enregistrée est celle d’Oughtred ” δ . π {displaystyle delta .pi } “, pour exprimer le rapport de la périphérie et du diamètre dans les éditions 1647 et ultérieures de Clavis Mathematicae . ^{[105] [104]} Barrow a également utilisé ” π δ {textstyle {frac {pi }{delta }}} ” pour représenter la constante 3,14…, ^[106] alors que Gregory utilisait à la place ” π ρ {textstyle {frac {pi }{rho }}} ” pour représenter 6,28… . ^{[107] [102]}

La première utilisation connue de la lettre grecque π seule pour représenter le rapport de la circonférence d’un cercle à son diamètre était par le mathématicien gallois William Jones dans son ouvrage de 1706 Synopsis Palmariorum Matheseos ; ou, une Nouvelle Introduction aux Mathématiques . ^{[3] [108]} La lettre grecque apparaît d’abord là dans l’expression “1/2 Périphérie ( π )” dans la discussion d’un cercle avec le rayon un. ^[109] Cependant, il écrit que ses équations pour π sont de la « plume prête du vraiment ingénieux M. John Machin », conduisant à la spéculation que Machin a peut-être employé la lettre grecque avant Jones. ^[104]La notation de Jones n’a pas été immédiatement adoptée par d’autres mathématiciens, la notation des fractions étant encore utilisée jusqu’en 1767. ^{[101] [110]}

Euler a commencé à utiliser la forme à une seule lettre à partir de son essai de 1727 expliquant les propriétés de l’air , bien qu’il ait utilisé π = 6,28… , le rapport de la périphérie au rayon, dans cet écrit et dans certains écrits ultérieurs. ^{[111] [112]} Euler a utilisé pour la première fois π = 3,14… dans son ouvrage de 1736 Mechanica , ^[113] et a continué dans son ouvrage largement lu de 1748 Introductio in analysin infinitorum (il a écrit : “par souci de brièveté, nous écrirons ce nombre comme π ; donc π est égal à la moitié de la circonférence d’un cercle de rayon 1″). ^[114]Parce qu’Euler correspondait fortement avec d’autres mathématiciens en Europe, l’utilisation de la lettre grecque se répandit rapidement, et la pratique fut universellement adoptée par la suite dans le monde occidental , ^[104] bien que la définition variait encore entre 3,14… et 6,28… comme tard en 1761. ^[115]

Quête moderne pour plus de chiffres

L’ère informatique et les algorithmes itératifs

L’ algorithme itératif de Gauss–Legendre :
Initialiser

a 0 = 1 , b 0 = 1 2 , t 0 = 1 4 , p 0 = 1. {displaystyle textstyle a_{0}=1,quad b_{0}={frac {1}{sqrt {2}}},quad t_{0}={frac {1}{4} },quad p_{0}=1.}

Répéter

a n + 1 = a n + b n 2 , b n + 1 = a n b n , {displaystyle textstyle a_{n+1}={frac {a_{n}+b_{n}}{2}},quad quad b_{n+1}={sqrt {a_{n} b_{n}}},} t n + 1 = t n − p n ( a n − a n + 1 ) 2 , p n + 1 = 2 p n . {displaystyle textstyle t_{n+1}=t_{n}-p_{n}(a_{n}-a_{n+1})^{2},quad quad p_{n+1}= 2p_{n}.}

Ensuite, une estimation de π est donnée par

π ≈ ( a n + b n ) 2 4 t n . {displaystyle textstyle pi approx {frac {(a_{n}+b_{n})^{2}}{4t_{n}}}.}

Le développement des ordinateurs au milieu du XXe siècle a de nouveau révolutionné la chasse aux chiffres de π . Les mathématiciens John Wrench et Levi Smith ont atteint 1 120 chiffres en 1949 à l’aide d’une calculatrice de bureau. ^[116] En utilisant une série infinie de tangente inverse (arctan), une équipe dirigée par George Reitwiesner et John von Neumann la même année a atteint 2 037 chiffres avec un calcul qui a pris 70 heures de temps d’ordinateur sur l’ ordinateur ENIAC . ^{[117] [118]} Le record, reposant toujours sur une série arctan, a été battu à plusieurs reprises (7 480 chiffres en 1957 ; 10 000 chiffres en 1958 ; 100 000 chiffres en 1961) jusqu’à ce que 1 million de chiffres soient atteints en 1973. ^[117]

Deux développements supplémentaires vers 1980 ont encore une fois accéléré la capacité de calculer π . Premièrement, la découverte de nouveaux algorithmes itératifs pour calculer π , beaucoup plus rapides que la série infinie ; et deuxièmement, l’invention d’ algorithmes de multiplication rapide qui pourraient multiplier très rapidement de grands nombres. ^[119] De tels algorithmes sont particulièrement importants dans les calculs π modernes car la majeure partie du temps de l’ordinateur est consacrée à la multiplication. ^[120] Ils incluent l’ algorithme de Karatsuba , la multiplication de Toom-Cook et les méthodes basées sur la transformée de Fourier . ^[121]

Les algorithmes itératifs ont été publiés indépendamment en 1975-1976 par le physicien Eugene Salamin et le scientifique Richard Brent . ^[122] Ceux-ci évitent de s’appuyer sur des séries infinies. Un algorithme itératif répète un calcul spécifique, chaque itération utilisant les sorties des étapes précédentes comme entrées, et produit un résultat à chaque étape qui converge vers la valeur souhaitée. L’approche a en fait été inventée plus de 160 ans plus tôt par Carl Friedrich Gauss , dans ce que l’on appelle maintenant la méthode de la moyenne arithmétique-géométrique (méthode AGM) ou l’algorithme de Gauss-Legendre . ^[122] Tel que modifié par Salamin et Brent, il est également appelé algorithme de Brent-Salamin.

Les algorithmes itératifs ont été largement utilisés après 1980 car ils sont plus rapides que les algorithmes de séries infinies : alors que les séries infinies augmentent généralement le nombre de chiffres corrects de manière additive par termes successifs, les algorithmes itératifs multiplient généralement le nombre de chiffres corrects à chaque étape. Par exemple, l’algorithme de Brent-Salamin double le nombre de chiffres à chaque itération. En 1984, les frères John et Peter Borwein ont produit un algorithme itératif qui quadruple le nombre de chiffres à chaque étape ; et en 1987, celui qui augmente le nombre de chiffres cinq fois à chaque étape. ^[123] Des méthodes itératives ont été utilisées par le mathématicien japonais Yasumasa Kanada pour établir plusieurs records de calcul de πentre 1995 et 2002. ^[124] Cette convergence rapide a un prix : les algorithmes itératifs nécessitent nettement plus de mémoire que les séries infinies. ^[124]

Motifs du calcul de π

Au fur et à mesure que les mathématiciens découvraient de nouveaux algorithmes et que les ordinateurs devenaient disponibles, le nombre de chiffres décimaux connus de π augmentait considérablement. L’échelle verticale est logarithmique .

Pour la plupart des calculs numériques impliquant π , une poignée de chiffres fournit une précision suffisante. Selon Jörg Arndt et Christoph Haenel, trente-neuf chiffres suffisent pour effectuer la plupart des calculs cosmologiques , car c’est la précision nécessaire pour calculer la circonférence de l’ univers observable avec une précision d’un atome. ^[125] Compte tenu des chiffres supplémentaires nécessaires pour compenser les erreurs d’arrondi de calcul , Arndt conclut que quelques centaines de chiffres suffiraient pour toute application scientifique. Malgré cela, les gens ont travaillé dur pour calculer π en milliers et en millions de chiffres. ^[126]Cet effort peut être en partie attribué à la compulsion humaine à battre des records, et de telles réalisations avec π font souvent les gros titres dans le monde entier. ^{[127] [128]} Ils ont également des avantages pratiques, tels que tester des supercalculateurs , tester des algorithmes d’analyse numérique (y compris des algorithmes de multiplication de haute précision ) ; et dans les mathématiques pures elles-mêmes, fournissant des données pour évaluer le caractère aléatoire des chiffres de π . ^[129]

Série rapidement convergente

Srinivasa Ramanujan , travaillant isolément en Inde, a produit de nombreuses séries innovantes pour le calcul de π .

Les calculatrices π modernes n’utilisent pas exclusivement des algorithmes itératifs. De nouvelles séries infinies ont été découvertes dans les années 1980 et 1990 qui sont aussi rapides que les algorithmes itératifs, mais sont plus simples et moins gourmandes en mémoire. ^[124] Les algorithmes itératifs rapides ont été anticipés en 1914, lorsque le mathématicien indien Srinivasa Ramanujan a publié des dizaines de nouvelles formules innovantes pour π , remarquables par leur élégance, leur profondeur mathématique et leur convergence rapide. ^[130] Une de ses formules, basée sur des équations modulaires , est

1 π = 2 2 9801 ∑ k = 0 ∞ ( 4 k ) ! ( 1103 + 26390 k ) k ! 4 ( 396 4 k ) . {displaystyle {frac {1}{pi }}={frac {2{sqrt {2}}}{9801}}sum _{k=0}^{infty }{frac {( 4k)!(1103+26390k)}{k!^{4}left(396^{4k}right)}}.}

Cette série converge beaucoup plus rapidement que la plupart des séries arctan, y compris la formule de Machin. ^[131] Bill Gosper a été le premier à l’utiliser pour des avancées dans le calcul de π , établissant un record de 17 millions de chiffres en 1985. ^[132] Les formules de Ramanujan ont anticipé les algorithmes modernes développés par les frères Borwein ( Jonathan et Peter ) et les Frères Chudnovsky . ^[133] La formule Chudnovsky développée en 1987 est

1 π = 12 640320 3 / 2 ∑ k = 0 ∞ ( 6 k ) ! ( 13591409 + 545140134 k ) ( 3 k ) ! k ! 3 ( − 640320 ) 3 k . {displaystyle {frac {1}{pi }}={frac {12}{640320^{3/2}}}sum _{k=0}^{infty}{frac {(6k )!(13591409+545140134k)}{(3k)!,k!^{3}(-640320)^{3k}}}.}

Il produit environ 14 chiffres de π par terme ^[134] et a été utilisé pour plusieurs calculs de π records , dont le premier à dépasser 1 milliard (10 ⁹ ) de chiffres en 1989 par les frères Chudnovsky, 10 billions (10 ¹³ ) chiffres en 2011 par Alexander Yee et Shigeru Kondo, ^[135] plus de 22 billions de chiffres en 2016 par Peter Trueb ^{[136] [137]} et 50 billions de chiffres par Timothy Mullican en 2020. ^[138] Pour des formules similaires, voir aussi le Ramanujan– Série Sato .

En 2006, le mathématicien Simon Plouffe a utilisé l’ algorithme de relation entière PSLQ ^[139] pour générer plusieurs nouvelles formules pour π , conformément au modèle suivant :

π k = ∑ n = 1 ∞ 1 n k ( a q n − 1 + b q 2 n − 1 + c q 4 n − 1 ) , {displaystyle pi ^{k}=sum _{n=1}^{infty }{frac {1}{n^{k}}}left({frac {a}{q^{ n}-1}}+{frac {b}{q^{2n}-1}}+{frac {c}{q^{4n}-1}}right),}

où q est e ^π (constante de Gelfond), k est un nombre impair et a , b , c sont certains nombres rationnels calculés par Plouffe. ^[140]

Méthodes de Monte Carlo

Aiguille de Buffon . Les aiguilles a et b sont lâchées au hasard. Des points aléatoires sont placés sur un carré et un cercle inscrit à l’intérieur.

Les méthodes de Monte Carlo , qui évaluent les résultats de plusieurs essais aléatoires, peuvent être utilisées pour créer des approximations de π . ^[141] L’aiguille de Buffon est l’une de ces techniques : si une aiguille de longueur l est lâchée n fois sur une surface sur laquelle des lignes parallèles sont tracées à t unités, et si x de ces fois elle s’immobilise en traversant une ligne ( x > 0 ), alors on peut approximer π en se basant sur les comptages : ^[142]

π ≈ 2 n l x t . {displaystyle pi approx {frac {2nell }{xt}}.}

Une autre méthode de Monte Carlo pour calculer π consiste à dessiner un cercle inscrit dans un carré et à placer au hasard des points dans le carré. Le rapport des points à l’intérieur du cercle au nombre total de points sera approximativement égal à π/4 . ^[143]

Cinq marches aléatoires de 200 pas. La moyenne de l’échantillon de | W ₂₀₀ | est μ = 56/5 , et donc 2(200)μ ⁻² ≈ 3,19 est à moins de 0,05 de π .

Une autre façon de calculer π en utilisant la probabilité est de commencer par une marche aléatoire , générée par une séquence de (justes) lancers de pièces : variables aléatoires indépendantes X _k telles que X _k ∈ {−1,1} avec des probabilités égales. La marche aléatoire associée est

W n = ∑ k = 1 n X k {displaystyle W_{n}=sum _{k=1}^{n}X_{k}}

de sorte que, pour chaque n , W _n est tiré d’une distribution binomiale décalée et mise à l’échelle . Lorsque n varie, W _n définit un processus stochastique (discret) . Alors π peut être calculé par ^[144]

π = lim n → ∞ 2 n E [ | W n | ] 2 . {displaystyle pi =lim _{nto infty }{frac {2n}{E[|W_{n}|]^{2}}}.}

Cette méthode de Monte Carlo est indépendante de toute relation avec les cercles et est une conséquence du théorème central limite , discuté ci- dessous .

Ces méthodes Monte Carlo d’approximation de π sont très lentes par rapport aux autres méthodes et ne fournissent aucune information sur le nombre exact de chiffres obtenus. Ainsi, ils ne sont jamais utilisés pour approximer π lorsque la vitesse ou la précision sont souhaitées. ^[145]

Algorithmes de robinet

Deux algorithmes ont été découverts en 1995 qui ont ouvert de nouvelles voies de recherche sur π . Ils sont appelés algorithmes de robinet car, comme l’eau s’égouttant d’un robinet , ils produisent des chiffres uniques de π qui ne sont pas réutilisés après leur calcul. ^{[146] [147]} Ceci est en contraste avec les séries infinies ou les algorithmes itératifs, qui conservent et utilisent tous les chiffres intermédiaires jusqu’à ce que le résultat final soit produit. ^[146]

Les mathématiciens Stan Wagon et Stanley Rabinowitz ont produit un simple algorithme de robinet en 1995. ^{[147] [148] [149]} Sa vitesse est comparable aux algorithmes arctan, mais pas aussi rapide que les algorithmes itératifs. ^[148]

Un autre algorithme de broche, l’ algorithme d’extraction de chiffres BBP , a été découvert en 1995 par Simon Plouffe : ^{[150] [151]}

π = ∑ k = 0 ∞ 1 16 k ( 4 8 k + 1 − 2 8 k + 4 − 1 8 k + 5 − 1 8 k + 6 ) . {displaystyle pi =sum _{k=0}^{infty }{frac {1}{16^{k}}}left({frac {4}{8k+1}}-{ frac {2}{8k+4}}-{frac {1}{8k+5}}-{frac {1}{8k+6}}right).}

Cette formule, contrairement à d’autres avant elle, peut produire n’importe quel chiffre hexadécimal individuel de π sans calculer tous les chiffres précédents. ^[150] Des chiffres binaires individuels peuvent être extraits de chiffres hexadécimaux individuels, et des chiffres octaux peuvent être extraits d’un ou deux chiffres hexadécimaux. Des variantes de l’algorithme ont été découvertes, mais aucun algorithme d’extraction de chiffres n’a encore été trouvé qui produit rapidement des chiffres décimaux. ^[152] Une application importante des algorithmes d’extraction de chiffres est de valider de nouvelles revendications d’enregistrement πcalculs : après la réclamation d’un nouvel enregistrement, le résultat décimal est converti en hexadécimal, puis un algorithme d’extraction de chiffres est utilisé pour calculer plusieurs chiffres hexadécimaux aléatoires vers la fin ; s’ils correspondent, cela fournit une mesure de confiance que l’ensemble du calcul est correct. ^[135]

Entre 1998 et 2000, le projet de calcul distribué PiHex a utilisé la formule de Bellard (une modification de l’algorithme BBP) pour calculer le quadrillionième (10 ¹⁵ ème) bit de π , qui s’est avéré être 0. ^[153] En septembre 2010, un Yahoo ! employé a utilisé l’ application Hadoop de l’entreprise sur un millier d’ordinateurs sur une période de 23 jours pour calculer 256 bits de π au deux quadrillionième (2×10 ¹⁵ ème) bit, qui est également égal à zéro. ^[154]

Rôle et caractérisations en mathématiques

Parce que π est étroitement lié au cercle, on le retrouve dans de nombreuses formules des domaines de la géométrie et de la trigonométrie, en particulier celles concernant les cercles, les sphères ou les ellipses. D’autres branches de la science, telles que les statistiques, la physique, l’analyse de Fourier et la théorie des nombres, incluent également π dans certaines de leurs formules importantes.

Géométrie et trigonométrie

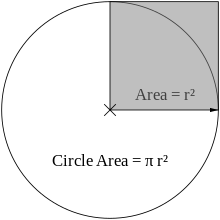
L’aire du cercle est égale à π fois l’aire ombrée. L’aire du cercle unité est π .

π apparaît dans les formules pour les aires et les volumes de formes géométriques basées sur des cercles, tels que les ellipses , les sphères , les cônes et les tores . Voici quelques-unes des formules les plus courantes qui impliquent π . ^[155]

• La circonférence d’un cercle de rayon r est 2π r .
• L’ aire d’un cercle de rayon r est π r ² .
• L’aire d’une ellipse de demi-grand axe a et de demi-petit axe b est π ab .
• Le volume d’une sphère de rayon r est 4/3π r ³ .
• La surface d’une sphère de rayon r est 4π r ² .

Certaines des formules ci-dessus sont des cas particuliers du volume de la boule à n dimensions et de la surface de sa frontière, la sphère à ( n −1) dimensions , données ci- dessous .

Outre les cercles, il existe d’autres courbes de largeur constante . D’ après le théorème de Barbier , toute courbe de largeur constante a pour périmètre π fois sa largeur. ^[156] Le triangle de Reuleaux (formé par l’intersection de trois cercles centrés chacun là où les deux autres cercles se croisent ^[157] ) a la plus petite aire possible pour sa largeur et le cercle le plus grand. Il existe aussi des lisses non circulaires non circulaires de largeur constante. ^[158]

Les intégrales définies qui décrivent la circonférence, l’aire ou le volume de formes générées par des cercles ont généralement des valeurs qui impliquent π . Par exemple, une intégrale qui spécifie la moitié de l’aire d’un cercle de rayon un est donnée par : ^[159]

∫ − 1 1 1 − x 2 d x = π 2 . {displaystyle int _{-1}^{1}{sqrt {1-x^{2}}},dx={frac {pi }{2}}.}

Dans cette intégrale, la fonction √ 1 − x ² représente la moitié supérieure d’un cercle (la racine carrée est une conséquence du théorème de Pythagore ), et l’intégrale ∫¹
₋₁calcule l’aire entre cette moitié d’un cercle et l’ axe x .

Unités d’angle

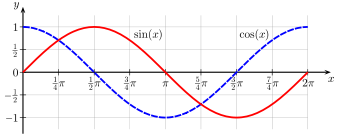
Les fonctions sinus et cosinus se répètent avec la période 2 π .

Les fonctions trigonométriques reposent sur les angles et les mathématiciens utilisent généralement les radians comme unités de mesure. π joue un rôle important dans les angles mesurés en radians , qui sont définis de sorte qu’un cercle complet couvre un angle de 2 π radians. ^[160] La mesure d’angle de 180° est égale à π radians, et 1° = π /180 radians. ^[160]

Les fonctions trigonométriques courantes ont des périodes multiples de π ; par exemple, sinus et cosinus ont une période 2 π , ^[161] donc pour tout angle θ et tout entier k ,

sin ⁡ θ = sin ⁡ ( θ + 2 π k ) and cos ⁡ θ = cos ⁡ ( θ + 2 π k ) . {displaystyle sin theta =sin left(theta +2pi kright){text{ and }}cos theta =cos left(theta +2pi kright) .} ^[161]

Valeurs propres

Les harmoniques d’une corde vibrante sont des fonctions propres de la dérivée seconde et forment une progression harmonique . Les valeurs propres associées forment la progression arithmétique des multiples entiers de π .

De nombreuses apparitions de π dans les formules des mathématiques et des sciences sont liées à sa relation étroite avec la géométrie. Cependant, π apparaît également dans de nombreuses situations naturelles n’ayant apparemment rien à voir avec la géométrie.

Dans de nombreuses applications, il joue un rôle distinct en tant que valeur propre . Par exemple, une corde vibrante idéalisée peut être modélisée comme le graphique d’une fonction f sur l’intervalle unitaire [0, 1] , avec des extrémités fixes f (0) = f (1) = 0 . Les modes de vibration de la corde sont des solutions de l’ équation différentielle f ′′ ( x ) + λ f ( x ) = 0 {displaystyle f”(x)+lambda f(x)=0} , ou alors f ′′ ( t ) = − λ f ( x ) {displaystyle f”(t)=-lambda f(x)} . Ainsi λ est une valeur propre de l’ opérateur de dérivée seconde f ↦ f ′′ {displaystyle fmapsto f”} , et est contraint par la théorie de Sturm-Liouville de ne prendre que certaines valeurs spécifiques. Il doit être positif, puisque l’opérateur est défini négatif , il est donc commode d’écrire λ = ν ² , où ν > 0 est appelé le nombre d’onde . Alors f ( x ) = sin( π x ) satisfait les conditions aux limites et l’équation différentielle avec ν = π . ^[162]

La valeur π est, en fait, la plus petite valeur du nombre d’onde, et est associée au mode fondamental de vibration de la corde. Une façon de le montrer est d’estimer l’ énergie , qui satisfait l’inégalité de Wirtinger : ^[163] pour une fonction f : [ 0 , 1 ] → C {displaystyle f :[0,1]à mathbb {C} } avec f (0) = f (1) = 0 et f , f ‘ de carré intégrable , on a :

π 2 ∫ 0 1 | f ( x ) | 2 d x ≤ ∫ 0 1 | f ′ ( x ) | 2 d x , {displaystyle pi ^{2}int _{0}^{1}|f(x)|^{2},dxleq int _{0}^{1}|f'(x) |^{2},dx,}

avec égalité précisément lorsque f est un multiple de sin(π x ) . Ici π apparaît comme une constante optimale dans l’inégalité de Wirtinger, et il s’ensuit qu’il s’agit du plus petit nombre d’onde, en utilisant la caractérisation variationnelle de la valeur propre. En conséquence, π est la plus petite valeur singulière de l’opérateur de dérivée sur l’espace des fonctions sur [0, 1] s’annulant aux deux extrémités (l’ espace de Sobolev H 0 1 [ 0 , 1 ] {displaystyle H_{0}^{1}[0,1]} ).

Inégalités

L’ antique cité de Carthage était la solution d’un problème d’isopérimétrie, selon une légende racontée par Lord Kelvin ( Thompson 1894 ) : ces terres bordant la mer que la reine Didon pouvait enfermer de tous les autres côtés dans une même peau de bœuf donnée, découpée en lanières.

Le nombre π sert apparaît dans des problèmes de valeurs propres similaires dans une analyse de dimension supérieure. Comme mentionné plus haut , elle peut être caractérisée par son rôle de meilleure constante de l ‘ inégalité isopérimétrique : l’ aire A délimitée par une courbe de Jordan plane de périmètre P satisfait l’ inégalité

4 π A ≤ P 2 , {displaystyle 4pi Aleq P^{2},}

et l’égalité est bien atteinte pour le cercle, puisque dans ce cas A = π r ² et P = 2π r .^[164]

En fin de compte, en conséquence de l’inégalité isopérimétrique, π apparaît dans la constante optimale de l’ inégalité critique de Sobolev à n dimensions, qui caractérise ainsi le rôle de π dans de nombreux phénomènes physiques également, par exemple ceux de la théorie classique du potentiel . ^{[165] [166] [167]} En deux dimensions, l’inégalité critique de Sobolev est

2 π ‖ f ‖ 2 ≤ ‖ ∇ f ‖ 1 {displaystyle 2pi |f|_{2}leq |nabla f|_{1}}

pour f une fonction lisse à support compact dans R ² , ∇ f {displaystylenabla f} est le gradient de f , et ‖ f ‖ 2 {displaystyle |f|_{2}} et ‖ ∇ f ‖ 1 {displaystyle |nabla f|_{1}} se référer respectivement aux L ² et L ¹ normes . L’inégalité de Sobolev est équivalente à l’inégalité isopérimétrique (en toute dimension), avec les mêmes meilleures constantes.

L’inégalité de Wirtinger se généralise également aux inégalités de Poincaré de dimension supérieure qui fournissent les meilleures constantes pour l’ énergie de Dirichlet d’une membrane à n dimensions. Plus précisément, π est la plus grande constante telle que

π ≤ ( ∫ G | ∇ u | 2 ) 1 / 2 ( ∫ G | u | 2 ) 1 / 2 {displaystyle pi leq {frac {left(int _{G}|nabla u|^{2}right)^{1/2}}{left(int _{G}| u|^{2}right)^{1/2}}}}

pour tous les sous- ensembles convexes G de R ⁿ de diamètre 1, et les fonctions carrées intégrables u sur G de moyenne nulle. ^[168] Tout comme l’inégalité de Wirtinger est la forme variationnelle du problème aux valeurs propres de Dirichlet en une dimension, l’inégalité de Poincaré est la forme variationnelle du problème de Neumann , en n’importe quelle dimension.

Transformée de Fourier et principe d’incertitude de Heisenberg

Une animation d’une géodésique dans le groupe de Heisenberg

La constante π apparaît également comme un paramètre spectral critique dans la transformée de Fourier . Il s’agit de la transformée intégrale , qui prend une fonction intégrable à valeurs complexes f sur la droite réelle jusqu’à la fonction définie comme :

f ^ ( ξ ) = ∫ − ∞ ∞ f ( x ) e − 2 π i x ξ d x . {displaystyle {hat {f}}(xi )=int _{-infty}^{infty}f(x)e^{-2pi ixxi },dx.}

Bien qu’il existe plusieurs conventions différentes pour la transformée de Fourier et son inverse, toute convention de ce type doit impliquer π quelque part . Ce qui précède est la définition la plus canonique, cependant, donnant l’unique opérateur unitaire sur L ² qui est aussi un homomorphisme d’algèbre de L ¹ à L ^∞ . ^[169]

Le principe d’incertitude de Heisenberg contient également le nombre π . Le principe d’incertitude donne une borne inférieure nette sur la mesure dans laquelle il est possible de localiser une fonction à la fois dans l’espace et en fréquence : avec nos conventions pour la transformée de Fourier,

( ∫ − ∞ ∞ x 2 | f ( x ) | 2 d x ) ( ∫ − ∞ ∞ ξ 2 | f ^ ( ξ ) | 2 d ξ ) ≥ ( 1 4 π ∫ − ∞ ∞ | f ( x ) | 2 d x ) 2 . {displaystyle left(int _{-infty}^{infty}x^{2}|f(x)|^{2},dxright)left(int _{-infty }^{infty}xi ^{2}|{hat {f}}(xi )|^{2},dxi right)geq left({frac {1}{4 pi }}int _{-infty }^{infty }|f(x)|^{2},dxright)^{2}.}

La conséquence physique, à propos de l’incertitude des observations simultanées de position et d’impulsion d’un système mécanique quantique , est discutée ci-dessous . L’apparition de π dans les formules de l’analyse de Fourier est finalement une conséquence du théorème de Stone-von Neumann , affirmant l’unicité de la représentation de Schrödinger du groupe de Heisenberg . ^[170]

Intégrales gaussiennes

Un graphique de la fonction gaussienne ƒ ( x ) = e ^{− x 2} . La région colorée entre la fonction et l’ axe des x a une aire √ π .

Les domaines de la probabilité et des statistiques utilisent fréquemment la distribution normale comme modèle simple pour des phénomènes complexes ; par exemple, les scientifiques supposent généralement que l’erreur d’observation dans la plupart des expériences suit une distribution normale. ^[171] La fonction gaussienne , qui est la fonction de densité de probabilité de la distribution normale de moyenne μ et d’écart type σ , contient naturellement π : ^[172]

f ( x ) = 1 σ 2 π e − ( x − μ ) 2 / ( 2 σ 2 ) . {displaystyle f(x)={1 over sigma {sqrt {2pi }}},e^{-(x-mu )^{2}/(2sigma ^{2}) }.}

Le facteur de 1 2 π {displaystyle {tfrac {1}{sqrt {2pi }}}} rend l’aire sous le graphique de f égale à un, comme cela est requis pour une distribution de probabilité. Cela découle d’un changement de variables dans l’ intégrale gaussienne : ^[172]

∫ − ∞ ∞ e − u 2 d u = π {displaystyle int _{-infty}^{infty}e^{-u^{2}},du={sqrt {pi }}}

qui dit que l’aire sous la courbe en cloche de base dans la figure est égale à la racine carrée de π .

Le théorème central limite explique le rôle central des distributions normales, et donc de π , dans les probabilités et les statistiques. Ce théorème est finalement lié à la caractérisation spectrale de π en tant que valeur propre associée au principe d’incertitude de Heisenberg, et au fait que l’égalité n’est valable dans le principe d’incertitude que pour la fonction gaussienne. ^[173] De manière équivalente, π est l’unique constante rendant la distribution normale gaussienne e ^{-π x 2} égale à sa propre transformée de Fourier. ^[174] En effet, selon Howe (1980), “toute l’affaire” d’établir les théorèmes fondamentaux de l’analyse de Fourier se réduit à l’intégrale gaussienne.

Géométrie projective

Soit V l’ensemble de toutes les fonctions réelles deux fois différentiables f : R → R {displaystyle f:mathbb {R} to mathbb {R} } qui satisfont l’ équation différentielle ordinaire f ′′ ( x ) + f ( x ) = 0 {displaystyle f”(x)+f(x)=0} . Alors V est un espace vectoriel réel à deux dimensions , avec deux paramètres correspondant à une paire de conditions initiales pour l’équation différentielle. Pour toute t ∈ R {displaystyle tin mathbb {R}} , laisser e t : V → R {displaystyle e_{t}:Vto mathbb {R} } soit la fonctionnelle d’évaluation, qui associe à chaque f ∈ V {displaystyle fen V} la valeur e t ( f ) = f ( t ) {displaystyle e_{t}(f)=f(t)} de la fonction f au point réel t . Alors, pour chaque t , le noyau de e t {displaystyle e_{t}} est un sous-espace linéaire unidimensionnel de V . Ainsi t ↦ ker ⁡ e t {displaystyle tmapsto ker e_{t}} définit une fonction à partir de R → P ( V ) {displaystyle mathbb {R} à mathbb {P} (V)} de la droite réelle à la droite projective réelle . Cette fonction est périodique et la quantité π peut être caractérisée comme la période de cette carte. ^[175]

Topologie

Uniformisation de la quartique de Klein , une surface de genre trois et de caractéristique d’Euler −4, en tant que quotient du plan hyperbolique par le groupe de symétrie PSL(2,7) du plan de Fano . L’aire hyperbolique d’un domaine fondamental est 8π , par Gauss–Bonnet.

La constante π apparaît dans la formule de Gauss-Bonnet qui relie la géométrie différentielle des surfaces à leur topologie . Plus précisément, si une surface compacte Σ a une courbure de Gauss K , alors

∫ Σ K d A = 2 π χ ( Σ ) {displaystyle int _{Sigma }K,dA=2pi chi (Sigma )}

où χ (Σ) est la caractéristique d’Euler , qui est un entier. ^[176] Un exemple est la surface d’une sphère S de courbure 1 (de sorte que son rayon de courbure , qui coïncide avec son rayon, est également 1.) La caractéristique d’Euler d’une sphère peut être calculée à partir de ses groupes d’homologie et est trouvée égale à deux. Ainsi nous avons

A ( S ) = ∫ S 1 d A = 2 π ⋅ 2 = 4 π {displaystyle A(S)=int _{S}1,dA=2pi cdot 2=4pi }

reproduisant la formule de l’aire d’une sphère de rayon 1.

La constante apparaît dans de nombreuses autres formules intégrales en topologie, en particulier celles impliquant des classes caractéristiques via l’ homomorphisme de Chern-Weil . ^[177]

Calcul vectoriel

Décompositions des harmoniques sphériques , un domaine du calcul vectoriel

Le calcul vectoriel est une branche du calcul qui s’intéresse aux propriétés des champs vectoriels et a de nombreuses applications physiques telles que l’ électricité et le magnétisme . Le potentiel newtonien d’une source ponctuelle Q située à l’origine d’un repère cartésien tridimensionnel est ^[178]

V ( x ) = − k Q | x | {displaystyle V(mathbf {x} )=-{frac {kQ}{|mathbf {x} |}}}

qui représente l’ énergie potentielle d’une unité de masse (ou charge) placée à une distance | x | de la source, et k est une constante dimensionnelle. Le champ, noté ici E , qui peut être le champ gravitationnel (newtonien) ou le champ électrique (coulombien) , est le gradient négatif du potentiel :

E = − ∇ V . {displaystyle mathbf {E} =-nabla V.}

Les cas particuliers incluent la loi de Coulomb et la loi de la gravitation universelle de Newton . La loi de Gauss stipule que le flux sortant du champ à travers toute surface lisse, simple, fermée et orientable S contenant l’origine est égal à 4 π kQ :

4 π k Q = {displaystyle 4pi kQ=} S {displaystyle {scriptstyle S}} E ⋅ d A . {displaystyle mathbf {E} cdot dmathbf {A} .}

Il est courant d’absorber ce facteur de 4π dans la constante k , mais cet argument montre pourquoi il doit apparaître quelque part . De plus, 4π est la surface de la sphère unité, mais nous n’avons pas supposé que S est la sphère. Cependant, en raison du théorème de divergence , parce que la région éloignée de l’origine est vide (sans source), ce n’est que la classe d’homologie de la surface S dans R ³ {0}qui importe dans le calcul de l’intégrale, elle peut donc être remplacée par n’importe quelle surface pratique dans la même classe d’homologie, en particulier une sphère, où les coordonnées sphériques peuvent être utilisées pour calculer l’intégrale.

Une conséquence de la loi de Gauss est que le Laplacien négatif du potentiel V est égal à 4π kQ fois la fonction delta de Dirac :

Δ V ( x ) = − 4 π k Q δ ( x ) . {displaystyle Delta V(mathbf {x} )=-4pi kQdelta (mathbf {x} ).}

Des distributions plus générales de matière (ou de charge) en sont obtenues par convolution , donnant l’ équation de Poisson

Δ V ( x ) = − 4 π k ρ ( x ) {displaystyle Delta V(mathbf {x} )=-4pi krho (mathbf {x} )}

où ρ est la fonction de distribution.

La constante π joue également un rôle analogue dans les potentiels quadridimensionnels associés aux équations d’ Einstein , une formule fondamentale qui constitue la base de la théorie générale de la relativité et décrit l’ interaction fondamentale de la gravitation résultant de la courbure de l’ espace – temps par la matière et l’énergie : ^[179]

R μ ν − 1 2 R g μ ν + Λ g μ ν = 8 π G c 4 T μ ν , {displaystyle R_{mu nu }-{frac {1}{2}}Rg_{mu nu }+Lambda g_{mu nu }={frac {8pi G}{c ^{4}}}T_{mu nu },}

où R _μν est le tenseur de courbure de Ricci , R est la courbure scalaire , g _μν est le tenseur métrique , Λ est la constante cosmologique , G est la constante gravitationnelle de Newton , c est la vitesse de la lumière dans le vide et T _μν est la contrainte– tenseur énergétique . Le côté gauche de l’équation d’Einstein est un analogue non linéaire du laplacien du tenseur métrique, et se réduit à celui de la limite de champ faible, avec le Λ g {displaystyle Lambda g} terme jouant le rôle d’un multiplicateur de Lagrange , et le membre de droite est l’analogue de la fonction de distribution, multiplié par 8π .

Formule intégrale de Cauchy

Les fonctions analytiques complexes peuvent être visualisées comme une collection de lignes de courant et d’équipotentielles, des systèmes de courbes se coupant à angle droit. Voici illustré le logarithme complexe de la fonction Gamma.

L’un des outils clés de l’analyse complexe est l’ intégration de contour d’une fonction sur une courbe de Jordan orientée positivement ( rectifiable ) γ . Une forme de la formule intégrale de Cauchy stipule que si un point z ₀ est intérieur à γ , alors ^[180]

∮ γ d z z − z 0 = 2 π i . {displaystyle oint _{gamma }{frac {dz}{z-z_{0}}}=2pi i.}

Bien que la courbe γ ne soit pas un cercle, et n’ait donc aucun lien évident avec la constante π , une preuve standard de ce résultat utilise le théorème de Morera , qui implique que l’intégrale est invariante par homotopie de la courbe, de sorte qu’elle peut être déformé en un cercle puis intégré explicitement en coordonnées polaires. Plus généralement, il est vrai que si une courbe fermée rectifiable γ ne contient pas z ₀ , alors l’intégrale ci-dessus vaut 2π i fois le nombre d’enroulement de la courbe.

La forme générale de la formule intégrale de Cauchy établit la relation entre les valeurs d’une fonction analytique complexe f ( z ) sur la courbe de Jordan γ et la valeur de f ( z ) en tout point intérieur z ₀ de γ : ^{[181] [182]}

∮ γ f ( z ) z − z 0 d z = 2 π i f ( z 0 ) {displaystyle oint _{gamma }{f(z) over z-z_{0}},dz=2pi if(z_{0})}

à condition que f ( z ) soit analytique dans la région délimitée par γ et s’étende continûment jusqu’à γ . La formule intégrale de Cauchy est un cas particulier du théorème des résidus , selon lequel si g ( z ) est une fonction méromorphe la région entourée par γ et est continue dans un voisinage de γ , alors

∮ γ g ( z ) d z = 2 π i ∑ Res ⁡ ( g , a k ) {displaystyle oint _{gamma}g(z),dz=2pi isum operatorname {Res} (g,a_{k})}

où la somme est celle des résidus aux pôles de g ( z ) .

La fonction gamma et l’approximation de Stirling

Tracé de la fonction gamma sur l’axe réel

La fonction factorielle n ! {displaystyle n !} est le produit de tous les entiers positifs par n . La fonction gamma étend le concept de factoriel (normalement défini uniquement pour les entiers non négatifs) à tous les nombres complexes, à l’exception des entiers réels négatifs, avec l’identité Γ ( n ) = ( n − 1 ) ! {displaystyleGamma (n)=(n-1) !} . Lorsque la fonction gamma est évaluée à des demi-entiers, le résultat contient π . Par example, Γ ( 1 / 2 ) = π {displaystyle Gamma (1/2)={sqrt {pi }}} et Γ ( 5 / 2 ) = 3 π 4 {textstyle Gamma (5/2)={frac {3{sqrt {pi }}}{4}}} . ^[183]

La fonction gamma est définie par son développement de produit Weierstrass : ^[184]

Γ ( z ) = e − γ z z ∏ n = 1 ∞ e z / n 1 + z / n {displaystyle Gamma (z)={frac {e^{-gamma z}}{z}}prod _{n=1}^{infty }{frac {e^{z/n} }{1+z/n}}}

où γ est la constante d’Euler–Mascheroni . Évaluée à z = 1/2 et au carré, l’équation Γ(1/2) ² = π se réduit à la formule du produit de Wallis. La fonction gamma est également reliée à la fonction zêta de Riemann et aux identités pour le déterminant fonctionnel , dans lequel la constante π joue un rôle important .

La fonction gamma est utilisée pour calculer le volume V _n ( r ) de la boule à n dimensions de rayon r dans l’espace euclidien à n dimensions, et la surface S _{n −1} ( r ) de sa frontière, la ( n −1 )-sphère dimensionnelle : ^[185]

V n ( r ) = π n / 2 Γ ( n 2 + 1 ) r n , {displaystyle V_{n}(r)={frac {pi ^{n/2}}{Gamma left({frac {n}{2}}+1right)}}r^{ n},} S n − 1 ( r ) = n π n / 2 Γ ( n 2 + 1 ) r n − 1 . {displaystyle S_{n-1}(r)={frac {npi ^{n/2}}{Gamma left({frac {n}{2}}+1right)}} r^{n-1}.}

De plus, il découle de l’ équation fonctionnelle que

2 π r = S n + 1 ( r ) V n ( r ) . {displaystyle 2pi r={frac {S_{n+1}(r)}{V_{n}(r)}}.}

La fonction gamma peut être utilisée pour créer une approximation simple de la fonction factorielle n ! pour grand n : n ! ∼ 2 π n ( n e ) n {textstyle n!sim {sqrt {2pi n}}left({frac {n}{e}}right)^{n}} qui est connue sous le nom d’approximation de Stirling . ^[186] De manière équivalente,

π = lim n → ∞ e 2 n n ! 2 2 n 2 n + 1 . {displaystyle pi =lim _{nto infty }{frac {e^{2n}n!^{2}}{2n^{2n+1}}}.}

Comme application géométrique de l’approximation de Stirling, soit Δ _n le simplexe standard dans l’espace euclidien à n dimensions, et ( n + 1)Δ _n le simplexe dont tous les côtés sont mis à l’échelle d’un facteur n + 1 . Puis

Vol ⁡ ( ( n + 1 ) Δ n ) = ( n + 1 ) n n ! ∼ e n + 1 2 π n . {displaystyle operatorname {Vol} ((n+1)Delta _{n})={frac {(n+1)^{n}}{n!}}sim {frac {e^{ n+1}}{sqrt {2pi n}}}.}

La conjecture de volume d’Ehrhart est qu’il s’agit de la limite supérieure (optimale) sur le volume d’un corps convexe contenant un seul point de réseau . ^[187]

Théorie des nombres et fonction zêta de Riemann

Chaque nombre premier a un groupe de Prüfer associé , qui sont des localisations arithmétiques du cercle. Les fonctions L de la théorie analytique des nombres sont également localisées en chaque nombre premier p . Résolution du problème de Bâle par la conjecture de Weil : la valeur de ζ (2) est l’ aire hyperbolique d’un domaine fondamental du groupe modulaire , multipliée par π /2 .

La fonction zêta de Riemann ζ ( s ) est utilisée dans de nombreux domaines des mathématiques. Lorsqu’il est évalué à s = ​​2 , il peut être écrit comme

ζ ( 2 ) = 1 1 2 + 1 2 2 + 1 3 2 + ⋯ {displaystyle zeta (2)={frac {1}{1^{2}}}+{frac {1}{2^{2}}}+{frac {1}{3^{2 }}}+cdots }

Trouver une solution simple pour cette série infinie était un problème célèbre en mathématiques appelé le problème de Bâle . Leonhard Euler l’a résolu en 1735 lorsqu’il a montré qu’il était égal à π ² /6 . ^[94] Le résultat d’Euler conduit au résultat de la théorie des nombres selon lequel la probabilité que deux nombres aléatoires soient relativement premiers (c’est-à-dire n’ayant aucun facteur partagé) est égale à 6/π ² . ^{[188] [189]} Cette probabilité est basée sur l’observation que la probabilité que tout nombre soit divisible par un nombre premier p est 1/ p(par exemple, chaque 7e entier est divisible par 7.) Par conséquent, la probabilité que deux nombres soient tous deux divisibles par ce nombre premier est 1/ p ² , et la probabilité qu’au moins l’un d’entre eux ne le soit pas est 1 − 1/ p ² . Pour des nombres premiers distincts, ces événements de divisibilité sont mutuellement indépendants ; donc la probabilité que deux nombres soient relativement premiers est donnée par un produit sur tous les nombres premiers : ^[190]

∏ p ∞ ( 1 − 1 p 2 ) = ( ∏ p ∞ 1 1 − p − 2 ) − 1 = 1 1 + 1 2 2 + 1 3 2 + ⋯ = 1 ζ ( 2 ) = 6 π 2 ≈ 61 % . {displaystyle {begin{aligned}prod _{p}^{infty}left(1-{frac {1}{p^{2}}}right)&=left(prod _ {p}^{infty }{frac {1}{1-p^{-2}}}right)^{-1}\[4pt]&={frac {1}{1+{ frac {1}{2^{2}}}+{frac {1}{3^{2}}}+cdots }}\[4pt]&={frac {1}{zeta ( 2)}}={frac {6}{pi ^{2}}}approx 61%.end{aligned}}}

Cette probabilité peut être utilisée en conjonction avec un générateur de nombres aléatoires pour approximer π en utilisant une approche de Monte Carlo. ^[191]

La solution du problème de Bâle implique que la quantité dérivée géométriquement π est liée de manière profonde à la distribution des nombres premiers. Il s’agit d’un cas particulier de la conjecture de Weil sur les nombres de Tamagawa , qui affirme l’égalité de tels produits infinis similaires de quantités arithmétiques , localisées à chaque nombre premier p , et d’une quantité géométrique : l’inverse du volume d’un certain espace localement symétrique . Dans le cas du problème de Bâle, il s’agit de la 3-variété hyperbolique SL ₂ ( R ) / SL ₂ ( Z ) . ^[192]

La fonction zêta satisfait également l’équation fonctionnelle de Riemann, qui implique π ainsi que la fonction gamma :

ζ ( s ) = 2 s π s − 1 sin ⁡ ( π s 2 ) Γ ( 1 − s ) ζ ( 1 − s ) . {displaystyle zeta (s)=2^{s}pi ^{s-1} sin left({frac {pi s}{2}}right) Gamma (1-s ) zeta (1-s).}

De plus, la dérivée de la fonction zêta satisfait

exp ⁡ ( − ζ ′ ( 0 ) ) = 2 π . {displaystyle exp(-zeta ‘(0))={sqrt {2pi }}.}

Une conséquence est que π peut être obtenu à partir du déterminant fonctionnel de l’ oscillateur harmonique . Ce déterminant fonctionnel peut être calculé via une expansion de produit et est équivalent à la formule du produit de Wallis. ^[193] Le calcul peut être refondu en mécanique quantique , en particulier l’ approche variationnelle du spectre de l’atome d’hydrogène . ^[194]

Série de Fourier

π apparaît en caractères de nombres p-adiques (illustrés), qui sont des éléments d’un groupe de Prüfer . La thèse de Tate fait un usage intensif de cette machinerie. ^[195]

La constante π apparaît aussi naturellement dans les séries de Fourier des fonctions périodiques . Les fonctions périodiques sont des fonctions sur le groupe T = R / Z de parties fractionnaires de nombres réels. La décomposition de Fourier montre qu’une fonction à valeurs complexes f sur T peut s’écrire comme une superposition linéaire infinie de caractères unitaires de T . C’est-à-dire des homomorphismes de groupes continus de T au groupe de cercles U (1) des nombres complexes de modules unitaires. C’est un théorème que tout caractère de Test l’une des exponentielles complexes e n ( x ) = e 2 π i n x {displaystyle e_{n}(x)=e^{2pi inx}} .

Il existe un caractère unique sur T , à conjugaison complexe près, c’est-à-dire un isomorphisme de groupe. En utilisant la mesure de Haar sur le groupe de cercles, la constante π est la moitié de l’amplitude de la dérivée Radon – Nikodym de ce caractère. Les autres caractères ont des dérivées dont les grandeurs sont des multiples entiers positifs de 2 π . ^[20] Par conséquent, la constante π est le nombre unique tel que le groupe T , muni de sa mesure de Haar, est Pontrjagin dual au treillis des multiples entiers de 2 π . ^[196] Il s’agit d’une version unidimensionnelleFormule de sommation de Poisson .

Formes modulaires et fonctions thêta

Les fonctions thêta se transforment sous le réseau de périodes d’une courbe elliptique.

La constante π est liée de manière profonde à la théorie des formes modulaires et des fonctions thêta . Par exemple, l’ algorithme de Chudnovsky fait intervenir de manière essentielle le j-invariant d’une courbe elliptique .

Les formes modulaires sont des fonctions holomorphes dans le demi-plan supérieur caractérisées par leurs propriétés de transformation sous le groupe modulaire S L 2 ( Z ) {displaystyle mathrm {SL} _{2}(mathbb {Z} )} (ou ses divers sous-groupes), un treillis dans le groupe S L 2 ( R ) {displaystyle mathrm {SL} _{2}(mathbb {R} )} . Un exemple est la fonction thêta de Jacobi

θ ( z , τ ) = ∑ n = − ∞ ∞ e 2 π i n z + i π n 2 τ {displaystyle theta (z,tau )=sum _{n=-infty}^{infty}e^{2pi inz+ipi n^{2}tau }}

qui est une sorte de forme modulaire appelée forme de Jacobi . ^[197] Ceci est parfois écrit en termes de nome q = e π i τ {displaystyle q=e^{pi jetau}} .

La constante π est l’unique constante faisant de la fonction thêta de Jacobi une forme automorphe , c’est-à-dire qu’elle se transforme d’une manière spécifique. Certaines identités sont valables pour toutes les formes automorphes. Un exemple est

θ ( z + τ , τ ) = e − π i τ − 2 π i z θ ( z , τ ) , {displaystyle theta (z+tau ,tau )=e^{-pi itau -2pi iz}theta (z,tau ),}

ce qui implique que θ se transforme en une représentation sous le groupe de Heisenberg discret . Les formes modulaires générales et d’autres fonctions thêta impliquent également π , encore une fois à cause du théorème de Stone-von Neumann . ^[197]

Distribution de Cauchy et théorie du potentiel

La Sorcière d’Agnesi , du nom de Maria Agnesi (1718–1799), est une construction géométrique du graphe de la distribution de Cauchy. La distribution de Cauchy régit le passage des particules browniennes à travers une membrane.

La distribution de Cauchy

g ( x ) = 1 π ⋅ 1 x 2 + 1 {displaystyle g(x)={frac {1}{pi }}cdot {frac {1}{x^{2}+1}}}

est un fonction de densité de probabilité . La probabilité totale est égale à un, du fait de l’intégrale :

∫ − ∞ ∞ 1 x 2 + 1 d x = π . {displaystyle int _{-infty }^{infty }{frac {1}{x^{2}+1}},dx=pi .}

L’ entropie de Shannon de la distribution de Cauchy est égale à ln(4π) , ce qui implique également π .

La distribution de Cauchy joue un rôle important dans la théorie du potentiel car c’est la mesure de Furstenberg la plus simple, le noyau de Poisson classique associé à un mouvement brownien dans un demi-plan. ^[198] Les fonctions harmoniques conjuguées et donc aussi la transformée de Hilbert sont associées aux asymptotiques du noyau de Poisson. La transformée de Hilbert H est la transformée intégrale donnée par la valeur principale de Cauchy de l’ intégrale singulière

H f ( t ) = 1 π ∫ − ∞ ∞ f ( x ) d x x − t . {displaystyle Hf(t)={frac {1}{pi }}int _{-infty }^{infty }{frac {f(x),dx}{xt}}.}

La constante π est l’unique facteur de normalisation (positif) tel que H définit une structure complexe linéaire sur l’espace de Hilbert de fonctions à valeurs réelles intégrables au carré sur la ligne réelle. ^[199] La transformée de Hilbert, comme la transformée de Fourier, peut être caractérisée uniquement par ses propriétés de transformation sur l’espace de Hilbert L ² ( R ) : à un facteur de normalisation près, c’est l’unique opérateur linéaire borné qui commute avec les dilatations positives et anti-commute avec toutes les réflexions de la ligne réelle. ^[200] La constante π est l’unique facteur de normalisation qui rend cette transformation unitaire.

Dans l’ensemble de Mandelbrot

Le ensemble de Mandelbrot peut être utilisé pour approximer π .

Une occurrence de π dans la fractale appelée l’ ensemble de Mandelbrot a été découverte par David Boll en 1991. ^[201] Il a examiné le comportement de l’ensemble de Mandelbrot près du “cou” à (−0,75, 0) . Lorsque le nombre d’itérations jusqu’à la divergence pour le point (−0,75, ε ) est multiplié par ε , le résultat se rapproche de π lorsque ε se rapproche de zéro. Le point (0,25 + ε , 0) à l’extrémité de la grande “vallée” du côté droit de l’ensemble de Mandelbrot se comporte de manière similaire : le nombre d’itérations jusqu’à la divergence multiplié par la racine carrée de εtend vers π . ^{[201] [202]}

En dehors des mathématiques

Décrire des phénomènes physiques

Bien qu’il ne s’agisse pas d’une constante physique , π apparaît régulièrement dans les équations décrivant les principes fondamentaux de l’univers, souvent en raison de la relation de π avec le cercle et les systèmes de coordonnées sphériques . Une formule simple du domaine de la mécanique classique donne la période approximative T d’un pendule simple de longueur L , oscillant avec une petite amplitude ( g est l’ accélération gravitationnelle de la Terre ): ^[203]

T ≈ 2 π L g . {displaystyle Tenviron 2pi {sqrt {frac {L}{g}}}.}

L’une des formules clés de la mécanique quantique est le principe d’incertitude de Heisenberg , qui montre que l’incertitude dans la mesure de la position d’une particule (Δ x ) et de la quantité de mouvement (Δ p ) ne peut pas être arbitrairement petite en même temps (où h est la constante de Planck ): ^[204]

Δ x Δ p ≥ h 4 π . {displaystyle Delta x,Delta pgeq {frac {h}{4pi }}.}

Le fait que π soit approximativement égal à 3 joue un rôle dans la durée de vie relativement longue de l’orthopositronium . La durée de vie inverse à l’ordre le plus bas dans la constante de structure fine α est ^[205]

1 τ = 2 π 2 − 9 9 π m α 6 , {displaystyle {frac {1}{tau}}=2{frac {pi ^{2}-9}{9pi }}malpha ^{6},}

où m est la masse de l’électron.

π est présent dans certaines formules d’ingénierie structurelle, telles que la formule de flambement dérivée d’Euler, qui donne la charge axiale maximale F qu’une colonne longue et élancée de longueur L , de module d’élasticité E et de moment d’inertie de zone I peut supporter sans flambage : ^[206]

F = π 2 E I L 2 . {displaystyle F={frac {pi ^{2}EI}{L^{2}}}.}

Le domaine de la dynamique des fluides contient π dans la loi de Stokes , qui se rapproche de la force de frottement F exercée sur de petits objets sphériques de rayon R , se déplaçant à la vitesse v dans un fluide de viscosité dynamique η : ^[207]

F = 6 π η R v . {displaystyle F=6pi eta Rv.}

En électromagnétisme, la constante de perméabilité au vide μ ₀ apparaît dans les équations de Maxwell , qui décrivent les propriétés des champs électriques et magnétiques et du rayonnement électromagnétique . Avant le 20 mai 2019, il était défini comme exactement

μ 0 = 4 π × 10 − 7 H/m ≈ 1.2566370614 … × 10 − 6 N/A 2 . {displaystyle mu _{0}=4pi times 10^{-7}{text{ H/m}}approx 1.2566370614ldots times 10^{-6}{text{ N/A }}^{2}.}

Une relation pour la vitesse de la lumière dans le vide, c peut être dérivée des équations de Maxwell dans le milieu du vide classique en utilisant une relation entre μ ₀ et la constante électrique (permittivité du vide) , ε ₀ en unités SI :

c = 1 μ 0 ε 0 . {displaystyle c={1 over {sqrt {mu _{0}varepsilon _{0}}}}.}

Dans des conditions idéales (pente douce uniforme sur un substrat érodable de manière homogène), la sinuosité d’une rivière sinueuse se rapproche de π . La sinuosité est le rapport entre la longueur réelle et la distance en ligne droite de la source à la bouche. Des courants plus rapides le long des bords extérieurs des virages d’une rivière provoquent plus d’érosion que le long des bords intérieurs, poussant ainsi les virages encore plus loin et augmentant le bouclage global de la rivière. Cependant, cette boucle finit par amener la rivière à se replier sur elle-même par endroits et à se “court-circuiter”, créant ainsi un lac à arc de bœuf. L’équilibre entre ces deux facteurs opposés conduit à un rapport moyen de π entre la longueur réelle et la distance directe entre la source et l’embouchure. ^{[208] [209]}

Mémorisation des chiffres

La piphilologie est la pratique consistant à mémoriser un grand nombre de chiffres de π , ^[210] et les records du monde sont conservés par le Guinness World Records . Le record de mémorisation des chiffres de π , certifié par Guinness World Records, est de 70 000 chiffres, récités en Inde par Rajveer Meena en 9 heures et 27 minutes le 21 mars 2015. ^[211] En 2006, Akira Haraguchi , un ingénieur japonais à la retraite, a affirmé avoir récité 100 000 décimales, mais l’affirmation n’a pas été vérifiée par Guinness World Records. ^[212]

Une technique courante consiste à mémoriser une histoire ou un poème dans lequel les longueurs des mots représentent les chiffres de π : le premier mot a trois lettres, le deuxième mot en a une, le troisième en a quatre, le quatrième en a une, le cinquième en a cinq, et bientôt. Ces aides à la mémorisation sont appelées mnémoniques . Un premier exemple d’un mnémonique pour pi, initialement conçu par le scientifique anglais James Jeans , est “Comment je veux un verre, alcoolisé bien sûr, après les lourdes conférences impliquant la mécanique quantique.” ^[210] Lorsqu’un poème est utilisé, il est parfois appelé un piem . ^[213] Des poèmes pour mémoriser π ont été composés dans plusieurs langues en plus de l’anglais. ^[210]Les mémorisateurs π d’établissement d’enregistrements ne reposent généralement pas sur des poèmes, mais utilisent plutôt des méthodes telles que la mémorisation des modèles de nombres et la méthode des lieux . ^[214]

Quelques auteurs ont utilisé les chiffres de π pour établir une nouvelle forme d’ écriture contrainte , où les longueurs de mots sont nécessaires pour représenter les chiffres de π . La Cadaeic Cadenza contient les 3835 premiers chiffres de π de cette manière, ^[215] et le livre complet Not a Wake contient 10 000 mots, chacun représentant un chiffre de π . ^[216]

Dans la culture populaire

Une tarte aux pis. Les tartes sont circulaires, et “pie” et π sont des homophones , faisant de pie un sujet fréquent de jeux de mots pi .

Peut-être en raison de la simplicité de sa définition et de sa présence omniprésente dans les formules, π a été représenté dans la culture populaire plus que d’autres constructions mathématiques. ^[217]

Dans la coproduction documentaire de 2008 de l’ Open University et de la BBC , The Story of Maths , diffusée en octobre 2008 sur BBC Four , le mathématicien britannique Marcus du Sautoy montre une visualisation de la formule – historiquement la première exacte – de calcul de π lors d’une visite en Inde et de l’exploration de ses contributions à la trigonométrie. ^[218]

Au Palais de la Découverte (musée des sciences à Paris), il y a une salle circulaire connue sous le nom de salle pi . Sur son mur sont inscrits 707 chiffres de π . Les chiffres sont de grands caractères en bois fixés au plafond en forme de dôme. Les chiffres étaient basés sur un calcul de 1873 du mathématicien anglais William Shanks , qui comprenait une erreur commençant au 528e chiffre. L’erreur a été détectée en 1946 et corrigée en 1949. ^[219]

Dans le roman Contact de 1985 de Carl Sagan , il est suggéré que le créateur de l’univers a enfoui un message profondément dans les chiffres de π . ^[220] Les chiffres de π ont également été incorporés dans les paroles de la chanson “Pi” de l’album de 2005 Aerial de Kate Bush . ^[221]

Dans l’ épisode de Star Trek de 1967 ” Wolf in the Fold “, un ordinateur hors de contrôle est contenu en recevant l’instruction de ” calculer jusqu’au dernier chiffre la valeur de π “, même si ” π est une figure transcendantale sans résolution “. ^[222]

Aux États-Unis, Pi Day tombe le 14 mars (écrit 3/14 dans le style américain) et est populaire parmi les étudiants. ^[223] π et sa représentation numérique sont souvent utilisés par les « geeks des mathématiques » autoproclamés pour des blagues internes parmi les groupes à l’esprit mathématique et technologique. Plusieurs acclamations universitaires au Massachusetts Institute of Technology incluent “3.14159”. ^[224] Pi Day en 2015 était particulièrement significatif parce que la date et l’heure 14/03/15 09:26:53 reflétaient beaucoup plus de chiffres de pi. ^{[225] [226]}Dans les régions du monde où les dates sont généralement notées au format jour/mois/année, le 22 juillet représente le “jour d’approximation Pi”, car 22/7 = 3,142857. ^[227]

Au cours de la vente aux enchères de 2011 pour le portefeuille de brevets technologiques précieux de Nortel , Google a fait une série d’offres inhabituellement spécifiques basées sur des constantes mathématiques et scientifiques, y compris π . ^[228]

En 1958 , Albert Eagle proposa de remplacer π par τ ( tau ), où τ = π /2 , pour simplifier les formules. ^[229] Cependant, aucun autre auteur n’est connu pour utiliser τ de cette manière. Certaines personnes utilisent une valeur différente, τ = 2 π = 6,28318… , ^[230] arguant que τ , comme le nombre de radians dans un tour , ou comme le rapport de la circonférence d’un cercle à son rayon plutôt que son diamètre, est plus naturel que π et simplifie de nombreuses formules. ^{[231] [232]}Des célébrations de ce nombre, car il équivaut approximativement à 6,28, en faisant le 28 juin “Tau Day” et en mangeant “deux fois le gâteau”, ^[233] ont été rapportées dans les médias. Cependant, cette utilisation de τ n’a pas fait son chemin dans les mathématiques traditionnelles. ^[234] Tau a été ajouté au langage de programmation Python (comme math.tau) dans la version 3.6. ^[235]

En 1897, un mathématicien amateur a tenté de persuader la législature de l’Indiana d’adopter l ‘ Indiana Pi Bill , qui décrivait une méthode pour quadriller le cercle et contenait un texte qui impliquait diverses valeurs incorrectes pour π , dont 3,2. Le projet de loi est connu comme une tentative d’établir une valeur de constante mathématique par décret législatif. Le projet de loi a été adopté par la Chambre des représentants de l’Indiana, mais rejeté par le Sénat, ce qui signifie qu’il n’est pas devenu une loi. ^[236]

Dans la culture informatique

Dans la culture Internet contemporaine , les individus et les organisations rendent fréquemment hommage au nombre π . Par exemple, l’ informaticien Donald Knuth a laissé les numéros de version de son programme TeX s’approcher de π . Les versions sont 3, 3.1, 3.14, etc. ^[237]

Voir également

• Approximations de π
• Chronologie du calcul de π
• Liste des constantes mathématiques

Références

Remarques

1. ^ En particulier, π est supposé être un nombre normal , ce qui implique un type spécifique de hasard statistique sur ses chiffres dans toutes les bases.
2. ^ L’intégrale précise utilisée par Weierstrass était π = ∫ − ∞ ∞ d x 1 + x 2 . {displaystyle pi =int _{-infty }^{infty }{frac {dx}{1+x^{2}}}.} Remmert 2012 , p. 148
3. ^ Le polynôme montré est les premiers termes de l’ expansion en série de Taylor du fonction sinus .
4. ↑ Prétendument construit pour que le cercle dont le rayon est égal à la hauteur de la pyramide ait une circonférence égale au périmètre de la base

Citations

1. ^ Andrews, Askey & Roy 1999 , p. 59.
2. ^ Gupta 1992 , pp. 68-71.
3. ^ ^{un b} Jones, Guillaume (1706). Synopsis Palmariorum Matheseos : ou, une Nouvelle Introduction aux Mathématiques . pp. 243, 263. Archivé de l’original le 25 mars 2012 . Récupéré le 15 octobre 2017 .
4. ^ “π ^e milliards de chiffres de π” . pi2e.ch . Archivé de l’original le 6 décembre 2016.
5. ^ Haruka Iwao, Emma (14 mars 2019). “Pi dans le ciel : calcul d’un record de 31,4 billions de chiffres de la constante d’Archimède sur Google Cloud” . Plate-forme Google Cloud . Archivé de l’original le 19 octobre 2019 . Récupéré le 12 avril 2019 .
6. ^ Arndt & Haenel 2006 , p. 17.
7. ^ Bailey et al. 1997 , p. 50–56.
8. ^ Boeing 2016 .
9. ^ “pi” . Dictionary.reference.com. 2 mars 1993. Archivé de l’original le 28 juillet 2014 . Récupéré le 18 juin 2012 .
10. ^ ^{un bc _} 2006 , p. 8.
11. ^ ^{un bc Weisstein} , Eric W. “Pi” . mathworld.wolfram.com . Récupéré le 10 août 2020 .
12. ^ Apostol, Tom (1967). Calculus, volume 1 (2e éd.). Wiley.. p. 102 : “D’un point de vue logique, cela n’est pas satisfaisant à ce stade car nous n’avons pas encore discuté de la notion de longueur d’arc.” La longueur de l’arc est introduite p. 529.
13. ^ ^{un bc Remmert} 2012 , p. 129.
14. ^ Baltzer, Richard (1870), Die Elemente der Mathematik [ Les éléments des mathématiques ] (en allemand), Hirzel, p. 195, archivé de l’original le 14 septembre 2016
15. ^ Landau, Edmund (1934), Einführung in die Differentialrechnung und Integralrechnung (en allemand), Noordoff, p. 193
16. ^ ^{un b} Rudin, Walter (1976). Principes d’analyse mathématique . McGraw-Hill. ISBN 978-0-07-054235-8., p. 183.
17. ^ Rudin, Walter (1986). Analyse réelle et complexe . McGraw-Hill. , p. 2.
18. ^ Ahlfors, Lars (1966), Analyse complexe , McGraw-Hill, p. 46
19. ^ Bourbaki, Nicolas (1981), Topologie générale , Springer, §VIII.2.
20. ^ ^{a b} Bourbaki, Nicolas(1979),Fonctions d’une variable réelle(en français), Springer , §II.3.
21. ^ ^{un b} Arndt & Haenel 2006, p. 5.
22. ^ Salikhov, V. (2008). “Sur la mesure d’irrationalité de pi”. Enquêtes mathématiques russes . 53 (3): 570–572. Bibcode : 2008RuMaS..63..570S . doi : 10.1070/RM2008v063n03ABEH004543 .
23. ^ ^{un b} Arndt & Haenel 2006 , pp. 22–23 Preuss, Paul (23 juillet 2001). “Les chiffres de Pi sont-ils aléatoires ? Un chercheur de laboratoire peut détenir la clé” . Laboratoire national Lawrence de Berkeley . Archivé de l’original le 20 octobre 2007 . Récupéré le 10 novembre 2007 .
24. ^ Arndt & Haenel 2006 , p. 22, 28–30.
25. ^ Arndt & Haenel 2006 , p. 3.
26. ^ Mayer, Steve. « La Transcendance de π » . Archivé de l’original le 29 septembre 2000 . Récupéré le 4 novembre 2007 .
27. ^ Posamentier & Lehmann 2004 , p. 25
28. ^ Eymard & Lafon 1999 , p. 129
29. ^ Beckman 1989 , p. 37 Schlager, Neil; Lauer, Josh (2001). La science et son temps : comprendre l’importance sociale de la découverte scientifique . Groupe Gale. ISBN
    978-0-7876-3933-4. Archivé de l’original le 13 décembre 2019 . Récupéré le 19 décembre 2019 ., p. 185.
30. ^ ^{un b} Eymard & Lafon 1999 , p. 78
31. ^ Sloane, N.J.A. (éd.). “Séquence A001203 (fraction continue pour Pi)” . L’ encyclopédie en ligne des séquences d’entiers . Fondation OEIS.Récupéré le 12 avril 2012.
32. ^ Lange, LJ (mai 1999). “Une fraction continue élégante pour π “. Le mensuel mathématique américain . 106 (5): 456–458. doi : 10.2307/2589152 . JSTOR 2589152 .
33. ^ Arndt & Haenel 2006 , p. 240.
34. ^ Arndt & Haenel 2006 , p. 242.
35. ^ Kennedy, ES (1978), “Abu-r-Raihan al-Biruni, 973-1048”, Journal pour l’Histoire de l’Astronomie , 9 : 65, Bibcode : 1978JHA…..9…65K , doi : 10.1177/002182867800900106 , S2CID 126383231. Ptolémée a utilisé une approximation à trois chiffres sexagésimaux, et Jamshīd al-Kāshī l’a étendue à neuf chiffres; voir Aaboe, Asger (1964), Episodes from the Early History of Mathematics , New Mathematical Library, vol. 13, New York : Random House, p. 125, ISBN 978-0-88385-613-0, archivé de l’original le 29 novembre 2016
36. ^ Ayers 1964 , p. 100
37. ^ ^{un b} Bronshteĭn & Semendiaev 1971 , p. 592
38. ^ Maor, Eli, E: L’histoire d’un nombre , Princeton University Press, 2009, p. 160, ISBN 978-0-691-14134-3 (les “cinq constantes les plus importantes”).
39. ^ Weisstein, Eric W. “Racines de l’unité” . MathWorld .
40. ^ Petrie, WMF Sagesse des Egyptiens (1940)
41. ^ Verner, Miroslav. Les pyramides : le mystère, la culture et la science des grands monuments égyptiens. presse bosquet. 2001 (1997). ISBN 0-8021-3935-3
42. ^ Rossi 2004 .
43. ^ Legon, JAR sur les dimensions et les proportions de la pyramide (1991) Discussions en égyptologie (20) 25–34 “Proportions de la pyramide égyptienne” . Archivé de l’original le 18 juillet 2011 . Récupéré le 7 juin 2011 .
44. ^ “Nous pouvons conclure que bien que les anciens Égyptiens ne pouvaient pas définir avec précision la valeur de π , en pratique ils l’utilisaient”. En ligneVerner, M. (2003). Les pyramides : leur archéologie et leur histoire ., p. 70. Petrie (1940). Sagesse des Égyptiens .
    , p. 30.
    Voir aussi Legon, JAR (1991). “Sur les dimensions et les proportions de la pyramide” . Discussions en égyptologie . 20 : 25–34. Archivé de l’original le 18 juillet 2011..
    Voir aussi Petrie, WMF (1925). “Enquêtes sur les Grandes Pyramides” . Nature . 116 (2930): 942. Bibcode : 1925Natur.116..942P . doi : 10.1038/116942a0 . S2CID 33975301 .
45. ^ Rossi 2004 , pp. 60-70, 200.
46. ^ Shermer, Michael , L’Encyclopédie Sceptique de la Pseudoscience , ABC-CLIO, 2002, pp. 407-408, ISBN 978-1-57607-653-8 . Voir aussi Fagan, Garrett G., Archaeological Fantasies: How Pseudoarchaeology Misrepresents The Past and Misleads the Public , Routledge, 2006, ISBN 978-0-415-30593-8 . Pour une liste d’explications de la forme qui n’impliquent pas π , voir Herz-Fischler, Roger (2000). La forme de la Grande Pyramide . Presses de l’Université Wilfrid Laurier. p. 67–77, 165–166. ISBN
    978-0-88920-324-2. Archived from the original on 29 November 2016. Retrieved 5 June 2013.
47. ^ ^{a b} Arndt & Haenel 2006, p. 167.
48. ^ Chaitanya, Krishna. A profile of Indian culture. Archived 29 November 2016 at the Wayback Machine Indian Book Company (1975). p. 133.
49. ^ Arndt & Haenel 2006, p. 169.
50. ^ Arndt & Haenel 2006, p. 170.
51. ^ Arndt & Haenel 2006, pp. 175, 205.
52. ^ “The Computation of Pi by Archimedes: The Computation of Pi by Archimedes – File Exchange – MATLAB Central”. Mathworks.com. Archived from the original on 25 February 2013. Retrieved 12 March 2013.
53. ^ Arndt & Haenel 2006, p. 171.
54. ^ Arndt & Haenel 2006, p. 176.
55. ^ Boyer & Merzbach 1991, p. 168.
56. ^ Arndt & Haenel 2006, pp. 15–16, 175, 184–186, 205. Grienberger achieved 39 digits in 1630; Sharp 71 digits in 1699.
57. ^ Arndt & Haenel 2006, pp. 176–177.
58. ^ ^{a b} Boyer & Merzbach 1991, p. 202
59. ^ Arndt & Haenel 2006, p. 177.
60. ^ Arndt & Haenel 2006, p. 178.
61. ^ Arndt & Haenel 2006, p. 179.
62. ^ ^{a b} Arndt & Haenel 2006, p. 180.
63. ^ Azarian, Mohammad K. (2010). “al-Risāla al-muhītīyya: A Summary”. Missouri Journal of Mathematical Sciences. 22 (2): 64–85. doi:10.35834/mjms/1312233136.
64. ^ O’Connor, John J.; Robertson, Edmund F. (1999). “Ghiyath al-Din Jamshid Mas’ud al-Kashi”. MacTutor History of Mathematics archive. Archived from the original on 12 April 2011. Retrieved 11 August 2012.
65. ^ ^{a b c} Arndt & Haenel 2006, p. 182.
66. ^ Arndt & Haenel 2006, pp. 182–183.
67. ^ Arndt & Haenel 2006, p. 183.
68. ^ Grienbergerus, Christophorus (1630). Elementa Trigonometrica (PDF) (in Latin). Archived from the original (PDF) on 1 February 2014. His evaluation was 3.14159 26535 89793 23846 26433 83279 50288 4196 < π < 3.14159 26535 89793 23846 26433 83279 50288 4199.
69. ^ Brezinski, C. (2009), “Some pioneers of extrapolation methods”, The Birth of Numerical Analysis, World Scientific, pp. 1–22, doi:10.1142/9789812836267_0001, ISBN 978-981-283-625-0
70. ^ Yoder, J. (1996). “Following in the footsteps of geometry: The mathematical world of Christiaan Huygens”. DBNL. Retrieved 28 August 2021.{{cite web}}: CS1 maint: url-status (link)
71. ^ ^{a b} Arndt & Haenel 2006, pp. 185–191
72. ^ Roy 1990, pp. 101–102.
73. ^ Arndt & Haenel 2006, pp. 185–186.
74. ^ ^{a b c} Roy 1990, pp. 101–102
75. ^ Joseph 1991, p. 264.
76. ^ ^{a b} Arndt & Haenel 2006, p. 188. Newton quoted by Arndt.
77. ^ ^{a b} Arndt & Haenel 2006, p. 187.
78. ^ OEIS: A060294
79. ^ Variorum de rebus mathematicis responsorum liber VIII.
80. ^ Arndt & Haenel 2006, pp. 188–189.
81. ^ ^{a b} Eymard & Lafon 1999, pp. 53–54
82. ^ Arndt & Haenel 2006, p. 189.
83. ^ Arndt & Haenel 2006, p. 156.
84. ^ Arndt & Haenel 2006, pp. 192–193.
85. ^ ^{a b} Arndt & Haenel 2006, pp. 72–74
86. ^ Arndt & Haenel 2006, pp. 192–196, 205.
87. ^ Arndt & Haenel 2006, pp. 194–196
88. ^ Hayes, Brian (September 2014). “Pencil, Paper, and Pi”. American Scientist. Vol. 102, no. 5. p. 342. doi:10.1511/2014.110.342. Retrieved 22 January 2022.
89. ^ ^{a b} Borwein, J.M.; Borwein, P.B. (1988). “Ramanujan and Pi”. Scientific American. 256 (2): 112–117. Bibcode:1988SciAm.258b.112B. doi:10.1038/scientificamerican0288-112.
    Arndt & Haenel 2006, pp. 15–17, 70–72, 104, 156, 192–197, 201–202
90. ^ Arndt & Haenel 2006, pp. 69–72.
91. ^ Borwein, J.M.; Borwein, P.B.; Dilcher, K. (1989). “Pi, Euler Numbers, and Asymptotic Expansions”. American Mathematical Monthly. 96 (8): 681–687. doi:10.2307/2324715. hdl:1959.13/1043679. JSTOR 2324715.
92. ^ Arndt & Haenel 2006, p. 223: (formula 16.10).
93. ^ Wells, David (1997). The Penguin Dictionary of Curious and Interesting Numbers (revised ed.). Penguin. p. 35. ISBN 978-0-14-026149-3.
94. ^ ^{a b} Posamentier & Lehmann 2004, p. 284
95. ^ Lambert, Johann, “Mémoire sur quelques propriétés remarquables des quantités transcendantes circulaires et logarithmiques”, reprinted in Berggren, Borwein & Borwein 1997, pp. 129–140
96. ^ Lindemann, F. (1882), “Über die Ludolph’sche Zahl”, Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin, 2: 679–682
97. ^ Arndt & Haenel 2006, p. 196.
98. ^ Hardy and Wright 1938 and 2000: 177 footnote § 11.13–14 references Lindemann’s proof as appearing at Math. Ann. 20 (1882), 213–225.
99. ^ cf Hardy and Wright 1938 and 2000:177 footnote § 11.13–14. The proofs that e and π are transcendental can be found on pp. 170–176. They cite two sources of the proofs at Landau 1927 or Perron 1910; see the “List of Books” at pp. 417–419 for full citations.
100. ^ Oughtred, William (1652). Theorematum in libris Archimedis de sphaera et cylindro declarario (in Latin). Excudebat L. Lichfield, Veneunt apud T. Robinson. δ.π :: semidiameter. semiperipheria
101. ^ ^{a b} Cajori, Florian (2007). A History of Mathematical Notations: Vol. II. Cosimo, Inc. pp. 8–13. ISBN 978-1-60206-714-1. the ratio of the length of a circle to its diameter was represented in the fractional form by the use of two letters … J.A. Segner … in 1767, he represented 3.14159… by δ:π, as did Oughtred more than a century earlier
102. ^ ^{a b} Smith, David E. (1958). History of Mathematics. Courier Corporation. p. 312. ISBN 978-0-486-20430-7.
103. ^ Archibald, R.C. (1921). “Historical Notes on the Relation e − ( π / 2 ) = i i {displaystyle e^{-(pi /2)}=i^{i}} “. The American Mathematical Monthly. 28 (3): 116–121. doi:10.2307/2972388. JSTOR 2972388. It is noticeable that these letters are never used separately, that is, π is not used for ‘Semiperipheria’
104. ^ ^{a b c d} Arndt & Haenel 2006, p. 166.
105. ^ See, for example, Oughtred, William (1648). Clavis Mathematicæ [The key to mathematics] (in Latin). London: Thomas Harper. p. 69. (English translation: Oughtred, William (1694). Key of the Mathematics. J. Salusbury.)
106. ^ Barrow, Isaac (1860). “Lecture XXIV”. In Whewell, William (ed.). The mathematical works of Isaac Barrow (in Latin). Harvard University. Cambridge University press. p. 381.
107. ^ Gregorii, Davidis (1695). “Davidis Gregorii M.D. Astronomiae Professoris Sauiliani & S.R.S. Catenaria, Ad Reverendum Virum D. Henricum Aldrich S.T.T. Decanum Aedis Christi Oxoniae”. Philosophical Transactions (in Latin). 19: 637–652. Bibcode:1695RSPT…19..637G. doi:10.1098/rstl.1695.0114. JSTOR 102382.
108. ^ Arndt & Haenel 2006, p. 165: A facsimile of Jones’ text is in Berggren, Borwein & Borwein 1997, pp. 108–109.
109. ^ See Schepler 1950, p. 220: William Oughtred used the letter π to represent the periphery (that is, the circumference) of a circle.
110. ^ Segner, Joannes Andreas (1756). Cursus Mathematicus (in Latin). Halae Magdeburgicae. p. 282. Archived from the original on 15 October 2017. Retrieved 15 October 2017.
111. ^ Euler, Leonhard (1727). “Tentamen explicationis phaenomenorum aeris” (PDF). Commentarii Academiae Scientiarum Imperialis Petropolitana (in Latin). 2: 351. E007. Archived (PDF) from the original on 1 April 2016. Retrieved 15 October 2017. Sumatur pro ratione radii ad peripheriem, I : π English translation by Ian Bruce Archived 10 June 2016 at the Wayback Machine: “π is taken for the ratio of the radius to the periphery [note that in this work, Euler’s π is double our π.]”
112. ^ Euler, Leonhard (1747). Henry, Charles (ed.). Lettres inédites d’Euler à d’Alembert. Bullettino di Bibliografia e di Storia delle Scienze Matematiche e Fisiche (in French). Vol. 19 (published 1886). p. 139. E858. Car, soit π la circonference d’un cercle, dout le rayon est = 1 English translation in Cajori, Florian (1913). “History of the Exponential and Logarithmic Concepts”. The American Mathematical Monthly. 20 (3): 75–84. doi:10.2307/2973441. JSTOR 2973441. Letting π be the circumference (!) of a circle of unit radius
113. ^ Euler, Leonhard (1736). “Ch. 3 Prop. 34 Cor. 1”. Mechanica sive motus scientia analytice exposita. (cum tabulis) (in Latin). Vol. 1. Academiae scientiarum Petropoli. p. 113. E015. Denotet 1 : π rationem diametri ad peripheriam English translation by Ian Bruce Archived 10 June 2016 at the Wayback Machine : “Let 1 : π denote the ratio of the diameter to the circumference”
114. ^ Euler, Leonhard (1707–1783) (1922). Leonhardi Euleri opera omnia. 1, Opera mathematica. Volumen VIII, Leonhardi Euleri introductio in analysin infinitorum. Tomus primus / ediderunt Adolf Krazer et Ferdinand Rudio (in Latin). Lipsae: B.G. Teubneri. pp. 133–134. E101. Archived from the original on 16 October 2017. Retrieved 15 October 2017.
115. ^ Segner, Johann Andreas von (1761). Cursus Mathematicus: Elementorum Analyseos Infinitorum Elementorum Analyseos Infinitorvm (in Latin). Renger. p. 374. Si autem π notet peripheriam circuli, cuius diameter est 2
116. ^ Arndt & Haenel 2006, p. 205.
117. ^ ^{a b} Arndt & Haenel 2006, p. 197.
118. ^ Reitwiesner 1950.
119. ^ Arndt & Haenel 2006, pp. 15–17.
120. ^ Arndt & Haenel 2006, p. 131.
121. ^ Arndt & Haenel 2006, pp. 132, 140.
122. ^ ^{a b} Arndt & Haenel 2006, p. 87.
123. ^ Arndt & Haenel 2006, pp. 111 (5 times), pp. 113–114 (4 times):See Borwein & Borwein 1987 for details of algorithms
124. ^ ^{a b c} Bailey, David H. (16 May 2003). “Some Background on Kanada’s Recent Pi Calculation” (PDF). Archived (PDF) from the original on 15 April 2012. Retrieved 12 April 2012.
125. ^ James Grime, Pi and the size of the Universe, Numberphile, archived from the original on 6 December 2017, retrieved 25 December 2017
126. ^ Arndt & Haenel 2006, pp. 17–19
127. ^ Schudel, Matt (25 March 2009). “John W. Wrench, Jr.: Mathematician Had a Taste for Pi”. The Washington Post. p. B5.
128. ^ Connor, Steve (8 January 2010). “The Big Question: How close have we come to knowing the precise value of pi?”. The Independent. London. Archived from the original on 2 April 2012. Retrieved 14 April 2012.
129. ^ Arndt & Haenel 2006, p. 18.
130. ^ Arndt & Haenel 2006, pp. 103–104
131. ^ Arndt & Haenel 2006, p. 104
132. ^ Arndt & Haenel 2006, pp. 104, 206
133. ^ Arndt & Haenel 2006, pp. 110–111
134. ^ Eymard & Lafon 1999, p. 254
135. ^ ^{a b} “Round 2… 10 Trillion Digits of Pi” Archived 1 January 2014 at the Wayback Machine, NumberWorld.org, 17 October 2011. Retrieved 30 May 2012.
136. ^ Timothy Revell (14 March 2017). “Celebrate pi day with 9 trillion more digits than ever before”. New Scientist. Archived from the original on 6 September 2018. Retrieved 6 September 2018.
137. ^ “Pi”. Archived from the original on 31 August 2018. Retrieved 6 September 2018.
138. ^ “The Pi Record Returns to the Personal Computer”. 20 January 2020. Retrieved 30 September 2020.
139. ^ PSLQ means Partial Sum of Least Squares.
140. ^ Plouffe, Simon (April 2006). “Identities inspired by Ramanujan’s Notebooks (part 2)” (PDF). Archived (PDF) from the original on 14 January 2012. Retrieved 10 April 2009.
141. ^ Arndt & Haenel 2006, p. 39
142. ^ Ramaley, J.F. (October 1969). “Buffon’s Noodle Problem”. The American Mathematical Monthly. 76 (8): 916–918. doi:10.2307/2317945. JSTOR 2317945.
143. ^ Arndt & Haenel 2006, pp. 39–40
     Posamentier & Lehmann 2004, p. 105
144. ^ Grünbaum, B. (1960), “Projection Constants”, Trans. Amer. Math. Soc., 95 (3): 451–465, doi:10.1090/s0002-9947-1960-0114110-9
145. ^ Arndt & Haenel 2006, pp. 43
     Posamentier & Lehmann 2004, pp. 105–108
146. ^ ^{a b} Arndt & Haenel 2006, pp. 77–84.
147. ^ ^{a b} Gibbons, Jeremy, “Unbounded Spigot Algorithms for the Digits of Pi” Archived 2 December 2013 at the Wayback Machine, 2005. Gibbons produced an improved version of Wagon’s algorithm.
148. ^ ^{a b} Arndt & Haenel 2006, p. 77.
149. ^ Rabinowitz, Stanley; Wagon, Stan (March 1995). “A spigot algorithm for the digits of Pi”. American Mathematical Monthly. 102 (3): 195–203. doi:10.2307/2975006. JSTOR 2975006. A computer program has been created that implements Wagon’s spigot algorithm in only 120 characters of software.
150. ^ ^{a b} Arndt & Haenel 2006, pp. 117, 126–128.
151. ^ Bailey, David H.; Borwein, Peter B.; Plouffe, Simon (April 1997). “On the Rapid Computation of Various Polylogarithmic Constants” (PDF). Mathematics of Computation. 66 (218): 903–913. Bibcode:1997MaCom..66..903B. CiteSeerX 10.1.1.55.3762. doi:10.1090/S0025-5718-97-00856-9. Archived (PDF) from the original on 22 July 2012.
152. ^ Arndt & Haenel 2006, p. 128. Plouffe did create a decimal digit extraction algorithm, but it is slower than full, direct computation of all preceding digits.
153. ^ Arndt & Haenel 2006, p. 20
     Bellards formula in: Bellard, Fabrice. “A new formula to compute the n^th binary digit of pi”. Archived from the original on 12 September 2007. Retrieved 27 October 2007.
154. ^ Palmer, Jason (16 September 2010). “Pi record smashed as team finds two-quadrillionth digit”. BBC News. Archived from the original on 17 March 2011. Retrieved 26 March 2011.
155. ^ Bronshteĭn & Semendiaev 1971, pp. 200, 209
156. ^ Lay, Steven R. (2007), Convex Sets and Their Applications, Dover, Theorem 11.11, pp. 81–82, ISBN 9780486458038.
157. ^ Gardner, Martin (1991). “Chapter 18: Curves of Constant Width”. The Unexpected Hanging and Other Mathematical Diversions. University of Chicago Press. pp. 212–221. ISBN 0-226-28256-2.
158. ^ Rabinowitz, Stanley (1997). “A polynomial curve of constant width” (PDF). Missouri Journal of Mathematical Sciences. 9 (1): 23–27. doi:10.35834/1997/0901023. MR 1455287.
159. ^ Weisstein, Eric W. “Semicircle”. MathWorld.
160. ^ ^{a b} Ayers 1964, p. 60
161. ^ ^{a b} Bronshteĭn & Semendiaev 1971, pp. 210–211
162. ^ Hilbert, David; Courant, Richard (1966), Methods of mathematical physics, volume 1, Wiley, pp. 286–290
163. ^ Dym, H.; McKean, H.P. (1972), Fourier series and integrals, Academic Press, p. 47
164. ^ Chavel, Isaac (2001), Isoperimetric inequalities, Cambridge University Press
165. ^ Talenti, Giorgio (1976), “Best constant in Sobolev inequality”, Annali di Matematica Pura ed Applicata, 110 (1): 353–372, CiteSeerX 10.1.1.615.4193, doi:10.1007/BF02418013, ISSN 1618-1891, S2CID 16923822
166. ^ L. Esposito; C. Nitsch; C. Trombetti (2011). “Best constants in Poincaré inequalities for convex domains”. arXiv:1110.2960 [math.AP].
167. ^ M. Del Pino; J. Dolbeault (2002), “Best constants for Gagliardo–Nirenberg inequalities and applications to nonlinear diffusions”, Journal de Mathématiques Pures et Appliquées, 81 (9): 847–875, CiteSeerX 10.1.1.57.7077, doi:10.1016/s0021-7824(02)01266-7
168. ^ Payne, L.E.; Weinberger, H.F. (1960), “An optimal Poincaré inequality for convex domains”, Archive for Rational Mechanics and Analysis, 5 (1): 286–292, Bibcode:1960ArRMA…5..286P, doi:10.1007/BF00252910, ISSN 0003-9527, S2CID 121881343
169. ^ Gerald Folland (1989), Harmonic analysis in phase space, Princeton University Press, p. 5
170. ^ Howe 1980
171. ^ Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, Wiley, 1968, pp. 174–190.
172. ^ ^{a b} Bronshteĭn & Semendiaev 1971, pp. 106–107, 744, 748
173. ^ H. Dym; H.P. McKean (1972), Fourier series and integrals, Academic Press; Section 2.7
174. ^ Elias Stein; Guido Weiss (1971), Fourier analysis on Euclidean spaces, Princeton University Press, p. 6; Theorem 1.13.
175. ^ V. Ovsienko; S. Tabachnikov (2004), Projective Differential Geometry Old and New: From the Schwarzian Derivative to the Cohomology of Diffeomorphism Groups, Cambridge Tracts in Mathematics, Cambridge University Press, ISBN 978-0-521-83186-4: Section 1.3
176. ^ Michael Spivak (1999), A comprehensive introduction to differential geometry, vol. 3, Publish or Perish Press; Chapter 6.
177. ^ Kobayashi, Shoshichi; Nomizu, Katsumi (1996), Foundations of Differential Geometry, vol. 2 (New ed.), Wiley Interscience, p. 293; Chapter XII Characteristic classes
178. ^ H. M. Schey (1996) Div, Grad, Curl, and All That: An Informal Text on Vector Calculus, ISBN 0-393-96997-5.
179. ^ Yeo, Adrian, The pleasures of pi, e and other interesting numbers, World Scientific Pub., 2006, p. 21, ISBN 978-981-270-078-0.
     Ehlers, Jürgen, Einstein’s Field Equations and Their Physical Implications, Springer, 2000, p. 7, ISBN 978-3-540-67073-5.
180. ^ Lars Ahlfors (1966), Complex analysis, McGraw-Hill, p. 115
181. ^ Weisstein, Eric W. “Cauchy Integral Formula”. MathWorld.
182. ^ Joglekar, S.D., Mathematical Physics, Universities Press, 2005, p. 166, ISBN 978-81-7371-422-1.
183. ^ Bronshteĭn & Semendiaev 1971, pp. 191–192
184. ^ Emil Artin (1964), The gamma function, Athena series; selected topics in mathematics (1st ed.), Holt, Rinehart and Winston
185. ^ Lawrence Evans (1997), Partial differential equations, AMS, p. 615.
186. ^ Bronshteĭn & Semendiaev 1971, p. 190
187. ^ Benjamin Nill; Andreas Paffenholz (2014), “On the equality case in Erhart’s volume conjecture”, Advances in Geometry, 14 (4): 579–586, arXiv:1205.1270, doi:10.1515/advgeom-2014-0001, ISSN 1615-7168, S2CID 119125713
188. ^ Arndt & Haenel 2006, pp. 41–43
189. ^ This theorem was proved by Ernesto Cesàro in 1881. For a more rigorous proof than the intuitive and informal one given here, see Hardy, G.H., An Introduction to the Theory of Numbers, Oxford University Press, 2008, ISBN 978-0-19-921986-5, theorem 332.
190. ^ Ogilvy, C.S.; Anderson, J.T., Excursions in Number Theory, Dover Publications Inc., 1988, pp. 29–35, ISBN 0-486-25778-9.
191. ^ Arndt & Haenel 2006, p. 43
192. ^ Vladimir Platonov; Andrei Rapinchuk (1994), Algebraic groups and number theory, Academic Press, pp. 262–265
193. ^ Sondow, J. (1994), “Analytic Continuation of Riemann’s Zeta Function and Values at Negative Integers via Euler’s Transformation of Series”, Proc. Amer. Math. Soc., 120 (2): 421–424, CiteSeerX 10.1.1.352.5774, doi:10.1090/s0002-9939-1994-1172954-7
194. ^ T. Friedmann; C.R. Hagen (2015). “Quantum mechanical derivation of the Wallis formula for pi”. Journal of Mathematical Physics. 56 (11): 112101. arXiv:1510.07813. Bibcode:2015JMP….56k2101F. doi:10.1063/1.4930800. S2CID 119315853.
195. ^ Tate, John T. (1950), “Fourier analysis in number fields, and Hecke’s zeta-functions”, Algebraic Number Theory (Proc. Instructional Conf., Brighton, 1965), Thompson, Washington, DC, pp. 305–347, ISBN 978-0-9502734-2-6, MR 0217026
196. ^ H. Dym; H.P. McKean (1972), Fourier series and integrals, Academic Press; Chapter 4
197. ^ ^{a b} Mumford, David (1983), Tata Lectures on Theta I, Boston: Birkhauser, pp. 1–117, ISBN 978-3-7643-3109-2
198. ^ Sidney Port; Charles Stone (1978), Brownian motion and classical potential theory, Academic Press, p. 29
199. ^ * Titchmarsh, E. (1948), Introduction to the theory of Fourier integrals (2nd ed.), Oxford University: Clarendon Press (published 1986), ISBN 978-0-8284-0324-5.
200. ^ Stein, Elias (1970), Singular integrals and differentiability properties of functions, Princeton University Press; Chapter II.
201. ^ ^{a b} Klebanoff, Aaron (2001). “Pi in the Mandelbrot set” (PDF). Fractals. 9 (4): 393–402. doi:10.1142/S0218348X01000828. Archived from the original (PDF) on 27 October 2011. Retrieved 14 April 2012.
202. ^ Peitgen, Heinz-Otto, Chaos and fractals: new frontiers of science, Springer, 2004, pp. 801–803, ISBN 978-0-387-20229-7.
203. ^ Halliday, David; Resnick, Robert; Walker, Jearl, Fundamentals of Physics, 5th Ed., John Wiley & Sons, 1997, p. 381, ISBN 0-471-14854-7.
204. ^ Imamura, James M. (17 August 2005). “Heisenberg Uncertainty Principle”. University of Oregon. Archived from the original on 12 October 2007. Retrieved 9 September 2007.
205. ^ Itzykson, C.; Zuber, J.-B. (1980). Quantum Field Theory (2005 ed.). Mineola, NY: Dover Publications. ISBN 978-0-486-44568-7. LCCN 2005053026. OCLC 61200849.
206. ^ Low, Peter, Classical Theory of Structures Based on the Differential Equation, CUP Archive, 1971, pp. 116–118, ISBN 978-0-521-08089-7.
207. ^ Batchelor, G.K., An Introduction to Fluid Dynamics, Cambridge University Press, 1967, p. 233, ISBN 0-521-66396-2.
208. ^ Hans-Henrik Stølum (22 March 1996). “River Meandering as a Self-Organization Process”. Science. 271 (5256): 1710–1713. Bibcode:1996Sci…271.1710S. doi:10.1126/science.271.5256.1710. S2CID 19219185.
209. ^ Posamentier & Lehmann 2004, pp. 140–141
210. ^ ^{a b c} Arndt & Haenel 2006, pp. 44–45
211. ^ “Most Pi Places Memorized” Archived 14 February 2016 at the Wayback Machine, Guinness World Records.
212. ^ Otake, Tomoko (17 December 2006). “How can anyone remember 100,000 numbers?”. The Japan Times. Archived from the original on 18 August 2013. Retrieved 27 October 2007.
213. ^ Rosenthal, Jeffrey S. (2018). “A Note About Piems”.
214. ^ Raz, A.; Packard, M.G. (2009). “A slice of pi: An exploratory neuroimaging study of digit encoding and retrieval in a superior memorist”. Neurocase. 15 (5): 361–372. doi:10.1080/13554790902776896. PMC 4323087. PMID 19585350.
215. ^ Keith, Mike. “Cadaeic Cadenza Notes & Commentary”. Archived from the original on 18 January 2009. Retrieved 29 July 2009.
216. ^ Keith, Michael; Diana Keith (17 February 2010). Not A Wake: A dream embodying (pi)’s digits fully for 10,000 decimals. Vinculum Press. ISBN 978-0-9630097-1-5.
217. ^ For instance, Pickover calls π “the most famous mathematical constant of all time”, and Peterson writes, “Of all known mathematical constants, however, pi continues to attract the most attention”, citing the Givenchy π perfume, Pi (film), and Pi Day as examples. See Pickover, Clifford A. (1995), Keys to Infinity, Wiley & Sons, p. 59, ISBN 978-0-471-11857-2; Peterson, Ivars (2002), Mathematical Treks: From Surreal Numbers to Magic Circles, MAA spectrum, Mathematical Association of America, p. 17, ISBN 978-0-88385-537-9, archived from the original on 29 November 2016
218. ^ BBC documentary “The Story of Maths”, second part Archived 23 December 2014 at the Wayback Machine, showing a visualization of the historically first exact formula, starting at 35 min and 20 sec into the second part of the documentary.
219. ^ Posamentier & Lehmann 2004, p. 118
     Arndt & Haenel 2006, p. 50
220. ^ Arndt & Haenel 2006, p. 14. This part of the story was omitted from the film adaptation of the novel.
221. ^ Gill, Andy (4 November 2005). “Review of Aerial”. The Independent. Archived from the original on 15 October 2006. the almost autistic satisfaction of the obsessive-compulsive mathematician fascinated by ‘Pi’ (which affords the opportunity to hear Bush slowly sing vast chunks of the number in question, several dozen digits long)
222. ^ Inverse (2018). “Pi Day 2018: Spock Uses Pi to Kill an Evil Computer on ‘Star Trek'”.
223. ^ Pi Day activities Archived 4 July 2013 at archive.today.
224. ^ MIT cheers Archived 19 January 2009 at the Wayback Machine. Retrieved 12 April 2012.
225. ^ “Happy Pi Day! Watch these stunning videos of kids reciting 3.14”. USAToday.com. 14 March 2015. Archived from the original on 15 March 2015. Retrieved 14 March 2015.
226. ^ Rosenthal, Jeffrey S. (February 2015). “Pi Instant”. Math Horizons. 22 (3): 22. doi:10.4169/mathhorizons.22.3.22. S2CID 218542599.
227. ^ Griffin, Andrew. “Pi Day: Why some mathematicians refuse to celebrate 14 March and won’t observe the dessert-filled day”. The Independent. Archived from the original on 24 April 2019. Retrieved 2 February 2019.
228. ^ “Google’s strange bids for Nortel patents”. FinancialPost.com. Reuters. 5 July 2011. Archived from the original on 9 August 2011. Retrieved 16 August 2011.
229. ^ Eagle, Albert (1958). The Elliptic Functions as They Should be: An Account, with Applications, of the Functions in a New Canonical Form. Galloway and Porter, Ltd. p. ix.
230. ^ Sequence OEIS: A019692
231. ^ Abbott, Stephen (April 2012). “My Conversion to Tauism” (PDF). Math Horizons. 19 (4): 34. doi:10.4169/mathhorizons.19.4.34. S2CID 126179022. Archived (PDF) from the original on 28 September 2013.
232. ^ Palais, Robert (2001). “π Is Wrong!” (PDF). The Mathematical Intelligencer. 23 (3): 7–8. doi:10.1007/BF03026846. S2CID 120965049. Archived (PDF) from the original on 22 June 2012.
233. ^ Tau Day: Why you should eat twice the pie – Light Years – CNN.com Blogs Archived 12 January 2013 at the Wayback Machine
234. ^ “Life of pi in no danger – Experts cold-shoulder campaign to replace with tau”. Telegraph India. 30 June 2011. Archived from the original on 13 July 2013.
235. ^ “PEP 628 — Add math.tau”.
236. ^ Arndt & Haenel 2006, pp. 211–212
     Posamentier & Lehmann 2004, pp. 36–37
     Hallerberg, Arthur (May 1977). “Indiana’s squared circle”. Mathematics Magazine. 50 (3): 136–140. doi:10.2307/2689499. JSTOR 2689499.
237. ^ Knuth, Donald (3 October 1990). “The Future of TeX and Metafont” (PDF). TeX Mag. 5 (1): 145. Archived (PDF) from the original on 13 April 2016. Retrieved 17 February 2017.

Sources

• Andrews, George E.; Askey, Richard; Roy, Ranjan (1999). Special Functions. Cambridge: University Press. ISBN 978-0-521-78988-2.
• Arndt, Jörg; Haenel, Christoph (2006). Pi Unleashed. Springer-Verlag. ISBN 978-3-540-66572-4. Retrieved 5 June 2013. English translation by Catriona and David Lischka.
• Ayers, Frank (1964). Calculus. McGraw-Hill. ISBN 978-0-07-002653-7.
• Bailey, David H.; Plouffe, Simon M.; Borwein, Peter B.; Borwein, Jonathan M. (1997). “The quest for PI”. The Mathematical Intelligencer. 19 (1): 50–56. CiteSeerX 10.1.1.138.7085. doi:10.1007/BF03024340. ISSN 0343-6993. S2CID 14318695.
• Beckmann, Peter (1989) [1974]. History of Pi. St. Martin’s Press. ISBN 978-0-88029-418-8.
• Berggren, Lennart; Borwein, Jonathan; Borwein, Peter (1997). Pi: a Source Book. Springer-Verlag. ISBN 978-0-387-20571-7.
• Boeing, Niels (14 March 2016). “Die Welt ist Pi” [The World is Pi]. Zeit Online (in German). Archived from the original on 17 March 2016. Die Ludolphsche Zahl oder Kreiszahl erhielt nun auch das Symbol, unter dem wir es heute kennen: William Jones schlug 1706 den griechischen Buchstaben π vor, in Anlehnung an perimetros, griechisch für Umfang. Leonhard Euler etablierte π schließlich in seinen mathematischen Schriften. [The Ludolphian number or circle number now also received the symbol under which we know it today: William Jones proposed in 1706 the Greek letter π, based on perimetros [περίμετρος], Greek for perimeter. Leonhard Euler firmly established π in his mathematical writings.]
• Borwein, Jonathan; Borwein, Peter (1987). Pi and the AGM: a Study in Analytic Number Theory and Computational Complexity. Wiley. ISBN 978-0-471-31515-5.
• Boyer, Carl B.; Merzbach, Uta C. (1991). A History of Mathematics (2 ed.). Wiley. ISBN 978-0-471-54397-8.
• Bronshteĭn, Ilia; Semendiaev, K.A. (1971). A Guide Book to Mathematics. Verlag Harri Deutsch. ISBN 978-3-87144-095-3.
• Eymard, Pierre; Lafon, Jean Pierre (1999). The Number Pi. American Mathematical Society. ISBN 978-0-8218-3246-2., English translation by Stephen Wilson.
• Gupta, R.C. (1992). “On the remainder term in the Madhava–Leibniz’s series”. Ganita Bharati. 14 (1–4): 68–71.
• Howe, Roger (1980), “On the role of the Heisenberg group in harmonic analysis”, Bulletin of the American Mathematical Society, 3 (2): 821–844, doi:10.1090/S0273-0979-1980-14825-9, MR 0578375.
• Joseph, George Gheverghese (1991). The Crest of the Peacock: Non-European Roots of Mathematics. Princeton University Press. ISBN 978-0-691-13526-7. Retrieved 5 June 2013.
• Posamentier, Alfred S.; Lehmann, Ingmar (2004). Pi: A Biography of the World’s Most Mysterious Number. Prometheus Books. ISBN 978-1-59102-200-8.
• Reitwiesner, George (1950). “An ENIAC Determination of pi and e to 2000 Decimal Places”. Mathematical Tables and Other Aids to Computation. 4 (29): 11–15. doi:10.2307/2002695. JSTOR 2002695.
• Remmert, Reinhold (2012). “Ch. 5 What is π?”. In Heinz-Dieter Ebbinghaus; Hans Hermes; Friedrich Hirzebruch; Max Koecher; Klaus Mainzer; Jürgen Neukirch; Alexander Prestel; Reinhold Remmert (eds.). Numbers. Springer. ISBN 978-1-4612-1005-4.
• Rossi, Corinna (2004). Architecture and Mathematics in Ancient Egypt. Cambridge: University Press. ISBN 978-1-107-32051-2.
• Roy, Ranjan (1990). “The Discovery of the Series Formula for pi by Leibniz, Gregory, and Nilakantha”. Mathematics Magazine. 63 (5): 291–306. doi:10.2307/2690896. JSTOR 2690896.
• Schepler, H.C. (1950). “The Chronology of Pi”. Mathematics Magazine. 23 (3): 165–170 (Jan/Feb), 216–228 (Mar/Apr), and 279–283 (May/Jun). doi:10.2307/3029284. JSTOR 3029284.. issue 3 Jan/Feb, issue 4 Mar/Apr, issue 5 May/Jun
• Thompson, William (1894), “Isoperimetrical problems”, Nature Series: Popular Lectures and Addresses, II: 571–592

Further reading

• Blatner, David (1999). The Joy of Pi. Walker & Company. ISBN 978-0-8027-7562-7.
• Borwein, Jonathan; Borwein, Peter (1984). “The Arithmetic-Geometric Mean and Fast Computation of Elementary Functions” (PDF). SIAM Review. 26 (3): 351–365. CiteSeerX 10.1.1.218.8260. doi:10.1137/1026073.
• Borwein, Jonathan; Borwein, Peter; Bailey, David H. (1989). “Ramanujan, Modular Equations, and Approximations to Pi or How to Compute One Billion Digits of Pi”. The American Mathematical Monthly (Submitted manuscript). 96 (3): 201–219. doi:10.2307/2325206. JSTOR 2325206.
• Chudnovsky, David V. and Chudnovsky, Gregory V., “Approximations and Complex Multiplication According to Ramanujan”, in Ramanujan Revisited (G.E. Andrews et al. Eds), Academic Press, 1988, pp. 375–396, 468–472
• Cox, David A. (1984). “The Arithmetic-Geometric Mean of Gauss”. L’Enseignement Mathématique. 30: 275–330.
• Delahaye, Jean-Paul (1997). Le Fascinant Nombre Pi. Paris: Bibliothèque Pour la Science. ISBN 2-902918-25-9.
• Engels, Hermann (1977). “Quadrature of the Circle in Ancient Egypt”. Historia Mathematica. 4 (2): 137–140. doi:10.1016/0315-0860(77)90104-5.
• Euler, Leonhard, “On the Use of the Discovered Fractions to Sum Infinite Series”, in Introduction to Analysis of the Infinite. Book I, translated from the Latin by J.D. Blanton, Springer-Verlag, 1964, pp. 137–153
• Hardy, G. H.; Wright, E. M. (2000). An Introduction to the Theory of Numbers (fifth ed.). Oxford, UK: Clarendon Press.
• Heath, T.L., The Works of Archimedes, Cambridge, 1897; reprinted in The Works of Archimedes with The Method of Archimedes, Dover, 1953, pp. 91–98
• Huygens, Christiaan, “De Circuli Magnitudine Inventa”, Christiani Hugenii Opera Varia I, Leiden 1724, pp. 384–388
• Lay-Yong, Lam; Tian-Se, Ang (1986). “Circle Measurements in Ancient China“. Historia Mathematica. 13 (4): 325–340. doi:10.1016/0315-0860(86)90055-8.
• Lindemann, Ferdinand (1882). “Ueber die Zahl pi”. Mathematische Annalen. 20 (2): 213–225. doi:10.1007/bf01446522. S2CID 120469397. Archived from the original on 22 January 2015.
• Matar, K. Mukunda; Rajagonal, C. (1944). “On the Hindu Quadrature of the Circle” (Appendix by K. Balagangadharan)”. Journal of the Bombay Branch of the Royal Asiatic Society. 20: 77–82.
• Niven, Ivan (July 1947). “A Simple Proof that pi Is Irrational”. Bulletin of the American Mathematical Society. 53 (7): 507. doi:10.1090/S0002-9904-1947-08821-2.
• Ramanujan, Srinivasa (1914). “Modular Equations and Approximations to π”. Quarterly Journal of Pure and Applied Mathematics. XLV: 350–372. Reprinted in Ramanujan, Srinivasa (2015) [1927]. Hardy, G. H.; Seshu Aiyar, P. V.; Wilson, B. M. (eds.). Srinivasa Ramanujan: Collected Papers. Cambridge University Press. pp. 23–29. ISBN 978-1-107-53651-7.
• Shanks, William, Contributions to Mathematics Comprising Chiefly of the Rectification of the Circle to 607 Places of Decimals, 1853, pp. i–xvi, 10
• Shanks, Daniel; Wrench, John William (1962). “Calculation of pi to 100,000 Decimals”. Mathematics of Computation. 16 (77): 76–99. doi:10.1090/s0025-5718-1962-0136051-9.
• Tropfke, Johannes (1906). Geschichte Der Elementar-Mathematik in Systematischer Darstellung [The history of elementary mathematics] (in German). Leipzig: Verlag Von Veit.
• Viete, Francois, Variorum de Rebus Mathematicis Reponsorum Liber VII. F. Viete, Opera Mathematica (reprint), Georg Olms Verlag, 1970, pp. 398–401, 436–446
• Wagon, Stan (1985). “Is Pi Normal?”. The Mathematical Intelligencer. 7 (3): 65–67. doi:10.1007/BF03025811. S2CID 189884448.
• Wallis, John (1655–1656). Arithmetica Infinitorum, sive Nova Methodus Inquirendi in Curvilineorum Quadratum, aliaque difficiliora Matheseos Problemata (in Latin). Oxford. Reprinted in Opera Mathematica. Vol. 1. Oxford: E Theatro Sheldoniano. 1695. pp. 357–478.
• Zebrowski, Ernest (1999). A History of the Circle: Mathematical Reasoning and the Physical Universe. Rutgers University Press. ISBN 978-0-8135-2898-4.

External links

Wikimedia Commons has media related to Pi.

• 10 million decimal places
• “Pi” at Wolfram Mathworld
• Representations of Pi at Wolfram Alpha
• Demonstration by Lambert (1761) of irrationality of π, online and analysed BibNum (PDF).
• π Search Engine 2 billion searchable digits of π, e and √2