Nombre irrationnel

En mathématiques , les nombres irrationnels (de in- préfixe assimilé à ir- (préfixe négatif, privatif ) + rationnel) sont tous les nombres réels qui ne sont pas des nombres rationnels . Autrement dit, les nombres irrationnels ne peuvent pas être exprimés comme le rapport de deux entiers . Lorsque le rapport des longueurs de deux segments de droite est un nombre irrationnel, les segments de droite sont également décrits comme étant incommensurables , ce qui signifie qu’ils ne partagent aucune “mesure” en commun, c’est-à-dire qu’il n’y a pas de longueur (“la mesure”), pas de quelle que soit sa longueur, cela pourrait être utilisé pour exprimer les longueurs des deux segments donnés sous forme de multiples entiers de lui-même.

Le nombre √ 2 est irrationnel.

Parmi les nombres irrationnels figurent le rapport π de la circonférence d’un cercle à son diamètre, le nombre d’Euler e , le nombre d’or φ et la Racine carrée de deux . ^{[1] [2] [3]} En fait, toutes les racines carrées des nombres naturels , autres que des Carrés parfaits , sont irrationnelles. ^[4]

Comme tous les nombres réels, les nombres irrationnels peuvent être exprimés en notation positionnelle , notamment sous forme décimale. Dans le cas des nombres irrationnels, le développement décimal ne se termine pas, ni ne se termine par une séquence répétitive . Par exemple, la représentation décimale de π commence par 3,14159, mais aucun nombre fini de chiffres ne peut représenter π exactement, ni ne se répète. Inversement, une expansion décimale qui se termine ou se répète doit être un nombre rationnel. Ce sont des propriétés prouvables des nombres rationnels et des systèmes de nombres positionnels, et ne sont pas utilisées comme définitions en mathématiques.

Les nombres irrationnels peuvent également être exprimés sous forme de fractions continues non terminales et de nombreuses autres manières.

En conséquence de la preuve de Cantor que les nombres réels sont indénombrables et les rationnels dénombrables, il s’ensuit que presque tous les nombres réels sont irrationnels. ^[5]

Histoire

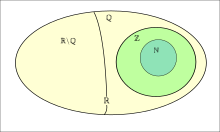
Ensemble de nombres réels (R), qui incluent les rationnels (Q), qui incluent les nombres entiers (Z), qui incluent les nombres naturels (N). Les nombres réels incluent également les irrationnels (RQ).

La Grèce ancienne

La première preuve de l’existence de nombres irrationnels est généralement attribuée à un Pythagoricien (peut-être Hippase de Métaponte ), ^[6] qui les a probablement découverts en identifiant les côtés du pentagramme . ^[7] La ​​méthode pythagoricienne alors en vigueur aurait affirmé qu’il doit y avoir une unité suffisamment petite et indivisible qui pourrait s’adapter uniformément à l’une de ces longueurs ainsi qu’à l’autre. Hippase, au Ve siècle av. J.-C., a cependant pu en déduire qu’il n’y avait en fait aucune unité de mesure commune, et que l’affirmation d’une telle existence était en fait une contradiction. Il l’a fait en démontrant que si l’ hypoténuse d’un Triangle rectangle isocèleétait en effet commensurable à une jambe, alors l’une de ces longueurs mesurées dans cette unité de mesure doit être à la fois impaire et paire, ce qui est impossible. Son raisonnement est le suivant :

• Commencez par un Triangle rectangle isocèle dont les côtés sont des nombres entiers a , b et c . Le rapport de l’hypoténuse à une jambe est représenté par c : b .
• Supposons que a , b et c soient dans les plus petits termes possibles ( c’est-à- dire qu’ils n’ont pas de facteurs communs).
• Par le théorème de Pythagore : c ² = a ² + b ² = b ² + b ² = 2 b ² . (Puisque le triangle est isocèle, a = b ).
• Comme c ² = 2 b ² , c ² est divisible par 2, donc pair.
• Puisque c ² est pair, c doit être pair.
• Comme c est pair, diviser c par 2 donne un entier. Soit y cet entier ( c = 2 y ).
• La mise au carré des deux côtés de c = 2 y donne c ² = (2 y ) ² , ou c ² = 4 y ² .
• Remplacer 4 y ² par c ² dans la première équation ( c ² = 2 b ² ) nous donne 4 y ² = 2 b ² .
• La division par 2 donne 2 y ² = b ² .
• Puisque y est un entier, et 2 y ² = b ² , b ² est divisible par 2, donc pair.
• Puisque b ² est pair, b doit être pair.
• Nous venons de montrer que b et c doivent être pairs. Par conséquent, ils ont un facteur commun de 2. Cependant, cela contredit l’hypothèse selon laquelle ils n’ont pas de facteurs communs. Cette contradiction prouve que c et b ne peuvent pas être tous les deux des entiers, et donc l’existence d’un nombre qui ne peut pas être exprimé comme un rapport de deux entiers. ^[8]

Les mathématiciens grecs appelaient ce rapport de grandeurs incommensurables alogos , ou inexprimable. Hippase, cependant, n’a pas été loué pour ses efforts: selon une légende, il a fait sa découverte en mer, et a ensuite été jeté par-dessus bord par ses compagnons pythagoriciens “… pour avoir produit un élément dans l’univers qui a nié le. .. doctrine selon laquelle tous les phénomènes de l’univers peuvent être réduits à des nombres entiers et à leurs rapports.” ^[9] Une autre légende déclare qu’Hippase a été simplement exilé pour cette révélation. Quelle que soit la conséquence pour Hippase lui-même, sa découverte posa un problème très sérieux aux mathématiques pythagoriciennes, car elle brisa l’hypothèse selon laquelle le nombre et la géométrie étaient inséparables – un fondement de leur théorie.

La découverte des rapports incommensurables était révélatrice d’un autre problème auquel étaient confrontés les Grecs : le rapport du discret au continu. Cela a été mis en lumière par Zénon d’Elée , qui a remis en question la conception selon laquelle les quantités sont discrètes et composées d’un nombre fini d’unités d’une taille donnée. Les conceptions grecques passées dictaient qu’elles devaient nécessairement l’être, car “les nombres entiers représentent des objets discrets, et un rapport commensurable représente une relation entre deux collections d’objets discrets”, ^[10] mais Zeno a constaté qu’en fait “[les quantités] en général ne sont pas des ensembles discrets d’unités ; c’est pourquoi apparaissent des rapports de [quantités] incommensurables… [c]es quantités sont, en d’autres termes, continues ». ^[dix]Cela signifie que, contrairement à la conception populaire de l’époque, il ne peut y avoir une plus petite unité de mesure indivisible pour toute quantité. Qu’en fait, ces divisions de quantité doivent nécessairement être infinies . Par exemple, considérons un segment de ligne : ce segment peut être divisé en deux, cette moitié divisée en deux, la moitié de la moitié en deux, et ainsi de suite. Ce processus peut se poursuivre indéfiniment, car il y a toujours une autre moitié à diviser. Plus le segment est divisé par deux, plus l’unité de mesure se rapproche de zéro, mais elle n’atteint jamais exactement zéro. C’est exactement ce que Zénon a cherché à prouver. Il a cherché à le prouver en formulant quatre paradoxes, qui a démontré les contradictions inhérentes à la pensée mathématique de l’époque. Alors que les paradoxes de Zénon ont démontré avec précision les lacunes des conceptions mathématiques actuelles, ils n’ont pas été considérés comme la preuve de l’alternative. Dans l’esprit des Grecs, réfuter la validité d’un point de vue ne prouvait pas nécessairement la validité d’un autre, et donc une enquête plus approfondie devait avoir lieu.

L’étape suivante a été franchie par Eudoxe de Cnide , qui a formalisé une nouvelle théorie des proportions prenant en compte les quantités commensurables et incommensurables. Au centre de son idée se trouvait la distinction entre la grandeur et le nombre. Une magnitude “… n’était pas un nombre mais représentait des entités telles que des segments de ligne, des angles, des aires, des volumes et du temps qui pouvaient varier, comme nous le dirions, de manière continue. Les magnitudes étaient opposées aux nombres, qui sautaient d’une valeur à un autre, à partir de 4 à 5”. ^[11]Les nombres sont composés d’une plus petite unité indivisible, alors que les grandeurs sont infiniment réductibles. Parce qu’aucune valeur quantitative n’a été attribuée aux grandeurs, Eudoxe a alors pu tenir compte à la fois des rapports commensurables et incommensurables en définissant un rapport en termes de grandeur et de proportion comme une égalité entre deux rapports. En retirant des valeurs quantitatives (nombres) de l’équation, il a évité le piège d’avoir à exprimer un nombre irrationnel comme un nombre. “La théorie d’Eudoxe a permis aux mathématiciens grecs de faire d’énormes progrès en géométrie en fournissant le fondement logique nécessaire aux rapports incommensurables”. ^[12] Cette incommensurabilité est traitée dans les Éléments d’Euclide, Livre X, Proposition 9. Ce n’est qu’Eudoxea développé une théorie des proportions qui a pris en compte les ratios irrationnels et rationnels qu’une base mathématique solide des nombres irrationnels a été créée. ^[13]

Du fait de la distinction entre nombre et grandeur, la géométrie est devenue la seule méthode capable de prendre en compte des rapports incommensurables. Parce que les fondements numériques précédents étaient encore incompatibles avec le concept d’incommensurabilité, l’attention grecque s’est éloignée de ces conceptions numériques telles que l’algèbre et s’est concentrée presque exclusivement sur la géométrie. En fait, dans de nombreux cas, les conceptions algébriques ont été reformulées en termes géométriques. Cela peut expliquer pourquoi nous concevons toujours x ² et x ³ comme x au carré et x au cube au lieu de x à la deuxième puissance et xà la troisième puissance. L’accent fondamental sur le raisonnement déductif qui a résulté de l’éclatement fondamental des mathématiques grecques antérieures était également crucial pour le travail de Zeno avec des ampleurs incommensurables. La prise de conscience qu’une conception de base de la théorie existante était en contradiction avec la réalité a nécessité une enquête complète et approfondie sur les axiomes et les hypothèses qui sous-tendent cette théorie. De cette nécessité, Eudoxe a développé sa méthode d’épuisement , une sorte de reductio ad absurdum qui “… a établi l’organisation déductive sur la base d’axiomes explicites…” ainsi que “… a renforcé la décision antérieure de s’appuyer sur le raisonnement déductif pour la preuve”. ^[14] Cette méthode d’épuisement est la première étape dans la création du calcul.

Théodore de Cyrène a prouvé l’irrationalité des surds de nombres entiers jusqu’à 17, mais s’est arrêté là probablement parce que l’algèbre qu’il utilisait ne pouvait s’appliquer à la racine carrée de 17. ^[15]

Inde

Les problèmes géométriques et mathématiques impliquant des nombres irrationnels tels que les racines carrées ont été abordés très tôt pendant la période védique en Inde. Il y a des références à de tels calculs dans les Samhitas , les Brahmanas et les Shulba Sutras (800 avant JC ou avant). (Voir Bag, Indian Journal of History of Science, 25(1-4), 1990).

Il est suggéré que le concept d’irrationalité a été implicitement accepté par les mathématiciens indiens depuis le 7ème siècle avant JC, lorsque Manava (vers 750 – 690 avant JC) croyait que les racines carrées de nombres tels que 2 et 61 ne pouvaient pas être déterminées avec précision. ^[16] L’historien Carl Benjamin Boyer , cependant, écrit que “de telles affirmations ne sont pas bien étayées et peu susceptibles d’être vraies”. ^[17]

Il est également suggéré qu’Aryabhata (5ème siècle après JC), en calculant une valeur de pi à 5 chiffres significatifs, a utilisé le mot āsanna (approche), pour signifier que non seulement c’est une approximation mais que la valeur est incommensurable (ou irrationnelle) .

Plus tard, dans leurs traités, les mathématiciens indiens ont écrit sur l’arithmétique des surds comprenant l’addition, la soustraction, la multiplication, la rationalisation, ainsi que la séparation et l’extraction des racines carrées. ^[18]

Des mathématiciens comme Brahmagupta (en 628 après JC) et Bhāskara I (en 629 après JC) ont apporté des contributions dans ce domaine, tout comme d’autres mathématiciens qui ont suivi. Au 12ème siècle , Bhāskara II a évalué certaines de ces formules et les a critiquées, identifiant leurs limites.

Au cours des XIVe au XVIe siècles, Madhava de Sangamagrama et l’ école d’astronomie et de mathématiques du Kerala ont découvert la Série infinie de plusieurs nombres irrationnels tels que π et certaines valeurs irrationnelles de fonctions trigonométriques . Jyeṣṭhadeva a fourni des preuves de ces séries infinies dans le Yuktibhāṣā . ^[19]

Moyen-âge

Au Moyen Age , le développement de l’ algèbre par les mathématiciens musulmans a permis de traiter les nombres irrationnels comme des objets algébriques . ^[20] Les mathématiciens du Moyen-Orient ont également fusionné les concepts de « nombre » et de « grandeur » dans une idée plus générale des nombres réels , critiqué l’idée d’Euclide des rapports , développé la théorie des rapports composés et étendu le concept de nombre aux rapports de nombres continus. ordre de grandeur. ^[21] Dans son commentaire du Livre 10 des Éléments , le mathématicien persan Al-Mahani(m. 874/884) a examiné et classé les irrationnels quadratiques et les irrationnels cubiques. Il a fourni des définitions pour les grandeurs rationnelles et irrationnelles, qu’il a traitées comme des nombres irrationnels. Il les traite librement mais les explique en termes géométriques comme suit : ^[21]

“Ce sera une (magnitude) rationnelle quand nous disons, par exemple, 10, 12, 3%, 6%, etc., parce que sa valeur est prononcée et exprimée quantitativement. Ce qui n’est pas rationnel est irrationnel et il est impossible de prononcer et représenter quantitativement sa valeur. Par exemple : les racines de nombres tels que 10, 15, 20 qui ne sont pas des carrés, les côtés de nombres qui ne sont pas des cubes etc.

Contrairement au concept d’Euclide des grandeurs comme des lignes, Al-Mahani considérait les nombres entiers et les fractions comme des grandeurs rationnelles, et les racines carrées et les racines cubiques comme des grandeurs irrationnelles. Il a également introduit une approche arithmétique du concept d’irrationalité, car il attribue ce qui suit aux grandeurs irrationnelles : ^[21]

“leurs sommes ou différences, ou les résultats de leur addition à une grandeur rationnelle, ou les résultats de la soustraction d’une grandeur de ce type à une grandeur irrationnelle, ou d’une grandeur rationnelle à celle-ci.”

Le mathématicien égyptien Abū Kāmil Shujā ibn Aslam (vers 850-930) fut le premier à accepter les nombres irrationnels comme solutions d’ équations quadratiques ou comme coefficients dans une équation , souvent sous la forme de racines carrées, de racines cubiques et de racines quatrièmes . ^[22] Au 10ème siècle, le mathématicien irakien Al-Hashimi a fourni des preuves générales (plutôt que des démonstrations géométriques) pour les nombres irrationnels, car il considérait la multiplication, la division et d’autres fonctions arithmétiques. ^[21] Mathématicien iranien, Abū Ja’far al-Khāzin(900–971) fournit une définition des grandeurs rationnelles et irrationnelles, indiquant que si une quantité définie est : ^[21]

“contenu dans une certaine grandeur donnée une ou plusieurs fois, alors cette grandeur (donnée) correspond à un nombre rationnel… Chaque fois que cette (dernière) grandeur comprend la moitié, ou un tiers, ou un quart de la grandeur donnée (de l’unité), ou, par rapport à (l’unité), comprend trois, cinq ou trois cinquièmes, c’est une grandeur rationnelle. Et, en général, chaque grandeur qui correspond à cette grandeur ( c’est-à -dire à l’unité), comme un nombre à un autre, est rationnel, mais si une grandeur ne peut pas être représentée comme un multiple, une partie (1/ n ) ou des parties ( m / n ) d’une grandeur donnée, elle est irrationnelle, c’est-à -dire qu’elle ne peut pas être exprimée autrement qu’au moyen de racines.”

Beaucoup de ces concepts ont finalement été acceptés par les mathématiciens européens quelque temps après les traductions latines du 12ème siècle . Al-Hassār , un mathématicien marocain de Fès spécialisé dans la jurisprudence de l’héritage islamique au XIIe siècle, mentionne pour la première fois l’utilisation d’une barre fractionnaire, où les numérateurs et les dénominateurs sont séparés par une barre horizontale. Dans sa discussion, il écrit: “…, par exemple, si on vous dit d’écrire trois cinquièmes et un tiers de cinquième, écrivez ainsi, 3 1 5 3 {displaystyle {frac {3quad 1}{5quad 3}}} .” ^[23] Cette même notation fractionnaire apparaît peu après dans l’œuvre de Leonardo Fibonacci au XIIIe siècle. ^[24]

Période moderne

Le 17ème siècle a vu les nombres imaginaires devenir un outil puissant entre les mains d’ Abraham de Moivre , et surtout de Leonhard Euler . L’achèvement de la théorie des nombres complexes au XIXe siècle a entraîné la différenciation des irrationnels en nombres algébriques et transcendants , la preuve de l’existence des nombres transcendants, et la résurgence de l’étude scientifique de la théorie des irrationnels, largement ignorée depuis Euclide . L’année 1872 voit la publication des théories de Karl Weierstrass (par son élève Ernst Kossak), Eduard Heine ( Crelle’s Journal , 74), Georg Cantor(Annalen, 5), et Richard Dedekind . Méray avait pris en 1869 le même point de départ que Heine, mais la théorie est généralement renvoyée à l’année 1872. La méthode de Weierstrass a été complètement exposée par Salvatore Pincherle en 1880, ^[25] et celle de Dedekind a reçu une importance supplémentaire à travers les travaux ultérieurs de l’auteur. travail (1888) et l’approbation par Paul Tannery (1894). Weierstrass, Cantor et Heine fondent leurs théories sur les séries infinies, tandis que Dedekind fonde la sienne sur l’idée d’une coupure (Schnitt) dans le système de tous les nombres rationnels , les séparant en deux groupes ayant certaines propriétés caractéristiques. Le sujet a reçu des contributions ultérieures de la part de Weierstrass,Léopold Kronecker (Crelle, 101), et Charles Méray .

Les fractions continues , étroitement liées aux nombres irrationnels (et dues à Cataldi, 1613), ont attiré l’attention d’Euler et, à l’ouverture du XIXe siècle, ont été mises en évidence grâce aux écrits de Joseph-Louis Lagrange . Dirichlet a également ajouté à la théorie générale, tout comme de nombreux contributeurs aux applications du sujet.

Johann Heinrich Lambert a prouvé (1761) que π ne peut pas être rationnel, et que e ⁿ est irrationnel si n est rationnel (sauf si n = 0). ^[26] Alors que la preuve de Lambert est souvent qualifiée d’incomplète, les évaluations modernes la soutiennent comme satisfaisante et, en fait, pour son époque, elle est exceptionnellement rigoureuse. Adrien-Marie Legendre (1794), après avoir introduit la fonction de Bessel-Clifford , a fourni une preuve pour montrer que π ² est irrationnel, d’où il s’ensuit immédiatement que π est irrationnel aussi. L’existence des Nombres transcendantaux a été établie pour la première fois par Liouville (1844, 1851). Plus tard, Georg Cantor(1873) ont prouvé leur existence par une méthode différente , qui a montré que tout intervalle dans les réels contient des nombres transcendants. Charles Hermite (1873) a d’abord prouvé e transcendantal, et Ferdinand von Lindemann (1882), à partir des conclusions d’Hermite, a montré la même chose pour π. La preuve de Lindemann a été très simplifiée par Weierstrass (1885), encore plus loin par David Hilbert (1893), et a finalement été rendue élémentaire par Adolf Hurwitz ^{[ la citation nécessaire ]} et Paul Gordan . ^[27]

Exemples

Apprendre encore plus Cette section ne cite aucune source . ( juin 2013 ) Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (Learn how and when to remove this template message)

Racines carrées

La racine carrée de 2 était le premier nombre prouvé irrationnel, et cet article contient un certain nombre de preuves. Le nombre d’or est un autre nombre Irrationnel quadratique célèbre. Les racines carrées de tous les nombres naturels qui ne sont pas des Carrés parfaits sont irrationnelles et une preuve peut être trouvée dans les irrationnels quadratiques .

Racines générales

La preuve ci-dessus pour la Racine carrée de deux peut être généralisée en utilisant le théorème fondamental de l’arithmétique . Cela affirme que chaque entier a une Factorisation unique en nombres premiers. En l’utilisant, nous pouvons montrer que si un nombre rationnel n’est pas un entier, alors aucune puissance intégrale de celui-ci ne peut être un entier, car dans les Termes les plus bas, il doit y avoir un nombre premier dans le dénominateur qui ne se divise pas en Numérateur quelle que soit la puissance à laquelle chacun est élevé . . Par conséquent, si un entier n’est pas une k ième puissance exacte d’un autre entier, alors la k ième racine de ce premier entier est irrationnelle.

Logarithmes

Peut-être que les nombres les plus faciles à prouver comme irrationnels sont certains logarithmes . Voici une preuve par contradiction que log ₂ 3 est irrationnel (log ₂ 3 ≈ 1,58 > 0).

Supposons que log ₂ 3 est rationnel. Pour certains entiers positifs m et n , nous avons

log 2 ⁡ 3 = m n . {displaystyle log _{2}3={frac {m}{n}}.}

Il s’ensuit que

2 m / n = 3 {displaystyle 2^{m/n}=3} ( 2 m / n ) n = 3 n {displaystyle (2^{m/n})^{n}=3^{n}} 2 m = 3 n . {displaystyle 2^{m}=3^{n}.}

Le nombre 2 élevé à toute puissance entière positive doit être pair (car il est divisible par 2) et le nombre 3 élevé à toute puissance entière positive doit être impair (car aucun de ses facteurs premiers ne sera 2). Il est clair qu’un entier ne peut pas être à la fois impair et pair : nous avons une contradiction. La seule hypothèse que nous avons faite était que log ₂ 3 est rationnel (et donc exprimable comme un quotient d’entiers m / n avec n ≠ 0). La contradiction signifie que cette hypothèse doit être fausse, c’est-à-dire que log ₂ 3 est irrationnel et ne peut jamais être exprimé comme un quotient d’entiers m / n avec n ≠ 0.

Des cas tels que log ₁₀ 2 peuvent être traités de la même manière.

Les types

• distinction théorique des nombres : transcendantal/algébrique
• normal / anormal (non normal)

Transcendantale/algébrique

Presque tous les nombres irrationnels sont transcendants et tous les nombres transcendants réels sont irrationnels (il existe aussi des nombres transcendants complexes) : l’article sur les nombres transcendants en énumère plusieurs exemples. Ainsi e ^r et π ^r sont irrationnels pour tout r rationnel non nul , et, par exemple, e ^π est également irrationnel.

Les nombres irrationnels peuvent également être trouvés dans l’ ensemble dénombrable des nombres algébriques réels (essentiellement définis comme les racines réelles de polynômes à coefficients entiers), c’est-à-dire comme des solutions réelles d’équations polynomiales

p ( x ) = a n x n + a n − 1 x n − 1 + ⋯ + a 1 x + a 0 = 0 , {displaystyle p(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+cdots +a_{1}x+a_{0}=0 ;, }

où les coefficients a i {displaystyle a_{i}} sont des entiers et a n ≠ 0 {displaystyle a_{n}neq 0} . Toute racine rationnelle de cette équation polynomiale doit être de la forme r / s , où r est un diviseur de a ₀ et s est un diviseur de a _n . Si une vraie racine x 0 {style d’affichage x_{0}} d’un polynôme p {displaystyle p} n’est pas parmi ces nombres finis de possibilités, il doit s’agir d’un nombre algébrique irrationnel. Un exemple de preuve de l’existence de tels irrationnels algébriques consiste à montrer que x ₀ = (2 ^1/2 + 1) ^1/3 est une racine irrationnelle d’un polynôme à coefficients entiers : elle satisfait ( x ³ − 1) ² = 2 et donc x ⁶ − 2 x ³ − 1 = 0, et ce dernier polynôme n’a pas de racines rationnelles (les seuls candidats à vérifier sont ±1, et x ₀ , étant supérieur à 1, n’est ni l’un ni l’autre), donc x ₀ est un nombre algébrique irrationnel.

Parce que les nombres algébriques forment un sous -champ des nombres réels, de nombreux nombres réels irrationnels peuvent être construits en combinant des Nombres transcendantaux et algébriques. Par exemple, 3 π + 2, π + √ 2 et e √ 3 sont irrationnels (et même transcendantaux).

Expansions décimales

L’expansion décimale d’un nombre irrationnel ne se répète ni ne se termine jamais (ce dernier étant équivalent à la répétition de zéros), contrairement à tout nombre rationnel. Il en va de même pour les développements binaires , octaux ou hexadécimaux , et en général pour les développements dans toutes les notations positionnelles avec des bases naturelles .

Pour le montrer, supposons que nous divisons les entiers n par m (où m est différent de zéro). Lorsque la division longue est appliquée à la division de n par m , il ne peut jamais y avoir de reste supérieur ou égal à m . Si 0 apparaît comme un reste, l’expansion décimale se termine. Si 0 ne se produit jamais, alors l’algorithme peut exécuter au plus m – 1 étapes sans utiliser de reste plus d’une fois. Après cela, un reste doit se reproduire, puis l’expansion décimale se répète.

Inversement, supposons que nous soyons confrontés à un nombre décimal répétitif , nous pouvons prouver qu’il s’agit d’une fraction de deux entiers. Par exemple, considérez :

A = 0.7 162 162 162 … {displaystyle A=0.7,162,162,162,ldots }

Ici, la répétition est de 162 et la longueur de la répétition est de 3. Tout d’abord, nous multiplions par une puissance appropriée de 10 pour déplacer la virgule vers la droite afin qu’elle soit juste devant une répétition. Dans cet exemple, nous multiplierions par 10 pour obtenir :

10 A = 7.162 162 162 … {displaystyle 10A=7.162,162,162,ldots }

Maintenant, nous multiplions cette équation par 10 ^r où r est la longueur de la répétition. Cela a pour effet de déplacer la virgule décimale devant la “prochaine” répétition. Dans notre exemple, multipliez par 10 ³ :

10 , 000 A = 7 162.162 162 … {displaystyle 10 000A=7,162.162,162,ldots }

Le résultat des deux multiplications donne deux expressions différentes avec exactement la même “partie décimale”, c’est-à-dire que la fin de 10 000 A correspond exactement à la fin de 10 A. Ici, 10 000 A et 10 A ont 0,162 162 162 … après la virgule.

Par conséquent, lorsque nous soustrayons l’équation 10 A de l’équation 10 000 A , la fin de 10 A annule la fin de 10 000 A nous laissant avec :

9990 A = 7155. {displaystyle 9990A=7155.}

Puis

A = 7155 9990 = 53 74 {displaystyle A={frac {7155}{9990}}={frac {53}{74}}}

est un rapport d’entiers et donc un nombre rationnel.

Pouvoirs irrationnels

Dov Jarden a donné une simple preuve non constructive qu’il existe deux nombres irrationnels a et b , tels que a ^b est rationnel : ^[28]

Considérons √ 2 ^{√ 2} ; si cela est rationnel, alors prenons a = b = √ 2 . Sinon, prenons a le nombre irrationnel √ 2 ^{√ 2} et b = √ 2 . Alors a ^b = ( √ 2 ^{√ 2} ) ^{√ 2} = √ 2 ^{√ 2 · √ 2} = √ 2 ² = 2, ce qui est rationnel.

Bien que l’argument ci-dessus ne tranche pas entre les deux cas, le théorème de Gelfond–Schneider montre que √ 2 ^{√ 2} est transcendantal , donc irrationnel. Ce théorème stipule que si a et b sont tous deux des nombres algébriques , et que a n’est pas égal à 0 ou 1, et que b n’est pas un nombre rationnel, alors toute valeur de a ^b est un nombre transcendant (il peut y avoir plus d’une valeur si l’exponentiation des nombres complexes est utilisée).

Un exemple qui fournit une preuve constructive simple est ^[29]

( 2 ) log 2 ⁡ 3 = 3. {displaystyle left({sqrt {2}}right)^{log _{sqrt {2}}3}=3.}

La base du côté gauche est irrationnelle et le côté droit est rationnel, il faut donc prouver que l’exposant du côté gauche, log 2 ⁡ 3 {displaystyle log _{sqrt {2}}3} , est irrationnel. Il en est ainsi parce que, par la formule reliant les logarithmes avec des bases différentes,

log 2 ⁡ 3 = log 2 ⁡ 3 log 2 ⁡ 2 = log 2 ⁡ 3 1 / 2 = 2 log 2 ⁡ 3 {displaystyle log _{sqrt {2}}3={frac {log _{2}3}{log _{2}{sqrt {2}}}}={frac {log _{2}3}{1/2}}=2log _{2}3}

que l’on peut supposer, pour établir une contradiction , égal à un rapport m/n d’entiers positifs. Puis log 2 ⁡ 3 = m / 2 n {displaystyle log _{2}3=m/2n} Par conséquent 2 log 2 ⁡ 3 = 2 m / 2 n {displaystyle 2^{log _{2}3}=2^{m/2n}} Par conséquent 3 = 2 m / 2 n {displaystyle 3=2^{m/2n}} Par conséquent 3 2 n = 2 m {displaystyle 3^{2n}=2^{m}} , qui est une paire contradictoire de factorisations premières et viole donc le théorème fondamental de l’arithmétique (factorisation première unique).

Un résultat plus fort est le suivant : ^[30] Tout nombre rationnel dans l’intervalle ( ( 1 / e ) 1 / e , ∞ ) {displaystyle ((1/e)^{1/e},infty)} peut s’écrire soit a ^a pour un nombre irrationnel a , soit n ⁿ pour un nombre naturel n . De même, ^[30] tout nombre rationnel positif peut s’écrire soit sous la forme a a a {displaystyle a^{a^{a}}} pour un certain nombre irrationnel a ou comme n n n {displaystyle n^{n^{n}}} pour un certain nombre naturel n .

Questions ouvertes

On ne sait pas si π + e {style d’affichage pi +e} (ou alors π − e { style d’affichage pi -e} ) est irrationnel. En fait, il n’y a pas de couple d’entiers non nuls m , n {displaystyle m,n} pour lequel on sait si m π + n e {displaystyle mpi +ne} est irrationnel. De plus, on ne sait pas si l’ensemble { π , e } {displaystyle {pi ,e}} est algébriquement indépendant sur Q {displaystyle mathbb {Q}} .

On ne sait pas si π e , π / e , 2 e , π e , π 2 , dans ⁡ π , {displaystyle pi e, pi /e, 2^{e}, pi ^{e}, pi ^{sqrt {2}}, ln pi ,} Constante de Catalan , ou constante d’Euler-Mascheroni γ {displaystylegamma} sont irrationnels. ^{[31] [32] [33]} On ne sait pas si l’une des tétrations n π {displaystyle ^{n}pi } ou alors n e {displaystyle ^{n}e} est rationnel pour un entier n > 1. {displaystyle n>1.} ^{[ citation nécessaire ]}

En mathématiques constructives

En mathématiques constructives , le tiers exclu n’est pas valide, il n’est donc pas vrai que tout nombre réel soit rationnel ou irrationnel. Ainsi, la notion de nombre irrationnel se bifurque en plusieurs notions distinctes. On pourrait prendre la définition traditionnelle d’un nombre irrationnel comme un nombre réel qui n’est pas rationnel. ^[34] Cependant, il existe une deuxième définition d’un nombre irrationnel utilisée en mathématiques constructives, selon laquelle un nombre réel r {displaystyle r} est un nombre irrationnel s’il est séparé de tout nombre rationnel, ou de manière équivalente, si la distance | r − q | {displaystyle vert rqvert } entre r {displaystyle r} et tout nombre rationnel q {displaystyle q} est positif. Cette définition est plus forte que la définition traditionnelle d’un nombre irrationnel. Cette deuxième définition est utilisée dans la preuve d’ Errett Bishop que la racine carrée de 2 est irrationnelle . ^[35]

Ensemble de tous les irrationnels

Puisque les réels forment un ensemble Indénombrable , dont les rationnels sont un sous-ensemble dénombrable , l’ensemble complémentaire des irrationnels est Indénombrable.

Sous la fonction de distance habituelle ( euclidienne ) d ( x , y ) = | x − y | {displaystyle d(x,y)=vert xyvert } , les nombres réels sont un espace métrique et donc aussi un espace topologique . La restriction de la fonction de distance euclidienne donne aux irrationnels la structure d’un espace métrique. Puisque le sous-espace des irrationnels n’est pas fermé, la métrique induite n’est pas complète . Étant un ensemble G-delta —c’est-à-dire une intersection dénombrable de sous-ensembles ouverts—dans un espace métrique complet, l’espace des irrationnels est complètement métrisable : c’est-à-dire qu’il existe une métrique sur les irrationnels induisant la même topologie que la restriction de l’Euclidienne métrique, mais par rapport à laquelle les irrationnels sont complets. On peut voir cela sans connaître le fait susmentionné sur les ensembles G-delta : la fraction continuel’expansion d’un nombre irrationnel définit un homéomorphisme de l’espace des irrationnels à l’espace de toutes les séquences d’entiers positifs, qui se voit facilement comme complètement métrisable.

De plus, l’ensemble de tous les irrationnels est un espace métrisable déconnecté. En fait, les irrationnels équipés de la topologie du sous-espace ont une base d’ ensembles clopen donc l’espace est zéro-dimensionnel .

Voir également

• Numéro Brjuno
• Nombre calculable
• Approximation diophantienne
• Preuve que e est irrationnel
• Preuve que π est irrationnel
• Racine carrée de 3
• Racine carrée de 5
• Nombre trigonométrique

Systèmes de numération Complexe : C {displaystyle :;mathbb {C} } Réel : R {displaystyle :;mathbb {R} } Rationnel : Q {displaystyle :;mathbb {Q}} Entier : Z {displaystyle :;mathbb {Z} } Naturel : N {displaystyle :;mathbb {N} } Zéro : 0 Un : 1 nombres premiers Nombres composés Entiers négatifs Fraction Décimal fini Dyadique (binaire fini) Décimal répétitif Irrationnel Algébrique irrationnel Transcendantal Imaginaire

Références

1. ^ Les 15 Nombres transcendantaux les plus célèbres . par Clifford A. Pickover . URL récupérée le 24 octobre 2007.
2. ^ http://www.mathsisfun.com/irrational-numbers.html ; URL récupérée le 24 octobre 2007.
3. ^ Weisstein, Eric W. “Nombre irrationnel” . MathWorld .URL récupérée le 26 octobre 2007.
4. ^ Jackson, Terence (2011-07-01). “95,42 Racines carrées irrationnelles des nombres naturels – une approche géométrique” . La Gazette Mathématique . 95 (533) : 327–330. doi : 10.1017/S0025557200003193 . ISSN 0025-5572 .
5. ^ Chanteur, Georg (1955) [1915]. Philippe Jourdain (éd.). Contributions à la fondation de la théorie des nombres transfinis . New York : Douvres. ISBN 978-0-486-60045-1.
6. ^ Kurt Von Fritz (1945). “La découverte de l’incommensurabilité par Hippase de Metapontum”. Les Annales de Mathématiques .
7. ^ James R. Choike (1980). “Le Pentagramme et la Découverte d’un Nombre Irrationnel”. Le Journal de mathématiques du Collège de deux ans . .
8. ^ Kline, M. (1990). La pensée mathématique de l’Antiquité à l’époque moderne , vol. 1. New York : Oxford University Press (ouvrage original publié en 1972), p. 33.
9. ^ Kline 1990, p. 32.
10. ^ ^{un b} Kline 1990, p. 34.
11. ^ Kline 1990, p. 48.
12. ^ Kline 1990, p. 49.
13. ^ Charles H. Edwards (1982). Le développement historique du calcul . Springer.
14. ^ Kline 1990, p. 50.
15. ^ Robert L. McCabe (1976). “Les preuves d’irrationalité de Theodorus”. Revue Mathématiques . .
16. ^ TK Puttaswamy, “Les réalisations des anciens mathématiciens indiens”, pp. 411–2, à Selin, Helaine ; D’Ambrosio, Ubiratan, éds. (2000). Mathématiques à travers les cultures : l’histoire des mathématiques non occidentales . Springer . ISBN 1-4020-0260-2..
17. ^ Boyer (1991). “La Chine et l’Inde”. Une histoire des mathématiques (2e éd.). p. 208. ISBN 0471093742. OCLC 414892 . Il a également été affirmé que la première reconnaissance des incommensurables apparaît en Inde pendant la période Sulbasutra , mais ces affirmations ne sont pas bien étayées. Le cas d’une prise de conscience hindoue précoce de grandeurs incommensurables est rendu très improbable par le manque de preuves que les mathématiciens indiens de cette période s’étaient emparés des concepts fondamentaux.
18. ^ Datta, Bibhutibhusan; Singh, Awadhesh Narayan (1993). “Surds en mathématiques hindoues” (PDF) . Journal indien d’histoire des sciences . 28 (3): 253–264. Archivé de l’original (PDF) le 2018-10-03 . Récupéré le 18 septembre 2018 .
19. ^ Katz, VJ (1995), “Ideas of Calculus in Islam and India”, Mathematics Magazine (Mathematical Association of America) 68 (3): 163–74.
20. ^ O’Connor, John J. ; Robertson, Edmund F. (1999). « Mathématiques arabes : génie oublié ? . Archives MacTutor Histoire des mathématiques . Université de St Andrews . .
21. ^ ^{un bcde Matvievskaya} , Galina ⁽ 1987) ^. “La théorie des irrationnels quadratiques dans les mathématiques orientales médiévales”. Annales de l’Académie des sciences de New York . 500 (1): 253–277. Bibcode : 1987NYASA.500..253M . doi : 10.1111/j.1749-6632.1987.tb37206.x . S2CID 121416910 . Voir notamment p. 254 & 259–260.
22. ↑ Jacques Sesiano, “Mathématiques islamiques”, p . 148, à Selin, Helaine ; D’Ambrosio, Ubiratan (2000). Mathématiques à travers les cultures : l’histoire des mathématiques non occidentales . Springer . ISBN 1-4020-0260-2..
23. ^ Cajori, Florian (1928). Une histoire des notations mathématiques (Vol.1) . La Salle, Illinois: La société d’édition Open Court. p. 269.
24. ^ ( Cajori 1928 , page 89)
25. ^ Salvatore Pincherle (1880). “Saggio di una introduzione alla theoria delle funzioni analitiche secondo i principii del prof. C. Weierstrass” . Giornale di Matematiche : 178–254, 317–320.
26. ^ Lambert, JH (1761). “Mémoire sur quelques propriétés remarquables des quantités transcendantes, circulaires et logarithmiques” (PDF) . Mémoires de l’Académie royale des sciences de Berlin (en français): 265–322. Archivé (PDF) de l’original le 2016-04-28.
27. ^ Gordon, Paul (1893). “Transcendenz von e et π” . Annales Mathématiques . Teubner. 43 (2–3): 222–224. doi : 10.1007/bf01443647 . S2CID 123203471 .
28. ^ George, Alexandre; En ligneVelleman, Daniel J. (2002). Philosophies des mathématiques (PDF) . Blackwell. p. 3–4. ISBN 0-631-19544-0.
29. ^ Lord, Nick, “Maths morsure: les pouvoirs irrationnels des nombres irrationnels peuvent être rationnels”, Mathematical Gazette 92, novembre 2008, p. 534.
30. ^ ^{a b} Marshall, Ash J. et Tan, Yiren, “Un nombre rationnel de la forme a ^a avec un irrationnel”, Mathematical Gazette 96, mars 2012, pp. 106-109.
31. ^ Weisstein, Eric W. “Pi” . MathWorld .
32. ^ Weisstein, Eric W. “Nombre irrationnel” . MathWorld .
33. ^ Albert, Jean. “Quelques problèmes non résolus en théorie des nombres” (PDF) . Département de mathématiques, Université de l’Oklahoma. (Séminaire supérieur de mathématiques, cours du printemps 2008)
34. ^ Mark Bridger (2007). Analyse réelle : une approche constructive par l’arithmétique d’intervalle . John Wiley et fils . ISBN 978-1-470-45144-8.
35. ^ Errett Bishop; Ponts Douglas (1985). Analyse constructive . Springer . ISBN 0-387-15066-8.

Lectures complémentaires

• Adrien-Marie Legendre , Éléments de Géométrie , Note IV, (1802), Paris
• Rolf Wallisser, “Sur la preuve de Lambert de l’irrationalité de π”, dans Théorie algébrique des nombres et analyse diophantienne , Franz Halter-Koch et Robert F. Tichy, (2000), Walter de Gruyer

Liens externes

Wikimedia Commons a des médias liés aux nombres irrationnels .

• Paradoxes et incommensurabilité de Zeno Archivé le 13/05/2016 à la Wayback Machine (nd). Récupéré le 1er avril 2008
• Weisstein, Eric W. “Nombre irrationnel” . MathWorld .