Distribution exponentielle

Dans la théorie des probabilités et les statistiques , la distribution exponentielle est la distribution de probabilité du temps entre les événements dans un processus ponctuel de Poisson , c’est-à-dire un processus dans lequel les événements se produisent de manière continue et indépendante à un taux moyen constant. C’est un cas particulier de la distribution gamma . C’est l’analogue continu de la distribution géométrique , et il a la propriété clé d’être Sans mémoire . En plus d’être utilisé pour l’analyse des processus ponctuels de Poisson, on le trouve dans divers autres contextes.

Exponentiel

Fonction de densité de probabilité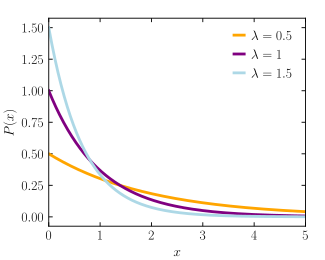
Fonction de distribution cumulative
Paramètres	λ > 0 , {displaystylelambda >0,} taux ou échelle inverse
Soutien	X ∈ [ 0 , ∞ ) {displaystyle xin [0,infty )}
PDF	λ e − λ x {displaystyle lambda e^{-lambda x}}
CDF	1 − e − λ x {displaystyle 1-e^{-lambda x}}
quantile	− ln ⁡ ( 1 − p ) λ {displaystyle -{frac {ln(1-p)}{lambda}}}
Moyenne	1 λ {displaystyle {frac {1}{lambda}}}
Médian	ln ⁡ 2 λ {displaystyle {frac {ln 2}{lambda}}}
Mode	0 {displaystyle 0}
Variance	1 λ 2 {displaystyle {frac {1}{lambda ^{2}}}}
Asymétrie	2 {displaystyle 2}
Ex. aplatissement	6 {displaystyle 6}
Entropie	1 − ln ⁡ λ {displaystyle 1-ln lambda}
FMG	λ λ − t , for t < λ {displaystyle {frac {lambda }{lambda -t}},{text{ for }}t<lambda }
FC	λ λ − i t {displaystyle {frac {lambda }{lambda -it}}}
Informations sur les pêcheurs	1 λ 2 {displaystyle {frac {1}{lambda ^{2}}}}
Divergence de Kullback-Leibler	ln ⁡ λ 0 λ + λ λ 0 − 1 {displaystyle ln {frac {lambda _{0}}{lambda }}+{frac {lambda }{lambda _{0}}}-1}

La distribution exponentielle n’est pas la même que la classe des familles de distributions exponentielles, qui est une grande classe de distributions de probabilité qui inclut la distribution exponentielle comme l’un de ses membres, mais comprend également la distribution normale , la distribution binomiale , la distribution gamma , Poisson , et plein d’autres.

Définitions

Fonction de densité de probabilité

La fonction de densité de probabilité (pdf) d’une distribution exponentielle est

F ( X ; λ ) = { λ e − λ X X ≥ 0 , 0 X < 0. {displaystyle f(x;lambda )={begin{cases}lambda e^{-lambda x}&xgeq 0,\0&x<0.end{cases}}}

Ici λ > 0 est le paramètre de la distribution, souvent appelé paramètre de taux . La distribution est supportée sur l’intervalle [0, ∞) . Si une variable aléatoire X a cette distribution, on écrit X ~ Exp( λ ) .

La distribution exponentielle présente une divisibilité infinie .

Fonction de distribution cumulative

La fonction de distribution cumulative est donnée par

F ( x ; λ ) = { 1 − e − λ x x ≥ 0 , 0 x < 0. {displaystyle F(x;lambda )={begin{cases}1-e^{-lambda x}&xgeq 0,\0&x<0.end{cases}}}

Paramétrage alternatif

La distribution exponentielle est parfois paramétrée en fonction du paramètre d’échelle β = 1/ λ , qui est également la moyenne :

f ( x ; β ) = { 1 β e − x / β x ≥ 0 , 0 x < 0. F ( x ; β ) = { 1 − e − x / β x ≥ 0 , 0 x < 0. {displaystyle f(x;beta )={begin{cases}{frac {1}{beta }}e^{-x/beta }&xgeq 0,\0&x<0.end {cas}}qquad qquad F(x;beta )={begin{cas}1-e^{-x/beta }&xgeq 0,\0&x<0.end{cas}} }

Propriétés

Moyenne, variance, moments et médiane

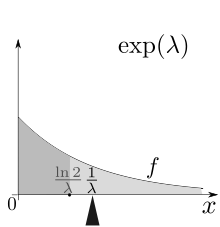
La moyenne est le centre de masse de probabilité, c’est-à-dire le premier moment . 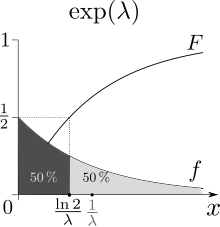La médiane est la Préimage F ⁻¹ (1/2).

La valeur moyenne ou attendue d’une variable aléatoire X à distribution exponentielle avec le paramètre de taux λ est donnée par

E ⁡ [ X ] = 1 λ . {displaystyle operatorname {E} [X]={frac {1}{lambda }}.}

À la lumière des exemples donnés ci- dessous , cela a du sens : si vous recevez des appels téléphoniques à un rythme moyen de 2 par heure, alors vous pouvez vous attendre à attendre une demi-heure pour chaque appel.

La variance de X est donnée par

Var ⁡ [ X ] = 1 λ 2 , {displaystyle operatorname {Var} [X]={frac {1}{lambda ^{2}}},} donc l’ écart type est égal à la moyenne.

Les moments de X , pour n ∈ N {displaystyle nin mathbb {N} } sont donnés par

E ⁡ [ X n ] = n ! λ n . {displaystyle operatorname {E} left[X^{n}right]={frac {n!}{lambda ^{n}}}.}

Les moments centraux de X , pour n ∈ N {displaystyle nin mathbb {N} } sont donnés par

μ n = ! n λ n = n ! λ n ∑ k = 0 n ( − 1 ) k k ! . {displaystyle mu _{n}={frac {!n}{lambda ^{n}}}={frac {n!}{lambda ^{n}}}sum _{k=0 }^{n}{frac {(-1)^{k}}{k!}}.} où ! n est la sous- factorielle de n

La médiane de X est donnée par

m ⁡ [ X ] = ln ⁡ ( 2 ) λ < E ⁡ [ X ] , {displaystyle operatorname {m} [X]={frac {ln(2)}{lambda }}<operatorname {E} [X],} où ln désigne le logarithme népérien . Ainsi, la différence absolue entre la moyenne et la médiane est | E ⁡ [ X ] − m ⁡ [ X ] | = 1 − ln ⁡ ( 2 ) λ < 1 λ = σ ⁡ [ X ] , {displaystyle left|operatorname {E} left[Xright]-operatorname {m} left[Xright]right|={frac {1-ln(2)}{lambda }}<{frac {1}{lambda }}=operatorname {sigma } [X],}

conformément à l’ inégalité médiane-moyenne .

Sans mémoire

Une variable aléatoire T exponentiellement distribuée obéit à la relation

Pr ( T > s + t ∣ T > s ) = Pr ( T > t ) , ∀ s , t ≥ 0. {displaystyle Pr left(T>s+tmid T>sright)=Pr(T>t),qquad forall s,tgeq 0.}

Ceci peut être vu en considérant la fonction de distribution cumulative complémentaire :

Pr ( T > s + t ∣ T > s ) = Pr ( T > s + t ∩ T > s ) Pr ( T > s ) = Pr ( T > s + t ) Pr ( T > s ) = e − λ ( s + t ) e − λ s = e − λ t = Pr ( T > t ) . {displaystyle {begin{aligned}Pr left(T>s+tmid T>sright)&={frac {Pr left(T>s+tcap T>sright)}{Pr left(T>sright)}}\[4pt]&={frac {Pr left(T>s+tright)}{Pr left(T>sright)}}\[4pt]&={frac {e^{-lambda (s+t)}}{e^{-lambda s}}}\[4pt]&=e^{-lambda t}\[4pt]&=Pr(T>t).end{aligned}}}

Lorsque T est interprété comme le temps d’attente pour qu’un événement se produise par rapport à un temps initial, cette relation implique que, si T est conditionné par une non-observation de l’événement sur une période de temps initiale s , la distribution du temps d’attente restant est identique à la distribution inconditionnelle d’origine. Par exemple, si un événement ne s’est pas produit après 30 secondes, la probabilité conditionnelle que l’occurrence prendra au moins 10 secondes de plus est égale à la probabilité inconditionnelle d’observer l’événement plus de 10 secondes après l’heure initiale.

La distribution exponentielle et la distribution géométrique sont les seules distributions de probabilité Sans mémoire .

La distribution exponentielle est par conséquent aussi nécessairement la seule distribution de probabilité continue qui a un taux d’échec constant .

Quantiles

Critères de Tukey pour les anomalies. ^{[ citation nécessaire ]}

La fonction quantile (fonction de distribution cumulative inverse) pour Exp( λ ) est

F − 1 ( p ; λ ) = − ln ⁡ ( 1 − p ) λ , 0 ≤ p < 1 {displaystyle F^{-1}(p;lambda )={frac {-ln(1-p)}{lambda }},qquad 0leq p<1}

Les quartiles sont donc :

• premier quartile : ln(4/3)/ λ
• médiane : ln(2)/ λ
• troisième quartile : ln(4)/ λ

Et par conséquent l’ écart interquartile est ln(3)/ λ .

Divergence Kullback-Leibler

La divergence dirigée Kullback – Leibler dans les nats de e λ {displaystyle e^{lambda }} (répartition “approximative”) de e λ 0 {displaystyle e^{lambda _{0}}} (distribution “vraie”) est donnée par

Δ ( λ 0 ∥ λ ) = E λ 0 ( log ⁡ p λ 0 ( x ) p λ ( x ) ) = E λ 0 ( log ⁡ λ 0 e λ 0 x λ e λ x ) = log ⁡ ( λ 0 ) − log ⁡ ( λ ) − ( λ 0 − λ ) E λ 0 ( x ) = log ⁡ ( λ 0 ) − log ⁡ ( λ ) + λ λ 0 − 1. {displaystyle {begin{aligned}Delta (lambda _{0}parallel lambda )&=mathbb {E} _{lambda _{0}}left(log {frac {p_{ lambda _{0}}(x)}{p_{lambda }(x)}}right)\&=mathbb {E} _{lambda _{0}}left(log { frac {lambda _{0}e^{lambda _{0}x}}{lambda e^{lambda x}}}right)\&=log(lambda _{0})- log(lambda )-(lambda _{0}-lambda )E_{lambda _{0}}(x)\&=log(lambda _{0})-log(lambda )+{frac {lambda }{lambda _{0}}}-1.end{aligned}}}

Distribution d’entropie maximale

Parmi toutes les distributions de probabilité continues avec support [0, ∞) et moyenne μ , la distribution exponentielle avec λ = 1/ μ a la plus grande entropie différentielle . En d’autres termes, il s’agit de la distribution de probabilité d’entropie maximale pour une variable aléatoire X supérieure ou égale à zéro et pour laquelle E[ X ] est fixe. ^[1]

Distribution du minimum de variables aléatoires exponentielles

Soit X ₁ , …, X _n des Variables aléatoires indépendantes distribuées exponentiellement avec des paramètres de taux λ ₁ , …, λ _n . Puis

min { X 1 , … , X n } {displaystyle min left{X_{1},dotsc ,X_{n}right}} est également distribué exponentiellement, avec le paramètre λ = λ 1 + ⋯ + λ n . {displaystyle lambda =lambda _{1}+dotsb +lambda _{n}.}

Ceci peut être vu en considérant la fonction de distribution cumulative complémentaire :

Pr ( min { X 1 , … , X n } > x ) = Pr ( X 1 > x , … , X n > x ) = ∏ i = 1 n Pr ( X i > x ) = ∏ i = 1 n exp ⁡ ( − x λ i ) = exp ⁡ ( − x ∑ i = 1 n λ i ) . {displaystyle {begin{aligned}&Pr left(min{X_{1},dotsc ,X_{n}}>xright)\={}&Pr left(X_ {1}>x,dotsc ,X_{n}>xright)\={}&prod _{i=1}^{n}Pr left(X_{i}>xright) \={}&prod _{i=1}^{n}exp left(-xlambda _{i}right)=exp left(-xsum _{i=1} ^{n}lambda _{i}right).end{aligned}}}

L’indice de la variable qui atteint le minimum est distribué selon la distribution catégorielle

Pr ( X k = min { X 1 , … , X n } ) = λ k λ 1 + ⋯ + λ n . {displaystyle Pr left(X_{k}=min{X_{1},dotsc ,X_{n}}right)={frac {lambda _{k}}{lambda _ {1}+dotsb +lambda _{n}}}.}

Une preuve peut être vue en laissant I = argmin i ∈ { 1 , ⋯ , n } ⁡ { X 1 , … , X n } {displaystyle I=operatorname {argmin} _{iin {1,dotsb ,n}}{X_{1},dotsc ,X_{n}}} . Puis,

Pr ( I = k ) = ∫ 0 ∞ Pr ( X k = x ) Pr ( ∀ i ≠ k X i > x ) d x = ∫ 0 ∞ λ k e − λ k x ( ∏ i = 1 , i ≠ k n e − λ i x ) d x = λ k ∫ 0 ∞ e − ( λ 1 + ⋯ + λ n ) x d x = λ k λ 1 + ⋯ + λ n . {displaystyle {begin{aligned}Pr(I=k)&=int _{0}^{infty}Pr(X_{k}=x)Pr(forall _{ineq k }X_{i}>x),dx\&=int _{0}^{infty }lambda _{k}e^{-lambda _{k}x}left(prod _ {i=1,ineq k}^{n}e^{-lambda _{i}x}right)dx\&=lambda _{k}int _{0}^{infty }e^{-left(lambda _{1}+dotsb +lambda _{n}right)x}dx\&={frac {lambda _{k}}{lambda _{ 1}+dotsb +lambda _{n}}}.end{aligned}}}

Noter que

max { X 1 , … , X n } {displaystyle max{X_{1},dotsc ,X_{n}}} n’est pas exponentiellement distribuée, si X ₁ , …, X _n ne sont pas tous de paramètre 0. ^[2]

Moments conjoints de statistiques d’ordre exponentiel iid

Laisser X 1 , … , X n {displaystyle X_{1},dotsc ,X_{n}} être n {displaystyle n} variables aléatoires exponentielles indépendantes et identiquement distribuées avec le paramètre de taux λ . Laisser X ( 1 ) , … , X ( n ) {displaystyle X_{(1)},dotsc ,X_{(n)}} désignent les statistiques de commande correspondantes . Pour i < j {displaystyle i<j} , le moment conjoint E ⁡ [ X ( i ) X ( j ) ] {displaystyle operatorname {E} left[X_{(i)}X_{(j)}right]} des statistiques de commande X ( i ) {displaystyle X_{(i)}} et X ( j ) {displaystyle X_{(j)}} est donné par

E ⁡ [ X ( i ) X ( j ) ] = ∑ k = 0 j − 1 1 ( n − k ) λ E ⁡ [ X ( i ) ] + E ⁡ [ X ( i ) 2 ] = ∑ k = 0 j − 1 1 ( n − k ) λ ∑ k = 0 i − 1 1 ( n − k ) λ + ∑ k = 0 i − 1 1 ( ( n − k ) λ ) 2 + ( ∑ k = 0 i − 1 1 ( n − k ) λ ) 2 . {displaystyle {begin{aligned}operatorname {E} left[X_{(i)}X_{(j)}right]&=sum _{k=0}^{j-1}{ frac {1}{(nk)lambda }}operatorname {E} left[X_{(i)}right]+operatorname {E} left[X_{(i)}^{2}right ]\&=sum _{k=0}^{j-1}{frac {1}{(nk)lambda }}sum _{k=0}^{i-1}{frac {1}{(nk)lambda }}+sum _{k=0}^{i-1}{frac {1}{((nk)lambda )^{2}}}+left( sum _{k=0}^{i-1}{frac {1}{(nk)lambda }}right)^{2}.end{aligned}}}

Cela peut être vu en invoquant la loi de l’espérance totale et la propriété Sans mémoire :

E ⁡ [ X ( i ) X ( j ) ] = ∫ 0 ∞ E ⁡ [ X ( i ) X ( j ) ∣ X ( i ) = x ] f X ( i ) ( x ) d x = ∫ x = 0 ∞ x E ⁡ [ X ( j ) ∣ X ( j ) ≥ x ] f X ( i ) ( x ) d x ( since X ( i ) = x ⟹ X ( j ) ≥ x ) = ∫ x = 0 ∞ x [ E ⁡ [ X ( j ) ] + x ] f X ( i ) ( x ) d x ( by the memoryless property ) = ∑ k = 0 j − 1 1 ( n − k ) λ E ⁡ [ X ( i ) ] + E ⁡ [ X ( i ) 2 ] . {displaystyle {begin{aligned}operatorname {E} left[X_{(i)}X_{(j)}right]&=int _{0}^{infty}operatorname {E} left[X_{(i)}X_{(j)}mid X_{(i)}=xright]f_{X_{(i)}}(x),dx\&=int _ {x=0}^{infty}xnomopérateur{E} left[X_{(j)}mid X_{(j)}geq xright]f_{X_{(i)}}(x ),dx&&left({textrm {depuis}}~X_{(i)}=ximplique X_{(j)}geq xright)\&=int _{x=0}^ {infty }xleft[operatorname {E} left[X_{(j)}right]+xright]f_{X_{(i)}}(x),dx&&left({ text{par la propriété Sans mémoire}}right)\&=sum _{k=0}^{j-1}{frac {1}{(nk)lambda }}operatorname {E} left [X_{(i)}right]+operatorname {E} left[X_{(i)}^{2}right].end{aligned}}}

La première équation découle de la loi de l’espérance totale . La deuxième équation exploite le fait qu’une fois que nous conditionnons sur X ( i ) = x {displaystyle X_{(i)}=x} , il doit s’ensuivre que X ( j ) ≥ x {displaystyle X_{(j)}geq x} . La troisième équation repose sur la propriété Sans mémoire pour remplacer E ⁡ [ X ( j ) ∣ X ( j ) ≥ x ] {displaystyle operatorname {E} left[X_{(j)}mid X_{(j)}geq xright]} avec E ⁡ [ X ( j ) ] + x {displaystyle operatorname {E} left[X_{(j)}right]+x} .

Somme de deux variables aléatoires exponentielles indépendantes

La fonction de distribution de probabilité (PDF) d’une somme de deux Variables aléatoires indépendantes est la convolution de leurs PDF individuelles . Si X 1 {displaystyle X_{1}} et X 2 {displaystyle X_{2}} sont des variables aléatoires exponentielles indépendantes avec des paramètres de taux respectifs λ 1 {style d’affichage lambda _{1}} et λ 2 , { style d’affichage lambda _ {2},} alors la densité de probabilité de Z = X 1 + X 2 {displaystyle Z=X_{1}+X_{2}} est donné par

f Z ( z ) = ∫ − ∞ ∞ f X 1 ( x 1 ) f X 2 ( z − x 1 ) d x 1 = ∫ 0 z λ 1 e − λ 1 x 1 λ 2 e − λ 2 ( z − x 1 ) d x 1 = λ 1 λ 2 e − λ 2 z ∫ 0 z e ( λ 2 − λ 1 ) x 1 d x 1 = { λ 1 λ 2 λ 2 − λ 1 ( e − λ 1 z − e − λ 2 z ) if λ 1 ≠ λ 2 λ 2 z e − λ z if λ 1 = λ 2 = λ . {displaystyle {begin{aligned}f_{Z}(z)&=int _{-infty }^{infty }f_{X_{1}}(x_{1})f_{X_{2} }(z-x_{1}),dx_{1}\&=int _{0}^{z}lambda _{1}e^{-lambda _{1}x_{1}} lambda _{2}e^{-lambda _{2}(z-x_{1})},dx_{1}\&=lambda _{1}lambda _{2}e^{ -lambda _{2}z}int _{0}^{z}e^{(lambda _{2}-lambda _{1})x_{1}},dx_{1}\ &={begin{cases}{dfrac {lambda _{1}lambda _{2}}{lambda _{2}-lambda _{1}}}left(e^{-lambda _{1}z}-e^{-lambda _{2}z}right)&{text{ if }}lambda _{1}neq lambda _{2}\[4pt] lambda ^{2}ze^{-lambda z}&{text{ if }}lambda _{1}=lambda _{2}=lambda .end{cases}}end{aligned}} } L’entropie de cette distribution est disponible sous forme fermée : en supposant λ 1 > λ 2 {displaystyle lambda _{1}>lambda _{2}} (sans perte de généralité), alors H ( Z ) = 1 + γ + ln ⁡ ( λ 1 − λ 2 λ 1 λ 2 ) + ψ ( λ 1 λ 1 − λ 2 ) , {displaystyle {begin{aligned}H(Z)&=1+gamma +ln left({frac {lambda _{1}-lambda _{2}}{lambda _{1} lambda _{2}}}right)+psi left({frac {lambda _{1}}{lambda _{1}-lambda _{2}}}right),end {aligné}}} où γ {displaystylegamma} est la Constante d’Euler-Mascheroni , et ψ ( ⋅ ) {displaystyle psi (cdot )} est la fonction digamma . ^[3]

Dans le cas de paramètres de taux égaux, le résultat est une distribution d’Erlang de forme 2 et de paramètre λ , { style d’affichage lambda ,} qui à son tour est un cas particulier de distribution gamma .

Distributions associées

• Si X ∼ Laplace ⁡ ( μ , β − 1 ) {displaystyle Xsim operatorname {Laplace} left(mu ,beta ^{-1}right)} alors | X − μ| ~ Exp(β).
• Si X ~ Pareto(1, λ) alors log( X ) ~ Exp(λ).
• Si X ~ SkewLogistic (θ), alors log ⁡ ( 1 + e − X ) ∼ Exp ⁡ ( θ ) {displaystyle log left(1+e^{-X}right)sim operatorname {Exp} (theta )} .
• Si X _i ~ U (0, 1) alors lim n → ∞ n min ( X 1 , … , X n ) ∼ Exp ⁡ ( 1 ) {displaystyle lim _{nto infty}nmin left(X_{1},ldots ,X_{n}right)sim operatorname {Exp} (1)}
• La distribution exponentielle est une limite d’une distribution bêta mise à l’échelle : lim n → ∞ n Beta ⁡ ( 1 , n ) = Exp ⁡ ( 1 ) . {displaystyle lim _{nto infty}noperatorname {Beta} (1,n)=operatorname {Exp} (1).}
• La distribution exponentielle est un cas particulier de la distribution de Pearson de type 3 .
• Si X ~ Exp(λ) et X _i ~ Exp(λ _i ) alors :
  • k X ∼ Exp ⁡ ( λ k ) {displaystyle kXsim operatorname {Exp} left({frac {lambda }{k}}right)} , fermeture sous mise à l’échelle par un facteur positif.
  • 1 + X ~ BenktanderWeibull (λ, 1), qui se réduit à une distribution exponentielle tronquée.
  • ke ^X ~ Pareto ( k , λ).
  • e ^−X ~ Bêta (λ, 1).
  • 1/ke ^X ~ PowerLaw ( k , λ)
  • X ∼ Rayleigh ⁡ ( 1 2 λ ) {displaystyle {sqrt {X}}sim operatorname {Rayleigh} left({frac {1}{sqrt {2lambda}}}right)} , la distribution de Rayleigh
  • X ∼ Weibull ⁡ ( 1 λ , 1 ) {displaystyle Xsim operatorname {Weibull} left({frac {1}{lambda}},1right)} , la distribution de Weibull
  • X 2 ∼ Weibull ⁡ ( 1 λ 2 , 1 2 ) {displaystyle X^{2}sim operatorname {Weibull} left({frac {1}{lambda ^{2}}},{frac {1}{2}}right)}
  • μ − β log(λ X ) ∼ Gumbel (μ, β) .
  • ⌊ X ⌋ ∼ Geometric ⁡ ( 1 − e − λ ) {displaystyle lfloor Xrfloor sim operatorname {Géométrique} left(1-e^{-lambda }right)} , une distribution géométrique sur 0,1,2,3,…
  • ⌈ X ⌉ ∼ Geometric ⁡ ( 1 − e − λ ) {displaystyle lceil Xrceil sim operatorname {Géométrique} left(1-e^{-lambda }right)} , une distribution géométrique sur 1,2,3,4,…
  • Si aussi Y ~ Erlang( n , λ) ou Y ∼ Γ ( n , 1 λ ) {displaystyle YsimGamma left(n,{frac {1}{lambda }}right)} alors X Y + 1 ∼ Pareto ⁡ ( 1 , n ) {displaystyle {frac {X}{Y}}+1sim operatorname {Pareto} (1,n)}
  • Si aussi λ ~ Gamma ( k , θ) (forme, paramétrisation d’échelle) alors la distribution marginale de X est Lomax ( k , 1/θ), le mélange gamma
  • λ ₁ X ₁ − λ ₂ Y ₂ ~ Laplace(0, 1) .
  • min{ X ₁ , …, X _n } ~ Exp(λ ₁ + … + λ _n ).
  • Si aussi λ _i = λ alors :
    • X 1 + ⋯ + X k = ∑ i X i ∼ {displaystyle X_{1}+cdots +X_{k}=sum _{i}X_{i}sim } Erlang ( k , λ) = Gamma ( k , λ ⁻¹ ) = Gamma( k , λ) (en paramétrisation ( k , θ) et (α, β), respectivement) avec un paramètre de forme entier k. ^[4]
    • X _i − X _j ~ Laplace(0, λ ⁻¹ ).
  • Si aussi X _i sont indépendants, alors :
    • X i X i + X j {displaystyle {frac {X_{i}}{X_{i}+X_{j}}}} ~ U (0, 1)
    • Z = λ i X i λ j X j {displaystyle Z={frac {lambda _{i}X_{i}}{lambda _{j}X_{j}}}} a une fonction de densité de probabilité f Z ( z ) = 1 ( z + 1 ) 2 {displaystyle f_{Z}(z)={frac {1}{(z+1)^{2}}}} . Cela peut être utilisé pour obtenir un intervalle de confiance pour λ i λ j {displaystyle {frac {lambda _{i}}{lambda _{j}}}} .
  • Si aussi λ = 1 :
    • μ − β log ⁡ ( e − X 1 − e − X ) ∼ Logistic ⁡ ( μ , β ) {displaystyle mu -beta log left({frac {e^{-X}}{1-e^{-X}}}right)sim operatorname {Logistique} (mu , bêta )} , la répartition logistique
    • μ − β log ⁡ ( X i X j ) ∼ Logistic ⁡ ( μ , β ) {displaystyle mu -beta log left({frac {X_{i}}{X_{j}}}right)sim operatorname {Logistique} (mu ,beta )}
    • μ − σ log( X ) ~ GEV(μ, σ, 0) .
    • De plus si Y ∼ Γ ( α , β α ) {displaystyle Ysim Gamma left(alpha ,{frac {beta }{alpha }}right)} alors X Y ∼ K ⁡ ( α , β ) {displaystyle {sqrt {XY}}sim operatorname {K} (alpha ,beta )} ( distribution K )
  • Si aussi λ = 1/2 alors X ∼ χ²
    ₂; c’est-à-dire que X a une distribution chi carré avec 2 degrés de liberté . Ainsi: Exp ⁡ ( λ ) = 1 2 λ Exp ⁡ ( 1 2 ) ∼ 1 2 λ χ 2 2 ⇒ ∑ i = 1 n Exp ⁡ ( λ ) ∼ 1 2 λ χ 2 n 2 {displaystyle operatorname {Exp} (lambda )={frac {1}{2lambda }}operatorname {Exp} left({frac {1}{2}}right)sim { frac {1}{2lambda }}chi _{2}^{2}Rightarrow sum _{i=1}^{n}operatorname {Exp} (lambda )sim {frac {1 }{2lambda }}chi _{2n}^{2}}
• Si X ∼ Exp ⁡ ( 1 λ ) {displaystyle Xsim operatorname {Exp} left({frac {1}{lambda }}right)} et Y ∣ X {displaystyle Ymilieu X} ~ Poisson( X ) alors Y ∼ Geometric ⁡ ( 1 1 + λ ) {displaystyle Ysim operatorname {Géométrique} left({frac {1}{1+lambda }}right)} ( répartition géométrique )
• La distribution de Hoyt peut être obtenue à partir de la distribution exponentielle et de la distribution arc sinus

Autres distributions associées :

• Distribution hyperexponentielle – la distribution dont la densité est une somme pondérée de densités exponentielles.
• Distribution hypoexponentielle – la distribution d’une somme générale de variables aléatoires exponentielles.
• Distribution exgaussienne – la somme d’une distribution exponentielle et d’une distribution normale .

Inférence statistique

Ci-dessous, supposons que la variable aléatoire X est distribuée de manière exponentielle avec le paramètre de taux λ, et x 1 , … , x n {displaystyle x_{1},dotsc ,x_{n}} sont n échantillons indépendants de X , avec une moyenne d’échantillon x ̄ {displaystyle {bar {x}}} .

Estimation des paramètres

L’ estimateur du maximum de vraisemblance pour λ est construit comme suit :

La fonction de vraisemblance pour λ, étant donné un échantillon indépendant et identiquement distribué x = ( x ₁ , …, x _n ) tiré de la variable, est :

L ( λ ) = ∏ i = 1 n λ exp ⁡ ( − λ x i ) = λ n exp ⁡ ( − λ ∑ i = 1 n x i ) = λ n exp ⁡ ( − λ n x ̄ ) , {displaystyle L(lambda )=prod _{i=1}^{n}lambda exp(-lambda x_{i})=lambda ^{n}exp left(-lambda somme _{i=1}^{n}x_{i}right)=lambda ^{n}exp left(-lambda n{overline {x}}right),}

où:

x ̄ = 1 n ∑ i = 1 n x i {displaystyle {overline {x}}={frac {1}{n}}sum _{i=1}^{n}x_{i}} est la moyenne de l’échantillon.

La dérivée du logarithme de la fonction de vraisemblance est :

d d λ ln ⁡ L ( λ ) = d d λ ( n ln ⁡ λ − λ n x ̄ ) = n λ − n x ̄ { > 0 , 0 < λ < 1 x ̄ , = 0 , λ = 1 x ̄ , < 0 , λ > 1 x ̄ . {displaystyle {frac {d}{dlambda }}ln L(lambda )={frac {d}{dlambda }}left(nln lambda -lambda n{overline {x}}right)={frac {n}{lambda }}-n{overline {x}} {begin{cases}>0,&0<lambda <{frac {1}{ overline {x}}},\[8pt]=0,&lambda ={frac {1}{overline {x}}},\[8pt]<0,&lambda >{frac {1}{overline {x}}}.end{cases}}}

Par conséquent, l’ estimation du maximum de vraisemblance pour le paramètre de taux est :

λ ^ mle = 1 x ̄ = n ∑ i x i {displaystyle {widehat {lambda}}_{text{mle}}={frac {1}{overline {x}}}={frac {n}{sum _{i}x_{ je}}}}

Il ne s’agit pas d’un Estimateur sans biais de λ , { style d’affichage lambda ,} même si x ̄ {displaystyle {overline {x}}} est un estimateur ^[5] MLE ^{[6] sans biais de} 1 / λ {displaystyle 1/lambda} et la moyenne de distribution.

Le biais de λ ^ mle {displaystyle {widehat {lambda}}_{text{mle}}} est égal à

b ≡ E ⁡ [ ( λ ^ mle − λ ) ] = λ n − 1 {displaystyle bequiv operatorname {E} left[left({widehat {lambda }}_{text{mle}}-lambda right)right]={frac {lambda } {n-1}}} qui donne l ‘ estimateur du maximum de vraisemblance corrigé du biais λ ^ mle ∗ = λ ^ mle − b ^ . {displaystyle {widehat {lambda }}_{text{mle}}^{*}={widehat {lambda }}_{text{mle}}-{widehat {b}}.}

Minimiseur approximatif de l’erreur quadratique attendue

Supposons que vous ayez au moins trois échantillons. Si nous recherchons un minimiseur de l’erreur quadratique moyenne attendue (voir aussi : Compromis biais-variance ) similaire à l’estimation du maximum de vraisemblance (c’est-à-dire une correction multiplicative de l’estimation de vraisemblance), nous avons :

λ ^ = ( n − 2 n ) ( 1 x ̄ ) = n − 2 ∑ i x i {displaystyle {widehat {lambda}}=left({frac {n-2}{n}}right)left({frac {1}{bar {x}}}right) ={frac {n-2}{somme _{i}x_{i}}}}

Ceci est dérivé de la moyenne et de la variance de la distribution gamma inverse : Inv-Gamma ( n , λ ) {textstyle {mbox{Inv-Gamma}}(n,lambda)} . ^[7]

Informations sur les pêcheurs

Les informations de Fisher , notées I ( λ ) {displaystyle {mathcal {I}}(lambda )} , pour un estimateur du paramètre taux λ {displaystylelambda} est donné comme suit :

I ( λ ) = E ⁡ [ ( ∂ ∂ λ log ⁡ f ( x ; λ ) ) 2 | λ ] = ∫ ( ∂ ∂ λ log ⁡ f ( x ; λ ) ) 2 f ( x ; λ ) d x {displaystyle {mathcal {I}}(lambda )=operatorname {E} left[left.left({frac {partial }{partial lambda }}log f(x; lambda )right)^{2}right|lambda right]=int left({frac {partial }{partial lambda }}log f(x;lambda )right)^ {2}f(x;lambda ),dx}

Brancher la distribution et la résolution donne:

I ( λ ) = ∫ 0 ∞ ( ∂ ∂ λ log ⁡ λ e − λ x ) 2 λ e − λ x d x = ∫ 0 ∞ ( 1 λ − x ) 2 λ e − λ x d x = λ − 2 . {displaystyle {mathcal {I}}(lambda )=int _{0}^{infty}left({frac {partial }{partial lambda }}log lambda e^{ -lambda x}right)^{2}lambda e^{-lambda x},dx=int _{0}^{infty}left({frac {1}{lambda } }-xright)^{2}lambda e^{-lambda x},dx=lambda ^{-2}.}

Cela détermine la quantité d’informations que chaque échantillon indépendant d’une distribution exponentielle porte sur le paramètre de taux inconnu λ {displaystylelambda} .

Intervalles de confiance

L’intervalle de confiance 100(1 − α)% pour le paramètre de taux d’une distribution exponentielle est donné par : ^[8]

2 n λ ^ χ 1 − α 2 , 2 n 2 < 1 λ < 2 n λ ^ χ α 2 , 2 n 2 {displaystyle {frac {2n}{{widehat {lambda}}chi _{1-{frac {alpha }{2}},2n}^{2}}}<{frac {1 }{lambda }}<{frac {2n}{{widehat {lambda }}chi _{{frac {alpha }{2}},2n}^{2}}}} qui est aussi égal à : 2 n x ̄ χ 1 − α 2 , 2 n 2 < 1 λ < 2 n x ̄ χ α 2 , 2 n 2 {displaystyle {frac {2n{overline {x}}}{chi _{1-{frac {alpha }{2}},2n}^{2}}}<{frac {1} {lambda}}<{frac {2n{overline {x}}}{chi _{{frac {alpha }{2}},2n}^{2}}}} où χ²
_{p , v}est le centile 100( p ) de la Distribution du chi carré avec v degrés de liberté , n est le nombre d’observations des temps entre les arrivées dans l’échantillon et x-bar est la moyenne de l’échantillon. Une approximation simple des extrémités exactes de l’intervalle peut être dérivée en utilisant une approximation normale du χ ²
_{p , v}Distribution. Cette approximation donne les valeurs suivantes pour un intervalle de confiance à 95 % : λ lower = λ ^ ( 1 − 1.96 n ) λ upper = λ ^ ( 1 + 1.96 n ) {displaystyle {begin{aligned}lambda _{text{lower}}&={widehat {lambda }}left(1-{frac {1.96}{sqrt {n}}}right )\lambda _{text{upper}}&={widehat {lambda }}left(1+{frac {1.96}{sqrt {n}}}right)end{aligned} }}

Cette approximation peut être acceptable pour des échantillons contenant au moins 15 à 20 éléments. ^[9]

Inférence bayésienne

L’ a priori conjugué pour la distribution exponentielle est la distribution gamma (dont la distribution exponentielle est un cas particulier). Le paramétrage suivant de la fonction de densité de probabilité gamma est utile :

Gamma ⁡ ( λ ; α , β ) = β α Γ ( α ) λ α − 1 exp ⁡ ( − λ β ) . {displaystyle operatorname {Gamma} (lambda ;alpha ,beta )={frac {beta ^{alpha }}{Gamma (alpha )}}lambda ^{alpha -1} exp(-lambdabeta ).}

La Distribution postérieure p peut alors être exprimée en fonction de la fonction de vraisemblance définie ci-dessus et d’un a priori gamma :

p ( λ ) ∝ L ( λ ) Γ ( λ ; α , β ) = λ n exp ⁡ ( − λ n x ̄ ) β α Γ ( α ) λ α − 1 exp ⁡ ( − λ β ) ∝ λ ( α + n ) − 1 exp ⁡ ( − λ ( β + n x ̄ ) ) . {displaystyle {begin{aligned}p(lambda )&propto L(lambda )Gamma (lambda ;alpha ,beta )\&=lambda ^{n}exp left(- lambda n{overline {x}}right){frac {beta ^{alpha }}{Gamma (alpha )}}lambda ^{alpha -1}exp(-lambda beta )\&propto lambda ^{(alpha +n)-1}exp(-lambda left(beta +n{overline {x}}right)).end{aligned} }}

Maintenant, la densité a posteriori p a été spécifiée jusqu’à une constante de normalisation manquante. Comme il a la forme d’un gamma pdf, celui-ci peut facilement être rempli, et on obtient :

p ( λ ) = Γ ( λ ; α + n , β + n x ̄ ) . {displaystyle p(lambda )=Gamma (lambda ;alpha +n,beta +n{overline {x}}).}

Ici, l’ hyperparamètre α peut être interprété comme le nombre d’observations antérieures et β comme la somme des observations antérieures. La moyenne postérieure est ici :

α + n β + n x ̄ . {displaystyle {frac {alpha +n}{beta +n{overline {x}}}}.}

Occurrence et applications

Survenance d’événements

La distribution exponentielle se produit naturellement lors de la description des longueurs des temps inter-arrivées dans un processus de Poisson homogène .

La distribution exponentielle peut être considérée comme une contrepartie continue de la distribution géométrique , qui décrit le nombre d’ essais de Bernoulli nécessaires pour qu’un processus discret change d’état. En revanche, la distribution exponentielle décrit le temps nécessaire à un processus continu pour changer d’état.

Dans les scénarios du monde réel, l’hypothèse d’un taux constant (ou probabilité par unité de temps) est rarement satisfaite. Par exemple, le taux d’appels téléphoniques entrants diffère selon l’heure de la journée. Mais si nous nous concentrons sur un intervalle de temps pendant lequel le taux est à peu près constant, comme de 14h à 16h pendant les jours de travail, la distribution exponentielle peut être utilisée comme un bon modèle approximatif pour le temps jusqu’à l’arrivée du prochain appel téléphonique. Des mises en garde similaires s’appliquent aux exemples suivants qui produisent des variables à distribution approximativement exponentielle :

• Le temps jusqu’à ce qu’une particule radioactive se désintègre , ou le temps entre les clics d’un compteur Geiger
• Le temps qu’il faut avant votre prochain appel téléphonique
• Le temps jusqu’au défaut (sur le paiement aux créanciers de l’entreprise) dans la modélisation du risque de crédit sous forme réduite

Les variables exponentielles peuvent également être utilisées pour modéliser des situations où certains événements se produisent avec une probabilité constante par unité de longueur, comme la distance entre les mutations sur un brin d’ADN ou entre les accidents de la route sur une route donnée.

Dans la théorie des files d’attente , les temps de service des agents dans un système (par exemple, combien de temps il faut à un caissier de banque, etc. pour servir un client) sont souvent modélisés comme des variables à distribution exponentielle. (L’arrivée de clients par exemple est également modélisée par la distribution de Poisson si les arrivées sont indépendantes et distribuées de manière identique.) La durée d’un processus qui peut être considéré comme une séquence de plusieurs tâches indépendantes suit la distribution d’Erlang (qui est la distribution de la somme de plusieurs variables indépendantes distribuées exponentiellement). La théorie de la fiabilité et l’ingénierie de la fiabilité font également un usage intensif de la distribution exponentielle. A cause des Sans mémoirepropriété de cette distribution, elle est bien adaptée pour modéliser la partie du taux de risque constant de la courbe de la baignoire utilisée dans la théorie de la fiabilité. C’est aussi très pratique car il est si facile d’ajouter des taux d’échec dans un modèle de fiabilité. La distribution exponentielle n’est cependant pas appropriée pour modéliser la durée de vie globale des organismes ou des dispositifs techniques, car les “taux de défaillance” ici ne sont pas constants : plus de défaillances se produisent pour les systèmes très jeunes et pour les systèmes très anciens.

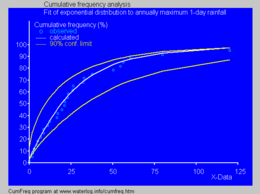
Ajustement de la distribution exponentielle cumulative aux précipitations annuelles maximales sur 1 jour à l’aide de CumFreq ^[10]

En physique , si vous observez un gaz à une température et une pression fixes dans un champ gravitationnel uniforme , les hauteurs des différentes molécules suivent également une distribution exponentielle approximative, connue sous le nom de formule barométrique . Ceci est une conséquence de la propriété d’entropie mentionnée ci-dessous.

En hydrologie , la distribution exponentielle est utilisée pour analyser les valeurs extrêmes de variables telles que les valeurs maximales mensuelles et annuelles des précipitations quotidiennes et les volumes de débit des rivières. ^[11]

L’image bleue illustre un exemple d’ajustement de la distribution exponentielle aux précipitations annuelles maximales sur une journée, montrant également la ceinture de confiance à 90 % basée sur la distribution binomiale . Les données pluviométriques sont représentées en traçant les positions dans le cadre de l’ analyse des fréquences cumulées .

Dans la gestion des blocs opératoires, la distribution de la durée d’une chirurgie pour une catégorie de chirurgies sans contenu de travail typique (comme dans une salle d’urgence, englobant tous les types de chirurgies).

Prédiction

Après avoir observé un échantillon de n points de données à partir d’une distribution exponentielle inconnue, une tâche courante consiste à utiliser ces échantillons pour faire des prédictions sur les données futures à partir de la même source. Une distribution prédictive commune sur les futurs échantillons est la distribution dite plug-in, formée en branchant une estimation appropriée pour le paramètre de taux λ dans la fonction de densité exponentielle. Un choix courant d’estimation est celui fourni par le principe du maximum de vraisemblance, et son utilisation donne la densité prédictive sur un échantillon futur x _{n +1} , conditionnée sur les échantillons observés x = ( x ₁ , …, x _n ) donné par

p M L ( x n + 1 ∣ x 1 , … , x n ) = ( 1 x ̄ ) exp ⁡ ( − x n + 1 x ̄ ) {displaystyle p_{rm {ML}}(x_{n+1}mid x_{1},ldots ,x_{n})=left({frac {1}{overline {x}} }right)exp left(-{frac {x_{n+1}}{overline {x}}}right)}

L’approche bayésienne fournit une distribution prédictive qui tient compte de l’incertitude du paramètre estimé, bien que cela puisse dépendre de manière cruciale du choix de l’a priori.

Une distribution prédictive exempte des problèmes de choix des a priori qui se posent dans le cadre de l’approche bayésienne subjective est

p C N M L ( x n + 1 ∣ x 1 , … , x n ) = n n + 1 ( x ̄ ) n ( n x ̄ + x n + 1 ) n + 1 , {displaystyle p_{rm {CNML}}(x_{n+1}mid x_{1},ldots ,x_{n})={frac {n^{n+1}left({ overline {x}}right)^{n}}{left(n{overline {x}}+x_{n+1}right)^{n+1}}},}

qui peut être considéré comme

1. une distribution de confiance fréquentiste , obtenue à partir de la distribution de la grandeur pivot x n + 1 / x ̄ {displaystyle {x_{n+1}}/{overline {x}}} ; ^[12]
2. une vraisemblance prédictive de profil, obtenue en éliminant le paramètre λ de la vraisemblance conjointe de x _{n +1} et λ par maximisation ; ^[13]
3. une distribution a posteriori prédictive bayésienne objective, obtenue à l’aide de l’a priori non informatif de Jeffreys 1/ λ ;
4. la distribution prédictive du maximum de vraisemblance normalisée conditionnelle (CNML), à partir de considérations théoriques de l’information. ^[14]

La précision d’une distribution prédictive peut être mesurée en utilisant la distance ou la divergence entre la vraie distribution exponentielle avec un paramètre de taux, λ ₀ , et la distribution prédictive basée sur l’échantillon x . La divergence Kullback – Leibler est une mesure couramment utilisée et sans paramétrisation de la différence entre deux distributions. En notant Δ( λ ₀ || p ) la Divergence de Kullback-Leibler entre une exponentielle de paramètre de taux λ ₀ et une distribution prédictive p , on peut montrer que

E λ 0 ⁡ [ Δ ( λ 0 ∥ p M L ) ] = ψ ( n ) + 1 n − 1 − log ⁡ ( n ) E λ 0 ⁡ [ Δ ( λ 0 ∥ p C N M L ) ] = ψ ( n ) + 1 n − log ⁡ ( n ) {displaystyle {begin{aligned}operatorname {E} _{lambda _{0}}left[Delta (lambda _{0}parallel p_{rm {ML}})right]& =psi (n)+{frac {1}{n-1}}-log(n)\operatorname {E} _{lambda _{0}}left[Delta (lambda _ {0}parallel p_{rm {CNML}})right]&=psi (n)+{frac {1}{n}}-log(n)end{aligned}}}

où l’espérance est prise par rapport à la distribution exponentielle avec le paramètre de taux λ ₀ ∈ (0, ∞) , et ψ( · ) est la fonction digamma. Il est clair que la distribution prédictive CNML est strictement supérieure à la distribution plug-in de maximum de vraisemblance en termes de divergence moyenne de Kullback-Leibler pour toutes les tailles d’échantillon n > 0 .

Méthodes de calcul

Génération de variables exponentielles

Une méthode conceptuellement très simple pour générer des variables exponentielles est basée sur l’échantillonnage par transformation inverse : étant donné une variable aléatoire U tirée de la distribution uniforme sur l’intervalle unitaire (0, 1) , la variable

T = F − 1 ( U ) {displaystyle T=F^{-1}(U)}

a une distribution exponentielle, où F ⁻¹ est la fonction quantile , définie par

F − 1 ( p ) = − ln ⁡ ( 1 − p ) λ . {displaystyle F^{-1}(p)={frac {-ln(1-p)}{lambda }}.}

De plus, si U est uniforme sur (0, 1), alors 1 − U l’est aussi . Cela signifie que l’on peut générer des variables exponentielles comme suit :

T = − ln ⁡ ( U ) λ . {displaystyle T={frac {-ln(U)}{lambda }}.}

D’autres méthodes pour générer des variables exponentielles sont discutées par Knuth ^[15] et Devroye. ^[16]

Une méthode rapide pour générer un ensemble de variables exponentielles prêtes à l’emploi sans utiliser de routine de tri est également disponible. ^[16]

Voir également

• Temps mort – une application de la distribution exponentielle à l’analyse des détecteurs de particules.
• Distribution de Laplace ou “distribution exponentielle double”.
• Relations entre les distributions de probabilité
• Distribution exponentielle de Marshall – Olkin

Références

1. ^ Parc, Sung Y.; En ligneBera, Anil K. (2009). “Modèle d’hétéroscédasticité conditionnelle autorégressive à entropie maximale” (PDF) . Journal d’économétrie . Elsevier. 150 (2): 219-230. doi : 10.1016/j.jeconom.2008.12.014 . Archivé de l’original (PDF) le 2016-03-07 . Récupéré le 02/06/2011 .
2. ^ Michel, Lugo. “L’espérance du maximum d’exponentielles” (PDF) . Archivé de l’original (PDF) le 20 décembre 2016 . Récupéré le 13 décembre 2016 .
3. ^ Eckford, Andrew W.; Thomas, Peter J. (2016). “Entropie de la somme de deux variables aléatoires exponentielles indépendantes et non distribuées de manière identique”. arXiv : 1609.02911 [ cs.IT ].
4. ^ Ibe, Oliver C. (2014). Fundamentals of Applied Probability and Random Processes (2e éd.). Presse académique. p. 128. ISBN 9780128010358.
5. ^ Richard Arnold Johnson; Dean W. Wichern (2007). Analyse statistique multivariée appliquée . Salle Pearson Prentice. ISBN 978-0-13-187715-3. Récupéré le 10 août 2012 .
6. ^ Manuel électronique NIST / SEMATECH des méthodes statistiques
7. ^ Elfessi, Abdulaziz; En ligneReineke, David M. (2001). “Un regard bayésien sur l’estimation classique : la distribution exponentielle” . Journal de l’éducation statistique . 9 (1). doi : 10.1080/10691898.2001.11910648 .
8. ^ Ross, Sheldon M. (2009). Introduction aux probabilités et aux statistiques pour les ingénieurs et les scientifiques (4e éd.). Presse associée. p. 267.ISBN _ 978-0-12-370483-2.
9. ^ Guerriero, V. (2012). “Distribution de la loi de puissance: méthode de statistiques inférentielles multi-échelles” . Journal de la Frontière des Mathématiques Modernes . 1 : 21–28.
10. ^ “Cumfreq, un programme informatique gratuit pour l’analyse de fréquence cumulative” .
11. ^ Ritzema, HP, éd. (1994). Analyse de fréquence et de régression . Chapitre 6 dans : Drainage Principles and Applications, Publication 16, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, Pays-Bas. p. 175–224 . ISBN 90-70754-33-9.
12. ^ Sans loi, JF; En ligneFredette, M. (2005). “Intervalles de prédictions fréquentistes et distributions prédictives” . Biométrie . 92 (3): 529–542. doi : 10.1093/biomet/92.3.529 .
13. ^ Bjornstad, JF (1990). “Probabilité prédictive : un examen” . Statiste. Sci . 5 (2): 242–254. doi : 10.1214/ss/1177012175 .
14. ^ DF Schmidt et E. Makalic, ” Modèles universels pour la distribution exponentielle “, IEEE Transactions on Information Theory , Volume 55, Numéro 7, pp. 3087–3090, 2009 doi : 10.1109/TIT.2009.2018331
15. ^ Donald E. Knuth (1998). L’art de la programmation informatique , volume 2 : Algorithmes semi -numériques , 3e éd. Boston : Addison-Wesley. ISBN 0-201-89684-2 . Voir section 3.4.1, p. 133.
16. ^ ^{un b} Luc Devroye (1986). Génération de variables aléatoires non uniformes . New York : Springer-Verlag. ISBN 0-387-96305-7 . Voir chapitre IX , section 2, p. 392–401.

Liens externes

• “Distribution exponentielle” , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Calculateur en ligne de distribution exponentielle