Densité relative

Densité relative , ou gravité spécifique , ^{[1] [2]} est le rapport de la densité (masse d’une unité de volume) d’une substance à la densité d’un matériau de référence donné. La gravité spécifique des liquides est presque toujours mesurée par rapport à l’eau la plus dense (à 4 ° C ou 39,2 ° F); pour les gaz, la référence est l’Air à température ambiante (20 °C ou 68 °F). Le terme “densité relative” est souvent préféré dans l’usage scientifique.

Gravité spécifique
Symboles communs	SG
Unité SI	Sans unité
Dérivations à partir d’ autres grandeurs	S G true = ρ sample ρ H 2 O {displaystyle SG_{text{true}}={frac {rho _{text{sample}}}{rho _{mathrm {H_{2}O} }}}}

Un maître de manœuvre de l’aviation de l’US Navy teste la gravité spécifique du carburant JP-5

Si la densité relative d’une substance est inférieure à 1, elle est alors moins dense que la référence ; si supérieur à 1 alors il est plus dense que la référence. Si la densité relative est exactement 1 alors les densités sont égales ; c’est-à-dire que des volumes égaux des deux substances ont la même masse. Si le matériau de référence est l’eau, alors une substance avec une densité relative (ou gravité spécifique) inférieure à 1 flottera dans l’eau. Par exemple, un glaçon, avec une densité relative d’environ 0,91, flottera. Une substance dont la densité relative est supérieure à 1 coulera.

La température et la pression doivent être spécifiées pour l’échantillon et la référence. La pression est presque toujours de 1 atm (101,325 kPa ). Là où ce n’est pas le cas, il est plus courant de spécifier directement la densité. Les températures pour l’échantillon et la référence varient d’une industrie à l’autre. Dans la pratique brassicole britannique, la gravité spécifique, comme spécifié ci-dessus, est multipliée par 1000. ^[3] La gravité spécifique est couramment utilisée dans l’industrie comme un moyen simple d’obtenir des informations sur la concentration de solutions de divers matériaux tels que les saumures , le poids du moût ( sirops , jus, miels, moût de bière , moût , etc.) et acides.

Calcul de base

Densité relative ( R D {displaystyle RD} ) ou gravité spécifique ( S G {displaystyle SG} ) est une quantité sans dimension , car c’est le rapport des densités ou des poids

R D = ρ s u b s t a n c e ρ r e f e r e n c e {displaystyle {mathit {RD}}={frac {rho _{mathrm {substance}}}{rho _{mathrm {référence} }}}} où R D {displaystyle RD} est la densité relative, ρ substance {displaystyle rho _{text{substance}}} est la masse volumique de la substance mesurée, et ρ reference {displaystyle rho _{text{référence}}} est la densité de la référence. (Par convention ρ {style d’affichage rho} , la lettre grecque rho , dénote la densité.)

Le matériel de référence peut être indiqué à l’aide d’indices : R D substance/reference {displaystyle RD_{text{substance/référence}}} qui signifie “la densité relative de la substance par rapport à la référence “. Si la référence n’est pas explicitement indiquée, on suppose normalement qu’il s’agit d’ eau à 4 ° C (ou, plus précisément, 3,98 ° C, qui est la température à laquelle l’eau atteint sa densité maximale). En unités SI , la masse volumique de l’eau est (approximativement) de 1000 kg / m ³ ou 1 g / cm ³ , ce qui rend les calculs de densité relative particulièrement pratiques : il suffit de diviser la masse volumique de l’objet par 1000 ou 1, selon la unités.

La densité relative des gaz est souvent mesurée par rapport à de l’ Air sec à une température de 20 °C et une pression de 101,325 kPa absolu, qui a une densité de 1,205 kg/m ³ . La densité relative par rapport à l’Air peut être obtenue par

R D = ρ g a s ρ a i r ≈ M g a s M a i r {displaystyle {mathit {RD}}={frac {rho _{mathrm {gaz} }}{rho _{mathrm {Air}}}}approx {frac {M_{mathrm { gaz} }}{M_{mathrm {Air} }}}} Air} }}}approx {frac {M_{mathrm {gas} }}{M_{mathrm {Air} }}}}” height=”0″ src=”” data-src=”https://wikimedia.org/api/rest_v1/media/math/render/svg/d206c1c0a1cb09b2c927151cff6b0f14d1d432b3″ width=”0″> où M {displaystyle M} est la masse molaire et le signe approximativement égal est utilisé car l’égalité ne vaut que si 1 mol de gaz et 1 mol d’Air occupent le même volume à une température et une pression données, c’est-à-dire qu’ils sont tous deux des gaz parfaits . Le comportement idéal n’est généralement observé qu’à très basse pression. Par exemple, une mole d’un gaz parfait occupe 22,414 L à 0 °C et 1 atmosphère alors que le dioxyde de carbone a un volume molaire de 22,259 L dans ces mêmes conditions.

Ceux dont le SG est supérieur à 1 sont plus denses que l’eau et, sans tenir compte des effets de tension de surface , s’y enfonceront. Ceux avec un SG inférieur à 1 sont moins denses que l’eau et flotteront dessus. Dans les travaux scientifiques, la relation entre la masse et le volume est généralement exprimée directement en termes de densité (masse par unité de volume) de la substance étudiée. C’est dans l’industrie que la gravité spécifique trouve une large application, souvent pour des raisons historiques.

La véritable gravité spécifique d’un liquide peut être exprimée mathématiquement comme suit :

S G true = ρ sample ρ H 2 O {displaystyle SG_{text{true}}={frac {rho _{text{sample}}}{rho _{mathrm {H_{2}O} }}}} où ρ sample {displaystyle rho _{text{échantillon}}} est la densité de l’échantillon et ρ H 2 O {displaystyle rho _{mathrm {H_{2}O} }} est la masse volumique de l’eau.

La gravité spécifique apparente est simplement le rapport des poids de volumes égaux d’échantillon et d’eau dans l’Air :

S G apparent = W A , sample W A , H 2 O {displaystyle SG_{text{apparent}}={frac {W_{mathrm {A} ,{text{sample}}}}{W_{mathrm {A} ,mathrm {H_{2}O } }}}} où W A , sample {displaystyle W_{A,{text{échantillon}}}} représente le poids de l’échantillon mesuré dans l’Air et W A , H 2 O {displaystyle {W_{mathrm {A} ,mathrm {H_{2}O} }}} le poids d’un volume égal d’eau mesuré dans l’Air.

On peut montrer que la gravité spécifique vraie peut être calculée à partir de différentes propriétés :

S G true = ρ sample ρ H 2 O = m sample V m H 2 O V = m sample m H 2 O g g = W V , sample W V , H 2 O {displaystyle SG_{text{true}}={frac {rho _{text{sample}}}{rho _{mathrm {H_{2}O} }}}={frac { frac {m_{text{échantillon}}}{V}}{frac {m_{mathrm {H_{2}O} }}{V}}}={frac {m_{text{échantillon}} }{m_{mathrm {H_{2}O} }}}{frac {g}{g}}={frac {W_{mathrm {V} ,{text{sample}}}}{W_ {mathrm {V} ,mathrm {H_{2}O} }}}}

où g est l’accélération locale due à la gravité, V est le volume de l’échantillon et de l’eau (le même pour les deux), ρ _échantillon est la densité de l’échantillon, ρ _{H 2 O} est la densité de l’eau, W _V représente un poids obtenu sous vide, m sample {displaystyle {mathit {m}}_{text{échantillon}}} est la masse de l’échantillon et m H 2 O {displaystyle {mathit {m}}_{mathrm {H_{2}O} }} est la masse d’un volume égal d’eau.

La densité de l’eau varie avec la température et la pression, tout comme la densité de l’échantillon. Il est donc nécessaire de préciser les températures et pressions auxquelles les densités ou poids ont été déterminés. C’est presque toujours le cas que les mesures sont effectuées à 1 atmosphère nominale (101,325 kPa ± variations dues aux conditions météorologiques changeantes). Mais comme la gravité spécifique fait généralement référence à des solutions aqueuses hautement incompressibles ou à d’autres substances incompressibles (telles que des produits pétroliers), les variations de densité causées par la pression sont généralement négligées au moins là où la gravité spécifique apparente est mesurée. Pour les vrais calculs de gravité spécifique ( sous vide ), la pression atmosphérique doit être prise en compte (voir ci-dessous). Les températures sont spécifiées par la notation ( T _s / T_r ), avec T _s représentant la température à laquelle la densité de l’échantillon a été déterminée et T _r la température à laquelle la densité de référence (de l’eau) est spécifiée. Par exemple, SG (20 °C/4 °C) signifierait que la densité de l’échantillon a été déterminée à 20 °C et celle de l’eau à 4 °C. En tenant compte des différentes températures d’échantillon et de référence, nous notons que, alors que SG _{H 2 O} =1.000 000 (20 °C/20 °C), c’est aussi le cas que SG _{H 2 O} =0,998 203 ⁄0,999 840 =0,998 363 (20 °C/4 °C). Ici, la température est spécifiée à l’aide de l’ échelle ITS-90 actuelle et les densités ^[4] utilisées ici et dans le reste de cet article sont basées sur cette échelle. Sur l’échelle IPTS-68 précédente, les densités à 20 °C et 4 °C sont0,998 2071 et0,999 9720 respectivement, résultant en une valeur SG (20 °C/4 °C) pour l’eau de0,998 2343 .

Étant donné que la principale utilisation des mesures de gravité spécifique dans l’industrie est la détermination des concentrations de substances dans des solutions aqueuses et que celles-ci se trouvent dans les tableaux de SG par rapport à la concentration, il est extrêmement important que l’analyste entre dans le tableau avec la forme correcte de gravité spécifique. Par exemple, dans l’industrie brassicole, le tableau de Plato répertorie la concentration en saccharose en poids par rapport au vrai SG, et était à l’origine (20 °C/4 °C) ^[5] c’est-à-dire basé sur des mesures de la densité de solutions de saccharose faites à la température du laboratoire ( 20 °C) mais référencé à la densité de l’eau à 4 °C qui est très proche de la température à laquelle l’eau a sa densité maximale, ρ _{H 2 O} égal à 999,972 kg/m ³en unités SI (0,999 972 g/cm ³ en unités cgs ou 62,43 lb/pi3 en unités usuelles aux États-Unis ). La table ASBC ^[6] utilisée aujourd’hui en Amérique du Nord, alors qu’elle est dérivée de la table originale de Platon, concerne les mesures de gravité spécifique apparente à (20 °C/20 °C) sur l’échelle IPTS-68 où la densité de l’eau est0,998 2071 g/ ^cm3 . Dans les industries du sucre, des boissons gazeuses, du miel, des jus de fruits et connexes, la concentration en saccharose en poids est tirée d’un tableau préparé par A. Brix , qui utilise SG (17,5 °C/17,5 °C). Comme dernier exemple, les unités SG britanniques sont basées sur des températures de référence et d’échantillon de 60 °F et sont donc (15,56 °C/15,56 °C).

Compte tenu de la gravité spécifique d’une substance, sa densité réelle peut être calculée en réorganisant la formule ci-dessus :

ρ substance = S G × ρ H 2 O . {displaystyle rho _{text{substance}}=SGtimes rho _{mathrm {H_{2}O}}.}

Parfois, une substance de référence autre que l’eau est spécifiée (par exemple, l’Air), auquel cas la gravité spécifique signifie la densité par rapport à cette référence.

Dépendance à la température

Voir Densité pour un tableau des densités mesurées de l’eau à différentes températures.

La densité des substances varie avec la température et la pression, de sorte qu’il est nécessaire de spécifier les températures et les pressions auxquelles les densités ou masses ont été déterminées. Il est presque toujours le cas que les mesures sont effectuées à nominalement 1 atmosphère (101,325 kPa en ignorant les variations causées par l’évolution des conditions météorologiques) mais comme la densité relative fait généralement référence à des solutions aqueuses hautement incompressibles ou à d’autres substances incompressibles (telles que les produits pétroliers), les variations de densité causées par la pression sont généralement négligées au moins là où la densité relative apparente est mesurée. Pour les vrais calculs de densité relative ( sous vide ), la pression atmosphérique doit être prise en compte (voir ci-dessous). Les températures sont spécifiées par la notation ( T _s / T _r) avec T _{s 2 O} =représentant la température à laquelle la densité de l’échantillon a été déterminée et T _r la température à laquelle la densité de référence (de l’eau) est spécifiée. Par exemple, SG (20 °C/4 °C) signifierait que la densité de l’échantillon a été déterminée à 20 °C et celle de l’eau à 4 °C. En tenant compte des différentes températures d’échantillon et de référence, nous notons que si SG _{H 2 O} = 1,000000 (20 °C/20 °C), il est également vrai que RD _H0,998203/0,998840= 0,998363 (20 °C/4 °C). Ici, la température est spécifiée en utilisant l’ échelle ITS-90 actuelle et les densités ^[7] utilisées ici et dans le reste de cet article sont basées sur cette échelle. Sur l’échelle IPTS-68 précédente, les densités à 20 °C et 4 °C sont respectivement de 0,9982071 et 0,9999720, ce qui donne une valeur RD (20 °C/4 °C) pour l’eau de 0,9982343.

Les températures des deux matériaux peuvent être explicitement indiquées dans les symboles de densité ; par exemple:

densité relative : 8,15 ^{20 °C}
_{4 °C}; ou densité : 2,432 ¹⁵
₀

où l’exposant indique la température à laquelle la masse volumique du matériau est mesurée et l’indice indique la température de la substance de référence à laquelle il est comparé.

Les usages

La densité relative peut également aider à quantifier la flottabilité d’une substance dans un fluide ou un gaz, ou à déterminer la densité d’une substance inconnue à partir de la densité connue d’une autre. La densité relative est souvent utilisée par les géologues et les minéralogistes pour aider à déterminer la teneur en minéraux d’une roche ou d’un autre échantillon. Les gemmologues l’utilisent comme aide à l’identification des pierres précieuses . L’eau est privilégiée comme référence car les mesures sont alors faciles à réaliser sur le terrain (voir ci-dessous pour des exemples de méthodes de mesure).

Comme la principale utilisation des mesures de densité relative dans l’industrie est la détermination des concentrations de substances dans les solutions aqueuses et que celles-ci se trouvent dans les tableaux de RD par rapport à la concentration, il est extrêmement important que l’analyste entre dans le tableau avec la forme correcte de densité relative. Par exemple, dans l’industrie brassicole, le tableau Plato , qui répertorie la concentration de saccharose en masse par rapport à la vraie RD, était à l’origine (20 °C/4 °C) ^[8] qui est basé sur des mesures de la densité de solutions de saccharose faites au laboratoire. température (20 °C) mais référencée à la densité de l’eau à 4 °C qui est très proche de la température à laquelle l’eau a sa densité maximale de ρ ( H₂O ) égal à 0,999972 g/cm ³ (ou 62,43 lb·ft ^-3 ). La table ASBC ^[9] utilisée aujourd’hui en Amérique du Nord, alors qu’elle est dérivée de la table originale de Platon, concerne les mesures de densité relative apparente à (20 °C/20 °C) sur l’échelle IPTS-68 où la densité de l’eau est 0,9982071 g/ ^cm3 . Dans les industries du sucre, des boissons gazeuses, du miel, des jus de fruits et des industries connexes, la concentration en masse de saccharose est tirée de ce travail ^[3] qui utilise SG (17,5 °C/17,5 °C). Comme dernier exemple, les unités britanniques RD sont basées sur des températures de référence et d’échantillon de 60 °F et sont donc (15,56 °C/15,56 °C). ^[3]

La mesure

La densité relative peut être calculée directement en mesurant la densité d’un échantillon et en la divisant par la densité (connue) de la substance de référence. La densité de l’échantillon est simplement sa masse divisée par son volume. Bien que la masse soit facile à mesurer, le volume d’un échantillon de forme irrégulière peut être plus difficile à déterminer. Une méthode consiste à placer l’échantillon dans un cylindre gradué rempli d’eau et à lire la quantité d’eau qu’il déplace. Alternativement, le récipient peut être rempli à ras bord, l’échantillon immergé et le volume de débordement mesuré. La tension superficielle de l’eau peut empêcher une quantité importante d’eau de déborder, ce qui est particulièrement problématique pour les petits échantillons. Pour cette raison, il est souhaitable d’utiliser un récipient à eau avec une bouche aussi petite que possible.

Pour chaque substance, la densité, ρ , est donnée par

ρ = Mass Volume = Deflection × Spring Constant Gravity Displacement W a t e r L i n e × Area C y l i n d e r {displaystyle rho ={frac {text{Masse}}{text{Volume}}}={frac {{text{Déflexion}}times {frac {text{Constante du ressort}}{ text{Gravité}}}}{{text{Déplacement}}_{mathrm {WaterLine} }times {text{Zone}}_{mathrm {Cylindre} }}}}

Lorsque ces densités sont divisées, les références à la constante du ressort, à la gravité et à la section transversale s’annulent simplement, laissant

R D = ρ o b j e c t ρ r e f = Deflection O b j . Displacement O b j . Deflection R e f . Displacement R e f . = 3 i n 20 m m 5 i n 34 m m = 3 i n × 34 m m 5 i n × 20 m m = 1.02 {displaystyle RD={frac {rho _{mathrm {object}}}{rho _{mathrm {ref} }}}={frac {frac {{text{Déflexion}}_{ mathrm {Obj.} }}{{text{Déplacement}}_{mathrm {Obj.} }}}{frac {{text{Déflexion}}_{mathrm {Ref.} }}{{ text{Déplacement}}_{mathrm {Réf.} }}}}={frac {frac {3 mathrm {in} }{20 mathrm {mm} }}{frac {5 mathrm {in} }{34 mathrm {mm} }}}={frac {3 mathrm {in} times 34 mathrm {mm} }{5 mathrm {in} times 20 mathrm {mm} }}=1.02}

Pesée hydrostatique

La densité relative est plus facilement et peut-être plus précisément mesurée sans mesurer le volume. À l’aide d’une balance à ressort, l’échantillon est d’abord pesé dans l’Air puis dans l’eau. La densité relative (par rapport à l’eau) peut alors être calculée à l’aide de la formule suivante :

R D = W a i r W a i r − W w a t e r {displaystyle RD={frac {W_{mathrm {Air} }}{W_{mathrm {Air} }-W_{mathrm {eau} }}}} Air} }}{W_{mathrm {Air} }-W_{mathrm {water} }}}}” height=”0″ src=”” data-src=”https://wikimedia.org/api/rest_v1/media/math/render/svg/1b6a35d12ba3a1ca4066f844ba0b8ccb3152d943″ width=”0″> où

• W _Air est le poids de l’échantillon dans l’Air (mesuré en newtons , livres-force ou une autre unité de force)
• W _eau est le poids de l’échantillon dans l’eau (mesuré dans les mêmes unités).

Cette technique ne peut pas facilement être utilisée pour mesurer des densités relatives inférieures à un, car l’échantillon flottera alors. _{L’ eau} W devient une quantité négative, représentant la force nécessaire pour maintenir l’échantillon sous l’eau.

Une autre méthode pratique utilise trois mesures. L’échantillon est pesé sec. Ensuite, un récipient rempli à ras bord d’eau est pesé, et pesé à nouveau avec l’échantillon immergé, après que l’eau déplacée a débordé et a été évacuée. En soustrayant la dernière lecture de la somme des deux premières lectures, on obtient le poids de l’eau déplacée. Le résultat de la densité relative est le poids de l’échantillon sec divisé par celui de l’eau déplacée. Cette méthode permet l’utilisation de balances qui ne peuvent pas manipuler un échantillon en suspension. Un échantillon moins dense que l’eau peut également être manipulé, mais il doit être maintenu enfoncé et l’erreur introduite par le matériau de fixation doit être prise en compte.

Hydromètre

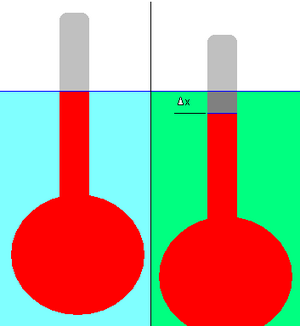
La densité relative d’un liquide peut être mesurée à l’aide d’un hydromètre. Il s’agit d’un bulbe attaché à une tige de section transversale constante, comme le montre le schéma ci-contre.

L’hydromètre est d’abord mis à flotter dans le liquide de référence (indiqué en bleu clair) et le déplacement (le niveau du liquide sur la tige) est marqué (ligne bleue). La référence peut être n’importe quel liquide, mais en pratique, il s’agit généralement d’eau.

L’hydromètre est ensuite mis à flotter dans un liquide de densité inconnue (en vert). Le changement de déplacement, Δ x , est noté. Dans l’exemple représenté, l’aréomètre a légèrement baissé dans le liquide vert ; sa densité est donc inférieure à celle du liquide de référence. Il est nécessaire que l’hydromètre flotte dans les deux liquides.

L’application de principes physiques simples permet de calculer la densité relative du liquide inconnu à partir du changement de déplacement. (En pratique la tige de l’aréomètre est pré-marquée de graduations pour faciliter cette mesure.)

Dans l’explication qui suit,

• ρ _ref est la masse volumique connue ( masse par unité de volume ) du liquide de référence (généralement de l’eau).
• ρ _new est la masse volumique inconnue du nouveau liquide (vert).
• RD _new/ref est la densité relative du nouveau liquide par rapport à la référence.
• V est le volume de liquide de référence déplacé, c’est-à-dire le volume rouge sur le diagramme.
• m est la masse de l’hydromètre entier.
• g est la constante gravitationnelle locale .
• Δ x est le changement de déplacement. Conformément à la manière dont les aréomètres sont habituellement gradués, Δ x est ici pris négatif si la droite de déplacement monte sur la tige de l’aréomètre, et positif si elle descend. Dans l’exemple représenté, Δ x est négatif.
• A est la section transversale de l’arbre.

Étant donné que l’hydromètre flottant est en Équilibre statique , la force gravitationnelle descendante agissant sur lui doit équilibrer exactement la force de flottabilité ascendante. La force gravitationnelle agissant sur l’hydromètre est simplement son poids, mg . D’après le principe de flottabilité d’ Archimède , la force de flottabilité agissant sur l’hydromètre est égale au poids du liquide déplacé. Ce poids est égal à la masse de liquide déplacée multipliée par g , qui dans le cas du liquide de référence est ρ _ref Vg . En les mettant égaux, nous avons

m g = ρ r e f V g {displaystyle mg=rho _{mathrm {ref} }Vg}

ou juste

m = ρ r e f V {displaystyle m=rho _{mathrm {ref} }V}

( 1 )

Exactement la même équation s’applique lorsque l’hydromètre flotte dans le liquide mesuré, sauf que le nouveau volume est V – A Δ x (voir la note ci-dessus sur le signe de Δ x ). Ainsi,

m = ρ n e w ( V − A Δ x ) {displaystyle m=rho _{mathrm {nouveau} }(VADelta x)}

( 2 )

La combinaison de ( 1 ) et ( 2 ) donne

R D n e w / r e f = ρ n e w ρ r e f = V V − A Δ x {displaystyle RD_{mathrm {new/ref} }={frac {rho _{mathrm {new} }}{rho _{mathrm {ref} }}}={frac {V}{ VADelta x}}}

( 3 )

Mais à partir de ( 1 ) nous avons V = m / ρ _ref . La substitution dans ( 3 ) donne

R D n e w / r e f = 1 1 − A Δ x m ρ r e f {displaystyle RD_{mathrm {new/ref} }={frac {1}{1-{frac {ADelta x}{m}}rho _{mathrm {ref} }}}}

( 4 )

Cette équation permet de calculer la densité relative à partir du changement de déplacement, de la densité connue du liquide de référence et des propriétés connues de l’hydromètre. Si Δ x est petit alors, comme approximation au premier ordre de la série géométrique, l’ équation ( 4 ) peut s’écrire :

R D n e w / r e f ≈ 1 + A Δ x m ρ r e f {displaystyle RD_{mathrm {new/ref} }approx 1+{frac {ADelta x}{m}}rho _{mathrm {ref} }}

Cela montre que, pour un petit Δ x , les changements de déplacement sont approximativement proportionnels aux changements de densité relative.

Pycnomètre

Un pycnomètre en verre vide et un bouchon Un pycnomètre rempli

Un pycnomètre (du grec : πυκνός ( puknos ) signifiant « dense »), également appelé pycnomètre ou bouteille de gravité spécifique , est un appareil utilisé pour déterminer la densité d’un liquide. Un pycnomètre est généralement en verre , avec un bouchon en verre dépoli bien ajusté avec un Tube capillaire à travers celui-ci, de sorte que des bulles d’Air puissent s’échapper de l’appareil. Cet appareil permet de mesurer avec précision la densité d’un liquide par référence à un fluide de travail approprié, tel que l’eau ou le mercure , à l’aide d’une balance analytique . ^{[citation nécessaire ]}

Si le ballon est pesé vide, plein d’eau et plein d’un liquide dont la densité relative est souhaitée, la densité relative du liquide peut facilement être calculée. La densité de particules d’une poudre, à laquelle la méthode habituelle de pesée ne peut pas être appliquée, peut également être déterminée avec un pycnomètre. La poudre est ajoutée au pycnomètre, qui est ensuite pesé, donnant le poids de l’échantillon de poudre. Le pycnomètre est alors rempli d’un liquide de densité connue, dans lequel la poudre est totalement insoluble. Le poids du liquide déplacé peut alors être déterminé, et donc la densité relative de la poudre.

Un pycnomètre à gaz , la manifestation à base de gaz d’un pycnomètre, compare le changement de pression provoqué par un changement mesuré dans un volume fermé contenant une référence (généralement une sphère en acier de volume connu) avec le changement de pression provoqué par l’échantillon sous le mêmes conditions. La différence de changement de pression représente le volume de l’échantillon par rapport à la sphère de référence, et est généralement utilisée pour les particules solides qui peuvent se dissoudre dans le milieu liquide de la conception du pycnomètre décrit ci-dessus, ou pour les matériaux poreux dans lesquels le liquide ne serait pas pénétrer entièrement.

Lorsqu’un pycnomètre est rempli à un volume spécifique, mais pas nécessairement connu avec précision, V et est placé sur une balance, il exercera une force

F b = g ( m b − ρ a m b ρ b ) {displaystyle F_{b}=gleft(m_{b}-rho _{a}{frac {m_{b}}{rho _{b}}}right)} où m _b est la masse de la bouteille et g l’ accélération gravitationnelle à l’endroit où les mesures sont effectuées. ρ _a est la masse volumique de l’Air à la pression ambiante et ρ _b est la masse volumique du matériau dont est faite la bouteille (généralement du verre) de sorte que le second terme est la masse d’Air déplacée par le verre de la bouteille dont le poids , par le principe d’Archimèdedoit être soustrait. La bouteille est remplie d’Air, mais comme cet Air déplace une quantité égale d’Air, le poids de cet Air est annulé par le poids de l’Air déplacé. Maintenant, nous remplissons la bouteille avec le fluide de référence, par exemple de l’eau pure. La force exercée sur le plateau de la balance devient : F w = g ( m b − ρ a m b ρ b + V ρ w − V ρ a ) . {displaystyle F_{w}=gleft(m_{b}-rho _{a}{frac {m_{b}}{rho _{b}}}+Vrho _{w}- Vrho _{a}right).}

Si l’on en soustrait la force mesurée sur la bouteille vide (ou tarer la balance avant de faire la mesure de l’eau) on obtient.

F w , n = g V ( ρ w − ρ a ) {displaystyle F_{w,n}=gV(rho _{w}-rho _{a})} où l’indice n indique que cette force est nette de la force de la bouteille vide. La bouteille est maintenant vidée, soigneusement séchée et remplie à nouveau avec l’échantillon. La force, nette de la bouteille vide, est maintenant : F s , n = g V ( ρ s − ρ a ) {displaystyle F_{s,n}=gV(rho _{s}-rho _{a})} où ρ _s est la densité de l’échantillon. Le rapport des forces de l’échantillon et de l’eau est : S G A = g V ( ρ s − ρ a ) g V ( ρ w − ρ a ) = ρ s − ρ a ρ w − ρ a . {displaystyle SG_{A}={frac {gV(rho _{s}-rho _{a})}{gV(rho _{w}-rho _{a})}}={ frac {rho _{s}-rho _{a}}{rho _{w}-rho _{a}}}.}

C’est ce qu’on appelle la densité relative apparente, désignée par l’indice A, car c’est ce que nous obtiendrions si nous prenions le rapport des pesées nettes dans l’Air d’une balance analytique ou utilisions un hydromètre (la tige déplace l’Air). Notez que le résultat ne dépend pas de l’étalonnage de la balance. La seule exigence est qu’il se lise linéairement avec force. RD _A ne dépend pas non plus du volume réel du pycnomètre.

Une manipulation plus poussée et enfin la substitution de RD _V , la vraie densité relative (l’indice V est utilisé car on l’appelle souvent la densité relative sous vide ), pour ρ _s / ρ _w donne la relation entre la densité relative apparente et vraie.

R D A = ρ s ρ w − ρ a ρ w 1 − ρ a ρ w = R D V − ρ a ρ w 1 − ρ a ρ w {displaystyle RD_{A}={{rho _{s} over rho _{w}}-{rho _{a} over rho _{w}} over 1-{rho _ {a} over rho _{w}}}={RD_{V}-{rho _{a} over rho _{w}} over 1-{rho _{a} over rho _{w}}}}

Dans le cas habituel, nous aurons des poids mesurés et nous voudrons la vraie densité relative. Cela se trouve à partir

R D V = R D A − ρ a ρ w ( R D A − 1 ) {displaystyle RD_{V}=RD_{A}-{rho _{a} over rho _{w}}(RD_{A}-1)}

Puisque la densité de l’Air sec à 101,325 kPa à 20 °C est de ^[10] 0,001205 g/cm ³ et celle de l’eau est de 0,998203 g/cm ³ , nous voyons que la différence entre les densités relatives vraies et apparentes pour une substance de densité relative ( 20 °C/20 °C) d’environ 1,100 serait 0,000120. Lorsque la densité relative de l’échantillon est proche de celle de l’eau (par exemple des solutions d’éthanol diluées), la correction est encore plus faible.

Le pycnomètre est utilisé dans la norme ISO : ISO 1183-1:2004, ISO 1014–1985 et la norme ASTM : ASTM D854.

Les types

• Gay-Lussac , piriforme, avec bouchon perforé, ajusté, contenance 1, 2, 5, 10, 25, 50 et 100 mL
• comme ci-dessus, avec thermomètre rodé , ajusté, tube latéral avec bouchon
• Hubbard, pour Bitume et pétroles bruts lourds , type cylindrique, ASTM D 70, 24 mL
• comme ci-dessus, type conique, ASTM D 115 et D 234, 25 mL
• Botte, avec enveloppe à vide et thermomètre, capacité 5, 10, 25 et 50 mL

Densimètres numériques

Instruments basés sur la pression hydrostatique : Cette technologie repose sur le principe de Pascal qui stipule que la différence de pression entre deux points dans une colonne verticale de fluide dépend de la distance verticale entre les deux points, de la densité du fluide et de la force gravitationnelle. Cette technologie est souvent utilisée pour les applications de jaugeage de réservoir comme moyen pratique de mesurer le niveau de liquide et la densité.

Transducteurs à élément vibrant : Ce type d’instrument nécessite qu’un élément vibrant soit placé en contact avec le fluide d’intérêt. La fréquence de résonance de l’élément est mesurée et est liée à la densité du fluide par une caractérisation qui dépend de la conception de l’élément. Dans les laboratoires modernes, des mesures précises de la densité relative sont effectuées à l’aide de d’un tube en U oscillantmètres. Ceux-ci sont capables de mesurer jusqu’à 5 à 6 décimales au-delà de la virgule et sont utilisés dans les industries de la brasserie, de la distillation, de la pharmacie, du pétrole et autres. Les instruments mesurent la masse réelle de fluide contenue dans un volume fixe à des températures comprises entre 0 et 80 ° C, mais comme ils sont basés sur un microprocesseur, ils peuvent calculer la densité relative apparente ou vraie et contenir des tableaux les reliant aux forces des acides courants, des solutions de sucre, etc. .

Transducteur à ultrasons : les ondes ultrasonores sont passées d’une source, à travers le fluide d’intérêt, et dans un détecteur qui mesure la spectroscopie acoustique des ondes. Les propriétés des fluides telles que la densité et la viscosité peuvent être déduites du spectre.

Jauge basée sur le rayonnement : le rayonnement est passé d’une source, à travers le fluide d’intérêt, et dans un détecteur de scintillation, ou un compteur. Au fur et à mesure que la densité du fluide augmente, le rayonnement détecté “compte” diminue. La source est généralement l’isotope radioactif césium-137 , avec une demi-vie d’environ 30 ans. L’un des principaux avantages de cette technologie est qu’il n’est pas nécessaire que l’instrument soit en contact avec le fluide. En général, la source et le détecteur sont montés à l’extérieur des réservoirs ou de la tuyauterie. ^[11]

Transducteur de force flottante: la force de flottabilité produite par un flotteur dans un liquide homogène est égale au poids du liquide déplacé par le flotteur. Étant donné que la force de flottabilité est linéaire par rapport à la densité du liquide dans lequel le flotteur est immergé, la mesure de la force de flottabilité donne une mesure de la densité du liquide. Une unité disponible dans le commerce affirme que l’instrument est capable de mesurer la densité relative avec une précision de ± 0,005 unités RD. La tête de sonde submersible contient un système à ressort-flotteur caractérisé mathématiquement. Lorsque la tête est immergée verticalement dans le liquide, le flotteur se déplace verticalement et la position du flotteur contrôle la position d’un aimant permanent dont le déplacement est détecté par un réseau concentrique de capteurs de déplacement linéaire à effet Hall.^[12]

Exemples

Matériel	Gravité spécifique
Bois de balsa	0,2
Bois de chêne	0,75
Éthanol	0,78
Huile d’olive	0,91
Eau	1
Bois de fer	1.5
Graphite	1.9–2.3
Sel de table	2.17
Aluminium	2.7
Ciment	3.15
Fer	7,87
Cuivre	8,96
Mener	11h35
Mercure	13.56
Uranium appauvri	19.1
Or	19.3
Osmium	22.59

(Les échantillons peuvent varier, et ces chiffres sont approximatifs.) Les substances avec une densité relative de 1 ont une flottabilité neutre, celles avec RD supérieur à un sont plus denses que l’eau, et donc (en ignorant les effets de tension superficielle ) y couleront, et celles avec un RD inférieur à un est moins dense que l’eau et flottera donc.

Exemple:

R D H 2 O = ρ M a t e r i a l ρ H 2 O = R D , {displaystyle RD_{mathrm {H_{2}O} }={frac {rho _{mathrm {Matériau}}}{rho _{mathrm {H_{2}O} }}}=RD ,}

L’hélium gazeux a une densité de 0,164 g/L ; ^[13] il est 0,139 fois plus dense que l’Air , qui a une densité de 1,18 g/L. ^[13]

• L’urine a normalement une densité comprise entre 1,003 et 1,030. Le test de diagnostic de gravité spécifique de l’urine est utilisé pour évaluer la capacité de concentration rénale pour l’évaluation du système urinaire. ^[14] Une faible concentration peut indiquer un diabète insipide , tandis qu’une concentration élevée peut indiquer une albuminurie ou une glycosurie . ^[14]
• Le sang a normalement une gravité spécifique d’environ 1,060. ^[15]
• La vodka 80° proof (40% v/v) a une densité de 0,9498. ^[16]

Voir également

• Gravité API
• Échelle Baumé
• Flottabilité
• Mécanique des fluides
• Gravité (bière)
• Hydromètre
• Bon équilibre
• Échelle de Platon

Références

1. ^ Dana, Edward Salisbury (1922). Un texte-livre de minéralogie : avec un traité étendu sur la cristallographie… New York, Londres(Chapman Hall) : John Wiley and Sons. p. 195–200, 316.
2. ^ Schetz, Joseph A.; Allen E. Fuhs (1999-02-05). Fondamentaux de la mécanique des fluides . Wiley, John & Sons, Incorporé. pages 111, 142, 144, 147, 109, 155, 157, 160, 175. ISBN 0-471-34856-2.
3. ^ ^{un bc Hough} , JS, Briggs, DE, Stevens, R et Young, TW Malting and Brewing Science, Vol. II Hopped Wort and Beer, Chapman and Hall, Londres, 1991, p. 881
4. ^ Bettin, H.; Spieweck, F. (1990). “Die Dichte des Wassers als Funktion der Temperatur nach Einführung des Internationalen Temperaturskala von 1990”. PTB-Mitteilungen 100 . p. 195–196.
5. ^ Méthodes d’analyse ASBC Préface au tableau 1: Extrait dans le moût et la bière, American Society of Brewing Chemists, St Paul, 2009
6. ^ Méthodes d’analyse ASBC op. cit. Tableau 1 : Extrait dans le moût et la bière
7. ^ Bettin, H.; Spieweck, F. (1990). Die Dichte des Wassers als Funktion der Temperatur nach Einführung des Internationalen Temperaturskala von 1990 (en allemand). PTB = Mitt. 100. pp. 195–196.
8. ^ Méthodes d’analyse ASBC Préface au tableau 1: Extrait dans le moût et la bière, American Society of Brewing Chemists, St Paul, 2009
9. ^ Méthodes d’analyse ASBC op. cit. Tableau 1 : Extrait dans le moût et la bière
10. ^ DIN51 757 (04.1994): Essais d’huiles minérales et de matériaux connexes ; détermination de la densité
11. ^ Densité – VEGA Americas, Inc . Ohmartvega.com. Consulté le 2011-09-30.
12. ^ Hydromètre électronique numérique de contrôle de processus . Garco. Consulté le 2011-09-30.
13. ^ ^{un b} “les Démonstrations de Conférence” . physique.ucsb.edu .
14. ^ ^{un b} Lewis, Sharon Mantik; Dirksen, Shannon Ruff; Heitkemper, Margaret M.; Bucher, Linda; Harding, Mariann (5 décembre 2013). Soins infirmiers médico-chirurgicaux : évaluation et prise en charge des problèmes cliniques (9e éd.). Saint Louis, Missouri. ISBN 978-0-323-10089-2. OCLC 228373703 .
15. ^ Shmukler, Michael (2004). Elert, Glenn (éd.). “Densité du sang” . Le Factbook de Physique . Récupéré le 23/01/2022 .
16. ^ “Gravité Spécifique des Liqueurs” . Bons cocktails.com .

Lectures complémentaires

• Principes fondamentaux de la mécanique des fluides Wiley, BR Munson, DF Young et TH Okishi
• Introduction à la mécanique des fluides quatrième édition, Wiley, version SI, RW Fox et AT McDonald
• Thermodynamique : une approche d’ingénierie deuxième édition, McGraw-Hill, édition internationale, YA Cengel et MA Boles
• Munson, BR; DF Young; TH Okishi (2001). Principes fondamentaux de la mécanique des fluides (4e éd.). Wiley. ISBN 978-0-471-44250-9.
• Fox, RW; McDonald, AT (2003). Introduction à la mécanique des fluides (4e éd.). Wiley. ISBN 0-471-20231-2.

Liens externes

• Poids de gravité spécifique des matériaux