Multilatération à plage réelle

La multilatération à plage réelle (également appelée plage-plage, rho-rho et multilatération sphérique) est une méthode permettant de déterminer l’emplacement d’un véhicule mobile ou d’un point stationnaire dans l’espace en utilisant plusieurs plages (distances) entre le véhicule/point et plusieurs espaces séparés. emplacements connus (souvent appelés « stations »). ^{[1] [2]} Les ondes d’énergie peuvent être impliquées dans la détermination de la portée, mais ne sont pas obligatoires.

La multilatération à plage vraie est à la fois un sujet mathématique et une technique appliquée utilisée dans plusieurs domaines. Une application pratique impliquant un emplacement fixe est la méthode d’ arpentage par trilatération . Les applications impliquant la localisation d’un véhicule sont appelées navigation lorsque les personnes/équipements à bord sont informés de sa position, et sont appelées surveillance lorsque des entités hors véhicule sont informées de la position du véhicule.

Deux plages obliques à partir de deux emplacements connus peuvent être utilisées pour localiser un troisième point dans un espace cartésien à deux dimensions (plan), qui est une technique fréquemment appliquée (par exemple, dans l’arpentage). De même, deux plages sphériques peuvent être utilisées pour localiser un point sur une sphère, ce qui est un concept fondamental de l’ancienne discipline de la navigation céleste – appelée problème d’ interception d’altitude . De plus, si plus que le nombre minimum de plages sont disponibles, il est recommandé de les utiliser également. Cet article aborde le problème général de la détermination de la position à l’aide de plusieurs plages.

En géométrie bidimensionnelle , on sait que si un point se trouve sur deux cercles, alors les centres des cercles et les deux rayons fournissent des informations suffisantes pour réduire les emplacements possibles à deux – dont l’un est la solution souhaitée et l’autre est un solution ambiguë. Des informations supplémentaires réduisent souvent les possibilités à un emplacement unique. En géométrie tridimensionnelle, lorsqu’on sait qu’un point se trouve sur les surfaces de trois sphères, les centres des trois sphères ainsi que leurs rayons fournissent également des informations suffisantes pour réduire les emplacements possibles à pas plus de deux (à moins que le les centres sont sur une droite).

La multilatération à plage réelle peut être opposée à la multilatération plus fréquemment rencontrée ( pseudo -distance ) , qui utilise des différences de plage pour localiser un point (généralement mobile). La multilatération de pseudo-distance est presque toujours mise en œuvre en mesurant les temps d’arrivée (TOA) des ondes d’énergie. La multilatération à plage vraie peut également être opposée à la triangulation , qui implique la mesure des angles .

Des termes multiples, parfois se chevauchant et contradictoires, sont employés pour des concepts similaires – par exemple, la multilatération sans modification a été utilisée pour les systèmes aéronautiques utilisant à la fois des distances réelles et des pseudo-distances. ^{[3] [4]} De plus, différents domaines d’activité peuvent employer des termes différents. En géométrie , la trilatération est définie comme le processus de détermination des emplacements absolus ou relatifs des points par la mesure des distances, en utilisant la géométrie des cercles , des sphères ou des triangles . En topographie, la trilatération est une technique particulière. ^{[5] [6] [7]}

Problèmes de mise en œuvre

Terminologie (nom)

Il n’y a pas de terme général accepté ou largement utilisé pour ce que l’on appelle ici la multilatération à plage vraie . Ce nom est choisi parce qu’il : (a) est une description précise et une terminologie partiellement familière ( la multilatération est souvent utilisée dans ce contexte) ; (b) évite de spécifier le nombre de gammes impliquées (comme le fait, par exemple, la gamme-gamme ; (c) évite d’impliquer une application (comme le font, par exemple, la navigation ou la trilatération DME/DME ) et (d) et évite la confusion avec les plus multilatération commune (Pseudo-gamme) .

Avantages et inconvénients pour la navigation et la surveillance des véhicules

Les systèmes de navigation et de surveillance impliquent généralement des véhicules et nécessitent qu’une entité gouvernementale ou une autre organisation déploie plusieurs stations qui emploient une forme de technologie radio (c.-à-d., utilisent des ondes électromagnétiques). Les avantages et les inconvénients de l’utilisation de la multilatération à plage réelle pour un tel système sont présentés dans le tableau suivant.

Avantages

Désavantages

Les emplacements des stations sont flexibles; ils peuvent être placés au centre ou à la périphérie La précision se dégrade lentement avec la distance de la station (généralement meilleure que la multilatération de pseudo-portée) Nécessite une station de moins qu’un système de multilatération à pseudo-portée La synchronisation de la station n’est pas exigeante (basée sur la vitesse du point d’intérêt et peut être traitée à l’ estime )

Souvent, un utilisateur doit disposer à la fois d’un émetteur et d’un récepteur La précision du système coopératif est sensible à l’erreur de rotation de l’équipement Ne peut pas être utilisé pour la surveillance furtive La surveillance non coopérative implique des pertes de trajet à la puissance quatre de la distance

La multilatération à plage réelle est souvent opposée à la multilatération (pseudo plage), car les deux nécessitent une forme de plages d’utilisateurs vers plusieurs stations. La complexité et le coût de l’équipement de l’utilisateur sont probablement les facteurs les plus importants pour limiter l’utilisation de la multilatération à portée réelle pour la navigation et la surveillance des véhicules. Certaines utilisations ne sont pas l’objectif initial du déploiement du système – par exemple, la navigation aérienne DME/DME.

Obtention de plages

Pour des distances et des erreurs de mesure similaires, un système de navigation et de surveillance basé sur la multilatération à distance réelle fournit un service à une zone 2D ou un volume 3D nettement plus grand que les systèmes basés sur la multilatération à pseudo-distance . Cependant, il est souvent plus difficile ou plus coûteux de mesurer les vrais = intervalles que de mesurer les pseudo intervalles. Pour des distances allant jusqu’à quelques kilomètres et des emplacements fixes, la plage réelle peut être mesurée manuellement. C’est ce qu’on fait en arpentage depuis plusieurs milliers d’années, par exemple en utilisant des cordes et des chaînes.

Pour les longues distances et/ou les véhicules en mouvement, un système radio/radar est généralement nécessaire. Cette technologie a été développée pour la première fois vers 1940 en conjonction avec le radar. Depuis lors, trois méthodes ont été employées :

• Mesure de distance bidirectionnelle, une partie active – Il s’agit de la méthode utilisée par les radars traditionnels (parfois appelés radars primaires ) pour déterminer la distance d’une cible non coopérative, et maintenant utilisée par les télémètres laser . Ses principales limites sont les suivantes : (a) la cible ne s’identifie pas, et dans une situation de cibles multiples, une mauvaise affectation d’un retour peut se produire ; (b) le signal de retour est atténué (par rapport au signal transmis) par la quatrième puissance de la portée véhicule-station (ainsi, pour des distances de plusieurs dizaines de kilomètres ou plus, les stations nécessitent généralement des émetteurs de forte puissance et/ou de grande taille/sensibles antennes); et (c) de nombreux systèmes utilisent la propagation en visibilité directe, ce qui limite leur portée à moins de 20 milles lorsque les deux parties se trouvent à des hauteurs similaires au-dessus du niveau de la mer.
• Mesure de distance bidirectionnelle, les deux parties actives – Cette méthode aurait été utilisée pour la première fois pour la navigation par le système de guidage d’avion Y-Gerät mis en service en 1941 par la Luftwaffe. Il est maintenant utilisé à l’échelle mondiale dans le contrôle du trafic aérien – par exemple, la surveillance radar secondaire et la navigation DME/DME. Cela nécessite que les deux parties aient à la fois des émetteurs et des récepteurs, et peut nécessiter que les problèmes d’interférence soient résolus.
• Mesure de distance unidirectionnelle – Le temps de vol (TOF) de l’énergie électromagnétique entre plusieurs stations et le véhicule est mesuré en fonction de la transmission par une partie et de la réception par l’autre. Il s’agit de la méthode la plus récemment développée et a été rendue possible par le développement des horloges atomiques ; il faut que le véhicule (utilisateur) et les stations aient des horloges synchronisées. Il a été démontré avec succès (expérimentalement) avec Loran-C et GPS. ^{[2] [8]}

Méthodes de résolution

Apprendre encore plus Cette section a besoin d’être agrandie . Vous pouvez aider en y ajoutant . ( juin 2017 )

Les algorithmes de multilatération à plage réelle peuvent être partitionnés en fonction de

• dimension de l’espace du problème (généralement deux ou trois),
• géométrie de l’espace du problème (généralement, cartésien ou sphérique) et
• présence de mesures redondantes (plus que la dimension de l’espace du problème).

Tout algorithme de multilatération de Pseudo-gamme peut être spécialisé pour être utilisé avec la multilatération de vraie gamme.

Deux dimensions cartésiennes, deux plages obliques mesurées (trilatération)

Fig. 1 Scénario de multilatération (trilatération) à plage vraie cartésienne 2D. C1 et C2 sont des centres de cercles ayant une séparation connue tu {displaystyle U} . P est le point dont ( X , y ) {displaystyle (x,y)} les coordonnées sont souhaitées en fonction de tu {displaystyle U} et plages mesurées r 1 {displaystyle r_{1}} et r 2 {displaystyle r_{2}} .

Une solution analytique est probablement connue depuis plus de 1 000 ans et est donnée dans plusieurs textes. ^[9] De plus, on peut facilement adapter des algorithmes pour un espace cartésien tridimensionnel.

L’algorithme le plus simple utilise la géométrie analytique et un cadre de coordonnées basé sur la station. Ainsi, considérons les centres de cercle (ou stations) C1 et C2 de la Fig. 1 qui ont des coordonnées connues (par exemple, ont déjà été relevés) et donc dont la séparation tu {displaystyle U} est connu. La figure ‘page’ contient C1 et C2 . Si un troisième “point d’intérêt” P (par exemple, un véhicule ou un autre point à surveiller) se trouve à un point inconnu ( X , y ) {displaystyle (x,y)} , alors le théorème de Pythagore donne

r 1 2 = x 2 + y 2 r 2 2 = ( U − x ) 2 + y 2 {displaystyle {begin{aligned}r_{1}^{2}&=x^{2}+y^{2}\[4pt]r_{2}^{2}&=(Ux)^{ 2}+y^{2}end{aligné}}}

Ainsi,

x = r 1 2 − r 2 2 + U 2 2 U y = ± r 1 2 − x 2 {displaystyle {begin{aligned}x&={frac {r_{1}^{2}-r_{2}^{2}+U^{2}}{2U}}\[4pt]y&= pm {sqrt {r_{1}^{2}-x^{2}}}end{aligné}}}

( 1 )

Noter que y {displaystyle y} a deux valeurs (c’est-à-dire que la solution est ambiguë) ; ce n’est généralement pas un problème.

Bien qu’il y ait de nombreuses améliorations, l’équation 1 est la relation de multilatération à plage vraie la plus fondamentale. La navigation DME/DME des aéronefs et la méthode d’arpentage par trilatération sont des exemples de son application. Pendant la Seconde Guerre mondiale, Oboe et pendant la guerre de Corée, SHORAN a utilisé le même principe pour guider les avions en fonction des distances mesurées vers deux stations au sol. SHORAN a ensuite été utilisé pour l’exploration pétrolière en mer et pour les levés aériens. Le système de levé aérien australien Aerodist a utilisé une multilatération cartésienne à portée réelle 2D. ^[10] Ce scénario 2D est suffisamment important pour que le terme trilatération soit souvent appliqué à toutes les applications impliquant une ligne de base connue et deux mesures de distance.

La ligne de base contenant les centres des cercles est une ligne de symétrie. Les solutions correctes et ambiguës sont perpendiculaires et également distantes de (sur les côtés opposés de) la ligne de base. Habituellement, la solution ambiguë est facilement identifiée. Par exemple, si P est un véhicule, tout mouvement vers ou loin de la ligne de base sera opposé à celui de la solution ambiguë ; ainsi, une mesure brute du cap du véhicule est suffisante. Un deuxième exemple : les géomètres savent bien de quel côté de la ligne de base se trouve P. Un troisième exemple : dans les applications où P est un avion et C1 et C2 sont au sol, la solution ambiguë est généralement sous le sol.

Si nécessaire, les angles intérieurs du triangle C1-C2-P peuvent être trouvés en utilisant la loi trigonométrique des cosinus . De plus, si nécessaire, les coordonnées de P peuvent être exprimées dans un deuxième système de coordonnées mieux connu – par exemple, le système Universal Transverse Mercator (UTM) – à condition que les coordonnées de C1 et C2 soient connues dans ce deuxième système. Les deux sont souvent effectués dans les levés lorsque la méthode de trilatération est utilisée. ^[11] Une fois les coordonnées de P établies, les droites C1-P et C2-Ppeuvent être utilisées comme nouvelles lignes de base et des points supplémentaires étudiés. Ainsi, de vastes zones ou distances peuvent être étudiées sur la base de plusieurs triangles plus petits, appelés cheminement .

Une hypothèse implicite pour que l’équation ci-dessus soit vraie est que r 1 {displaystyle r_{1}} et r 2 {displaystyle r_{2}} se rapportent à la même position de P . Lorsque P est un véhicule, alors typiquement r 1 {displaystyle r_{1}} et r 2 {displaystyle r_{2}} doit être mesuré dans une tolérance de synchronisation qui dépend de la vitesse du véhicule et de l’erreur de position du véhicule admissible. Alternativement, le mouvement du véhicule entre les mesures de distance peut être pris en compte, souvent à l’estime.

Une solution trigonométrique est également possible (cas côté-côté-côté). De plus, une solution employant des graphiques est possible. Une solution graphique est parfois employée lors de la navigation en temps réel, en superposition sur une carte.

Trois dimensions cartésiennes, trois plages d’inclinaison mesurées

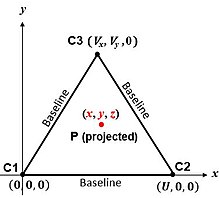
Fig. 2 Scénario de multilatération 3-D True-Range. C1, C2 et C3 sont des centres connus de sphères dans le plan x,y. P est le point dont les coordonnées (x, y, z) sont souhaitées en fonction de ses plages à C1, C2 et C3. La trilatération 3-D limite le nombre de positions potentielles à deux (ici A ou B)

Il existe plusieurs algorithmes qui résolvent directement le problème de multilatération à plage vraie cartésienne 3D (c’est-à-dire sous forme fermée) – par exemple, Fang. ^[12] De plus, on peut adopter des algorithmes de forme fermée développés pour la multilatération de pseudo-distance . ^{[13] [9]} L’algorithme de Bancroft ^[14] (adapté) emploie des vecteurs, ce qui est un avantage dans certaines situations.

L’algorithme le plus simple correspond aux centres des sphères de la Fig. 2. La figure ‘page’ est le plan contenant C1 , C2 et C3 . Si P est un « point d’intérêt » (par exemple, un véhicule) à ( x , y , z ) {displaystyle (x,y,z)} , alors le théorème de Pythagore donne les plages obliques entre P et les centres de la sphère :

r 1 2 = x 2 + y 2 + z 2 r 2 2 = ( x − U ) 2 + y 2 + z 2 r 3 2 = ( x − V x ) 2 + ( y − V y ) 2 + z 2 {displaystyle {begin{aligned}r_{1}^{2}&=x^{2}+y^{2}+z^{2}\[4pt]r_{2}^{2}& =(xU)^{2}+y^{2}+z^{2}\[4pt]r_{3}^{2}&=(x-V_{x})^{2}+(y -V_{y})^{2}+z^{2}end{aligné}}}

Ainsi, les coordonnées de P sont :

x = r 1 2 − r 2 2 + U 2 2 U y = r 1 2 − r 3 2 + V x 2 + V y 2 − 2 V x x 2 V y z = ± r 1 2 − x 2 − y 2 {displaystyle {begin{aligned}x&={frac {r_{1}^{2}-r_{2}^{2}+U^{2}}{2U}}\[4pt]y&= {frac {r_{1}^{2}-r_{3}^{2}+V_{x}^{2}+V_{y}^{2}-2V_{x}x}{2V_{y }}}\[4pt]z&=pm {sqrt {r_{1}^{2}-x^{2}-y^{2}}}end{aligned}}}

( 2 )

Le plan contenant les centres des sphères est un plan de symétrie. Les solutions correctes et ambiguës lui sont perpendiculaires et également distantes de lui, sur des côtés opposés.

De nombreuses applications de la multilatération 3D à plage vraie impliquent de courtes plages, par exemple, la fabrication de précision. ^[15] L’intégration des mesures de distance à partir de trois radars ou plus (p. ex. l’ ERAM de la FAA ) est une application de surveillance d’aéronefs en 3D. La multilatération 3D à distance réelle a été utilisée à titre expérimental avec des satellites GPS pour la navigation aérienne. ^[8] L’exigence qu’un aéronef soit équipé d’une horloge atomique exclut son utilisation générale. Cependant, l’aide à l’horloge du récepteur GPS est un domaine de recherche active, y compris l’aide sur un réseau. Ainsi, les conclusions peuvent changer. ^[16]La multilatération 3D à plage réelle a été évaluée par l’ Organisation de l’aviation civile internationale en tant que système d’atterrissage d’avion, mais une autre technique s’est avérée plus efficace. ^[17] La ​​mesure précise de l’altitude des aéronefs pendant l’approche et l’atterrissage nécessite de nombreuses stations au sol le long de la trajectoire de vol.

Deux dimensions sphériques, deux plages sphériques mesurées ou plus

Fig. 3 Exemple de problème d’interception d’altitude de navigation céleste (les lignes de position sont déformées par la projection cartographique)

Il s’agit d’un problème classique de navigation céleste (ou astronomique), appelé problème d’ interception d’altitude (Fig. 3). C’est l’équivalent géométrique sphérique de la méthode d’arpentage par trilatération (bien que les distances impliquées soient généralement beaucoup plus grandes). Une solution en mer (n’impliquant pas nécessairement le soleil et la lune) a été rendue possible par le chronomètre de marine (introduit en 1761) et la découverte de la “ligne de position” (LOP) en 1837. La méthode de résolution maintenant la plus enseignée dans les universités ( par exemple, US Naval Academy) utilise la trigonométrie sphérique pour résoudre un triangle sphérique oblique basé sur des mesures sextantes de « l’altitude » de deux corps célestes. ^{[18] [19]} Ce problème peut également être résolu en utilisant l’analyse vectorielle.^[20] Historiquement, des techniques graphiques – par exemple, la méthode d’interception – ont été employées. Ceux-ci peuvent accueillir plus de deux « altitudes » mesurées. En raison de la difficulté des mesures en mer, 3 à 5 « altitudes » sont souvent préconisées.

Comme la Terre est mieux modélisée comme un ellipsoïde de révolution que comme une sphère, des techniques itératives peuvent être utilisées dans les implémentations modernes. ^[21] Dans les avions et les missiles à haute altitude, un sous-système de navigation céleste est souvent intégré à un sous-système de navigation inertielle pour effectuer une navigation automatisée, par exemple, US Air Force SR-71 Blackbird et B-2 Spirit .

Bien qu’il soit conçu comme un système de multilatération à pseudo-portée « sphérique », le Loran-C a également été utilisé comme système de multilatération à portée réelle « sphérique » par des utilisateurs bien équipés (par exemple, le Service hydrographique du Canada). ^[2] Cela a permis d’étendre considérablement la zone de couverture d’une triade de stations Loran-C (par exemple, de doubler ou de tripler) et de réduire le nombre minimum d’émetteurs disponibles de trois à deux. Dans l’aviation moderne, les distances obliques plutôt que les distances sphériques sont plus souvent mesurées; cependant, lorsque l’altitude de l’aéronef est connue, les distances obliques sont facilement converties en distances sphériques. ^[9]

Mesures de plage redondantes

Lorsqu’il y a plus de mesures de distance disponibles que de dimensions problématiques, soit à partir des mêmes stations C1 et C2 (ou C1 , C2 et C3 ), soit à partir de stations supplémentaires, au moins ces avantages s’accumulent :

• Les “mauvaises” mesures peuvent être identifiées et rejetées
• Les solutions ambiguës peuvent être identifiées automatiquement (c’est-à-dire sans intervention humaine) — nécessite une station supplémentaire
• Les erreurs dans les “bonnes” mesures peuvent être moyennées, ce qui réduit leur effet.

L’algorithme itératif de Gauss – Newton pour résoudre les problèmes des moindres carrés non linéaires (NLLS) est généralement préféré lorsqu’il y a plus de «bonnes» mesures que le minimum nécessaire. Un avantage important de la méthode de Gauss-Newton par rapport à de nombreux algorithmes de forme fermée est qu’elle traite les erreurs de plage de manière linéaire, ce qui est souvent leur nature, réduisant ainsi l’effet des erreurs de plage en faisant la moyenne. ^[13] La méthode de Gauss-Newton peut également être utilisée avec le nombre minimum de plages mesurées. Puisqu’elle est itérative, la méthode de Gauss-Newton nécessite une estimation initiale de la solution.

Dans l’espace cartésien 3D, une quatrième sphère élimine la solution ambiguë qui se produit avec trois plages, à condition que son centre ne soit pas coplanaire avec les trois premiers. Dans l’espace cartésien ou sphérique 2D, un troisième cercle élimine la solution ambiguë qui se produit avec deux plages, à condition que son centre ne soit pas colinéaire avec les deux premiers.

Application unique versus application répétitive

Cet article décrit en grande partie l’application “ponctuelle” de la technique de multilatération à plage réelle, qui est l’utilisation la plus basique de la technique. En référence à la figure 1, la caractéristique des situations « ponctuelles » est que le point P et au moins l’un de C1 et C2 changent d’une application de la technique de multilatération à plage vraie à la suivante. Ceci est approprié pour l’arpentage, la navigation céleste à l’aide de visées manuelles et la navigation DME/DME de certains aéronefs.

Cependant, dans d’autres situations, la technique de multilatération à plage vraie est appliquée de manière répétitive (essentiellement en continu). Dans ces situations, C1 et C2 (et peut-être Cn, n = 3,4,… ) restent constants et P est le même véhicule. Des exemples d’applications (et des intervalles sélectionnés entre les mesures) sont : la surveillance radar multiple des aéronefs (5 et 12 secondes, selon la plage de couverture radar), les relevés aériens, la navigation Loran-C avec une horloge utilisateur de haute précision (environ 0,1 seconde) et certains navigation DME/DME de l’avion (environ 0,1 seconde). Généralement, les implémentations pour une utilisation répétitive : (a) emploient un algorithme de « suivi » ^[22](en plus de l’algorithme de solution de multilatération), qui permet de comparer et de moyenner d’une certaine manière les mesures collectées à différents moments ; et (b) utilisent un algorithme de solution itératif, car ils (b1) admettent un nombre variable de mesures (y compris des mesures redondantes) et (b2) ont intrinsèquement une estimation initiale chaque fois que l’algorithme de solution est invoqué.

Systèmes hybrides de multilatération

Les systèmes de multilatération hybrides – ceux qui ne sont ni des systèmes à plage réelle ni à pseudo-distance – sont également possibles. Par exemple, dans la Fig. 1, si les centres des cercles sont décalés vers la gauche pour que C1 soit à x 1 ′ = − 1 2 U , y 1 ′ = 0 {displaystyle x_{1}^{prime }=-{tfrac {1}{2}}U,y_{1}^{prime }=0} et C2 est à x 2 ′ = 1 2 U , y 2 ′ = 0 {displaystyle x_{2}^{prime }={tfrac {1}{2}}U,y_{2}^{prime }=0} alors le point d’intérêt P est à

x ′ = ( r 1 ′ + r 2 ′ ) ( r 1 ′ − r 2 ′ ) 2 U y ′ = ± ( r 1 ′ + r 2 ′ ) 2 − U 2 U 2 − ( r 1 ′ − r 2 ′ ) 2 2 U {displaystyle {begin{aligned}x^{prime}&={frac {(r_{1}^{prime }+r_{2}^{prime})(r_{1}^{ premier }-r_{2}^{prime })}{2U}}\[4pt]y^{prime}&=pm {frac {{sqrt {(r_{1}^{prime }+r_{2}^{prime })^{2}-U^{2}}}{sqrt {U^{2}-(r_{1}^{prime }-r_{2}^ {prime })^{2}}}}{2U}}end{aligned}}}

Cette forme de la solution dépend explicitement de la somme et de la différence de r 1 ′ {displaystyle r_{1}^{prime}} et r 2 ′ {displaystyle r_{2}^{prime}} et ne nécessite pas de « chaînage » à partir du x ′ {displaystyle x^{prime}} -solution à la y ′ {displaystyle y^{prime}} -Solution. Il pourrait être implémenté comme un système de multilatération à plage réelle en mesurant r 1 ′ {displaystyle r_{1}^{prime}} et r 2 ′ {displaystyle r_{2}^{prime}} .

Cependant, il pourrait également être mis en œuvre en tant que système de multilatération hybride en mesurant r 1 ′ + r 2 ′ {displaystyle r_{1}^{prime }+r_{2}^{prime }} et r 1 ′ − r 2 ′ {displaystyle r_{1}^{prime }-r_{2}^{prime }} utilisant des équipements différents – par exemple, pour la surveillance par un radar multistatique avec un émetteur et deux récepteurs (plutôt que deux radars monostatiques ). Bien que l’élimination d’un émetteur soit un avantage, il existe un “coût” compensatoire : la tolérance de synchronisation pour les deux stations dépend de la vitesse de propagation (généralement, la vitesse de la lumière) plutôt que de la vitesse du point P , afin de mesurer avec précision tous les deux r 1 ′ ± r 2 ′ {displaystyle r_{1}^{prime }pm r_{2}^{prime }} .

Bien qu’ils ne soient pas mis en œuvre de manière opérationnelle, les systèmes de multilatération hybrides ont été étudiés pour la surveillance des aéronefs à proximité des aéroports et comme système de sauvegarde de navigation GPS pour l’aviation. ^[23]

Calculs préliminaires et finaux

Apprendre encore plus Cette section a besoin d’être agrandie . Vous pouvez aider en y ajoutant . ( juin 2018 )

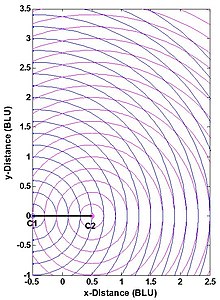
Fig. 4 Mesures de télémétrie du système de multi-latération (trilatération) à plage vraie 2D

La précision de position d’un système de multilatération à plage réelle, par exemple la précision de la ( x , y ) {displaystyle (x,y)} coordonnées du point P sur la Fig. 1 — dépend de deux facteurs : (1) la précision de la mesure de la distance et (2) la relation géométrique de P avec les stations C1 et C2 du système . Cela peut être compris à partir de la Fig. 4. Les deux stations sont représentées par des points et BLU désigne les unités de base. (Le modèle de mesure est symétrique à la fois par rapport à la ligne de base et à la bissectrice perpendiculaire de la ligne de base, et est tronqué sur la figure.) Comme cela se fait couramment, les erreurs de mesure de distance individuelles sont considérées comme indépendantes de la plage, statistiquement indépendantes et distribuées de manière identique. Cette hypothèse raisonnable sépare les effets de la géométrie de la station utilisateur et des erreurs de mesure de distance sur l’erreur dans le calcul ( x , y ) {displaystyle (x,y)} coordonnées de P . Ici, la géométrie de mesure est simplement l’angle auquel deux cercles se croisent ou, de manière équivalente, l’angle entre les lignes P-C1 et P-C2 . Lorsque le point P- n’est pas sur un cercle, l’erreur sur sa position est approximativement proportionnelle à la surface délimitée par les deux cercles bleus les plus proches et les deux cercles magenta les plus proches.

Sans mesures redondantes, un système de multilatération à plage réelle ne peut pas être plus précis que les mesures de plage, mais peut être nettement moins précis si la géométrie de mesure n’est pas choisie correctement. En conséquence, certaines applications imposent des restrictions sur l’emplacement du point P . Pour une situation cartésienne 2D (trilatération), ces restrictions prennent l’une des deux formes équivalentes :

• L’angle intérieur autorisé en P entre les lignes P-C1 et P-C2 : L’idéal est un angle droit, qui se produit à des distances de la ligne de base égales ou inférieures à la moitié de la longueur de la ligne de base ; les écarts maximaux admissibles par rapport aux 90 degrés idéaux peuvent être spécifiés.
• La dilution horizontale de précision (HDOP), qui multiplie l’erreur de distance dans la détermination de l’erreur de position : pour deux dimensions, l’idéal (minimum) HDOP est la racine carrée de 2 ( 2 ≈ 1.414 {displaystyle {sqrt {2}}environ 1.414} ), qui se produit lorsque l’angle entre P-C1 et P-C2 est de 90 degrés ; une valeur HDOP maximale autorisée peut être spécifiée. (Ici, les HDOP égaux sont simplement le lieu des points de la Fig. 4 ayant le même angle de croisement.)

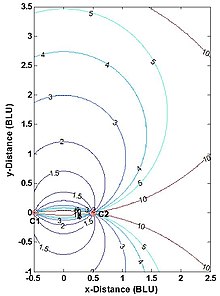
Fig. 5 Contours HDOP pour un système de multilatération (trilatération) à plage vraie 2D

La planification d’un système de navigation ou de surveillance multilatération à portée réelle implique souvent une analyse de dilution de la précision (DOP) pour éclairer les décisions sur le nombre et l’emplacement des stations et la zone de service du système (deux dimensions) ou le volume de service (trois dimensions). ^{[24] [25]} La figure 5 montre des DOP horizontaux (HDOP) pour un système de multilatération à plage réelle 2D à deux stations. HDOP est infini le long de la ligne de base et de ses extensions, car une seule des deux dimensions est réellement mesurée. Un utilisateur d’un tel système devrait être à peu près au large de la ligne de base et dans une bande de portée dépendante de l’application. Par exemple, pour les repères de navigation DME/DME par avion, le HDOP maximal autorisé par la FAA des États-Unis est le double de la valeur minimale possible, soit 2,828, ^[26]ce qui limite la plage d’utilisation maximale (qui se produit le long de la bissectrice de la ligne de base) à 1,866 fois la longueur de la ligne de base. (L’avion contenant deux stations au sol DME et un avion n’est pas strictement horizontal, mais l’est généralement presque. ) ).

Les erreurs dans les enquêtes de trilatération sont discutées dans plusieurs documents. ^{[27] [28]} Généralement, l’accent est mis sur les effets des erreurs de mesure de distance, plutôt que sur les effets des erreurs numériques d’algorithme.

Exemples d’application

• Arpentage par la méthode de trilatération
• Levé aérien
• Recherche d’archéologie maritime ^[29]
• Navigation aérienne DME/DME RNAV ^{[26] [30]}
• Intégration de plusieurs radars (par exemple, FAA ERAM ) ^[4]
• Navigation céleste utilisant la méthode d’interception d’altitude
• Méthode d’interception – Solution graphique au problème d’interception d’altitude
• Étalonnage des interféromètres laser ^[15]
• SHORAN , Oboe , Gee-H —Systèmes de guidage d’aéronefs développés pour les bombardements “à l’aveugle”
• JTIDS ( Joint Tactical Information Distribution System ) – Système US/OTAN qui (entre autres capacités) localise les participants dans un réseau à l’aide de plages inter-participants
• Avion SR-71 Blackbird de l’ USAF – Utilise la navigation astro-inertielle
• Avion USAF B-2 Spirit – Utilise la navigation astro-inertielle
• Technique Loran-C expérimentale ^[2]

Voir également

• Problème de géométrie de distance , technique similaire appliquée aux molécules
• Navigation céleste – ancienne technique de navigation basée sur les corps célestes
• Équipement de mesure de distance (DME) — Système utilisé pour mesurer la distance entre un aéronef et une station au sol
• Distance euclidienne
• Méthode d’interception – Technique graphique utilisée dans la navigation céleste
• Télémètre laser
• Multilatération – Adresses pseudo-range multilatération
• Télémètre —Systèmes utilisés pour mesurer la distance entre deux points au sol
• Résection (orientation)
• SHORAN — Développé en tant que système de navigation d’avions militaires, utilisé plus tard à des fins civiles
• Arpentage
• Telluromètre – Premier télémètre électronique à micro-ondes
• Triangulation – Méthode d’arpentage basée sur la mesure des angles

Références

1. ^ Limites de précision des systèmes de multilatération de gamme-gamme (sphériques) , Harry B. Lee, Massachusetts Institute of Technology, Lincoln Laboratory, Numéro de rapport : DOT/TSC-RA-3-8-(1) (Note technique 1973-43), 11 octobre 1973
2. ^ ^{un bcd} ” ^Rho -Rho Loran-C Combiné avec la Navigation par Satellite pour les Enquêtes Offshore ^“ . ST Grant, Revue hydrographique internationale , sans date
3. ^ “Concept d’utilisation de la multilatération (MLAT)”, Organisation de l’aviation civile internationale, 2007
4. ^ ^{un b} “Radar Basics” , Christian Wolff, non daté
5. ^ Encyclopædia Britannica
6. ^ diracdelta Archivé le 12/08/2010 à la Wayback Machine
7. ^ dictionnaire gratuit
8. ^ ^{un b} Impact d’Aide d’Horloge de Rubidium sur la Navigation de Véhicule Augmentée GPS , Zhaonian Zhang; Université de Calgary; décembre 1997.
9. ^ ^{un bc Geyer} , Michael (juin 2016). Analyse de la navigation et de la surveillance des aéronefs à référence terrestre . Bibliothèque nationale des transports US DOT : US DOT John A. Volpe National Transportation Systems Center.
10. ^ Adastra Aerial Surveys récupéré le 22 janvier 2019.
11. ^ “La nature des informations géographiques: trilatération” , Pennsylvania State Univ., 2018.
12. ^ “Trilatération et extension à la navigation du système de positionnement global”, BT Fang, Journal of Guidance, Control, and Dynamics , vol. 9 (1986), pages 715 à 717.
13. ^ ^{a b} ” Algorithmes de forme fermée dans le positionnement mobile : mythes et idées fausses “, Niilo Sirola, Actes du 7e atelier sur le positionnement, la navigation et la communication 2010 (WPNC’10) , 11 mars 2010.
14. ^ “Une solution algébrique des équations GPS” , Stephen Bancroft, Transactions IEEE sur les systèmes aérospatiaux et électroniques , Volume : AES-21, Numéro : 7 (janvier 1985), pp 56–59.
15. ^ ^{a b} LaserTracer – Un nouveau type d’interféromètre laser à suivi automatique , Carl-Thomas Schneider, IWAA2004, CERN, Genève, octobre 2004
16. ^ “Comment une horloge atomique à l’échelle de la puce peut aider à atténuer les interférences à large bande” ; Fang-Cheng Chan, Mathieu Joerger, Samer Khanafseh, Boris Pervan et Ondrej Jakubov ; Monde GPS — Innovations ; Mai 2014.
17. ^ “Système d’atterrissage à micro-ondes” ; Thomas E. Evans; Magazine de l’IEEE sur les systèmes aérospatiaux et électroniques ; Vol. 1, numéro 5 ; Mai 1986.
18. ^ Trigonométrie sphérique , Isaac Todhunter, MacMillan; 5e édition, 1886.
19. ↑ Un traité sur la trigonométrie sphérique et son application à la géodésie et à l’astronomie, avec de nombreux exemples , John Casey, Dublin, Hodges, Figgis & Co., 1889.
20. ^ “Géodésie basée sur les vecteurs” , Chris Veness. 2016.
21. ^ “STELLA (Système pour estimer la latitude et la longitude astronomiquement)”, George Kaplan, John Bangert, Nancy Oliversen; Observatoire naval américain, 1999.
22. ^ Suivi et fusion de données : un manuel d’algorithmes ; Y. Bar-Shalom, PK Willett, X. Tian ; 2011
23. ^ “Position alternative, navigation et synchronisation : le besoin d’une radionavigation robuste” ; MJ Narins, LV Eldredge, P. Enge, SC Lo, MJ Harrison et R. Kenagy ; Chapitre deatelier conjoint sur les systèmes mondiaux de navigation par satellite de l’Académie nationale d’ingénierie et de l’Académie chinoise d’ingénierie (2012).
24. ^ “Dilution de précision” , Richard Langeley, GPS World , mai 1999, pp 52–59.
25. ^ Limitations de précision des systèmes de multilatération gamme-gamme (sphérique) , Harry B. Lee, Massachusetts Institute of Technology, Lincoln Laboratory, note technique 1973-43, 11 octobre 1973.
26. ^ ^{un b} “DME/DME pour Alternate Position, Navigation, and Timing (APNT)” , Robert W. Lilley et Robert Erikson, Federal Aviation Administration, Livre blanc, 23 juillet 2012.
27. ^ Méthodes statistiques d’enquête par trilatération ; William Navidi, William S Murphy, Jr et Willy Hereman ; 20 décembre 1999.
28. ^ Comparaison de la précision de la triangulation, de la trilatération et de la triangulation-trilatération ; KL Provoro; Novosibirsk Institute of Engineers of Geodesy; 1960.
29. ^ “Trilatération dans l’archéologie maritime” , YouTube, US National Oceanic and Atmospheric Administration, 2006.
30. ^ “Précision DME / DME”, Michael Tran, Actes de la réunion technique nationale de 2008 de l’Institut de navigation , San Diego, Californie, janvier 2008, pp. 443–451.

Liens externes

• stackexchange.com , Implémentation PHP / Python