Unité imaginaire
L’ unité imaginaire ou nombre imaginaire unitaire ( i ) est une solution de l’ équation quadratique x 2 + 1 = 0 . Bien qu’il n’y ait pas de nombre réel avec cette propriété, i peut être utilisé pour étendre les nombres réels à ce qu’on appelle des nombres complexes , en utilisant l’ addition et la multiplication . Un exemple simple de l’utilisation de i dans un nombre complexe est 2 + 3 i .
 i dans le plan complexe ou cartésien . Les nombres réels se trouvent sur l’axe horizontal et les nombres imaginaires se trouvent sur l’axe vertical.
i dans le plan complexe ou cartésien . Les nombres réels se trouvent sur l’axe horizontal et les nombres imaginaires se trouvent sur l’axe vertical.
Les nombres imaginaires sont un concept mathématique important; ils étendent le système des nombres réels R {displaystyle mathbb {R} } 

Il y a deux racines carrées complexes de −1 , à savoir i et − i , tout comme il y a deux racines carrées complexes de tout nombre réel autre que Zéro (qui a une double racine carrée ).
Dans les contextes où l’utilisation de la lettre i est ambiguë ou problématique, la lettre j ou le grec ι est parfois utilisé à la place. [a] Par exemple, en génie électrique et en génie des systèmes de contrôle , l’unité imaginaire est normalement notée j au lieu de i , car i est couramment utilisé pour désigner le courant électrique .
Définition
| Les puissances de i renvoient des valeurs cycliques : |
|---|
| … (répète le motif de la zone bleue en gras ) |
| je −3 = je |
| je −2 = −1 |
| je −1 = − je |
| je 0 = 1 |
| je 1 = je |
| je 2 = −1 |
| je 3 = – je |
| je 4 = 1 |
| je 5 = je |
| je 6 = −1 |
| … (répète le motif de la zone bleue en gras ) |
Le nombre imaginaire i est défini uniquement par la propriété que son carré est −1 :
je 2 = − 1. {displaystyle i^{2}=-1.} 
Avec i défini de cette manière, il découle directement de l’algèbre que i et − i sont tous deux des racines carrées de −1.
Bien que la construction soit dite « imaginaire », et bien que le concept de nombre imaginaire puisse être intuitivement plus difficile à appréhender que celui de nombre réel, la construction est parfaitement valable d’un point de vue mathématique. Les opérations sur les nombres réels peuvent être étendues aux nombres imaginaires et complexes, en traitant i comme une quantité inconnue tout en manipulant une expression (et en utilisant la définition pour remplacer toute occurrence de i 2 par −1). Les puissances intégrales supérieures de i peuvent également être remplacées par − i , 1, i ou −1 :
je 3 = je 2 je = ( − 1 ) je = − je {displaystyle i^{3}=i^{2}i=(-1)i=-i} 
je 4 = je 3 je = ( − je ) je = − ( je 2 ) = − ( − 1 ) = 1 {displaystyle i^{4}=i^{3}i=(-i)i=-(i^{2})=-(-1)=1}

ou équivalent, je 4 = ( je 2 ) ( je 2 ) = ( − 1 ) ( − 1 ) = 1 {displaystyle i^{4}=(i^{2})(i^{2})=(-1)(-1)=1}

je 5 = je 4 je = ( 1 ) je = je {displaystyle i^{5}=i^{4}i=(1)i=i}

De même, comme pour tout nombre réel non nul :
je 0 = je 1 − 1 = i 1 i − 1 = i 1 1 i = i 1 i = i i = 1 {displaystyle i^{0}=i^{1-1}=i^{1}i^{-1}=i^{1}{frac {1}{i}}=i{frac { 1}{i}}={frac {i}{i}}=1} 
En tant que nombre complexe, i est représenté sous forme rectangulaire par 0 + 1 i , avec une composante réelle nulle et une composante imaginaire unitaire. Sous Forme polaire , i est représenté par 1⋅ e iπ /2 (ou simplement e iπ /2 ), avec une valeur absolue (ou grandeur) de 1 et un argument (ou angle) de π /2 . Dans le plan complexe (également connu sous le nom de plan d’Argand), qui est une interprétation spéciale d’un plan cartésien , jeest le point situé à une unité de l’origine le long de l’ Axe imaginaire (qui est orthogonal à l’ Axe réel ).
je contre – je
Étant un Polynôme quadratique sans Racine multiple , l’équation de définition x 2 = −1 a deux solutions distinctes, qui sont également valables et qui se trouvent être des inverses additifs et multiplicatifs l’un de l’autre. Une fois qu’une solution i de l’équation a été fixée, la valeur − i , qui est distincte de i , est également une solution. Puisque l’équation est la seule définition de i , il apparaît que la définition est ambiguë (plus précisément, pas bien définie). Cependant, aucune ambiguïté n’en résultera tant que l’une ou l’autre des solutions est choisie et étiquetée ” i “, l’autre étant alors étiquetée – i . [3] Après tout, bien que − i et + i ne soient pas quantitativement équivalents (ils sont négatifs l’un de l’autre), il n’y a pas de différence algébrique entre + i et − i , car les deux nombres imaginaires ont la même prétention d’être le nombre dont le carré est −1.
En fait, si tous les manuels de mathématiques et la littérature publiée faisant référence aux nombres imaginaires ou complexes devaient être réécrits avec − i remplaçant chaque occurrence de + i (et donc chaque occurrence de − i remplacée par −(− i ) = + i ), tous les faits et les théorèmes resteraient valables. La distinction entre les deux racines x de x 2 + 1 = 0 , dont l’une est étiquetée avec un signe moins, est purement une relique notationnelle ; aucune racine ne peut être considérée comme plus primaire ou fondamentale que l’autre, et aucune d’entre elles n’est “positive” ou “négative”. [4]
Le problème peut être subtil : l’explication la plus précise est de dire que bien que le corps complexe , défini comme R [ x ]/( x 2 + 1) (voir nombre complexe ), soit unique à isomorphisme près , il n’est pas unique à un isomorphisme unique près : Il existe exactement deux automorphismes de corps de R [ x ]/( x 2 + 1) qui maintiennent chaque nombre réel fixe : L’identité et l’automorphisme envoyant x vers − x. Pour plus d’informations, voir conjugué complexe et groupe de Galois .
Matrices

 ( x , y ) est limité par l’hyperbole xy = –1 pour une matrice unitaire imaginaire.
( x , y ) est limité par l’hyperbole xy = –1 pour une matrice unitaire imaginaire.
Un problème similaire se pose si les nombres complexes sont interprétés comme des matrices réelles 2 × 2 (voir représentation matricielle des nombres complexes ), car alors les deux
X = ( 0 − 1 1 0 ) {displaystyle X={begin{pmatrix}0&-1\1&0end{pmatrix}}} 
et X = ( 0 1 − 1 0 ) {displaystyle X={begin{pmatrix}0&1\-1&0end{pmatrix}}}

seraient les solutions de l’équation matricielle X 2 = − I = − ( 1 0 0 1 ) = ( − 1 0 0 − 1 ) . {displaystyle X^{2}=-I=-{begin{pmatrix}1&0\0&1end{pmatrix}}={begin{pmatrix}-1&0\0&-1end{pmatrix}}. }

Dans ce cas, l’ambiguïté résulte du choix géométrique dont la « direction » autour du cercle unité est la rotation « positive ». Une explication plus précise est de dire que le groupe d’ automorphismes du groupe orthogonal spécial SO(2, R ) a exactement deux éléments : L’identité et l’automorphisme qui échange les rotations “CW” (sens horaire) et “CCW” (sens anti-horaire) . Pour plus d’informations, voir groupe orthogonal .
Toutes ces ambiguïtés peuvent être résolues en adoptant une définition plus rigoureuse du nombre complexe et en choisissant explicitement l’une des solutions de l’équation comme unité imaginaire. Par exemple, le couple ordonné (0, 1), dans la construction habituelle des nombres complexes avec des vecteurs à deux dimensions.
Considérez l’équation matricielle
( z x y − z ) 2 = ( − 1 0 0 − 1 ) . {displaystyle {begin{pmatrix}z&x\y&-zend{pmatrix}}^{2}={begin{pmatrix}-1&0\0&-1end{pmatrix}}.} 
Ici, z 2 + xy = –1 , donc le produit xy est négatif car xy = –(1 + z 2 ) , donc le point ( x , y ) se trouve dans le quadrant II ou IV. En outre, z 2 = − ( 1 + x y ) ≥ 0 ⟹ x y ≤ − 1 {displaystyle z^{2}=-(1+xy)geq 0implique xyleq -1}

donc ( x , y ) est borné par l’hyperbole xy = –1 .
Utilisation appropriée
L’unité imaginaire s’écrit parfois − 1 {displaystyle {sqrt {-1}}} 
dans des contextes mathématiques avancés [3] (ainsi que dans des textes populaires moins avancés). Cependant, il faut être très prudent lors de la manipulation de formules impliquant des radicaux . La notation de signe radical est réservée soit à la fonction racine carrée principale, qui n’est définie que pour le réel x ≥ 0 , soit à la branche principale de la fonction racine carrée complexe. Tenter d’appliquer les règles de calcul de la fonction racine carrée principale (réelle) pour manipuler la branche principale de la fonction racine carrée complexe peut produire de faux résultats : [5]
− 1 = i ⋅ i = − 1 ⋅ − 1 = ( − 1 ) ⋅ ( − 1 ) = 1 = 1 (incorrect). {displaystyle -1=icdot i={sqrt {-1}}cdot {sqrt {-1}}={sqrt {(-1)cdot (-1)}}={sqrt {1}}=1qquad {text{(incorrect).}}} 
De la même manière:
1 i = 1 − 1 = 1 − 1 = − 1 1 = − 1 = i (incorrect). {displaystyle {frac {1}{i}}={frac {sqrt {1}}{sqrt {-1}}}={sqrt {frac {1}{-1}}}= {sqrt {frac {-1}{1}}}={sqrt {-1}}=iqquad {text{(incorrect).}}} 
Les règles de calcul
a ⋅ b = a ⋅ b {displaystyle {sqrt {a}}cdot {sqrt {b}}={sqrt {acdot b}}} 
et
a b = a b {displaystyle {frac {sqrt {a}}{sqrt {b}}}={sqrt {frac {a}{b}}}} 
ne sont valables que pour des valeurs réelles et positives de a et b . [6] [7] [8]
Ces problèmes peuvent être évités en écrivant et en manipulant des expressions telles que i 7 {displaystyle je{sqrt {7}}} 
, plutôt que − 7 {displaystyle {sqrt {-7}}}

. Pour une discussion plus approfondie, voir racine carrée et point de ramification .
Propriétés
Racines carrées

 Les deux racines carrées de i dans le plan complexe
Les deux racines carrées de i dans le plan complexe 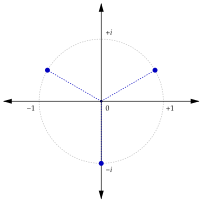
 Les trois racines cubiques de i dans le plan complexe
Les trois racines cubiques de i dans le plan complexe
Comme tous les nombres complexes non nuls, i a deux racines carrées : elles sont [b]
± ( 2 2 + 2 2 i ) = ± 2 2 ( 1 + i ) . {displaystyle pm left({frac {sqrt {2}}{2}}+{frac {sqrt {2}}{2}}iright)=pm {frac {sqrt {2}}{2}}(1+i).} 
En effet, la mise au carré des deux expressions donne :
( ± 2 2 ( 1 + i ) ) 2 = ( ± 2 2 ) 2 ( 1 + i ) 2 = 1 2 ( 1 + 2 i + i 2 ) = 1 2 ( 1 + 2 i − 1 ) = i . {displaystyle {begin{aligned}left(pm {frac {sqrt {2}}{2}}(1+i)right)^{2} &=left(pm { frac {sqrt {2}}{2}}right)^{2}(1+i)^{2} \&={frac {1}{2}}(1+2i+i^ {2})\&={frac {1}{2}}(1+2i-1) \&=i.end{aligné}}} 
En utilisant le signe radical de la racine carrée principale , on obtient :
i = 2 2 ( 1 + i ) . {displaystyle {sqrt {i}}={frac {sqrt {2}}{2}}(1+i).} 
Racines cubiques
Les trois racines cubiques de i sont :
− i , {displaystyle -i,} 


Semblables à toutes les racines de 1 , toutes les racines de i sont les sommets de polygones réguliers , qui sont inscrits dans le cercle unité du plan complexe.
Multiplication et division
Multiplier un nombre complexe par i donne :
i ( a + b i ) = a i + b i 2 = − b + a i . {displaystyle i(a+bi)=ai+bi^{2}=-b+ai.} 
(Cela équivaut à une rotation de 90° dans le sens inverse des aiguilles d’une montre d’un vecteur autour de l’origine dans le plan complexe.)
Diviser par i revient à multiplier par l’ inverse de i :
1 i = 1 i ⋅ i i = i i 2 = i − 1 = − i . {displaystyle {frac {1}{i}}={frac {1}{i}}cdot {frac {i}{i}}={frac {i}{i^{2}} }={frac{i}{-1}}=-i~.} 
L’utilisation de cette identité pour généraliser la division par i à tous les nombres complexes donne :
a + b i i = − i ( a + b i ) = − a i − b i 2 = b − a i . {displaystyle {frac {a+bi}{i}}=-i(a+bi)=-ai-bi^{2}=b-ai.} 
(Cela équivaut à une rotation de 90° dans le sens des aiguilles d’une montre d’un vecteur autour de l’origine dans le plan complexe.)
Pouvoirs
Les puissances de i se répètent dans un cycle exprimable avec le modèle suivant, où n est un nombre entier :
i 4 n = 1 {displaystyle i^{4n}=1} 
i 4 n + 1 = i {displaystyle je^{4n+1}=i}

i 4 n + 2 = − 1 {displaystyle i^{4n+2}=-1}

i 4 n + 3 = − i , {displaystyle i^{4n+3}=-i,}

Cela conduit à la conclusion que
i n = i ( n mod 4 ) {displaystyle i^{n}=i^{(n{bmod {4}})}} 
où mod représente l’ opération modulo . Équivalent :
i n = cos ( n π / 2 ) + i sin ( n π / 2 ) {displaystyle i^{n}=cos(npi /2)+isin(npi /2)} 
J’ai élevé au pouvoir de moi
En utilisant la formule d’Euler , i i est
i i = ( e i ( π / 2 + 2 k π ) ) i = e i 2 ( π / 2 + 2 k π ) = e − ( π / 2 + 2 k π ) {displaystyle i^{i}=left(e^{i(pi /2+2kpi )}right)^{i}=e^{i^{2}(pi /2+2k pi )}=e^{-(pi /2+2kpi )}} 
où k ∈ Z , l’ensemble des entiers .
La valeur principale (pour k = 0 ) est e − π /2 , soit environ 0,207879576. [dix]
Factoriel
La factorielle de l’unité imaginaire i est le plus souvent donnée en fonction de la fonction gamma évaluée en 1 + i :
i ! = Γ ( 1 + i ) ≈ 0.4980 − 0.1549 i . {displaystyle i!=Gamma (1+i)environ 0,4980-0,1549i~.} 
Aussi,
| i ! | = π sinh π {displaystyle |i!|={sqrt {frac {pi }{sinh pi }}}} 
[11]
Autres opérations
De nombreuses opérations mathématiques pouvant être effectuées avec des nombres réels peuvent également être effectuées avec i , telles que l’exponentiation, les racines, les logarithmes et les fonctions trigonométriques. Toutes les fonctions suivantes sont des fonctions complexes à valeurs multiples , et il convient d’indiquer clairement sur quelle branche de la surface de Riemann la fonction est définie en pratique. Vous trouverez ci-dessous les résultats pour la branche la plus couramment choisie.
Un nombre élevé à la puissance ni est :
x n i = cos ( n ln x ) + i sin ( n ln x ) . {displaystyle x^{ni}=cos(nln x)+isin(nln x).} 
La racine ni ième d’un nombre est :
x n i = cos ( ln x n ) − i sin ( ln x n ) . {displaystyle {sqrt[{ni}]{x}}=cos left({frac {ln x}{n}}right)-isin left({frac {ln x }{n}}right)~.} ![{displaystyle {sqrt[{ni}]{x}}=cos left({frac {ln x}{n}}right)-isin left({frac {ln x}{n}}right)~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85698bb8407b1e6c4da720b6ea4e1838624d79e3)
Le Logarithme à base imaginaire d’un nombre est :
log i x = 2 ln x i π . {displaystyle log _{i}x={frac {2ln x}{ipi }}~.} 
Comme pour tout logarithme complexe , la base de journal i n’est pas définie de manière unique.
Le Cosinus de i est un nombre réel :
cos i = cosh 1 = e + 1 / e 2 = e 2 + 1 2 e ≈ 1.54308064 … {displaystyle cos i=cosh 1={frac {e+1/e}{2}}={frac {e^{2}+1}{2e}}approx 1.54308064ldots } 
Et le Sinus de i est purement imaginaire :
sin i = i sinh 1 = e − 1 / e 2 i = e 2 − 1 2 e i ≈ ( 1.17520119 … ) i . {displaystyle sin i=isinh 1={frac {e-1/e}{2}}i={frac {e^{2}-1}{2e}}iapprox (1.17520119 ldots )i~.} 
Histoire Voir également
- L’identité d’Euler
- Constante mathématique
- Multiplicité (mathématiques)
- Racine d’unité
- Numéro complexe d’unité
Remarques
- ^ Quelques textes [ lesquels ? ] utilisez la lettre grecque iota ( ι ) pour l’unité imaginaire afin d’éviter toute confusion, en particulier avec les indices et les indices.
En génie électrique et dans les domaines connexes, l’unité imaginaire est normalement notée j pour éviter toute confusion avec le courant électrique en fonction du temps, qui est classiquement représenté par i ( t ) ou simplement i . [1]
Le langage de programmation Python utilise également j pour marquer la partie imaginaire d’un nombre complexe.
MATLABassocie à la fois i et j à l’unité imaginaire, bien que l’entrée 1 i ou 1 j soit préférable, pour une analyse rapide et plus robuste des expressions. [2]
Dans les quaternions , Chacun de i , j , et k est une unité imaginaire distincte.
Dans les bivecteurs et les biquaternions , une unité imaginaire supplémentaire h ou l est utilisée. - ^ Pour trouver un tel nombre, on peut résoudre l’équation ( X + je ) 2 = je où x et y sont des paramètres réels à déterminer, ou de manière équivalente X 2 + 2 ixy − y 2 = je . Parce que les parties réelles et imaginaires sont toujours séparées, nous regroupons les termes : x 2 − y 2 + 2 ixy = 0 + je et en égalant les coefficients , la partie réelle et le coefficient réel de la partie imaginaire séparément, on obtient un système de deux équations : x 2 – y 2 = 0 2 xy = 1 . En substituant y = 1⁄2 x dans la première équation, on obtient x 2 −1⁄4 x 2 = 0 x 2 = 1⁄4 x 2 4 x 4 = 1 Comme x est un nombre réel, cette équation a deux solutions réelles pour x : x = 1/ √ 2 et x = −1/ √ 2 . En substituant l’un ou l’autre de ces résultats dans l’équation 2 xy = 1 à son tour, nous obtiendrons le résultat correspondant pour y . Ainsi, les racines carrées de i sont les nombres 1/ √ 2 + i / √ 2 et −1/ √ 2 − i / √ 2 . [9]
Références
- ^ Boas, Mary L. (2006). Méthodes mathématiques en sciences physiques (3e éd.). New York [ua] : Wiley. p. 49 . ISBN 0-471-19826-9.
- ^ “Documentation du produit MATLAB” .
- ^ un b Weisstein, Eric W. “Unité Imaginaire” . mathworld.wolfram.com . Récupéré le 10 août 2020 .
- ^ Doxiades, Apostolos K.; Mazur, Barry (2012). Cercles perturbés : l’interaction des mathématiques et de la narration (éd. illustrée). Presse universitaire de Princeton. p. 225 . ISBN 978-0-691-14904-2– via Google Livres.
- ^ Bouquet, Bryan (2012). Erreurs mathématiques et paradoxes (éd. illustré). Société de messagerie. p. 31 -34. ISBN 978-0-486-13793-3– via Google Livres.
- ^ Kramer, Arthur (2012). Mathématiques pour l’électricité et l’électronique (4e éd.). Cengage Apprentissage. p. 81 . ISBN 978-1-133-70753-0– via Google Livres.
- ↑ Picciotto, Henri ; Wah, Anita (1994). Algèbre : Thèmes, outils, concepts (éd. des enseignants). Henri Picciotto. p. 424 . ISBN 978-1-56107-252-1– via Google Livres.
- ^ Nahin, Paul J. (2010). An Imaginary Tale: L’histoire de ” i ” [la racine carrée de moins un] . Presse universitaire de Princeton. p. 12 . ISBN 978-1-4008-3029-9– via Google Livres.
- ^ “Quelle est la racine carrée de i ?” . Réseau de mathématiques de l’Université de Toronto . Récupéré le 26 mars 2007 .
- ^ Wells, David (1997) [1986]. Le dictionnaire Penguin des nombres curieux et intéressants (édition révisée). Royaume-Uni : Penguin Books. p. 26. ISBN 0-14-026149-4.
- ^ “abs (je!)” . Wolfram Alpha .
Lectures complémentaires
- En ligneNahin, Paul J. (1998). An Imaginary Tale: L’histoire de i [la racine carrée de moins un] . Chichester : Presse universitaire de Princeton. ISBN 0-691-02795-1– via Archive.org.
Liens externes
- Euler, Leonhard . “Racines imaginaires des polynômes” .à “Convergence” . mathdl.maa.org . Association mathématique d’Amérique. Archivé de l’original le 13 juillet 2007.
