Rhombe

En géométrie euclidienne plane , un losange (pluriel losanges ou losanges ) est un quadrilatère dont les quatre côtés ont tous la même longueur. Un autre nom est quadrilatère équilatéral , car équilatéral signifie que tous ses côtés sont de longueur égale. Le losange est souvent appelé un “diamant”, d’après le costume de diamants dans les cartes à jouer qui ressemble à la projection d’un diamant octaédrique ou d’un losange (forme) , bien que le premier se réfère parfois spécifiquement à un losange avec un angle de 60° (ce que certains les auteurs appellent un calisson aprèsle bonbon français ^[1] – voir aussi Polyiamond ), et ce dernier se réfère parfois spécifiquement à un losange avec un angle de 45°.

Rhombe
Un losange dans deux orientations différentes
Taper	quadrilatère , trapèze , parallélogramme , cerf -volant
Arêtes et sommets	4
Symbole Schläfli	{ } + { } {2 _α }
Diagrammes de Coxeter – Dynkin
Groupe Symétrie	Dièdre (D ₂ ), [2], (*22), ordre 4
Région	K = p ⋅ q 2 {displaystyle K={frac {pcdot q}{2}}} ${displaystyle K={frac {pcdot q}{2}}}$ (la moitié du produit des diagonales)
Propriétés	convexe , Isotoxique

Le losange a un carré comme cas particulier, et est un cas particulier de cerf -volant et de parallélogramme .

Chaque losange est simple (non auto-sécant) et est un cas particulier d’un parallélogramme et d’un cerf -volant . Un losange à angles droits est un carré . ^{[2] [3]}

Étymologie

Le mot « losange » vient du grec ancien : ῥόμβος , romanisé : rhombos , signifiant quelque chose qui tourne, ^[4] qui dérive du verbe ῥέμβω , romanisé : rhémbō , signifiant « tourner en rond ». ^[5] Le mot a été utilisé à la fois par Euclide et Archimède , qui ont utilisé le terme “losange solide” pour un bicône , deux cônes circulaires droits partageant une base commune. ^[6]

La surface que nous appelons aujourd’hui losange est une coupe transversale du bicône sur un plan passant par les sommets des deux cônes.

Caractérisations

Un quadrilatère simple (non auto-sécant ) est un losange si et seulement s’il est l’un des suivants : ^{[7] [8]}

un parallélogramme dans lequel une diagonale coupe en son milieu un angle intérieur
un parallélogramme dont au moins deux côtés consécutifs ont la même longueur
un parallélogramme dont les diagonales sont perpendiculaires (un parallélogramme orthodiagonal )
un quadrilatère à quatre côtés de même longueur (par définition)
un quadrilatère dont les diagonales sont perpendiculaires et se coupent en leur milieu
un quadrilatère dont chaque diagonale coupe en son milieu deux angles intérieurs opposés
un quadrilatère ABCD possédant un point P dans son plan tel que les quatre triangles ABP , BCP , CDP et DAP soient tous congrus ^[9]
un quadrilatère ABCD dans lequel les cercles inscrits des triangles ABC , BCD , CDA et DAB ont un point commun ^[10]

Propriétés de base

Chaque losange a deux diagonales reliant des paires de sommets opposés et deux paires de côtés parallèles. En utilisant des triangles congruents , on peut prouver que le losange est symétrique sur chacune de ces diagonales. Il s’ensuit que tout losange a les propriétés suivantes :

Les angles opposés d’un losange ont la même mesure.
Les deux diagonales d’un losange sont perpendiculaires ; c’est-à-dire qu’un losange est un quadrilatère orthodiagonal .
Ses diagonales coupent en deux des angles opposés.

La première propriété implique que tout losange est un parallélogramme . Un losange a donc toutes les propriétés d’un parallélogramme : par exemple, les côtés opposés sont parallèles ; les angles adjacents sont supplémentaires ; les deux diagonales se coupent en leur milieu ; toute ligne passant par le milieu coupe l’aire en deux; et la somme des carrés des côtés est égale à la somme des carrés des diagonales ( loi du parallélogramme ). Désignant ainsi le côté commun par a et les diagonales par p et q , dans chaque losange

4 un 2 = p 2 + q 2 . {displaystyle displaystyle 4a^{2}=p^{2}+q^{2}.} $displaystyle 4a^{2}=p^{2}+q^{2}.$ $displaystyle 4a^{2}=p^{2}+q^{2}.$

Tous les parallélogrammes ne sont pas des losanges, bien que tout parallélogramme avec des diagonales perpendiculaires (la deuxième propriété) soit un losange. En général, tout quadrilatère avec des diagonales perpendiculaires, dont l’une est un axe de symétrie, est un cerf -volant . Tout losange est un cerf-volant, et tout quadrilatère qui est à la fois un cerf-volant et un parallélogramme est un losange.

Un losange est un quadrilatère tangentiel . ^[11] C’est-à-dire qu’il a un cercle Inscrit qui est tangent aux quatre côtés.

Un losange. Chaque angle marqué d’un point noir est un angle droit. La hauteur h est la distance perpendiculaire entre deux côtés non adjacents quelconques, qui est égale au diamètre du cercle Inscrit. Les diagonales de longueurs p et q sont les segments de ligne en pointillés rouges.

Diagonales

La longueur des diagonales p = AC et q = BD peut être exprimée en fonction du côté du losange a et d’un angle au sommet α comme

p = un 2 + 2 parce que ⁡ α {displaystyle p=a{sqrt {2+2cos {alpha}}}}

q = un 2 − 2 parce que ⁡ α . {displaystyle q=a{sqrt {2-2cos {alpha }}}.}

Ces formules sont une conséquence directe de la loi des cosinus .

Inradius

L’inradius (le rayon d’un cercle Inscrit dans le losange), noté r , peut être exprimé en termes de diagonales p et q comme ^[11]

r = p ⋅ q 2 p 2 + q 2 , {displaystyle r={frac {pcdot q}{2{sqrt {p^{2}+q^{2}}}}},} ${displaystyle r={frac {pcdot q}{2{sqrt {p^{2}+q^{2}}}}},}$ ${displaystyle r={frac {pcdot q}{2{sqrt {p^{2}+q^{2}}}}},}$

ou en termes de longueur de côté a et de tout angle au sommet α ou β comme

r = a sin ⁡ α 2 = a sin ⁡ β 2 . {displaystyle r={frac {asin alpha }{2}}={frac {asin beta }{2}}.} ${displaystyle r={frac {asin alpha }{2}}={frac {asin beta }{2}}.}$ ${displaystyle r={frac {asin alpha }{2}}={frac {asin beta }{2}}.}$

Région

Comme pour tous les parallélogrammes , l’ aire K d’un losange est le produit de sa base et de sa hauteur ( h ). La base est simplement n’importe quelle longueur de côté a :

K = a ⋅ h . {displaystyle K=acdot h.}

L’aire peut également être exprimée comme la base au carré multipliée par le sinus de n’importe quel angle :

K = a 2 ⋅ sin ⁡ α = a 2 ⋅ sin ⁡ β , {displaystyle K=a^{2}cdot sin alpha =a^{2}cdot sin beta ,} ${displaystyle K=a^{2}cdot sin alpha =a^{2}cdot sin beta ,}$ ${displaystyle K=a^{2}cdot sin alpha =a^{2}cdot sin beta ,}$

soit en termes de hauteur et d’ angle au sommet :

K = h 2 sin ⁡ α , {displaystyle K={frac {h^{2}}{sin alpha }},} ${displaystyle K={frac {h^{2}}{sin alpha }},}$ ${displaystyle K={frac {h^{2}}{sin alpha }},}$

ou comme la moitié du produit des diagonales p , q :

K = p ⋅ q 2 , {displaystyle K={frac {pcdot q}{2}},} ${displaystyle K={frac {pcdot q}{2}},}$ ${displaystyle K={frac {pcdot q}{2}},}$

ou comme le demi- périmètre multiplié par le rayon du cercle Inscrit dans le losange (inradius):

K = 2 a ⋅ r . {displaystyle K=2acdot r.}

Une autre façon, en commun avec les parallélogrammes, est de considérer deux côtés adjacents comme des vecteurs, formant un bivecteur , donc l’aire est la grandeur du bivecteur (la grandeur du produit vectoriel des deux vecteurs), qui est le déterminant des deux coordonnées cartésiennes des vecteurs : K = x ₁y ₂ – x ₂y ₁ . ^[12]

Double propriétés

Le polygone dual d’un losange est un rectangle : ^[13]

Un losange a tous les côtés égaux, tandis qu’un rectangle a tous les angles égaux.
Un losange a des angles opposés égaux, tandis qu’un rectangle a des côtés opposés égaux.
Un losange a un cercle Inscrit, tandis qu’un rectangle a un cercle circonscrit .
Un losange a un axe de symétrie passant par chaque paire d’angles de sommet opposés, tandis qu’un rectangle a un axe de symétrie passant par chaque paire de côtés opposés.
Les diagonales d’un losange se coupent à angles égaux, tandis que les diagonales d’un rectangle ont la même longueur.
La figure formée en joignant les milieux des côtés d’un losange est un rectangle , et vice versa.

Équation cartésienne

Les côtés d’un losange centré à l’origine, dont les diagonales tombent chacune sur un axe, sont constitués de tous les points ( x, y ) satisfaisant

| x a | + | y b | = 1. {displaystyle left|{frac {x}{a}}right|!+left|{frac {y}{b}}right|!=1.} ${displaystyle left|{frac {x}{a}}right|!+left|{frac {y}{b}}right|!=1.}$ ${displaystyle left|{frac {x}{a}}right|!+left|{frac {y}{b}}right|!=1.}$

Les sommets sont à ( ± a , 0 ) {displaystyle (pm a,0)} et ( 0 , ± b ) . {displaystyle (0,pm b).} C’est un cas particulier de superellipse , d’exposant 1.

Autres propriétés

L’un des cinq types de réseau 2D est le réseau rhombique, également appelé réseau rectangulaire centré .
Des losanges identiques peuvent paver le plan 2D de trois manières différentes, y compris, pour le losange à 60°, le pavage en losange .

Comme pavages carrés topologiques	Comme carrelage en losange de 30 à 60 degrés

Les analogues tridimensionnels d’un losange comprennent la bipyramide et le bicône .
Plusieurs Polyèdres ont des faces rhombiques, comme le dodécaèdre rhombique et le dodécaèdre trapézo-rhombique .

Quelques Polyèdres à toutes faces rhombiques

Polyèdres isoédriques	Polyèdres non isoédriques
Losanges identiques	Losanges dorés identiques	Deux types de losanges	Trois types de losanges

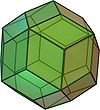
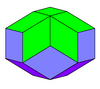
Dodécaèdre rhombique	Triacontaèdre rhombique	Icosaèdre rhombique	Ennéacontaèdre rhombique	Rhomboèdre

Comme les faces d’un polyèdre

Un rhomboèdre (également appelé hexaèdre rhombique) est une figure tridimensionnelle comme un cuboïde (également appelé parallélépipède rectangle), sauf que ses 3 paires de faces parallèles sont jusqu’à 3 types de losanges au lieu de rectangles.

Le dodécaèdre rhombique est un Polyèdre convexe avec 12 losanges congrus comme faces .

Le triacontaèdre rhombique est un Polyèdre convexe avec 30 losanges dorés (losanges dont les diagonales sont dans le nombre d’or ) comme faces.

Le grand triacontaèdre rhombique est un polyèdre isoèdre isotoxal non convexe à 30 faces rhombiques sécantes.

L’ hexecontaèdre rhombique est une stellation du triacontaèdre rhombique. Il est non convexe avec 60 faces rhombiques dorées à symétrie icosaédrique .

L’ ennéacontaèdre rhombique est un polyèdre composé de 90 faces rhombiques, avec trois, cinq ou six losanges se rencontrant à chaque sommet. Il a 60 larges losanges et 30 minces.

Le dodécaèdre trapézo-rhombique est un Polyèdre convexe à 6 faces rhombiques et 6 faces trapézoïdales .

L’ icosaèdre rhombique est un polyèdre composé de 20 faces rhombiques, dont trois, quatre ou cinq se rejoignent à chaque sommet. Il a 10 faces sur l’axe polaire avec 10 faces suivant l’équateur.

Voir également

Merkel Raute
Losange de Michaelis , dans l’anatomie humaine
Rhomboïde , soit un parallélépipède, soit un parallélogramme qui n’est ni un losange ni un rectangle
Antenne rhombique
Échecs rhombiques
Drapeau du département du nord de Santander en Colombie, contenant quatre étoiles en forme de losange
Superellipse (comprend un losange aux coins arrondis)

Références

^ Alsina, Claudi; Nelsen, Roger B. (31 décembre 2015). Une Odyssée Mathématique de l’Espace : la Géométrie Solide au 21ème Siècle . ISBN 9781614442165.
^ Remarque: la définition originale d’ Euclide et la définition de losange de certains dictionnaires anglais excluent les carrés, mais les mathématiciens modernes préfèrent la définition inclusive.
^ Weisstein, Eric W. “Carré” . MathWorld . utilisation inclusive
^ ῥόμβος Archivé le 08/11/2013 à la Wayback Machine , Henry George Liddell, Robert Scott, A Greek-English Lexicon , sur Persée
^ ρέμβω Archivé le 08/11/2013 à la Wayback Machine , Henry George Liddell, Robert Scott, A Greek-English Lexicon , sur Persée
^ “L’origine du losange” . Archivé de l’original le 2015-04-02 . Récupéré le 25/01/2005 .
^ Zalman Usiskin et Jennifer Griffin, ” La classification des quadrilatères. Une étude de définition archivée le 26/02/2020 à la Wayback Machine “, Information Age Publishing, 2008, pp. 55-56.
^ Owen Byer, Felix Lazebnik et Deirdre Smeltzer , Méthodes de géométrie euclidienne Archivé le 01/09/2019 à la Wayback Machine , Mathematical Association of America, 2010, p. 53.
^ Paris Pamfilos (2016), “Une caractérisation du losange”, Forum Geometricorum 16 , pp. 331–336, [1] Archivé le 23/10/2016 à la Wayback Machine
^ “IMOmath,” 26-ème Olympiade mathématique brésilienne 2004 ” ” (PDF) . Archivé (PDF) de l’original le 18/10/2016 . Récupéré le 06/01/2020 .
^ ^un ^b Weisstein, Eric W. “Rhombe” . MathWorld .
^ WildLinAlg épisode 4 Archivé le 05/02/2017 à la Wayback Machine , Norman J Wildberger, Univ. of New South Wales, 2010, conférence via youtube
^ de Villiers, Michael, “Polygones circonscrits cycliques équiangulaires et équilatéraux”, Mathematical Gazette 95, mars 2011, 102-107.

Liens externes

Recherchez losange dans Wiktionary, le dictionnaire gratuit.

Wikimedia Commons a des médias liés à Rhombi .

Parallélogramme et Losange – Parcours animé (Construction, Circonférence, Aire)
Définition Rhombus, Math Open Reference avec applet interactive.
Zone de losange , Math Open Reference – montre trois façons différentes de calculer la surface d’un losange, avec une applet interactive