Numéro
Un nombre est un objet mathématique utilisé pour compter , mesurer et étiqueter . Les exemples originaux sont les nombres naturels 1 , 2 , 3 , 4 , etc. [1] Les nombres peuvent être représentés dans un langage avec des Mots numériques . Plus universellement, les nombres individuels peuvent être représentés par des symboles , appelés chiffres ; par exemple, “5” est un chiffre qui représente le nombre cinq . Comme seul un nombre relativement restreint de symboles peut être mémorisé, les chiffres de base sont généralement organisés en unsystème numérique , qui est une manière organisée de représenter n’importe quel nombre. Le système numérique le plus courant est le système numérique hindou-arabe , qui permet la représentation de n’importe quel nombre à l’aide d’une combinaison de dix symboles numériques fondamentaux, appelés chiffres . [2] [3] En plus de leur utilisation dans le comptage et la mesure, les chiffres sont souvent utilisés pour les étiquettes (comme pour les numéros de téléphone ), pour la commande (comme pour les numéros de série ) et pour les codes (comme pour les ISBN ). Dans l’usage courant, un chiffre ne se distingue pas clairement du nombre qu’il représente.
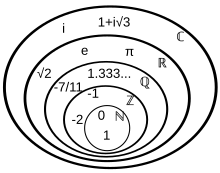 Sous -ensembles des nombres complexes
Sous -ensembles des nombres complexes
En mathématiques , la notion de nombre s’est étendue au cours des siècles pour inclure 0 , [4] les nombres négatifs , [5] les nombres rationnels comme un demi ( 1 2 ) {displaystyle left({tfrac {1}{2}}right)} 

Outre leurs utilisations pratiques, les nombres ont une signification culturelle dans le monde entier. [8] [9] Par exemple, dans la société occidentale, le nombre 13 est souvent considéré comme un porte- bonheur , et ” un million ” peut signifier “beaucoup” plutôt qu’une quantité exacte. [8] Bien qu’elle soit maintenant considérée comme une pseudoscience , la croyance en une signification mystique des nombres, connue sous le nom de numérologie , a imprégné la pensée antique et médiévale. [10] La numérologie a fortement influencé le développement des mathématiques grecques , stimulant l’étude de nombreux problèmes de théorie des nombres qui sont encore d’intérêt aujourd’hui. [dix]
Au cours du XIXe siècle, les mathématiciens ont commencé à développer de nombreuses abstractions différentes qui partagent certaines propriétés des nombres et peuvent être considérées comme une extension du concept. Parmi les premiers figurent les nombres hypercomplexes , qui consistent en diverses extensions ou modifications du système des nombres complexes . En mathématiques modernes, les systèmes de nombres sont considérés comme des exemples spéciaux importants de structures algébriques plus générales telles que les anneaux et les champs , et l’application du terme « nombre » est une question de convention, sans signification fondamentale. [11]
Histoire
| L’ exactitude factuelle de cette section est contestée . ( novembre 2014 ) Relevant discussion may be found on Talk:Number. Please help to ensure that disputed statements are reliably sourced. (Learn how and when to remove this template message) |
Chiffres
Les nombres doivent être distingués des chiffres , les symboles utilisés pour représenter les nombres. Les Égyptiens ont inventé le premier système numérique chiffré, et les Grecs ont suivi en cartographiant leurs nombres de comptage sur les alphabets ionien et dorique. [12] Les chiffres romains, un système qui utilisait des combinaisons de lettres de l’alphabet romain, sont restés dominants en Europe jusqu’à la diffusion du système numérique supérieur hindou-arabe vers la fin du 14e siècle, et le système numérique hindou-arabe reste le plus courant. système de représentation des nombres dans le monde d’aujourd’hui. [13] [ meilleure source nécessaire ] La clé de l’efficacité du système était le symbole du zéro, qui a été développé par d’anciens mathématiciens indiens vers 500 après JC. [13]
Première utilisation des nombres
Des os et d’autres artefacts ont été découverts avec des marques découpées que beaucoup pensent être des marques de pointage . [14] Ces marques de pointage peuvent avoir été utilisées pour compter le temps écoulé, comme le nombre de jours, les cycles lunaires ou pour tenir des registres de quantités, comme des animaux.
Un système de comptage n’a pas de concept de valeur de position (comme dans la notation décimale moderne ), ce qui limite sa représentation des grands nombres. Néanmoins, les systèmes de pointage sont considérés comme le premier type de système numérique abstrait.
Le premier système connu avec une valeur de position était le système mésopotamien de base 60 ( vers 3400 av. J.-C.) et le premier système connu de base 10 date de 3100 av. J.-C. en Égypte . [15]
Zéro
La première utilisation documentée connue de zéro date de l’an 628 et est apparue dans le Brāhmasphuṭasiddhānta , l’ouvrage principal du mathématicien indien Brahmagupta . Il a traité 0 comme un nombre et a discuté des opérations qui l’impliquent, y compris la division . À cette époque (le 7ème siècle), le concept avait clairement atteint le Cambodge sous forme de chiffres khmers , et la documentation montre que l’idée s’est ensuite répandue en Chine et dans le monde islamique .

 Le nombre 605 en chiffres khmers , d’après une inscription de 683 après JC. Utilisation précoce du zéro comme chiffre décimal.
Le nombre 605 en chiffres khmers , d’après une inscription de 683 après JC. Utilisation précoce du zéro comme chiffre décimal.
Le Brāhmasphuṭasiddhānta de Brahmagupta est le premier livre qui mentionne zéro comme nombre, c’est pourquoi Brahmagupta est généralement considéré comme le premier à formuler le concept de zéro. Il a donné des règles d’utilisation de zéro avec des nombres négatifs et positifs, telles que “zéro plus un nombre positif est un nombre positif, et un nombre négatif plus zéro est le nombre négatif”. Le Brāhmasphuṭasiddhānta est le premier texte connu à traiter le zéro comme un nombre à part entière, plutôt que comme un simple chiffre fictif représentant un autre nombre comme cela a été fait par les Babyloniens ou comme un symbole d’un manque de quantité comme cela a été fait par Ptolémée et les Romains.
L’utilisation de 0 comme nombre doit être distinguée de son utilisation comme chiffre d’espace réservé dans les systèmes de valeur de position . De nombreux textes anciens utilisaient 0. Les textes babyloniens et égyptiens l’utilisaient. Les Égyptiens utilisaient le mot nfr pour désigner un solde nul dans la comptabilité en partie double . Les textes indiens utilisaient un mot sanskrit Shunye ou shunya pour désigner le concept de vide . Dans les textes de mathématiques, ce mot fait souvent référence au chiffre zéro. [16] Dans le même ordre d’idées, Pāṇini (Ve siècle av. J.-C.) a utilisé l’opérateur nul (zéro) dans l’ Ashtadhyayi , un des premiers exemples de grammaire algébriquepour la langue sanskrite (voir aussi Pingala ).
Il existe d’autres utilisations du zéro avant Brahmagupta, bien que la documentation ne soit pas aussi complète que dans le Brāhmasphuṭasiddhānta .
Les archives montrent que les Grecs de l’Antiquité semblaient incertains du statut de 0 en tant que nombre : ils se sont demandé “comment le “rien” peut-il être quelque chose ?” conduisant à d’intéressants arguments philosophiques et, à l’époque médiévale, religieux sur la nature et l’existence de 0 et du vide . Les paradoxes de Zénon d’Elée dépendent en partie de l’interprétation incertaine du 0. (Les anciens Grecs se demandaient même si 1 était un nombre.)
Le peuple Olmèque tardif du centre-sud du Mexique a commencé à utiliser un symbole pour zéro, un glyphe de coquillage , dans le Nouveau Monde, peut-être au 4ème siècle avant JC mais certainement en 40 avant JC, qui est devenu une partie intégrante des chiffres mayas et du calendrier maya . . L’arithmétique maya utilisait la base 4 et la base 5 écrites en base 20. George I. Sánchez en 1961 a rapporté un boulier “doigt” de base 4, base 5. [17] [ meilleure source nécessaire ]
En 130 après JC, Ptolémée , influencé par Hipparque et les Babyloniens, utilisait un symbole pour 0 (un petit cercle avec une longue barre supérieure) dans un système numérique sexagésimal utilisant autrement des chiffres grecs alphabétiques . Parce qu’il était utilisé seul, et pas seulement comme un espace réservé, ce zéro hellénistique était la première utilisation documentée d’un vrai zéro dans l’Ancien Monde. Dans les manuscrits byzantins ultérieurs de sa Syntaxis Mathematica ( Almagest ), le zéro hellénistique s’était transformé en la lettre grecque Omicron (autrement signifiant 70).
Un autre vrai zéro était utilisé dans les tableaux aux côtés des chiffres romains vers 525 (première utilisation connue par Dionysius Exiguus ), mais en tant que mot, nulla ne signifiant rien , pas en tant que symbole. Lorsque la division produisait 0 comme reste, nihil , signifiant également rien , était utilisé. Ces zéros médiévaux ont été utilisés par tous les futurs calculateurs médiévaux ( calculatrices de Pâques ). Une utilisation isolée de leur initiale, N, a été utilisée dans un tableau de chiffres romains par Bede ou un collègue vers 725, un vrai symbole zéro.
Nombres négatifs
Le concept abstrait des nombres négatifs a été reconnu dès 100-50 avant JC en Chine. Les neuf chapitres sur l’art mathématique contiennent des méthodes pour trouver les aires des figures; des bâtonnets rouges ont été utilisés pour désigner les coefficients positifs , le noir pour les négatifs. [18] La première référence dans un ouvrage occidental remonte au IIIe siècle de notre ère en Grèce. Diophante a fait référence à l’équation équivalente à 4 x + 20 = 0 (la solution est négative) dans Arithmetica , disant que l’équation donnait un résultat absurde.
Au cours des années 600, des nombres négatifs étaient utilisés en Inde pour représenter les dettes. La référence précédente de Diophantus a été discutée plus explicitement par le mathématicien indien Brahmagupta , dans Brāhmasphuṭasiddhānta en 628, qui a utilisé des nombres négatifs pour produire la formule quadratique de forme générale qui reste en usage aujourd’hui. Cependant, au 12ème siècle en Inde, Bhaskara donne des racines négatives pour les équations quadratiques mais dit que la valeur négative “n’est pas dans ce cas à prendre, car elle est inadéquate; les gens n’approuvent pas les racines négatives”.
Les mathématiciens européens, pour la plupart, ont résisté au concept de nombres négatifs jusqu’au XVIIe siècle, bien que Fibonacci ait permis des solutions négatives aux problèmes financiers où elles pouvaient être interprétées comme des dettes (chapitre 13 du Liber Abaci , 1202) et plus tard comme des pertes (dans Flos ). René Descartes les appelait les fausses racines car elles apparaissaient dans les polynômes algébriques, mais il a également trouvé un moyen d’échanger les vraies racines et les fausses racines. Dans le même temps, les Chinois indiquaient les nombres négatifs en traçant un trait diagonal à travers le chiffre non nul le plus à droite du chiffre du nombre positif correspondant. [19] La première utilisation des nombres négatifs dans une œuvre européenne est celle de Nicolas Chuquetau cours du XVe siècle. Il les a utilisés comme exposants , mais les a qualifiés de “nombres absurdes”.
Aussi récemment qu’au 18e siècle, il était courant d’ignorer tout résultat négatif renvoyé par des équations en supposant qu’elles n’avaient pas de sens.
Nombres rationnels
Il est probable que le concept de nombres fractionnaires remonte à la préhistoire . Les anciens Égyptiens utilisaient leur notation de fraction égyptienne pour les nombres rationnels dans des textes mathématiques tels que le papyrus mathématique Rhind et le papyrus Kahun . Les mathématiciens grecs et indiens classiques ont étudié la théorie des nombres rationnels, dans le cadre de l’étude générale de la théorie des nombres . [20] Le plus connu d’entre eux est les Éléments d’Euclide , datant d’environ 300 av. Parmi les textes indiens, le plus pertinent est le Sthananga Sutra , qui aborde également la théorie des nombres dans le cadre d’une étude générale des mathématiques.
Le concept de fractions décimales est étroitement lié à la notation décimale des valeurs de position ; les deux semblent s’être développés en tandem. Par exemple, il est courant que le sutra mathématique Jain inclue des calculs d’approximations de fraction décimale de pi ou de la racine carrée de 2 . [ citation nécessaire ] De même, les textes mathématiques babyloniens utilisaient des fractions sexagésimales (base 60) avec une grande fréquence.
Nombres irrationnels
La première utilisation connue des nombres irrationnels était dans les Sulba Sutras indiens composés entre 800 et 500 av. [21] [ meilleure source nécessaire ] Les premières preuves d’existence de nombres irrationnels sont généralement attribuées à Pythagore , plus précisément au pythagoricien Hippase de Métaponte , qui a produit une preuve (probablement géométrique) de l’irrationalité de la racine carrée de 2 . L’histoire raconte qu’Hippase a découvert des nombres irrationnels en essayant de représenter la racine carrée de 2 sous forme de fraction. Cependant, Pythagore croyait au caractère absolu des nombres et ne pouvait accepter l’existence de nombres irrationnels. Il ne pouvait pas réfuter leur existence par la logique, mais il ne pouvait pas accepter les nombres irrationnels, et ainsi, prétendument et fréquemment rapporté, il condamna Hippase à mort par noyade, pour empêcher la diffusion de cette nouvelle déconcertante. [22] [ meilleure source nécessaire ]
Le 16ème siècle a apporté l’acceptation européenne définitive des nombres entiers et fractionnaires négatifs . Au 17ème siècle, les mathématiciens utilisaient généralement des fractions décimales avec une notation moderne. Ce n’est cependant qu’au XIXe siècle que les mathématiciens ont séparé les irrationnels en parties algébriques et transcendantales, et ont à nouveau entrepris l’étude scientifique des irrationnels. Il était resté presque en sommeil depuis Euclide . En 1872, la publication des théories de Karl Weierstrass (par son élève E. Kossak), Eduard Heine , [23] Georg Cantor , [24] et Richard Dedekind [25] est provoquée. En 1869, Charles Méray avait pris le même point de départ que Heine, mais la théorie se réfère généralement à l’année 1872. La méthode de Weierstrass a été complètement exposée par Salvatore Pincherle (1880), et celle de Dedekind a reçu une importance supplémentaire à travers les travaux ultérieurs de l’auteur (1888) et approbation par Paul Tannery (1894). Weierstrass, Cantor et Heine fondent leurs théories sur les séries infinies, tandis que Dedekind fonde la sienne sur l’idée d’une coupure (Schnitt) dans le système des nombres réels , séparant tous les nombres rationnels en deux groupes ayant certaines propriétés caractéristiques. Le sujet a reçu des contributions ultérieures de la part de Weierstrass, Kronecker , [26]et Méray.
La recherche des racines des équations quintiques et de degré supérieur a été un développement important, le théorème d’Abel-Ruffini ( Ruffini 1799, Abel 1824) a montré qu’elles ne pouvaient pas être résolues par des radicaux (formules impliquant uniquement des opérations arithmétiques et des racines). Il était donc nécessaire de considérer l’ensemble plus large des nombres algébriques (toutes les solutions aux équations polynomiales). Galois (1832) a lié les équations polynomiales à la théorie des groupes donnant naissance au domaine de la théorie de Galois .
Les fractions continues , étroitement liées aux nombres irrationnels (et dues à Cataldi, 1613), ont attiré l’attention d’ Euler , [27] et à l’ouverture du XIXe siècle ont été mises en évidence par les écrits de Joseph Louis Lagrange . D’autres contributions notables ont été faites par Druckenmüller (1837), Kunze (1857), Lemke (1870) et Günther (1872). Ramus [28] a d’abord relié le sujet aux déterminants , résultant, avec les contributions ultérieures de Heine, [29] Möbius , et Günther, [30] dans la théorie de Kettenbruchdeterminanten .
Nombres et réels transcendantaux
L’existence des nombres transcendantaux [31] a été établie pour la première fois par Liouville (1844, 1851). Hermite a prouvé en 1873 que e est transcendant et Lindemann a prouvé en 1882 que π est transcendant. Enfin, Cantor a montré que l’ensemble de tous les nombres réels est infiniment indénombrable mais que l’ensemble de tous les nombres algébriques est infiniment dénombrable , il existe donc un nombre indénombrable infini de nombres transcendants.
Infini et infinitésimaux
La première conception connue de l’ infini mathématique apparaît dans le Yajur Veda , une ancienne écriture indienne, qui à un moment donné déclare: “Si vous supprimez une partie de l’infini ou ajoutez une partie à l’infini, ce qui reste est l’infini.” L’infini était un sujet d’étude philosophique populaire parmi les mathématiciens jaïns c. 400 av. Ils distinguaient cinq types d’infini : infini dans une et deux directions, infini en surface, infini partout et infini perpétuellement. Le symbole ∞ {displaystyle {text{∞}}} 
est souvent utilisé pour représenter une quantité infinie.
Aristote a défini la notion occidentale traditionnelle d’infini mathématique. Il a fait la distinction entre l’ infini réel et l’infini potentiel – le consensus général étant que seul ce dernier avait une vraie valeur. Galileo Galilei ‘s Two New Sciences a discuté de l’idée de correspondances biunivoques entre des ensembles infinis. Mais la prochaine avancée majeure dans la théorie a été faite par Georg Cantor ; en 1895, il publie un livre sur sa nouvelle théorie des ensembles , introduisant, entre autres, les nombres transfinis et formulant l’ hypothèse du continu .
Dans les années 1960, Abraham Robinson a montré comment les nombres infiniment grands et infinitésimaux peuvent être rigoureusement définis et utilisés pour développer le domaine de l’analyse non standard. Le système des nombres hyperréels représente une méthode rigoureuse de traitement des idées sur les nombres infinis et infinitésimaux qui avaient été utilisées avec désinvolture par les mathématiciens, les scientifiques et les ingénieurs depuis l’invention du calcul infinitésimal par Newton et Leibniz .
Une version géométrique moderne de l’infini est donnée par la géométrie projective , qui introduit des “points idéaux à l’infini”, un pour chaque direction spatiale. Chaque famille de droites parallèles dans une direction donnée est supposée converger vers le point idéal correspondant. Ceci est étroitement lié à l’idée de points de fuite dans le dessin en perspective .
Nombres complexes
La première référence fugace aux racines carrées des nombres négatifs s’est produite dans les travaux du mathématicien et inventeur Héron d’Alexandrie au 1er siècle après JC , lorsqu’il considérait le volume d’un tronc de pyramide impossible . Ils sont devenus plus importants lorsqu’au XVIe siècle, des formules fermées pour les racines des polynômes du troisième et du quatrième degré ont été découvertes par des mathématiciens italiens tels que Niccolò Fontana Tartaglia et Gerolamo Cardano . On s’est vite rendu compte que ces formules, même si l’on ne s’intéressait qu’aux solutions réelles, nécessitaient parfois la manipulation de racines carrées de nombres négatifs.
C’était doublement troublant car ils ne considéraient même pas que les nombres négatifs étaient sur un terrain solide à l’époque. Lorsque René Descartes a inventé le terme “imaginaire” pour ces quantités en 1637, il l’a voulu péjoratif. (Voir nombre imaginaire pour une discussion sur la “réalité” des nombres complexes.) Une autre source de confusion était que l’équation
( − 1 ) 2 = − 1 − 1 = − 1 {displaystyle left({sqrt {-1}}right)^{2}={sqrt {-1}}{sqrt {-1}}=-1} 
paraissait capricieusement incompatible avec l’identité algébrique
a b = a b , {displaystyle {sqrt {a}}{sqrt {b}}={sqrt {ab}},} 
qui est valable pour les nombres réels positifs a et b , et a également été utilisé dans les calculs de nombres complexes avec l’un parmi a , b positif et l’autre négatif. L’utilisation incorrecte de cette identité et de l’identité associée
1 a = 1 a {displaystyle {frac {1}{sqrt {a}}}={sqrt {frac {1}{a}}}} 
dans le cas où a et b sont négatifs, même embêté Euler . Cette difficulté l’a finalement conduit à la convention d’utiliser le symbole spécial i à la place de − 1 {displaystyle {sqrt {-1}}} 
pour se prémunir contre cette erreur.
Le XVIIIe siècle voit l’œuvre d’ Abraham de Moivre et de Leonhard Euler . La formule de De Moivre (1730) stipule :
( cos θ + i sin θ ) n = cos n θ + i sin n θ {displaystyle (cos theta +isin theta )^{n}=cos ntheta +isin ntheta } 
tandis que la formule d’ analyse complexe d’Euler (1748) nous donnait :
cos θ + i sin θ = e i θ . {displaystyle cos theta +isin theta =e^{itheta }.} 
L’existence des nombres complexes n’a été complètement acceptée que lorsque Caspar Wessel a décrit l’interprétation géométrique en 1799. Carl Friedrich Gauss l’a redécouvert et popularisé plusieurs années plus tard, et par conséquent la théorie des nombres complexes a reçu une expansion notable. L’idée de la représentation graphique des nombres complexes était pourtant apparue dès 1685, dans le De algebra tractatus de Wallis .
Toujours en 1799, Gauss a fourni la première preuve généralement acceptée du théorème fondamental de l’algèbre , montrant que chaque polynôme sur les nombres complexes a un ensemble complet de solutions dans ce domaine. L’acceptation générale de la théorie des nombres complexes est due aux travaux d’ Augustin Louis Cauchy et de Niels Henrik Abel , et surtout de ce dernier, qui fut le premier à utiliser hardiment les nombres complexes avec un succès bien connu. [ prose de paon ]
Gauss a étudié les nombres complexes de la forme a + bi , où a et b sont entiers ou rationnels (et i est l’une des deux racines de x 2 + 1 = 0 ). Son élève, Gotthold Eisenstein , a étudié le type a + bω , où ω est une racine complexe de x 3 − 1 = 0. D’autres classes de ce type (appelées champs cyclotomiques ) de nombres complexes dérivent des racines de l’unité x k − 1 = 0 pour des valeurs plus élevées de k. Cette généralisation est largement due à Ernst Kummer , qui a également inventé les nombres idéaux , qui ont été exprimés sous forme d’entités géométriques par Felix Klein en 1893.
En 1850 , Victor Alexandre Puiseux franchit l’étape clé de la distinction entre les pôles et les points de ramification, et introduit le concept de points singuliers essentiels . [ clarification nécessaire ] Cela a finalement conduit au concept de plan complexe étendu .
nombres premiers
Les nombres premiers ont été étudiés tout au long de l’histoire enregistrée. [ la citation nécessaire ] Euclid a consacré un livre des Éléments à la théorie de nombres premiers; il y prouva l’infinitude des nombres premiers et le théorème fondamental de l’arithmétique , et présenta l’ algorithme d’Euclide pour trouver le plus grand diviseur commun de deux nombres.
En 240 av. J.-C., Ératosthène utilisa le crible d’Ératosthène pour isoler rapidement les nombres premiers. Mais la plupart des développements ultérieurs de la théorie des nombres premiers en Europe remontent à la Renaissance et aux époques ultérieures. [ citation nécessaire ]
En 1796, Adrien-Marie Legendre conjecture le théorème des nombres premiers décrivant la distribution asymptotique des nombres premiers. D’autres résultats concernant la distribution des nombres premiers incluent la preuve d’Euler que la somme des réciproques des nombres premiers diverge, et la conjecture de Goldbach , qui prétend que tout nombre pair suffisamment grand est la somme de deux nombres premiers. Encore une autre conjecture liée à la distribution des nombres premiers est l’ hypothèse de Riemann , formulée par Bernhard Riemann en 1859. Le théorème des nombres premiers a finalement été prouvé par Jacques Hadamard et Charles de la Vallée-Poussinen 1896. Les conjectures de Goldbach et Riemann restent non prouvées et non réfutées.
Classement principal
|
Les nombres peuvent être classés en ensembles , appelés systèmes de numération , tels que les nombres naturels et les nombres réels . [32] Les principales catégories de nombres sont les suivantes :
N {displaystyle mathbb {N} }  |
Naturel | 0, 1, 2, 3, 4, 5, … ou 1, 2, 3, 4, 5, …
N 0 {displaystyle mathbb {N} _{0}} |
|---|---|---|
Z {displaystyle mathbb {Z} }  |
Entier | …, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, … |
Q {displaystyle mathbb {Q}}  |
Rationnel | un/boù a et b sont des entiers et b n’est pas 0 |
R {displaystyle mathbb {R} }  |
Réel | La limite d’une suite convergente de nombres rationnels |
C {displaystyle mathbb {C} }  |
Complexe | a + bi où a et b sont des nombres réels et i est une racine carrée formelle de −1 |
Il n’y a généralement aucun problème à identifier chaque système numérique avec un sous-ensemble approprié du suivant (par abus de notation ), car chacun de ces systèmes numériques est canoniquement isomorphe à un sous-ensemble approprié du suivant. [ citation nécessaire ] La hiérarchie résultante permet, par exemple, de parler, formellement correctement, de nombres réels qui sont des nombres rationnels, et s’exprime symboliquement en écrivant
N ⊂ Z ⊂ Q ⊂ R ⊂ C {displaystyle mathbb {N} subset mathbb {Z} subset mathbb {Q} subset mathbb {R} subset mathbb {C} } 
.
Nombres naturels

 Les nombres naturels, commençant par 1
Les nombres naturels, commençant par 1
Les nombres les plus connus sont les nombres naturels (parfois appelés nombres entiers ou nombres à compter) : 1, 2, 3, etc. Traditionnellement, la séquence des nombres naturels commençait par 1 (0 n’était même pas considéré comme un nombre pour les Grecs de l’Antiquité .) Cependant, au XIXe siècle, les théoriciens des ensembles et autres mathématiciens ont commencé à inclure 0 ( cardinalité de l’ ensemble vide , c’est-à-dire 0 éléments, où 0 est donc le plus petit nombre cardinal ) dans l’ensemble des nombres naturels. [33] [34] Aujourd’hui, différents mathématiciens utilisent le terme pour décrire les deux ensembles, y compris 0 ou non. Le symbole mathématique de l’ensemble de tous les nombres naturels estN , également écrit N {displaystyle mathbb {N} } 
, et parfois N 0 {displaystyle mathbb {N} _{0}}

ou alors N 1 {displaystyle mathbb {N} _{1}}

lorsqu’il est nécessaire d’indiquer si l’ensemble doit commencer par 0 ou 1, respectivement.
Dans le système de numération en base 10 , d’usage presque universel aujourd’hui pour les opérations mathématiques, les symboles des nombres naturels s’écrivent à l’aide de dix chiffres : 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9. La base ou base est le nombre de chiffres numériques uniques, y compris zéro, qu’un système numérique utilise pour représenter les nombres (pour le système décimal, la base est 10). Dans ce système de base 10, le chiffre le plus à droite d’un nombre naturel a une valeur de position de 1, et tous les autres chiffres ont une valeur de position dix fois celle de la valeur de position du chiffre à sa droite.
Dans la théorie des ensembles , qui est capable d’agir comme fondement axiomatique des mathématiques modernes, [35] les nombres naturels peuvent être représentés par des classes d’ensembles équivalents. Par exemple, le nombre 3 peut être représenté comme la classe de tous les ensembles qui ont exactement trois éléments. Alternativement, dans l’arithmétique de Peano , le nombre 3 est représenté par sss0, où s est la fonction “successeur” (c’est-à-dire que 3 est le troisième successeur de 0). De nombreuses représentations différentes sont possibles; tout ce qui est nécessaire pour représenter formellement 3 est d’inscrire trois fois un certain symbole ou un certain ensemble de symboles.
Entiers
Le négatif d’un entier positif est défini comme un nombre qui produit 0 lorsqu’il est ajouté à l’entier positif correspondant. Les nombres négatifs sont généralement écrits avec un signe négatif (un signe moins ). A titre d’exemple, le négatif de 7 s’écrit −7, et 7 + (−7) = 0 . Lorsque l’ ensemble des nombres négatifs est combiné avec l’ensemble des nombres naturels (y compris 0), le résultat est défini comme l’ensemble des nombres entiers , Z également écrit Z {displaystyle mathbb {Z} } 
. Ici, la lettre Z vient du “chiffre” allemand Zahl . L’ensemble des entiers forme un anneau avec les opérations addition et multiplication. [36]
Les nombres naturels forment un sous- ensemble des nombres entiers. Comme il n’y a pas de norme commune pour l’inclusion ou non de zéro dans les nombres naturels, les nombres naturels sans zéro sont communément appelés entiers positifs et les nombres naturels avec zéro sont appelés entiers non négatifs .
Nombres rationnels
Un nombre rationnel est un nombre qui peut être exprimé sous forme de fraction avec un numérateur entier et un dénominateur entier positif. Les dénominateurs négatifs sont autorisés, mais sont généralement évités, car chaque nombre rationnel est égal à une fraction avec un dénominateur positif. Les fractions sont écrites sous la forme de deux nombres entiers, le numérateur et le dénominateur, avec une barre de séparation entre eux. La fraction m/nreprésente m parties d’un tout divisé en n parties égales. Deux fractions différentes peuvent correspondre au même nombre rationnel ; par exemple 1/2et 2/4sont égaux, c’est-à-dire :
1 2 = 2 4 . {displaystyle {1 plus de 2}={2 plus de 4}.} 
En général,
a b = c d {displaystyle {a over b}={c over d}} 
si et seulement si a × d = c × b . {displaystyle {afois d}={cfois b}.}

Si la valeur absolue de m est supérieure à n (supposée positive), alors la valeur absolue de la fraction est supérieure à 1. Les fractions peuvent être supérieures, inférieures ou égales à 1 et peuvent également être positives, négatives, ou 0. L’ensemble de tous les nombres rationnels comprend les entiers puisque chaque entier peut être écrit comme une fraction avec le dénominateur 1. Par exemple −7 peut être écrit −7/1. Le symbole des nombres rationnels est Q (pour quotient ), également écrit Q {displaystyle mathbb {Q}} 
.
Nombres réels
Le symbole des nombres réels est R , également écrit comme R . {displaystyle mathbb{R} .} 
Ils comprennent tous les numéros de mesure. Chaque nombre réel correspond à un point sur la droite numérique . Le paragraphe suivant se concentrera principalement sur les nombres réels positifs. Le traitement des nombres réels négatifs est conforme aux règles générales de l’arithmétique et leur dénotation préfixe simplement le nombre positif correspondant par un signe moins , par exemple −123,456.
La plupart des nombres réels ne peuvent être approximés que par des chiffres décimaux , dans lesquels un point décimal est placé à droite du chiffre avec la valeur de position 1. Chaque chiffre à droite du point décimal a une valeur de position un dixième de la valeur de position de le chiffre à sa gauche. Par exemple, 123,456 représente 123456/1000, ou, en mots, cent, deux dizaines, trois unités, quatre dixièmes, cinq centièmes et six millièmes. Un nombre réel ne peut être exprimé par un nombre fini de chiffres décimaux que s’il est rationnel et que sa partie fractionnaire a un dénominateur dont les facteurs premiers sont 2 ou 5 ou les deux, car ce sont les facteurs premiers de 10, la base du système décimal . Ainsi, par exemple, un demi vaut 0,5, un cinquième vaut 0,2, un dixième vaut 0,1 et un cinquantième vaut 0,02. Représenter d’autres nombres réels sous forme de décimales nécessiterait une séquence infinie de chiffres à droite de la virgule décimale. Si cette séquence infinie de chiffres suit un modèle, elle peut être écrite avec des points de suspension ou une autre notation qui indique le modèle répétitif. Un tel nombre décimal est appelé un nombre décimal répétitif . Ainsi 1/3peut s’écrire 0,333…, avec des points de suspension pour indiquer que le motif continue. Les 3 répétés indéfiniment s’écrivent également sous la forme 0. 3 . [37]
Il s’avère que ces décimales répétitives (y compris la répétition de zéros ) dénotent exactement les nombres rationnels, c’est-à-dire que tous les nombres rationnels sont aussi des nombres réels, mais ce n’est pas le cas que chaque nombre réel est rationnel. Un nombre réel qui n’est pas rationnel est dit irrationnel . Un nombre réel irrationnel célèbre est le nombre π , le rapport de la circonférence de tout cercle à son diamètre . Lorsque pi s’écrit
π = 3.14159265358979 … , {displaystyle pi =3.14159265358979dots ,} 
comme c’est parfois le cas, les points de suspension ne signifient pas que les décimales se répètent (elles ne le font pas), mais plutôt qu’elles n’ont pas de fin. Il a été prouvé que π est irrationnel . Un autre nombre bien connu, avéré être un nombre réel irrationnel, est
2 = 1.41421356237 … , {displaystyle {sqrt {2}}=1.41421356237points,} 
la racine carrée de 2 , c’est-à-dire l’unique nombre réel positif dont le carré est 2. Ces deux nombres ont été approchés (par ordinateur) en trillions ( 1 trillion = 10 12 = 1 000 000 000 000 ) de chiffres.
Non seulement ces exemples importants, mais presque tous les nombres réels sont irrationnels et n’ont donc pas de motifs répétitifs et donc pas de nombre décimal correspondant. Ils ne peuvent être approchés que par des chiffres décimaux, désignant des nombres réels arrondis ou tronqués . Tout nombre arrondi ou tronqué est nécessairement un nombre rationnel, dont il n’y a qu’un nombre dénombrable . Toutes les mesures sont, de par leur nature, des approximations et ont toujours une marge d’erreur . Ainsi 123,456 est considéré comme une approximation de tout nombre réel supérieur ou égal à 1234555/10000et strictement inférieur à 1234565/10000(arrondi à 3 décimales), ou de tout nombre réel supérieur ou égal à 123456/1000et strictement inférieur à 123457/1000(troncature après la 3ème décimale). Les chiffres qui suggèrent une plus grande précision que la mesure elle-même doivent être supprimés. Les chiffres restants sont alors appelés chiffres significatifs . Par exemple, les mesures avec une règle peuvent rarement être effectuées sans une marge d’erreur d’au moins 0,001 m . Si les côtés d’un rectangle mesurent 1,23 m et 4,56 m, la multiplication donne une aire pour le rectangle entre 5,614591 m 2 et 5,603011 m 2 . Étant donné que même le deuxième chiffre après la virgule n’est pas conservé, les chiffres suivants ne sont pas significatifs . Par conséquent, le résultat est généralement arrondi à 5,61.
Tout comme la même fraction peut être écrite de plusieurs façons, le même nombre réel peut avoir plusieurs représentations décimales. Par exemple, 0,999…, 1.0, 1.00, 1.000, …, représentent tous le nombre naturel 1. Un nombre réel donné n’a que les représentations décimales suivantes : une approximation à un nombre fini de décimales, une approximation dans laquelle un modèle est établi qui continue pour un nombre illimité de décimales ou une valeur exacte avec seulement un nombre fini de décimales. Dans ce dernier cas, le dernier chiffre non nul peut être remplacé par le chiffre un plus petit suivi d’un nombre illimité de 9, ou le dernier chiffre non nul peut être suivi d’un nombre illimité de zéros. Ainsi, le nombre réel exact 3,74 peut aussi s’écrire 3,7399999999… et 3,74000000000…. De même, un nombre décimal avec un nombre illimité de 0 peut être réécrit en laissant tomber les 0 à droite de la décimale, et un nombre décimal avec un nombre illimité de 9′ s peut être réécrit en augmentant de un le chiffre -9 le plus à droite, en remplaçant tous les 9 à droite de ce chiffre par des 0. Enfin, une séquence illimitée de 0 à droite de la décimale peut être supprimée. Par exemple, 6,849999999999… = 6,85 et 6,850000000000… = 6,85. Enfin, si tous les chiffres d’un chiffre sont 0, le nombre est 0, et si tous les chiffres d’un chiffre sont une chaîne sans fin de 9, vous pouvez déposer les neuf à droite de la décimale et ajouter un à la chaîne de 9 à gauche de la décimale. Par exemple, 99,999… = 100. Enfin, si tous les chiffres d’un chiffre sont 0, le nombre est 0, et si tous les chiffres d’un chiffre sont une chaîne sans fin de 9, vous pouvez déposer les neuf à droite de la décimale et ajouter un à la chaîne de 9 à gauche de la décimale. Par exemple, 99,999… = 100. Enfin, si tous les chiffres d’un chiffre sont 0, le nombre est 0, et si tous les chiffres d’un chiffre sont une chaîne sans fin de 9, vous pouvez déposer les neuf à droite de la décimale et ajouter un à la chaîne de 9 à gauche de la décimale. Par exemple, 99,999… = 100.
Les nombres réels ont également une propriété importante mais hautement technique appelée propriété de borne supérieure .
On peut montrer que tout corps ordonné , qui est aussi complet , est isomorphe aux nombres réels. Les nombres réels ne sont cependant pas un champ algébriquement clos , car ils n’incluent pas de solution (souvent appelée racine carrée de moins un ) à l’équation algébrique x 2 + 1 = 0 {displaystyle x^{2}+1=0} 
.
Nombres complexes
Passant à un plus haut niveau d’abstraction, les nombres réels peuvent être étendus aux nombres complexes . Cet ensemble de nombres est né historiquement de la tentative de trouver des formules fermées pour les racines des polynômes cubiques et quadratiques . Cela a conduit à des expressions impliquant les racines carrées de nombres négatifs, et finalement à la définition d’un nouveau nombre : une racine carrée de −1, notée i , un symbole attribué par Leonhard Euler , et appelée l’ unité imaginaire . Les nombres complexes sont constitués de tous les nombres de la forme
a + b i {displaystyle,a+bi} 
où a et b sont des nombres réels. De ce fait, les nombres complexes correspondent à des points sur le plan complexe , un espace vectoriel à deux dimensions réelles . Dans l’expression a + bi , le nombre réel a est appelé la partie réelle et b est appelé la partie imaginaire . Si la partie réelle d’un nombre complexe est 0, alors le nombre est appelé nombre imaginaire ou est dit purement imaginaire ; si la partie imaginaire est 0, alors le nombre est un nombre réel. Ainsi les nombres réels sont un sous- ensembledes nombres complexes. Si les parties réelle et imaginaire d’un nombre complexe sont toutes deux des entiers, alors le nombre est appelé un entier gaussien . Le symbole des nombres complexes est C ou C {displaystyle mathbb {C} } 
.
Le théorème fondamental de l’algèbre affirme que les nombres complexes forment un corps algébriquement clos , ce qui signifie que tout polynôme à coefficients complexes a une racine dans les nombres complexes. Comme les réels, les nombres complexes forment un corps , qui est complet , mais contrairement aux nombres réels, il n’est pas ordonné . C’est-à-dire qu’il n’y a pas de sens cohérent pouvant être attribué à dire que i est supérieur à 1, ni de sens à dire que i est inférieur à 1. En termes techniques, les nombres complexes manquent d’un ordre total compatible avec les opérations sur le terrain .
Sous-classes des entiers
Nombres pairs et impairs
Un nombre pair est un entier “équidivisible” par deux, c’est-à-dire divisible par deux sans reste ; un nombre impair est un nombre entier qui n’est pas pair. (Le terme démodé “également divisible” est maintenant presque toujours abrégé en ” divisible “.) Tout nombre impair n peut être construit par la formule n = 2 k + 1, pour un entier approprié k . À partir de k = 0, les premiers nombres impairs non négatifs sont {1, 3, 5, 7, …}. Tout nombre pair m a la forme m = 2 k où k est à nouveau unentier . De même, les premiers nombres pairs non négatifs sont {0, 2, 4, 6, …}.
nombres premiers
Un nombre premier , souvent abrégé en prime , est un entier supérieur à 1 qui n’est pas le produit de deux entiers positifs plus petits. Les premiers nombres premiers sont 2, 3, 5, 7 et 11. Il n’existe pas de formule aussi simple que pour les nombres impairs et pairs pour générer les nombres premiers. Les nombres premiers ont été largement étudiés depuis plus de 2000 ans et ont conduit à de nombreuses questions, dont seules certaines ont trouvé une réponse. L’étude de ces questions relève de la théorie des nombres . La conjecture de Goldbach est un exemple d’une question encore sans réponse : “Tout nombre pair est-il la somme de deux nombres premiers ?”
Une réponse à la question de savoir si chaque entier supérieur à un est un produit de nombres premiers d’une seule manière, à l’exception d’un réarrangement des nombres premiers, a été confirmée; cette affirmation prouvée est appelée le théorème fondamental de l’arithmétique . Une preuve apparaît dans les Éléments d’Euclide .
Autres classes d’entiers
De nombreux sous-ensembles des nombres naturels ont fait l’objet d’études spécifiques et ont été nommés, souvent d’après le premier mathématicien qui les a étudiés. Des exemples de tels ensembles d’entiers sont les nombres de Fibonacci et les nombres parfaits . Pour plus d’exemples, consultez Séquence d’entiers .
Sous-classes des nombres complexes
Nombres algébriques, irrationnels et transcendantaux
Les nombres algébriques sont ceux qui sont solution d’une équation polynomiale à coefficients entiers. Les nombres réels qui ne sont pas des nombres rationnels sont appelés nombres irrationnels . Les nombres complexes qui ne sont pas algébriques sont appelés nombres transcendants . Les nombres algébriques qui sont des solutions d’une équation polynomiale unitaire à coefficients entiers sont appelés entiers algébriques .
Numéros constructibles
Motivés par les problèmes classiques de constructions à la règle et au compas , les nombres constructibles sont les nombres complexes dont les parties réelles et imaginaires peuvent être construites à la règle et au compas, à partir d’un segment donné d’unité de longueur, en un nombre fini d’étapes.
Nombres calculables
Un nombre calculable , également appelé nombre récursif , est un nombre réel tel qu’il existe un algorithme qui, étant donné un nombre positif n en entrée, produit les n premiers chiffres de la représentation décimale du nombre calculable. Des définitions équivalentes peuvent être données à l’aide de fonctions μ-récursives , de machines de Turing ou de λ-calcul . Les nombres calculables sont stables pour toutes les opérations arithmétiques usuelles, y compris le calcul des racines d’un polynôme , et forment ainsi un véritable corps fermé qui contient les nombres algébriques réels .
Les nombres calculables peuvent être considérés comme les nombres réels qui peuvent être exactement représentés dans un ordinateur : un nombre calculable est exactement représenté par ses premiers chiffres et un programme pour calculer les chiffres suivants. Cependant, les nombres calculables sont rarement utilisés dans la pratique. Une des raisons est qu’il n’y a pas d’algorithme pour tester l’égalité de deux nombres calculables. Plus précisément, il ne peut exister d’algorithme qui prenne en entrée n’importe quel nombre calculable, et décide dans tous les cas si ce nombre est égal à zéro ou non.
L’ensemble des nombres calculables a la même cardinalité que les nombres naturels. Par conséquent, presque tous les nombres réels ne sont pas calculables. Cependant, il est très difficile de produire explicitement un nombre réel qui ne soit pas calculable.
Extensions du concept
nombres p -adiques
Les nombres p -adiques peuvent avoir des développements infiniment longs à gauche de la virgule décimale, de la même manière que les nombres réels peuvent avoir des développements infiniment longs à droite. Le système numérique qui en résulte dépend de la base utilisée pour les chiffres : n’importe quelle base est possible, mais une base de nombres premiers fournit les meilleures propriétés mathématiques. L’ensemble des nombres p -adiques contient les nombres rationnels, mais n’est pas contenu dans les nombres complexes.
Les éléments d’un champ de fonction algébrique sur un corps fini et les nombres algébriques ont de nombreuses propriétés similaires (voir Analogie du champ de fonction ). Par conséquent, ils sont souvent considérés comme des nombres par les théoriciens des nombres. Les nombres p -adiques jouent un rôle important dans cette analogie.
Nombres hypercomplexes
Certains systèmes de nombres qui ne sont pas inclus dans les nombres complexes peuvent être construits à partir des nombres réels d’une manière qui généralise la construction des nombres complexes. Ils sont parfois appelés nombres hypercomplexes . Ils comprennent les quaternions H , introduits par Sir William Rowan Hamilton , dans lesquels la multiplication n’est pas commutative , les octonions , dans lesquels la multiplication n’est pas associative en plus de ne pas être commutative , et les sedenions , dans lesquels la multiplication n’est ni alternative , ni associative ni commutatif.
Nombres transfinis
Pour traiter des ensembles infinis , les nombres naturels ont été généralisés aux nombres ordinaux et aux nombres cardinaux . Le premier donne l’ordre de l’ensemble, tandis que le second donne sa taille. Pour les ensembles finis, les nombres ordinaux et cardinaux sont identifiés avec les nombres naturels. Dans le cas infini, plusieurs nombres ordinaux correspondent au même nombre cardinal.
Numéros non standard
Les nombres hyperréels sont utilisés dans les analyses non standard . Les hyperréels, ou réels non standard (généralement notés * R ), désignent un champ ordonné qui est une extension appropriée du champ ordonné de nombres réels R et satisfait le principe de transfert . Ce principe permet aux vraies déclarations du premier ordre sur R d’être réinterprétées comme de vraies déclarations du premier ordre sur * R .
Les nombres surréalistes et surréalistes étendent les nombres réels en ajoutant des nombres infiniment petits et des nombres infiniment grands, mais forment toujours des champs .
Voir également
-
![icon]()
![icon]() Portail des mathématiques
Portail des mathématiques
- Numéro concret
- Liste des numéros
- Liste des numéros dans différentes langues
- Liste des types de nombres
- Constante mathématique – Nombre fixe qui a reçu un nom
- Nombres complexes
- Cognition numérique
- Ordres de grandeur
- Constante physique – Quantité physique universelle et immuable
- Pi – Nombre, environ 3,14
- Notation positionnelle – Méthode de représentation ou d’encodage des nombres
- Nombre premier – Nombre dont le seul plus petit diviseur est 1
- Scalaire (mathématiques) – Éléments d’un champ, par exemple des nombres réels, dans le contexte de l’algèbre linéaire
- Subiter et compter
Remarques
- ^ “nombre, n.” ODE en ligne . Presse universitaire d’Oxford. Archivé de l’original le 2018-10-04 . Récupéré le 16/05/2017 .
- ^ “chiffre, adj. et n.” ODE en ligne . Presse universitaire d’Oxford.
- ↑ En linguistique , un chiffre peut faire référence à un symbole comme 5, mais aussi à un mot ou une phrase qui nomme un nombre, comme « cinq cents » ; les chiffres incluent également d’autres mots représentant des nombres, comme “douzaine”.
- ^ Matson, John. “L’Origine du Zéro” . Scientifique américain . Archivé de l’original le 2017-08-26 . Récupéré le 16/05/2017 .
- ^ un b Hodgkin, Luc (2005-06-02). Une histoire des mathématiques : de la Mésopotamie à la modernité . OUP Oxford. p. 85–88. ISBN 978-0-19-152383-0. Archivé de l’original le 2019-02-04 . Récupéré le 16/05/2017 .
- ^ Mathématiques à travers les cultures : l’histoire des mathématiques non-occidentales . Dordrecht : Kluwer Académique. 2000. pp. 410–411. ISBN 1-4020-0260-2.
- ^ Descartes, René (1954) [1637], La Géométrie | La Géométrie de René Descartes avec un fac-similé de la première édition , Dover Publications , ISBN 0-486-60068-8, récupéré le 20 avril 2011
- ^ un b Gilsdorf, Thomas E.Introduction aux mathématiques culturelles: avec des études de cas dans les Otomies et les Incas, John Wiley & Sons, 24 février 2012.
- ^ Restivo, S. Mathématiques dans la société et l’histoire , Springer Science & Business Media, 30 novembre 1992.
- ^ un minerai b , Oystein. La théorie des nombres et son histoire, Courier Dover Publications.
- ^ Gouvéa, Fernando Q. The Princeton Companion to Mathematics , Chapitre II.1, “Les origines des mathématiques modernes” , p. 82. Princeton University Press, 28 septembre 2008. ISBN 978-0-691-11880-2 . “Aujourd’hui, il n’est plus si facile de décider ce qui compte comme un ‘nombre’. Les objets de la séquence originale de “entier, rationnel, réel et complexe” sont certainement des nombres, mais les p -adiques le sont aussi. Les quaternions sont rarement appelés “nombres”, d’autre part, bien qu’ils puissent être utilisés coordonner certaines notions mathématiques.
- ^ Chrisomalis, Stephen (2003-09-01). “L’origine égyptienne des chiffres alphabétiques grecs”. Antiquité . 77 (297): 485–96. doi : 10.1017/S0003598X00092541 . ISSN 0003-598X .
- ^ un b Bulliet, Richard; Crossley, Pamela; Headrick, Daniel; Hirsch, Steven; Johnson, Lyman (2010). La Terre et ses peuples : Une histoire globale, Volume 1 . Cengage Apprentissage. p. 192. ISBN 978-1-4390-8474-8. Archivé de l’original le 2017-01-28 . Récupéré le 16/05/2017 . Les mathématiciens indiens ont inventé le concept de zéro et ont développé les chiffres “arabes” et le système de notation de la valeur de position utilisés dans la plupart des régions du monde aujourd’hui
- ^ Marshak, A., Les racines de la civilisation ; Cognitive Beginnings of Man’s First Art, Symbol and Notation , (Weidenfeld & Nicolson, Londres: 1972), 81ff.
- ^ “Papyrus mathématiques égyptiens – Mathématiciens de la diaspora africaine” . Math.buffalo.edu. Archivé de l’original le 2015-04-07 . Récupéré le 30/01/2012 .
- ^ “Historia Matematica Mailing List Archive: Re: [HM] The Zero Story: a question” . Sunsite.utk.edu. 1999-04-26. Archivé de l’original le 12/01/2012 . Récupéré le 30/01/2012 .
- ^ Sánchez, George I. (1961). Arithmétique en Maya . Austin, Texas : auto-publié.
- ^ Staszkow, Ronald; Robert Bradshaw (2004). La palette mathématique (3e éd.) . Brooks Cole. p. 41. ISBN 0-534-40365-4.
- ^ Smith, David Eugène (1958). Histoire des Mathématiques Modernes . Publications de Douvres. p. 259. ISBN 0-486-20429-4.
- ^ “Culture grecque classique (article)” . Académie Khan . Récupéré le 04/05/2022 .
- ^ Selin, Helaine , éd. (2000). Mathématiques à travers les cultures : l’histoire des mathématiques non occidentales . Éditeurs académiques Kluwer. p. 451.ISBN _ 0-7923-6481-3.
- ^ Bernard Frischer (1984). “Horace et les Monuments : Une Nouvelle Interprétation de l’ Ode d’Archytas “. Dans DR Shackleton Bailey (éd.). Études de Harvard en philologie classique . Presse universitaire de Harvard. p. 83. ISBN 0-674-37935-7.
- ^ Eduard Heine, “Die Elemente der Functionenlehre” , [Crelle’s] Journal für die reine und angewandte Mathematik , No 74 (1872): 172–188.
- ^ Georg Cantor, “Ueber unendliche, lineare Punktmannichfaltigkeiten”, pt. 5 , Mathematische Annalen , 21, 4 (1883‐12) : 545–591.
- ^ Richard Dedekind, Stetigkeit & irrationnel Zahlen (Braunschweig : Friedrich Vieweg & Sohn, 1872). Publié ultérieurement dans : ———, Gesammelte mathematische Werke , éd. Robert Fricke, Emmy Noether & Öystein Ore (Braunschweig : Friedrich Vieweg & Sohn, 1932), vol. 3, p. 315–334.
- ^ L. Kronecker, “Ueber den Zahlbegriff” , [Crelle’s] Journal für die reine und angewandte Mathematik , No 101 (1887): 337–355.
- ^ Leonhard Euler, “Conjectura circa naturam aeris, pro explicandis phaenomenis in atmosphaera observatis”, Acta Academiae Scientiarum Imperialis Petropolitanae , 1779, 1 (1779): 162–187.
- ^ Ramus, “Determinanternes Anvendelse til at bes temme Loven for de convergerende Bröker”, dans: Det Kongelige Danske Videnskabernes Selskabs naturvidenskabelige og mathematiske Afhandlinger (Kjoebenhavn: 1855), p. 106.
- ^ Eduard Heine, “Einige Eigenschaften der Lamé schen Funktionen” , [Crelle’s] Journal für die reine und angewandte Mathematik , No 56 (janvier 1859): 87–99 à 97.
- ^ Siegmund Günther, Darstellung der Näherungswerthe von Kettenbrüchen sous forme indépendante (Erlangen: Eduard Besold, 1873); ———, “Kettenbruchdeterminanten”, dans : Lehrbuch der Determinanten-Theorie : Für Studirende (Erlangen : Eduard Besold, 1875), c. 6, p. 156–186.
- ^ Bogomolny, A. “Qu’est-ce qu’un nombre?” . Mathématiques interactives Divers et Puzzles . Archivé de l’original le 23 septembre 2010 . Récupéré le 11 juillet 2010 .
- ^ “Eine Menge, ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens – welche Elemente der Menge genannt werden – zu einem Ganzen.” [https://web.archive.org/web/20110610133240/http://brinkmann-du.de/mathe/fos/fos01_03.htm Archivé le 10/06/2011 à la Wayback Machine [1]]
- ^ Weisstein, Eric W. “Nombre naturel” . MathWorld .
- ^ “nombre naturel” , Merriam-Webster.com , Merriam-Webster , archivé de l’original le 13 décembre 2019 , récupéré le 4 octobre 2014
- ^ Suppes, Patrick (1972). Théorie axiomatique des ensembles . Courrier Douvres Publications. p. 1 . ISBN 0-486-61630-4.
- ^ Weisstein, Eric W. “Entier” . MathWorld .
- ^ Weisstein, Eric W. “Répéter la décimale” . mathworld.wolfram.com . Récupéré le 23/07/2020 .
Références
- Tobias Dantzig , Le nombre, le langage de la science ; une étude critique écrite pour le non-mathématicien cultivé , New York, The Macmillan Company, 1930. [ ISBN manquant ]
- Erich Friedman, Quelle est la particularité de ce numéro ?
- Steven Galovich, Introduction aux structures mathématiques , Harcourt Brace Javanovich, 1989, ISBN 0-15-543468-3 .
- Paul Halmos , Théorie naïve des ensembles , Springer, 1974, ISBN 0-387-90092-6 .
- Morris Kline , La pensée mathématique des temps anciens aux temps modernes , Oxford University Press, 1990. ISBN 978-0195061352
- Alfred North Whitehead et Bertrand Russell , Principia Mathematica à *56, Cambridge University Press, 1910. [ ISBN manquant ]
- Leo Cory, Une brève histoire des nombres , Oxford University Press, 2015, ISBN 978-0-19-870259-7 .
Liens externes
| Wikimedia Commons a des médias liés aux nombres . |
| Wikiquote a des citations liées au nombre . |
| Recherchez un numéro dans Wiktionary, le dictionnaire gratuit. |
| Wikiversité a des ressources d’apprentissage sur les mathématiques primaires : les nombres |
- Nechaev, VI (2001) [1994], “Nombre” , Encyclopédie des mathématiques , EMS Press
- Talant, Jonathan. “Est-ce que les nombres existent?” . Numérophile . Brady Haran . Archivé de l’original le 2016-03-08 . Récupéré le 06/04/2013 .
- BBC Radio 4, À notre époque : nombres négatifs
- ‘4000 Years of Numbers’ , conférence de Robin Wilson, 07/11/07, Gresham College (disponible en téléchargement en MP3 ou MP4, et en fichier texte).
- Krulwich, Robert (2011-06-22). “Quel est le numéro préféré du monde ?” . NPR . Récupéré le 17/09/2011 .; “Câliner avec 9, bécoter avec 8, faire un clin d’œil à 7” . NPR . 2011-08-11 . Récupéré le 17/09/2011 .
- Encyclopédie en ligne des séquences d’entiers





