Le numéro de Reynold

Le nombre de Reynolds ( Re ) permet de prédire les schémas d’écoulement dans différentes situations d’écoulement de fluide. À de faibles nombres de Reynolds, les écoulements ont tendance à être dominés par un écoulement laminaire (en forme de feuille) , tandis qu’à des nombres de Reynolds élevés, les écoulements ont tendance à être turbulents . La turbulence résulte de différences de vitesse et de direction du fluide, qui peuvent parfois se croiser ou même aller à l’encontre de la direction générale de l’écoulement ( courants de Foucault ). Ces courants de Foucault commencent à brasser le flux, consommant de l’énergie dans le processus, ce qui, pour les liquides, augmente les risques de cavitation . Les nombres de Reynolds sont une grandeur sans dimension importante en mécanique des fluides .

Le panache de cette flamme de bougie passe de laminaire à turbulent. Le nombre de Reynolds peut être utilisé pour prédire où cette transition aura lieu. Écoulement turbulent et laminaire de l’eau du robinet Une rue tourbillonnaire autour d’un cylindre. Cela peut se produire autour des cylindres et des sphères, pour n’importe quel fluide, taille de cylindre et vitesse de fluide, à condition qu’il ait un nombre de Reynolds compris entre environ 40 et 1000. ^[1] George Stokes a introduit les nombres de Reynolds. Osborne Reynolds a popularisé le concept.

Le nombre de Reynolds a de nombreuses applications, allant de l’écoulement de liquide dans un tuyau au passage de l’air au-dessus d’une aile d’avion. Il est utilisé pour prédire la transition d’ un écoulement laminaire à un Écoulement turbulent , et est utilisé dans la mise à l’échelle de situations d’écoulement similaires mais de tailles différentes, comme entre un modèle d’avion dans une soufflerie et la version grandeur nature. Les prédictions de l’apparition de la turbulence et la capacité de calculer les effets d’échelle peuvent être utilisées pour aider à prédire le comportement des fluides à plus grande échelle, comme dans le mouvement local ou global de l’air ou de l’eau et ainsi les effets météorologiques et climatologiques associés.

Le concept a été introduit par George Stokes en 1851, ^[2] mais le nombre de Reynolds a été nommé par Arnold Sommerfeld en 1908 ^[3] d’après Osborne Reynolds (1842–1912), qui a popularisé son utilisation en 1883. ^{[4] [5]}

Définition

Le nombre de Reynolds est le rapport des forces d’ inertie aux forces visqueuses dans un fluide qui est soumis à un mouvement interne relatif dû à différentes vitesses de fluide. Une région où ces forces changent de comportement est connue sous le nom de couche limite , telle que la surface de délimitation à l’intérieur d’un tuyau. Un effet similaire est créé par l’introduction d’un flux de fluide à grande vitesse dans un fluide à faible vitesse, tel que les gaz chauds émis par une flamme dans l’air. Ce mouvement relatif génère des frottements fluides, facteur de développement des écoulements turbulents. Contrecarrer cet effet est la viscositédu fluide, ce qui tend à inhiber les turbulences. Le nombre de Reynolds quantifie l’importance relative de ces deux types de forces pour des conditions d’écoulement données et indique quand un Écoulement turbulent se produira dans une situation particulière. ^[6]

Cette capacité à prédire le début d’un Écoulement turbulent est un outil de conception important pour des équipements tels que des systèmes de tuyauterie ou des ailes d’avion, mais le nombre de Reynolds est également utilisé dans la mise à l’échelle des problèmes de dynamique des fluides et est utilisé pour déterminer la Similitude dynamique entre deux cas différents de flux de fluide, comme entre un modèle réduit d’avion et sa version grandeur nature. Une telle mise à l’échelle n’est pas linéaire et l’application des nombres de Reynolds aux deux situations permet de développer des facteurs de mise à l’échelle.

En ce qui concerne les régimes d’écoulement laminaire et turbulent :

l’écoulement laminaire se produit à de faibles nombres de Reynolds, où les forces visqueuses sont dominantes, et se caractérise par un mouvement fluide constant et régulier ;
un Écoulement turbulent se produit à des nombres de Reynolds élevés et est dominé par des forces d’inertie, qui ont tendance à produire des tourbillons chaotiques , des tourbillons et d’autres instabilités d’écoulement. ^[7]

Le nombre de Reynolds est défini comme ^[3]

R e = u L ν = ρ u L μ {displaystyle mathrm {Re} ={frac {uL}{nu }}={frac {rho uL}{mu }}} ${displaystyle mathrm {Re} ={frac {uL}{nu }}={frac {rho uL}{mu }}}$ ${displaystyle mathrm {Re} ={frac {uL}{nu }}={frac {rho uL}{mu }}}$

où:

ρ est la masse volumique du fluide ( Unités SI : kg/m³ )
u est la Vitesse d’écoulement (m/s)
L est une dimension linéaire caractéristique (m) (voir les sections ci-dessous de cet article pour des exemples)
μ est la Viscosité dynamique du fluide (Pa·s ou N·s/m² ou kg/(m·s))
ν est la Viscosité cinématique du fluide (m² /s).

L’équation de Brezina

Le nombre de Reynolds peut être défini pour plusieurs situations différentes où un fluide est en mouvement relatif par rapport à une surface. ^{[n 1]} Ces définitions incluent généralement les propriétés du fluide de densité et de viscosité, plus une vitesse et une longueur caractéristique ou une dimension caractéristique (L dans l’équation ci-dessus). Cette dimension est une question de convention – par exemple, le rayon et le diamètre sont également valables pour décrire des sphères ou des cercles, mais l’un est choisi par convention. Pour les avions ou les navires, la longueur ou la largeur peut être utilisée. Pour un écoulement dans un tuyau, ou pour une sphère se déplaçant dans un fluide, le diamètre intérieur est généralement utilisé aujourd’hui. D’autres formes telles que des tuyaux rectangulaires ou des objets non sphériques ont un diamètre équivalentdéfini. Pour les fluides de densité variable comme les gaz compressibles ou les fluides de viscosité variable comme les fluides non newtoniens , des règles particulières s’appliquent. La vitesse peut également être une question de convention dans certaines circonstances, notamment les cuves agitées.

En pratique, l’appariement du nombre de Reynolds n’est pas suffisant à lui seul pour garantir la similitude. L’écoulement des fluides est généralement chaotique, et de très petits changements de forme et de rugosité de surface des surfaces de délimitation peuvent entraîner des écoulements très différents. Néanmoins, les nombres de Reynolds sont un guide très important et sont largement utilisés.

Histoire

L’appareil d’Osborne Reynolds de 1883 démontrant le début d’un Écoulement turbulent. L’appareil est toujours à l’Université de Manchester. Schéma de l’article de Reynolds de 1883 montrant le début d’un Écoulement turbulent.

Osborne Reynolds a étudié les conditions dans lesquelles l’écoulement de fluide dans les tuyaux est passé d’ un écoulement laminaire à un Écoulement turbulent . Dans son article de 1883, Reynolds a décrit la transition d’un écoulement laminaire à un Écoulement turbulent dans une expérience classique dans laquelle il a examiné le comportement de l’écoulement de l’eau sous différentes vitesses d’écoulement en utilisant un petit courant d’eau colorée introduit au centre de l’écoulement d’eau claire dans un tuyau plus grand.

Le plus gros tuyau était en verre, de sorte que le comportement de la couche du flux teinté pouvait être observé. À l’extrémité de ce tuyau, il y avait une vanne de contrôle de débit utilisée pour faire varier la vitesse de l’eau à l’intérieur du tube. Lorsque la vitesse était faible, la couche colorée restait distincte sur toute la longueur du grand tube. Lorsque la vitesse a été augmentée, la couche s’est brisée en un point donné et s’est diffusée dans toute la section transversale du fluide. Le point auquel cela s’est produit était le point de transition de l’écoulement laminaire à l’Écoulement turbulent.

De ces expériences est venu le nombre de Reynolds sans dimension pour la similarité dynamique – le rapport des forces d’ inertie aux forces visqueuses . Reynolds a également proposé ce que l’on appelle maintenant la moyenne de Reynolds des écoulements turbulents, où des quantités telles que la vitesse sont exprimées comme la somme des composantes moyennes et fluctuantes. Une telle moyenne permet une description «en vrac» de l’Écoulement turbulent, par exemple en utilisant les équations de Navier – Stokes moyennées de Reynolds .

Écoulement dans un tuyau

Pour un écoulement dans un tuyau ou un tube, le nombre de Reynolds est généralement défini comme ^[8]

R e = u D H ν = ρ u D H μ = ρ Q D H μ A = W D H μ A , {displaystyle mathrm {Re} ={frac {uD_{text{H}}}{nu }}={frac {rho uD_{text{H}}}{mu }}={ frac {rho QD_{text{H}}}{mu A}}={frac {WD_{text{H}}}{mu A}},} ${displaystyle mathrm {Re} ={frac {uD_{text{H}}}{nu }}={frac {rho uD_{text{H}}}{mu }}={frac {rho QD_{text{H}}}{mu A}}={frac {WD_{text{H}}}{mu A}},}$ ${displaystyle mathrm {Re} ={frac {uD_{text{H}}}{nu }}={frac {rho uD_{text{H}}}{mu }}={ frac {rho QD_{text{H}}}{mu A}}={frac {WD_{text{H}}}{mu A}},}$

où

D _H est le diamètre hydraulique de la conduite (le diamètre intérieur si la conduite est circulaire) (m),
Q est le débit volumétrique(m³ /s),
A est l’aire de la section transversale du tuyau( A =πD ²/4) (m ² ),
u est la vitesse moyenne du fluide (m/s),
μ (mu) est la Viscosité dynamique du fluide (Pa·s = N·s/m² = kg/(m·s)),
ν (nu) est la Viscosité cinématique ( ν = μ/ρ) (m ² /s),
ρ (rho) est la masse volumique du fluide (kg/m³ ),
W est le débit massique du fluide (kg/s).

Pour des formes telles que des conduits carrés, rectangulaires ou annulaires où la hauteur et la largeur sont comparables, la dimension caractéristique pour les situations d’écoulement interne est considérée comme étant le diamètre hydraulique , D _H , défini comme

D H = 4 A P , {displaystyle D_{text{H}}={frac {4A}{P}},} ${displaystyle D_{text{H}}={frac {4A}{P}},}$ ${displaystyle D_{text{H}}={frac {4A}{P}},}$

où A est l’aire de la section transversale et P est le périmètre mouillé . Le périmètre mouillé d’un canal est le périmètre total de toutes les parois du canal qui sont en contact avec l’écoulement. ^[9] Cela signifie que la longueur du canal exposé à l’air n’est pas incluse dans le périmètre mouillé.

Pour un tuyau circulaire, le diamètre hydraulique est exactement égal au diamètre intérieur du tuyau :

D H = D . {displaystyle D_{text{H}}=D.} ${displaystyle D_{text{H}}=D.}$ ${displaystyle D_{text{H}}=D.}$

Pour un conduit annulaire, tel que le canal extérieur d’un échangeur de chaleur tube dans tube , le diamètre hydraulique peut être représenté algébriquement pour se réduire à

D H,annulus = D o − D i , {displaystyle D_{text{H,annulus}}=D_{text{o}}-D_{text{i}},} ${displaystyle D_{text{H,annulus}}=D_{text{o}}-D_{text{i}},}$ ${displaystyle D_{text{H,annulus}}=D_{text{o}}-D_{text{i}},}$

où

D _o est le diamètre extérieur du tuyau extérieur,
D _i est le diamètre intérieur du tuyau intérieur.

Pour le calcul impliquant un écoulement dans des conduits non circulaires, le diamètre hydraulique peut être remplacé par le diamètre d’un conduit circulaire, avec une précision raisonnable, si le rapport d’aspect AR de la section du conduit reste dans la plage 1/4< AR < 4. ^[10]

Transition laminaire-turbulente

Dans un écoulement de couche limite sur une plaque plane, les expériences confirment qu’après une certaine longueur d’écoulement, une couche limite laminaire deviendra instable et turbulente. Cette instabilité se produit à différentes échelles et avec différents fluides, généralement lorsque Re _x ≈5 × 10 ⁵ , ^[11] où x est la distance depuis le bord d’attaque de la plaque plate, et la Vitesse d’écoulement est la vitesse libre du fluide à l’extérieur de la couche limite.

Pour un écoulement dans une conduite de diamètre D , les observations expérimentales montrent que pour un écoulement “pleinement développé”, ^{[n 2]} un écoulement laminaire se produit lorsque Re _D < 2300 et un Écoulement turbulent se produit lorsque Re _D > 2900. ^{[12] [13]}A l’extrémité inférieure de cette plage, un Écoulement turbulent continu se formera, mais seulement à une très grande distance de l’entrée du tuyau. Le flux intermédiaire commencera à passer de laminaire à turbulent, puis de nouveau à laminaire à intervalles irréguliers, appelé flux intermittent. Cela est dû aux différentes vitesses et conditions du fluide dans différentes zones de la section transversale du tuyau, en fonction d’autres facteurs tels que la rugosité du tuyau et l’uniformité du débit. L’écoulement laminaire a tendance à dominer dans le centre à déplacement rapide du tuyau, tandis que l’Écoulement turbulent à déplacement plus lent domine près de la paroi. À mesure que le nombre de Reynolds augmente, l’Écoulement turbulent continu se rapproche de l’entrée et l’intermittence entre les augmentations, jusqu’à ce que l’écoulement devienne complètement turbulent à Re _D > 2900. ^[12]Ce résultat est généralisé aux canaux non circulaires en utilisant le diamètre hydraulique , permettant de calculer un nombre de Reynolds de transition pour d’autres formes de canal. ^[12]

Ces nombres de Reynolds de transition sont également appelés nombres de Reynolds critiques et ont été étudiés par Osborne Reynolds vers 1895. ^[5] Le nombre de Reynolds critique est différent pour chaque géométrie. ^[14]

Écoulement dans un conduit large

Pour un fluide se déplaçant entre deux surfaces parallèles planes – où la largeur est bien supérieure à l’espace entre les plaques – alors la dimension caractéristique est égale à la distance entre les plaques. ^[15] Ceci est cohérent avec les cas de conduit annulaire et de conduit rectangulaire ci-dessus pris à un rapport d’aspect limite.

Écoulement dans un canal ouvert

Pour un écoulement de liquide à surface libre, le Rayon hydraulique doit être déterminé. Il s’agit de la section transversale du canal divisée par le périmètre mouillé. Pour un canal semi-circulaire, il s’agit du quart du diamètre (en cas d’écoulement complet de la conduite). Pour un canal rectangulaire, le Rayon hydraulique est la surface de la section transversale divisée par le périmètre mouillé. Certains textes utilisent alors une dimension caractéristique égale à quatre fois le Rayon hydraulique, choisie parce qu’elle donne la même valeur de Re pour l’apparition de la turbulence qu’en écoulement en conduite ^[16] , tandis que d’autres utilisent le Rayon hydraulique comme échelle de longueur caractéristique avec par conséquent différentes valeurs de Re pour la transition et l’Écoulement turbulent.

Écoulement autour des profils aérodynamiques

Les nombres de Reynolds sont utilisés dans la conception des profils aérodynamiques pour (entre autres) gérer “l’effet d’échelle” lors du calcul/de la comparaison des caractéristiques (une petite aile, dimensionnée pour être énorme, fonctionnera différemment). ^[17] Les dynamiques des fluides définissent le nombre de Reynolds d’accord R comme ceci : R = Vc/v, où V est la vitesse de vol, c est la longueur de la corde et ν est la Viscosité cinématique du fluide dans lequel le profil aérodynamique fonctionne, qui est1,460 × 10 ⁻⁵ m ² /s pour l’atmosphère au niveau de la mer . ^[18] Dans certaines études spéciales, une longueur caractéristique autre que la corde peut être utilisée; rare est le “nombre de Reynolds d’envergure”, qui ne doit pas être confondu avec les stations d’envergure sur une aile, où l’accord est toujours utilisé. ^[19]

Objet dans un fluide

La viscosité élevée du miel se traduit par un écoulement parfaitement laminaire lorsqu’il est versé à partir d’un seau, tandis que la faible tension superficielle lui permet de rester en forme de feuille même après avoir atteint le fluide en dessous. Analogue à la turbulence, lorsque le flux rencontre une résistance, il ralentit et commence à osciller d’avant en arrière, s’empilant sur lui-même.

Le nombre de Reynolds d’un objet en mouvement dans un fluide, appelé nombre de Reynolds particulaire et souvent noté Re _p , caractérise la nature de l’écoulement environnant et sa vitesse de chute.

Dans les fluides Visqueux

Apprendre encore plus Cette section ne cite aucune source . ( février 2014 ) Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (Learn how and when to remove this template message)

Ecoulement rampant au-delà d’une sphère en chute : lignes de courant , force de traînée F _d et force de gravité F _g .

Lorsque la viscosité est naturellement élevée, comme dans le cas des solutions polymères et des polymères fondus, l’écoulement est normalement laminaire. Le nombre de Reynolds est très petit et la loi de Stokes peut être utilisée pour mesurer la viscosité du fluide. Les sphères peuvent tomber à travers le fluide et elles atteignent rapidement la vitesse terminale , à partir de laquelle la viscosité peut être déterminée.

Le flux laminaire des solutions de polymères est exploité par des animaux tels que les poissons et les dauphins, qui exsudent des solutions visqueuses de leur peau pour faciliter l’écoulement sur leur corps tout en nageant. Il a été utilisé dans les courses de yachts par des propriétaires qui souhaitent obtenir un avantage de vitesse en pompant une solution polymère telle que du Polyoxyéthylène de faible poids moléculaire dans l’eau, sur la surface mouillée de la coque.

C’est cependant un problème pour le mélange des polymères, car la turbulence est nécessaire pour répartir la charge fine (par exemple) à travers le matériau. Des inventions telles que le “mélangeur à transfert à cavité” ont été développées pour produire de multiples plis dans une masse fondue en mouvement afin d’améliorer l’ efficacité du mélange . Le dispositif peut être monté sur des extrudeuses pour faciliter le mélange.

Sphère dans un fluide

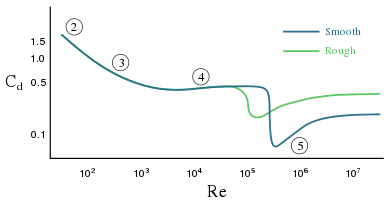
Coefficient de traînée C _d pour une sphère en fonction du nombre de Reynolds Re , obtenu à partir d’expériences en laboratoire. La ligne sombre est pour une sphère avec une surface lisse, tandis que la ligne plus claire est pour le cas d’une surface rugueuse (par exemple avec de petites fossettes). Il existe une gamme de vitesses de fluide où une balle de golf à surface rugueuse subit moins de traînée qu’une balle lisse. Les nombres le long de la ligne indiquent plusieurs régimes d’écoulement et les changements associés du coefficient de traînée :

écoulement attaché ( écoulement de Stokes ) et écoulement séparé stable ,
écoulement instationnaire séparé, présentant une couche limite d’ écoulement laminaire en amont de la séparation, et produisant une rue tourbillonnaire ,
écoulement instationnaire séparé avec une couche limite laminaire en amont, avant la séparation de l’écoulement, avec en aval de la sphère un sillage turbulent chaotique ,
écoulement séparé post-critique, avec une couche limite turbulente.

Pour une sphère dans un fluide, l’échelle de longueur caractéristique est le diamètre de la sphère et la vitesse caractéristique est celle de la sphère par rapport au fluide à une certaine distance de la sphère, de sorte que le mouvement de la sphère ne perturbe pas cette référence colis de fluide. La densité et la viscosité sont celles propres au fluide. ^[20] Notez que l’écoulement purement laminaire n’existe que jusqu’à Re = 10 selon cette définition.

Sous la condition de faible Re , la relation entre la force et la vitesse du mouvement est donnée par la loi de Stokes . ^[21]

À des nombres de Reynolds plus élevés, la traînée sur une sphère dépend de la rugosité de la surface. Ainsi, par exemple, l’ajout de fossettes sur la surface d’une balle de golf amène la couche limite sur le côté amont de la balle à passer de laminaire à turbulente. La couche limite turbulente est capable de rester attachée à la surface de la balle beaucoup plus longtemps qu’une limite laminaire et crée ainsi un sillage basse pression plus étroit et donc moins de traînée de pression. La réduction de la traînée de pression fait que la balle se déplace plus loin. ^[22]

Objet rectangulaire dans un fluide

L’équation d’un objet rectangulaire est identique à celle d’une sphère, l’objet étant approché comme un ellipsoïde et l’axe de longueur étant choisi comme échelle de longueur caractéristique. De telles considérations sont importantes dans les cours d’eau naturels, par exemple, où il y a peu de grains parfaitement sphériques. Pour les grains dans lesquels la mesure de chaque axe n’est pas pratique, les diamètres de tamis sont utilisés à la place comme échelle de longueur caractéristique des particules. Les deux approximations modifient les valeurs du nombre critique de Reynolds.

Vitesse de chute

Le nombre de Reynolds des particules est important pour déterminer la vitesse de chute d’une particule. Lorsque le nombre de Reynolds des particules indique un écoulement laminaire, la loi de Stokes peut être utilisée pour calculer sa vitesse de chute. Lorsque le nombre de Reynolds des particules indique un Écoulement turbulent, une loi de traînée turbulente doit être construite pour modéliser la vitesse de sédimentation appropriée.

Lit emballé

Pour un écoulement de fluide à travers un lit, de particules approximativement sphériques de diamètre D en contact, si le vide est ε et la vitesse superficielle est v _s , le nombre de Reynolds peut être défini comme ^[23]

Learn more.

Nombre irrationnel

Jul 10, 2022

Décimal

Jul 10, 2022

Exponentation

Jul 8, 2022

Numéro

Jul 8, 2022

R e = ρ v s D μ , {displaystyle mathrm {Re} ={frac {rho v_{text{s}}D}{mu }},} ${displaystyle mathrm {Re} ={frac {rho v_{text{s}}D}{mu }},}$ ${displaystyle mathrm {Re} ={frac {rho v_{text{s}}D}{mu }},}$

ou alors

R e = ρ v s D μ ε , {displaystyle mathrm {Re} ={frac {rho v_{text{s}}D}{mu varepsilon }},} ${displaystyle mathrm {Re} ={frac {rho v_{text{s}}D}{mu varepsilon }},}$ ${displaystyle mathrm {Re} ={frac {rho v_{text{s}}D}{mu varepsilon }},}$

ou alors

R e = ρ v s D μ ( 1 − ε ) . {displaystyle mathrm {Re} ={frac {rho v_{text{s}}D}{mu (1-varepsilon )}}.} ${displaystyle mathrm {Re} ={frac {rho v_{text{s}}D}{mu (1-varepsilon )}}.}$ ${displaystyle mathrm {Re} ={frac {rho v_{text{s}}D}{mu (1-varepsilon )}}.}$

Le choix de l’équation dépend du système impliqué : la première réussit à corréler les données pour différents types de lits tassés et fluidisés , la deuxième nombre de Reynolds convient aux données en phase liquide, tandis que la troisième réussit à corréler le lit fluidisé. données, introduites pour la première fois pour le système à lit fluidisé liquide. ^[23]

Les conditions laminaires s’appliquent jusqu’à Re = 10, entièrement turbulentes à partir de Re = 2000. ^[20]

Récipient agité

Dans une cuve cylindrique agitée par une pale rotative centrale, turbine ou hélice, la dimension caractéristique est le diamètre de l’agitateur D . La vitesse V est ND où N est la vitesse de rotation en rad par seconde. Alors le nombre de Reynolds est :

R e = ρ N D 2 μ = ρ V D μ . {displaystyle mathrm {Re} ={frac {rho ND^{2}}{mu }}={frac {rho VD}{mu }}.} ${displaystyle mathrm {Re} ={frac {rho ND^{2}}{mu }}={frac {rho VD}{mu }}.}$ ${displaystyle mathrm {Re} ={frac {rho ND^{2}}{mu }}={frac {rho VD}{mu }}.}$

Le système est entièrement turbulent pour des valeurs de Re supérieures à10 000 . ^[24]

Frottement du tuyau

Le diagramme de Moody , qui décrit le facteur de frottement Darcy – Weisbach f en fonction du nombre de Reynolds et de la rugosité relative du tuyau.

Les chutes de pression ^[25] observées pour un écoulement de fluides pleinement développé dans les conduites peuvent être prédites à l’aide du diagramme de Moody qui trace le facteur de frottement de Darcy – Weisbach f par rapport au nombre de Reynolds Re et à la rugosité relative ε/ré. Le diagramme montre clairement les régimes d’écoulement laminaire, de transition et turbulent à mesure que le nombre de Reynolds augmente. La nature de l’écoulement du tuyau dépend fortement du fait que l’écoulement soit laminaire ou turbulent.

Similitude des flux

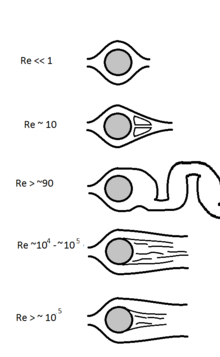
Les comportements qualitatifs de l’écoulement de fluide sur un cylindre dépendent dans une large mesure du nombre de Reynolds ; des modèles d’écoulement similaires apparaissent souvent lorsque la forme et le nombre de Reynolds correspondent, bien que d’autres paramètres comme la rugosité de surface aient un effet important.

Pour que deux écoulements soient similaires, ils doivent avoir la même géométrie et des nombres de Reynolds et d’Euler égaux . Lors de la comparaison du comportement des fluides aux points correspondants d’un modèle et d’un écoulement à grande échelle, les éléments suivants sont valables :

R e m = R e , E u m = E u , {displaystyle {begin{aligned}mathrm {Re} _{text{m}}&=mathrm {Re} ,\mathrm {Eu} _{text{m}}&=mathrm { Eu} ,end{aligné}}} ${displaystyle {begin{aligned}mathrm {Re} _{text{m}}&=mathrm {Re} ,\mathrm {Eu} _{text{m}}&=mathrm {Eu} ,end{aligned}}}$ ${displaystyle {begin{aligned}mathrm {Re} _{text{m}}&=mathrm {Re} ,\mathrm {Eu} _{text{m}}&=mathrm {Eu} ,end{aligned}}}$

où R e m {displaystyle mathrm {Re} _{text{m}}} ${displaystyle mathrm {Re} _{text{m}}}$ ${displaystyle mathrm {Re} _{text{m}}}$ est le nombre de Reynolds du modèle, et R e {displaystyle mathrm {Re} } {mathrm {Re}} est le nombre de Reynolds à pleine échelle, et de même pour les nombres d’Euler.

Les numéros de modèle et les numéros de conception doivent être dans la même proportion, donc

p m ρ m v m 2 = p ρ v 2 . {displaystyle {frac {p_{text{m}}}{rho _{text{m}}v_{text{m}}^{2}}}={frac {p}{ rho v^{2}}}.} ${displaystyle {frac {p_{text{m}}}{rho _{text{m}}v_{text{m}}^{2}}}={frac {p}{rho v^{2}}}.}$ ${displaystyle {frac {p_{text{m}}}{rho _{text{m}}v_{text{m}}^{2}}}={frac {p}{rho v^{2}}}.}$

Cela permet aux ingénieurs d’effectuer des expériences avec des modèles à échelle réduite dans des canaux d’eau ou des souffleries et de corréler les données aux débits réels, ce qui permet d’économiser sur les coûts d’expérimentation et sur le temps de laboratoire. Notez que la véritable Similitude dynamique peut également nécessiter la correspondance d’autres nombres sans dimension , tels que le nombre de Mach utilisé dans les écoulements compressibles ou le nombre de Froudequi régit les flux à ciel ouvert. Certains écoulements impliquent plus de paramètres sans dimension que ce qui peut être pratiquement satisfait avec l’appareil et les fluides disponibles, on est donc obligé de décider quels paramètres sont les plus importants. Pour que la modélisation expérimentale des flux soit utile, elle nécessite une bonne dose d’expérience et de jugement de la part de l’ingénieur.

Un exemple où le simple nombre de Reynolds n’est pas suffisant pour la similarité des écoulements (ou même le régime d’écoulement – laminaire ou turbulent) sont les écoulements limités, c’est-à-dire les écoulements qui sont limités par des murs ou d’autres limites. Un exemple classique de ceci est le flux de Taylor-Couette , où le rapport sans dimension des rayons des cylindres englobants est également important, et de nombreuses applications techniques où ces distinctions jouent un rôle important. ^{[26] [27]} Les principes de ces restrictions ont été développés par Maurice Marie Alfred Couette et Geoffrey Ingram Taylor et développés plus loin par Floris Takens et David Ruelle .

Valeurs typiques du nombre de Reynolds ^{[28] [29]}

Bactérie ~ 1 × 10 ⁻⁴
Cilié ~ 1 × 10 ⁻¹
Plus petit poisson ~ 1
Flux sanguin dans le cerveau ~ 1 × 10 ²
Débit sanguin dans l’ aorte ~ 1 × 10 ³
Début de l’Écoulement turbulent ~ 2,3 × 10 ³ à 5,0 × 10 ⁴ pour l’écoulement du tuyau à 10 ⁶ pour les couches limites
Terrain typique en Major League Baseball ~ 2 × 10 ⁵
Personne nageant ~ 4 × 10 ⁶
Poisson le plus rapide ~ 1 × 10 ⁸
Rorqual bleu ~ 4 × 10 ⁸
Un grand navire ( Queen Elizabeth 2 ) ~ 5 × 10 ⁹
Cyclone tropical atmosphérique ~ 1 x 10 ¹²

Les plus petites échelles de mouvement turbulent

Apprendre encore plus Cette section ne cite aucune source . ( janvier 2019 ) Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (Learn how and when to remove this template message)

Dans un Écoulement turbulent, il existe une gamme d’échelles de mouvement de fluide variant dans le temps. La taille des plus grandes échelles de mouvement fluide (parfois appelées tourbillons) est définie par la géométrie globale de l’écoulement. Par exemple, dans une cheminée industrielle, les plus grandes échelles de mouvement de fluide sont aussi grandes que le diamètre de la cheminée elle-même. La taille des plus petites échelles est définie par le nombre de Reynolds. À mesure que le nombre de Reynolds augmente, des échelles de plus en plus petites du flux sont visibles. Dans une cheminée, la fumée peut sembler avoir de nombreuses perturbations ou tourbillons de vitesse très faibles, en plus de grands tourbillons volumineux. En ce sens, le nombre de Reynolds est un indicateur de la gamme d’échelles dans le flux. Plus le nombre de Reynolds est élevé, plus la plage d’échelles est grande. Les plus grands tourbillons auront toujours la même taille ;

Quelle est l’explication de ce phénomène ? Un grand nombre de Reynolds indique que les forces visqueuses ne sont pas importantes à grande échelle de l’écoulement. Avec une forte prédominance des forces d’inertie sur les forces visqueuses, les plus grandes échelles de mouvement de fluide ne sont pas amorties – il n’y a pas assez de viscosité pour dissiper leurs mouvements. L’énergie cinétique doit “cascader” de ces grandes échelles vers des échelles progressivement plus petites jusqu’à ce qu’un niveau soit atteint pour lequel l’échelle est suffisamment petite pour que la viscosité devienne importante (c’est-à-dire que les forces visqueuses deviennent de l’ordre des forces inertielles). C’est à ces petites échelles que se produit finalement la dissipation d’énergie par action visqueuse. Le nombre de Reynolds indique à quelle échelle cette dissipation visqueuse se produit.

En physiologie

Apprendre encore plus Cette section ne cite aucune source . ( décembre 2014 ) Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (Learn how and when to remove this template message)

La loi de Poiseuille sur la circulation sanguine dans le corps est dépendante du flux laminaire . ^[30] En Écoulement turbulent, le débit est proportionnel à la racine carrée du gradient de pression, par opposition à sa proportionnalité directe au gradient de pression en écoulement laminaire.

En utilisant la définition du nombre de Reynolds, nous pouvons voir qu’un grand diamètre à écoulement rapide, où la densité du sang est élevée, tend vers la turbulence. Des changements rapides du diamètre du vaisseau peuvent conduire à un Écoulement turbulent, par exemple lorsqu’un vaisseau plus étroit s’élargit en un plus grand. De plus, un renflement d’ athérome peut être la cause d’un Écoulement turbulent, où une turbulence audible peut être détectée avec un stéthoscope.

Systèmes complexes

L’interprétation des nombres de Reynolds a été étendue au domaine des Systèmes complexes arbitraires . Tels que les flux financiers, ^[31] réseaux non linéaires, ^{[ citation nécessaire ]} etc. Dans ce dernier cas, une viscosité artificielle est réduite à un mécanisme non linéaire de distribution d’énergie dans des réseaux complexes . Le nombre de Reynolds représente alors un paramètre de contrôle de base qui exprime un équilibre entre les flux d’énergie injectés et dissipés pour un système à frontière ouverte. Il a été montré que le régime critique de Reynolds sépare deux types de mouvement dans l’espace des phases : accélérateur (attracteur) et décélérateur. ^[32] Un nombre de Reynolds élevé conduit à une transition de régime chaotique uniquement dans le cadre d’ un attracteur étrangemaquette.

Dérivation

Le nombre de Reynolds peut être obtenu lorsque l’on utilise la forme adimensionnelle des équations incompressibles de Navier–Stokes pour un fluide newtonien exprimée en fonction de la dérivée lagrangienne :

ρ D v D t = − ∇ p + μ ∇ 2 v + ρ f . {displaystyle rho {frac {Dmathbf {v} }{Dt}}=-nabla p+mu nabla ^{2}mathbf {v} +rho mathbf {f} .} $rho {frac {Dmathbf {v} }{Dt}}=-nabla p+mu nabla ^{2}mathbf {v} +rho mathbf {f} .$ $rho {frac {Dmathbf {v} }{Dt}}=-nabla p+mu nabla ^{2}mathbf {v} +rho mathbf {f} .$

Chaque terme de l’équation ci-dessus a les unités d’une “force corporelle” (force par unité de volume) avec les mêmes dimensions d’une densité multipliée par une accélération. Chaque terme est donc dépendant des mesures exactes d’un débit. Lorsqu’on rend l’équation adimensionnelle, c’est-à-dire lorsqu’on la multiplie par un facteur d’unités inverses de l’équation de base, on obtient une forme qui ne dépend pas directement des grandeurs physiques. Une façon possible d’obtenir une équation non dimensionnelle est de multiplier l’équation entière par le facteur

L ρ V 2 , {displaystyle {frac {L}{rho V^{2}}},} ${displaystyle {frac {L}{rho V^{2}}},}$ ${displaystyle {frac {L}{rho V^{2}}},}$

où

V est la vitesse moyenne, v ou v , par rapport au fluide (m/s),
L est la longueur caractéristique (m),
ρ est la masse volumique du fluide (kg/m³ ).

Si nous fixons maintenant

v ′ = v V , p ′ = p 1 ρ V 2 , f ′ = f L V 2 , ∂ ∂ t ′ = L V ∂ ∂ t , ∇ ′ = L ∇ , {displaystyle {begin{aligned}mathbf {v} ‘&={frac {mathbf {v} }{V}},&p’&=p{frac {1}{rho V^{2 }}},&mathbf {f} ‘&=mathbf {f} {frac {L}{V^{2}}},&{frac {partial }{partial t’}}&= {frac {L}{V}}{frac {partial }{partial t}},&nabla ‘&=Lnabla ,end{aligned}}} ${displaystyle {begin{aligned}mathbf {v} '&={frac {mathbf {v} }{V}},&p'&=p{frac {1}{rho V^{2}}},&mathbf {f} '&=mathbf {f} {frac {L}{V^{2}}},&{frac {partial }{partial t'}}&={frac {L}{V}}{frac {partial }{partial t}},&nabla '&=Lnabla ,end{aligned}}}$ ${displaystyle {begin{aligned}mathbf {v} '&={frac {mathbf {v} }{V}},&p'&=p{frac {1}{rho V^{2}}},&mathbf {f} '&=mathbf {f} {frac {L}{V^{2}}},&{frac {partial }{partial t'}}&={frac {L}{V}}{frac {partial }{partial t}},&nabla '&=Lnabla ,end{aligned}}}$

on peut réécrire l’équation de Navier-Stokes sans dimensions :

D v ′ D t ′ = − ∇ ′ p ′ + μ ρ L V ∇ ′ 2 v ′ + f ′ , {displaystyle {frac {Dmathbf {v} ‘}{Dt’}}=-nabla ‘p’+{frac {mu }{rho LV}}nabla ‘^{2}mathbf {v} ‘+mathbf {f} ‘,} ${displaystyle {frac {Dmathbf {v} '}{Dt'}}=-nabla 'p'+{frac {mu }{rho LV}}nabla '^{2}mathbf {v} '+mathbf {f} ',}$ ${displaystyle {frac {Dmathbf {v} '}{Dt'}}=-nabla 'p'+{frac {mu }{rho LV}}nabla '^{2}mathbf {v} '+mathbf {f} ',}$

où le terme μ/ρLV= 1/Concernant.

Enfin, en supprimant les nombres premiers pour faciliter la lecture :

D v D t = − ∇ p + 1 R e ∇ 2 v + f . {displaystyle {frac {Dmathbf {v} }{Dt}}=-nabla p+{frac {1}{mathrm {Re}}}nabla ^{2}mathbf {v} + mathbf {f} .} ${frac {Dmathbf {v} }{Dt}}=-nabla p+{frac {1}{mathrm {Re} }}nabla ^{2}mathbf {v} +mathbf {f} .$ ${frac {Dmathbf {v} }{Dt}}=-nabla p+{frac {1}{mathrm {Re}}}nabla ^{2}mathbf {v} +mathbf {f } .$ Équation universelle de sédimentation – coefficient de traînée, fonction du nombre de Reynolds et du facteur de forme, diagramme 2D Équation universelle de sédimentation – coefficient de traînée, fonction du nombre de Reynolds et du facteur de forme, diagramme 3D

C’est pourquoi mathématiquement tous les écoulements newtoniens incompressibles avec le même nombre de Reynolds sont comparables. Notez également que dans l’équation ci-dessus, les termes Visqueux s’annulent pour Re → ∞ . Ainsi, les flux avec des nombres de Reynolds élevés sont approximativement non Visqueux dans le flux libre.

Relation avec d’autres paramètres sans dimension

Il existe de nombreux nombres sans dimension en mécanique des fluides . Le nombre de Reynolds mesure le rapport des effets d’advection et de diffusion sur les structures dans le champ de vitesse, et est donc étroitement lié aux nombres de Péclet , qui mesurent le rapport de ces effets sur d’autres champs portés par l’écoulement, par exemple la température et les champs magnétiques. Remplacement de la Viscosité cinématique ν = μ/ρen Re par la diffusivité thermique ou magnétique se traduit respectivement par le nombre de Péclet thermique et le nombre de Reynolds magnétique . Ceux-ci sont donc liés aux sous-produits de Re avec des rapports de diffusivités, à savoir le nombre de Prandtl et le nombre de Prandtl magnétique .

Voir également

Théorème de transport de Reynolds – Généralisation 3D de la règle intégrale de Leibniz
Coefficient de traînée – Paramètre sans dimension pour quantifier la résistance du fluide
Dépôt (géologie) – Processus géologique dans lequel des sédiments, du sol et des roches sont ajoutés à un relief ou à une masse continentale
Instabilité de Kelvin-Helmholtz

Références

Notes de bas de page

^ La définition du nombre de Reynolds ne doit pas être confondue avec l’ équation de Reynolds ou l’équation de lubrification.
^ Le développement complet de l’écoulement se produit lorsque l’écoulement pénètre dans le tuyau, la couche limite s’épaissit puis se stabilise après plusieurs diamètres de distance dans le tuyau.

Citations

^ Tansley & Marshall 2001 , pp. 3274–3283.
^ Stokes 1851 , pp. 8–106.
^ ^un ^b Sommerfeld 1908 , pp. 116–124.
^ Reynolds 1883 , pp. 935–982.
^ ^un ^b Rott 1990 , pp. 1-11.
^ Falkovich 2018 .
^ Salle, Nancy (5 mai 2015). “Couche limite” . Centre de recherche Glenn . Récupéré le 17 septembre 2019 .
^ “Numéro de Reynolds” . Engineeringtoolbox.com . 2003.
^ Holman 2002 .
^ Renard, McDonald & Pritchard 2004 , p. 348.
^ Incropera & DeWitt 1981 .
^ ^un ^bc ^Schlichting & Gersten 2017 , pp. 416-419.
^ Holman 2002 , p. 207.
^ Potier, Wiggert et Ramadan 2012 , p. 105.
^ Seshadri, K (février 1978). “Ecoulement laminaire entre plaques parallèles avec injection d’un réactif à haut nombre de reynolds”. Journal international de transfert de chaleur et de masse . 21 (2): 251-253. doi : 10.1016/0017-9310(78)90230-2 .
^ Rueter 1965 .
^ Lissaman 1983 , pp. 223-239.
^ “Atmosphère standard internationale” . eng.cam.ac.uk . Récupéré le 17 septembre 2019 .
^ Ehrenstein & Eloy 2013 , pp. 321–346.
^ ^un ^b Rhodes 1989 , p. 29.
^ Dusenbery 2009 , p. 49.
^ “Bossettes de balle de golf et traînée” . Aerospaceweb.org . Récupéré le 11 août 2011 .
^ ^un ^b Dwivedi 1977 , pp. 157–165.
^ Sinnott, Coulson & Richardson 2005 , p. 73.
^ “Perte de tête majeure – Perte de friction” . L’énergie nucléaire . Récupéré le 17 septembre 2019 .
^ “Flux laminaire, transitionnel et turbulent” . rheologic.net . Récupéré le 17 septembre 2019 .
^ Manneville & Pomeau 2009 , p. 2072.
^ Patel, Rodi & Scheuerer 1985 , pp. 1308–1319.
^ Dusenbery 2009 , p. 136.
^ Aide, EPW; McDonald, DA (1954-06-28). “Observations sur le flux laminaire dans les veines” . Le Journal de Physiologie . 124 (3): 631–639. doi : 10.1113/jphysiol.1954.sp005135 . PMC 1366298 . PMID 13175205 .
^ Los 2006 , p. 369.
^ Gómez Blazquez, Alberto (2016-06-23). “Analyse aérodynamique du plancher plat” . {{cite journal}}: Cite journal requires |journal= (help)

Sources

Oiseau, R. Byron; Stewart, Warren E.; Lightfoot, Edwin N. (2006). Phénomènes de transport . John Wiley et fils. ISBN 978-0-470-11539-8.
En ligneDusenbery, David B. (2009). Vivre à Micro Échelle . Cambridge, Massachusetts : Harvard University Press. ISBN 9780674031166.
Dwivedi, PN (1977). “Transfert de masse particule-fluide dans des lits fixes et fluidisés”. Conception et développement de procédés de chimie industrielle et mécanique . 16 (2): 157–165. doi : 10.1021/i260062a001 .
Ehrenstein, Uwe; Eloy, Christophe (2013). “Le frottement de la peau sur une paroi en mouvement et ses implications pour les animaux nageurs” (PDF) . Journal de mécanique des fluides . 718 : 321–346. Bibcode : 2013JFM…718..321E . doi : 10.1017/jfm.2012.613 . ISSN 0022-1120 . S2CID 56331294 . Archivé de l’original (PDF) le 2019-03-02.
Falkovitch, Grégoire (2018). Mécanique des fluides . La presse de l’Universite de Cambridge. ISBN 978-1-107-12956-6.
Fox, RW; McDonald, AT ; En lignePritchard, Phillip J. (2004). Introduction à la mécanique des fluides (6e éd.). Hoboken : John Wiley et fils. p. 348. ISBN 978-0-471-20231-8.
Holman, JP (2002). Transfert de chaleur (éd. Unités SI). McGraw-Hill Education (Inde) Pvt Limited. ISBN 978-0-07-106967-0.
Incropera, Frank P.; En ligneDeWitt, David P. (1981). Fondamentaux du transfert de chaleur . New York : Wiley. ISBN 978-0-471-42711-7.
Lissaman, PBS (1983). “Profils aérodynamiques à faible nombre de Reynolds”. Annu. Rév. Fluid Mech . 15 (15): 223–239. Bibcode : 1983AnRFM..15..223L . CiteSeerX 10.1.1.506.1131 . doi : 10.1146/annurev.fl.15.010183.001255 .
Los, Cornelis (2006). Risque de marché financier : mesure et analyse . Routledge. ISBN 978-1-134-46932-1.
Manneville, Paul; Pomeau, Yves (25 mars 2009). “Passage aux turbulences” . Scholarpédia . 4 (3): 2072. Bibcode : 2009SchpJ…4.2072M . doi : 10.4249/scholarpedia.2072 .
Patel, VC ; Rodi, W.; En ligneScheuerer, G. (1985). “Modèles de turbulence pour les flux proches du mur et à faible nombre de Reynolds – Un examen”. Revue AIAA . 23 (9): 1308-1319. Bibcode : 1985AIAAJ..23.1308P . doi : 10.2514/3.9086 .
Potter, Merle C.; Wiggert, David C.; En ligneRamadan, Bassem H. (2012). Mécanique des fluides (4e, Unités SI éd.). Cengage Apprentissage. ISBN 978-0-495-66773-5.
Reynolds, Osborne (1883). “Une étude expérimentale des circonstances qui déterminent si le mouvement de l’eau doit être direct ou sinueux, et de la loi de résistance dans les canaux parallèles” . Transactions philosophiques de la Royal Society . 174 : 935–982. Bibcode : 1883RSPT..174..935R . doi : 10.1098/rstl.1883.0029 . JSTOR 109431 .
En ligneRhodes, M. (1989). Introduction à la technologie des particules . Wiley. ISBN 978-0-471-98482-5.
En ligneRott, N. (1990). “Note sur l’histoire du nombre de Reynolds” (PDF) . Revue annuelle de mécanique des fluides . 22 (1): 1–11. Bibcode : 1990AnRFM..22….1R . doi : 10.1146/annurev.fl.22.010190.000245 . S2CID 54583669 . Archivé de l’original (PDF) le 2019-02-25.
Schlichting, Hermann; Gersten, Klaus (2017). Théorie de la couche limite . Springer. ISBN 978-3-662-52919-5.
Sinnott, RK; Coulson, John Metcalfe; Richardson, John Francis (2005). Conception en génie chimique . Vol. 6 (4e éd.). Elsevier Butterworth-Heinemann. ISBN 978-0-7506-6538-4.
Sommerfeld, Arnold (1908). “Ein Beitrag zur hydrodynamischen Erkläerung der turbulenten Flüssigkeitsbewegüngen (Une contribution à l’explication hydrodynamique des mouvements de fluides turbulents)” (PDF) . Congrès international des mathématiciens . 3 : 116–124. Archivé de l’original (PDF) le 2016-11-15.
Stokes, George (1851). “Sur l’effet du frottement interne des fluides sur le mouvement des pendules”. Transactions de la Cambridge Philosophical Society . 9 : 8–106. Bibcode : 1851TCaPS…9….8S .
Streeter, Victor Lyle (1965). Mécanique des fluides (3e éd.). New York : McGraw Hill. OCLC 878734937 .
Tansley, Claire E.; En ligneMarshall, David P. (2001). « Écoulement devant un cylindre sur un avion, avec application à la séparation du Gulf Stream et au courant circumpolaire antarctique » (PDF) . Journal d’océanographie physique . 31 (11): 3274–3283. Bibcode : 2001JPO….31.3274T . doi : 10.1175/1520-0485(2001)031<3274:FPACOA>2.0.CO;2 . Archivé de l’original (PDF) le 2011-04-01.

Lectures complémentaires

Batchelor, GK (1967). Une introduction à la dynamique des fluides . La presse de l’Universite de Cambridge. p. 211–215.
Brezina, Jiri, 1979, Distributions de la taille des particules et du taux de sédimentation des matériaux de la taille du sable : 2e Symposium européen sur la caractérisation des particules ( PARTEC ), Nürnberg, Allemagne de l’Ouest.
Brezina, Jiri, 1980, Interprétation sédimentologique des erreurs dans l’analyse granulométrique des sables ; 1ère réunion européenne de l’Association internationale des sédimentologues, Université de la Ruhr à Bochum, République fédérale d’Allemagne, mars 1980.
Brezina, Jiri, 1980, Distribution granulométrique du sable – interprétation sédimentologique ; 26e Congrès géologique international, Paris , juillet 1980, Résumés, vol. 2.
Fouz, Infaz “Fluid Mechanics”, Département de génie mécanique, Université d’Oxford, 2001, p. 96
Hughes, Roger “Civil Engineering Hydraulics”, Département civil et environnemental, Université de Melbourne 1997, pp. 107–152
Jermy M., “Fluid Mechanics A Course Reader”, Département de génie mécanique, Université de Canterbury, 2005, pp. d5.10.
Purcell, EM “La vie à faible nombre de Reynolds”, American Journal of Physics vol 45, pp. 3–11 (1977) [1]
Truskey, GA, Yuan, F, Katz, DF (2004). Phénomènes de transport dans les systèmes biologiques Prentice Hall, pp. 7. ISBN 0-13-042204-5 . ISBN 978-0-13-042204-0 .
Zagarola, MV et Smits, AJ, “Expériences dans un écoulement de tuyau turbulent à nombre de Reynolds élevé.” Article AIAA # 96-0654, 34e réunion des sciences aérospatiales de l’AIAA, Reno, Nevada, 15-18 janvier 1996.
Isobel Clark , 1977, ROKE, un programme informatique pour la décomposition non linéaire des moindres carrés de mélanges de distributions ; Informatique et géosciences (Pergamon Press), vol. 3, p. 245 – 256.
BC Colby et RP Christensen, 1957, Quelques principes fondamentaux de l’analyse de la taille des particules ; Laboratoire hydraulique de St. Anthony Falls, Minneapolis, Minnesota, États-Unis, rapport n°. 12/décembre, 55 pages.
Arthur T. Corey , 1949, Influence de la forme sur la vitesse de chute des grains de sable ; Thèse de maîtrise, Colorado Agricultural and Mechanical College, Fort Collins, Colorado, États-Unis, décembre 102 pages.
Joseph R. Curray , 1961, Traçage des masses sédimentaires par modes granulométriques ; Proc. Internat. Association de sédimentologie, Rapport de la 21e session Norden, Internat. Géol. Congrès, p. 119 – 129.
Burghard Walter Flemming & Karen Ziegler, 1995, Modèles de distribution granulométrique à haute résolution et tendances texturales dans l’environnement de la barrière arrière de l’île Spiekeroog (sud de la mer du Nord); Senckenbergiana Maritima, vol. 26, n° 1+2, p. 1 – 24.
Robert Louis Folk , 1962, Des asymétries et des sables ; Jour. Sédiment. Essence., vol. 8, n° 3/septembre, p. 105 – 111
FOLK, Robert Louis & William C. WARD, 1957 : Brazos River bar : une étude sur l’importance des paramètres granulométriques ; Jour. Sédiment. Essence., vol. 27, n° 1/mars, p. 3 – 26
George Herdan , ML Smith et WH Hardwick (1960) : Statistiques des petites particules. 2e édition révisée, Butterworths (Londres, Toronto, etc.), 418 p.
Douglas Inman , 1952 : Mesures pour décrire la distribution granulométrique des sédiments. Jour. Sédiment. Pétrologie, vol. 22, n° 3/septembre, p. 125 – 145
Miroslaw Jonasz , 1991 : Taille, forme, composition et structure des microparticules issues de la diffusion de la lumière ; dans SYVITSKI, James PM, 1991, Principes, méthodes et application de l’analyse de la taille des particules ; Université de Cambridge. Press, Cambridge , 368 pages, p. 147.
William C. Krumbein , 1934 : Distribution des fréquences granulométriques des sédiments ; Jour. Sédiment. Essence., vol. 4, n° 2/août, p. 65 – 77.
Krumbein, William Christian & Francis J. Pettijohn, 1938 : Manuel de pétrographie sédimentaire ; Appleton-Century-Crofts, Inc., New York ; 549 p.
John S. McNown & Pin-Nam Lin, 1952, Concentration des sédiments et vitesse de chute ; Proc. de la 2e Midwest Conf. sur la mécanique des fluides, Ohio State University , Columbus, Ohio ; Université d’État. of Iowa Reprints in Engineering, réimpression n° 109/1952, p. 401 – 411.
McNownn, John S. & J. Malaika, 1950, Effets de la forme des particules de la vitesse de sédimentation aux faibles nombres de Reynolds ; Transactions de l’Union géophysique américaine, vol. 31, n° 1/février, p. 74 – 82.
Gerard V. Middleton 1967, Expériences sur les courants de densité et de turbidité, III ; Déposition; Journée canadienne. des Sciences de la Terre, vol. 4, p. 475 – 505 (définition PSI : p. 483 – 485).
Osborne Reynolds , 1883 : Une étude expérimentale des circonstances qui déterminent si le mouvement de l’eau doit être direct ou sinueux, et de la loi de résistance dans les canaux parallèles. Phil. Trans. Roy. Soc., 174, Cahiers, vol. 2, p. 935 – 982
EF Schultz , RH Wilde & ML Albertson, 1954, Influence de la forme sur la vitesse de chute des particules sédimentaires ; Colorado Agricultural & Mechanical College, Fort Collins, Colorado, MRD Sediment Series, n° 5/juillet (CER 54EFS6), 161 pages.
HJ Skidmore , 1948, Développement d’une technique de suspension stratifiée pour l’analyse de fréquence de taille ; Thèse, Département de mécanique et d’hydraulique, State Univ. de l’Iowa, p. 2 (? pages).
James PM Syvitski , 1991, Principes, méthodes et application de l’analyse de la taille des particules ; Université de Cambridge. Press, Cambridge, 368 p.

Liens externes

Wikimedia Commons a des médias liés au nombre de Reynolds .

Le nombre de Reynolds à soixante symboles
Mini-biographie de Reynolds et photo de l’appareil original à l’Université de Manchester.