JPEG
JPEG ( / ˈ dʒ eɪ p ɛ ɡ / JAY -peg ) [2] est une méthode couramment utilisée de compression avec perte pour les images numériques , en particulier pour les images produites par la photographie numérique . Le degré de compression peut être ajusté, permettant un compromis sélectionnable entre la taille de stockage et la qualité d’image . JPEG atteint généralement une compression de 10:1 avec peu de perte perceptible de qualité d’image. [3] Depuis son introduction en 1992, JPEG est la norme de compression d’image la plus utilisée au monde, [4] [5]et le Format d’image numérique le plus largement utilisé , avec plusieurs milliards d’images JPEG produites chaque jour à partir de 2015. [6]
 Une photo d’un chat sauvage européen avec le taux de compression diminuant et donc la qualité augmentant, de gauche à droite Une photo d’un chat sauvage européen avec le taux de compression diminuant et donc la qualité augmentant, de gauche à droite |
|
| Extension de nom de fichier | .jpg, .jpeg, .jpe .jif, .JFIF, .jfi |
|---|---|
| Type de média Internet | image/jpeg |
| Tapez le code | JPEG |
| Identificateur de type uniforme (UTI) | public.jpeg |
| nombre magique | ff d8 ff |
| Développé par | Groupe conjoint d’experts en photographie , IBM , Mitsubishi Electric , AT&T , Canon Inc. [1] |
| Première version | 18 septembre 1992 ; il y a 29 ans ( 1992-09-18 ) |
| Type de format | Format de compression d’image avec perte |
| Standard | ISO/CEI 10918, UIT-T T.81, UIT-T T.83, UIT-T T.84, UIT-T T.86 |
| Site Internet | www .jpeg .org /jpeg / |
Le terme “JPEG” est un acronyme pour le Joint Photographic Experts Group , qui a créé la norme en 1992. La compression d’image avec perte de JPEG est basée sur la transformée en cosinus discrète (DCT), [7] [8] une technique qui a été proposée pour la première fois par Nasir Ahmed en 1972. [9] [8] JPEG était en grande partie responsable de la prolifération des images numériques et des photos numériques sur Internet, et plus tard sur les réseaux sociaux . [dix]
La compression JPEG est utilisée dans un certain nombre de formats de fichiers image . JPEG/ Exif est le Format d’image le plus couramment utilisé par les appareils photo numériques et autres appareils de capture d’images photographiques ; avec JPEG/ JFIF , c’est le format le plus courant pour stocker et transmettre des images photographiques sur le World Wide Web . [11] Ces variations de format ne sont souvent pas distinguées et sont simplement appelées JPEG.
Le type de média MIME pour JPEG est image/jpeg , sauf dans les anciennes versions d’ Internet Explorer , qui fournit un type MIME image/pjpeg lors du téléchargement d’images JPEG. [12] Les fichiers JPEG ont généralement une extension de nom de fichier .jpgou .jpeg. JPEG / JFIF prend en charge une taille d’image maximale de 65 535 × 65 535 pixels, [13] donc jusqu’à 4 gigapixels pour un rapport d’aspect de 1: 1. En 2000, le groupe JPEG a introduit un format destiné à lui succéder, JPEG 2000 , mais il n’a pas été en mesure de remplacer le JPEG original comme norme d’image dominante. [14]
Histoire
Arrière-plan
La spécification JPEG originale publiée en 1992 met en œuvre des processus issus de divers Documents de recherche et Brevets antérieurs cités par le CCITT (maintenant ITU-T ) et le Joint Photographic Experts Group. [1] La base principale de l’ algorithme de compression avec perte de JPEG est la transformée en cosinus discrète (DCT), [1] [8] qui a été proposée pour la première fois par Nasir Ahmed comme technique de compression d’image en 1972. [9] [8] Ahmed a développé une algorithme DCT pratique avec T. Natarajan de la Kansas State University et KR Raode l’ Université du Texas en 1973. [9] Leur article de 1974 [15] est cité dans la spécification JPEG, ainsi que plusieurs articles de recherche ultérieurs qui ont poursuivi leurs travaux sur le DCT, notamment un article de 1977 de Wen-Hsiung Chen, CH Smith et SC Fralick qui a décrit un algorithme DCT rapide, [1] [16] ainsi qu’un article de 1978 de NJ Narasinha et SC Fralick, et un article de 1984 de BG Lee. [1] La spécification cite également un article de 1984 de Wen-Hsiung Chen et WK Pratt comme une influence sur son algorithme de quantification , [1] [17] et l’article de David A. Huffman de 1952 pour son algorithme de codage Huffman .[1]
La spécification JPEG cite des Brevets de plusieurs sociétés. Les Brevets suivants ont fourni la base de son algorithme de codage arithmétique . [1]
- IBM
- Brevet américain 4 652 856 – 4 février 1986 – Kottappuram MA Mohiuddin et Jorma J. Rissanen – Code arithmétique multi-alphabet sans multiplication
- Brevet américain 4 905 297 – 27 février 1990 – G. Langdon, JL Mitchell, WB Pennebaker et Jorma J. Rissanen – Système d’encodeur et de décodeur de codage arithmétique
- Brevet américain 4 935 882 – 19 juin 1990 – WB Pennebaker et JL Mitchell – Adaptation de probabilité pour les codeurs arithmétiques
- Mitsubishi Électrique
- JP H02202267 ( 1021672 ) – 21 janvier 1989 – Toshihiro Kimura, Shigenori Kino, Fumitaka Ono, Masayuki Yoshida – Système de codage
- JP H03247123 ( 2-46275 ) – 26 février 1990 – Fumitaka Ono, Tomohiro Kimura, Masayuki Yoshida et Shigenori Kino – Appareil de codage et méthode de codage
La spécification JPEG cite également trois autres Brevets d’IBM. AT&T (deux Brevets) et Canon Inc. [1] Absent de la liste est le brevet US 4,698,672 , déposé par Compression Labs ‘ Wen-Hsiung Chen et Daniel J. Klenke en octobre 1986. Le brevet décrit un Algorithme de compression d’image basé sur DCT, et serait plus tard une cause de controverse en 2002 (voir la controverse sur les Brevets ci-dessous). [18] Cependant, la spécification JPEG cite deux articles de recherche antérieurs de Wen-Hsiung Chen, publiés en 1977 et 1984. [1]
Norme JPEG
“JPEG” signifie Joint Photographic Experts Group , le nom du comité qui a créé la norme JPEG ainsi que d’autres normes de codage d’images fixes. Le “Joint” signifiait ISO TC97 WG8 et CCITT SGVIII. Fondé en 1986, le groupe a développé la norme JPEG à la fin des années 1980. Parmi plusieurs techniques de codage par transformée qu’ils ont examinées, ils ont sélectionné la transformée en cosinus discrète (DCT), car c’était de loin la technique de compression pratique la plus efficace. Le groupe a publié la norme JPEG en 1992. [4]
En 1987, l’ISO TC 97 est devenu l’ISO/CEI JTC1 et, en 1992, le CCITT est devenu l’UIT-T. Actuellement du côté du JTC1, JPEG est l’un des deux sous-groupes du Comité technique mixte ISO / CEI 1 , Sous-comité 29, Groupe de travail 1 ( ISO/CEI JTC 1/SC 29 /WG 1) – intitulé Codage des images fixes . [19] [20] [21] Du côté d’ITU-T, ITU-T SG16 est le corps respectif. Le groupe JPEG original a été organisé en 1986, [22] publiant la première norme JPEG en 1992, qui a été approuvée en septembre 1992 en tant que recommandation UIT-T T.81 [23] et, en 1994, en tant qu’ISO / CEI 10918-1 .
La norme JPEG spécifie le codec , qui définit la façon dont une image est compressée en un flux d’ octets et décompressée en une image, mais pas le format de fichier utilisé pour contenir ce flux. [24] Les normes Exif et JFIF définissent les formats de fichiers couramment utilisés pour l’échange d’images compressées JPEG.
Les normes JPEG sont officiellement nommées Technologies de l’information – Compression numérique et codage d’images fixes à tons continus . L’ISO/CEI 10918 comprend les parties suivantes :
| Partie | Norme ISO/CEI | UIT-T Rec. | Première date de sortie publique | Dernier amendement | Titre | La description |
|---|---|---|---|---|---|---|
| Partie 1 | ISO/CEI 10918-1:1994 | T.81 (09/92) | 18 septembre 1992 | Exigences et lignes directrices | ||
| Partie 2 | ISO/CEI 10918-2:1995 | T.83 (11/94) | 11 novembre 1994 | Tests de conformité | Règles et contrôles de conformité du logiciel (à la partie 1). | |
| Partie 3 | ISO/CEI 10918-3:1997 | T.84 (07/96) | 3 juillet 1996 | 1 avril 1999 | Rallonges | Ensemble d’extensions pour améliorer la partie 1, y compris le format de fichier d’échange d’images fixes (SPIFF). [26] |
| Partie 4 | ISO/CEI 10918-4:1999 | T.86 (06/98) | 18 juin 1998 | 29 juin 2012 | Enregistrement des profils JPEG, des profils SPIFF, des balises SPIFF, des espaces colorimétriques SPIFF, des marqueurs APPn, des types de compression SPIFF et des autorités d’enregistrement (REGAUT) | méthodes d’enregistrement de certains des paramètres utilisés pour étendre JPEG |
| Partie 5 | ISO/CEI 10918-5:2013 | T.871 (05/11) | 14 mai 2011 | Format d’échange de fichiers JPEG (JFIF) | Un format populaire qui a été le format de fichier de facto pour les images encodées par la norme JPEG. En 2009, le comité JPEG a officiellement créé un groupe ad hoc pour normaliser JFIF en tant que JPEG Part 5. [27] | |
| Partie 6 | ISO/CEI 10918-6:2013 | T.872 (06/12) | juin 2012 | Application aux systèmes d’impression | Spécifie un sous-ensemble de fonctionnalités et d’outils d’application pour l’échange d’images codées conformément à la norme ISO/IEC 10918-1 pour l’impression. |
Ecma International TR /98 spécifie le format d’échange de fichiers JPEG (JFIF) ; la première édition a été publiée en juin 2009. [28]
Controverse sur les Brevets
En 2002, Forgent Networks a affirmé qu’il possédait et ferait respecter les droits de brevet sur la technologie JPEG, découlant d’un brevet qui avait été déposé le 27 octobre 1986 et accordé le 6 octobre 1987 : brevet américain 4 698 672 par Compression Labs ‘ Wen- Hsiung Chen et Daniel J. Klenke. [18] [29] Alors que Forgent ne possédait pas Compression Labs à l’époque, Chen a ensuite vendu Compression Labs à Forgent, avant que Chen ne continue à travailler pour Cisco . Cela a conduit Forgent à acquérir la propriété du brevet. [18] L’annonce de Forgent en 2002 a créé une fureur qui rappelle Unisys’ tente de faire valoir ses droits sur la norme de compression d’image GIF.
Le comité JPEG a enquêté sur les revendications du brevet en 2002 et a estimé qu’elles étaient invalidées par l’état de la technique [30] , un point de vue partagé par divers experts. [18] [31] Le brevet décrit un algorithme de compression d’image basé sur la transformée en cosinus discrète (DCT), [32] une technique de compression d’image avec perte issue d’un article de 1974 de Nasir Ahmed , T. Natarajan et KR Rao . [1] [8] [15] Wen-Hsiung Chen a développé sa technique DCT, décrivant un algorithme DCT rapide dans un article de 1977 avec CH Smith et SC Fralick. [16] [18]La spécification JPEG de 1992 cite à la fois l’article d’Ahmed de 1974 et l’article de Chen de 1977 pour son algorithme DCT, ainsi qu’un article de 1984 de Chen et WK Pratt pour son algorithme de quantification . [1] [17] Au moment où Chen avait déposé son brevet pour un algorithme de compression d’image basé sur DCT avec Klenke en 1986, la plupart de ce qui deviendrait plus tard la norme JPEG avait déjà été formulée dans la littérature antérieure. [18] Le représentant de JPEG, Richard Clark, a également affirmé que Chen lui-même siégeait dans l’un des comités JPEG, mais Forgent a nié cette affirmation. [18]
Entre 2002 et 2004, Forgent a pu obtenir environ 105 millions de dollars américains en licenciant son brevet à une trentaine d’entreprises. En avril 2004, Forgent a poursuivi 31 autres sociétés pour faire appliquer de nouveaux paiements de licence. En juillet de la même année, un consortium de 21 grandes sociétés informatiques a déposé une contre-poursuite, dans le but d’invalider le brevet. De plus, Microsoft a lancé une action en justice distincte contre Forgent en avril 2005. [33] En février 2006, l’ Office américain des Brevets et des marques a accepté de réexaminer le brevet JPEG de Forgent à la demande de la Public Patent Foundation. [34] Le 26 mai 2006, l’USPTO a déclaré le brevet invalide sur la base de l’état de la technique . L’USPTO a également constaté que Forgent était au courant de l’ état de la technique, mais il a intentionnellement évité de le dire à l’Office des Brevets. Cela rend tout appel visant à rétablir le brevet très peu susceptible d’aboutir. [35]
Forgent possède également un brevet similaire délivré par l’ Office européen des Brevets en 1994, bien qu’il ne soit pas clair dans quelle mesure il est exécutoire. [36]
Depuis le 27 octobre 2006, la durée de 20 ans du brevet américain semble avoir expiré et, en novembre 2006, Forgent a accepté d’abandonner l’application des revendications de brevet contre l’utilisation de la norme JPEG. [37]
Le comité JPEG a pour objectif explicite que leurs normes (en particulier leurs méthodes de base) puissent être mises en œuvre sans paiement de frais de licence, et ils ont obtenu les droits de licence appropriés pour leur norme JPEG 2000 auprès de plus de 20 grandes organisations.
À partir d’août 2007, une autre société, Global Patent Holdings, LLC a affirmé que son brevet ( brevet américain 5 253 341 ) délivré en 1993 était enfreint par le téléchargement d’images JPEG sur un site Web ou par courrier électronique. S’il n’est pas invalidé, ce brevet pourrait s’appliquer à tout site Web affichant des images JPEG. Le brevet a fait l’objet d’un réexamen par l’Office américain des Brevets et des marques de 2000 à 2007 ; en juillet 2007, l’Office des Brevets a révoqué toutes les revendications initiales du brevet, mais a conclu qu’une revendication supplémentaire proposée par Global Patent Holdings (revendication 17) était valide. [38] Global Patent Holdings a alors intenté un certain nombre de poursuites fondées sur la revendication 17 de son brevet.
Dans ses deux premières poursuites à la suite du réexamen, toutes deux déposées à Chicago, dans l’Illinois, Global Patent Holdings a poursuivi les Green Bay Packers , CDW , Motorola , Apple , Orbitz , Officemax , Caterpillar , kraft et Peapod en tant que défendeurs. Une troisième action en justice a été déposée le 5 décembre 2007 dans le sud de la Floride contre ADT Security Services , AutoNation , Florida Crystals Corp., HearUSA, MovieTickets.com , Ocwen Financial Corp. et Tire Kingdom ., et un quatrième procès le 8 janvier 2008, dans le sud de la Floride contre le Boca Raton Resort & Club . Un cinquième procès a été intenté contre Global Patent Holdings au Nevada. Cette action en justice a été déposée par Zappos.com , Inc., qui aurait été menacée par Global Patent Holdings, et a demandé une déclaration judiciaire selon laquelle le brevet ‘341 est invalide et non violé.
Global Patent Holdings avait également utilisé le brevet ‘341 pour poursuivre ou menacer les critiques virulents de larges Brevets logiciels, y compris Gregory Aharonian [39] et l’opérateur anonyme d’un blog de site Web connu sous le nom de « Patent Troll Tracker ». [40] Le 21 décembre 2007, l’avocat en Brevets Vernon Francissen de Chicago a demandé au Bureau américain des Brevets et des marques de réexaminer la seule revendication restante du brevet ‘341 sur la base d’un nouvel art antérieur. [41]
Le 5 mars 2008, l’Office américain des Brevets et des marques a accepté de réexaminer le brevet ‘341, estimant que le nouvel état de la technique soulevait de nouvelles questions importantes concernant la validité du brevet. [42] À la lumière du réexamen, les contrevenants accusés dans quatre des cinq poursuites en cours ont déposé des requêtes pour suspendre (suspendre) leurs affaires jusqu’à l’achèvement de l’examen du brevet ‘341 par l’Office américain des Brevets et des marques. Le 23 avril 2008, un juge présidant les deux poursuites à Chicago, dans l’Illinois, a accordé les requêtes dans ces affaires. [43] Le 22 juillet 2008, l’Office des Brevets a publié la première “action de l’Office” du deuxième réexamen, concluant que la revendication était invalide sur la base de dix-neuf motifs distincts. [44]Le 24 novembre 2009, un certificat de réexamen a été délivré annulant toutes les réclamations.
À partir de 2011 et au début de 2013, une entité connue sous le nom de Princeton Digital Image Corporation, [45] basée dans l’est du Texas, a commencé à poursuivre un grand nombre d’entreprises pour violation présumée du brevet américain 4 813 056.. Princeton affirme que la norme de compression d’image JPEG enfreint le brevet ‘056 et a poursuivi un grand nombre de sites Web, de détaillants, de fabricants et de revendeurs d’appareils photo et d’appareils photo. Le brevet appartenait à l’origine et était attribué à General Electric. Le brevet a expiré en décembre 2007, mais Princeton a poursuivi un grand nombre d’entreprises pour “contrefaçon passée” de ce brevet. (En vertu des lois américaines sur les Brevets, un titulaire de brevet peut intenter une action en justice pour “contrefaçon passée” jusqu’à six ans avant le dépôt d’une action en justice, de sorte que Princeton aurait pu théoriquement continuer à poursuivre des entreprises jusqu’en décembre 2013.) En mars 2013, Princeton avait des poursuites en cours en New York et Delaware contre plus de 55 entreprises. L’implication de General Electric dans la poursuite est inconnue,[46]
Utilisation typique
L’algorithme de compression JPEG fonctionne au mieux sur des photographies et des peintures de scènes réalistes avec des variations douces de tons et de couleurs. Pour une utilisation Web, où la réduction de la quantité de données utilisées pour une image est importante pour une présentation réactive, les avantages de la compression JPEG rendent JPEG populaire. JPEG/ Exif est également le format le plus courant enregistré par les appareils photo numériques.
Cependant, JPEG n’est pas bien adapté aux dessins au trait et autres graphiques textuels ou iconiques, où les contrastes nets entre les pixels adjacents peuvent provoquer des artefacts notables. Il est préférable d’enregistrer ces images dans un format graphique sans perte tel que TIFF , GIF , PNG ou un Format d’image brute . La norme JPEG inclut un mode de codage sans perte, mais ce mode n’est pas pris en charge dans la plupart des produits.
Comme l’utilisation typique de JPEG est une méthode de compression avec perte , qui réduit la fidélité de l’image, elle est inappropriée pour la reproduction exacte des données d’imagerie (comme certaines applications d’imagerie scientifique et médicale et certains travaux techniques de traitement d’image ).
JPEG n’est pas non plus bien adapté aux fichiers qui subiront de multiples modifications, car une certaine qualité d’image est perdue à chaque fois que l’image est recompressée, en particulier si l’image est recadrée ou décalée, ou si les paramètres d’encodage sont modifiés – voir la perte de génération numérique pour plus de détails. Pour éviter la perte d’informations d’image lors de l’édition séquentielle et répétitive, la première édition peut être enregistrée dans un format sans perte, ensuite éditée dans ce format, puis finalement publiée au format JPEG pour distribution.
Compression JPEG
JPEG utilise une forme de compression avec perte basée sur la transformée en cosinus discrète(DCT). Cette opération mathématique convertit chaque image/champ de la source vidéo du domaine spatial (2D) dans le domaine fréquentiel (domaine de transformation). Un modèle perceptif basé vaguement sur le système psychovisuel humain rejette les informations à haute fréquence, c’est-à-dire les transitions nettes d’intensité et de teinte de couleur. Dans le domaine de la transformée, le processus de réduction de l’information est appelé quantification. En termes plus simples, la quantification est une méthode pour réduire de manière optimale une grande échelle de nombres (avec différentes occurrences de chaque nombre) en une plus petite, et le domaine de transformation est une représentation pratique de l’image car les coefficients haute fréquence, qui contribuent moins à l’image globale que d’autres coefficients, sont généralement de petites valeurs avec une compressibilité élevée. Les coefficients quantifiés sont ensuite séquencés et emballés sans perte dans le flux binaire de sortie. Presque toutes les implémentations logicielles de JPEG permettent à l’utilisateur de contrôler le taux de compression (ainsi que d’autres paramètres facultatifs), permettant à l’utilisateur de troquer la qualité d’image contre une taille de fichier plus petite. Dans les applications embarquées (telles que miniDV, qui utilise un schéma de compression DCT similaire), les paramètres sont présélectionnés et fixés pour l’application.
La méthode de compression est généralement avec perte , ce qui signifie que certaines informations de l’image d’origine sont perdues et ne peuvent pas être restaurées, ce qui peut affecter la qualité de l’image. Il existe un mode optionnel sans perte défini dans la norme JPEG. Cependant, ce mode n’est pas largement pris en charge dans les produits.
Il existe également un format JPEG progressif entrelacé , dans lequel les données sont compressées en plusieurs passes de détails progressivement plus élevés. Ceci est idéal pour les grandes images qui seront affichées lors du téléchargement via une connexion lente, permettant un aperçu raisonnable après avoir reçu seulement une partie des données. Cependant, la prise en charge des JPEG progressifs n’est pas universelle. Lorsque des JPEG progressifs sont reçus par des programmes qui ne les prennent pas en charge (comme les versions d’ Internet Explorer antérieures à Windows 7 ) [47] , le logiciel n’affiche l’image qu’après son téléchargement complet.
Il existe également de nombreuses applications d’imagerie médicale, de trafic et de caméra qui créent et traitent des images JPEG 12 bits à la fois en niveaux de gris et en couleur. Le format JPEG 12 bits est inclus dans une partie étendue de la spécification JPEG. Le codec libjpeg supporte le JPEG 12 bits et il existe même une version performante. [48]
Édition sans perte
Plusieurs modifications d’une image JPEG peuvent être effectuées sans perte (c’est-à-dire sans recompression et perte de qualité associée) tant que la taille de l’image est un multiple de 1 bloc MCU (unité codée minimale) (généralement 16 pixels dans les deux sens, pour 4 :2:0 sous-échantillonnage de chrominance ). Les utilitaires qui implémentent cela incluent :
- jpegtranet son interface graphique, Jpegcrop.
- IrfanViewen utilisant “JPG Lossless Crop (PlugIn)” et “JPG Lossless Rotation (PlugIn)”, qui nécessitent l’installation du plugin JPG_TRANSFORM.
- FastStone Image Vieweren utilisant « Lossless Crop to File » et « JPEG Lossless Rotate ».
- XnViewMPen utilisant des “transformations JPEG sans perte”.
- ACDSeeprend en charge la rotation sans perte (mais pas le recadrage sans perte) avec son option “Forcer les opérations JPEG sans perte”.
Les blocs peuvent être tournés par incréments de 90 degrés, retournés dans les axes horizontal, vertical et diagonal et déplacés dans l’image. Tous les blocs de l’image d’origine n’ont pas besoin d’être utilisés dans l’image modifiée.
Les bords supérieur et gauche d’une image JPEG doivent se trouver sur une limite de bloc de 8 × 8 pixels, mais les bords inférieur et droit n’ont pas besoin de le faire. Cela limite les opérations de recadrage sans perte possibles et empêche également les retournements et les rotations d’une image dont le bord inférieur ou droit ne se trouve pas sur une limite de bloc pour tous les canaux (car le bord se retrouverait en haut ou à gauche, où – comme mentionné ci-dessus – un limite de bloc est obligatoire).
Les rotations où l’image n’est pas un multiple de 8 ou 16, dont la valeur dépend du sous-échantillonnage de la chrominance, ne sont pas sans perte. La rotation d’une telle image entraîne le recalcul des blocs, ce qui entraîne une perte de qualité. [49]
Lors de l’utilisation du recadrage sans perte, si le bas ou le côté droit de la zone de recadrage ne se trouve pas sur une limite de bloc, le reste des données des blocs partiellement utilisés sera toujours présent dans le fichier recadré et pourra être récupéré. Il est également possible de passer du format de base au format progressif sans aucune perte de qualité, puisque la seule différence est l’ordre dans lequel les coefficients sont placés dans le fichier.
De plus, plusieurs images JPEG peuvent être jointes sans perte, tant qu’elles ont été enregistrées avec la même qualité et que les bords coïncident avec les limites des blocs.
Fichiers JPEG
Le format de fichier dit “JPEG Interchange Format” (JIF) est spécifié dans l’annexe B de la norme. Cependant, ce format de fichier « pur » est rarement utilisé, principalement en raison de la difficulté de programmer des encodeurs et des décodeurs qui implémentent pleinement tous les aspects de la norme et en raison de certaines lacunes de la norme :
- Définition de l’espace colorimétrique
- Enregistrement du sous-échantillonnage des composants
- Définition du rapport hauteur/largeur des pixels.
Plusieurs normes supplémentaires ont été élaborées pour résoudre ces problèmes. Le premier d’entre eux, sorti en 1992, était le format d’ échange de fichiers JPEG (ou JFIF), suivi ces dernières années par le format de fichier image échangeable (Exif) et les profils de couleurs ICC . Ces deux formats utilisent la disposition d’octets JIF réelle, composée de différents marqueurs , mais utilisent en outre l’un des points d’extension de la norme JIF, à savoir les marqueurs d’application : JFIF utilise APP0, tandis qu’Exif utilise APP1. Dans ces segments du fichier qui ont été laissés pour une utilisation future dans la norme JIF et qui ne sont pas lus par celle-ci, ces normes ajoutent des métadonnées spécifiques.
Ainsi, à certains égards, JFIF est une version réduite de la norme JIF en ce sens qu’il spécifie certaines contraintes (telles que ne pas autoriser tous les différents modes de codage), tandis que d’autres manières, il s’agit d’une extension de JIF en raison de l’ajout métadonnées. La documentation de la norme JFIF d’origine indique : [50]
Le format d’échange de fichiers JPEG est un format de fichier minimal qui permet d’échanger des flux binaires JPEG entre une grande variété de plates-formes et d’applications. Ce format minimal n’inclut aucune des fonctionnalités avancées trouvées dans la spécification TIFF JPEG ou tout format de fichier spécifique à l’application. Il ne devrait pas non plus, car le seul but de ce format simplifié est de permettre l’échange d’images compressées JPEG.
Les fichiers d’image qui utilisent la compression JPEG sont communément appelés “fichiers JPEG” et sont stockés dans des variantes du Format d’image JIF. La plupart des appareils de capture d’images (tels que les appareils photo numériques) qui génèrent des fichiers JPEG créent en fait des fichiers au format Exif , le format sur lequel l’industrie de l’appareil photo a normalisé l’échange de métadonnées. D’autre part, comme la norme Exif n’autorise pas les profils de couleur, la plupart des logiciels d’édition d’images stockent JPEG au format JFIF et incluent également le segment APP1 du fichier Exif pour inclure les métadonnées de manière presque conforme. la norme JFIF est interprétée avec une certaine souplesse. [51]
Strictement parlant, les normes JFIF et Exif sont incompatibles, car chacune spécifie que son segment marqueur (APP0 ou APP1, respectivement) apparaît en premier. En pratique, la plupart des fichiers JPEG contiennent un segment marqueur JFIF qui précède l’en-tête Exif. Cela permet aux lecteurs plus âgés de gérer correctement le segment JFIF au format plus ancien, tandis que les lecteurs plus récents décodent également le segment Exif suivant, étant moins stricts quant à l’exigence qu’il apparaisse en premier.
Extensions de nom de fichier JPEG
Les extensions de nom de fichier les plus courantes pour les fichiers utilisant la compression JPEG sont .jpget .jpeg, cependant .jpe, .jfifet .jifsont également utilisées. Il est également possible que des données JPEG soient intégrées dans d’autres types de fichiers – les fichiers encodés TIFF intègrent souvent une image JPEG sous forme de vignette de l’image principale ; et les fichiers MP3 peuvent contenir un JPEG de la pochette dans la balise ID3v2 .
Profil de couleur
De nombreux fichiers JPEG intègrent un profil de couleur ICC ( espace colorimétrique ). Les profils de couleurs couramment utilisés incluent sRVB et Adobe RVB . Étant donné que ces espaces colorimétriques utilisent une transformation non linéaire, la plage dynamique d’un fichier JPEG 8 bits est d’environ 11 arrêts ; voir courbe gamma .
Si l’image ne spécifie pas d’informations sur le profil de couleur ( untagged ), l’espace colorimétrique est supposé être sRGB pour les besoins de l’affichage sur les pages Web. [52] [53]
Syntaxe et structure
Une image JPEG se compose d’une séquence de segments , chacun commençant par un marqueur , chacun commençant par un octet 0xFF, suivi d’un octet indiquant de quel type de marqueur il s’agit. Certains marqueurs se composent uniquement de ces deux octets ; d’autres sont suivis de deux octets (haut puis bas), indiquant la longueur des données de charge utile spécifiques au marqueur qui suivent. (La longueur inclut les deux octets pour la longueur, mais pas les deux octets pour le marqueur.) Certains marqueurs sont suivis de données codées entropie ; la longueur d’un tel marqueur n’inclut pas les données codées par entropie. Notez que les octets 0xFF consécutifs sont utilisés comme octets de remplissage pour le remplissagefins, bien que ce rembourrage d’octets de remplissage ne doive avoir lieu que pour les marqueurs qui suivent immédiatement les données de numérisation codées entropie (voir les sections B.1.1.2 et E.1.2 de la spécification JPEG pour plus de détails ; en particulier “Dans tous les cas où des marqueurs sont ajoutés après les données compressées données, des octets de remplissage facultatifs 0xFF peuvent précéder le marqueur”).
Dans les données codées entropie, après tout octet 0xFF, un octet 0x00 est inséré par l’encodeur avant l’octet suivant, de sorte qu’il ne semble pas y avoir de marqueur là où aucun n’est prévu, empêchant les erreurs de cadrage. Les décodeurs doivent sauter cet octet 0x00. Cette technique, appelée bourrage d’octets (voir la section F.1.2.3 de la spécification JPEG), n’est appliquée qu’aux données codées par entropie, et non aux données de charge utile du marqueur. Notez cependant que les données codées par entropie ont leurs propres marqueurs ; spécifiquement les marqueurs de réinitialisation (0xD0 à 0xD7), qui sont utilisés pour isoler des blocs indépendants de données codées entropie pour permettre un décodage parallèle, et les encodeurs sont libres d’insérer ces marqueurs de réinitialisation à intervalles réguliers (bien que tous les encodeurs ne le fassent pas).
| Nom court | Octets | Charge utile | Nom | commentaires |
|---|---|---|---|---|
| DONC JE | 0xFF, 0xD8 | rien | Début de l’image | |
| SOF0 | 0xFF, 0xC0 | taille variable | Début de trame ( DCT de base ) | Indique qu’il s’agit d’un JPEG basé sur DCT de base et spécifie la largeur, la hauteur, le nombre de composants et le sous-échantillonnage des composants (par exemple, 4:2:0). |
| SOF2 | 0xFF, 0xC2 | taille variable | Début de trame (DCT progressif) | Indique qu’il s’agit d’un JPEG progressif basé sur DCT et spécifie la largeur, la hauteur, le nombre de composants et le sous-échantillonnage des composants (par exemple, 4:2:0). |
| DHT | 0xFF, 0xC4 | taille variable | Définir la ou les tables de Huffman | Spécifie une ou plusieurs tables de Huffman. |
| DQT | 0xFF, 0xDB | taille variable | Définir la ou les tables de quantification | Spécifie une ou plusieurs tables de quantification. |
| DRI | 0xFF, 0xDD | 4 octets | Définir l’intervalle de redémarrage | Spécifie l’intervalle entre les marqueurs RST n , en unités codées minimales (MCU). Ce marqueur est suivi de deux octets indiquant la taille fixe afin qu’il puisse être traité comme n’importe quel autre segment de taille variable. |
| SOS | 0xFF, 0xDA | taille variable | Début de l’analyse | Commence un balayage de haut en bas de l’image. Dans les images DCT JPEG de base, il y a généralement une seule numérisation. Les images JPEG DCT progressives contiennent généralement plusieurs numérisations. Ce marqueur spécifie quelle tranche de données il contiendra et est immédiatement suivi de données codées entropiquement. |
| TVD n | 0xFF, 0xD n ( n =0..7) | rien | Redémarrer | Inséré tous les r macroblocs, où r est l’intervalle de redémarrage défini par un marqueur DRI. Non utilisé s’il n’y avait pas de marqueur DRI. Les trois bits de poids faible du code marqueur changent de valeur de 0 à 7. |
| APP n | 0xFF, 0xE n | taille variable | Spécifique à l’application | Par exemple, un fichier Exif JPEG utilise un marqueur APP1 pour stocker les métadonnées, disposées dans une structure étroitement basée sur TIFF . |
| COM | 0xFF, 0xFE | taille variable | Commenter | Contient un commentaire textuel. |
| déclaration d’intérêt | 0xFF, 0xD9 | rien | Fin de l’image |
Il existe d’autres marqueurs de début de trame qui introduisent d’autres types d’encodages JPEG.
Étant donné que plusieurs fournisseurs peuvent utiliser le même type de marqueur APP n , les marqueurs spécifiques à l’application commencent souvent par un nom standard ou de fournisseur (par exemple, “Exif” ou “Adobe”) ou une autre chaîne d’identification.
Au niveau d’un marqueur de redémarrage, les variables de prédiction bloc à bloc sont réinitialisées et le flux binaire est synchronisé sur une limite d’octet. Les marqueurs de redémarrage fournissent des moyens de récupération après une erreur de flux binaire, telle qu’une transmission sur un réseau non fiable ou une corruption de fichier. Etant donné que les séquences de macroblocs entre les marqueurs de redémarrage peuvent être décodées indépendamment, ces séquences peuvent être décodées en parallèle.
Exemple de codec JPEG
Bien qu’un fichier JPEG puisse être encodé de différentes manières, le plus souvent, il se fait avec l’encodage JFIF. Le processus d’encodage comprend plusieurs étapes :
- La représentation des couleurs dans l’image est convertie de RVB en Y′C B C R , consistant en une composante luma (Y’), représentant la luminosité, et deux composantes chroma (C B et C R ), représentant la couleur. Cette étape est parfois ignorée.
- La résolution des données de chrominance est réduite, généralement d’un facteur 2 ou 3. Cela reflète le fait que l’œil est moins sensible aux détails de couleur fins qu’aux détails de luminosité fins.
- L’image est découpée en blocs de 8×8 pixels, et pour chaque bloc, chacune des données Y, C B et C R subit la transformée en cosinus discrète (DCT). Une DCT est similaire à une transformée de Fourier en ce sens qu’elle produit une sorte de spectre de fréquences spatiales.
- Les amplitudes des composantes fréquentielles sont quantifiées . La vision humaine est beaucoup plus sensible aux petites variations de couleur ou de luminosité sur de grandes surfaces qu’à la force des variations de luminosité à haute fréquence. Par conséquent, les amplitudes des composants haute fréquence sont stockées avec une précision inférieure à celle des composants basse fréquence. Le réglage de qualité de l’encodeur (par exemple 50 ou 95 sur une échelle de 0 à 100 dans la bibliothèque de l’Independent JPEG Group [55] ) affecte dans quelle mesure la résolution de chaque composante de fréquence est réduite. Si un réglage de qualité excessivement bas est utilisé, les composants haute fréquence sont complètement ignorés.
- Les données résultantes pour tous les blocs 8 × 8 sont encore compressées avec un algorithme sans perte, une variante du codage Huffman .
Le processus de décodage inverse ces étapes, sauf la quantification car elle est irréversible. Dans le reste de cette section, les processus de codage et de décodage sont décrits plus en détail.
Codage
De nombreuses options de la norme JPEG ne sont pas couramment utilisées et, comme mentionné ci-dessus, la plupart des logiciels d’image utilisent le format JFIF plus simple lors de la création d’un fichier JPEG, qui spécifie entre autres la méthode d’encodage. Voici une brève description de l’une des méthodes de codage les plus courantes lorsqu’elle est appliquée à une entrée de 24 bits par pixel (huit de rouge, vert et bleu ). Cette option particulière est une méthode de compression de données avec perte .
Transformation de l’espace colorimétrique
Tout d’abord, l’image doit être convertie de RVB (par défaut sRGB, [52] [53] mais d’autres espaces colorimétriques sont possibles) en un espace colorimétrique différent appelé Y′C B C R (ou, de manière informelle, YCbCr). Il comporte trois composantes Y’, C B et C R : la composante Y’ représente la luminosité d’un pixel, et les composantes C B et C R représentent la chrominance (décomposée en composantes bleue et rouge). Il s’agit essentiellement du même espace colorimétrique que celui utilisé par la télévision couleur numérique ainsi que la vidéo numérique, y compris les DVD vidéo . Le Y′C BLa conversion de l’espace colorimétrique C R permet une plus grande compression sans effet significatif sur la qualité perceptuelle de l’image (ou une meilleure qualité perceptuelle de l’image pour la même compression). La compression est plus efficace car l’information de luminosité, qui est plus importante pour la qualité perceptuelle finale de l’image, est confinée à un seul canal. Cela correspond plus étroitement à la perception de la couleur dans le système visuel humain. La transformation des couleurs améliore également la compression par décorrélation statistique .
Une conversion particulière en Y′C B C R est spécifiée dans la norme JFIF et doit être effectuée pour que le fichier JPEG résultant ait une compatibilité maximale. Cependant, certaines implémentations JPEG en mode “qualité la plus élevée” n’appliquent pas cette étape et conservent à la place les informations de couleur dans le modèle de couleur RVB , [56] où l’image est stockée dans des canaux séparés pour les composants de luminosité rouge, vert et bleu. Cela entraîne une compression moins efficace et ne serait probablement pas utilisé lorsque la taille du fichier est particulièrement importante.
Sous-échantillonnage
En raison des densités de récepteurs sensibles à la couleur et à la luminosité dans l’œil humain, les humains peuvent voir beaucoup plus de détails fins dans la luminosité d’une image (la composante Y’) que dans la teinte et la saturation des couleurs d’une image (le Cb et Composants Cr). Grâce à ces connaissances, les encodeurs peuvent être conçus pour compresser les images plus efficacement.
La transformation dans le modèle de couleur Y’C B C R permet l’étape suivante usuelle, qui est de réduire la résolution spatiale des composantes Cb et Cr (appelée « downsampling » ou « chroma subsampling »). Les rapports auxquels le sous-échantillonnage est généralement effectué pour les images JPEG sont 4:4:4 (pas de sous-échantillonnage), 4:2:2 (réduction d’un facteur 2 dans le sens horizontal) ou (le plus souvent) 4:2 : 0 (diminution d’un facteur 2 dans le sens horizontal et vertical). Pour le reste du processus de compression, Y’, Cb et Cr sont traités séparément et de manière très similaire.
Fractionnement de blocs
Après le sous- échantillonnage , chaque canal doit être divisé en blocs de 8 × 8. En fonction du sous-échantillonnage de la chrominance, cela donne des blocs d’unité codée minimale (MCU) de taille 8 × 8 (4: 4: 4 – pas de sous-échantillonnage), 16 × 8 (4: 2: 2) ou le plus souvent 16 × 16 (4: 2:0). Dans la compression vidéo, les MCU sont appelés macroblocs .
Si les données pour un canal ne représentent pas un nombre entier de blocs, alors le codeur doit remplir la zone restante des blocs incomplets avec une certaine forme de données fictives. Remplir les bords avec une couleur fixe (par exemple, le noir) peut créer des artefacts de sonnerie le long de la partie visible de la bordure ; la répétition des pixels de bord est une technique courante qui réduit (mais n’élimine pas nécessairement) ces artefacts, et des techniques de remplissage de bordure plus sophistiquées peuvent également être appliquées.
Transformée discrète en cosinus 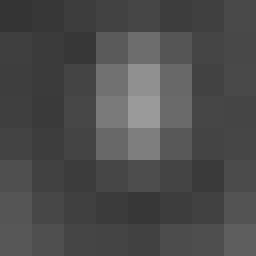
 La sous-image 8 × 8 affichée en niveaux de gris 8 bits
La sous-image 8 × 8 affichée en niveaux de gris 8 bits
Ensuite, chaque bloc 8 × 8 de chaque composant (Y, Cb, Cr) est converti en une représentation dans le domaine fréquentiel , à l’aide d’une transformée en cosinus discrète bidimensionnelle normalisée de type II (DCT), voir Citation 1 dans la transformée en cosinus discrète . Le DCT est parfois appelé “DCT de type II” dans le contexte d’une famille de transformées comme dans la transformée en cosinus discrète , et l’inverse correspondant (IDCT) est désigné par “DCT de type III”.
Par exemple, une telle sous-image 8 × 8 8 bits pourrait être :
[ 52 55 61 66 70 61 64 73 63 59 55 90 109 85 69 72 62 59 68 113 144 104 66 73 63 58 71 122 154 106 70 69 67 61 68 104 126 88 68 70 79 65 60 70 77 68 58 75 85 71 64 59 55 61 65 83 87 79 69 68 65 76 78 94 ] . {displaystyle left[{begin{array}{rrrrrrrr}52&55&61&66&70&61&64&73\63&59&55&90&109&85&69&72\62&59&68&113&144&104&66&73\63&58&71&122&154&106&70&69\67&61&68&104&126&88&68&70\79&65&60&70&77&68&58&75\85&71&64&59&55&61&65&83\87&79&69&68&65&76&78&94end{array}}right].} ![left[{begin{array}{rrrrrrrr}52&55&61&66&70&61&64&73\63&59&55&90&109&85&69&72\62&59&68&113&144&104&66&73\63&58&71&122&154&106&70&69\67&61&68&104&126&88&68&70\79&65&60&70&77&68&58&75\85&71&64&59&55&61&65&83\87&79&69&68&65&76&78&94end{array}}right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/eed8c00e62db6618fd452d3905a03f842c30ce34)
Avant de calculer le DCT du bloc 8 × 8, ses valeurs sont décalées d’une plage positive à une plage centrée sur zéro. Pour une image 8 bits, chaque entrée du bloc d’origine tombe dans la plage [ 0 , 255 ] {displaystyle [0,255]} ![[0,255]](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b92f49fdc420e36b9d62c711c3c6ebe7d9fcebc)
. Le milieu de la plage (dans ce cas, la valeur 128) est soustrait de chaque entrée pour produire une plage de données centrée sur zéro, de sorte que la plage modifiée est [ − 128 , 127 ] {displaystyle [-128,127]}
![[-128,127]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3709f640eb5df69afe38bd25ef8e4bfa189a99b)
. Cette étape réduit les exigences de plage dynamique dans l’étape de traitement DCT qui suit.
Cette étape donne les valeurs suivantes :
g = x ⟶ [ − 76 − 73 − 67 − 62 − 58 − 67 − 64 − 55 − 65 − 69 − 73 − 38 − 19 − 43 − 59 − 56 − 66 − 69 − 60 − 15 16 − 24 − 62 − 55 − 65 − 70 − 57 − 6 26 − 22 − 58 − 59 − 61 − 67 − 60 − 24 − 2 − 40 − 60 − 58 − 49 − 63 − 68 − 58 − 51 − 60 − 70 − 53 − 43 − 57 − 64 − 69 − 73 − 67 − 63 − 45 − 41 − 49 − 59 − 60 − 63 − 52 − 50 − 34 ] ↓ y . {displaystyle g={begin{array}{c}x\longrightarrow \left[{begin{array}{rrrrrrrr}-76&-73&-67&-62&-58&-67&-64&-55\-65&-69&-73&-38&-19&-43&-59&-56\-66&-69&-60&-15&16&-24&-62&-55\-65&-70&-57&-6&26&-22&-58&-59\-61&-67&-60&-24&-2&-40&-60&-58\-49&-63&-68&-58&-51&-60&-70&-53\-43&-57&-64&-69&-73&-67&-63&-45\-41&-49&-59&-60&-63&-52&-50&-34end{array}}right]end{array}}{Bigg downarrow }y.} ![g={begin{array}{c}x\longrightarrow \left[{begin{array}{rrrrrrrr}-76&-73&-67&-62&-58&-67&-64&-55\-65&-69&-73&-38&-19&-43&-59&-56\-66&-69&-60&-15&16&-24&-62&-55\-65&-70&-57&-6&26&-22&-58&-59\-61&-67&-60&-24&-2&-40&-60&-58\-49&-63&-68&-58&-51&-60&-70&-53\-43&-57&-64&-69&-73&-67&-63&-45\-41&-49&-59&-60&-63&-52&-50&-34end{array}}right]end{array}}{Bigg downarrow }y.](https://wikimedia.org/api/rest_v1/media/math/render/svg/f69a5e277c8e5d58ea12abdf1b102668b9bb5bf1)

 Le DCT transforme un bloc 8 × 8 de valeurs d’entrée en une combinaison linéaire de ces 64 modèles. Les modèles sont appelés fonctions de base DCT bidimensionnelles et les valeurs de sortie sont appelées coefficients de transformation . L’indice horizontal est u {displaystyle u}
Le DCT transforme un bloc 8 × 8 de valeurs d’entrée en une combinaison linéaire de ces 64 modèles. Les modèles sont appelés fonctions de base DCT bidimensionnelles et les valeurs de sortie sont appelées coefficients de transformation . L’indice horizontal est u {displaystyle u} 
et l’indice vertical est v {style d’affichage v}

.
L’étape suivante consiste à prendre le DCT bidimensionnel, qui est donné par :
G u , v = 1 4 α ( u ) α ( v ) ∑ x = 0 7 ∑ y = 0 7 g x , y cos [ ( 2 x + 1 ) u π 16 ] cos [ ( 2 y + 1 ) v π 16 ] {displaystyle G_{u,v}={frac {1}{4}}alpha (u)alpha (v)sum _{x=0}^{7}sum _{y=0 }^{7}g_{x,y}cos left[{frac {(2x+1)upi }{16}}right]cos left[{frac {(2y+1) vpi }{16}}right]} ![G_{u,v}={frac {1}{4}}alpha (u)alpha (v)sum _{x=0}^{7}sum _{y=0}^{7}g_{x,y}cos left[{frac {(2x+1)upi }{16}}right]cos left[{frac {(2y+1)vpi }{16}}right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e06f6ee04c9c879a283edcbb7b1fc18b86fcec5b)
où
- u {displaystyleu}
est la fréquence spatiale horizontale , pour les entiers 0 ≤ u < 8 {displaystyle 0leq u<8}
.
- v {displaystylev}
est la fréquence spatiale verticale, pour les entiers 0 ≤ v < 8 {displaystyle 0leq v<8}
.
- α ( u ) = { 1 2 , if u = 0 1 , otherwise {displaystyle alpha (u)={begin{cases}{frac {1}{sqrt {2}}},&{mbox{if }}u=0\1,&{mbox{ sinon}}end{cases}}}
est un facteur d’échelle de normalisation pour rendre la transformation orthonormée
- g x , y {displaystyle g_{x,y}}
est la valeur du pixel aux coordonnées ( x , y ) { style d’affichage (x, y)}
- G u , v {displaystyle G_{u,v}}
est le coefficient DCT aux coordonnées ( u , v ) . {displaystyle(u,v).}
Si nous effectuons cette transformation sur notre matrice ci-dessus, nous obtenons ce qui suit (arrondi aux deux chiffres les plus proches après la virgule):
G = u ⟶ [ − 415.38 − 30.19 − 61.20 27.24 56.12 − 20.10 − 2.39 0.46 4.47 − 21.86 − 60.76 10.25 13.15 − 7.09 − 8.54 4.88 − 46.83 7.37 77.13 − 24.56 − 28.91 9.93 5.42 − 5.65 − 48.53 12.07 34.10 − 14.76 − 10.24 6.30 1.83 1.95 12.12 − 6.55 − 13.20 − 3.95 − 1.87 1.75 − 2.79 3.14 − 7.73 2.91 2.38 − 5.94 − 2.38 0.94 4.30 1.85 − 1.03 0.18 0.42 − 2.42 − 0.88 − 3.02 4.12 − 0.66 − 0.17 0.14 − 1.07 − 4.19 − 1.17 − 0.10 0.50 1.68 ] ↓ v . {displaystyle G={begin{array}{c}u\longrightarrow \left[{begin{array}{rrrrrrrr}-415.38&-30.19&-61.20&27.24&56.12&-20.10&-2.39&0.46\4.47&-21.86&-60.76&10.25&13.15&-7.09&-8.54&4.88\-46.83&7.37&77.13&-24.56&-28.91&9.93&5.42&-5.65\-48.53&12.07&34.10&-14.76&-10.24&6.30&1.83&1.95\12.12&-6.55&-13.20&-3.95&-1.87&1.75&-2.79&3.14\-7.73&2.91&2.38&-5.94&-2.38&0.94&4.30&1.85\-1.03&0.18&0.42&-2.42&-0.88&-3.02&4.12&-0.66\-0.17&0.14&-1.07&-4.19&-1.17&-0.10&0.50&1.68end{array}}right]end{array}}{Bigg downarrow }v.} ![G={begin{array}{c}u\longrightarrow \left[{begin{array}{rrrrrrrr}-415.38&-30.19&-61.20&27.24&56.12&-20.10&-2.39&0.46\4.47&-21.86&-60.76&10.25&13.15&-7.09&-8.54&4.88\-46.83&7.37&77.13&-24.56&-28.91&9.93&5.42&-5.65\-48.53&12.07&34.10&-14.76&-10.24&6.30&1.83&1.95\12.12&-6.55&-13.20&-3.95&-1.87&1.75&-2.79&3.14\-7.73&2.91&2.38&-5.94&-2.38&0.94&4.30&1.85\-1.03&0.18&0.42&-2.42&-0.88&-3.02&4.12&-0.66\-0.17&0.14&-1.07&-4.19&-1.17&-0.10&0.50&1.68end{array}}right]end{array}}{Bigg downarrow }v.](https://wikimedia.org/api/rest_v1/media/math/render/svg/46ee57df2a309dd59e0a10c9ab83e8b86d712e3e)
Notez l’entrée du coin supérieur gauche avec la magnitude plutôt grande. Il s’agit du coefficient DC (également appelé composante constante), qui définit la teinte de base pour l’ensemble du bloc. Les 63 coefficients restants sont les coefficients AC (également appelés composants alternatifs). [57] L’avantage du DCT est sa tendance à agréger la majeure partie du signal dans un coin du résultat, comme on peut le voir ci-dessus. L’étape de quantification à suivre accentue cet effet tout en réduisant simultanément la taille globale des coefficients DCT, résultant en un signal facile à compresser efficacement dans l’étage d’entropie.
Le DCT augmente temporairement la profondeur de bits des données, car les coefficients DCT d’une image 8 bits / composante prennent jusqu’à 11 bits ou plus (selon la fidélité du calcul DCT) pour être stockés. Cela peut forcer le codec à utiliser temporairement des nombres de 16 bits pour conserver ces coefficients, doublant la taille de la représentation de l’image à ce stade ; ces valeurs sont généralement ramenées à des valeurs de 8 bits par l’étape de quantification. L’augmentation temporaire de la taille à ce stade n’est pas un problème de performances pour la plupart des implémentations JPEG, car généralement seule une très petite partie de l’image est stockée sous forme DCT complète à un moment donné pendant le processus de codage ou de décodage de l’image.
Quantification
L’œil humain est doué pour voir de petites différences de luminositésur une zone relativement grande, mais pas aussi bon pour distinguer l’intensité exacte d’une variation de luminosité à haute fréquence. Cela permet de réduire considérablement la quantité d’informations dans les composants à haute fréquence. Cela se fait en divisant simplement chaque composant dans le domaine fréquentiel par une constante pour ce composant, puis en arrondissant à l’entier le plus proche. Cette opération d’arrondi est la seule opération avec perte dans l’ensemble du processus (autre que le sous-échantillonnage de chrominance) si le calcul DCT est effectué avec une précision suffisamment élevée. En conséquence, il arrive généralement que de nombreuses composantes de fréquence plus élevée soient arrondies à zéro, et la plupart des autres deviennent de petits nombres positifs ou négatifs, qui nécessitent beaucoup moins de bits pour être représentés.
Les éléments de la matrice de quantification contrôlent le taux de compression, des valeurs plus élevées produisant une plus grande compression. Une matrice de quantification typique (pour une qualité de 50 % telle que spécifiée dans la norme JPEG d’origine) est la suivante :
Q = [ 16 11 10 16 24 40 51 61 12 12 14 19 26 58 60 55 14 13 16 24 40 57 69 56 14 17 22 29 51 87 80 62 18 22 37 56 68 109 103 77 24 35 55 64 81 104 113 92 49 64 78 87 103 121 120 101 72 92 95 98 112 100 103 99 ] . {displaystyle Q={begin{bmatrix}16&11&10&16&24&40&51&61\12&12&14&19&26&58&60&55\14&13&16&24&40&57&69&56\14&17&22&29&51&87&80&62\18&22&37&56&68&109&103&77\24&35&55&64&81&104&113&92\49&64&78&87&103&121&120&101\72&92&95&98&112&100&103&99end{bmatrix}}.} 
Les coefficients DCT quantifiés sont calculés avec
B j , k = r o u n d ( G j , k Q j , k ) for j = 0 , 1 , 2 , … , 7 ; k = 0 , 1 , 2 , … , 7 {displaystyle B_{j,k}=mathrm {rond} left({frac {G_{j,k}}{Q_{j,k}}}right){mbox{ for }}j= 0,1,2,ldots ,7;k=0,1,2,ldots ,7} 
où G {displaystyle G} 
est les coefficients DCT non quantifiés ; Q {displaystyle Q}

est la matrice de quantification ci-dessus ; et B {displaystyle B}

est les coefficients DCT quantifiés.
L’utilisation de cette matrice de quantification avec la matrice de coefficients DCT ci-dessus donne :

 A gauche : une image finale est construite à partir d’une série de fonctions de base. À droite : chacune des fonctions de base DCT qui composent l’image, et le coefficient de pondération correspondant. Milieu : la fonction de base, après multiplication par le coefficient : cette composante est ajoutée à l’image finale. Pour plus de clarté, le macrobloc 8×8 dans cet exemple est agrandi de 10x en utilisant une interpolation bilinéaire. B = [ − 26 − 3 − 6 2 2 − 1 0 0 0 − 2 − 4 1 1 0 0 0 − 3 1 5 − 1 − 1 0 0 0 − 3 1 2 − 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ] . {displaystyle B=left[{begin{array}{rrrrrrrr}-26&-3&-6&2&2&-1&0&0\0&-2&-4&1&1&0&0&0\-3&1&5&-1&-1&0&0&0\-3&1&2&-1&0&0&0&0\1&0&0&0&0&0&0&0\ �&0&0&0&0&0&0&0\0&0&0&0&0&0&0&0\0&0&0&0&0&0&0&0end{tableau}}right].}
A gauche : une image finale est construite à partir d’une série de fonctions de base. À droite : chacune des fonctions de base DCT qui composent l’image, et le coefficient de pondération correspondant. Milieu : la fonction de base, après multiplication par le coefficient : cette composante est ajoutée à l’image finale. Pour plus de clarté, le macrobloc 8×8 dans cet exemple est agrandi de 10x en utilisant une interpolation bilinéaire. B = [ − 26 − 3 − 6 2 2 − 1 0 0 0 − 2 − 4 1 1 0 0 0 − 3 1 5 − 1 − 1 0 0 0 − 3 1 2 − 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ] . {displaystyle B=left[{begin{array}{rrrrrrrr}-26&-3&-6&2&2&-1&0&0\0&-2&-4&1&1&0&0&0\-3&1&5&-1&-1&0&0&0\-3&1&2&-1&0&0&0&0\1&0&0&0&0&0&0&0\ �&0&0&0&0&0&0&0\0&0&0&0&0&0&0&0\0&0&0&0&0&0&0&0end{tableau}}right].} ![B=left[{begin{array}{rrrrrrrr}-26&-3&-6&2&2&-1&0&0\0&-2&-4&1&1&0&0&0\-3&1&5&-1&-1&0&0&0\-3&1&2&-1&0&0&0&0\1&0&0&0&0&0&0&0\0&0&0&0&0&0&0&0\0&0&0&0&0&0&0&0\0&0&0&0&0&0&0&0end{array}}right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfedb02fc67c95d021b46c13f4fb21c55a361671)
Par exemple, en utilisant −415 (le coefficient DC) et en arrondissant à l’entier le plus proche
r o u n d ( − 415.37 16 ) = r o u n d ( − 25.96 ) = − 26. {displaystyle mathrm {rond} left({frac {-415.37}{16}}right)=mathrm {rond} left(-25.96right)=-26.} 
Notez que la plupart des éléments de fréquence plus élevée du sous-bloc (c’est-à-dire ceux avec une fréquence spatiale x ou y supérieure à 4) sont quantifiés en valeurs nulles.
Codage entropique 
 Ordre en zigzag des composants d’image JPEG
Ordre en zigzag des composants d’image JPEG
Le codage entropique est une forme spéciale de compression de données sans perte . Cela implique de disposer les composants de l’image dans un ordre ” en zigzag ” en utilisant un algorithme de codage de longueur de plage (RLE) qui regroupe des fréquences similaires, en insérant des zéros de codage de longueur, puis en utilisant le codage de Huffman sur ce qui reste.
La norme JPEG permet également, mais n’exige pas, que les décodeurs prennent en charge l’utilisation du codage arithmétique , qui est mathématiquement supérieur au codage Huffman. Cependant, cette fonctionnalité a rarement été utilisée, car elle était historiquement couverte par des Brevets nécessitant des licences payantes, et parce qu’elle est plus lente à encoder et à décoder par rapport au codage Huffman. Le codage arithmétique réduit généralement la taille des fichiers d’environ 5 à 7 %.
Le coefficient DC quantifié précédent est utilisé pour prédire le coefficient DC quantifié actuel. La différence entre les deux est codée plutôt que la valeur réelle. Le codage des 63 coefficients AC quantifiés n’utilise pas une telle différenciation de prédiction.
La séquence en zigzag pour les coefficients quantifiés ci-dessus est illustrée ci-dessous. (Le format indiqué est juste pour faciliter la compréhension/visualisation.)
| −26 | |||||||
| −3 | 0 | ||||||
| −3 | −2 | −6 | |||||
| 2 | −4 | 1 | −3 | ||||
| 1 | 1 | 5 | 1 | 2 | |||
| −1 | 1 | −1 | 2 | 0 | 0 | ||
| 0 | 0 | 0 | −1 | −1 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | |||||
| 0 | 0 | ||||||
| 0 |
Si le bloc i est représenté par B i {displaystyle B_{i}} 
et les positions dans chaque bloc sont représentées par ( p , q ) {displaystyle (p, q)}

où p = 0 , 1 , . . . , 7 {displaystyle p=0,1,…,7}

et q = 0 , 1 , . . . , 7 {displaystyle q=0,1,…,7}

, alors tout coefficient dans l’image DCT peut être représenté comme B i ( p , q ) {displaystyle B_{i}(p, q)}

. Ainsi, dans le schéma ci-dessus, l’ordre de codage des pixels (pour le i -ème bloc) est B i ( 0 , 0 ) {displaystyle B_{i}(0,0)}

, B i ( 0 , 1 ) {displaystyle B_{i}(0,1)}

, B i ( 1 , 0 ) {displaystyle B_{i}(1,0)}

, B i ( 2 , 0 ) {displaystyle B_{i}(2,0)}

, B i ( 1 , 1 ) {displaystyle B_{i}(1,1)}

, B i ( 0 , 2 ) {displaystyle B_{i}(0,2)}

, B i ( 0 , 3 ) {displaystyle B_{i}(0,3)}

, B i ( 1 , 2 ) {displaystyle B_{i}(1,2)}

etc.

 Processus de codage et de décodage JPEG séquentiels de base
Processus de codage et de décodage JPEG séquentiels de base
Ce mode de codage est appelé codage séquentiel de base . Le JPEG de base prend également en charge l’ encodage progressif . Alors que le codage séquentiel code les coefficients d’un seul bloc à la fois (en zigzag), le codage progressif code un lot de coefficients de position similaire de tous les blocs en une seule fois (appelé balayage ), suivi du lot suivant de coefficients de tous les blocs , etc. Par exemple, si l’image est découpée en N blocs 8×8 B 0 , B 1 , B 2 , . . . , B n − 1 {displaystyle B_{0},B_{1},B_{2},…,B_{n-1}} 
, puis un codage progressif à 3 balayages code la composante continue, B i ( 0 , 0 ) {displaystyle B_{i}(0,0)}

pour tous les blocs, c’est-à-dire pour tous i = 0 , 1 , 2 , . . . , N − 1 {displaystyle i=0,1,2,…,N-1}

, lors du premier balayage. Ceci est suivi par la deuxième analyse qui encode quelques composants supplémentaires (en supposant quatre composants supplémentaires, ils sont B i ( 0 , 1 ) {displaystyle B_{i}(0,1)}

pour B i ( 1 , 1 ) {displaystyle B_{i}(1,1)}

, toujours en zigzag) les coefficients de tous les blocs (donc la séquence est : B 0 ( 0 , 1 ) , B 0 ( 1 , 0 ) , B 0 ( 2 , 0 ) , B 0 ( 1 , 1 ) , B 1 ( 0 , 1 ) , B 1 ( 1 , 0 ) , . . . , B N ( 2 , 0 ) , B N ( 1 , 1 ) {displaystyle B_{0}(0,1),B_{0}(1,0),B_{0}(2,0),B_{0}(1,1),B_{1}(0, 1),B_{1}(1,0),…,B_{N}(2,0),B_{N}(1,1)}

), suivi de tous les coefficients restants de tous les blocs du dernier balayage.
Une fois que tous les coefficients positionnés de manière similaire ont été codés, la position suivante à coder est celle qui se produit ensuite dans la traversée en zigzag, comme indiqué dans la figure ci-dessus. Il a été constaté que le codage JPEG progressif de base donne généralement une meilleure compression par rapport au JPEG séquentiel de base en raison de la possibilité d’utiliser différentes tables de Huffman (voir ci-dessous) adaptées à différentes fréquences sur chaque “balayage” ou “passe” (qui inclut des coefficients positionnés), bien que la différence ne soit pas trop grande.
Dans la suite de l’article, on suppose que le motif de coefficients généré est dû au mode séquentiel.
Afin de coder le modèle de coefficient généré ci-dessus, JPEG utilise le codage Huffman. La norme JPEG fournit des tables de Huffman à usage général ; les codeurs peuvent également choisir de générer des tables de Huffman optimisées pour les distributions de fréquences réelles dans les images en cours de codage.
Le processus de codage des données quantifiées en zigzag commence par un codage de longueur d’exécution expliqué ci-dessous, où :
- x est le coefficient AC quantifié non nul.
- RUNLENGTH est le nombre de zéros qui précèdent ce coefficient AC non nul.
- SIZE est le nombre de bits requis pour représenter x .
- AMPLITUDE est la représentation binaire de x .
Le codage de longueur de plage fonctionne en examinant chaque coefficient AC non nul x et en déterminant combien de zéros sont venus avant le coefficient AC précédent. Avec ces informations, deux symboles sont créés :
| Symbole 1 | Symbole 2 |
|---|---|
| (LONGUEUR, TAILLE) | (AMPLITUDE) |
RUNLENGTH et SIZE reposent tous deux sur le même octet, ce qui signifie que chacun ne contient que quatre bits d’information. Les bits supérieurs traitent du nombre de zéros, tandis que les bits inférieurs indiquent le nombre de bits nécessaires pour coder la valeur de x .
Cela a pour conséquence immédiate que le symbole 1 ne peut stocker que des informations concernant les 15 premiers zéros précédant le coefficient AC non nul. Cependant, JPEG définit deux mots de code Huffman spéciaux. L’un consiste à terminer la séquence prématurément lorsque les coefficients restants sont nuls (appelé “End-of-Block” ou “EOB”), et un autre lorsque la série de zéros dépasse 15 avant d’atteindre un coefficient AC non nul. Dans un tel cas où 16 zéros sont rencontrés avant un coefficient AC non nul donné, le symbole 1 est codé “spécialement” comme suit : (15, 0)(0).
Le processus global se poursuit jusqu’à ce que “EOB” – désigné par (0, 0) – soit atteint.
Dans cet esprit, la séquence de plus tôt devient :
(0, 2)(-3);(1, 2)(-3);(0, 1)(-2);(0, 2)(-6);(0, 1)(2);( 0, 1)(-4);(0, 1)(1);(0, 2)(-3);(0, 1)(1);(0, 1)(1); (0, 2)(5);(0, 1)(1);(0, 1)(2);(0, 1)(-1);(0, 1)(1);(0, 1 )(-1);(0, 1)(2);(5, 1)(-1);(0, 1)(-1);(0, 0);
(La première valeur de la matrice, −26, est le coefficient DC ; il n’est pas codé de la même manière. Voir ci-dessus.)
À partir de là, les calculs de fréquence sont effectués sur la base des occurrences des coefficients. Dans notre exemple de bloc, la plupart des coefficients quantifiés sont des petits nombres qui ne sont pas immédiatement précédés d’un coefficient nul. Ces cas plus fréquents seront représentés par des mots de code plus courts.
Taux de compression et artefacts

 Cette image montre les pixels qui sont différents entre une image non compressée et la même image JPEG compressée avec un réglage de qualité de 50. Plus sombre signifie une plus grande différence. Notez en particulier les changements qui se produisent près des arêtes vives et qui ont la forme d’un bloc.
Cette image montre les pixels qui sont différents entre une image non compressée et la même image JPEG compressée avec un réglage de qualité de 50. Plus sombre signifie une plus grande différence. Notez en particulier les changements qui se produisent près des arêtes vives et qui ont la forme d’un bloc. 
 L’image originale
L’image originale 
 Les carrés 8 × 8 compressés sont visibles dans l’image agrandie, ainsi que d’autres artefacts visuels de la compression avec perte .
Les carrés 8 × 8 compressés sont visibles dans l’image agrandie, ainsi que d’autres artefacts visuels de la compression avec perte .
Le taux de compression résultant peut varier selon les besoins en étant plus ou moins agressif dans les diviseurs utilisés dans la phase de quantification. La compression dix pour un donne généralement une image qui ne peut pas être distinguée à l’œil nu de l’original. Un taux de compression de 100: 1 est généralement possible, mais il aura l’air nettement artefacté par rapport à l’original. Le niveau de compression approprié dépend de l’utilisation qui sera faite de l’image.
| Image externe |
|---|
| |
Ceux qui utilisent le World Wide Web connaissent peut-être les irrégularités connues sous le nom d’artefacts de compression qui apparaissent dans les images JPEG, qui peuvent prendre la forme de bruit autour des bords contrastés (en particulier les courbes et les coins) ou d’images “blocs”. Celles-ci sont dues à l’étape de quantification de l’algorithme JPEG. Ils sont particulièrement visibles autour des angles vifs entre des couleurs contrastées (le texte en est un bon exemple, car il contient de nombreux angles de ce type). Les artefacts analogues dans la vidéo MPEG sont appelés bruit de moustique , car l ‘«activité de bord» qui en résulte et les points parasites, qui changent avec le temps, ressemblent à des moustiques grouillant autour de l’objet. [58] [59]
Ces artefacts peuvent être réduits en choisissant un niveau de compression inférieur ; ils peuvent être complètement évités en enregistrant une image à l’aide d’un format de fichier sans perte , bien que cela se traduira par une taille de fichier plus grande. Les images créées avec des programmes de lancer de rayons ont des formes de blocs visibles sur le terrain. Certains artefacts de compression de faible intensité peuvent être acceptables lors de la simple visualisation des images, mais peuvent être accentués si l’image est ensuite traitée, ce qui entraîne généralement une qualité inacceptable. Considérez l’exemple ci-dessous, démontrant l’effet de la compression avec perte sur une étape de traitement de détection de bord .
| Image | Compression sans perte | La compression avec perte |
|---|---|---|
| Original |   |
  |
| Traité par le détecteur de bord Canny |
  |
  |
Certains programmes permettent à l’utilisateur de faire varier la quantité de compression des blocs individuels. Une compression plus forte est appliquée aux zones de l’image qui présentent moins d’artefacts. De cette façon, il est possible de réduire manuellement la taille du fichier JPEG avec moins de perte de qualité.
Étant donné que l’étape de quantification entraîne toujours une perte d’informations, la norme JPEG est toujours un codec de compression avec perte. (Des informations sont perdues à la fois lors de la quantification et de l’arrondi des nombres à virgule flottante.) Même si la matrice de quantification est une matrice de uns , des informations seront toujours perdues lors de l’étape d’arrondi.
Décodage
Le décodage pour afficher l’image consiste à faire tout ce qui précède en sens inverse.
Prendre la matrice de coefficients DCT (après avoir ajouté la différence du coefficient DC)
[ − 26 − 3 − 6 2 2 − 1 0 0 0 − 2 − 4 1 1 0 0 0 − 3 1 5 − 1 − 1 0 0 0 − 3 1 2 − 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ] {displaystyle left[{begin{array}{rrrrrrr}-26&-3&-6&2&2&-1&0&0\0&-2&-4&1&1&0&0&0\-3&1&5&-1&-1&0&0&0\-3&1&2&-1&0&0&0&0\1&0&0&0&0&0&0&0\0&0&0 \0&0&0&0&0&0&0&0\0&0&0&0&0&0&0&0end{tableau}}right]} ![left[{begin{array}{rrrrrrrr}-26&-3&-6&2&2&-1&0&0\0&-2&-4&1&1&0&0&0\-3&1&5&-1&-1&0&0&0\-3&1&2&-1&0&0&0&0\1&0&0&0&0&0&0&0\0&0&0&0&0&0&0&0\0&0&0&0&0&0&0&0\0&0&0&0&0&0&0&0end{array}}right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d681176f165171c22d40b070b93cee3e7d627cc8)
et en prenant le produit entrée pour entrée avec la matrice de quantification ci-dessus, on obtient
[ − 416 − 33 − 60 32 48 − 40 0 0 0 − 24 − 56 19 26 0 0 0 − 42 13 80 − 24 − 40 0 0 0 − 42 17 44 − 29 0 0 0 0 18 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ] {displaystyle left[{begin{array}{rrrrrrrr}-416&-33&-60&32&48&-40&0&0\0&-24&-56&19&26&0&0&0\-42&13&80&-24&-40&0&0&0\-42&17&44&-29&0&0&0&0\18&0&0&0&0&0&0&0\0&0&0&0&0&0&0&0 \0&0&0&0&0&0&0&0\0&0&0&0&0&0&0&0end{tableau}}right]} ![left[{begin{array}{rrrrrrrr}-416&-33&-60&32&48&-40&0&0\0&-24&-56&19&26&0&0&0\-42&13&80&-24&-40&0&0&0\-42&17&44&-29&0&0&0&0\18&0&0&0&0&0&0&0\0&0&0&0&0&0&0&0\0&0&0&0&0&0&0&0\0&0&0&0&0&0&0&0end{array}}right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1336551027236825e4e96dad3e5da329b567f18)
qui ressemble étroitement à la matrice de coefficients DCT d’origine pour la partie supérieure gauche.
L’étape suivante consiste à prendre le DCT inverse bidimensionnel (un DCT 2D de type III), qui est donné par :
f x , y = 1 4 ∑ u = 0 7 ∑ v = 0 7 α ( u ) α ( v ) F u , v cos [ ( 2 x + 1 ) u π 16 ] cos [ ( 2 y + 1 ) v π 16 ] {displaystyle f_{x,y}={frac {1}{4}}sum _{u=0}^{7}sum _{v=0}^{7}alpha (u) alpha (v)F_{u,v}cos left[{frac {(2x+1)upi }{16}}right]cos left[{frac {(2y+1)v pi }{16}}right]} ![f_{x,y}={frac {1}{4}}sum _{u=0}^{7}sum _{v=0}^{7}alpha (u)alpha (v)F_{u,v}cos left[{frac {(2x+1)upi }{16}}right]cos left[{frac {(2y+1)vpi }{16}}right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b57a66586a29b5d371243341173f5fd1c00822b9)
où
- x {displaystylex}
est la rangée de pixels, pour les entiers 0 ≤ x < 8 {displaystyle�leq x<8}
.
- y {displaystyle y}
est la colonne de pixels, pour les entiers 0 ≤ y < 8 {displaystyle 0leq y<8}
.
- α ( u ) {displaystyle\alpha (u)}
est défini comme ci-dessus, pour les entiers 0 ≤ u < 8 {displaystyle 0leq u<8}
.
- F u , v {displaystyle F_{u,v}}
est le coefficient approximatif reconstruit aux coordonnées ( u , v ) . {displaystyle(u,v).}
- f x , y {displaystyle f_{x,y}}
est la valeur de pixel reconstruite aux coordonnées ( x , y ) { style d’affichage (x, y)}
Arrondir la sortie à des valeurs entières (puisque l’original avait des valeurs entières) donne une image avec des valeurs (toujours décalées de 128)



 De légères différences sont perceptibles entre l’image d’origine (en haut) et l’image décompressée (en bas), ce qui est plus facilement visible dans le coin inférieur gauche. [ − 66 − 63 − 71 − 68 − 56 − 65 − 68 − 46 − 71 − 73 − 72 − 46 − 20 − 41 − 66 − 57 − 70 − 78 − 68 − 17 20 − 14 − 61 − 63 − 63 − 73 − 62 − 8 27 − 14 − 60 − 58 − 58 − 65 − 61 − 27 − 6 − 40 − 68 − 50 − 57 − 57 − 64 − 58 − 48 − 66 − 72 − 47 − 53 − 46 − 61 − 74 − 65 − 63 − 62 − 45 − 47 − 34 − 53 − 74 − 60 − 47 − 47 − 41 ] {displaystyle left[{begin{array}{rrrrrrrr}-66&-63&-71&-68&-56&-65&-68&-46\-71&-73&-72&-46&-20&-41&-66&-57 -70&-78&-68&-17&20&-14&-61&-63\-63&-73&-62&-8&27&-14&-60&-58\-58&-65&-61&-27&-6&-40&-68&-50 -57&-57&-64&-58&-48&-66&-72&-47\-53&-46&-61&-74&-65&-63&-62&-45\-47&-34&-53&-74&-60&-47&- 47&-41end{tableau}}right]}
De légères différences sont perceptibles entre l’image d’origine (en haut) et l’image décompressée (en bas), ce qui est plus facilement visible dans le coin inférieur gauche. [ − 66 − 63 − 71 − 68 − 56 − 65 − 68 − 46 − 71 − 73 − 72 − 46 − 20 − 41 − 66 − 57 − 70 − 78 − 68 − 17 20 − 14 − 61 − 63 − 63 − 73 − 62 − 8 27 − 14 − 60 − 58 − 58 − 65 − 61 − 27 − 6 − 40 − 68 − 50 − 57 − 57 − 64 − 58 − 48 − 66 − 72 − 47 − 53 − 46 − 61 − 74 − 65 − 63 − 62 − 45 − 47 − 34 − 53 − 74 − 60 − 47 − 47 − 41 ] {displaystyle left[{begin{array}{rrrrrrrr}-66&-63&-71&-68&-56&-65&-68&-46\-71&-73&-72&-46&-20&-41&-66&-57 -70&-78&-68&-17&20&-14&-61&-63\-63&-73&-62&-8&27&-14&-60&-58\-58&-65&-61&-27&-6&-40&-68&-50 -57&-57&-64&-58&-48&-66&-72&-47\-53&-46&-61&-74&-65&-63&-62&-45\-47&-34&-53&-74&-60&-47&- 47&-41end{tableau}}right]} ![left[{begin{array}{rrrrrrrr}-66&-63&-71&-68&-56&-65&-68&-46\-71&-73&-72&-46&-20&-41&-66&-57\-70&-78&-68&-17&20&-14&-61&-63\-63&-73&-62&-8&27&-14&-60&-58\-58&-65&-61&-27&-6&-40&-68&-50\-57&-57&-64&-58&-48&-66&-72&-47\-53&-46&-61&-74&-65&-63&-62&-45\-47&-34&-53&-74&-60&-47&-47&-41end{array}}right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3122f79ddeb024d01857afa1326287ef6ef8259e)
et en ajoutant 128 à chaque entrée
[ 62 65 57 60 72 63 60 82 57 55 56 82 108 87 62 71 58 50 60 111 148 114 67 65 65 55 66 120 155 114 68 70 70 63 67 101 122 88 60 78 71 71 64 70 80 62 56 81 75 82 67 54 63 65 66 83 81 94 75 54 68 81 81 87 ] . {displaystyle left[{begin{array}{rrrrrrrr}62&65&57&60&72&63&60&82\57&55&56&82&108&87&62&71\58&50&60&111&148&114&67&65\65&55&66&120&155&114&68&70\70&63&67&101&122&88&60&78\71&71&64&70&80&62&56&81\75&82&67&54&63&65&66&83\81&94&75&54&68&81&81&87end{array}}right].} ![left[{begin{array}{rrrrrrrr}62&65&57&60&72&63&60&82\57&55&56&82&108&87&62&71\58&50&60&111&148&114&67&65\65&55&66&120&155&114&68&70\70&63&67&101&122&88&60&78\71&71&64&70&80&62&56&81\75&82&67&54&63&65&66&83\81&94&75&54&68&81&81&87end{array}}right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/97c63837bcedc3e999e024b101278c9ad8789553)
Il s’agit de la sous-image décompressée. En général, le processus de décompression peut produire des valeurs en dehors de la plage d’entrée d’origine de [ 0 , 255 ] {displaystyle [0,255]} ![[0,255]](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b92f49fdc420e36b9d62c711c3c6ebe7d9fcebc)
. Si cela se produit, le décodeur doit écrêter les valeurs de sortie afin de les maintenir dans cette plage pour éviter un débordement lors du stockage de l’image décompressée avec la profondeur de bits d’origine.
La sous-image décompressée peut être comparée à la sous-image d’origine (voir également les images à droite) en prenant les résultats de différence (original – non compressé) dans les valeurs d’erreur suivantes :
[ − 10 − 10 4 6 − 2 − 2 4 − 9 6 4 − 1 8 1 − 2 7 1 4 9 8 2 − 4 − 10 − 1 8 − 2 3 5 2 − 1 − 8 2 − 1 − 3 − 2 1 3 4 0 8 − 8 8 − 6 − 4 − 0 − 3 6 2 − 6 10 − 11 − 3 5 − 8 − 4 − 1 − 0 6 − 15 − 6 14 − 3 − 5 − 3 7 ] {displaystyle left[{begin{array}{rrrrrrrr}-10&-10&4&6&-2&-2&4&-9\6&4&-1&8&1&-2&7&1\4&9&8&2&-4&-10&-1&8\-2&3&5&2&-1&-8&2&- 1\-3&-2&1&3&4&0&8&-8\8&-6&-4&-0&-3&6&2&-6\10&-11&-3&5&-8&-4&-1&-0\6&-15&-6&14&-3&-5&-3&7 end{tableau}}right]} ![left[{begin{array}{rrrrrrrr}-10&-10&4&6&-2&-2&4&-9\6&4&-1&8&1&-2&7&1\4&9&8&2&-4&-10&-1&8\-2&3&5&2&-1&-8&2&-1\-3&-2&1&3&4&0&8&-8\8&-6&-4&-0&-3&6&2&-6\10&-11&-3&5&-8&-4&-1&-0\6&-15&-6&14&-3&-5&-3&7end{array}}right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/57b41af069e9b6354156d2640bf40825c80b1b4a)
avec une erreur absolue moyenne d’environ 5 valeurs par pixel (c’est-à-dire, 1 64 ∑ x = 0 7 ∑ y = 0 7 | e ( x , y ) | = 4.8750 {displaystyle {frac {1}{64}}sum _{x=0}^{7}sum _{y=0}^{7}|e(x,y)|=4.8750} 
).
L’erreur est plus visible dans le coin inférieur gauche où le pixel inférieur gauche devient plus sombre que le pixel immédiatement à sa droite.
Précision requise
La description de l’encodage dans la norme JPEG ne fixe pas la précision nécessaire pour l’image compressée de sortie. Cependant, la norme JPEG (et les normes MPEG similaires) inclut certaines exigences de précision pour le de , y compris toutes les parties du processus de décodage (décodage à longueur variable, DCT inverse, déquantification, renormalisation des sorties) ; la sortie de l’algorithme de référence ne doit pas dépasser :
- un maximum d’un bit de différence pour chaque composant de pixel
- faible erreur quadratique moyenne sur chaque bloc de 8 × 8 pixels
- erreur moyenne très faible sur chaque bloc de 8 × 8 pixels
- erreur quadratique moyenne très faible sur toute l’image
- erreur moyenne extrêmement faible sur toute l’image
Ces assertions sont testées sur un grand nombre d’images d’entrée aléatoires, pour gérer les pires cas. L’ancienne norme IEEE 1180–1990 contenait des exigences de précision similaires. La précision a une conséquence sur la mise en oeuvre des décodeurs, et elle est critique car certains procédés d’encodage (notamment utilisés pour encoder des séquences d’images comme MPEG) doivent pouvoir construire, côté encodeur, une image décodée de référence. Afin de prendre en charge une précision de 8 bits par sortie de composant de pixel, la déquantification et les transformées DCT inverses sont généralement mises en œuvre avec une précision d’au moins 14 bits dans des décodeurs optimisés.
Effets de la compression JPEG
Les artefacts de compression JPEG se fondent bien dans les photographies avec des textures détaillées non uniformes, permettant des taux de compression plus élevés. Remarquez comment un taux de compression plus élevé affecte d’abord les textures haute fréquence dans le coin supérieur gauche de l’image, et comment les lignes contrastées deviennent plus floues. Le taux de compression très élevé affecte gravement la qualité de l’image, bien que les couleurs globales et la forme de l’image soient toujours reconnaissables. Cependant, la précision des couleurs souffre moins (pour un œil humain) que la précision des contours (basée sur la luminance). Ceci justifie le fait que les images doivent d’abord être transformées dans un modèle de couleur séparant la luminance de l’information chromatique,
Exemples de photographies

 Impact visuel d’une compression jpeg sur Photoshop sur une image de 4480×4480 pixels
Impact visuel d’une compression jpeg sur Photoshop sur une image de 4480×4480 pixels
Pour information, l’image bitmap RVB 24 bits non compressée ci-dessous (73 242 pixels) nécessiterait 219 726 octets (à l’exclusion de tous les autres en-têtes d’informations). Les tailles de fichiers indiquées ci-dessous incluent les en-têtes d’informations JPEG internes et certaines métadonnées. Pour des images de la plus haute qualité (Q=100), environ 8,25 bits par pixel de couleur sont nécessaires. Sur les images en niveaux de gris, un minimum de 6,5 bits par pixel est suffisant (une information de couleur de qualité Q = 100 comparable nécessite environ 25 % de bits encodés en plus). L’image de la plus haute qualité ci-dessous (Q=100) est codée à neuf bits par pixel de couleur, l’image de qualité moyenne (Q=25) utilise un bit par pixel de couleur. Pour la plupart des applications, le facteur de qualité ne doit pas descendre en dessous de 0,75 bit par pixel (Q=12,5), comme en témoigne la faible qualité de l’image. L’image de qualité la plus basse n’utilise que 0,13 bit par pixel et affiche des couleurs très médiocres. Ceci est utile lorsque l’image sera affichée dans une taille considérablement réduite. Un procédé pour créer de meilleures matrices de quantification pour une qualité d’image donnée à l’aide du PSNRau lieu du facteur Q est décrit dans Minguillón & Pujol (2001). [60]
| Image | Qualité | Taille (octets) | Ratio de compression | Commenter |
|---|---|---|---|---|
  |
Qualité la plus élevée (Q = 100) | 81 447 | 2.7:1 | Artefacts extrêmement mineurs |
  |
Haute qualité (Q = 50) | 14 679 | 15:1 | Premiers signes d’artefacts de sous-image |
  |
Qualité moyenne (Q = 25) | 9 407 | 23:1 | Artefacts plus puissants ; perte d’informations à haute fréquence |
  |
Qualité médiocre (Q = 10) | 4 787 | 46:1 | Une forte perte de haute fréquence conduit à des artefacts évidents sur les limites de la sous-image (“macroblocage”) |
  |
Qualité la plus basse (Q = 1) | 1 523 | 144:1 | Perte extrême de couleurs et de détails ; les feuilles sont presque méconnaissables. |
La photo de qualité moyenne n’utilise que 4,3 % de l’espace de stockage requis pour l’image non compressée, mais présente peu de perte notable de détails ou d’artefacts visibles. Cependant, une fois un certain seuil de compression passé, les images compressées présentent des défauts de plus en plus visibles. Voir l’article sur la théorie taux-distorsion pour une explication mathématique de cet effet de seuil. Une limitation particulière de JPEG à cet égard est sa structure de transformée de bloc 8 × 8 non superposée. Des conceptions plus modernes telles que JPEG 2000 et JPEG XR présentent une dégradation plus gracieuse de la qualité à mesure que l’utilisation des bits diminue – en utilisant des transformées avec une plus grande étendue spatiale pour les coefficients de fréquence inférieurs et en utilisant des fonctions de base de transformation qui se chevauchent.
Compression supplémentaire sans perte
De 2004 à 2008, de nouvelles recherches ont émergé sur les moyens de compresser davantage les données contenues dans les images JPEG sans modifier l’image représentée. [61] [62] [63] [64] Cela a des applications dans des scénarios où l’image originale n’est disponible qu’au format JPEG, et sa taille doit être réduite pour l’archivage ou la transmission. Les outils de compression standard à usage général ne peuvent pas compresser de manière significative les fichiers JPEG.
En règle générale, ces schémas tirent parti des améliorations apportées au schéma naïf de codage des coefficients DCT, qui ne prend pas en compte :
- Corrélations entre les grandeurs des coefficients adjacents dans le même bloc ;
- Corrélations entre les grandeurs du même coefficient dans des blocs adjacents ;
- Corrélations entre les grandeurs du même coefficient/bloc dans différents canaux ;
- Les coefficients DC, lorsqu’ils sont pris ensemble, ressemblent à une version à échelle réduite de l’image originale multipliée par un facteur d’échelle. Des schémas bien connus de codage sans perte d’images à tons continus peuvent être appliqués, obtenant une compression quelque peu meilleure que le DPCM codé de Huffman utilisé dans JPEG.
Certaines options standard mais rarement utilisées existent déjà en JPEG pour améliorer l’efficacité du codage des coefficients DCT : l’ option de codage arithmétique et l’option de codage progressif (qui produit des débits inférieurs car les valeurs de chaque coefficient sont codées indépendamment, et chaque coefficient a une valeur significativement différente Distribution). Les méthodes modernes ont amélioré ces techniques en réordonnant les coefficients pour regrouper les coefficients de plus grande amplitude; [61] utilisant des coefficients et des blocs adjacents pour prédire de nouvelles valeurs de coefficients ; [63] diviser des blocs ou des coefficients entre un petit nombre de modèles codés indépendamment en fonction de leurs statistiques et valeurs adjacentes ; [62] [63]et plus récemment, en décodant les blocs, en prédisant les blocs suivants dans le domaine spatial, puis en les codant pour générer des prédictions pour les coefficients DCT. [64]
En règle générale, ces méthodes peuvent compresser les fichiers JPEG existants entre 15 et 25 %, et pour les fichiers JPEG compressés avec des paramètres de faible qualité, peuvent produire des améliorations allant jusqu’à 65 %. [63] [64]
Un outil disponible gratuitement appelé packJPG [65] est basé sur l’article de 2007 “Amélioration de la réduction de la redondance pour les fichiers JPEG”.
Formats dérivés pour la 3D stéréoscopique
JPEG Stéréoscopique

 Un exemple de fichier .JPS stéréoscopique
Un exemple de fichier .JPS stéréoscopique
JPS est une image JPEG stéréoscopique utilisée pour créer des effets 3D à partir d’images 2D. Il contient deux images statiques, une pour l’œil gauche et une pour l’œil droit ; encodé sous forme de deux images côte à côte dans un seul fichier JPG. JPEG Stéréoscopique (JPS, extension .jps) est un format basé sur JPEG pour les images stéréoscopiques . [66] [67] Il a une gamme de configurations stockées dans le champ de marqueur JPEG APP3, mais contient généralement une image de double largeur, représentant deux images de taille identique dans les yeux croisés (c’est-à-dire le cadre gauche sur la moitié droite de l’image et vice versa) disposition côte à côte. Ce format de fichier peut être visualisé au format JPEG sans aucun logiciel spécial, ou peut être traité pour le rendu dans d’autres modes.
Format multi-images JPEG
Le format JPEG multi-images (MPO, extension .mpo) est un format basé sur JPEG pour stocker plusieurs images dans un seul fichier. Il contient deux ou plusieurs fichiers JPEG concaténés. [68] [69] Il définit également un segment marqueur JPEG APP2 pour la description de l’image. Divers appareils l’utilisent pour stocker des images 3D, tels que Fujifilm FinePix Real 3D W1 , HTC Evo 3D , caméscope d’extension JVC GY-HMZ1U AVCHD/MVC, Nintendo 3DS , Panasonic Lumix DMC-TZ20 , DMC-TZ30 , DMC-TZ60 , DMC- TS4 (FT4) et Sony DSC-HX7V. D’autres appareils l’utilisent pour stocker des “images de prévisualisation” qui peuvent être affichées sur un téléviseur.
Au cours des dernières années, en raison de l’utilisation croissante des images stéréoscopiques, de nombreux efforts ont été déployés par la communauté scientifique pour développer des algorithmes de compression d’images stéréoscopiques . [70] [71]
Implémentations
Une implémentation très importante d’un codec JPEG est la bibliothèque de programmation libre libjpeg du Independent JPEG Group. Il a été publié pour la première fois en 1991 et a été la clé du succès de la norme. [72] Cette bibliothèque ou un dérivé direct de celle-ci est utilisée dans d’innombrables applications. Les versions récentes introduisent des extensions propriétaires qui rompent la compatibilité ABI avec les versions précédentes .
En mars 2017, Google a publié le projet open source Guetzli , qui échange un temps d’encodage beaucoup plus long pour une taille de fichier plus petite (similaire à ce que Zopfli fait pour PNG et d’autres formats de données sans perte). [73]
L’ISO/IEC Joint Photography Experts Group maintient une implémentation logicielle de référence qui peut coder à la fois les extensions JPEG de base (ISO/IEC 10918-1 et 18477–1) et JPEG XT (ISO/IEC 18477 Parties 2 et 6–9), ainsi que JPEG-LS (ISO/CEI 14495). [74]
JPEG XT
JPEG XT (ISO/IEC 18477) a été publié en juin 2015 ; il étend le format JPEG de base avec la prise en charge de profondeurs de bits entiers plus élevées (jusqu’à 16 bits), l’imagerie à plage dynamique élevée et le codage en virgule flottante, le codage sans perte et le codage de canal alpha. Les extensions sont rétrocompatibles avec le format de fichier JPEG/JFIF de base et l’image compressée avec perte de 8 bits. JPEG XT utilise un format de fichier extensible basé sur JFIF. Les couches d’extension sont utilisées pour modifier la couche de base JPEG 8 bits et restaurer l’image haute résolution. Le logiciel existant est compatible avec les versions ultérieures et peut lire le flux binaire JPEG XT, bien qu’il ne décode que la couche de base 8 bits. [75]
JPEGXL
| Apprendre encore plus Cette rubrique doit être mise à jour . ( avril 2022 ) Please help update this article to reflect recent events or newly available information. |
Depuis août 2017, JTC1/SC29/WG1 a publié une série de projets d’appels à propositions sur JPEG XL – la norme de compression d’image de nouvelle génération avec une efficacité de compression nettement meilleure (amélioration de 60 %) par rapport à JPEG. [76] On s’attend à ce que la norme dépasse les performances de compression d’images fixes présentées par HEVC HM, Daala et WebP , et contrairement aux efforts précédents visant à remplacer JPEG, pour fournir une option de transport et de stockage de recompression plus efficace et sans perte pour les images JPEG traditionnelles. [77] [78] [79]Les principales exigences incluent la prise en charge d’images à très haute résolution (au moins 40 MP), 8 à 10 bits par composant, le codage couleur RVB/YCbCr/ICtCp, les images animées, le codage de canal alpha, Rec. Espace colorimétrique 709 ( sRGB ) et fonction gamma (puissance 2,4), Rec. Espace colorimétrique à large gamme de couleurs 2100 (Rec. 2020) et fonctions de transfert à plage dynamique élevée (PQ et HLG), et compression de haute qualité des images synthétiques, telles que les polices bitmap et les dégradés. La norme devrait également offrir des profondeurs de bits plus élevées (entier 12–16 bits et virgule flottante), des espaces colorimétriques supplémentaires et des fonctions de transfert (telles que Log C de Arri), images d’aperçu intégrées, codage de canal alpha sans perte, codage de région d’image et codage de faible complexité. Toute technologie brevetée ferait l’objet d’une licence libre de droits . Les propositions ont été soumises en septembre 2018, ce qui a conduit à un projet de comité en juillet 2019, avec une date de publication cible actuelle en octobre 2019. [ Nécessite une mise à jour ] [80] [79]
Voir également
- Better Portable Graphics , un format basé sur l’encodage intra-frame du HEVC
- C-Cube , un des premiers implémenteurs de JPEG sous forme de puce
- Comparaison des formats de fichiers graphiques
- Comparaison des moteurs de mise en page (graphiques)
- Filtre de déblocage (vidéo) , les méthodes de déblocage similaires pourraient être appliquées au JPEG
- Règle de conception pour le système de fichiers de caméra (DCF)
- Extensions de fichiers
- Programme d’édition graphique
- Format de fichier d’image à haute efficacité , format de conteneur d’image pour HEVC et autres formats de codage d’image
- Lenna (image de test) , l’image standard traditionnelle utilisée pour tester les algorithmes de traitement d’image
- Codec d’image sans perte FELICS
- Mouvement JPEG
- WebP
Références
- ^ un bcd e f g h i j k l “T.81 – COMPRESSION NUMÉRIQUE ET CODAGE DES IMAGES FIXES À TON CONTINU – EXIGENCES ET DIRECTIVES” (PDF) . CCITT . Septembre 1992 . Récupéré le 12 juillet 2019 .
- ^ “Définition de “JPEG” ” . Collins English Dictionary . Récupéré le 23/05/2013 .
- ^ Haines, Richard F.; Chuang, Sherry L. (1er juillet 1992). Les effets de la compression vidéo sur l’acceptabilité des images pour le suivi d’expériences en sciences de la vie (rapport technique). NASA . NASA-TP-3239, A-92040, NAS 1.60:3239 . Récupéré le 13/03/2016 . Les niveaux de compression d’images fixes JPEG, même avec la large plage de 5: 1 à 120: 1 dans cette étude, ont donné des niveaux d’acceptabilité tout aussi élevés
- ^ un b Hudson, Graham; Léger, Alain; Niss, Birger ; Sebestyén, Istvan ; Vaaben, Jørgen (31 août 2018). “Norme JPEG-1 25 ans: raisons passées, présentes et futures d’un succès”. Journal d’imagerie électronique . 27 (4) : 1. doi : 10.1117/1.JEI.27.4.040901 . S2CID 52164892 .
- ^ “Le Format d’image JPEG expliqué” . BT.com . Groupe BT . 31 mai 2018. Archivé de l’original le 5 août 2019 . Récupéré le 5 août 2019 .
- ^ Baraniuk, Chris (15 octobre 2015). “Des protections contre la copie pourraient venir sur les JPEG” . Nouvelles de la BBC . BBC . Récupéré le 13 septembre 2019 .
- ^ “T.81 – COMPRESSION NUMÉRIQUE ET CODAGE DES IMAGES FIXES À TON CONTINU – EXIGENCES ET DIRECTIVES” (PDF) . CCITT . Septembre 1992. p. 14 . Récupéré le 12 juillet 2019 . La présente spécification spécifie deux classes de processus de codage et de décodage, les processus avec et sans perte . Celles basées sur la transformée en cosinus discrète (DCT) sont avec perte, ce qui permet d’obtenir une compression substantielle tout en produisant une image reconstruite avec une fidélité visuelle élevée à l’image source du codeur.
- ^ un bcde ” JPEG : 25 Jahre und kein bisschen alt” . Heise en ligne (en allemand). Octobre 2016 . Récupéré le 5 septembre 2019 .
- ^ un bc Ahmed, Nasir ( janvier 1991). “Comment j’ai trouvé la transformation en cosinus discrète” . Traitement numérique du signal . 1 (1): 4–5. doi : 10.1016/1051-2004(91)90086-Z .
- ^ “Qu’est-ce qu’un JPEG ? L’objet invisible que vous voyez tous les jours” . L’Atlantique . 24 septembre 2013 . Récupéré le 13 septembre 2019 .
- ^ “Archive HTTP – Statistiques intéressantes” . httparchive.org . Récupéré le 06/04/2016 .
- ^ Détection de type MIME dans Internet Explorer : types MIME téléchargés (msdn.microsoft.com)
- ^ “Format d’échange de fichiers JPEG” (PDF) . 3 septembre 2014. Archivé de l’original le 3 septembre 2014 . Récupéré le 16 octobre 2017 . {{cite web}}: CS1 maint: bot: original URL status unknown (link)
- ^ “Pourquoi JPEG 2000 n’a jamais décollé” . Institut national américain des normes . 10 juillet 2018 . Récupéré le 13 septembre 2019 .
- ^ un b Ahmed, Nasir ; Natarajan, T.; Rao, KR (janvier 1974), ” Discrete Cosine Transform “, IEEE Transactions on Computers , C-23 (1): 90–93, doi : 10.1109 / TC.1974.223784
- ^ un b Chen, Wen-Hsiung; Smith, C.; Fralick, S. (1977). “Un algorithme de calcul rapide pour la transformée discrète en cosinus”. Transactions IEEE sur les communications . 25 (9) : 1004-1009. doi : 10.1109/TCOM.1977.1093941 . ISSN 0090-6778 .
- ^ un b Chen, Wen-Hsiung; Pratt, WK (1984). “Codeur adaptatif de scène”. Transactions IEEE sur les communications . 32 (3): 225–232. doi : 10.1109/TCOM.1984.1096066 . ISSN 0090-6778 .
- ^ un bcdefg Lemos , Robert ( 23 juillet 2002). “Trouver la vérité patente dans la revendication JPEG” . CNET . Récupéré le 13 juillet 2019 .
- ^ ISO/CEI JTC 1/SC 29 (2009-05-07). “ISO/IEC JTC 1/SC 29/WG 1 – Codage des images fixes (SC 29/WG 1 Structure)” . Archivé de l’original le 2013-12-31 . Récupéré le 11/11/2009 .
- ^ un b ISO/IEC JTC 1/SC 29. “Programme de Travail, (Alloué à SC 29/WG 1)” . Archivé de l’original le 2013-12-31 . Récupéré le 07/11/2009 .
- ^ ISO. “JTC 1/SC 29 – Codage des informations audio, image, multimédia et hypermédia” . Récupéré le 11/11/2009 .
- ^ un b JPEG. “Groupe d’experts photographiques conjoints, page d’accueil JPEG” . Récupéré le 08/11/2009 .
- ^ “T.81 : Technologies de l’information – Compression numérique et codage d’images fixes à ton continu – Exigences et directives” . ITU.int . Récupéré le 07/11/2009 .
- ^ William B. Pennebaker; Joan L. Mitchell (1993). Norme de compression de données d’images fixes JPEG (3e éd.). Springer. p. 291.ISBN _ 978-0-442-01272-4.
- ^ ISO. “JTC 1/SC 29 – Codage des informations audio, image, multimédia et hypermédia” . Récupéré le 07/11/2009 .
- ^ “SPIFF, format de fichier d’échange d’images fixes” . Bibliothèque du Congrès . 30 janvier 2012. Archivé de l’original le 2018-07-31 . Récupéré le 31/07/2018 .
- ^ JPEG (2009-04-24). “JPEG XR entre dans le statut FDIS : le format d’échange de fichiers JPEG (JFIF) sera normalisé en tant que JPEG Part 5″ (Communiqué de presse). Archivé de l’original le 2009-10-08 . Récupéré le 09/11/2009 .
- ^ “Format d’échange de fichiers JPEG (JFIF)” . ECMA TR/98 1ère éd . Ecma International . 2009 . Récupéré le 01/08/2011 .
- ^ “Le brevet JPEG de Forgent” . SourceForge . 2002 . Récupéré le 13 juillet 2019 .
- ^ “Concernant les revendications de brevet récentes” . Jpeg.org . 2002-07-19. Archivé de l’original le 14/07/2007 . Récupéré le 29/05/2011 .
- ^ “JPEG et JPEG2000 – Entre querelle de brevet et changement de technologie” . Archivé de l’original le 17 août 2004 . Récupéré le 16/04/2017 . {{cite web}}: CS1 maint: bot: original URL status unknown (link)
- ^ Lemos, Robert (23 juillet 2002). “Trouver la vérité patente dans la revendication JPEG” . CNET . Récupéré le 13 juillet 2019 . Certains experts lui attribuent la création d’un type spécifique de manipulation d’image – la transformée en cosinus discrète – utilisée dans le format JPEG.
- ^ Kawamoto, Aube (22 avril 2005). “La poursuite en matière de Brevets graphiques se retourne contre Microsoft” . Nouvelles CNET . Récupéré le 28/01/2009 .
- ^ “Le Bureau des marques réexamine le brevet JPEG Forgent” . Publier.com . 3 février 2006. Archivé de l’original le 2016-05-15 . Récupéré le 28/01/2009 .
- ^ “USPTO : les déclarations les plus larges de Forgent contre la norme JPEG sont invalides” . Groklaw.net . 26 mai 2006 . Récupéré le 21/07/2007 .
- ^ “Système de codage pour réduire la redondance” . Gauss.ffii.org . Archivé de l’original le 12/06/2011 . Récupéré le 29/05/2011 .
- ^ “Revendication de brevet JPEG abandonnée” . Fondation publique des Brevets. 2 novembre 2006 . Récupéré le 03/11/2006 .
- ^ “Certificat de réexamen ex parte pour le brevet américain n ° 5 253 341” . Archivé de l’original le 2 juin 2008.
- ^ Groupe de travail. “Rozmanith : Utilisation des Brevets logiciels pour faire taire les critiques” . Eupat.ffii.org . Archivé de l’original le 16/07/2011 . Récupéré le 29/05/2011 .
- ^ “Une prime de 5 000 $ pour nommer Troll Tracker: Ray Niro veut savoir qui dit toutes ces choses désagréables à son sujet” . Law.com . Récupéré le 29/05/2011 .
- ^ Reimer, Jérémy (2008-02-05). “Chasse aux trolls : l’USPTO a demandé de réexaminer le brevet d’image large” . Arstechnica.com . Récupéré le 29/05/2011 .
- ^ Office des Brevets des États-Unis – Octroi d’un réexamen sur 5 253 341 C1
- ^ “Le juge met le brevet JPEG sur la glace” . Techdirt.com . 2008-04-30 . Récupéré le 29/05/2011 .
- ^ “La revendication unique du brevet JPEG a été rejetée (et rejetée pour faire bonne mesure)” . Techdirt.com . 2008-08-01 . Récupéré le 29/05/2011 .
- ^ Groupe de travail. “Page d’accueil de Princeton Digital Image Corporation” . Archivé de l’original le 11/04/2013 . Récupéré le 01/05/2013 .
- ^ Groupe de travail. “Article sur la décision du tribunal de Princeton concernant l’accord de licence GE” . Archivé de l’original le 2016-03-09 . Récupéré le 01/05/2013 .
- ^ “Vue d’ensemble du décodage progressif” . Réseau de développeurs Microsoft . Microsoft . Récupéré le 23/03/2012 .
- ^ Fastvideo (mai 2019). “Encodeur JPEG 12 bits sur GPU” . Récupéré le 06/05/2019 .
- ^ “Pourquoi vous devriez toujours faire pivoter les photos JPEG originales sans perte” . Petapixel.com . 14 août 2012 . Récupéré le 16 octobre 2017 .
- ^ “Format de fichier JFIF au format PDF” (PDF) .
- ^ Tom Lane (1999-03-29). “Foire aux questions sur la compression d’images JPEG” . Récupéré le 11/09/2007 . (q. 14 : “Pourquoi tous ces arguments sur les formats de fichiers ?”)
- ^ un b “Un espace colorimétrique standard par défaut pour Internet – sRGB” . www.w3.org .
- ^ un b “IEC 61966-2-1:1999/AMD1:2003 | CEI Webstore” . boutique en ligne.iec.ch .
- ^ “ISO/CEI 10918-1 : 1993(E) p.36″ .
- ^ Thomas G. Lane. “Fonctionnalités avancées : sélection des paramètres de compression” . Utilisation de la bibliothèque IJG JPEG .
- ^ Ryan, Dan (2012-06-20). Modules d’apprentissage en ligne : Série Dlr Associates . AuthorHouse. ISBN 9781468575200.
- ^ “Questions de fréquence DC / AC – Forum de Doom9” . forum.doom9.org . Récupéré le 16 octobre 2017 .
- ^ un b Phuc-Tue Le Dinh et Jacques Patry. Artefacts de compression vidéo et réduction du bruit MPEG Archivé le 14/03/2006 sur la Wayback Machine . DesignLine d’imagerie vidéo. 24 février 2006. Consulté le 28 mai 2009.
- ^ “ 3.9 bruit de moustique : forme de distorsion d’activité des bords parfois associée au mouvement, caractérisée par des artefacts en mouvement et/ou des motifs de bruit tachetés superposés sur les objets (ressemblant à un moustique volant autour de la tête et des épaules d’une personne).” UIT-T Rec. P.930 (08/96) Principes d’un système de dégradation de référence pour la vidéo Archivé le 16/02/2010 sur la Wayback Machine
- ^ Julià Minguillón, Jaume Pujol (avril 2001). “Modélisation d’erreur de quantification uniforme standard JPEG avec applications aux modes de fonctionnement séquentiel et progressif” (PDF) . Imagerie électronique . 10 (2): 475–485. Bibcode : 2001JEI….10..475M . doi : 10.1117/1.1344592 . hdl : 10609/6263 .
- ^ un b I. Bauermann et E. Steinbacj. Compression sans perte supplémentaire des images JPEG. Proc. du Picture Coding Symposium (PCS 2004), San Francisco, États-Unis, du 15 au 17 décembre 2004.
- ^ un b N. Ponomarenko, K. Egiazarian, V. Lukin et J. Astola. Compression supplémentaire sans perte d’images JPEG, Proc. du 4ème Intl. Symposium on Image and Signal Processing and Analysis (ISPA 2005), Zagreb, Croatie, pp. 117–120, 15–17 septembre 2005.
- ^ un bcd M. Stirner et G. Seelmann . Amélioration de la réduction de redondance pour les fichiers JPEG. Proc. du Picture Coding Symposium (PCS 2007), Lisbonne, Portugal, du 7 au 9 novembre 2007
- ^ un bc Ichiro Matsuda, Yukio Nomoto, Kei Wakabayashi et Susumu Itoh. Réencodage sans perte d’images JPEG à l’aide d’une prédiction intra adaptative par bloc. Actes de la 16e conférence européenne sur le traitement du signal (EUSIPCO 2008).
- ^ “Dernières versions binaires de packJPG : V2.3a” . 3 janvier 2008. Archivé de l’original le 23 janvier 2009.
- ^ J. Siragusa, DC Swift (1997). “Descripteur de données stéréoscopiques à usage général” (PDF) . VRex, Inc., Elmsford, New York, États-Unis . Archivé de l’original (PDF) le 2011-10-30. {{cite web}}: CS1 maint: uses authors parameter (link)
- ^ Tim Kemp, fichiers JPS
- ^ “Format multi-images” (PDF) . 2009. Archivé de l’original (PDF) le 2016-04-05 . Récupéré le 30/12/2015 .
- ^ “MPO2Stereo: Convertir les fichiers Fujifilm MPO en paires stéréo JPEG” , Mtbs3d.com , récupéré le 12 janvier 2010
- ^ Alessandro Ortis; Sebastiano Battiato (2015), Sitnik, Robert; Puech, William (eds.), “Une nouvelle méthode de mise en correspondance rapide pour la compression adaptative d’images stéréoscopiques” , Traitement d’ images tridimensionnelles , Traitement d’images tridimensionnelles, Mesure (3DIPM) et Applications 2015, SPIE – Traitement d’images tridimensionnelles , Measurement (3DIPM), and Applications 2015, 9393 : 93930K, Bibcode : 2015SPIE.9393E..0KO , doi : 10.1117/12.2086372 , S2CID 18879942 , récupéré le 30 avril 2015
- ^ Alessandro Ortis; Francesco Rundo; Giuseppe Di Giore; Sebastiano Battiato, Adaptive Compression of Stereoscopic Images , International Conference on Image Analysis and Processing (ICIAP) 2013 , récupéré le 30 avril 2015
- ^ “Aperçu de JPEG” . jpeg.org . Récupéré le 16/10/2017 .
- ^ “Annoncer Guetzli : Un nouvel encodeur JPEG Open Source” . Research.googleblog.com . Récupéré le 16 octobre 2017 .
- ^ “JPEG-JPEG XT” . jpeg.org .
- ^ “JPEG-JPEG XT” . jpeg.org .
- ^ “JPEG – Compression d’image de nouvelle génération (JPEG XL) Projet final d’appel à propositions” . Jpeg.org . Récupéré le 29 mai 2018 .
- ^ Alakuijala, Jyrki; van Asseldonk, Ruud; Boukortt, Sami ; Brusé, Martin ; Comşa, Iulia-Maria ; Firsching, Moritz; Fischbacher, Thomas; Kliuchnikov, Evgenii; Gomez, Sébastien ; Obryk, Robert; Potempa, Krzysztof; Rhatushniak, Alexandre ; Sneyers, Jon ; Szabadka, Zoltan; Vandervenne, Lode; Versari, Luca; Wassenberg, janvier (2019-09-06). “Architecture de compression d’image et outils de codage de nouvelle génération JPEG XL” . Dans Tescher, Andrew G; Ebrahimi, Touradj (dir.). Applications du traitement numérique des images XLII . p. 20. doi : 10.1117/12.2529237 . ISBN 9781510629677. S2CID 202785129 .
- ^ “Copie archivée” . Archivé de l’original le 22 août 2019 . Récupéré le 22 août 2019 . {{cite web}}: CS1 maint: archived copy as title (link)
- ^ un b Rhatushnyak, Alexandre; Wassenberg, Jan; Sneyers, Jon ; Alakuijala, Jyrki ; Vandevenne, Lode; Versari, Luca; Obryk, Robert; Szabadka, Zoltan; Kliuchnikov, Evgenii; Comsa, Iulia-Maria ; Potempa, Krzysztof; Brusé, Martin ; Firsching, Moritz; Khasanova, Renata; Ruud van Asseldonk; Boukortt, Sami ; Gomez, Sébastien ; Fischbacher, Thomas (2019). “Projet de comité du système de codage d’image JPEG XL”. arXiv : 1908.03565 [ eess.IV ].
- ^ “N79010 Dernier appel à propositions pour une norme de codage d’image de nouvelle génération (JPEG XL)” (PDF) . ISO/CEI JTC 1/SC 29/WG 1 (UIT-T SG16) . Récupéré le 29 mai 2018 .
Liens externes
| Wikimedia Commons a des médias liés à la compression JPEG . |
- Norme JPEG (JPEG ISO/IEC 10918-1 Recommandation ITU-T T.81) sur W3.org
- Site officiel du Groupe conjoint d’experts en photographie (JPEG)
- Format de fichier JFIF sur W3.org
- Visualiseur JPEG en 250 lignes de code Python facile à comprendre
- Exemples d’images sur toute la gamme des niveaux de quantification de 1 à 100 sur visengi.com
- Compresseur JPEG du domaine public dans un seul fichier source C++, avec un décompresseur correspondant sur code.google.com
- Code source ouvert du décodeur JPEG, copyright (C) 1995–1997, Thomas G. Lane
















