Inertie

L’ inertie est la résistance de tout objet physique à un changement de sa vitesse . Cela inclut les modifications de la vitesse ou de la direction du mouvement de l’objet. Un aspect de cette propriété est la tendance des objets à continuer à se déplacer en ligne droite à une vitesse constante lorsqu’aucune force n’agit sur eux.

L’inertie vient du mot latin, iners , qui signifie paresseux, paresseux. L’inertie est l’une des principales manifestations de la masse , qui est une propriété quantitative des systèmes physiques . Isaac Newton a défini l’inertie comme une force, avant sa première loi dans la monumentale Philosophiæ Naturalis Principia Mathematica . Là, on lit :

DÉFINITION III. La vis insita , ou force innée de la matière, est un pouvoir de résistance par lequel tout corps, autant qu’il se trouve en lui, s’efforce de persévérer dans son état présent, qu’il soit de repos ou d’avancer uniformément dans une ligne droite. ^[1]

Après quelques autres définitions, Newton énonce (traduction anglaise de Motte-Cajori p.83) sa Première loi du mouvement :

LOI I. Tout corps persévère dans son état de repos ou de mouvement uniforme en ligne droite, à moins qu’il ne soit obligé de changer cet état par des forces qui lui sont imprimées.

Notez que Newton utilise la forme verbale active “persévérer”, plutôt que d’autres formes passives telles que “continuer” ou “rester”, que l’on trouve couramment dans les manuels modernes. Cela découle de certains changements dans la mécanique originale de Newton (comme indiqué dans les Principia) apportés par Euler , D’Alembert et d’autres Cartésiens .

Dans l’usage courant, le terme “inertie” peut faire référence à la “quantité de résistance d’un objet au changement de vitesse” ou, pour des termes plus simples, à la “résistance à un changement de mouvement” (qui est quantifiée par sa masse), ou parfois à son élan , selon le contexte. Le terme “inertie” est plus correctement compris comme un raccourci pour “le principe d’inertie” tel que décrit par Newton dans sa Première loi du mouvement , énoncée ci-dessus, selon laquelle un objet continuera à se déplacer à sa vitesse actuelle jusqu’à ce qu’une force provoque sa vitesse . ou direction à changer.

À la surface de la Terre, l’inertie est souvent masquée par la gravité et les effets du frottement et de la résistance de l’air, qui ont tous deux tendance à diminuer la vitesse des objets en mouvement (généralement jusqu’au point de repos). Cela a induit le philosophe Aristote en erreur en lui faisant croire que les objets ne bougeraient que tant qu’une force leur serait appliquée. ^{[2] [3]}

Le principe d’inertie est l’un des principes fondamentaux de la physique classique qui est encore utilisé aujourd’hui pour décrire le mouvement des objets et la manière dont ils sont affectés par les forces qui leur sont appliquées.

Histoire et évolution du concept

Compréhension précoce du mouvement

Le sinologue Joseph Needham attribue au Mozi (un texte chinois de la période des Royaumes combattants (475-221 av. J.-C.) la première description de l’inertie. ^[4] Avant la Renaissance européenne, la théorie dominante du mouvement dans la philosophie occidentale était celle d’ Aristote (335 Aristote a dit que tous les objets en mouvement (sur Terre) finissent par s’immobiliser à moins qu’une puissance (force) externe ne continue à les déplacer ^[5] Aristote a expliqué le mouvement continu des projectiles, après avoir été séparés de leur projecteur, comme une action (elle-même inexpliquée) du milieu environnant continuant à déplacer le projectile ^[6].

Malgré son acceptation générale, le concept de mouvement d’Aristote a été contesté à plusieurs reprises par des philosophes notables pendant près de deux Millénaires . Par exemple, Lucrèce (à la suite, vraisemblablement, d’ Épicure ) a déclaré que “l’état par défaut” de la matière était le mouvement, pas la stase. ^[7] Au VIe siècle, Jean Philoponusa critiqué l’incohérence entre la discussion d’Aristote sur les projectiles, où le médium fait avancer les projectiles, et sa discussion sur le vide, où le médium entraverait le mouvement d’un corps. Philoponus a proposé que le mouvement n’était pas maintenu par l’action d’un milieu environnant, mais par une propriété conférée à l’objet lorsqu’il était mis en mouvement. Bien que ce ne soit pas le concept moderne d’inertie, car il y avait encore besoin d’un pouvoir pour maintenir un corps en mouvement, cela s’est avéré un pas fondamental dans cette direction. ^{[8] [9] [10]} Cette vue a été fortement opposée par Averroes et par beaucoup de philosophes scolastiques qui ont soutenu Aristotle. Cependant, ce point de vue n’est pas resté incontesté dans le monde islamique, où Philoponus avait plusieurs partisans qui ont développé ses idées.

Au 11ème siècle, le polymathe persan Ibn Sina (Avicenne) a affirmé qu’un projectile dans le vide ne s’arrêterait pas à moins d’agir. ^[11]

Théorie de l’impulsion

Au XIVe siècle, Jean Buridan rejette l’idée qu’une propriété génératrice de mouvement, qu’il nomme impulsion , se dissipe spontanément. La position de Buridan était qu’un objet en mouvement serait arrêté par la résistance de l’air et le poids du corps qui s’opposeraient à son impulsion. ^[12] Buridan a également soutenu que l’impulsion augmentait avec la vitesse; ainsi, son idée initiale de l’impulsion était similaire à bien des égards au concept moderne de l’élan. Malgré les similitudes évidentes avec des idées plus modernes sur l’inertie, Buridan considérait sa théorie comme une simple modification de la philosophie de base d’Aristote, maintenant de nombreuses autres théories itinérantes .opinions, y compris la croyance qu’il y avait encore une différence fondamentale entre un objet en mouvement et un objet au repos. Buridan croyait également que l’impulsion pouvait être non seulement linéaire mais aussi circulaire, provoquant le déplacement d’objets (tels que des corps célestes) en cercle.

La pensée de Buridan a été suivie par son élève Albert de Saxe (1316-1390) et les calculatrices d’Oxford , qui ont effectué diverses expériences qui ont encore sapé le modèle aristotélicien. Leur travail à son tour a été élaboré par Nicole Oresme qui a été la pionnière de la pratique consistant à illustrer les lois du mouvement avec des graphiques.

Peu de temps avant la théorie de l’inertie de Galilée, Giambattista Benedetti a modifié la théorie croissante de l’impulsion pour impliquer uniquement le mouvement linéaire :

“… [Toute] portion de matière corporelle qui se déplace d’elle-même lorsqu’une impulsion lui a été imprimée par une force motrice externe a une tendance naturelle à se déplacer sur un chemin rectiligne et non courbe.” ^[13]

Benedetti cite le mouvement d’un rocher dans une fronde comme exemple du mouvement linéaire inhérent des objets, contraints à un mouvement circulaire.

Inertie classique

Selon l’historien des sciences Charles Coulston Gillispie , l’inertie “est entrée dans la science comme une conséquence physique de la géométrisation de l’espace-matière par Descartes , combinée à l’immuabilité de Dieu”. ^[14]

Galilée

Le principe d’inertie, qui trouve son origine avec Aristote pour les “mouvements dans le vide”, ^[15] stipule qu’un objet a tendance à résister à un changement de mouvement. Selon Newton, un objet restera au repos ou restera en mouvement (c’est-à-dire maintiendra sa vitesse) à moins qu’il ne soit soumis à une force externe nette, qu’elle résulte de la gravité , du frottement , du contact ou d’une autre force. La division aristotélicienne du mouvement en mondain et céleste est devenue de plus en plus problématique face aux conclusions de Nicolas Copernic au XVIe siècle, qui soutenait que la Terre n’est jamais au repos, mais est en fait en mouvement constant autour du Soleil. ^[16] Galilée , dans son développement ultérieur du Modèle copernicien, a reconnu ces problèmes avec la nature alors acceptée du mouvement et, au moins partiellement, a par conséquent inclus une reformulation de la description d’Aristote du mouvement dans le vide en tant que principe physique de base :

Un corps se déplaçant sur une surface plane continuera dans la même direction à une vitesse constante à moins d’être dérangé. ^[17]

Galilée écrit que “tout obstacle extérieur ôté, un corps pesant sur une surface sphérique concentrique à la terre se maintiendra dans l’état où il a été ; s’il est mis en mouvement vers l’ouest (par exemple), il se maintiendra dans cet état”. mouvement.” ^[18] Cette notion appelée “inertie circulaire” ou “inertie circulaire horizontale” par les historiens des sciences, est un précurseur, mais distinct de la notion newtonienne d’inertie rectiligne. ^{[19] [20]} Pour Galilée, un mouvement est ” horizontal ” s’il n’entraîne pas le mobile vers ou loin du centre de la terre, et pour lui, “un navire, par exemple, ayant reçu une fois une certaine impulsion à travers la mer tranquille,^{[21] [22]}

Il convient également de noter que Galilée plus tard (en 1632) a conclu que sur la base de cette prémisse initiale d’inertie, il est impossible de faire la différence entre un objet en mouvement et un objet stationnaire sans une référence extérieure pour le comparer. ^[23] Cette observation est finalement devenue la base d’ Albert Einstein pour développer la théorie de la relativité restreinte .

Le premier physicien à rompre complètement avec le modèle aristotélicien du mouvement fut Isaac Beeckman en 1614. ^[24]

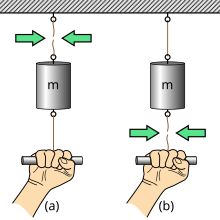
L’effet de la masse d’inertie : s’il est tiré lentement, le fil supérieur casse (a). S’il est tiré rapidement, le fil inférieur casse (b)

Les concepts d’inertie dans les écrits de Galilée seront plus tard affinés, modifiés et codifiés par Isaac Newton comme la première de ses lois du mouvement (publiée pour la première fois dans l’ouvrage de Newton, Philosophiæ Naturalis Principia Mathematica , en 1687) :

Tout corps persévère dans son état de repos ou de mouvement uniforme en ligne droite, à moins qu’il ne soit obligé de changer cet état par des forces qui lui sont imprimées. ^[25]

Depuis la publication initiale, les lois du mouvement de Newton (et par inclusion, cette première loi) en sont venues à former la base de la branche de la physique connue sous le nom de mécanique classique . ^[26]

Le terme « inertie » a été introduit pour la première fois par Johannes Kepler dans son Epitome Astronomiae Copernicanae ^[27] (publié en trois parties de 1617 à 1621) ; cependant, la signification du terme de Kepler (qu’il a dérivé du mot latin pour «oisiveté» ou «paresse») n’était pas tout à fait la même que son interprétation moderne. Kepler a défini l’inertie uniquement en termes de résistance au mouvement, une fois de plus en partant du principe que le repos était un état naturel qui n’avait pas besoin d’explication. Ce n’est que lorsque les travaux ultérieurs de Galilée et de Newton ont unifié le repos et le mouvement en un seul principe que le terme «inertie» a pu être appliqué à ces concepts tels qu’ils sont aujourd’hui. ^[28]

Néanmoins, malgré la définition si élégante du concept dans ses lois du mouvement, même Newton n’a pas utilisé le terme “inertie” pour désigner sa première loi. En fait, Newton considérait à l’origine le phénomène qu’il décrivait dans sa Première loi du mouvement comme étant causé par des “forces innées” inhérentes à la matière, qui résistaient à toute accélération. Compte tenu de cette perspective, et empruntant à Kepler, Newton a attribué le terme «inertie» pour signifier «la force innée possédée par un objet qui résiste aux changements de mouvement»; ainsi, Newton a défini «inertie» comme signifiant la cause du phénomène, plutôt que le phénomène lui-même. Cependant, les idées originales de Newton sur la “force de résistance innée” étaient finalement problématiques pour diverses raisons, et donc la plupart des physiciens ne pensent plus en ces termes. Comme aucun mécanisme alternatif n’a été facilement accepté, et il est maintenant généralement admis qu’il n’y en a peut-être pas un que nous puissions connaître, le terme «inertie» en est venu à signifier simplement le phénomène lui-même, plutôt que tout mécanisme inhérent. Ainsi, finalement, “l’inertie” dans la physique classique moderne est devenue un nom pour le même phénomène décrit par la Première loi du mouvement de Newton, et les deux concepts sont maintenant considérés comme équivalents.

Relativité

La théorie de la relativité restreinte d’ Albert Einstein , telle que proposée dans son article de 1905 intitulé ” Sur l’électrodynamique des corps en mouvement“, a été fondée sur la compréhension des cadres de référence inertiels développés par Galilée et Newton. Bien que cette théorie révolutionnaire ait considérablement modifié la signification de nombreux concepts newtoniens tels que la masse , l’énergie et la distance , le concept d’inertie d’Einstein est resté inchangé par rapport à la signification originale de Newton. Cependant, cela entraînait une limitation inhérente à la relativité restreinte : le principe de relativité ne pouvait s’appliquer qu’aux Référentiels inertiels. Pour remédier à cette limitation, Einstein a développé sonthéorie générale de la relativité (“The Foundation of the General Theory of Relativity”, 1916), qui a fourni une théorie comprenant des cadres de référence non inertiels (accélérés). ^[29]

Inertie de rotation

Inertie de rotation

Une quantité liée à l’inertie est l’inertie de rotation (→ moment d’inertie ), la propriété selon laquelle un corps rigide en rotation maintient son état de mouvement de rotation uniforme . Son moment cinétique reste inchangé, à moins qu’un couple externe ne soit appliqué ; c’est ce qu’on appelle aussi la conservation du moment cinétique. L’inertie de rotation est souvent considérée par rapport à un corps rigide. Par exemple, un gyroscope utilise la propriété qu’il résiste à tout changement de l’axe de rotation.

Voir également

• Dispositifs de stockage d’énergie à volant d’inertie qui peuvent également être connus sous le nom de batterie à inertie
• Relativité générale
• Vertical et horizontal
• Système de navigation inertielle
• Réponse inertielle des générateurs synchrones dans un réseau électrique
• Énergie cinétique
• Liste des moments d’inertie
• Le principe de Mach
• Les lois du mouvement de Newton
• Physique newtonienne
• Relativité restreinte
• Théorème de Steiner

Références

1. ^ Traduction anglaise d’Andrew Motte : Newton, Isaac (1846), Principia de Newton : les principes mathématiques de la philosophie naturelle (3e édition) , New York : Daniel Adee, p. 73
2. ^ Aristote: Œuvres mineures (1936), Mechanical Problems ( Mechanica ) , University of Chicago Library : Loeb Classical Library Cambridge (Mass.) and London, p. 407, …il [un corps] s’arrête lorsque la force qui pousse le mobile n’a plus le pouvoir de le faire avancer…
3. ^ Pages 2 à 4, Section 1.1, “Skating”, Chapitre 1, “Things that Move”, Louis Bloomfield, professeur de physique à l’ Université de Virginie , How Everything Works: Making Physics Out of the Ordinary , John Wiley & Sons ( 2007), couverture rigide, ISBN 978-0-471-74817-5
4. ^ “N° 2080 La Survie de l’Invention” . www.uh.edu .
5. ^ Byrne, Christophe (2018). Science de la matière et du mouvement d’Aristote . Presse de l’Université de Toronto. p. 21. ISBN 978-1-4875-0396-3. Extrait de la page 21
6. ^ Aristote, Physique , 8.10, 267a1–21 ; Aristote, Physique , trad. par RP Hardie et RK Gaye Archivé le 29/01/2007 à la Wayback Machine .
7. ^ Lucrèce, Sur la nature des choses (Londres: Penguin, 1988), pp. 60-65
8. ^ Sorabji, Richard (1988). Matière, espace et mouvement : théories dans l’antiquité et leur suite (1ère éd.). Ithaca, NY : Cornell University Press. p. 227–228. ISBN 978-0801421945.
9. ^ “John Philoponus” . Encyclopédie de philosophie de Stanford . 8 juin 2007 . Récupéré le 26 juillet 2012 .
10. ^ Chéri, David (2006). L’arc de gravité : l’histoire de la gravité, d’Aristote à Einstein et au-delà . John Wiley et fils. pp. 17 , 50. ISBN 978-0-471-71989-2.
11. ^ Espinoza, Fernando. “Une analyse du développement historique des idées sur le mouvement et ses implications pour l’enseignement”. Enseignement de la physique. Vol. 40(2).
12. ^ Jean Buridan: Quaestiones on Aristote’s Physics (cité à Impetus Theory )
13. ^ Giovanni Benedetti, sélection de Speculationum , dans Stillman Drake et IE Drabkin, Mechanics in XVIth-Century Italy University of Wisconsin Press , 1969, p. 156.
14. ^ Gillispie, Charles Coulston (1960). Aux confins de l’objectivité : un essai sur l’histoire des idées scientifiques . Presse universitaire de Princeton. p. 367–68 . ISBN 0-691-02350-6.
15. ^ 7e paragraphe de la section 8, livre 4 de Physica
16. ^ Nicolas Copernic, Les révolutions des sphères célestes , 1543
17. ↑ Pour une analyse détaillée concernant cette question, voir l’article d’Alan Chalmers “Galilean Relativity and Galileo’s Relativity”, in Correspondence, Invariance and Heuristics: Essays in Honor of Heinz Post , eds. Steven French et Harmke Kamminga, Kluwer Academic Publishers, Dordrecht, 1991, ISBN 0792320859 .
18. ^ Drake, S. Découvertes et opinions de Galilée , Doubleday Anchor, New York, 1957, pp. 113-114
19. ^ Voir l’article d’Alan Chalmers “Galilean Relativity and Galileo’s Relativity”, in Correspondence, Invariance and Heuristics: Essays in Honor of Heinz Post , eds. Steven French et Harmke Kamminga, Kluwer Academic Publishers, Dordrecht, 1991, pp. 199–200, ISBN 0792320859 . Chalmers ne croit cependant pas que la physique de Galilée ait un principe général d’inertie, circulaire ou autre.
20. ^ Dijksterhuis EJ La mécanisation de l’image mondiale , Oxford University Press, Oxford, 1961, p. 352
21. ^ Galileo, Letters on Sunspots , 1613 cité dans Drake, S. Discoveries and Opinions of Galileo , Doubleday Anchor, New York, 1957, pp. 113–114.
22. ↑ Selon la mécanique newtonienne, si un projectile sur une planète sphérique lisse reçoit une vitesse horizontale initiale, il ne restera pas à la surface de la planète. Différentes courbes sont possibles en fonction de la vitesse initiale et de la hauteur de lancement. Voir Harris Benson University Physics , New York 1991, page 268. S’il est contraint de rester à la surface, en étant pris en sandwich, disons, entre deux sphères concentriques, il suivra un grand cercle à la surface de la terre, c’est-à-dire ne maintiendra que une direction ouest s’il est tiré le long de l’équateur. Voir “Utilisation des grands cercles” Utilisation des grands cercles
23. ^ Galilée, Dialogue concernant les deux principaux systèmes mondiaux , 1632 ( texte intégral ).
24. ^ van Berkel, Klaas (2013), Isaac Beeckman sur la matière et le mouvement: la philosophie mécanique en devenir , Johns Hopkins University Press, pp. 105-110, ISBN 9781421409368
25. ^ Traduction anglaise d’Andrew Motte : Newton, Isaac (1846), Principia de Newton : les principes mathématiques de la philosophie naturelle , New York : Daniel Adee, p. 83Cette déclaration habituelle de la loi de Newton à partir de la traduction de Motte-Cajori est cependant trompeuse en donnant l’impression que «l’état» se réfère uniquement au repos et non au mouvement alors qu’il se réfère aux deux. Ainsi, la virgule devrait venir après ‘state’ et non ‘rest’ (Koyre: Newtonian Studies London 1965 Chap III, App A)
26. ^ Dourmaskin, Peter (décembre 2013). “Mécanique classique: Notes de cours MIT 8.01” . MIT Physique 8.01 . Consulté le 9 septembre 2016 .
27. ^ Lawrence Nolan (éd.), The Cambridge Descartes Lexicon , Cambridge University Press, 2016, “Inertia”.
28. ^ Biad, Abder-Rahim (2018-01-26). Restauration de la machine bioélectrique . Lulu Press, Inc. ISBN 9781365447709.
29. ^ Alfred Engel English Translation: Einstein, Albert (1997), The Foundation of the General Theory of Relativité (PDF) , New Jersey: Princeton University Press, p. 57 , récupéré le 30 mai 2014

Lectures complémentaires

• Butterfield, H (1957), Les origines de la science moderne , ISBN 0-7135-0160-X .
• Clement, J (1982), “Les idées préconçues des étudiants en mécanique d’introduction”, American Journal of Physics vol 50, pp 66–71
• Crombie, AC (1959), Medieval and Early Modern Science , vol. 2.
• McCloskey, M (1983), “Physique intuitive”, Scientific American , avril, pp. 114–123.
• McCloskey, M & Carmazza, A (1980), “Mouvement curviligne en l’absence de forces externes: croyances naïves sur le mouvement des objets”, Science vol. 210, p. 1139–1141.
• Pfister, Herbert; Roi, Markus (2015). Inertie et Gravitation. La nature fondamentale et la structure de l’espace-temps . Vol. Les notes de cours en physique . Tome 897. Heidelberg : Springer. doi : 10.1007/978-3-319-15036-9 . ISBN 978-3-319-15035-2.
• En ligneRagep, F. Jamil (2001a). “Tusi et Copernic: le mouvement de la Terre en contexte”. Sciences en contexte . Presse universitaire de Cambridge . 14 (1–2): 145–163. doi : 10.1017/S0269889701000060 . S2CID 145372613 .
• Ragep, F. Jamil (2001b). “Libérer l’astronomie de la philosophie: un aspect de l’influence islamique sur la science” . Osiris . 2e série. 16 (Science dans des contextes théistes : dimensions cognitives) : 49–64 et 66–71. Bibcode : 2001Osir…16…49R . doi : 10.1086/649338 . S2CID 142586786 .

Liens externes

• Citations liées à l’ inertie sur Wikiquote
• Pourquoi la Terre tourne-t-elle ? (Youtube)