Estimation de vraisemblance maximale

En statistique, l’estimation du maximum de vraisemblance ( MLE ) est une méthode d’ estimation des paramètres d’une distribution de probabilité supposée , compte tenu de certaines données observées. Ceci est réalisé en maximisant une fonction de vraisemblance de sorte que, sous le modèle statistique supposé , les données observées soient les plus probables. Le point dans l’ espace des paramètres qui maximise la fonction de vraisemblance est appelé estimation du maximum de vraisemblance. ^[1] La logique du maximum de vraisemblance est à la fois intuitive et flexible, et en tant que telle la méthode est devenue un moyen dominant deinférence statistique . ^{[2] [3] [4]}

Si la fonction de vraisemblance est différentiable , le test dérivé pour déterminer les maxima peut être appliqué. Dans certains cas, les conditions de premier ordre de la fonction de vraisemblance peuvent être résolues explicitement ; par exemple, l’ estimateur des moindres carrés ordinaires maximise la vraisemblance du modèle de régression linéaire . ^[5] Dans la plupart des cas, cependant, des méthodes numériques seront nécessaires pour trouver le maximum de la fonction de vraisemblance.

Du point de vue de l’inférence bayésienne , MLE est généralement équivalente à l’estimation maximale a posteriori (MAP) sous une distribution a priori uniforme sur les paramètres. Dans l’inférence fréquentiste , MLE est un cas particulier d’ estimateur extremum , la fonction objectif étant la vraisemblance.

Des principes

Nous modélisons un ensemble d’observations comme un échantillon aléatoire à partir d’une distribution de probabilité jointe inconnue qui est exprimée en termes d’un ensemble de paramètres . L’objectif de l’estimation du maximum de vraisemblance est de déterminer les paramètres pour lesquels les données observées ont la probabilité conjointe la plus élevée. Nous écrivons les paramètres régissant la distribution conjointe sous forme de vecteur θ = [ θ 1 , θ 2 , … , θ k ] T {displaystyle ;theta =left[theta _{1},,theta _{2},,ldots ,,theta _{k}right]^{mathsf {T} };} de sorte que cette distribution tombe dans une famille paramétrique { f ( ⋅ ; θ ) ∣ θ ∈ Θ } , {displaystyle ;{f(cdot ,;theta )mid theta in Theta };,} où Θ {displaystyle ,Thêta ,} est appelé l’ espace des paramètres , un sous-ensemble de dimension finie de l’ espace euclidien . Évaluation de la densité des joints au niveau de l’échantillon de données observé y = ( y 1 , y 2 , … , y n ) {displaystyle ;mathbf {y} =(y_{1},y_{2},ldots ,y_{n});} donne une fonction à valeurs réelles,

L n ( θ ) = L n ( θ ; y ) = f n ( y ; θ ) , {displaystyle {mathcal {L}}_{n}(theta )={mathcal {L}}_{n}(theta ;mathbf {y} )=f_{n}(mathbf {y } ;thêta );,}

qui s’appelle la fonction de vraisemblance . Pour des variables aléatoires indépendantes et identiquement distribuées , f n ( y ; θ ) {displaystyle f_{n}(mathbf {y} ;theta )} sera le produit de fonctions de densité univariées :

f n ( y ; θ ) = ∏ k = 1 n f k u n i v a r ( y k ; θ ) . {displaystyle f_{n}(mathbf {y} ;theta )=prod _{k=1}^{n},f_{k}^{mathsf {univar}}(y_{k} ; thêta )~.}

Le but de l’estimation du maximum de vraisemblance est de trouver les valeurs des paramètres du modèle qui maximisent la fonction de vraisemblance sur l’espace des paramètres, ^[6] c’est-à-dire

θ ^ = a r g m a x θ ∈ Θ L ^ n ( θ ; y ) . {displaystyle {hat {theta }}={underset {theta in Theta }{operatorname {arg;max} }},{widehat {mathcal {L}}}_{n }(theta ,;mathbf {y} )~.}

Intuitivement, cela sélectionne les valeurs des paramètres qui rendent les données observées les plus probables. La valeur spécifique θ ^ = θ ^ n ( y ) ∈ Θ {displaystyle ~{hat {theta }}={hat {theta }}_{n}(mathbf {y} )in Theta ~} qui maximise la fonction de vraisemblance L n {displaystyle ,{mathcal {L}}_{n},} est appelée estimation du maximum de vraisemblance. De plus, si la fonction θ ^ n : R n → Θ {displaystyle ;{hat {theta}}_{n} :mathbb {R} ^{n}to Theta ;} ainsi défini est mesurable , alors on l’appelle l’ estimateur du maximum de vraisemblance . Il s’agit généralement d’une fonction définie sur l’ espace des échantillons , c’est-à-dire prenant un échantillon donné comme argument. Une condition suffisante mais non nécessaire pour son existence est que la fonction de vraisemblance soit continue sur un espace de paramètres Θ {displaystyle ,Thêta ,} c’est compact . ^[7] Pour une ouverture Θ {displaystyle ,Thêta ,} la fonction de vraisemblance peut augmenter sans jamais atteindre une valeur suprême.

En pratique, il est souvent commode de travailler avec le logarithme népérien de la fonction de vraisemblance, appelé log-vraisemblance :

l ( θ ; y ) = ln ⁡ L n ( θ ; y ) . {displaystyle ell (theta ,;mathbf {y} )=ln {mathcal {L}}_{n}(theta ,;mathbf {y} )~.}

Comme le logarithme est une fonction monotone , le maximum de l ( θ ; y ) {displaystyle ;ell (theta ,;mathbf {y} );} se produit à la même valeur de θ {displaystyle thêta} tout comme le maximum de L n . {displaystyle,{mathcal{L}}_{n}~.} ^[8] Si l ( θ ; y ) {displaystyle ell (theta ,;mathbf {y} )} est différentiable en Θ , {displaystyle ,Thêta ,,} les conditions nécessaires à l’apparition d’un maximum (ou d’un minimum) sont

∂ l ∂ θ 1 = 0 , ∂ l ∂ θ 2 = 0 , … , ∂ l ∂ θ k = 0 , {displaystyle {frac {partial ell }{partial theta _{1}}}=0,quad {frac {partial ell }{partial theta _{2}}}=0 ,quad ldots ,quad {frac {partial ell }{partial theta _{k}}}=0~,}

connues sous le nom d’équations de vraisemblance. Pour certains modèles, ces équations peuvent être explicitement résolues pour θ ^ , {displaystyle ,{widehat {theta ,}},,} mais en général, aucune solution de forme fermée au problème de maximisation n’est connue ou disponible, et un MLE ne peut être trouvé que par optimisation numérique . Un autre problème est que dans des échantillons finis, il peut exister plusieurs racines pour les équations de vraisemblance. ^[9] Si la racine identifiée θ ^ {displaystyle ,{widehat {theta ,}},} des équations de vraisemblance est en effet un maximum (local) dépend si la matrice des dérivées partielles et croisées du second ordre, la matrice dite Hessienne

H ( θ ^ ) = [ ∂ 2 l ∂ θ 1 2 | θ = θ ^ ∂ 2 l ∂ θ 1 ∂ θ 2 | θ = θ ^ … ∂ 2 l ∂ θ 1 ∂ θ k | θ = θ ^ ∂ 2 l ∂ θ 2 ∂ θ 1 | θ = θ ^ ∂ 2 l ∂ θ 2 2 | θ = θ ^ … ∂ 2 l ∂ θ 2 ∂ θ k | θ = θ ^ ⋮ ⋮ ⋱ ⋮ ∂ 2 l ∂ θ k ∂ θ 1 | θ = θ ^ ∂ 2 l ∂ θ k ∂ θ 2 | θ = θ ^ … ∂ 2 l ∂ θ k 2 | θ = θ ^ ] , {displaystyle mathbf {H} left({widehat {theta ,}}right)={begin{bmatrix}left.{frac {partial ^{2}ell }{partial theta _{1}^{2}}}right|_{theta ={widehat {theta ,}}}&left.{frac {partial ^{2}ell }{partial theta _{1},partial theta _{2}}}right|_{theta ={widehat {theta ,}}}&dots &left.{frac {partial ^{2}ell }{partial theta _{1},partial theta _{k}}}right|_{theta ={widehat {theta ,}}}\left.{frac {partial ^{2}ell }{partial theta _{2},partial theta _{1}}}right|_{theta ={widehat {theta ,}}}&left.{frac {partial ^{2}ell }{partial theta _{2}^{2}}}right|_{theta ={widehat {theta ,}}}&dots &left.{frac {partial ^{2}ell }{partial theta _{2},partial theta _{k}}}right|_{theta ={widehat {theta ,}}}\vdots &vdots &ddots &vdots \left.{frac {partial ^{2}ell }{partial theta _{k},partial theta _{1}}}right|_{theta ={widehat {theta ,}}}&left.{frac {partial ^{2}ell }{partial theta _{k},partial theta _{2}}}right|_{theta ={widehat {theta ,}}}&dots &left.{frac {partial ^{2}ell }{partial theta _{k}^{2}}}right|_{theta ={widehat {theta ,}}}end{bmatrix}}~,}

est semi-défini négatif en θ ^ {displaystyle {widehat {thêta ,}}} , car cela indique une concavité locale . De manière pratique, la plupart des distributions de probabilité courantes – en particulier la famille exponentielle – sont logarithmiquement concaves . ^{[10] [11]}

Espace de paramètre restreint

Alors que le domaine de la fonction de vraisemblance – l’ espace des paramètres – est généralement un sous-ensemble de dimension finie de l’ espace euclidien , des restrictions supplémentaires doivent parfois être incorporées dans le processus d’estimation. L’espace des paramètres peut être exprimé comme

Θ = { θ : θ ∈ R k , h ( θ ) = 0 } , {displaystyle Theta =left{theta :theta in mathbb {R} ^{k},;h(theta )=0right}~,}

où h ( θ ) = [ h 1 ( θ ) , h 2 ( θ ) , … , h r ( θ ) ] {displaystyle ;h(theta )=left[h_{1}(theta ),h_{2}(theta ),ldots ,h_{r}(theta )right];} est un mappage de fonction à valeur vectorielle R k {displaystyle ,mathbb {R} ^{k},} dans R r . {displaystyle ;mathbb {R} ^{r}~.} Estimation du vrai paramètre θ {displaystyle thêta} appartenir à Θ {displaystyle thêta} puis, en pratique, signifie trouver le maximum de la fonction de vraisemblance soumise à la contrainte h ( θ ) = 0 . {displaystyle ~h(theta )=0~.}

Théoriquement, l’approche la plus naturelle de ce problème d’optimisation sous contrainte est la méthode de substitution, c’est-à-dire “remplir” les restrictions h 1 , h 2 , … , h r {displaystyle ;h_{1},h_{2},ldots ,h_{r};} à un ensemble h 1 , h 2 , … , h r , h r + 1 , … , h k {displaystyle ;h_{1},h_{2},ldots ,h_{r},h_{r+1},ldots ,h_{k};} de telle sorte que h ∗ = [ h 1 , h 2 , … , h k ] {displaystyle ;h^{ast }=left[h_{1},h_{2},ldots ,h_{k}right];} est une fonction biunivoque de R k {displaystyle mathbb {R} ^{k}} à lui-même, et reparamétrer la fonction de vraisemblance en fixant φ i = h i ( θ 1 , θ 2 , … , θ k ) . {displaystyle ;phi _{i}=h_{i}(theta _{1},theta _{2},ldots ,theta _{k})~.} ^[12] En raison de l’équivariance de l’estimateur du maximum de vraisemblance, les propriétés de l’EML s’appliquent également aux estimations restreintes. ^[13] Par exemple, dans une distribution normale multivariée, la matrice de covariance Σ {displaystyle,Sigma,} doit être défini positif ; cette restriction peut être imposée en remplaçant Σ = Γ T Γ , {displaystyle ;Sigma =Gamma ^{mathsf {T}}Gamma ;,} où Γ {displaystylegamma} est une vraie matrice triangulaire supérieure et Γ T {displaystyle Gamma ^{mathsf {T}}} est sa transposée . ^[14]

En pratique, les restrictions sont généralement imposées à l’aide de la méthode de Lagrange qui, compte tenu des contraintes telles que définies ci-dessus, conduit aux équations de vraisemblance restreintes

∂ l ∂ θ − ∂ h ( θ ) T ∂ θ λ = 0 {displaystyle {frac {partial ell }{partial theta }}-{frac {partial h(theta )^{mathsf {T}}}{partial theta }}lambda = 0} et h ( θ ) = 0 , {displaystyle h(theta )=0;,}

où λ = [ λ 1 , λ 2 , … , λ r ] T {displaystyle ~lambda =left[lambda _{1},lambda _{2},ldots ,lambda _{r}right]^{mathsf {T}}~} est un vecteur-colonne de multiplicateurs de Lagrange et ∂ h ( θ ) T ∂ θ {displaystyle ;{frac {partial h(theta )^{mathsf {T}}}{partial theta }};} est la matrice jacobienne k × r des dérivées partielles. ^[12] Naturellement, si les contraintes ne sont pas contraignantes au maximum, les multiplicateurs de Lagrange doivent être nuls. ^[15] Cela permet à son tour un test statistique de la “validité” de la contrainte, connu sous le nom de test du multiplicateur de Lagrange .

Propriétés

Un estimateur du maximum de vraisemblance est un estimateur extremum obtenu en maximisant, en fonction de θ , la fonction objectif l ^ ( θ ; x ) {displaystyle {widehat {ell ,}}(theta ,;x)} . Si les données sont indépendantes et identiquement distribuées , alors on a

l ^ ( θ ; x ) = 1 n ∑ i = 1 n ln ⁡ f ( x i ∣ θ ) , {displaystyle {widehat {ell ,}}(theta ,;x)={frac {1}{n}}sum _{i=1}^{n}ln f(x_{ je}mid theta ),}

ceci étant l’analogue de l’échantillon de la log-vraisemblance attendue l ( θ ) = E ⁡ [ ln ⁡ f ( x i ∣ θ ) ] {displaystyle ell (theta )=operatorname {mathbb {E} } [,ln f(x_{i}mid theta ),]} , où cette espérance est prise par rapport à la vraie densité.

Les estimateurs du maximum de vraisemblance n’ont pas de propriétés optimales pour les échantillons finis, en ce sens que (lorsqu’ils sont évalués sur des échantillons finis), d’autres estimateurs peuvent avoir une plus grande concentration autour de la vraie valeur du paramètre. ^[16] Cependant, comme d’autres méthodes d’estimation, l’estimation du maximum de vraisemblance possède un certain nombre de propriétés limitantes intéressantes : lorsque la taille de l’échantillon augmente jusqu’à l’infini, les séquences d’estimateurs du maximum de vraisemblance ont ces propriétés :

• Cohérence : la séquence des MLE converge en probabilité vers la valeur estimée.
• Equivariance fonctionnelle : Si θ ^ {displaystyle {chapeau {thêta}}} est l’estimateur du maximum de vraisemblance pour θ {displaystyle thêta} , et si g ( θ ) {displaystyle g(thêta)} est toute transformation de θ {displaystyle thêta} , alors l’estimateur du maximum de vraisemblance pour α = g ( θ ) {displaystyle alpha =g(theta )} est α ^ = g ( θ ^ ) {displaystyle {chapeau {alpha}}=g({chapeau {thêta}})} .
• Efficience , c’est-à-dire qu’elle atteint la borne inférieure de Cramér–Rao lorsque la taille de l’échantillon tend vers l’infini. Cela signifie qu’aucun estimateur cohérent n’a une erreur quadratique moyenne asymptotique inférieure à celle du MLE (ou d’autres estimateurs atteignant cette limite), ce qui signifie également que le MLE a une normalité asymptotique .
• Efficacité de second ordre après correction du biais.

Cohérence

Dans les conditions décrites ci-dessous, l’estimateur du maximum de vraisemblance est cohérent . La cohérence signifie que si les données ont été générées par f ( ⋅ ; θ 0 ) {displaystyle f(cdot ,;theta _{0})} et que l’on dispose d’un nombre suffisamment grand d’observations n , alors il est possible de trouver la valeur de θ ₀ avec une précision arbitraire. En termes mathématiques, cela signifie que lorsque n tend vers l’infini, l’estimateur θ ^ {displaystyle {widehat {thêta ,}}} converge en probabilité vers sa vraie valeur :

θ ^ m l e → p θ 0 . {displaystyle {widehat {theta ,}}_{mathrm {mle} } {xrightarrow {text{p}}} theta _{0}.}

Dans des conditions légèrement plus fortes, l’estimateur converge presque sûrement (ou fortement ):

θ ^ m l e → a.s. θ 0 . {displaystyle {widehat {theta ,}}_{mathrm {mle} } {xrightarrow {text{as}}} theta _{0}.}

Dans les applications pratiques, les données ne sont jamais générées par f ( ⋅ ; θ 0 ) {displaystyle f(cdot ,;theta _{0})} . Plutôt, f ( ⋅ ; θ 0 ) {displaystyle f(cdot ,;theta _{0})} est un modèle, souvent sous forme idéalisée, du processus généré par les données. C’est un aphorisme courant dans les statistiques que tous les modèles sont faux . Ainsi, la véritable cohérence ne se produit pas dans les applications pratiques. Néanmoins, la cohérence est souvent considérée comme une propriété souhaitable pour un estimateur.

Pour établir la cohérence, les conditions suivantes sont suffisantes. ^[17]

1. Identification du modèle : θ ≠ θ 0 ⇔ f ( ⋅ ∣ θ ) ≠ f ( ⋅ ∣ θ 0 ) . {displaystyle theta neq theta _{0}quad Leftrightarrow quad f(cdot mid theta )neq f(cdot mid theta _{0}).} En d’autres termes, différentes valeurs de paramètres θ correspondent à différentes distributions au sein du modèle. Si cette condition n’était pas vérifiée, il y aurait une certaine valeur θ ₁ telle que θ ₀ et θ ₁ génèrent une distribution identique des données observables. Nous ne serions alors pas en mesure de faire la distinction entre ces deux paramètres même avec une quantité infinie de données – ces paramètres auraient été équivalents d’un point de vue observationnel .
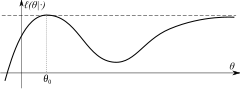
   La condition d’identification est absolument nécessaire pour que l’estimateur ML soit cohérent. Lorsque cette condition est vérifiée, la fonction de vraisemblance limite l ( θ |·) a un maximum global unique en θ ₀ .
2. Compacité : l’espace des paramètres Θ du modèle est compact . La condition d’identification établit que la log-vraisemblance a un maximum global unique. La compacité implique que la vraisemblance ne peut pas s’approcher de la valeur maximale arbitrairement proche en un autre point (comme le montre par exemple l’image de droite).La compacité n’est qu’une condition suffisante et non une condition nécessaire. La compacité peut être remplacée par d’autres conditions, telles que :
   • à la fois la concavité de la fonction de log-vraisemblance et la compacité de certains ensembles de niveau supérieur (non vides) de la fonction de log-vraisemblance, ou
   • existence d’un voisinage compact N de θ ₀ tel qu’en dehors de N la fonction de log-vraisemblance est inférieure au maximum d’au moins quelques ε > 0 .
3. Continuité : la fonction ln f ( x | θ ) est continue en θ pour presque toutes les valeurs de x : P ⁡ [ ln ⁡ f ( x ∣ θ ) ∈ C 0 ( Θ ) ] = 1. {displaystyle operatorname {mathbb {P} } {Bigl [};ln f(xmid theta );in ​​;C^{0}(Theta );{Bigr ] }=1.} La continuité ici peut être remplacée par une condition légèrement plus faible de semi-continuité supérieure .
4. Dominance : il existe D ( x ) intégrable par rapport à la distribution f ( x | θ ₀ ) tel que | ln ⁡ f ( x ∣ θ ) | < D ( x ) for all θ ∈ Θ . {displaystyle {Bigl |}ln f(xmid theta ){Bigr |}<D(x)quad {text{ for all }}theta in Theta .} Par la Loi uniforme des grands nombres , la condition de dominance ainsi que la continuité établissent la convergence uniforme en probabilité de la log-vraisemblance : sup θ ∈ Θ | l ^ ( θ ∣ x ) − l ( θ ) | → p 0. {displaystyle sup _{theta in Theta }left|{widehat {ell ,}}(theta mid x)-ell (theta ),right| {xrightarrow {text{p}}} 0.}

La condition de dominance peut être employée dans le cas d’ observations iid . Dans le cas non iid, la convergence uniforme en probabilité peut être vérifiée en montrant que la suite l ^ ( θ ∣ x ) {displaystyle {widehat {ell ,}}(theta mid x)} est stochastiquement équicontinu . Si l’on veut démontrer que l’estimateur ML θ ^ {displaystyle {widehat {thêta ,}}} converge vers θ ₀ presque sûrement , alors une condition plus forte de convergence uniforme presque sûrement doit être imposée :

sup θ ∈ Θ ‖ l ^ ( θ ∣ x ) − l ( θ ) ‖ → a.s. 0. {displaystyle sup _{theta in Theta }left|;{widehat {ell ,}}(theta mid x)-ell (theta );right| xrightarrow {text{as}} 0.}

De plus, si (comme supposé ci-dessus) les données ont été générées par f ( ⋅ ; θ 0 ) {displaystyle f(cdot ,;theta _{0})} , alors sous certaines conditions, on peut aussi montrer que l’estimateur du maximum de vraisemblance converge en distribution vers une distribution normale. Plus précisément, ^[18]

n ( θ ^ m l e − θ 0 ) → d N ( 0 , I − 1 ) {displaystyle {sqrt {n}}left({widehat {theta ,}}_{mathrm {mle} }-theta _{0}right) xrightarrow {d} { mathcal {N}}left(0,,I^{-1}right)}

où I est la matrice d’information de Fisher .

Equivariance fonctionnelle

L’estimateur du maximum de vraisemblance sélectionne la valeur du paramètre qui donne aux données observées la plus grande probabilité possible (ou densité de probabilité, dans le cas continu). Si le paramètre se compose d’un certain nombre de composantes, nous définissons alors leurs estimateurs du maximum de vraisemblance distincts, comme la composante correspondante de l’EML du paramètre complet. Conformément à cela, si θ ^ {displaystyle {widehat {thêta ,}}} est le MLE pour θ {displaystyle thêta} , et si g ( θ ) {displaystyle g(thêta)} est toute transformation de θ {displaystyle thêta} , puis le MLE pour α = g ( θ ) {displaystyle alpha =g(theta )} est par définition ^[19]

α ^ = g ( θ ^ ) . {displaystyle {widehat {alpha }}=g(,{widehat {theta ,}},).,}

Il maximise la vraisemblance dite du profil :

L ̄ ( α ) = sup θ : α = g ( θ ) L ( θ ) . {displaystyle {bar {L}}(alpha )=sup _{theta :alpha =g(theta )}L(theta ).,}

Le MLE est également équivariant vis-à-vis de certaines transformations des données. Si y = g ( x ) {displaystyle y=g(x)} où g {displaystyle g} est un à un et ne dépend pas des paramètres à estimer, alors les fonctions de densité satisfont

f Y ( y ) = f X ( x ) | g ′ ( x ) | {displaystyle f_{Y}(y)={frac {f_{X}(x)}{|g'(x)|}}}

et donc les fonctions de vraisemblance pour X {displaystyle X} et Y {displaystyle Y} ne diffèrent que par un facteur qui ne dépend pas des paramètres du modèle.

Par exemple, les paramètres MLE de la distribution log-normale sont les mêmes que ceux de la distribution normale ajustée au logarithme des données.

Efficacité

Comme supposé ci-dessus, si les données ont été générées par f ( ⋅ ; θ 0 ) , {displaystyle ~f(cdot ,;theta _{0})~,} puis sous certaines conditions, on peut aussi montrer que l’estimateur du maximum de vraisemblance converge en distribution vers une distribution normale. Elle est √ n -cohérente et asymptotiquement efficace, c’est-à-dire qu’elle atteint la borne de Cramér–Rao . Plus précisément, ^[18]

n ( θ ^ mle − θ 0 ) → d N ( 0 , I − 1 ) , {displaystyle {sqrt {n,}},left({widehat {theta ,}}_{text{mle}}-theta _{0}right) xrightarrow { ré} {mathcal {N}}left(0, {mathcal {I}}^{-1}right)~,}

où I {displaystyle ~{mathcal {I}}~} est la matrice d’information de Fisher :

I j k = E [ − ∂ 2 ln ⁡ f θ 0 ( X t ) ∂ θ j ∂ θ k ] . {displaystyle {mathcal {I}}_{jk}=operatorname {mathbb {E} } ,{biggl [};-{frac {partial ^{2}ln f_{theta _{0}}(X_{t})}{partial theta _{j},partial theta _{k}}};{biggr ]}~.}

En particulier, cela signifie que le biais de l’estimateur du maximum de vraisemblance est égal à zéro jusqu’à l’ordre1/√ n .

Efficacité de second ordre après correction du biais

Cependant, lorsque l’on considère les termes d’ordre supérieur dans le développement de la distribution de cet estimateur, il s’avère que θ _mle a un biais d’ordre 1 ⁄ n . Ce biais est égal à (par composante) ^[20]

b h ≡ E ⁡ [ ( θ ^ m l e − θ 0 ) h ] = 1 n ∑ i , j , k = 1 m I h i I j k ( 1 2 K i j k + J j , i k ) {displaystyle b_{h};equiv ;operatorname {mathbb {E} } {biggl [};left({widehat {theta}}_{mathrm {mle} }- theta _{0}right)_{h};{biggr ]};=;{frac {1}{,n,}},sum _{i,j,k= 1}^{m};{mathcal {I}}^{hi};{mathcal {I}}^{jk}left({frac {1}{,2,}} ,K_{ijk};+;J_{j,ik}right)}

où I j k {displaystyle {mathcal {I}}^{jk}} (avec exposants) désigne la ( j,k )-ième composante de la matrice d’information inverse de Fisher I − 1 {displaystyle {mathcal {I}}^{-1}} , et

1 2 K i j k + J j , i k = E [ 1 2 ∂ 3 ln ⁡ f θ 0 ( X t ) ∂ θ i ∂ θ j ∂ θ k + ∂ ln ⁡ f θ 0 ( X t ) ∂ θ j ∂ 2 ln ⁡ f θ 0 ( X t ) ∂ θ i ∂ θ k ] . {displaystyle {frac {1}{,2,}},K_{ijk};+;J_{j,ik};=;operatorname {mathbb {E} } , {biggl [} ;{frac {1}{2}}{frac {partial ^{3}ln f_{theta _{0}}(X_{t})}{partial theta _{i};partial theta _{j};partial theta _{k}}}+{frac {;partial ln f_{theta _{0}}(X_{t });}{partial theta _{j}}},{frac {;partial ^{2}ln f_{theta _{0}}(X_{t});} {partial theta _{i},partial theta _{k}}};{biggr ]}~.}

En utilisant ces formules, il est possible d’estimer le biais de second ordre de l’estimateur du maximum de vraisemblance et de corriger ce biais en le soustrayant :

θ ^ mle ∗ = θ ^ mle − b ^ . {displaystyle {widehat {theta ,}}_{text{mle}}^{*}={widehat {theta ,}}_{text{mle}}-{widehat {b ,}}~.}

Cet estimateur est sans biais jusqu’aux termes de la commande 1/ n , et est appelé estimateur du maximum de vraisemblance corrigé du biais.

Cet estimateur corrigé du biais est efficace au second ordre (au moins dans la famille exponentielle courbe), ce qui signifie qu’il a une erreur quadratique moyenne minimale parmi tous les estimateurs corrigés du biais du second ordre, jusqu’aux termes de l’ordre 1/ n ² . Il est possible de poursuivre ce processus, c’est-à-dire de dériver le terme de correction de biais du troisième ordre, et ainsi de suite. Cependant, l’estimateur du maximum de vraisemblance n’est pas efficace au troisième ordre. ^[21]

Relation avec l’inférence bayésienne

Un estimateur du maximum de vraisemblance coïncide avec l’ estimateur bayésien le plus probable compte tenu d’une distribution a priori uniforme sur les paramètres . En effet, l’ estimation a posteriori maximale est le paramètre θ qui maximise la probabilité de θ compte tenu des données, donné par le théorème de Bayes :

P ⁡ ( θ ∣ x 1 , x 2 , … , x n ) = f ( x 1 , x 2 , … , x n ∣ θ ) P ⁡ ( θ ) P ⁡ ( x 1 , x 2 , … , x n ) {displaystyle operatorname {mathbb {P}} (theta mid x_{1},x_{2},ldots ,x_{n})={frac {f(x_{1},x_{2 },ldots ,x_{n}mid theta )operatorname {mathbb {P} } (theta )}{operatorname {mathbb {P} } (x_{1},x_{2}, ldots ,x_{n})}}}

où P ⁡ ( θ ) {displaystyle operatorname {mathbb {P}} (theta)} est la distribution a priori pour le paramètre θ et où P ⁡ ( x 1 , x 2 , … , x n ) {displaystyle operatorname {mathbb {P} } (x_{1},x_{2},ldots ,x_{n})} est la probabilité des données moyennées sur tous les paramètres. Puisque le dénominateur est indépendant de θ , l’estimateur bayésien est obtenu en maximisant f ( x 1 , x 2 , … , x n ∣ θ ) P ⁡ ( θ ) {displaystyle f(x_{1},x_{2},ldots ,x_{n}mid theta )operatorname {mathbb {P} } (theta )} par rapport à θ . Si nous supposons en outre que le précédent P ⁡ ( θ ) {displaystyle operatorname {mathbb {P}} (theta)} est une distribution uniforme, l’estimateur bayésien est obtenu en maximisant la fonction de vraisemblance f ( x 1 , x 2 , … , x n ∣ θ ) {displaystyle f(x_{1},x_{2},ldots ,x_{n}mid theta)} . Ainsi, l’estimateur bayésien coïncide avec l’estimateur du maximum de vraisemblance pour une distribution a priori uniforme P ⁡ ( θ ) {displaystyle operatorname {mathbb {P}} (theta)} .

Application de l’estimation du maximum de vraisemblance dans la théorie de la décision de Bayes

Dans de nombreuses applications pratiques de l’apprentissage automatique , l’estimation du maximum de vraisemblance est utilisée comme modèle pour l’estimation des paramètres.

La théorie de la décision bayésienne consiste à concevoir un classificateur qui minimise le risque total attendu, en particulier lorsque les coûts (la fonction de perte) associés à différentes décisions sont égaux, le classificateur minimise l’erreur sur l’ensemble de la distribution. ^[22]

Ainsi, la règle de décision de Bayes est énoncée comme

“décider w 1 {displaystyle ;w_{1};} si P ⁡ ( w 1 | x ) > P ⁡ ( w 2 | x ) ; {displaystyle ~operatorname {mathbb {P} } (w_{1}|x);>;operatorname {mathbb {P} } (w_{2}|x)~;~} sinon décider w 2 {displaystyle ;w_{2};} ”

où w 1 , w 2 {displaystyle ;w_{1},,w_{2};} sont des prédictions de différentes classes. Du point de vue de la minimisation des erreurs, on peut également dire que

w = a r g m a x w ∫ − ∞ ∞ P ⁡ ( error ∣ x ) P ⁡ ( x ) d ⁡ x {displaystyle w={underset {w}{operatorname {arg;max} }};int _{-infty }^{infty}operatorname {mathbb {P} } ({text { erreur}}mid x)nom de l’opérateur {mathbb {P} } (x),nom de l’opérateur {d} x~}

où

P ⁡ ( error ∣ x ) = P ⁡ ( w 1 ∣ x ) {displaystyle operatorname {mathbb {P} } ({text{ error}}mid x)=operatorname {mathbb {P} } (w_{1}mid x)~}

si nous décidons w 2 {displaystyle ;w_{2};} et P ⁡ ( error ∣ x ) = P ⁡ ( w 2 ∣ x ) {displaystyle ;operatorname {mathbb {P} } ({text{ error}}mid x)=operatorname {mathbb {P} } (w_{2}mid x);} si nous décidons w 1 . {displaystyle ;w_{1};.}

En appliquant le théorème de Bayes

P ⁡ ( w i ∣ x ) = P ⁡ ( x ∣ w i ) P ⁡ ( w i ) P ⁡ ( x ) {displaystyle operatorname {mathbb {P} } (w_{i}mid x)={frac {operatorname {mathbb {P} } (xmid w_{i})operatorname {mathbb { P} } (w_{i})}{nomopérateur {mathbb {P} } (x)}}} ,

et si nous supposons en outre la fonction de perte zéro ou un, qui est une même perte pour toutes les erreurs, la règle de la décision de Bayes peut être reformulée comme suit :

h Bayes = a r g m a x w [ P ⁡ ( x ∣ w ) P ⁡ ( w ) ] , {displaystyle h_{text{Bayes}}={underset {w}{operatorname {arg;max} }},{bigl [},operatorname {mathbb {P} } (x milieu w),operatorname {mathbb {P} } (w),{bigr ]};,}

où h Bayes {displaystyle h_{text{Baies}}} est la prédiction et P ⁡ ( w ) {displaystyle ;operatorname {mathbb {P} } (w);} est la probabilité a priori .

Relation avec la minimisation de la divergence Kullback – Leibler et de l’entropie croisée

Découverte θ ^ {displaystyle {chapeau {thêta}}} qui maximise la vraisemblance est asymptotiquement équivalent à trouver la θ ^ {displaystyle {chapeau {thêta}}} qui définit une distribution de probabilité ( Q θ ^ {displaystyle Q_{hat {theta}}} ) qui a une distance minimale, en termes de divergence Kullback-Leibler , à la distribution de probabilité réelle à partir de laquelle nos données ont été générées (c’est-à-dire générées par P θ 0 {displaystyle P_{thêta _{0}}} ). ^[23] Dans un monde idéal, P et Q sont identiques (et la seule chose inconnue est θ {displaystyle thêta} qui définit P), mais même s’ils ne le sont pas et que le modèle que nous utilisons est mal spécifié, le MLE nous donnera toujours la distribution “la plus proche” (dans la restriction d’un modèle Q qui dépend de θ ^ {displaystyle {chapeau {thêta}}} ) à la distribution réelle P θ 0 {displaystyle P_{thêta _{0}}} . ^[24]

Preuve.

Pour simplifier la notation, supposons que P=Q. Soit n échantillons de données i.id y = ( y 1 , y 2 , … , y n ) {displaystyle mathbf {y} =(y_{1},y_{2},ldots ,y_{n})} d’une certaine probabilité y ∼ P θ 0 {displaystyle ysim P_{theta _{0}}} , que nous essayons d’estimer en trouvant θ ^ {displaystyle {chapeau {thêta}}} qui maximisera la probabilité en utilisant P θ {displaystyle P_{thêta}} , alors: θ ^ = a r g m a x θ L P θ ( y ) = a r g m a x θ P θ ( y ) = a r g m a x θ P ( y ∣ θ ) = a r g m a x θ ∏ i = 1 n P ( y i ∣ θ ) = a r g m a x θ ∑ i = 1 n log ⁡ P ( y i ∣ θ ) = a r g m a x θ ( ∑ i = 1 n log ⁡ P ( y i ∣ θ ) − ∑ i = 1 n log ⁡ P ( y i ∣ θ 0 ) ) = a r g m a x θ ∑ i = 1 n ( log ⁡ P ( y i ∣ θ ) − log ⁡ P ( y i ∣ θ 0 ) ) = a r g m a x θ ∑ i = 1 n log ⁡ P ( y i ∣ θ ) P ( y i ∣ θ 0 ) = a r g m i n θ ∑ i = 1 n log ⁡ P ( y i ∣ θ 0 ) P ( y i ∣ θ ) = a r g m i n θ 1 n ∑ i = 1 n log ⁡ P ( y i ∣ θ 0 ) P ( y i ∣ θ ) = a r g m i n θ 1 n ∑ i = 1 n h θ ( y i ) ⟶ n → ∞ a r g m i n θ E [ h θ ( y ) ] = a r g m i n θ ∫ P θ 0 ( y ) h θ ( y ) d y = a r g m i n θ ∫ P θ 0 ( y ) log ⁡ P ( y ∣ θ 0 ) P ( y ∣ θ ) d y = a r g m i n θ D KL ( P θ 0 ∥ P θ ) {displaystyle {begin{aligned}{hat {theta }}&={underset {theta }{operatorname {arg,max} }},L_{P_{theta }}(mathbf {y} )={underset {theta }{operatorname {arg,max} }},P_{theta }(mathbf {y} )={underset {theta }{operatorname {arg,max} }},P(mathbf {y} mid theta )\&={underset {theta }{operatorname {arg,max} }},prod _{i=1}^{n}P(y_{i}mid theta )={underset {theta }{operatorname {arg,max} }},sum _{i=1}^{n}log P(y_{i}mid theta )\&={underset {theta }{operatorname {arg,max} }},left(sum _{i=1}^{n}log P(y_{i}mid theta )-sum _{i=1}^{n}log P(y_{i}mid theta _{0})right)={underset {theta }{operatorname {arg,max} }},sum _{i=1}^{n}left(log P(y_{i}mid theta )-log P(y_{i}mid theta _{0})right)\&={underset {theta }{operatorname {arg,max} }},sum _{i=1}^{n}log {frac {P(y_{i}mid theta )}{P(y_{i}mid theta _{0})}}={underset {theta }{operatorname {arg,min} }},sum _{i=1}^{n}log {frac {P(y_{i}mid theta _{0})}{P(y_{i}mid theta )}}={underset {theta }{operatorname {arg,min} }},{frac {1}{n}}sum _{i=1}^{n}log {frac {P(y_{i}mid theta _{0})}{P(y_{i}mid theta )}}\&={underset {theta }{operatorname {arg,min} }},{frac {1}{n}}sum _{i=1}^{n}h_{theta }(y_{i})quad {underset {nto infty }{longrightarrow }}quad {underset {theta }{operatorname {arg,min} }},E[h_{theta }(y)]\&={underset {theta }{operatorname {arg,min} }},int P_{theta _{0}}(y)h_{theta }(y)dy={underset {theta }{operatorname {arg,min} }},int P_{theta _{0}}(y)log {frac {P(ymid theta _{0})}{P(ymid theta )}}dy\&={underset {theta }{operatorname {arg,min} }},D_{text{KL}}(P_{theta _{0}}parallel P_{theta })end{aligned}}} Où h θ ( x ) = log ⁡ P ( x ∣ θ 0 ) P ( x ∣ θ ) {displaystyle h_{theta }(x)=log {frac {P(xmid theta _{0})}{P(xmid theta )}}} . L’utilisation de h aide à voir comment nous utilisons la loi des grands nombres pour passer de la moyenne de h ( x ) à l’ espérance de celui-ci en utilisant la loi du statisticien inconscient . Les premières transitions ont à voir avec les lois du logarithme et que trouver θ ^ {displaystyle {chapeau {thêta}}} qui maximise une fonction sera également celle qui maximise une transformation monotone de cette fonction (c’est-à-dire : addition/multiplication par une constante).

Puisque l’ entropie croisée n’est que l’entropie de Shannon plus la divergence KL, et puisque l’entropie de P θ 0 {displaystyle P_{thêta _{0}}} est constant, alors le MLE minimise aussi asymptotiquement l’entropie croisée. ^[25]

Exemples

Distribution uniforme discrète

Considérons un cas où n tickets numérotés de 1 à n sont placés dans une boîte et un est tiré au sort ( voir distribution uniforme ) ; ainsi, la taille de l’échantillon est 1. Si n est inconnu, alors l’estimateur du maximum de vraisemblance n ^ {displaystyle {widehat {n}}} de n est le nombre m sur le ticket tiré. (La vraisemblance est 0 pour n < m , 1 ⁄ n pour n ≥ m , et c’est le plus grand quand n = m . Notez que l’estimation de vraisemblance maximale de n se produit à l’extrémité inférieure des valeurs possibles { m , m + 1, …}, plutôt que quelque part au “milieu” de la plage des valeurs possibles, ce qui entraînerait moins de biais.) La valeur attendue du nombre m sur le ticket tiré, et donc la valeur attendue de n ^ {displaystyle {widehat {n}}} , est ( n + 1)/2. Par conséquent, avec une taille d’échantillon de 1, l’estimateur du maximum de vraisemblance pour n sous-estimera systématiquement n de ( n − 1)/2.

Distribution discrète, espace paramétrique fini

Supposons que l’on souhaite déterminer à quel point une pièce injuste est biaisée. Appelez la probabilité de lancer une ‘ tête ‘ p . Le but devient alors de déterminer p .

Supposons que la pièce soit lancée 80 fois : c’est-à-dire que l’échantillon pourrait être quelque chose comme x ₁ = H, x ₂ = T, …, x ₈₀ = T, et le décompte du nombre de faces “H” est observé.

La probabilité de lancer pile est 1 − p (donc ici p est θ ci-dessus). Supposons que le résultat soit 49 pile et 31 pile , et supposons que la pièce a été tirée d’une boîte contenant trois pièces : une qui donne face avec probabilité p = 1 ⁄ 3 , une qui donne face avec probabilité p = 1 ⁄ 2 et une autre qui donne face avec probabilité p = 2 ⁄ 3. Les pièces ont perdu leurs étiquettes, donc laquelle est inconnue. En utilisant l’estimation du maximum de vraisemblance, la pièce qui a la plus grande probabilité peut être trouvée, compte tenu des données qui ont été observées. En utilisant la fonction de masse de probabilité de la distribution binomiale avec une taille d’échantillon égale à 80, un nombre de succès égal à 49 mais pour différentes valeurs de p (la « probabilité de succès »), la fonction de vraisemblance (définie ci-dessous) prend l’une des trois valeurs suivantes :

P ⁡ [ H = 49 ∣ p = 1 3 ] = ( 80 49 ) ( 1 3 ) 49 ( 1 − 1 3 ) 31 ≈ 0.000 , P ⁡ [ H = 49 ∣ p = 1 2 ] = ( 80 49 ) ( 1 2 ) 49 ( 1 − 1 2 ) 31 ≈ 0.012 , P ⁡ [ H = 49 ∣ p = 2 3 ] = ( 80 49 ) ( 2 3 ) 49 ( 1 − 2 3 ) 31 ≈ 0.054 . {displaystyle {begin{aligned}operatorname {mathbb {P} } {bigl [};mathrm {H} =49mid p={tfrac {1}{3}};{ bigr ]}&={binom {80}{49}}({tfrac {1}{3}})^{49}(1-{tfrac {1}{3}})^{31} environ 0,000,\[6pt]operatorname {mathbb {P} } {bigl [};mathrm {H} =49mid p={tfrac {1}{2}};{bigr ]}&={binom {80}{49}}({tfrac {1}{2}})^{49}(1-{tfrac {1}{2}})^{31}approx 0.012,\[6pt]operatorname {mathbb {P} } {bigl [};mathrm {H} =49mid p={tfrac {2}{3}};{bigr ] }&={binom {80}{49}}({tfrac {2}{3}})^{49}(1-{tfrac {2}{3}})^{31}environ 0,054 ~.end{aligné}}}

La vraisemblance est maximisée lorsque p = 2 ⁄ 3 , et il s’agit donc de l’ estimation de vraisemblance maximale pour p .

Distribution discrète, espace paramétrique continu

Supposons maintenant qu’il n’y avait qu’une seule pièce mais que son p aurait pu être n’importe quelle valeur 0 ≤ p ≤ 1 . La fonction de vraisemblance à maximiser est

L ( p ) = f D ( H = 49 ∣ p ) = ( 80 49 ) p 49 ( 1 − p ) 31 , {displaystyle L(p)=f_{D}(mathrm {H} =49mid p)={binom {80}{49}}p^{49}(1-p)^{31}~ ,}

et la maximisation est sur toutes les valeurs possibles 0 ≤ p ≤ 1 .

fonction de vraisemblance pour la valeur de proportion d’un processus binomial ( n = 10)

Une façon de maximiser cette fonction consiste à différencier par rapport à p et à mettre à zéro :

0 = ∂ ∂ p ( ( 80 49 ) p 49 ( 1 − p ) 31 ) , 0 = 49 p 48 ( 1 − p ) 31 − 31 p 49 ( 1 − p ) 30 = p 48 ( 1 − p ) 30 [ 49 ( 1 − p ) − 31 p ] = p 48 ( 1 − p ) 30 [ 49 − 80 p ] . {displaystyle {begin{aligned}0&={frac {partial }{partial p}}left({binom {80}{49}}p^{49}(1-p)^{31}right)~,\[8pt]0&=49p^{48}(1-p)^{31}-31p^{49}(1-p)^{30}\[8pt]&=p^{48}(1-p)^{30}left[49(1-p)-31pright]\[8pt]&=p^{48}(1-p)^{30}left[49-80pright]~.end{aligned}}}

C’est un produit de trois termes. Le premier terme vaut 0 quand p = 0. Le second vaut 0 quand p = 1. Le troisième vaut zéro quand p = 49 ⁄ 80 . La solution qui maximise la vraisemblance est clairement p = 49 ⁄ 80 (puisque p = 0 et p = 1 donnent une vraisemblance de 0). Ainsi, l’ estimateur du maximum de vraisemblance pour p est 49 ⁄ 80 .

Ce résultat est facilement généralisable en substituant une lettre telle que s à la place de 49 pour représenter le nombre observé de “succès” de nos essais de Bernoulli , et une lettre telle que n à la place de 80 pour représenter le nombre d’essais de Bernoulli. Exactement le même calcul donne s ⁄ n qui est l’estimateur du maximum de vraisemblance pour toute séquence de n essais de Bernoulli résultant en s ‘succès’.

Distribution continue, espace de paramètre continu

Pour la distribution normale N ( μ , σ 2 ) {displaystyle {mathcal {N}}(mu ,sigma ^{2})} qui a une fonction de densité de probabilité

f ( x ∣ μ , σ 2 ) = 1 2 π σ 2 exp ⁡ ( − ( x − μ ) 2 2 σ 2 ) , {displaystyle f(xmid mu ,sigma ^{2})={frac {1}{{sqrt {2pi sigma ^{2}}} }}exp left(- {frac {(x-mu )^{2}}{2sigma ^{2}}}right),}

la fonction de densité de probabilité correspondante pour un échantillon de n variables aléatoires normales indépendantes distribuées de manière identique (la vraisemblance) est

f ( x 1 , … , x n ∣ μ , σ 2 ) = ∏ i = 1 n f ( x i ∣ μ , σ 2 ) = ( 1 2 π σ 2 ) n / 2 exp ⁡ ( − ∑ i = 1 n ( x i − μ ) 2 2 σ 2 ) . {displaystyle f(x_{1},ldots ,x_{n}mid mu ,sigma ^{2})=prod _{i=1}^{n}f(x_{i}mid mu ,sigma ^{2})=left({frac {1}{2pi sigma ^{2}}}right)^{n/2}exp left(-{frac {sum _{i=1}^{n}(x_{i}-mu )^{2}}{2sigma ^{2}}}right).}

Cette famille de distributions a deux paramètres : θ = ( μ , σ ) ; donc on maximise la vraisemblance, L ( μ , σ ) = f ( x 1 , … , x n ∣ μ , σ ) {displaystyle {mathcal {L}}(mu ,sigma )=f(x_{1},ldots ,x_{n}mid mu ,sigma )} , sur les deux paramètres simultanément ou, si possible, individuellement.

Étant donné que la fonction logarithme elle-même est une fonction continue strictement croissante sur la plage de probabilité, les valeurs qui maximisent la probabilité maximiseront également son logarithme (la log-vraisemblance elle-même n’est pas nécessairement strictement croissante). La log-vraisemblance peut s’écrire comme suit :

log ⁡ ( L ( μ , σ ) ) = − n 2 log ⁡ ( 2 π σ 2 ) − 1 2 σ 2 ∑ i = 1 n ( x i − μ ) 2 {displaystyle log {Bigl (}{mathcal {L}}(mu ,sigma ){Bigr )}=-{frac {,n,}{2}}log(2 pi sigma ^{2})-{frac {1}{2sigma ^{2}}}sum _{i=1}^{n}(,x_{i}-mu ,) ^{2}}

(Remarque : la log-vraisemblance est étroitement liée à l’entropie de l’information et à l’ information de Fisher .)

Nous calculons maintenant les dérivées de cette log-vraisemblance comme suit.

0 = ∂ ∂ μ log ⁡ ( L ( μ , σ ) ) = 0 − − 2 n ( x ̄ − μ ) 2 σ 2 . {displaystyle {begin{aligned}0&={frac {partial }{partial mu }}log {Bigl (}{mathcal {L}}(mu ,sigma ){Bigr ) }=0-{frac {;-2!n({bar {x}}-mu );}{2sigma ^{2}}}.end{aligned}}}

où x ̄ {displaystyle {bar {x}}} est la moyenne de l’échantillon . Ceci est résolu par

μ ^ = x ̄ = ∑ i = 1 n x i n . {displaystyle {widehat {mu }}={bar {x}}=sum _{i=1}^{n}{frac {,x_{i},}{n}}. }

C’est bien le maximum de la fonction, puisque c’est le seul tournant en μ et que la dérivée seconde est strictement inférieure à zéro. Sa valeur attendue est égale au paramètre μ de la distribution donnée,

E ⁡ [ μ ^ ] = μ , {displaystyle operatorname {mathbb {E} } {bigl [};{widehat {mu }};{bigr ]}=mu ,,}

ce qui signifie que l’estimateur du maximum de vraisemblance μ ^ {displaystyle {widehat {mu }}} est impartial.

De même, nous différencions la log-vraisemblance par rapport à σ et égalons à zéro :

0 = ∂ ∂ σ log ⁡ ( L ( μ , σ ) ) = − n σ + 1 σ 3 ∑ i = 1 n ( x i − μ ) 2 . {displaystyle {begin{aligned}0&={frac {partial }{partial sigma }}log {Bigl (}{mathcal {L}}(mu ,sigma ){Bigr ) }=-{frac {,n,}{sigma }}+{frac {1}{sigma ^{3}}}sum _{i=1}^{n}(,x_ {i}-mu ,)^{2}.end{aligné}}}

qui est résolu par

σ ^ 2 = 1 n ∑ i = 1 n ( x i − μ ) 2 . {displaystyle {widehat {sigma}}^{2}={frac {1}{n}}sum _{i=1}^{n}(x_{i}-mu )^{2 }.}

Insertion du devis μ = μ ^ {displaystyle mu ={widehat {mu }}} on obtient

σ ^ 2 = 1 n ∑ i = 1 n ( x i − x ̄ ) 2 = 1 n ∑ i = 1 n x i 2 − 1 n 2 ∑ i = 1 n ∑ j = 1 n x i x j . {displaystyle {widehat {sigma}}^{2}={frac {1}{n}}sum _{i=1}^{n}(x_{i}-{bar {x} })^{2}={frac {1}{n}}sum _{i=1}^{n}x_{i}^{2}-{frac {1}{n^{2} }}somme _{i=1}^{n}somme _{j=1}^{n}x_{i}x_{j}.}

Pour calculer sa valeur attendue, il convient de réécrire l’expression en termes de variables aléatoires à moyenne nulle ( erreur statistique ) δ i ≡ μ − x i {displaystyle delta _{i}equiv mu -x_{i}} . L’expression de l’estimation dans ces variables donne

σ ^ 2 = 1 n ∑ i = 1 n ( μ − δ i ) 2 − 1 n 2 ∑ i = 1 n ∑ j = 1 n ( μ − δ i ) ( μ − δ j ) . {displaystyle {widehat {sigma }}^{2}={frac {1}{n}}sum _{i=1}^{n}(mu -delta _{i})^ {2}-{frac {1}{n^{2}}}sum _{i=1}^{n}sum _{j=1}^{n}(mu -delta _{ je})(mu -delta _{j}).}

En simplifiant l’expression ci-dessus, en utilisant les faits qui E ⁡ [ δ i ] = 0 {displaystyle operatorname {mathbb {E} } {bigl [};delta _{i};{bigr ]}=0} et E ⁡ [ δ i 2 ] = σ 2 {displaystyle operatorname {E} {bigl [};delta _{i}^{2};{bigr ]}=sigma ^{2}} , permet d’obtenir

E ⁡ [ σ ^ 2 ] = n − 1 n σ 2 . {displaystyle operatorname {mathbb {E} } {bigl [};{widehat {sigma}}^{2};{bigr ]}={frac {,n-1, }{n}}sigma ^{2}.}

Cela signifie que l’estimateur σ ^ 2 {displaystyle {widehat {sigma}}^{2}} est biaisé pour σ 2 {displaystyle sigma ^{2}} . On peut aussi montrer que σ ^ {displaystyle {widehat {sigma}}} est biaisé pour σ {displaystylesigma} , mais que les deux σ ^ 2 {displaystyle {widehat {sigma}}^{2}} et σ ^ {displaystyle {widehat {sigma}}} sont consistant.

Formellement, nous disons que l’ estimateur du maximum de vraisemblance pour θ = ( μ , σ 2 ) {displaystyle theta =(mu ,sigma ^{2})} est

θ ^ = ( μ ^ , σ ^ 2 ) . {displaystyle {widehat {theta ,}}=left({widehat {mu }},{widehat {sigma}}^{2}right).}

Dans ce cas, les MLE pourraient être obtenus individuellement. En général, cela peut ne pas être le cas et les MLE devraient être obtenus simultanément.

La log-vraisemblance normale à son maximum prend une forme particulièrement simple :

log ⁡ ( L ( μ ^ , σ ^ ) ) = − n 2 ( log ⁡ ( 2 π σ ^ 2 ) + 1 ) {displaystyle log {Bigl (}{mathcal {L}}({widehat {mu }},{widehat {sigma }}){Bigr )}={frac {,-n ;;}{2}}{bigl (},log(2pi {widehat {sigma }}^{2})+1,{bigr )}}

Cette log-vraisemblance maximale peut être démontrée comme étant la même pour les moindres carrés plus généraux , même pour les moindres carrés non linéaires . Ceci est souvent utilisé pour déterminer les intervalles de confiance approximatifs basés sur la vraisemblance et les régions de confiance , qui sont généralement plus précis que ceux utilisant la normalité asymptotique discutée ci-dessus.

Variables non indépendantes

Il se peut que les variables soient corrélées, c’est-à-dire non indépendantes. Deux variables aléatoires y 1 {displaystyle y_{1}} et y 2 {displaystyle y_{2}} ne sont indépendants que si leur fonction de densité de probabilité conjointe est le produit des fonctions de densité de probabilité individuelles, c’est-à-dire

f ( y 1 , y 2 ) = f ( y 1 ) f ( y 2 ) {displaystyle f(y_{1},y_{2})=f(y_{1})f(y_{2}),}

Supposons que l’on construise un vecteur gaussien d’ordre n à partir de variables aléatoires ( y 1 , … , y n ) {displaystyle (y_{1},ldots ,y_{n})} , où chaque variable a des moyennes données par ( μ 1 , … , μ n ) {displaystyle (mu _{1},ldots ,mu _{n})} . De plus, notons la matrice de covariance par Σ {displaystyle {mathit {Sigma}}} . La fonction de densité de probabilité jointe de ces n variables aléatoires suit alors une distribution normale multivariée donnée par :

f ( y 1 , … , y n ) = 1 ( 2 π ) n / 2 det ( Σ ) exp ⁡ ( − 1 2 [ y 1 − μ 1 , … , y n − μ n ] Σ − 1 [ y 1 − μ 1 , … , y n − μ n ] T ) {displaystyle f(y_{1},ldots ,y_{n})={frac {1}{(2pi )^{n/2}{sqrt {det({mathit {Sigma }})}}}}exp left(-{frac {1}{2}}left[y_{1}-mu _{1},ldots ,y_{n}-mu _{ n}right]{mathit {Sigma}}^{-1}left[y_{1}-mu _{1},ldots ,y_{n}-mu _{n}right] ^{mathrm {T} }right)}

Dans le cas bivarié , la fonction de densité de probabilité jointe est donnée par :

f ( y 1 , y 2 ) = 1 2 π σ 1 σ 2 1 − ρ 2 exp ⁡ [ − 1 2 ( 1 − ρ 2 ) ( ( y 1 − μ 1 ) 2 σ 1 2 − 2 ρ ( y 1 − μ 1 ) ( y 2 − μ 2 ) σ 1 σ 2 + ( y 2 − μ 2 ) 2 σ 2 2 ) ] {displaystyle f(y_{1},y_{2})={frac {1}{2pi sigma _{1}sigma _{2}{sqrt {1-rho ^{2} }}}}exp left[-{frac {1}{2(1-rho ^{2})}}left({frac {(y_{1}-mu _{1}) ^{2}}{sigma _{1}^{2}}}-{frac {2rho (y_{1}-mu _{1})(y_{2}-mu _{2 })}{sigma _{1}sigma _{2}}}+{frac {(y_{2}-mu _{2})^{2}}{sigma _{2}^{ 2}}}droite)droite]}

Dans ce cas et dans d’autres où une fonction de densité conjointe existe, la fonction de vraisemblance est définie comme ci-dessus, dans la section ” principes “, en utilisant cette densité.

Exemple

X 1 , X 2 , … , X m {displaystyle X_{1}, X_{2},ldots , X_{m}} sont les comptages dans les cellules/boîtes de 1 à m ; chaque boîte a une probabilité différente (pensez que les boîtes sont plus grandes ou plus petites) et nous fixons le nombre de balles qui tombent pour être n {displaystyle n} : x 1 + x 2 + ⋯ + x m = n {displaystyle x_{1}+x_{2}+cdots +x_{m}=n} . La probabilité de chaque case est p i {displaystyle p_{i}} , avec une contrainte : p 1 + p 2 + ⋯ + p m = 1 {displaystyle p_{1}+p_{2}+cdots +p_{m}=1} . Il s’agit d’un cas où le X i {displaystyle X_{i}} s ne sont pas indépendants, la probabilité jointe d’un vecteur x 1 , x 2 , … , x m {displaystyle x_{1}, x_{2},ldots ,x_{m}} est appelé le multinôme et a la forme :

f ( x 1 , x 2 , … , x m ∣ p 1 , p 2 , … , p m ) = n ! ∏ x i ! ∏ p i x i = ( n x 1 , x 2 , … , x m ) p 1 x 1 p 2 x 2 ⋯ p m x m {displaystyle f(x_{1},x_{2},ldots ,x_{m}mid p_{1},p_{2},ldots ,p_{m})={frac {n!} {prod x_{i} !}}prod p_{i}^{x_{i}}={binom {n}{x_{1},x_{2},ldots ,x_{m}}} p_{1}^{x_{1}}p_{2}^{x_{2}}cdots p_{m}^{x_{m}}}

Chaque case prise séparément de toutes les autres cases est un binôme et c’est une extension de celui-ci.

La log-vraisemblance de ceci est :

l ( p 1 , p 2 , … , p m ) = log ⁡ n ! − ∑ i = 1 m log ⁡ x i ! + ∑ i = 1 m x i log ⁡ p i {displaystyle ell (p_{1},p_{2},ldots ,p_{m})=log n!-sum _{i=1}^{m}log x_{i}!+ somme _{i=1}^{m}x_{i}log p_{i}}

La contrainte doit être prise en compte et utiliser les multiplicateurs de Lagrange :

L ( p 1 , p 2 , … , p m , λ ) = l ( p 1 , p 2 , … , p m ) + λ ( 1 − ∑ i = 1 m p i ) {displaystyle L(p_{1},p_{2},ldots ,p_{m},lambda )=ell (p_{1},p_{2},ldots ,p_{m})+ lambda left(1-sum _{i=1}^{m}p_{i}right)}

En posant toutes les dérivées à 0, l’estimation la plus naturelle est dérivée

p ^ i = x i n {displaystyle {hat {p}}_{i}={frac {x_{i}}{n}}}

Maximiser le log de vraisemblance, avec et sans contraintes, peut être un problème insoluble sous forme fermée, alors nous devons utiliser des procédures itératives.

Procédures itératives

Sauf cas particuliers, les équations de vraisemblance

∂ l ( θ ; y ) ∂ θ = 0 {displaystyle {frac {partial ell (theta ;mathbf {y} )}{partial theta}}=0}

ne peut pas être résolu explicitement pour un estimateur θ ^ = θ ^ ( y ) {displaystyle {widehat {theta }}={widehat {theta }}(mathbf {y} )} . Au lieu de cela, ils doivent être résolus de manière itérative : en partant d’une estimation initiale de θ {displaystyle thêta} (dire θ ^ 1 {displaystyle {widehat {theta}}_{1}} ), on cherche à obtenir une suite convergente { θ ^ r } {displaystyle left{{widehat {theta}}_{r}right}} . De nombreuses méthodes pour ce type de problème d’optimisation sont disponibles, ^{[26] [27]} mais les plus couramment utilisées sont des algorithmes basés sur une formule de mise à jour de la forme

θ ^ r + 1 = θ ^ r + η r d r ( θ ^ ) {displaystyle {widehat {theta}}_{r+1}={widehat {theta}}_{r}+eta _{r}mathbf {d} _{r}left({ widehat {thêta}}right)}

où le vecteur d r ( θ ^ ) {displaystyle mathbf {d} _{r}left({widehat {theta}}right)} indique la direction de descente du r ième “pas”, et le scalaire η r {displaystyle eta _{r}} capture la “longueur du pas”, ^{[28] [29]} également connue sous le nom de taux d’apprentissage . ^[30] En général, la fonction de vraisemblance est non convexe avec plusieurs maxima locaux. Les méthodes de recherche déterministes basées sur les dérivées ne peuvent généralement identifier qu’un maximum local de la fonction de vraisemblance. La localisation d’un maximum global d’une fonction non convexe est un problème NP-complet et ne peut donc pas être résolu en un temps raisonnable. Des techniques d’optimisation d’inspiration biologique et d’autres heuristiques peuvent être utilisées pour explorer plusieurs maxima locaux et identifier un maximum acceptable dans la pratique. ^[31]

Méthode de descente en dégradé

(Remarque : ici, il s’agit d’un problème de maximisation, donc le signe avant le dégradé est inversé)

η r ∈ R + {displaystyle eta _{r}in mathbb {R} ^{+}} qui est assez petit pour la convergence et d r ( θ ^ ) = ∇ l ( θ ^ r ; y ) {displaystyle mathbf {d} _{r}left({widehat {theta }}right)=nabla ell left({widehat {theta }}_{r};mathbf { y} droite)}

La méthode de descente de gradient nécessite de calculer le gradient à la rième itération, mais pas besoin de calculer l’inverse de la dérivée du second ordre, c’est-à-dire la matrice hessienne. Par conséquent, il est plus rapide en termes de calcul que la méthode de Newton-Raphson.

Méthode de Newton-Raphson

η r = 1 {displaystyle eta _{r}=1} et d r ( θ ^ ) = − H r − 1 ( θ ^ ) s r ( θ ^ ) {displaystyle mathbf {d} _{r}left({widehat {theta}}right)=-mathbf {H} _{r}^{-1}left({widehat { thêta }}right)mathbf {s} _{r}left({widehat {theta }}right)}

où s r ( θ ^ ) {displaystyle mathbf {s} _{r}({widehat {theta}})} est le score et H r − 1 ( θ ^ ) {displaystyle mathbf {H} _{r}^{-1}left({widehat {theta }}right)} est l’ inverse de la matrice hessienne de la fonction log-vraisemblance, toutes deux évaluées à la r ième itération. ^{[32] [33]} Mais parce que le calcul de la matrice hessienne est coûteux en calcul , de nombreuses alternatives ont été proposées. L’algorithme populaire de Berndt – Hall – Hall – Hausman se rapproche de la Hessienne avec le produit extérieur du gradient attendu, de sorte que

d r ( θ ^ ) = − [ 1 n ∑ t = 1 n ∂ l ( θ ; y ) ∂ θ ( ∂ l ( θ ; y ) ∂ θ ) T ] − 1 s r ( θ ^ ) {displaystyle mathbf {d} _{r}left({widehat {theta}}right)=-left[{frac {1}{n}}sum _{t=1}^ {n}{frac {partial ell (theta ;mathbf {y} )}{partial theta }}left({frac {partial ell (theta ;mathbf {y}) }{partial theta }}right)^{mathsf {T}}right]^{-1}mathbf {s} _{r}left({widehat {theta }}right) }

Méthodes quasi-Newton

D’autres méthodes quasi-Newton utilisent des mises à jour sécantes plus élaborées pour donner une approximation de la matrice hessienne.

Formule de Davidson – Fletcher – Powell

La formule DFP trouve une solution symétrique, définie positive et la plus proche de la valeur approximative actuelle de la dérivée de second ordre :

H k + 1 = ( I − γ k y k s k T ) H k ( I − γ k s k y k T ) + γ k y k y k T , {displaystyle mathbf {H} _{k+1}=left(I-gamma _{k}y_{k}s_{k}^{mathsf {T}}right)mathbf {H} _{k}left(I-gamma _{k}s_{k}y_{k}^{mathsf {T}}right)+gamma _{k}y_{k}y_{k}^ {mathsf {T}},}

où

y k = ∇ l ( x k + s k ) − ∇ l ( x k ) , {displaystyle y_{k}=nabla ell (x_{k}+s_{k})-nabla ell (x_{k}),} γ k = 1 y k T s k , {displaystyle gamma _{k}={frac {1}{y_{k}^{T}s_{k}}},} s k = x k + 1 − x k . {displaystyle s_{k}=x_{k+1}-x_{k}.} Algorithme de Broyden – Fletcher – Goldfarb – Shanno

BFGS donne également une solution symétrique et définie positive :

B k + 1 = B k + y k y k T y k T s k − B k s k s k T B k T s k T B k s k , {displaystyle B_{k+1}=B_{k}+{frac {y_{k}y_{k}^{mathsf {T}}}{y_{k}^{mathsf {T}}s_ {k}}}-{frac {B_{k}s_{k}s_{k}^{mathsf {T}}B_{k}^{mathsf {T}}}{s_{k}^{ mathsf {T}}B_{k}s_{k}}} ,}

où

y k = ∇ l ( x k + s k ) − ∇ l ( x k ) , {displaystyle y_{k}=nabla ell (x_{k}+s_{k})-nabla ell (x_{k}),} s k = x k + 1 − x k . {displaystyle s_{k}=x_{k+1}-x_{k}.}

La convergence de la méthode BFGS n’est pas garantie à moins que la fonction n’ait un développement de Taylor quadratique proche d’un optimum. Cependant, BFGS peut avoir des performances acceptables même pour les instances d’optimisation non fluides

Le score de Fisher

Une autre méthode populaire consiste à remplacer le hessien par la matrice d’information de Fisher , I ( θ ) = E ⁡ [ H r ( θ ^ ) ] {displaystyle {mathcal {I}}(theta )=operatorname {mathbb {E} } left[mathbf {H} _{r}left({widehat {theta }}right) à droite]} , nous donnant l’algorithme de score de Fisher. Cette procédure est standard dans l’estimation de nombreuses méthodes, telles que les modèles linéaires généralisés .

Bien que populaires, les méthodes quasi-Newton peuvent converger vers un point stationnaire qui n’est pas nécessairement un maximum local ou global, ^[34] mais plutôt un minimum local ou un point de selle . Il est donc important d’évaluer la validité de la solution obtenue aux équations de vraisemblance, en vérifiant que la Hessienne, évaluée à la solution, est à la fois définie négative et bien conditionnée . ^[35]

Histoire

Ronald Fisher en 1913

Les premiers utilisateurs du maximum de vraisemblance étaient Carl Friedrich Gauss , Pierre-Simon Laplace , Thorvald N. Thiele et Francis Ysidro Edgeworth . ^{[36] [37]} Cependant, son utilisation répandue a augmenté entre 1912 et 1922 lorsque Ronald Fisher a recommandé, largement popularisé et soigneusement analysé l’estimation du maximum de vraisemblance (avec des tentatives infructueuses de preuves ). ^[38]

L’estimation du maximum de vraisemblance a finalement transcendé la justification heuristique dans une preuve publiée par Samuel S. Wilks en 1938, maintenant appelée théorème de Wilks . ^[39] Le théorème montre que l’erreur dans le logarithme des valeurs de vraisemblance pour les estimations de plusieurs observations indépendantes est asymptotiquement χ ² -distribuée , ce qui permet de déterminer facilement une région de confiance autour de toute estimation des paramètres. La seule partie difficile de la preuve de Wilks dépend de la valeur attendue de la matrice d’ information de Fisher , qui est fournie par un théorème prouvé par Fisher . ^[40]Wilks a continué à améliorer la généralité du théorème tout au long de sa vie, avec sa preuve la plus générale publiée en 1962. ^[41]

Des revues du développement de l’estimation du maximum de vraisemblance ont été fournies par un certain nombre d’auteurs. ^{[42] [43] [44] [45] [46] [47] [48] [49]}

Voir également

• Portail des mathématiques

Notions connexes

• Critère d’information d’Akaike : un critère de comparaison de modèles statistiques, basé sur MLE
• Estimateur extrême : une classe plus générale d’estimateurs à laquelle MLE appartient
• Informations de Fisher : matrice d’informations, sa relation avec la matrice de covariance des estimations de ML
• Erreur quadratique moyenne : une mesure de la “bonne” qualité d’un estimateur d’un paramètre distributionnel (que ce soit l’estimateur du maximum de vraisemblance ou un autre estimateur)
• RANSAC : une méthode pour estimer les paramètres d’un modèle mathématique à partir de données contenant des valeurs aberrantes
• Théorème de Rao-Blackwell : donne un processus pour trouver le meilleur estimateur sans biais possible (dans le sens d’avoir une erreur quadratique moyenne minimale ); le MLE est souvent un bon point de départ pour le processus
• Théorème de Wilks : fournit un moyen d’estimer la taille et la forme de la région d’estimations à peu près également probables pour les valeurs des paramètres de la population, en utilisant les informations d’un seul échantillon, en utilisant une distribution du chi carré

Autres méthodes d’estimation

• Méthode généralisée des moments : méthodes liées à l’équation de vraisemblance dans l’estimation du maximum de vraisemblance
• M-estimator : une approche utilisée dans les statistiques robustes
• Estimateur maximum a posteriori (MAP) : pour un contraste dans la manière de calculer les estimateurs lorsque la connaissance préalable est postulée
• Estimation de l’espacement maximal : une méthode connexe plus robuste dans de nombreuses situations
• Estimation de l’entropie maximale
• Méthode des moments (statistiques) : une autre méthode populaire pour trouver des paramètres de distributions
• Méthode de prise en charge , une variante de la technique du maximum de vraisemblance
• Estimation de la distance minimale
• Méthodes de vraisemblance partielle pour les données de panel
• Estimateur de vraisemblance quasi-maximale : un estimateur MLE mal spécifié, mais toujours cohérent
• Maximum de vraisemblance restreint : une variation utilisant une fonction de vraisemblance calculée à partir d’un ensemble de données transformé

Références

1. ^ Rossi, Richard J. (2018). Statistiques mathématiques : une introduction à l’inférence basée sur la vraisemblance . New York : John Wiley & Fils. p. 227. ISBN 978-1-118-77104-4.
2. ^ Hendry, David F. ; Nielsen, Bent (2007). Modélisation économétrique : une approche de probabilité . Princeton : Presse universitaire de Princeton. ISBN 978-0-691-13128-3.
3. ^ Chambres, Raymond L.; Steel, David G.; Wang, Suojin ; Gallois, Alan (2012). Estimation du maximum de vraisemblance pour les enquêtes par sondage . Boca Raton : CRC Press. ISBN 978-1-58488-632-7.
4. ^ Salle, Michael Don ; En ligneAhlquist, John S. (2018). Maximum de vraisemblance pour les sciences sociales : stratégies d’analyse . New York : Cambridge University Press. ISBN 978-1-107-18582-1.
5. ^ Presse, WH; Flannery, BP; Teukolsky, SA; Vetterling, WT (1992). “Les moindres carrés comme estimateur du maximum de vraisemblance” . Recettes numériques en FORTRAN: L’art du calcul scientifique (2e éd.). Cambridge : Cambridge University Press. pages 651–655. ISBN 0-521-43064-X.
6. ^ Myung, IJ (2003). “Tutoriel sur l’estimation du maximum de vraisemblance”. Journal de psychologie mathématique . 47 (1): 90-100. doi : 10.1016/S0022-2496(02)00028-7 .
7. ↑ Gourieroux, chrétien ; Montfort, Alain (1995). Modèles statistiques et économétriques . La presse de l’Universite de Cambridge. p. 161 . ISBN 0-521-40551-3.
8. ^ Kane, Edward J. (1968). Statistiques économiques et économétrie . New York, NY : Harper & Row. p. 179 .
9. ^ Petit, Christopher G.; Wang, Jinfang (2003). “Travailler avec les racines” . Méthodes numériques pour les équations d’estimation non linéaires . Presse universitaire d’Oxford. p. 74–124. ISBN 0-19-850688-0.
10. ^ Kass, Robert E.; Vos, Paul W. (1997). Fondements géométriques de l’inférence asymptotique . New York, NY : John Wiley & Sons. p. 14. ISBN 0-471-82668-5.
11. ^ Papadopoulos, Alecos (25 septembre 2013). “Pourquoi mettons-nous toujours log() avant le pdf joint lorsque nous utilisons MLE (Estimation du maximum de vraisemblance) ?” . Échange de pile .
12. ^ ^{un b} Silvey, SD (1975). Inférence statistique . Londres, Royaume-Uni : Chapman et Hall. p. 79. ISBN 0-412-13820-4.
13. ^ Olive, David (2004). “Est-ce que le MLE maximise la vraisemblance ?” (PDF) . {{cite journal}}: Cite journal requires |journal= (help)
14. ^ Schwallie, Daniel P. (1985). “Estimateurs de covariance de vraisemblance maximum définis positifs”. Lettres d’économie . 17 (1–2): 115–117. doi : 10.1016/0165-1765(85)90139-9 .
15. ^ Magnus, Jan R. (2017). Introduction à la théorie de l’économétrie . Amsterdam : presse universitaire VU. p. 64–65. ISBN 978-90-8659-766-6.
16. ^ Pfanzagl (1994 , p. 206) harvtxt error: no target: CITEREFPfanzagl1994 (help)
17. ^ Par le théorème 2.5 dans Newey, Whitney K. ; McFadden, Daniel (1994). “Chapitre 36: Estimation d’un grand échantillon et test d’hypothèse”. En Angleterre, Robert; McFadden, Dan (éd.). Manuel d’économétrie, Vol.4 . Sciences Elsevier. pages 2111–2245. ISBN 978-0-444-88766-5.
18. ^ ^{un b} Par le Théorème 3.3 dans Newey, Whitney K.; McFadden, Daniel (1994). “Chapitre 36: Estimation d’un grand échantillon et test d’hypothèse”. En Angleterre, Robert; McFadden, Dan (éd.). Manuel d’économétrie, Vol.4 . Sciences Elsevier. pages 2111–2245. ISBN 978-0-444-88766-5.
19. ^ Zacks, Shelemyahu (1971). La théorie de l’inférence statistique . New York : John Wiley & Fils. p. 223. ISBN 0-471-98103-6.
20. ^ Voir la formule 20 dans Cox, David R. ; En ligneSnell, E. Joyce (1968). “Une définition générale des résidus”. Journal de la Royal Statistical Society, série B . 30 (2): 248–275. JSTOR 2984505 .
21. ^ Kano, Yutaka (1996). “L’efficacité du troisième ordre implique l’efficacité du quatrième ordre” . Journal de la Société statistique du Japon . 26 : 101–117. doi : 10.14490/jjss1995.26.101 .
22. ^ Christensen, Henrikt I. “Reconnaissance de formes” (PDF) (conférence). Théorie de la décision bayésienne – CS 7616. Georgia Tech.
23. ^ cmplx96 ( https://stats.stackexchange.com/users/177679/cmplx96 ), divergence Kullback-Leibler, URL (version : 2017-11-18) : https://stats.stackexchange.com/q/314472 ( à la vidéo youtube, regardez les minutes 13 à 25)
24. ^ Introduction à l’inférence statistique | Stanford (Conférence 16 – MLE sous spécification erronée du modèle)
25. ^ Sycorax dit Réintégrer Monica ( https://stats.stackexchange.com/users/22311/sycorax-says-reinstate-monica ), la relation entre la maximisation de la probabilité et la minimisation de l’entropie croisée, URL (version : 2019-11- 06): https://stats.stackexchange.com/q/364237
26. ^ Fletcher, R. (1987). Méthodes pratiques d’optimisation (deuxième éd.). New York, NY : John Wiley & Sons. ISBN 0-471-91547-5.
27. ^ Nocedal, Jorge ; En ligneWright, Stephen J. (2006). Optimisation numérique (deuxième éd.). New York, NY : Springer. ISBN 0-387-30303-0.
28. ^ Daganzo, Carlos (1979). Probit multinomial : la théorie et son application à la prévision de la demande . New York : Presse académique. p. 61–78. ISBN 0-12-201150-3.
29. ^ Gould, Guillaume; Pitblado, Jeffrey; Poi, Brian (2010). Estimation du maximum de vraisemblance avec Stata (quatrième éd.). Station College : Stata Press. p. 13–20. ISBN 978-1-59718-078-8.
30. ^ Murphy, Kevin P. (2012). Apprentissage automatique : une perspective probabiliste . Cambridge : Presse du MIT. p. 247. ISBN 978-0-262-01802-9.
31. ^ Noël, MM; Joshi, PP ; Jannett, TC (avril 2006). “Amélioration de l’estimation de la vraisemblance maximale de la position cible dans les réseaux de capteurs sans fil à l’aide de l’optimisation de l’essaim de particules” . Troisième conférence internationale sur les technologies de l’information : nouvelles générations (ITNG’06) : 274–279. doi : 10.1109/ITNG.2006.72 . ISBN 0-7695-2497-4. S2CID 17322072 .
32. ^ Amemiya, Takeshi (1985). Économétrie avancée . Cambridge : Harvard University Press. p. 137–138 . ISBN 0-674-00560-0.
33. ^ Sargan, Denis (1988). “Méthodes d’optimisation numérique”. Notes de cours sur la théorie économétrique avancée . Oxford : Basil Blackwell. p. 161–169. ISBN 0-631-14956-2.
34. ^ Voir le théorème 10.1 dans Avriel, Mordecai (1976). Programmation non linéaire : analyse et méthodes . Falaises d’Englewood, New Jersey : Prentice-Hall. p. 293–294. ISBN 9780486432274.
35. ^ Gill, Philip E.; Murray, Walter; En ligneWright, Margaret H. (1981). Optimisation pratique . Londres, Royaume-Uni : Academic Press. pages 312-313 . ISBN 0-12-283950-1.
36. ^ Edgeworth, Francis Y. (septembre 1908). “Sur les erreurs probables des constantes de fréquence” . Journal de la Société royale de statistique . 71 (3): 499–512. doi : 10.2307/2339293 . JSTOR 2339293 .
37. ^ Edgeworth, Francis Y. (décembre 1908). “Sur les erreurs probables des constantes de fréquence” . Journal de la Société royale de statistique . 71 (4): 651–678. doi : 10.2307/2339378 . JSTOR 2339378 .
38. ^ Pfanzagl, Johann; En ligneHamboker, R. (1994). Théorie statistique paramétrique . Walter de Gruyter . p. 207–208. ISBN 978-3-11-013863-4.
39. ^ Wilks, SS (1938). “La distribution à grand échantillon du rapport de vraisemblance pour tester les hypothèses composites” . Annales de statistiques mathématiques . 9 : 60–62. doi : 10.1214/aoms/1177732360 .
40. ^ Owen, Art B. (2001). Vraisemblance empirique . Londres, Royaume-Uni; Boca Raton, Floride : Chapman & Hall ; Presse CRC. ISBN 978-1584880714.
41. ^ Wilks, Samuel S. (1962). Statistiques mathématiques . New York, NY : John Wiley & Sons. ISBN 978-0471946502.
42. ^ Savage, Leonard J. (1976). “En relisant RA Fisher” . Les Annales de la statistique . 4 (3): 441–500. doi : 10.1214/aos/1176343456 . JSTOR 2958221 .
43. ^ Pratt, John W. (1976). “FY Edgeworth et RA Fisher sur l’efficacité de l’estimation du maximum de vraisemblance” . Les Annales de la statistique . 4 (3): 501–514. doi : 10.1214/aos/1176343457 . JSTOR 2958222 .
44. ^ Stigler, Stephen M. (1978). “Francis Ysidro Edgeworth, statisticien”. Journal de la Royal Statistical Society, série A . 141 (3): 287–322. doi : 10.2307/2344804 . JSTOR 2344804 .
45. ^ Stigler, Stephen M. (1986). L’histoire des statistiques : la mesure de l’incertitude avant 1900 . Presse universitaire de Harvard. ISBN 978-0-674-40340-6.
46. ^ Stigler, Stephen M. (1999). Statistiques sur la table : l’histoire des concepts et des méthodes statistiques . Presse universitaire de Harvard. ISBN 978-0-674-83601-3.
47. ^ Hald, Anders (1998). Une histoire de la statistique mathématique de 1750 à 1930 . New York, NY : Wiley. ISBN 978-0-471-17912-2.
48. ^ Hald, Anders (1999). “Sur l’histoire du maximum de vraisemblance par rapport à la probabilité inverse et aux moindres carrés” . Sciences statistiques . 14 (2): 214–222. doi : 10.1214/ss/1009212248 . JSTOR 2676741 .
49. ^ Aldrich, John (1997). “RA Fisher et la réalisation du maximum de vraisemblance 1912–1922” . Sciences statistiques . 12 (3): 162–176. doi : 10.1214/ss/1030037906 . M. 1617519 .

Lectures complémentaires

• Cramer, JS (1986). Applications économétriques des méthodes du maximum de vraisemblance . New York, NY : Cambridge University Press. ISBN 0-521-25317-9.
• En ligneEliason, Scott R. (1993). Estimation du maximum de vraisemblance : logique et pratique . Newbury Park : Sauge. ISBN 0-8039-4107-2.
• Roi, Gary (1989). Méthodologie politique unificatrice : la théorie de la vraisemblance de l’inférence statistique . La presse de l’Universite de Cambridge. ISBN 0-521-36697-6.
• Le Cam, Lucien (1990). “Le maximum de vraisemblance : Une Introduction”. Revue ISI . 58 (2): 153–171. doi : 10.2307/1403464 . JSTOR 1403464 .
• Magnus, Jan R. (2017). “Plausibilité maximum”. Introduction à la théorie de l’économétrie . Amsterdam, Pays-Bas : VU University Press. p. 53–68. ISBN 978-90-8659-766-6.
• Millar, Russell B. (2011). Estimation et inférence du maximum de vraisemblance . Hoboken, New Jersey : Wiley. ISBN 978-0-470-09482-2.
• Cornichons, Andrew (1986). Une introduction à l’analyse de vraisemblance . Norwich : WH Hutchins & Sons. ISBN 0-86094-190-6.
• En ligneSeverini, Thomas A. (2000). Méthodes de vraisemblance en statistique . New York, NY : Oxford University Press. ISBN 0-19-850650-3.
• Ward, Michael D. ; En ligneAhlquist, John S. (2018). Maximum de vraisemblance pour les sciences sociales : stratégies d’analyse . La presse de l’Universite de Cambridge. ISBN 978-1-316-63682-4.

Liens externes

• Lesser, Lawrence M. (2007). “Paroles de chanson ‘MLE'” . Sciences mathématiques / Collège des sciences. math.utep.edu . El Paso, TX : Université du Texas . Récupéré le 06/03/2021 .{{cite web}}: CS1 maint: url-status (link)
• “Méthode du maximum de vraisemblance” , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Purcell, S. “Estimation du maximum de vraisemblance” .
• Sargent, Thomas ; Stachurski, John. “Estimation du maximum de vraisemblance” . Economie quantitative avec Python .
• Tomet, Ott ; Henningsen, Arne (2019-05-19). “maxLik : un package pour l’estimation du maximum de vraisemblance dans R” .