Ensemble dénombrable

En mathématiques , un ensemble est dénombrable s’il a la même cardinalité (le nombre d’éléments de l’ensemble) qu’un sous- ensemble de l’ensemble des Nombres naturels N = {0, 1, 2, 3, …}. De manière équivalente, un ensemble S est dénombrable s’il existe une fonction injective f : S → N de S dans N ; cela signifie simplement que chaque élément de S correspond à un élément différent de N .

Un ensemble dénombrable est soit un ensemble fini, soit un ensemble dénombrable infini . Qu’ils soient finis ou infinis, les éléments d’un ensemble dénombrable peuvent toujours être comptés un par un et – bien que le décompte puisse ne jamais se terminer en raison du nombre infini d’éléments à dénombrer – chaque élément de l’ensemble est associé à un naturel unique. Numéro.

Georg Cantor a introduit le concept d’ensembles dénombrables, opposant les ensembles qui sont dénombrables à ceux qui ne le sont pas . Aujourd’hui, les ensembles dénombrables forment la base d’une branche des mathématiques appelée mathématiques discrètes .

Une note sur la terminologie

Bien que les termes “dénombrable” et “dénombrable infini” tels que définis ici soient assez courants, la terminologie n’est pas universelle. ^[1] Un style alternatif utilise dénombrable pour signifier ce qu’on appelle ici dénombrable infini, et au plus dénombrable pour signifier ce qu’on appelle ici dénombrable. ^{[2] [3]} Pour éviter l’ambiguïté, on peut se limiter aux termes « au plus dénombrable » et « dénombrable infini », bien qu’en ce qui concerne la concision c’est le pire des deux mondes. ^{[ citation nécessaire ]} Le lecteur est invité à vérifier la définition en usage lorsqu’il rencontre le terme “dénombrable” dans la littérature.

Les termes dénombrable ^[4] et dénombrable ^{[5] [6]} peuvent également être utilisés, par exemple se référant respectivement à dénombrable et dénombrable infini ^[7] mais comme les définitions varient, le lecteur est à nouveau invité à vérifier la définition utilisée. ^[8]

Définition

La définition la plus concise est en termes de cardinalité . Un ensemble S est dénombrable si sa cardinalité |S| est inférieur ou égal à א 0 {displaystyle aleph _{0}} $aleph _{0}$ $aleph _{0}$ ( aleph-null ), la cardinalité de l’ensemble des Nombres naturels N . Un ensemble S est dénombrable infini si | S | = א 0 {displaystyle |S|=aleph _{0}} ${displaystyle |S|=aleph _{0}}$ ${displaystyle |S|=aleph _{0}}$ . Un ensemble est Indénombrable s’il n’est pas dénombrable, c’est-à-dire que sa cardinalité est supérieure à א 0 {displaystyle aleph _{0}} $aleph _{0}$ $aleph _{0}$ ; le lecteur est renvoyé à Uncountable set pour une discussion plus approfondie. ^[9]

Pour tout ensemble S , les propositions suivantes sont équivalentes :

S est dénombrable. ^[5]
Il existe une fonction injective de S dans N . ^{[10] [11]}
S est vide ou il existe une fonction surjective de N dans S . ^[11]
Il existe une application bijective entre S et un sous-ensemble de N . ^[12]
S est soit fini soit dénombrable infini. ^[13]

De même, les propositions suivantes sont équivalentes :

S est dénombrable infini.
Il existe une application injective et surjective (et donc bijective ) entre S et N .
S a une correspondance biunivoque avec N . ^[14]
Les éléments de S peuvent être arrangés dans une séquence infinie a 0 , a 1 , a 2 , … {displaystyle a_{0},a_{1},a_{2},ldots } ${displaystyle a_{0},a_{1},a_{2},ldots }$ ${displaystyle a_{0},a_{1},a_{2},ldots }$ , où a i {displaystyle a_{i}} $a_{i}$ $a_{i}$ est distinct de a j {displaystyle a_{j}} $a_{j}$ $a_{j}$ pour i ≠ j {displaystyle ineq j} et chaque élément de S est listé. ^{[15] [16]}

Histoire

En 1874, dans son premier article sur la théorie des ensembles , Cantor a prouvé que l’ensemble des nombres réels est Indénombrable, montrant ainsi que tous les ensembles infinis ne sont pas dénombrables. ^[17] En 1878, il a utilisé des correspondances biunivoques pour définir et comparer des cardinalités. ^[18] En 1883, il étendit les Nombres naturels avec ses ordinaux infinis et utilisa des ensembles d’ordinaux pour produire une infinité d’ensembles ayant des cardinalités infinies différentes. ^[19]

Introduction

Un ensemble est une collection d’ éléments et peut être décrit de plusieurs façons. Une façon consiste simplement à énumérer tous ses éléments; par exemple, l’ensemble constitué des nombres entiers 3, 4 et 5 peut être noté {3, 4, 5}, appelé formulaire de liste. ^[20] Ceci n’est cependant efficace que pour les petits ensembles; pour des ensembles plus grands, cela prendrait du temps et serait source d’erreurs. Au lieu d’énumérer chaque élément, parfois des points de suspension (“…”) sont utilisés pour représenter de nombreux éléments entre l’élément de départ et l’élément de fin dans un ensemble, si l’auteur pense que le lecteur peut facilement deviner ce que … représente ; par exemple, {1, 2, 3, …, 100} désigne vraisemblablement l’ensemble des nombres entiers de 1 à 100. Même dans ce cas, cependant, il est toujours possiblepour lister tous les éléments, car le nombre d’éléments dans l’ensemble est fini.

Certains ensembles sont infinis ; ces ensembles ont plus de n éléments où n est n’importe quel nombre entier qui peut être spécifié. (Peu importe la taille de l’entier spécifié n , tel que n =9 × 10 ³² , les ensembles infinis ont plus de n éléments.) Par exemple, l’ensemble des Nombres naturels, dénoté par {0, 1, 2, 3, 4, 5, …},^[a] a une infinité d’éléments , et nous ne pouvons utiliser aucun nombre naturel pour donner sa taille. Néanmoins, il s’avère que les ensembles infinis ont une notion bien définie de taille (ou plus correctement, de cardinalité , le terme technique désignant le nombre d’éléments dans un ensemble), et que tous les ensembles infinis n’ont pas la même cardinalité.

Mappage Bijectif des nombres entiers aux nombres pairs

Pour comprendre ce que cela signifie, examinons d’abord ce que cela ne signifie pas. Par exemple, il existe une infinité d’entiers impairs, une infinité d’entiers pairs et (donc) une infinité d’entiers au total. Cependant, il s’avère que le nombre d’entiers pairs, qui est le même que le nombre d’entiers impairs, est également le même que le nombre d’entiers globaux. C’est parce que nous pouvons arranger les choses de telle sorte que, pour chaque entier, il existe un entier pair distinct :

… − 2 → − 4 , − 1 → − 2 , 0 → 0 , 1 → 2 , 2 → 4 ⋯ {displaystyle ldots ,-!2!rightarrow !-!4,,-!1!rightarrow !-!2,,0!rightarrow !0, ,1!flèchedroite !2,,2!flèchedroite !4,cdots } ou, plus généralement, n → 2 n {displaystyle nrightarrow 2n} (voir l’image). Ce que nous avons fait ici est d’organiser les nombres entiers et les nombres entiers pairs dans une correspondance un à un (ou bijection ), qui est une fonction qui mappe entre deux ensembles de telle sorte que chaque élément de chaque ensemble correspond à un seul élément dans l’autre Positionner.

Cependant, tous les ensembles infinis n’ont pas la même cardinalité. Par exemple, Georg Cantor (qui a introduit ce concept) a démontré que les nombres réels ne peuvent pas être mis en correspondance biunivoque avec les Nombres naturels (entiers non négatifs), et donc que l’ensemble des nombres réels a une plus grande cardinalité que l’ensemble des Nombres naturels.

Aperçu formel

Par définition, un ensemble S est dénombrable s’il existe une fonction injective f : S → N de S aux entiers naturels N = {0, 1, 2, 3, …}. Cela signifie simplement que chaque élément de S correspond à un élément différent de N .

Il peut sembler naturel de répartir les ensembles en différentes classes : regrouper tous les ensembles contenant un élément ; tous les ensembles contenant deux éléments ensemble ; … ; enfin, rassemblez tous les ensembles infinis et considérez-les comme ayant la même taille. Ce point de vue n’est cependant pas défendable dans le cadre de la définition naturelle de la taille.

Pour élaborer cela, nous avons besoin du concept de bijection . Bien qu’une “bijection” puisse sembler un concept plus avancé qu’un nombre, le développement habituel des mathématiques en termes de théorie des ensembles définit les fonctions avant les nombres, car elles sont basées sur des ensembles beaucoup plus simples. C’est là qu’intervient le concept de bijection : définir la correspondance

une ↔ 1, b ↔ 2, c ↔ 3

Puisque chaque élément de { a , b , c } est apparié avec précisément un élément de {1, 2, 3}, et vice versa, cela définit une bijection.

Nous généralisons maintenant cette situation; on définit que deux ensembles sont de même taille, si et seulement s’il existe une bijection entre eux. Pour tous les ensembles finis, cela nous donne la définition habituelle de “la même taille”.

Comme pour le cas des ensembles infinis, considérons les ensembles A = {1, 2, 3, … }, l’ensemble des entiers positifs , et B = {2, 4, 6, … }, l’ensemble des nombres pairs entiers positifs. Nous affirmons que, selon notre définition, ces ensembles ont la même taille, et que donc B est dénombrable infini. Rappelons que pour le prouver, nous devons montrer une bijection entre eux. Ceci peut être réalisé en utilisant l’affectation n ↔ 2 n , de sorte que

1 ↔ 2, 2 ↔ 4, 3 ↔ 6, 4 ↔ 8, ….

Comme dans l’exemple précédent, chaque élément de A a été apparié avec précisément un élément de B, et vice versa. Ils ont donc la même taille. Ceci est un exemple d’ensemble de même taille que l’un de ses propres sous-ensembles , ce qui est impossible pour les ensembles finis.

De même, l’ensemble de toutes les paires ordonnées de Nombres naturels (le produit cartésien de deux ensembles de Nombres naturels, N × N ) est dénombrable infini, comme on peut le voir en suivant un chemin comme celui de l’image :

La fonction d’appariement de Cantor attribue un nombre naturel à chaque paire de Nombres naturels

Le mappage résultant se déroule comme suit :

0 ↔ (0, 0), 1 ↔ (1, 0), 2 ↔ (0, 1), 3 ↔ (2, 0), 4 ↔ (1, 1), 5 ↔ (0, 2), 6 ↔ (3, 0), ….

Ce mappage couvre toutes ces paires ordonnées.

Cette forme de mappage triangulaire se généralise récursivement à n – tuples de Nombres naturels, c’est-à-dire ( a ₁ , a ₂ , a ₃ , …, a _n ) où a _i et n sont des Nombres naturels, en mappant à plusieurs reprises les deux premiers éléments d’un n – uplet à un nombre naturel. Par exemple, (0, 2, 3) peut être écrit comme ((0, 2), 3). Alors (0, 2) correspond à 5 donc ((0, 2), 3) correspond à (5, 3), puis (5, 3) correspond à 39. Puisqu’un 2-tuple différent, c’est une paire telle que ( un , b), correspond à un nombre naturel différent, une différence entre deux n-uplets par un seul élément suffit à garantir que les n-uplets sont mappés à des Nombres naturels différents. Ainsi, une injection de l’ensemble des n -uplets à l’ensemble des Nombres naturels N est prouvée. Pour l’ensemble de n-uplets constitué par le produit cartésien d’un nombre fini d’ensembles différents, chaque élément de chaque tuple a la correspondance avec un nombre naturel, de sorte que chaque tuple peut être écrit en Nombres naturels, puis la même logique est appliquée pour prouver le théorème .

Théorème — Le produit cartésien d’un nombre fini d’ensembles dénombrables est dénombrable. ^{[21] [c]}

L’ensemble de tous les entiers Z et l’ensemble de tous les nombres rationnels Q peuvent intuitivement sembler beaucoup plus grands que N . Mais les apparences peuvent être trompeuses. Si une paire est traitée comme le Numérateur et le Dénominateur d’une Fraction vulgaire (une fraction sous la forme a / b où a et b ≠ 0 sont des entiers), alors pour chaque fraction positive, nous pouvons trouver un nombre naturel distinct correspondant à elle. Cette représentation comprend également les Nombres naturels, puisque tout nombre naturel est aussi une fraction N/1. On peut donc conclure qu’il y a exactement autant de nombres rationnels positifs qu’il y a d’entiers positifs. Ceci est également vrai pour tous les nombres rationnels, comme on peut le voir ci-dessous.

Théorème — Z (l’ensemble de tous les nombres entiers) et Q (l’ensemble de tous les nombres rationnels) sont dénombrables. ^[c]

De la même manière, l’ensemble des nombres algébriques est dénombrable. ^{[23] [d]}

Learn more.

Premier article sur la théorie des ensembles de Cantor

Jul 12, 2022

Nombre réel

Jul 11, 2022

Nombre irrationnel

Jul 10, 2022

Décimal

Jul 10, 2022

Parfois, plusieurs mappages sont utiles : un ensemble A à afficher comme dénombrable est mappé un à un (injection) à un autre ensemble B, puis A est prouvé comme dénombrable si B est mappé un à un à l’ensemble de Nombres naturels. Par exemple, l’ensemble de nombres rationnels positifs peut facilement être mappé un à un avec l’ensemble de paires de Nombres naturels (2-uplets) car p / q correspond à ( p , q ). Étant donné que l’ensemble de paires de Nombres naturels est mappé un à un (en fait une correspondance ou une bijection un à un) à l’ensemble de Nombres naturels comme indiqué ci-dessus, l’ensemble de nombres rationnels positifs est prouvé comme dénombrable.

Théorème — Toute union finie d’ensembles dénombrables est dénombrable. ^{[24] [25] [e]}

Avec la clairvoyance de savoir qu’il existe des ensembles innombrables, on peut se demander si ce dernier résultat peut ou non être poussé plus loin. La réponse est “oui” et “non”, nous pouvons l’étendre, mais nous devons supposer un nouvel axiome pour le faire.

Théorème — (En supposant l’ axiome du choix dénombrable ) L’union d’un nombre dénombrable d’ensembles dénombrables est dénombrable. ^[F]

Par exemple, étant donnés des ensembles dénombrables a , b , c , …

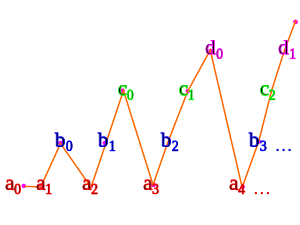
Énumération pour un nombre dénombrable d’ensembles dénombrables

En utilisant une variante de l’énumération triangulaire que nous avons vue ci-dessus :

un ₀ correspond à 0
a ₁ correspond à 1
b ₀ correspond à 2
a ₂ cartes à 3
b ₁ cartes à 4
c ₀ correspond à 5
a ₃ cartes à 6
b ₂ cartes à 7
c ₁ correspond à 8
d ₀ correspond à 9
a ₄ cartes à 10
…

Cela ne fonctionne que si les ensembles a , b , c , … sont disjoints . Sinon, alors l’union est encore plus petite et est donc également dénombrable par un théorème précédent.

Nous avons besoin de l’ axiome du choix dénombrable pour indexer tous les ensembles a , b , c , … simultanément.

Théorème — L’ensemble de toutes les suites de longueur finie de Nombres naturels est dénombrable.

Cet ensemble est l’union des suites de longueur 1, des suites de longueur 2, des suites de longueur 3, dont chacune est un ensemble dénombrable (produit cartésien fini). Nous parlons donc d’une union dénombrable d’ensembles dénombrables, qui est dénombrable par le théorème précédent.

Théorème — L’ensemble de tous les sous- ensembles finis des Nombres naturels est dénombrable.

Les éléments de tout sous-ensemble fini peuvent être ordonnés en une séquence finie. Il n’y a qu’un nombre dénombrable de séquences finies, donc il n’y a qu’un nombre dénombrable de sous-ensembles finis.

Théorème — Soient S et T des ensembles.

Si la fonction f : S → T est injective et T est dénombrable alors S est dénombrable.
Si la fonction g : S → T est surjective et S est dénombrable alors T est dénombrable.

Celles-ci découlent des définitions de l’ensemble dénombrable en tant que fonctions injectives / surjectives. ^[g]

Le théorème de Cantor affirme que si A est un ensemble et P ( A ) est son ensemble de puissance , c’est-à-dire l’ensemble de tous les sous-ensembles de A , alors il n’y a pas de fonction surjective de A vers P ( A ). Une preuve est donnée dans l’article Théorème de Cantor . En conséquence immédiate de ceci et du théorème de base ci-dessus, nous avons :

Proposition — L’ensemble P ( N ) n’est pas dénombrable ; c’est-à-dire qu’il est Indénombrable .

Pour une élaboration de ce résultat, voir l’argument diagonal de Cantor .

L’ensemble des nombres réels est Indénombrable, ^[h] et est donc l’ensemble de toutes les séquences infinies de Nombres naturels.

Le modèle minimal de la théorie des ensembles est dénombrable

S’il existe un ensemble qui est un modèle standard (voir modèle interne ) de la théorie des ensembles ZFC, alors il existe un modèle standard minimal ( voir Univers constructible ). Le théorème de Löwenheim-Skolem peut être utilisé pour montrer que ce modèle minimal est dénombrable. Le fait que la notion d’« indénombrabilité » ait un sens même dans ce modèle, et en particulier que ce modèle M contienne des éléments qui sont :

sous-ensembles de M , donc dénombrables,
mais Indénombrable du point de vue de M ,

était considéré comme paradoxal aux débuts de la théorie des ensembles, voir le paradoxe de Skolem pour en savoir plus.

Le modèle standard minimal comprend tous les nombres algébriques et tous les nombres transcendantaux effectivement calculables , ainsi que de nombreux autres types de nombres.

Commandes totales

Les ensembles dénombrables peuvent être totalement ordonnés de différentes manières, par exemple :

Bien-commandes (voir aussi nombre ordinal ):
- L’ordre habituel des Nombres naturels (0, 1, 2, 3, 4, 5, …)
- Les entiers dans l’ordre (0, 1, 2, 3, …; −1, −2, −3, …)
Autre ( pas bien commandé):
- L’ordre habituel des entiers (…, −3, −2, −1, 0, 1, 2, 3, …)
- L’ordre habituel des nombres rationnels (ne peut pas être explicitement écrit comme une liste ordonnée !)

Dans les deux exemples d’ordres de puits ici, tout sous-ensemble a un moindre élément ; et dans les deux exemples d’ordres hors puits, certains sous-ensembles n’ont pas de moindre élément . Il s’agit de la définition clé qui détermine si une commande totale est également une commande de puits.

Voir également

Numéro Aleph
Compte
Le paradoxe de Hilbert du Grand Hôtel
Ensemble Indénombrable

Remarques

^ Puisqu’il existe une bijection évidente entre N et N * = {1, 2, 3, … }, cela ne fait aucune différence que l’on considère 0 comme un nombre naturel ou non. Dans tous les cas, cet article suit la norme ISO 31-11 et la convention standard en logique mathématique , qui prend 0 comme nombre naturel.
^ Preuve : Observez que N × N est dénombrable en conséquence de la définition car la fonction f : N × N → N donnée par f ( m , n ) = 2 ^m 3 ⁿ est injective. ^[22] Il s’ensuit alors que le produit cartésien de deux ensembles dénombrables quelconques est dénombrable, car si A et B sont deux ensembles dénombrables il y a des surjections f : N → A et g : N →B. _ Alors f × g : N × N → A × B
est une surjection de l’ensemble dénombrable N × N à l’ensemble A × B et le corollaire implique que A × B est dénombrable. Ce résultat se généralise au produit cartésien de toute collection finie d’ensembles dénombrables et la preuve s’ensuit par induction sur le nombre d’ensembles de la collection.
^ Preuve : Les entiers Z sont dénombrables car la fonction f : Z → N donnée par f ( n ) = 2 ⁿ si n est non négatif et f ( n ) = 3 ^{− n} si n est négatif, est une fonction injective. Les nombres rationnels Q sont dénombrables car la fonction g : Z × N → Q donnée par g ( m , n ) = m /(n + 1) est une surjection de l’ensemble dénombrable Z × N aux rationnels Q .
^ Preuve : Par définition, chaque nombre algébrique (y compris les nombres complexes) est une racine d’un polynôme à coefficients entiers. Étant donné un nombre algébrique α {displaystylealpha} , laisser a 0 x 0 + a 1 x 1 + a 2 x 2 + ⋯ + a n x n {displaystyle a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+cdots +a_{n}x^{n}} ${displaystyle a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+cdots +a_{n}x^{n}}$ ${displaystyle a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+cdots +a_{n}x^{n}}$ un polynôme à coefficients entiers tel que α {displaystylealpha} est la k ème racine du polynôme, où les racines sont triées par valeur absolue de petit à grand, puis triées par argument de petit à grand. On peut définir une fonction d’injection (ie biunivoque) f : A → Q donnée par f ( α ) = 2 k − 1 ⋅ 3 a 0 ⋅ 5 a 1 ⋅ 7 a 2 ⋯ p n + 2 a n {displaystyle f(alpha )=2^{k-1}cdot 3^{a_{0}}cdot 5^{a_{1}}cdot 7^{a_{2}}cdots {p_ {n+2}}^{a_{n}}} ${displaystyle f(alpha )=2^{k-1}cdot 3^{a_{0}}cdot 5^{a_{1}}cdot 7^{a_{2}}cdots {p_{n+2}}^{a_{n}}}$ ${displaystyle f(alpha )=2^{k-1}cdot 3^{a_{0}}cdot 5^{a_{1}}cdot 7^{a_{2}}cdots {p_{n+2}}^{a_{n}}}$ , pendant que p n {displaystyle p_{n}} $p_{n}$ $p_{n}$ est le n -ième premier .
^ Preuve : Si A _i est un ensemble dénombrable pour chaque i dans I ={1,…,n}, alors pour chaque n il existe une fonction surjective g _i : N → A _i et donc la fonction G : I × N → ⋃ i ∈ I A i , {displaystyle G:Itimes mathbf {N} to bigcup _{iin I}A_{i},} ${displaystyle G:Itimes mathbf {N} to bigcup _{iin I}A_{i},}$ ${displaystyle G:Itimes mathbf {N} to bigcup _{iin I}A_{i},}$ donnée par G ( i , m ) = g _i ( m ) est une surjection. Comme I × N est dénombrable, l’union ⋃ i ∈ I A i {textstyle bigcup _{iin I}A_{i}} ${textstyle bigcup _{iin I}A_{i}}$ ${textstyle bigcup _{iin I}A_{i}}$ est dénombrable.
^ Preuve : Comme dans le cas fini, mais I = N et on utilise l’ axiome du choix dénombrable pour choisir pour chaque i dans N une surjection g _i de la collection non vide des surjections de N vers A _i .
^ Preuve : Pour (1) observer que si T est dénombrable il existe une fonction injective h : T → N . Alors si f : S → T est injective la composition h o f : S → N est injective, donc S est dénombrable. Pour (2) observer que si S est dénombrable, soit S est vide, soit il existe une fonction surjective h : N → S . Alors si g : S → Test surjectif, soit S et T sont tous les deux vides, soit la composition g o h : N → T est surjective. Dans les deux cas, T est dénombrable.
^ Voir La première preuve d’indénombrabilité de Cantor , ainsi que la propriété d’intersection finie # Applications pour une preuve topologique.

Citations

^ Manetti, Marco (19 juin 2015). Topologie . Springer. p. 26. ISBN 978-3-319-16958-3.
^ Rudin 1976 , chapitre 2
^ Tao 2016 , p. 181
^ Kamke 1950 , p. 2
^ ^un ^b Lang 1993 , §2 du chapitre I
^ Apostol 1969 , p. 23, chapitre 1.14
^ Thierry, Vialar (4 avril 2017). Manuel de Mathématiques . BoD – Livres à la demande. p. 24. ISBN 978-2-9551990-1-5.
^ Mukherjee, Subir Kumar (2009). Premier cours d’analyse réelle . Éditeurs académiques. p. 22. ISBN 978-81-89781-90-3.
^ Yaqub, Aladdin M. (24 octobre 2014). Une introduction à la métalogie . Presse Broadview. ISBN 978-1-4604-0244-3.
^ Singh, Tej Bahadur (17 mai 2019). Introduction à la topologie . Springer. p. 422.ISBN _ 978-981-13-6954-4.
^ ^un ^b Katzourakis, Nikolaos; Varvaruca, Eugen (2 janvier 2018). Une introduction illustrative à l’analyse moderne . Presse CRC. ISBN 978-1-351-76532-9.
^ Halmos 1960 , p. 91
^ Weisstein, Eric W. “Ensemble dénombrable” . mathworld.wolfram.com . Récupéré le 06/09/2020 .
^ Kamke 1950 , p. 2
^ Dlab, Vlastimil; Williams, Kenneth S. (9 juin 2020). Invitation à l’algèbre : un recueil de ressources pour les enseignants, les étudiants avancés de premier cycle et les étudiants diplômés en mathématiques . Scientifique mondial. p. 8. ISBN 978-981-12-1999-3.
^ Tao 2016 , p. 182
^ Stillwell, John C. (2010), Roads to Infinity: The Mathematics of Truth and Proof , CRC Press, p. 10, ISBN 9781439865507, la découverte par Cantor d’ensembles innombrables en 1874 fut l’un des événements les plus inattendus de l’histoire des mathématiques. Avant 1874, l’infini n’était même pas considéré comme un sujet mathématique légitime par la plupart des gens, de sorte que la nécessité de faire la distinction entre les infinis dénombrables et indénombrables n’aurait pas pu être imaginée.
^ Chantre 1878, p. 242.
^ Ferreirós 2007, pp. 268, 272–273.
^ “Que sont les ensembles et la forme de liste?” . expii . 2021-05-09. Archivé de l’original le 2020-09-18.
^ Halmos 1960 , p. 92
^ Avelsgaard 1990 , p. 182
^ Kamke 1950 , p. 3–4
^ Avelsgaard 1990 , p. 180
^ Fletcher & Patty 1988 , p. 187

Références

Apostol, Tom M. (juin 1969), Calcul multi-variable et algèbre linéaire avec applications , Calculus, vol. 2 (2e éd.), New York : John Wiley + Sons, ISBN 978-0-471-00007-5
Avelsgaard, Carol (1990), Fondations pour les mathématiques avancées , Scott, Foresman and Company, ISBN 0-673-38152-8
Cantor, Georg (1878), “Ein Beitrag zur Mannigfaltigkeitslehre” , Journal für die Reine und Angewandte Mathematik , 1878 (84): 242–248, doi : 10.1515/crelle-1878-18788413
Ferreirós, José (2007), Labyrinth of Thought: A History of Set Theory and Its Role in Mathematical Thought (2e éd. révisée), Birkhäuser, ISBN 978-3-7643-8349-7
Fletcher, Peter; Patty, C. Wayne (1988), Fondements des mathématiques supérieures , Boston: PWS-KENT Publishing Company, ISBN 0-87150-164-3
Halmos, Paul R. (1960), Théorie des ensembles naïfs , D. Van Nostrand Company, IncRéimprimé par Springer-Verlag, New York, 1974. ISBN 0-387-90092-6 (édition Springer-Verlag). Réimprimé par Martino Fine Books, 2011. ISBN 978-1-61427-131-4 (édition de poche).
Kamke, Erich (1950), Theory of Sets , série Dover en mathématiques et physique, New York: Dover, ISBN 978-0486601410
Lang, Serge (1993), Analyse réelle et fonctionnelle , Berlin, New York: Springer-Verlag, ISBN 0-387-94001-4
Rudin, Walter (1976), Principes d’analyse mathématique , New York : McGraw-Hill, ISBN 0-07-054235-X
Tao, Térence (2016). “Ensembles infinis” . Analyse I (troisième éd.). Singapour : Springer. pp. 181–210. ISBN 978-981-10-1789-6.

Recherchez dénombrable dans Wiktionary, le dictionnaire gratuit.

Portails : Arithmétique Mathématiques