Boîte Edgeworth

En économie , une boîte Edgeworth, parfois appelée boîte Edgeworth-Bowley, est une représentation graphique d’un marché avec seulement deux produits, X et Y , et deux consommateurs. Les dimensions de la boîte sont les quantités totales Ω _x et Ω _y des deux marchandises.

Fig. 1. Une boîte Edgeworth

Que les consommateurs soient Octavio et Abby. Le coin supérieur droit de la boîte représente la répartition dans laquelle Octavio détient tous les biens, tandis que le coin inférieur gauche correspond à la propriété complète par Abby. Les points à l’intérieur de la case représentent les manières de répartir les biens entre les deux consommateurs.

Le comportement du marché sera déterminé par les courbes d’indifférence des consommateurs . Les courbes bleues du diagramme représentent les courbes d’indifférence d’Octavio, et sont montrées comme convexes de son point de vue (c’est-à-dire vues du bas à gauche). Les courbes orange s’appliquent à Abby et sont convexes comme on le voit en haut à droite. Se déplacer vers le haut et vers la droite augmente l’allocation d’Octavio et le place sur une courbe d’indifférence plus souhaitable tout en plaçant Abby sur une courbe moins souhaitable.

Les courbes d’indifférence convexes sont considérées comme le cas habituel. Ils correspondent à des rendements décroissants pour chaque bien par rapport à l’autre.

L’échange au sein du marché commence à partir d’une allocation initiale connue sous le nom de dotation .

L’utilisation principale de la boîte d’Edgeworth est d’introduire des sujets dans la théorie de l’équilibre général sous une forme dans laquelle les propriétés peuvent être visualisées graphiquement. Cela peut aussi montrer la difficulté d’évoluer vers un résultat efficace en présence d’ un monopole bilatéral . ^[1] Dans ce dernier cas, il sert de précurseur au Problème de négociation de la théorie des jeux qui permet une solution numérique unique. ^{[2] [3]}

Histoire

Développement de la boîte Edgeworth

La boîte Edgeworth porte le nom de Francis Ysidro Edgeworth , ^[4] qui l’a présentée dans son livre Mathematical Psychics: An Essay on the Application of Mathematics to the Moral Sciences , 1881. ^[5] La représentation originale à deux axes d’Edgeworth a été développée dans le maintenant diagramme en boîte familier de Pareto dans son Manuel d’économie politique de 1906 et a été popularisé dans une exposition ultérieure de Bowley . La version moderne du diagramme est communément appelée la boîte Edgeworth-Bowley . ^[6]

La théorie mathématique de l’équilibre économique

Le cadre conceptuel de l’équilibre dans une économie de marché a été développé par Léon Walras ^[7] et étendu par Vilfredo Pareto . ^[8] Elle a été examinée avec un souci de généralité et de rigueur par des économistes mathématiciens du XXe siècle dont Abraham Wald , ^[9] Paul Samuelson , ^[10] Kenneth Arrow et Gérard Debreu . ^[11] Cela faisait partie d’un mouvement plus large dans lequel Wald a également cherché à apporter une plus grande rigueur à la théorie de la décision et de nombreux mathématiciens se sont concentrés sur la minimisation de la dépendance à l’ axiome du choix .

La théorie des marchés walrasiens s’est efforcée de trouver les prémisses les plus générales à partir desquelles une conclusion donnée peut être obtenue. Les domaines dans lesquels les locaux peuvent être renforcés ou affaiblis comprennent :

• Si les fonctions sont différentiables;
• Si les courbes d’indifférence sont primitives ou dérivables de fonctions d’utilité ; et
• Si les courbes d’indifférence sont convexes.

Des hypothèses sont également faites de nature plus technique, par exemple la non-réversibilité, la saturation , etc.

La recherche de la rigueur n’est pas toujours propice à l’intelligibilité. Dans cet article, les courbes d’indifférence seront traitées comme primitives. Dans un premier temps, nous les considérerons comme convexes et différentiables et nous nous concentrerons sur les équilibres intérieurs, mais nous relâcherons ensuite ces hypothèses.

L’équilibre du marché

Fig. 2. Marché des boîtes Edgeworth

Puisqu’il n’y a que deux produits, le prix effectif est le taux de change entre eux. Notre objectif est de trouver le prix auquel l’équilibre du marché peut être atteint, qui sera un point auquel aucune autre transaction n’est souhaitée, à partir d’une dotation donnée. Ces quantités seront déterminées par les courbes d’indifférence des deux consommateurs comme le montre la Fig. 2.

Nous supposerons que chaque jour Octavio et Abby vont au marché avec des dotations (ω _x ,ω _y ) et (Ω _x – ω _x , Ω _y – ω _y ) des deux marchandises, correspondant à la position ω dans le diagramme. Les deux consommateurs échangeront entre eux dans le cadre d’un comportement de marché concurrentiel. Cette hypothèse nécessite une certaine suspension de l’incrédulité puisque les conditions d’ une concurrence parfaite – qui incluent un nombre infini de consommateurs – ne sont pas réunies.

Si deux X s’échangent contre un seul Y , alors la transaction d’Octavio et d’Abby les amènera à un certain point le long de la ligne grise continue, connue sous le nom de ligne budgétaire . (Pour être plus précis, une ligne budgétaire peut être définie comme une ligne droite passant par le point de dotation représentant les allocations pouvant être obtenues par échange à un certain prix.) Les lignes budgétaires pour quelques autres prix sont également représentées par des lignes pointillées et pointillées sur la Fig. 2.

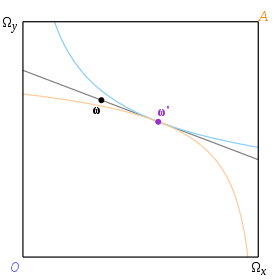
Fig. 3. Équilibre dans une boîte d’Edgeworth

L’équilibre correspondant à une dotation ω donnée est déterminé par le couple de courbes d’indifférence qui ont une tangente commune telle que cette tangente passe par ω . Nous utiliserons le terme « ligne de prix » pour désigner une tangente commune à deux courbes d’indifférence. Un équilibre correspond donc à une droite budgétaire qui est aussi une droite de prix, et le prix à l’équilibre est la pente de la droite. Dans la figure 3, ω est la dotation et ω ‘ est l’allocation d’équilibre.

Le raisonnement sous-jacent est le suivant.

Fig. 4. Découpage d’un quartier par croisement de courbes d’indifférence

Tout d’abord, tout point de la boîte doit se trouver exactement sur une des courbes d’indifférence d’Abby et sur exactement une des courbes d’Octavio. Si les courbes se croisent (comme illustré à la Fig. 4), elles divisent le voisinage immédiat en quatre régions, dont l’une (indiquée en vert pâle) est préférable pour les deux consommateurs ; donc un point auquel les courbes d’indifférence se croisent ne peut pas être un équilibre, et un équilibre doit être un point de tangence.

Deuxièmement, le seul prix qui peut tenir sur le marché au point de tangence est celui donné par le gradient de la tangente, car à ce prix seulement les consommateurs seront prêts à accepter des échanges limités.

Et troisièmement (le point le plus difficile) tous les échanges amenant les consommateurs sur le chemin de ω vers l’équilibre doivent avoir lieu au même prix. Si cela est accepté, alors ce prix doit être celui opérant au point de tangence, et le résultat suit.

Dans une économie à deux, rien ne garantit que tous les échanges se feront au même prix. Mais le but de l’encadré Edgeworth n’est pas d’illustrer la fixation des prix qui peut avoir lieu lorsqu’il n’y a pas de concurrence, mais plutôt d’illustrer une économie concurrentielle dans un cas minimal. Nous pouvons donc imaginer qu’au lieu d’une seule Abby et d’un seul Octavio, nous avons un nombre infini de clones de chacun, tous arrivant sur le marché avec des dotations identiques à des moments différents et négociant progressivement leur chemin vers l’équilibre. Un Octavio nouvellement arrivé peut échanger au prix du marché avec une Abby qui est proche de l’équilibre, et tant qu’une Abby nouvellement arrivée échange avec un Octavio presque satisfait, les chiffres s’équilibreront. Pour que l’échange fonctionne dans une grande économie concurrentielle, il faut que le même prix règne pour tous.^[12]

La recherche d’un équilibre concurrentiel se réduit donc à la recherche d’un point de tangence entre deux courbes d’indifférence dont la tangente passe par un point donné. L’utilisation des courbes d’offre (décrites ci-dessous) fournit une procédure systématique pour ce faire.

Ensemble de Pareto

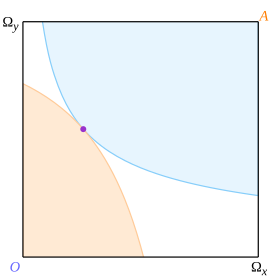
Fig. 5. Division de la boîte par deux courbes d’indifférence tangentielle

On dit qu’une allocation de biens en « domine Pareto » une autre si elle est préférable pour un consommateur et pas pire pour l’autre. Une allocation est dite « Pareto optimale » (ou « Pareto efficace ») si aucune autre allocation Pareto ne la domine. L’ensemble des allocations optimales de Pareto est connu sous le nom d’ ensemble de Pareto (ou «locus efficace»).

Considérez une paire de courbes tangentielles, une pour chaque consommateur, comme illustré à la Fig. 5, où le point de tangence est indiqué par le point violet. Alors la convexité garantit que les courbes ne peuvent s’intercepter qu’au point de tangence, et la boîte est donc divisée en 3 régions. La zone bleu pâle est préférable au point de tangence pour Octavio mais pire pour Abby; la zone orange pâle est préférable pour Abby mais pire pour Octavio ; et la zone blanche est pire pour les deux. Des considérations similaires s’appliquent aux frontières. Il s’ensuit que le point de tangence est Pareto optimal.

Fig 6. Ensemble de Pareto (ligne violette) pour une boîte Edgeworth

Ainsi l’ensemble de Pareto est le lieu des points de tangence des courbes. Il s’agit d’une ligne reliant l’origine d’Octavio (O) à celle d’Abby (A). Un exemple est illustré à la Fig. 6, où la ligne violette est l’ensemble de Pareto correspondant aux courbes d’indifférence pour les deux consommateurs.

Le vocabulaire utilisé pour décrire les différents objets qui font partie de la boîte Edgeworth diverge. L’ensemble de Pareto est parfois appelé courbe de contrat , tandis que Mas-Colell et al. restreindre la définition de la courbe de contrat aux seuls points de l’ensemble de Pareto qui rendent Abby et Octavio au moins aussi bien lotis qu’ils le sont à leur dotation initiale. D’autres auteurs qui ont un penchant plus théorique pour les jeux , tels que Martin Osborne et Ariel Rubinstein , ^[13] utilisent le terme noyau pour la section de l’ensemble de Pareto qui est au moins aussi bonne pour chaque consommateur que la dotation initiale.

Puisque l’ensemble de Pareto est l’ensemble des points où les courbes d’indifférence des consommateurs sont tangentielles, c’est aussi l’ensemble des points où le taux marginal de substitution de chaque consommateur est égal à celui de l’autre personne. ^[14]

Le premier théorème fondamental de l’économie du bien-être

Nous avons vu que les points de tangence des courbes d’indifférence sont les optima de Pareto, mais nous avons également vu précédemment que les équilibres économiques sont les points où les courbes d’indifférence sont tangentes à une ligne de prix commune. Il s’ensuit que les équilibres sont précisément les optima de Pareto.

Cet argument s’applique avec une restriction même si les courbes sont indifférenciables ou si l’équilibre est sur la frontière. La condition d’équilibre est qu’aucun autre échange n’aura lieu, et la condition pour qu’aucun autre échange n’ait lieu est qu’il n’y ait aucune direction de mouvement qui profite à un consommateur sans nuire à l’autre ; et cela équivaut à la définition d’un optimum de Pareto. ^[15]

La restriction est que l’équilibre implique qu’aucune amélioration locale ne peut être apportée – en d’autres termes, que le point est ‘localement’ Pareto optimal. Mais l’optimalité de Pareto est aujourd’hui considérée comme globale par définition. ^[16] Ainsi, si la nature des courbes d’indifférence permet à des optima non globaux de se produire (ce qui ne peut pas arriver si elles sont convexes), alors il est possible que les équilibres ne soient pas optimaux de Pareto.

La concurrence parfaite n’est pas une condition préalable au théorème. Tant que les consommateurs sont libres d’échanger, et continueront à le faire jusqu’à ce qu’aucun échange mutuellement acceptable ne soit disponible, l’équilibre sera atteint et sera (au moins « localement ») Pareto optimal. ^[17]

Le deuxième théorème fondamental de l’économie du bien-être

Fig. 7. Le deuxième théorème du bien-être

Considérons maintenant une économie dans laquelle les consommateurs ont des dotations ω comme le montre la figure 7. Laissé à lui-même, un marché libre les amènera à ω’ . Mais supposons qu’une autre position dans la boîte – disons α’ – soit considérée comme socialement préférable. On peut supposer que la position socialement souhaitée est optimale au sens de Pareto.

Nous pouvons considérer les lignes de prix (indiquées en pointillés dans le diagramme) comme correspondant à différentes distributions du revenu réel, et le mouvement le long de celles-ci comme une réaffectation des ressources alors que les revenus restent fixes.

Alors pour repositionner la société au point α’ souhaité, il n’est pas nécessaire que le gouvernement redistribue les ressources de manière à ce qu’Octavio tienne (α’ _x ,α’ _y ) et qu’Abby tienne le complément : il suffit de réallouer les ressources amener l’économie à n’importe quel point (disons α ) sur la ligne des prix passant par α’ , puis laisser le marché trouver son propre équilibre. En effet, tant que le gouvernement reconnaît une répartition souhaitable des revenus, il n’a pas besoin d’avoir une idée de l’allocation optimale des ressources.

Dans un énoncé d’économie plus générale, le théorème serait interprété comme disant que α’ peut être atteint par un transfert monétaire suivi du libre jeu des échanges marchands ; mais l’argent est absent de la boîte Edgeworth.

Le deuxième théorème fondamental ne fournit pas de modèle pour redresser les maux de la société. Le gouvernement peut décider de réaffecter les ressources entre Octavio et Abby, en les déplaçant de ω à α avant les échanges du jour ; et en conséquence, celui qui perd peut décider d’en emporter moins sur le marché le lendemain. Le deuxième théorème fondamental ne tient pas compte des distorsions introduites par la réallocation. ^[18]

Courbes d’offre

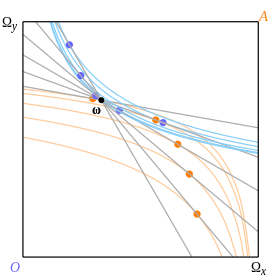
Fig. 8. Points privilégiés sur différentes lignes budgétaires

Les courbes d’offre permettent de trouver des points d’équilibre et sont également utiles pour étudier leur existence et leur unicité.

Deux de ces courbes, une pour chaque consommateur et les deux en fonction de la dotation, peuvent être tracées dans l’encadré. Nous faisons pivoter la ligne budgétaire autour de ω et traçons les points les plus favorisés par les deux consommateurs le long de la ligne, comme indiqué par les points colorés de la Fig. 8. Ce sont des points auxquels la ligne est tangentielle à leurs propres courbes d’indifférence.

Fig. 9. Courbes d’offre

Le lieu des points les plus favorisés d’un consommateur est sa courbe d’offre. La figure 9 montre la courbe d’offre d’Octavio en bleu foncé et celle d’Abby en marron. Elles se rejoignent au point ω ‘ et la ligne budgétaire d’équilibre (tracée en gris) est celle passant par ce point. Les courbes d’indifférence passant par ω ‘ pour les deux consommateurs sont représentées dans des couleurs plus claires.

Une courbe d’offre passe nécessairement par le point de dotation ω . Si nous prenons Abby comme exemple, nous notons qu’une de ses courbes d’indifférence doit passer par ω et qu’une ligne budgétaire peut être choisie pour avoir le même gradient que la courbe d’indifférence ici, faisant de ω un point le plus favorisé pour cette ligne.

En conséquence, les deux courbes d’offre des consommateurs se coupent nécessairement en ω ; mais la propriété qui rend cela possible est que ω est le seul point d’intersection possible compatible avec des lignes budgétaires de gradient différent, et qu’il ne constitue donc pas nécessairement un équilibre.

Toute intersection des courbes d’offre en un point autre que ω détermine un équilibre stable. Si les deux courbes d’offre sont tangentes au point de dotation, alors ce point est bien un équilibre et leur tangente commune est la ligne budgétaire correspondante. ^[19]

Terminologie des courbes d’offre

Les courbes d’offre ont été utilisées pour la première fois par Vilfredo Pareto – voir son Manuale / Manuel Chap. III, §97. Il les appelait « courbes d’échange » ( linee dei baratti / lignes des échanges ), et son nom pour l’allocation préférée d’Octavio le long d’une ligne budgétaire était son « point d’équilibre ».

Cette allocation préférentielle est parfois appelée aujourd’hui la « demande » d’Octavio, qui constitue une description asymétrique d’un fait symétrique. Une allocation détermine la possession d’Abby autant que celle d’Octavio, et est donc autant une offre qu’une demande.

Offre est le français pour «offre», donc appeler une courbe d’offre un lieu de demandes revient à appeler une courbe d’offre un lieu de demandes.

Unicité des équilibres

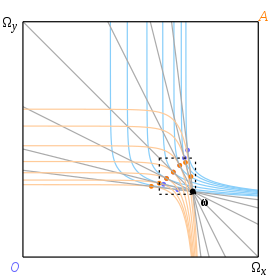
Fig. 10. Une boîte d’Edgeworth avec plusieurs équilibres Fig. 11. Une boîte d’Edgeworth à équilibres multiples (détail)

On pourrait supposer, à partir de considérations économiques, que si une tangente commune existe à travers une dotation donnée, et si les courbes d’indifférence ne sont pas pathologiques dans leur forme, alors le point de tangence sera unique. Cela s’avère faux. Les conditions d’unicité d’équilibre ont fait l’objet de recherches approfondies: voir Théorie générale de l’équilibre .

Figues. 9 et 10 illustrent un exemple de Mas-Colell et al. dans laquelle trois équilibres distincts correspondent au point de dotation ω . Les courbes d’indifférence sont :

X − 1 8 y − 8 = tu {displaystyle quad x-{tfrac {1}{8}}y^{-8}=u} (Octave)

y − 1 8 X − 8 = tu {displaystyle quad y-{tfrac {1}{8}}x^{-8}=u} (Abby).

Les courbes d’indifférence remplissent la case mais ne sont affichées que lorsqu’elles sont tangentielles à certaines lignes budgétaires représentatives. Les courbes d’offre, dessinées à la Fig. 11, se croisent en trois points matérialisés par de gros points gris et correspondant à des taux de change de 1 ⁄ 2 , 1 et 2.

Généralisations

Les premiers examens des propriétés de l’équilibre étaient basés sur une définition implicite de tangence, et la convexité semble avoir été implicitement supposée. ^[20] Il ne faisait aucun doute que l’équilibre serait atteint : l’ ascension du gradient y conduirait. Mais les résultats manquaient de généralité.

Equilibres aux frontières et courbes non différentiables

Fig. 12. Lignes de prix pour une boîte avec des équilibres aux frontières

Kenneth Arrow et Gérard Debreu ont publié des articles indépendamment en 1951 attirant l’attention sur les limites des preuves de calcul des théorèmes d’équilibre. ^[21] Arrow mentionne spécifiquement la difficulté causée par les équilibres sur la frontière, et Debreu le problème des courbes d’indifférence non différenciables.

Sans viser l’exhaustivité, il est aisé de voir intuitivement comment étendre nos méthodes pour les appliquer à ces cas. Il faut élargir le concept de tangente à toute droite qui touche la courbe : une tangente au sens étymologique plutôt qu’au sens du calcul différentiel. Dans l’exemple de la Fig. 12, il existe un arc de lignes de prix légaux passant par un point de contact, chacune touchant des courbes d’indifférence sans les couper à l’intérieur de la boîte, et en conséquence il existe une gamme d’équilibres possibles pour une dotation donnée.

Équilibre concurrentiel

Les équilibres de la figure 12 ne sont pas des points auxquels les courbes sont de vraies tangentes les unes aux autres. Elles ont cependant une propriété qui généralise la définition en termes de tangentes, à savoir que les deux courbes peuvent être localement séparées par une droite.

Arrow et Debreu ont défini l’équilibre de la même manière que l’autre dans leurs articles (indépendants) de 1951 sans fournir aucune source ou justification de leur définition. Ils ont conservé leur définition dans leur article commun (sur l’existence de l’équilibre) de 1954. ^[22] La nouvelle définition a nécessité un changement de technique mathématique du calcul différentiel à la théorie des ensembles convexes .

Leur définition était en fait la suivante : un équilibre pouvant être atteint à partir d’une dotation ω consiste en une allocation x et une ligne budgétaire passant par x et ω tels qu’il n’y a aucun point le long de la ligne que l’un ou l’autre des consommateurs (strictement) préfère à x . Un couple composé d’une allocation et d’une droite qui vérifie cette propriété est appelé équilibre « walrasien » ou « compétitif » .

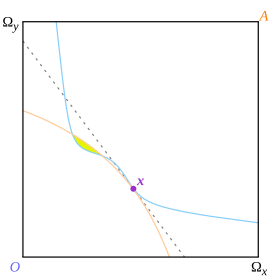
Fig. 13. Un équilibre « local »

La ligne budgétaire de cette définition est une ligne qui sépare les courbes d’indifférence des deux consommateurs, mais elle le fait globalement plutôt que localement. Arrow et Debreu n’expliquent pas pourquoi ils nécessitent une séparation globale, ce qui a peut-être facilité leurs preuves mais peut avoir des conséquences inattendues. Sur la figure 13, le point x est un point de tangence qui est également un point auquel les courbes d’indifférence sont localement séparées par la ligne de prix en pointillés ; mais comme ils ne sont pas globalement séparés, le point n’est pas un équilibre selon la définition d’Arrow et Debreu.

Fig. 14. Un optimum de Pareto qui n’est pas un « équilibre compétitif »

Dans la figure 14, le point x est un optimum de Pareto qui ne satisfait pas la définition de l’équilibre concurrentiel. La question de savoir si l’économie s’établirait à un tel point est tout à fait distincte de celle de savoir si elle satisfait à une définition donnée de l’équilibre ; évidemment dans ce cas il s’y installerait bien.

Arrow et Debreu ont toujours inclus la convexité des courbes d’indifférence parmi leurs « hypothèses ». Le terme «hypothèses» est vague et pourrait faire référence à une présupposition sous-jacente aux définitions ainsi qu’aux théorèmes, ou à une prémisse qui n’est nécessaire que pour ces derniers. Étant donné que leur définition n’inclut pas tous les équilibres qui peuvent exister lorsque les courbes peuvent être non convexes, il est possible qu’ils signifiaient l’hypothèse de convexité dans le premier sens. Qu’il en soit ainsi ou non, la définition a été largement adoptée sans aucune restriction de domaine.

Il a parfois été constaté que les résultats peuvent être dérivés sous leur définition sans supposer de convexité dans la preuve (le premier théorème fondamental de l’économie du bien-être en est un exemple).

Existence d’un équilibre concurrentiel

Dans certaines économies, il n’y aura pas de point de repos accessible à partir d’une dotation donnée par échange à des prix uniformes ; il n’existe donc aucun point d’arrêt satisfaisant à la définition de l’équilibre concurrentiel. Les familles de courbes du motif de la figure 14 en sont un exemple.

Les théorèmes fondamentaux de l’économie du bien-être

L’équilibre étant défini comme «équilibre compétitif», le premier théorème fondamental peut être prouvé même si les courbes d’indifférence n’ont pas besoin d’être convexes: tout équilibre compétitif est (globalement) Pareto optimal. Cependant la preuve n’est plus évidente, et le lecteur est renvoyé à l’article sur les Théorèmes fondamentaux de l’économie du bien-être .

Le même résultat n’aurait pas été considéré comme valable (avec des courbes d’indifférence non convexes) sous la définition de tangence de l’équilibre. Le point x de la Fig. 13 aurait été considéré comme un équilibre qui n’était pas (globalement) optimal puisque la région jaune de Pareto le domine.

Il ne s’ensuit pas que le résultat ait été renforcé puisque la possibilité d’atteindre l’équilibre a été rendue douteuse. Dans la figure 13, le point x n’est peut-être pas un « équilibre concurrentiel », mais l’économie peut y rester bloquée, l’empêchant d’atteindre le « véritable » équilibre (et Optimal de Pareto) dans la région jaune.

Il a toujours été considéré comme essentiel au premier théorème du bien-être que l’équilibre soit effectivement atteint. L’interprétation de Lerner du théorème était que “Heureusement, l’allocation optimale des biens peut être atteinte automatiquement”. ^[23] Cependant, rien ne peut garantir qu’un optimum global sera atteint lorsque des optima locaux sont présents. Si le concept d’équilibre inclut des optima locaux tels que x , alors l’équilibre peut être réalisable mais sous-optimal ; si de tels points sont exclus, alors l’équilibre peut être optimal mais inaccessible.

Les différences causées par la non-convexité deviennent plus profondes lorsque nous examinons le deuxième théorème fondamental. Tous les optimums de Pareto ne sont pas un équilibre concurrentiel (bien qu’il puisse encore s’agir d’un lieu de repos pour l’économie). Par conséquent, il faut soit donner au théorème la convexité des préférences comme prémisse, soit l’énoncer de telle manière que « l’équilibre » ne soit pas compris comme « l’équilibre concurrentiel » tel que défini ci-dessus.

Remarques

1. ^ John Creedy, 2008. “Francis Ysidro Edgeworth (1845–1926)”, Le New Palgrave Dictionary of Economics , 2e édition. Résumé .
2. ^ John F. Nash, Jr. , 1950. “Le problème de la négociation”, Econometrica , 18(2), pp. 155-162 .
3. ^ Roberto Serrano, 2008. “négociation,” Le Nouveau Dictionnaire Palgrave d’Économie , 2ème Édition. Résumé .
4. ^ Schotter, Andrew (2008), Microéconomie : une approche moderne , Cengage Learning , p. 524, ISBN 978-0-324-31584-4
5. ↑ Lluís Barbé (2010), Francis Ysidro Edgeworth : un portrait en famille et entre amis , Edward Elgar Publishing , p. 12, ISBN 978-1-84844-716-5
6. ^ Humphrey, Thomas M. “La première histoire du diagramme de boîte” (PDF) . Trimestriel économique . Récupéré le 30 octobre 2016 .
7. ^ L. Walras, ‘Éléments d’Économie Politique Pure, ou Théorie de la Richesse Sociale’ (1874).
8. ^ V. Pareto, Manuale / Manuel (1906/9).
9. ^ A. Wald, ‘Über einige Gleichungssysteme der mathematischen Ökonomie’ (1936), tr. comme “Sur certains systèmes d’équations d’économie mathématique” (1951).
10. ^ P. Samuelson, “Fondements de l’analyse économique” (1947).
11. ^ K. Arrow et G. Debreu, “Existence d’un équilibre pour une économie compétitive” (1954).
12. ↑ Voir Pareto, Manuale / Manuel , chap. III, §170. Notez que Pareto prend soin de ne pas dire que les prix constants sont généraux, mais simplement qu’ils sont le cas le plus courant et le plus important.
13. ^ Osborne, Martin J.; Rubinstein, Ariel (1994). Un cours de théorie des jeux . Cambridge : Presse du MIT. ISBN 0-262-65040-1.
14. ^ Les Cobb-Douglas αs pour les illustrations sont 0·35 (Octavio) et 0·65 (Abby).
15. ^ Voir K. Wicksell, “Conférences sur l’économie politique” I (1906), Eng. tr. (1934), p. 82 et suiv.
16. ^ Pareto lui-même l’a défini comme une propriété locale. Manuel / Manuel Chap III, §22 .
17. ↑ Voir Paul Samuelson , « Fondements de l’analyse économique » (1947), p. 204.
18. ↑ Voir la discussion aux pages 556 et suivantes. de Mas-Colell et al.
19. ^ Ce récit est basé sur la section 15.B de Mas-Colell et al. L’illustration est leur exemple 15.B.1 avec son Cobb-Douglas α réglé égal à 0,275.
20. ^ Oscar Lange , “Les fondements de l’économie du bien-être” (1942).
21. ^ K. Arrow, “Une extension des théorèmes de base de l’économie classique du bien-être” (1951); G. Debreu, “Le coefficient d’utilisation des ressources” (1951).
22. ^ K. Arrow et G. Debreu, “Existence d’un équilibre pour une économie compétitive” (1954).
23. ^ A. Lerner, “L’économie du contrôle” (1944), p. 15.

Références

• Mas-Colell, Andreu ; Whinston, Michael D.; Jerry R. Green (1995). Théorie microéconomique . New York : presse universitaire d’Oxford. ISBN 0-19-507340-1.
• Vilfredo Pareto , Manuale di Economia Politica con una Introduzione alla Scienza Sociale (1906) / Manuel d’Économie Politique (1909) (en fait une deuxième édition de la version italienne), Eng. tr. (des Français) comme “Manuel d’économie politique” (1971). Le texte italien est disponible en ligne sur https://archive.org/details/manualedieconomi00pareuoft .

Liens externes

• Simulation sur Wolfram.com
• Explication de la boîte d’Edgeworth à la vérité économique
• Explication de la boîte Edgeworth chez Digital Economist