Nombre complexe

En mathématiques , un nombre complexe est un élément d’un système numérique qui contient les nombres réels et un élément spécifique noté i , appelé l’ unité imaginaire , et satisfaisant l’ équation i ² = −1 . De plus, tout nombre complexe peut être exprimé sous la forme a + bi , où a et b sont des nombres réels. Parce qu’aucun nombre réel ne satisfait l’équation ci-dessus, j’ai été appelé un nombre imaginaire par René Descartes . Pour le nombre complexe a+ bi , a est appelé lepartie réelle etbest appelé la partie imaginaire . L’ensemble des nombres complexes est désigné par l’un des symboles C {displaystyle mathbb {C} } ou C. _ Malgré la nomenclature historique “imaginaire”, les nombres complexes sont considérés dans les sciences mathématiques comme tout aussi “réels” que les nombres réels et sont fondamentaux dans de nombreux aspects de la description scientifique du monde naturel. ^{[1] [un]}

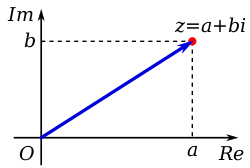Un nombre complexe peut être représenté visuellement comme une paire de nombres ( a , b ) formant un vecteur sur un diagramme appelé diagramme d’ Argand , représentant le plan complexe . Re est l’axe réel, Im est l’axe imaginaire, et i est ” l’unité imaginaire “, qui satisfait i ² = −1 .

Les nombres complexes permettent de résoudre toutes les équations polynomiales , même celles qui n’ont pas de solution en nombres réels. Plus précisément, le théorème fondamental de l’algèbre affirme que toute équation polynomiale non constante à coefficients réels ou complexes a une solution qui est un nombre complexe. Par exemple, l’équation ( x + 1 ) 2 = − 9 {displaystyle (x+1)^{2}=-9} n’a pas de solution réelle, puisque le carré d’un nombre réel ne peut pas être négatif, mais a les deux solutions complexes non réelles −1 + 3 i et −1 − 3 i .

L’addition, la soustraction et la multiplication des nombres complexes peuvent être naturellement définies en utilisant la règle i ² = −1 combinée avec les lois associatives , commutatives et distributives . Chaque nombre complexe non nul a un inverse multiplicatif . Cela fait des nombres complexes un champ qui a les nombres réels comme sous-champ. Les nombres complexes forment également un espace vectoriel réel de dimension deux, avec {1, i } comme base standard .

Cette base standard fait des nombres complexes un plan cartésien , appelé plan complexe . Cela permet une interprétation géométrique des nombres complexes et de leurs opérations, et inversement d’exprimer en termes de nombres complexes certaines propriétés et constructions géométriques. Par exemple, les nombres réels forment la droite réelle qui s’identifie à l’axe horizontal du plan complexe. Les nombres complexes de valeur absolue un forment le cercle unitaire . L’addition d’un nombre complexe est une translation dans le plan complexe, et la multiplication par un nombre complexe est une similarité centrée à l’origine. La conjugaison complexe est lasymétrie de réflexion par rapport à l’axe réel. La valeur absolue complexe est une norme euclidienne .

En résumé, les nombres complexes forment une structure riche qui est à la fois un corps algébriquement clos , une algèbre commutative sur les réels et un espace vectoriel euclidien de dimension deux.

Définition

Une illustration du nombre complexe z = x + iy sur le plan complexe . La partie réelle est x et sa partie imaginaire est y .

Un nombre complexe est un nombre de la forme a + bi , où a et b sont des nombres réels , et i est une indéterminée satisfaisant i ² = −1 . Par exemple, 2 + 3 i est un nombre complexe. ^[3]

Ainsi, un nombre complexe est défini comme un polynôme à coefficients réels dans l’unique indéterminée i , pour lequel la relation i ² + 1 = 0 est imposée. Sur la base de cette définition, les nombres complexes peuvent être additionnés et multipliés, en utilisant l’addition et la multiplication pour les polynômes. La relation i ² + 1 = 0 induit les égalités i ^{4 k} = 1, i ^{4 k +1} = i , i ^{4 k +2} = −1, et i ^{4 k +3} = − i ,qui sont valables pour tous les entiers k ; ceux-ci permettent de réduire tout polynôme résultant de l’addition et de la multiplication de nombres complexes à un polynôme linéaire en i , toujours de la forme a + bi à coefficients réels a, b.

Le nombre réel a est appelé la partie réelle du nombre complexe a + bi ; le nombre réel b est appelé sa partie imaginaire . Pour souligner, la partie imaginaire ne comprend pas de facteur i ; c’est-à-dire que la partie imaginaire est b , pas bi . ^{[4] [5]}

Formellement, les nombres complexes sont définis comme l’ anneau quotient de l’ anneau polynomial dans l’indéterminé i , par l’ idéal engendré par le polynôme i ² + 1 (voir ci- dessous ). ^[6]

Notation

Un nombre réel a peut être considéré comme un nombre complexe a + 0 i , dont la partie imaginaire est 0. Un nombre purement imaginaire bi est un nombre complexe 0 + bi , dont la partie réelle est nulle. Comme pour les polynômes, il est courant d’écrire a pour a + 0 i et bi pour 0 + bi . De plus, lorsque la partie imaginaire est négative, c’est-à-dire que b = − |b| < 0 , il est courant d’écrire a − |b|i au lieu de a + (− |b| ) i; par exemple, pour b = −4 , 3 − 4 i peut s’écrire au lieu de 3 + (−4) i .

Comme la multiplication de l’indéterminée i par un réel est commutative en polynômes à coefficients réels, le polynôme a + bi peut s’écrire a + ib . Ceci est souvent utile pour les parties imaginaires désignées par des expressions, par exemple, lorsque b est un radical. ^[7]

La partie réelle d’un nombre complexe z est notée Re( z ) , R e ( z ) {displaystyle {mathcal {Re}}(z)} , ou alors R ( z ) {displaystyle {mathfrak {R}}(z)} ; la partie imaginaire d’un nombre complexe z est notée Im( z ) , I m ( z ) {displaystyle {mathcal {Je}}(z)} , ou alors I ( z ) . {displaystyle {mathfrak {I}}(z).} Par example,

Re ⁡ ( 2 + 3 i ) = 2 and Im ⁡ ( 2 + 3 i ) = 3 . {displaystyle operatorname {Re} (2+3i)=2quad {text{ et }}quad operatorname {Im} (2+3i)=3~.}

L’ ensemble de tous les nombres complexes est noté C {displaystyle mathbb {C} } ( tableau gras ) ou C (vertical gras).

Dans certaines disciplines, notamment en électromagnétisme et en génie électrique , j est utilisé à la place de i car i est fréquemment utilisé pour représenter le courant électrique . ^[8] Dans ces cas, les nombres complexes s’écrivent sous la forme a + bj , ou a + jb .

Visualisation

Un nombre complexe z , sous la forme d’un point (noir) et de son vecteur de position (bleu)

Un nombre complexe z peut ainsi être identifié à un couple ordonné ( R ( z ) , I ( z ) ) {displaystyle (Re (z),Im (z))} de nombres réels, qui à leur tour peuvent être interprétés comme les coordonnées d’un point dans un espace à deux dimensions. L’espace le plus immédiat est le plan euclidien de coordonnées convenables, qui est alors appelé plan complexe ou diagramme d’Argand , ^{[9] [b] [10]} du nom de Jean-Robert Argand . Un autre espace proéminent sur lequel les coordonnées peuvent être projetées est la surface bidimensionnelle d’une sphère, qui est alors appelée sphère de Riemann .

Plan complexe cartésien

La définition des nombres complexes impliquant deux valeurs réelles arbitraires suggère immédiatement l’utilisation de coordonnées cartésiennes dans le plan complexe. L’axe horizontal ( réel ) est généralement utilisé pour afficher la partie réelle, avec des valeurs croissantes vers la droite, et la partie imaginaire marque l’axe vertical ( imaginaire ), avec des valeurs croissantes vers le haut.

Un numéro cartographié peut être considéré soit comme le point coordonné , soit comme un vecteur de position de l’origine à ce point. Les valeurs des coordonnées d’un nombre complexe z peuvent donc être exprimées sous sa forme cartésienne , rectangulaire ou algébrique .

Notamment, les opérations d’addition et de multiplication prennent un caractère géométrique très naturel, lorsque les nombres complexes sont considérés comme des vecteurs de position : l’addition correspond à l’ addition vectorielle , tandis que la multiplication (voir ci- dessous ) correspond à la multiplication de leurs grandeurs et à l’addition des angles qu’ils font avec le axe réel. Vue sous cet angle, la multiplication d’un nombre complexe par i correspond à la rotation du vecteur position dans le sens inverse des aiguilles d’une montre d’un quart de tour ( 90° ) autour de l’origine, ce qui peut s’exprimer algébriquement comme suit :

( a + b i ) ⋅ i = a i + b ( i ) 2 = − b + a i . {displaystyle (a+bi)cdot i=ai+b(i)^{2}=-b+ai.}

Plan complexe polaire

L’argument φ et le module r localisent un point dans le plan complexe. Module et argument

Une option alternative pour les coordonnées dans le plan complexe est le système de coordonnées polaires qui utilise la distance du point z à l’ origine ( O ) et l’angle sous-tendu entre l’ axe réel positif et le segment de ligne Oz dans le sens antihoraire. Cela conduit à la forme polaire

z = r e i φ = r ( cos ⁡ φ + i sin ⁡ φ ) {displaystyle z=re^{ivarphi }=r(cos varphi +isin varphi )}

d’un nombre complexe, où r est la valeur absolue de z , et φ {displaystylevarphi } est l’ argument de z .

La valeur absolue (ou module ou magnitude ) d’un nombre complexe z = x + yi est ^[11]

r = | z | = x 2 + y 2 . {displaystyle r=|z|={sqrt {x^{2}+y^{2}}}.} Si z est un nombre réel (c’est-à-dire si y = 0 ), alors r = | x | . Autrement dit, la valeur absolue d’un nombre réel est égale à sa valeur absolue en tant que nombre complexe.

Selon le théorème de Pythagore , la valeur absolue d’un nombre complexe est la distance à l’origine du point représentant le nombre complexe dans le plan complexe .

L’ argument de z (dans de nombreuses applications appelé “phase” φ ) ^[10] est l’angle du rayon Oz avec l’axe réel positif, et s’écrit arg z . Comme pour le module, l’argument peut être trouvé à partir de la forme rectangulaire x + yi ^[12] — en appliquant l’inverse tangente au quotient des parties imaginaires par parties réelles. En utilisant une identité demi-angle, une seule branche de l’arctan suffit pour couvrir la plage (− π , π ] de la fonction arg , et évite une analyse au cas par cas plus subtile

φ = arg ⁡ ( x + y i ) = { 2 arctan ⁡ ( y x 2 + y 2 + x ) if y ≠ 0 or x > 0 , π if x < 0 and y = 0 , undefined if x = 0 and y = 0. {displaystyle varphi =arg(x+yi)={begin{cases}2arctan left({dfrac {y}{{sqrt {x^{2}+y^{2}}}+x}}right)&{text{if }}yneq 0{text{ or }}x>0,\pi &{text{if }}x<0{text{ and }}y=0,\{text{undefined}}&{text{if }}x=0{text{ and }}y=0.end{cases}}}

Normalement, comme indiqué ci-dessus, la valeur principale dans l’intervalle (− π , π ] est choisie. Si la valeur arg est négative, les valeurs dans la plage (− π , π ] ou [0, 2 π ) peuvent être obtenues en ajoutant 2 π . La valeur de φ est exprimée en radians dans cet article, elle peut augmenter de tout multiple entier de 2 π et donner toujours le même angle, vu comme sous-tendu par les rayons de l’axe réel positif et de l’origine passant par z . Par conséquent, la fonction arg est parfois considérée commemultivalué . L’angle polaire pour le nombre complexe 0 est indéterminé, mais le choix arbitraire de l’angle polaire 0 est courant.

La valeur de φ est égale au résultat de atan2 :

φ = atan2 ⁡ ( Im ⁡ ( z ) , Re ⁡ ( z ) ) . {displaystyle varphi =operatorname {atan2} left(operatorname {Im} (z),operatorname {Re} (z)right).}

Ensemble, r et φ donnent une autre façon de représenter les nombres complexes, la forme polaire , car la combinaison du module et de l’argument spécifie entièrement la position d’un point sur le plan. La récupération des coordonnées rectangulaires d’origine à partir de la forme polaire se fait par la formule appelée forme trigonométrique

z = r ( cos ⁡ φ + i sin ⁡ φ ) . {displaystyle z=r(cos varphi +isin varphi ).}

En utilisant la formule d’Euler, cela peut être écrit comme

z = r e i φ or z = r exp ⁡ i φ . {displaystyle z=re^{ivarphi }{text{ ou }}z=rexp ivarphi .}

En utilisant la fonction cis , cela est parfois abrégé en

z = r c i s ⁡ φ . {displaystyle z=roperatorname {mathrm {cis} } varphi .}

En notation angulaire , souvent utilisée en électronique pour représenter un phaseur d’amplitude r et de phase φ , elle s’écrit ^[13]

z = r ∠ φ . {displaystyle z=rangle varphi .}

Graphiques complexes

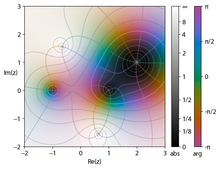
Un graphique de roue de couleur de l’expression ( z ² – 1)( z – 2 – je ) ²/z ² + 2 + 2 je

Lors de la visualisation de fonctions complexes , une entrée et une sortie complexes sont nécessaires. Étant donné que chaque nombre complexe est représenté en deux dimensions, la représentation graphique visuelle d’une fonction complexe nécessiterait la perception d’un espace à quatre dimensions , ce qui n’est possible que dans les projections. Pour cette raison, d’autres façons de visualiser des fonctions complexes ont été conçues.

Dans la coloration de domaine , les dimensions de sortie sont représentées respectivement par la couleur et la luminosité. Chaque point du plan complexe en tant que domaine est orné , généralement avec une couleur représentant l’argument du nombre complexe et une luminosité représentant la magnitude. Les taches sombres marquent des modules proches de zéro, les taches plus claires sont plus éloignées de l’origine, la gradation peut être discontinue, mais est supposée monotone. Les couleurs varient souvent par étapes de π/3pour 0 à 2 π du rouge, jaune, vert, cyan, bleu, au magenta. Ces tracés sont appelés graphiques à roues chromatiques . Cela fournit un moyen simple de visualiser les fonctions sans perdre d’informations. L’image montre des zéros pour ±1, (2 + i ) et des pôles à ± √ −2 −2 i .

Les surfaces de Riemann sont une autre façon de visualiser des fonctions complexes. ^{[ plus d’explications nécessaires ]} Les surfaces de Riemann peuvent être considérées comme des déformations du plan complexe ; tandis que les axes horizontaux représentent les entrées réelles et imaginaires, l’axe vertical unique ne représente que la sortie réelle ou imaginaire. Cependant, les surfaces de Riemann sont construites de telle sorte que leur rotation de 180 degrés montre la sortie imaginaire, et vice versa. Contrairement à la coloration de domaine, les surfaces de Riemann peuvent représenter des fonctions multivaluées comme √ z .

Histoire

La solution en radicaux (sans fonctions trigonométriques ) d’une équation cubique générale , lorsque ses trois racines sont des nombres réels, contient les racines carrées des nombres négatifs , une situation qui ne peut pas être corrigée par la factorisation à l’aide du test de la racine rationnelle , si la cubique est irréductible ; c’est ce qu’on appelle casus irreducibilis (“cas irréductible”). Cette énigme a conduit le mathématicien italien Gerolamo Cardano à concevoir des nombres complexes vers 1545 dans son Ars Magna , ^[14]bien que sa compréhension était rudimentaire; de plus, il a par la suite rejeté les nombres complexes comme “subtiles car inutiles”. ^[15]

Les travaux sur le problème des polynômes généraux ont finalement conduit au théorème fondamental de l’algèbre , qui montre qu’avec les nombres complexes, une solution existe pour chaque équation polynomiale de degré un ou plus. Les nombres complexes forment ainsi un corps algébriquement clos , où toute équation polynomiale a une racine .

De nombreux mathématiciens ont contribué au développement des nombres complexes. Les règles d’addition, de soustraction, de multiplication et d’extraction de racine des nombres complexes ont été développées par le mathématicien italien Rafael Bombelli . ^[16] Un formalisme plus abstrait pour les nombres complexes a été développé par le mathématicien irlandais William Rowan Hamilton , qui a étendu cette abstraction à la théorie des quaternions . ^[17]

On peut dire que la première référence fugitive aux racines carrées des nombres négatifs se produit dans l’œuvre du mathématicien grec Héro d’Alexandrie au 1er siècle après JC , où dans son Stereometrica il considérait, apparemment par erreur, le volume d’un impossible tronc de une pyramide pour arriver au terme 81 − 144 {displaystyle {sqrt {81-144}}} dans ses calculs, qui se simplifieraient aujourd’hui à − 63 = 3 i 7 {displaystyle {sqrt {-63}}=3i{sqrt {7}}} . Les quantités négatives n’étaient pas conçues dans les mathématiques hellénistiques et Hero les a simplement remplacées par leur valeur positive. 144 − 81 = 3 7 . {displaystyle {sqrt {144-81}}=3{sqrt {7}}.} ^[18]

L’impulsion pour étudier les nombres complexes en tant que sujet en soi est apparue pour la première fois au XVIe siècle lorsque des solutions algébriques pour les racines des polynômes cubiques et quartiques ont été découvertes par des mathématiciens italiens (voir Niccolò Fontana Tartaglia , Gerolamo Cardano ). On s’est vite rendu compte (mais on l’a prouvé bien plus tard) ^[19] que ces formules, même si l’on ne s’intéressait qu’aux solutions réelles, nécessitaient parfois la manipulation de racines carrées de nombres négatifs. A titre d’exemple, la formule de Tartaglia pour une équation cubique de la forme x ³ = px + q ^[c] donne la solution de l’équationx ³ = x comme

1 3 ( ( − 1 ) 1 / 3 + ( − 1 ) − 1 / 3 ) . {displaystyle {tfrac {1}{sqrt {3}}}left(left({sqrt {-1}}right)^{1/3}+left({sqrt {-1 }}right)^{-1/3}right).}

À première vue, cela ressemble à un non-sens. Cependant, des calculs formels avec des nombres complexes montrent que l’équation z ³ = i a trois solutions : − i , 3 + i 2 , − 3 + i 2 . {displaystyle -i,{frac {{sqrt {3}}+i}{2}},{frac {-{sqrt {3}}+i}{2}}.} En les remplaçant tour à tour par − 1 1 / 3 {displaystyle {sqrt {-1}}^{1/3}} dans la formule cubique de Tartaglia et en simplifiant, on obtient 0, 1 et −1 comme solutions de x ³ − x = 0 . Bien sûr, cette équation particulière peut être résolue à vue, mais elle illustre que lorsque des formules générales sont utilisées pour résoudre des équations cubiques avec des racines réelles, alors, comme les mathématiciens ultérieurs l’ont montré rigoureusement, ^[d] l’utilisation de nombres complexes est inévitable . Rafael Bombelli a été le premier à aborder explicitement ces solutions apparemment paradoxales d’équations cubiques et a développé les règles de l’arithmétique complexe essayant de résoudre ces problèmes.

Le terme “imaginaire” pour ces grandeurs a été inventé par René Descartes en 1637, qui s’est efforcé d’insister sur leur caractère irréel ^[20]

… parfois seulement imaginaire, c’est-à-dire qu’on peut en imaginer autant que je l’ai dit dans chaque équation, mais parfois il n’existe aucune quantité qui corresponde à celle que l’on imagine.
[ … quelquefois seulement imaginaires c’est-à-dire que l’on peut toujours en imaginer autant que j’ai dit en chaque équation, mais qu’il n’y a quelquefois aucune quantité qui corresponde à celle qu’on imaginer. ]

Une autre source de confusion était que l’équation − 1 2 = − 1 − 1 = − 1 {displaystyle {sqrt {-1}}^{2}={sqrt {-1}}{sqrt {-1}}=-1} semblait être capricieusement incompatible avec l’identité algébrique a b = a b {displaystyle {sqrt {a}}{sqrt {b}}={sqrt {ab}}} , qui est valable pour les nombres réels non négatifs a et b , et qui a également été utilisé dans les calculs de nombres complexes avec l’un parmi a , b positif et l’autre négatif. L’utilisation incorrecte de cette identité (et de l’identité associée 1 a = 1 a {textstyle {frac {1}{sqrt {a}}}={sqrt {frac {1}{a}}}} ) dans le cas où a et b sont tous deux négatifs, même embêté Euler. Cette difficulté a finalement conduit à la convention d’utiliser le symbole spécial i à la place de − 1 {displaystyle {sqrt {-1}}} pour se prémunir contre cette erreur. ^{[ citation nécessaire ]} Même ainsi, Euler considérait qu’il était naturel d’initier les étudiants aux nombres complexes beaucoup plus tôt que nous ne le faisons aujourd’hui. Dans son manuel d’algèbre élémentaire, Elements of Algebra , il introduit ces nombres presque immédiatement, puis les utilise de manière naturelle tout au long.

Au 18e siècle, les nombres complexes ont gagné en utilisation, car on a remarqué que la manipulation formelle d’expressions complexes pouvait être utilisée pour simplifier les calculs impliquant des fonctions trigonométriques. Par exemple, en 1730, Abraham de Moivre nota que les identités compliquées reliant les fonctions trigonométriques d’un multiple entier d’un angle aux puissances des fonctions trigonométriques de cet angle pouvaient être simplement réexprimées par la formule bien connue suivante qui porte son nom, de La formule de Moivre :

( cos ⁡ θ + i sin ⁡ θ ) n = cos ⁡ n θ + i sin ⁡ n θ . {displaystyle (cos theta +isin theta )^{n}=cos ntheta +isin ntheta .}

En 1748 , Leonhard Euler va plus loin et obtient la formule d’ analyse complexe d’Euler : ^[21]

cos ⁡ θ + i sin ⁡ θ = e i θ {displaystyle cos theta +isin theta =e^{itheta }}

en manipulant formellement des séries de puissances complexes et a observé que cette formule pouvait être utilisée pour réduire toute identité trigonométrique à des identités exponentielles beaucoup plus simples.

L’idée d’un nombre complexe comme un point dans le plan complexe ( ci- dessus ) a été décrite pour la première fois par le mathématicien dano – norvégien Caspar Wessel en 1799, ^[22] bien qu’elle ait été anticipée dès 1685 dans A Treatise of Algebra de Wallis . ^[23]

Les mémoires de Wessel sont apparus dans les Actes de l’ Académie de Copenhague mais sont passés largement inaperçus. En 1806 , Jean-Robert Argand a publié indépendamment une brochure sur les nombres complexes et a fourni une preuve rigoureuse du théorème fondamental de l’algèbre . ^[24] Carl Friedrich Gauss avait publié plus tôt une preuve essentiellement topologique du théorème en 1797 mais avait exprimé ses doutes à l’époque sur “la vraie métaphysique de la racine carrée de −1”. ^[25] Ce n’est qu’en 1831 qu’il surmonte ces doutes et publie son traité sur les nombres complexes comme points dans le plan, ^[26] établissant largement la notation et la terminologie modernes : ^[27]

Si autrefois on considérait ce sujet d’un faux point de vue et qu’on y trouvait donc une obscurité mystérieuse, c’est en grande partie imputable à une terminologie maladroite. Si quelqu’un n’avait pas appelé +1, -1, − 1 {displaystyle {sqrt {-1}}} des unités positives, négatives ou imaginaires (ou même impossibles), mais plutôt, disons, des unités directes, inverses ou latérales, alors on n’aurait guère pu parler d’une telle obscurité.

Au début du XIXe siècle, d’autres mathématiciens découvrent indépendamment la représentation géométrique des nombres complexes : Buée, ^{[28] [29]} Mourey , ^[30] Warren , ^{[31] [32] [33]} Français et son frère, Bellavitis . ^{[34] [35]}

Le mathématicien anglais GH Hardy a fait remarquer que Gauss était le premier mathématicien à utiliser les nombres complexes d’une « manière vraiment confiante et scientifique », bien que des mathématiciens tels que le Norvégien Niels Henrik Abel et Carl Gustav Jacob Jacobi les utilisaient nécessairement régulièrement avant que Gauss ne publie son traité de 1831. ^[36]

Augustin Louis Cauchy et Bernhard Riemann ont amené ensemble les idées fondamentales de l’analyse complexe à un état d’achèvement élevé, commençant vers 1825 dans le cas de Cauchy.

Les termes communs utilisés dans la théorie sont principalement dus aux fondateurs. Argand a appelé cos φ + i sin φ le facteur de direction , et r = a 2 + b 2 {displaystyle r={sqrt {a^{2}+b^{2}}}} le module ; ^{[e] [37]} Cauchy (1821) appelle cos φ + i sin φ la forme réduite (l’expression réduite) ^[38] et introduit apparemment le terme argument ; Gauss a utilisé i pour − 1 {displaystyle {sqrt {-1}}} , ^[f] a introduit le terme nombre complexe pour a + bi , ^[g] et a appelé a ² + b ² la norme . ^[h] L’expression coefficient de direction , souvent utilisée pour cos φ + i sin φ , est due à Hankel (1867), ^[42] et la valeur absolue, pour le module, est due à Weierstrass.

Les écrivains classiques ultérieurs sur la théorie générale comprennent Richard Dedekind , Otto Hölder , Felix Klein , Henri Poincaré , Hermann Schwarz , Karl Weierstrass et bien d’autres. D’importants travaux (y compris une systématisation) en calcul multivarié complexe ont été lancés au début du XXe siècle. Des résultats importants ont été obtenus par Wilhelm Wirtinger en 1927.

Relations et opérations

Égalité

Les nombres complexes ont une définition similaire de l’égalité aux nombres réels ; deux nombres complexes a ₁ + b ₁ i et a ₂ + b ₂ i sont égaux si et seulement si leurs parties réelle et imaginaire sont égales, c’est-à-dire si a ₁ = a ₂ et b ₁ = b ₂ . Les nombres complexes non nuls écrits sous forme polaire sont égaux si et seulement s’ils ont la même grandeur et si leurs arguments diffèrent d’un multiple entier de 2 π .

Commande

Contrairement aux nombres réels, il n’y a pas d’ordre naturel des nombres complexes. En particulier, il n’y a pas d’ordre linéaire sur les nombres complexes compatible avec l’addition et la multiplication. Par conséquent, les nombres complexes n’ont pas la structure d’un champ ordonné. Une explication à cela est que chaque somme de carrés non triviale dans un champ ordonné est non nulle, et i ² + 1 ² = 0 est une somme de carrés non triviale. Ainsi, les nombres complexes sont naturellement considérés comme existant sur un plan bidimensionnel.

Conjuguer

Représentation géométrique de z et de son conjugué z dans le plan complexe

Le conjugué complexe du nombre complexe z = x + yi est donné par x − yi . Il est noté z ou z * . ^[43] Cette opération unaire sur les nombres complexes ne peut être exprimée en appliquant uniquement leurs opérations de base addition, soustraction, multiplication et division.

Géométriquement, z est la “réflexion” de z autour de l’axe réel. Conjuguer deux fois donne le nombre complexe d’origine

z ̄ ̄ = z , {displaystyle {overline {overline {z}}}=z,}

ce qui fait de cette opération une involution . La réflexion laisse à la fois la partie réelle et la magnitude de z inchangées, c’est-à-dire

Re ⁡ ( z ̄ ) = Re ⁡ ( z ) {displaystyle operatorname {Re} ({overline {z}})=operatorname {Re} (z)quad } et | z ̄ | = | z | . {displaystyle quad |{overline {z}}|=|z|.}

La partie imaginaire et l’argument d’un nombre complexe z changent de signe par conjugaison

Im ⁡ ( z ̄ ) = − Im ⁡ ( z ) and arg ⁡ z ̄ ≡ − arg ⁡ z ( mod 2 π ) . {displaystyle operatorname {Im} ({overline {z}})=-operatorname {Im} (z)quad {text{ and }}quad operatorname {arg} {overline {z}} equiv -nomopérateur {arg} z{pmod {2pi }}.}

Pour plus de détails sur l’argument et la magnitude, voir la section sur la forme polaire .

Le produit d’un nombre complexe z = x + yi et de son conjugué est appelé carré absolu . C’est toujours un nombre réel non négatif et égal au carré de la magnitude de chacun :

z ⋅ z ̄ = x 2 + y 2 = | z | 2 = | z ̄ | 2 . {displaystyle zcdot {overline {z}}=x^{2}+y^{2}=|z|^{2}=|{overline {z}}|^{2}.}

Cette propriété peut être utilisée pour convertir une fraction avec un dénominateur complexe en une fraction équivalente avec un dénominateur réel en développant à la fois le numérateur et le dénominateur de la fraction par le conjugué du dénominateur donné. Ce processus est parfois appelé « rationalisation » du dénominateur (bien que le dénominateur de l’expression finale puisse être un nombre réel irrationnel), car il ressemble à la méthode pour supprimer les racines d’expressions simples dans un dénominateur.

Les parties réelle et imaginaire d’un nombre complexe z peuvent être extraites à l’aide de la conjugaison :

Re ⁡ ( z ) = z + z ̄ 2 , and Im ⁡ ( z ) = z − z ̄ 2 i . {displaystyle operatorname {Re} (z)={dfrac {z+{overline {z}}}{2}},quad {text{ et }}quad operatorname {Im} (z)= {dfrac {z-{overline {z}}}{2i}}.} De plus, un nombre complexe est réel si et seulement s’il est égal à son propre conjugué.

La conjugaison se répartit sur les opérations arithmétiques complexes de base :

z ± w ̄ = z ̄ ± w ̄ , z ⋅ w ̄ = z ̄ ⋅ w ̄ , z / w ̄ = z ̄ / w ̄ . {displaystyle {begin{aligned}{overline {zpm w}}&={overline {z}}pm {overline {w}},\{overline {zcdot w}} &={overline {z}}cdot {overline {w}},\{overline {z/w}}&={overline {z}}/{overline {w}}.end {aligné}}}

La conjugaison est également employée en géométrie inversive , une branche de la géométrie étudiant les réflexions plus générales que celles autour d’une ligne. Dans l’ analyse de réseau de circuits électriques , le conjugué complexe est utilisé pour trouver l’impédance équivalente lorsque le théorème de transfert de puissance maximum est recherché.

Addition et soustraction

L’addition de deux nombres complexes peut se faire géométriquement en construisant un parallélogramme.

Deux nombres complexes a = x + y i {displaystyle a=x+yi} et b = u + v i {displaystyle b=u+vi} sont le plus facilement ajoutés en ajoutant séparément leurs parties réelles et imaginaires. C’est-à-dire:

a + b = ( x + y i ) + ( u + v i ) = ( x + u ) + ( y + v ) i . {displaystyle a+b=(x+yi)+(u+vi)=(x+u)+(y+v)i.} De même, la soustraction peut être effectuée comme a − b = ( x + y i ) − ( u + v i ) = ( x − u ) + ( y − v ) i . {displaystyle ab=(x+yi)-(u+vi)=(xu)+(yv)i.}

Multiplication d’un nombre complexe a = x + y i {displaystyle a=x+yi} et un nombre réel r peut être fait de manière similaire en multipliant séparément r et les parties réelle et imaginaire de a :

r a = r ( x + y i ) = r x + r y i . {displaystyle ra=r(x+yi)=rx+ryi.} En particulier, la soustraction peut être effectuée en annulant la soustraction (c’est-à-dire en la multipliant par –1 ) et en ajoutant le résultat à la diminuende : a − b = a + ( − 1 ) b . {displaystyle ab=a+(-1),b.}

Utilisant la visualisation des nombres complexes dans le plan complexe, l’addition a l’interprétation géométrique suivante : la somme de deux nombres complexes a et b , interprétés comme des points dans le plan complexe, est le point obtenu en construisant un parallélogramme à partir des trois sommets O , et les pointes des flèches marquées a et b (à condition qu’elles ne soient pas alignées). De manière équivalente, en appelant ces points A , B , respectivement et le quatrième point du parallélogramme X les triangles OAB et XBA sont congruents .

Multiplication et carré

Les règles de la propriété distributive , les propriétés commutatives (d’addition et de multiplication) et la propriété de définition i ² = −1 s’appliquent aux nombres complexes. Il s’ensuit que

( x + y i ) ( u + v i ) = ( x u − y v ) + ( x v + y u ) i . {displaystyle (x+yi),(u+vi)=(xu-yv)+(xv+yu)i.}

En particulier,

( x + y i ) 2 = x 2 − y 2 + 2 x y i . {displaystyle (x+yi)^{2}=x^{2}-y^{2}+2xyi.}

Réciproque et division

En utilisant la conjugaison, l’ inverse d’un nombre complexe non nul z = x + yi peut toujours être décomposé en

1 z = z ̄ z z ̄ = z ̄ | z | 2 = z ̄ x 2 + y 2 = x x 2 + y 2 − y x 2 + y 2 i , {displaystyle {frac {1}{z}}={frac {overline {z}}{z{overline {z}}}}={frac {overline {z}}{|z| ^{2}}}={frac {overline {z}}{x^{2}+y^{2}}}={frac {x}{x^{2}+y^{2} }}-{frac {y}{x^{2}+y^{2}}}i,}

puisque non nul implique que x ² + y ² est supérieur à zéro.

Cela peut être utilisé pour exprimer une division d’un nombre complexe arbitraire w = u + vi par un nombre complexe non nul z comme

w z = w ⋅ 1 z = ( u + v i ) ⋅ ( x x 2 + y 2 − y x 2 + y 2 i ) = ( u x + v y ) + ( v x − u y ) i x 2 + y 2 . {displaystyle {frac {w}{z}}=wcdot {frac {1}{z}}=(u+vi)cdot left({frac {x}{x^{2} +y^{2}}}-{frac {y}{x^{2}+y^{2}}}iright)={frac {(ux+vy)+(vx-uy)i }{x^{2}+y^{2}}}.}

Multiplication et division sous forme polaire

Multiplication de 2 + i (triangle bleu) et 3 + i (triangle rouge). Le triangle rouge est tourné pour correspondre au sommet du bleu (l’addition des deux angles dans les termes φ ₁ + φ ₂ dans l’équation) et étiré de la longueur de l’ hypoténuse du triangle bleu (la multiplication des deux rayons, selon le terme r ₁ r ₂ dans l’équation).

Les formules de multiplication, de division et d’exponentiation sont plus simples sous forme polaire que les formules correspondantes en coordonnées cartésiennes. Étant donné deux nombres complexes z ₁ = r ₁ (cos φ ₁ + i sin φ ₁ ) et z ₂ = r ₂ (cos φ ₂ + i sin φ ₂ ) , à cause des identités trigonométriques

cos ⁡ a cos ⁡ b − sin ⁡ a sin ⁡ b = cos ⁡ ( a + b ) cos ⁡ a sin ⁡ b + sin ⁡ a cos ⁡ b = sin ⁡ ( a + b ) . {displaystyle {begin{alignedat}{4}cos acos b&-sin asin b&{}={}&cos(a+b)\cos asin b&+sin a cos b&{}={}&sin(a+b).end{alignedat}}}

nous pouvons dériver

z 1 z 2 = r 1 r 2 ( cos ⁡ ( φ 1 + φ 2 ) + i sin ⁡ ( φ 1 + φ 2 ) ) . {displaystyle z_{1}z_{2}=r_{1}r_{2}(cos(varphi _{1}+varphi _{2})+isin(varphi _{1}+ varphi _{2})).} En d’autres termes, les valeurs absolues sont multipliées et les arguments sont ajoutés pour donner la forme polaire du produit. Par exemple, multiplier par i correspond à un quart de tour dans le sens inverse des aiguilles d’une montre, ce qui donne i ² = −1 . L’image de droite illustre la multiplication de ( 2 + i ) ( 3 + i ) = 5 + 5 i . {displaystyle (2+i)(3+i)=5+5i.} Puisque la partie réelle et imaginaire de 5 + 5 i sont égales, l’argument de ce nombre est de 45 degrés, ou π /4 (en radian ). D’autre part, c’est aussi la somme des angles à l’origine des triangles rouge et bleu qui sont arctan (1/3) et arctan(1/2), respectivement. Ainsi, la formule π 4 = arctan ⁡ ( 1 2 ) + arctan ⁡ ( 1 3 ) {displaystyle {frac {pi }{4}}=arctan left({frac {1}{2}}right)+arctan left({frac {1}{3}} à droite)} tient. Comme la fonction arctan peut être approximée très efficacement, des formules comme celle-ci – connues sous le nom de formules de type Machin – sont utilisées pour des approximations de haute précision de π .

De même, la division est donnée par

z 1 z 2 = r 1 r 2 ( cos ⁡ ( φ 1 − φ 2 ) + i sin ⁡ ( φ 1 − φ 2 ) ) . {displaystyle {frac {z_{1}}{z_{2}}}={frac {r_{1}}{r_{2}}}left(cos(varphi _{1}- varphi _{2})+isin(varphi _{1}-varphi _{2})right).}

Racine carrée

Les racines carrées de a + bi (avec b ≠ 0 ) sont ± ( γ + δ i ) {displaystyle pm (gamma +delta i)} , où

γ = a + a 2 + b 2 2 {displaystyle gamma ={sqrt {frac {a+{sqrt {a^{2}+b^{2}}}}{2}}}}

et

δ = ( sgn ⁡ b ) − a + a 2 + b 2 2 , {displaystyle delta =(operatorname {sgn} b){sqrt {frac {-a+{sqrt {a^{2}+b^{2}}}}{2}}},}

où sgn est la fonction signum . Cela se voit en quadrillant ± ( γ + δ i ) {displaystyle pm (gamma +delta i)} pour obtenir a + bi . ^{[44] [45]} Ici a 2 + b 2 {displaystyle {sqrt {a^{2}+b^{2}}}} est appelé le module de a + bi , et le signe de la racine carrée indique la racine carrée à partie réelle non négative, appelée racine carrée principale ; aussi a 2 + b 2 = z z ̄ , {displaystyle {sqrt {a^{2}+b^{2}}}={sqrt {z{overline {z}}}},} où z = a + bi . ^[46]

Fonction exponentielle

La fonction exponentielle exp : C → C ; z ↦ exp ⁡ z {displaystyle exp deux-points mathbb {C} to mathbb {C} ;zmapsto exp z} peut être défini pour tout nombre complexe z par la série de puissance

exp ⁡ z = ∑ n = 0 ∞ z n n ! , {displaystyle exp z=sum _{n=0}^{infty }{frac {z^{n}}{n!}},} qui a un rayon de convergence infini .

La valeur à 1 de la fonction exponentielle est le nombre d’Euler

e = exp ⁡ 1 = ∑ n = 0 ∞ 1 n ! ≈ 2.71828. {displaystyle e=exp 1=sum _{n=0}^{infty }{frac {1}{n!}}approx 2.71828.} Si z est réel, on a exp ⁡ z = e z . {displaystyle exp z=e^{z}.} La continuation analytique permet d’étendre cette égalité pour toute valeur complexe de z , et donc de définir l’exponentiation complexe de base e comme e z = exp ⁡ z . {displaystyle e^{z}=exp z.} Équation fonctionnelle

La fonction exponentielle satisfait l’ équation fonctionnelle e z + t = e z e t . {displaystyle e^{z+t}=e^{z}e^{t}.} Cela peut être prouvé soit en comparant le développement de la série de puissance des deux membres, soit en appliquant la continuation analytique à partir de la restriction de l’équation aux arguments réels.

La formule d’Euler

La formule d’Euler stipule que, pour tout nombre réel y ,

e i y = cos ⁡ y + i sin ⁡ y . {displaystyle e^{iy}=cos y+isin y.}

L’équation fonctionnelle implique donc que, si x et y sont réels, on a

e x + i y = e x ( cos ⁡ y + i sin ⁡ y ) = e x cos ⁡ y + i e x sin ⁡ y , {displaystyle e^{x+iy}=e^{x}(cos y+isin y)=e^{x}cos y+ie^{x}sin y,} qui est la décomposition de la fonction exponentielle en ses parties réelles et imaginaires.

Logarithme complexe

Dans le cas réel, le logarithme naturel peut être défini comme l’ inverse ln : R + → R ; x ↦ ln ⁡ x {displaystyle ln deux points mathbb {R} ^{+}to mathbb {R} ;xmapsto ln x} de la fonction exponentielle. Pour étendre cela au domaine complexe, on peut partir de la formule d’Euler. Cela implique que, si un nombre complexe z ∈ C × {displaystyle zin mathbb {C} ^{fois }} s’écrit sous la forme polaire

z = r ( cos ⁡ φ + i sin ⁡ φ ) {displaystyle z=r(cos varphi +isin varphi )} avec r , φ ∈ R , {displaystyle r,varphi in mathbb {R} ,} puis avec ln ⁡ z = ln ⁡ r + i φ {displaystyle ln z=ln r+ivarphi } comme logarithme complexe on a une inverse propre : exp ⁡ ln ⁡ z = exp ⁡ ( ln ⁡ r + i φ ) = r exp ⁡ i φ = r ( cos ⁡ φ + i sin ⁡ φ ) = z . {displaystyle exp ln z=exp(ln r+ivarphi )=rexp ivarphi =r(cos varphi +isin varphi )=z.}

Cependant, comme le cosinus et le sinus sont des fonctions périodiques, l’addition d’un multiple entier de 2 π à φ ne change pas z . Par exemple, e ^iπ = e ^{3 iπ} = −1 , donc iπ et 3 iπ sont des valeurs possibles pour le logarithme naturel de −1 .

Par conséquent, si le logarithme complexe ne doit pas être défini comme une fonction multivaluée

ln ⁡ z = { ln ⁡ r + i ( φ + 2 π k ) ∣ k ∈ Z } , {displaystyle ln z=left{ln r+i(varphi +2pi k)mid kin mathbb {Z} right},} il faut utiliser une coupe de branche et restreindre le codomaine , ce qui donne la fonction bijective ln : C × → R + + i ( − π , π ] . {displaystyle ln colon ;mathbb {C} ^{times };to ;;;mathbb {R} ^{+}+;i,left(-pi ,pi droite].}

Si z ∈ C ∖ ( − R ≥ 0 ) {displaystyle zin mathbb {C} setminus left(-mathbb {R} _{geq 0}right)} n’est pas un nombre réel non positif (un nombre positif ou non réel), la valeur principale résultante du logarithme complexe est obtenue avec − π < φ < π . C’est une fonction analytique en dehors des nombres réels négatifs, mais elle ne peut pas être prolongée en une fonction continue à tout nombre réel négatif z ∈ − R + {displaystyle zin -mathbb {R} ^{+}} , où la valeur principale est ln z = ln(− z ) + iπ . ^[je]

Exponentation

Si x > 0 est réel et z complexe, l’exponentiation est définie comme

x z = e z ln ⁡ x , {displaystyle x^{z}=e^{zln x},} où ln désigne le logarithme népérien.

Il semble naturel d’étendre cette formule à des valeurs complexes de x , mais il y a quelques difficultés résultant du fait que le logarithme complexe n’est pas vraiment une fonction, mais une fonction multivaluée .

Il s’ensuit que si z est comme ci-dessus, et si t est un autre nombre complexe, alors l’ exponentiation est la fonction multivaluée

z t = { e t ln ⁡ r ( cos ⁡ ( φ t + 2 π k t ) + i sin ⁡ ( φ t + 2 π k t ) ) } ∣ k ∈ Z } {displaystyle z^{t}=left{e^{tln r},(cos(varphi t+2pi kt)+isin(varphi t+2pi kt) )}mid kin mathbb {Z} right}} Exposants entiers et fractionnaires Représentation géométrique des racines 2ème à 6ème d’un nombre complexe z , sous forme polaire re ^iφ où r = | z | et φ = arg z . Si z est réel, φ = 0 ou π . Les racines principales sont représentées en noir.

Si, dans la formule précédente, t est un entier, alors le sinus et le cosinus sont indépendants de k . Ainsi, si l’exposant n est un entier, alors z ⁿ est bien défini, et la formule d’exponentiation se simplifie en la formule de de Moivre :

z n = ( r ( cos ⁡ φ + i sin ⁡ φ ) ) n = r n ( cos ⁡ n φ + i sin ⁡ n φ ) . {displaystyle z^{n}=(r(cos varphi +isin varphi ))^{n}=r^{n},(cos nvarphi +isin nvarphi ) .}

Les n n ièmes racines d’un nombre complexe z sont données par

z 1 / n = r n ( cos ⁡ ( φ + 2 k π n ) + i sin ⁡ ( φ + 2 k π n ) ) {displaystyle z^{1/n}={sqrt[{n}]{r}}left(cos left({frac {varphi +2kpi }{n}}right)+ isin left({frac {varphi +2kpi }{n}}right)right)} pour 0 ≤ k ≤ n − 1 . (Ici r n {displaystyle {sqrt[{n}]{r}}} est la n ième racine habituelle (positive) du nombre réel positif r .) Parce que le sinus et le cosinus sont périodiques, les autres valeurs entières de k ne donnent pas d’autres valeurs.

Alors que la n ième racine d’un nombre réel positif r est choisie comme étant le nombre réel positif c satisfaisant c ⁿ = r , il n’existe aucun moyen naturel de distinguer une n ième racine complexe particulière d’un nombre complexe. Par conséquent, la n ième racine est une fonction à n valeurs de z . Cela implique que, contrairement au cas des nombres réels positifs, on a

( z n ) 1 / n ≠ z , {displaystyle (z^{n})^{1/n}neq z,} puisque le côté gauche est constitué de n valeurs et que le côté droit est une valeur unique.

Propriétés

Structuration du champ

L’ensemble C {displaystyle mathbb {C} } de nombres complexes est un champ . ^[47] Brièvement, cela signifie que les faits suivants sont valables : premièrement, deux nombres complexes peuvent être additionnés et multipliés pour donner un autre nombre complexe. Deuxièmement, pour tout nombre complexe z , son inverse additif – z est également un nombre complexe ; et troisièmement, chaque nombre complexe différent de zéro a un nombre complexe réciproque . De plus, ces opérations satisfont à un certain nombre de lois, par exemple la loi de commutativité de l’addition et de la multiplication pour deux nombres complexes quelconques z ₁ et z ₂ :

z 1 + z 2 = z 2 + z 1 , z 1 z 2 = z 2 z 1 . {displaystyle {begin{aligned}z_{1}+z_{2}&=z_{2}+z_{1},\z_{1}z_{2}&=z_{2}z_{1} .end{aligné}}} Ces deux lois et les autres exigences sur un champ peuvent être prouvées par les formules données ci-dessus, en utilisant le fait que les nombres réels eux-mêmes forment un champ.

Contrairement aux réels, C {displaystyle mathbb {C} } n’est pas un corps ordonné , c’est-à-dire qu’il n’est pas possible de définir une relation z ₁ < z ₂ compatible avec l’addition et la multiplication. En fait, dans tout corps ordonné, le carré de tout élément est nécessairement positif, donc i ² = −1 exclut l’existence d’un ordre sur C . {displaystyle mathbb{C} .} ^[48]

Lorsque le champ sous-jacent d’un sujet ou d’une construction mathématique est le champ des nombres complexes, le nom du sujet est généralement modifié pour refléter ce fait. Par exemple : analyse complexe , matrice complexe , polynôme complexe et algèbre de Lie complexe .

Solutions d’équations polynomiales

Étant donné tous les nombres complexes (appelés coefficients ) a ₀ , …, a _n , l’équation

a n z n + ⋯ + a 1 z + a 0 = 0 {displaystyle a_{n}z^{n}+dotsb +a_{1}z+a_{0}=0} a au moins une solution complexe z , à condition qu’au moins un des coefficients supérieurs a ₁ , …, a _n soit non nul. ^[6] C’est l’énoncé du théorème fondamental de l’algèbre , de Carl Friedrich Gauss et Jean le Rond d’Alembert . A cause de ce fait, C {displaystyle mathbb {C} } est appelé corps algébriquement clos . Cette propriété n’est pas valable pour le corps des nombres rationnels Q {displaystyle mathbb {Q}} (le polynôme x ² − 2 n’a pas de racine rationnelle, puisque √2 n’est pas un nombre rationnel) ni les nombres réels R {displaystyle mathbb {R} } (le polynôme x ² + a n’a pas de racine réelle pour a > 0 , puisque le carré de x est positif pour tout nombre réel x ).

Il existe différentes preuves de ce théorème, soit par des méthodes analytiques comme le théorème de Liouville , soit par des méthodes topologiques comme le nombre d’enroulement , soit par une preuve combinant la théorie de Galois et le fait que tout polynôme réel de degré impair a au moins une racine réelle.

De ce fait, les théorèmes valables pour tout champ algébriquement clos s’appliquent à C . {displaystyle mathbb{C} .} Par exemple, toute matrice carrée complexe non vide a au moins une valeur propre (complexe) .

Caractérisation algébrique

Le champ C {displaystyle mathbb {C} } possède les trois propriétés suivantes :

• Premièrement, il a la caractéristique 0. Cela signifie que 1 + 1 + ⋯ + 1 ≠ 0 pour n’importe quel nombre de sommations (toutes égales à un).
• Deuxièmement, son degré de transcendance sur Q {displaystyle mathbb {Q}} , le champ principal de C , {displaystyle mathbb{C} ,} est la cardinalité du continuum .
• Troisièmement, il est algébriquement clos (voir ci-dessus).

On peut montrer que tout champ ayant ces propriétés est isomorphe (en tant que champ) à C . {displaystyle mathbb{C} .} Par exemple, la clôture algébrique du champ Q p {displaystyle mathbb {Q} _{p}} du nombre p -adique satisfait aussi ces trois propriétés, donc ces deux champs sont isomorphes (en tant que champs, mais pas en tant que champs topologiques). ^[49] Aussi, C {displaystyle mathbb {C} } est isomorphe au domaine des séries de Puiseux complexes . Cependant, la spécification d’un isomorphisme nécessite l’ axiome de choix . Une autre conséquence de cette caractérisation algébrique est que C {displaystyle mathbb {C} } contient de nombreux sous-champs propres qui sont isomorphes à C {displaystyle mathbb {C} } .

Caractérisation en tant que champ topologique

La caractérisation précédente de C {displaystyle mathbb {C} } ne décrit que les aspects algébriques de C . {displaystyle mathbb{C} .} C’est-à-dire que les propriétés de proximité et de continuité , qui comptent dans des domaines tels que l’analyse et la topologie , ne sont pas traitées. La description suivante de C {displaystyle mathbb {C} } car un champ topologique (c’est-à-dire un champ muni d’une topologie , ce qui permet la notion de convergence) prend en compte les propriétés topologiques. C {displaystyle mathbb {C} } contient un sous-ensemble P (à savoir l’ensemble des nombres réels positifs) d’éléments non nuls satisfaisant les trois conditions suivantes :

• P est fermé par addition, multiplication et prise d’inverses.
• Si x et y sont des éléments distincts de P , alors soit x − y soit y − x est dans P .
• Si S est un sous-ensemble non vide de P , alors S + P = x + P pour un certain x dans C . {displaystyle mathbb{C} .}

En outre, C {displaystyle mathbb {C} } a un automorphisme involutif non trivial x ↦ x * (à savoir la conjugaison complexe), tel que x x * est dans P pour tout x non nul dans C . {displaystyle mathbb{C} .}

Tout champ F possédant ces propriétés peut être doté d’une topologie en prenant les ensembles B ( x , p ) = { y | p − ( y − x )( y − x )* ∈ P } comme base , où x s’étend sur le champ et p s’étend sur P . Avec cette topologie F est isomorphe en tant que champ topologique à C . {displaystyle mathbb{C} .}

Les seuls champs topologiques localement compacts connectés sont R {displaystyle mathbb {R} } et C . {displaystyle mathbb{C} .} Cela donne une autre caractérisation de C {displaystyle mathbb {C} } comme champ topologique, puisque C {displaystyle mathbb {C} } peut être distingué de R {displaystyle mathbb {R} } parce que les nombres complexes non nuls sont connectés , alors que les nombres réels non nuls ne le sont pas. ^[50]

Construction formelle

Construction par paires ordonnées

William Rowan Hamilton a introduit l’approche pour définir l’ensemble C {displaystyle mathbb {C} } des nombres complexes ^[51] comme l’ensemble R 2 {displaystyle mathbb {R} ^{2}} de couples ordonnés ( a , b ) de nombres réels, dans lesquels les règles d’addition et de multiplication suivantes sont imposées : ^[47]

( a , b ) + ( c , d ) = ( a + c , b + d ) ( a , b ) ⋅ ( c , d ) = ( a c − b d , b c + a d ) . {displaystyle {begin{aligned}(a,b)+(c,d)&=(a+c,b+d)\(a,b)cdot (c,d)&=(ac- bd,bc+ad).end{aligné}}}

C’est alors juste une question de notation pour exprimer ( a , b ) comme a + bi .

Construction comme champ de quotient

Bien que cette construction de bas niveau décrive avec précision la structure des nombres complexes, la définition équivalente suivante révèle la nature algébrique de C {displaystyle mathbb {C} } plus immédiatement. Cette caractérisation repose sur la notion de champs et de polynômes. Un champ est un ensemble doté d’opérations d’addition, de soustraction, de multiplication et de division qui se comportent de la manière habituelle, disons, des nombres rationnels. Par exemple, la loi distributive

( x + y ) z = x z + y z {displaystyle (x+y)z=xz+yz} doit être valable pour trois éléments x , y et z d’un champ. L’ensemble R {displaystyle mathbb {R} } de nombres réels forme un champ. Un polynôme p ( X ) à coefficients réels est une expression de la forme a n X n + ⋯ + a 1 X + a 0 , {displaystyle a_{n}X^{n}+dotsb +a_{1}X+a_{0},} où les a ₀ , …, a _n sont des nombres réels. L’addition et la multiplication habituelles de polynômes confèrent à l’ensemble R [ X ] {displaystyle mathbb {R} [X]} de tous ces polynômes avec une structure en anneau . Cet anneau s’appelle l’ anneau polynomial sur les nombres réels.

L’ensemble des nombres complexes est défini comme l’ anneau quotient R [ X ] / ( X 2 + 1 ) . {displaystyle mathbb {R} [X]/(X^{2}+1).} ^[6] Ce champ d’extension contient deux racines carrées de −1 , à savoir (les cosets de) X et − X , respectivement. (Les cosets de) 1 et X forment une base de R {displaystyle mathbb {R} } [ X ]/( X ² + 1) comme un espace vectoriel réel , ce qui signifie que chaque élément du champ d’extension peut être écrit de manière unique comme une combinaison linéaire dans ces deux éléments. De manière équivalente, les éléments du champ d’extension peuvent être écrits sous forme de paires ordonnées ( a , b ) de nombres réels. L’anneau quotient est un corps, car X ² + 1 est irréductible sur R , { displaystyle mathbb {R} ,} donc l’idéal qu’il génère est maximal .

Les formules d’addition et de multiplication dans l’anneau R [ X ] , {displaystyle mathbb {R} [X],} modulo la relation X ² = −1 , correspondent aux formules d’addition et de multiplication de nombres complexes définis comme des couples ordonnés. Donc les deux définitions du champ C {displaystyle mathbb {C} } sont isomorphes (comme des champs).

Accepter que C {displaystyle mathbb {C} } est algébriquement clos, puisque c’est une extension algébrique de R {displaystyle mathbb {R} } dans cette démarche, C {displaystyle mathbb {C} } est donc la clôture algébrique de R . {displaystyle mathbb{R} .}

Représentation matricielle des nombres complexes

Les nombres complexes a + bi peuvent aussi être représentés par des matrices 2 × 2 de la forme :

( a − b b a ) {displaystyle {begin{pmatrix}a&-b\b&;;aend{pmatrix}}} Ici, les entrées a et b sont des nombres réels. Comme la somme et le produit de deux de ces matrices sont à nouveau de cette forme, ces matrices forment un sous- anneau de l’anneau 2 × 2 matrices.

Un simple calcul montre que la carte :

a + i b ↦ ( a − b b a ) {displaystyle a+ibmapsto {begin{pmatrix}a&-b\b&;;aend{pmatrix}}} est un isomorphisme en anneau du corps des nombres complexes à l’anneau de ces matrices. Cet isomorphisme associe le carré de la valeur absolue d’un nombre complexe au déterminant de la matrice correspondante, et le conjugué d’un nombre complexe à la transposée de la matrice.

La description géométrique de la multiplication des nombres complexes peut également être exprimée en termes de matrices de rotation en utilisant cette correspondance entre les nombres complexes et ces matrices. L’action de la matrice sur un vecteur ( x , y ) correspond à la multiplication de x + iy par a + ib . En particulier, si le déterminant est 1 , il existe un nombre réel t tel que la matrice ait la forme :

( cos ⁡ t − sin ⁡ t sin ⁡ t cos ⁡ t ) {displaystyle {begin{pmatrix}cos t&-sin t\sin t&;;cos tend{pmatrix}}} Dans ce cas, l’action de la matrice sur les vecteurs et la multiplication par le nombre complexe cos ⁡ t + i sin ⁡ t {displaystyle cos t+isin t} sont à la fois la rotation de l’angle t .

Analyse complexe

Graphique de la roue chromatique de sin(1/ z ) . Les parties noires à l’intérieur font référence à des nombres ayant de grandes valeurs absolues.

L’étude des fonctions d’une variable complexe est connue sous le nom d’ analyse complexe et a une énorme utilité pratique en mathématiques appliquées ainsi que dans d’autres branches des mathématiques. Souvent, les preuves les plus naturelles des déclarations en analyse réelle ou même en théorie des nombres utilisent des techniques d’analyse complexe (voir le théorème des nombres premiers pour un exemple). Contrairement aux fonctions réelles, qui sont généralement représentées sous forme de graphiques à deux dimensions, les fonctions complexes ont des graphiques à quatre dimensions et peuvent être utilement illustrées par un codage couleur d’un graphique à trois dimensions. pour suggérer quatre dimensions, ou en animant la transformation dynamique de la fonction complexe du avion complexe.

Fonctions exponentielles complexes et fonctions connexes

Les notions de séries convergentes et de fonctions continues en analyse (réelle) ont des analogues naturels en analyse complexe. Une suite de nombres complexes est dite converger si et seulement si ses parties réelle et imaginaire le font. Ceci est équivalent à la (ε, δ)-définition des limites , où la valeur absolue des nombres réels est remplacée par celle des nombres complexes. D’un point de vue plus abstrait, C {displaystyle mathbb {C} } , muni de la métrique

d ⁡ ( z 1 , z 2 ) = | z 1 − z 2 | {displaystyle operatorname {d} (z_{1},z_{2})=|z_{1}-z_{2}|} est un espace métrique complet , qui inclut notamment l’ inégalité triangulaire | z 1 + z 2 | ≤ | z 1 | + | z 2 | {displaystyle |z_{1}+z_{2}|leq |z_{1}|+|z_{2}|} pour deux nombres complexes quelconques z ₁ et z ₂ .

Comme en analyse réelle, cette notion de convergence est utilisée pour construire un certain nombre de fonctions élémentaires : la fonction exponentielle exp z , également notée e ^z , est définie comme la série infinie

exp ⁡ z := 1 + z + z 2 2 ⋅ 1 + z 3 3 ⋅ 2 ⋅ 1 + ⋯ = ∑ n = 0 ∞ z n n ! . {displaystyle exp z :=1+z+{frac {z^{2}}{2cdot 1}}+{frac {z^{3}}{3cdot 2cdot 1}}+ cdots =sum _{n=0}^{infty }{frac {z^{n}}{n!}}.}

Les séries définissant les fonctions trigonométriques réelles sinus et cosinus , ainsi que les fonctions hyperboliques sinh et cosh, sont également reportées sur des arguments complexes sans changement. Pour les autres fonctions trigonométriques et hyperboliques, telles que tangente , les choses sont légèrement plus compliquées, car les séries de définition ne convergent pas pour toutes les valeurs complexes. Il faut donc les définir soit en termes de sinus, cosinus et exponentielle, soit, de manière équivalente, en utilisant la méthode de continuation analytique .

La formule d’Euler indique :

exp ⁡ ( i φ ) = cos ⁡ φ + i sin ⁡ φ {displaystyle exp(ivarphi )=cos varphi +isin varphi } pour tout nombre réel φ , en particulier exp ⁡ ( i π ) = − 1 {displaystyle exp(jepi)=-1} , qui est l’identité d’Euler . Contrairement à la situation des nombres réels, il existe une infinité de solutions complexes z de l’équation exp ⁡ z = w {displaystyle exp z=w} pour tout nombre complexe w ≠ 0 . On peut montrer que toute solution de ce type z – appelée logarithme complexe de w – satisfait log ⁡ w = ln ⁡ | w | + i arg ⁡ w , {displaystyle log w=ln |w|+iarg w,} où arg est l’ argument défini ci- dessus , et ln le (réel) logarithme népérien . Comme arg est une fonction multivaluée , unique uniquement jusqu’à un multiple de 2 π , log est également multivalué. La valeur principale de log est souvent prise en restreignant la partie imaginaire à l’ intervalle (− π , π ] .

L’ exponentiation complexe z ^ω est définie comme

z ω = exp ⁡ ( ω log ⁡ z ) , {displaystyle z^{omega }=exp(omega log z),} et est à plusieurs valeurs, sauf lorsque ω est un entier. Pour ω = 1 / n , pour un entier naturel n , cela récupère la non-unicité de n ièmes racines mentionnée ci-dessus.

Les nombres complexes, contrairement aux nombres réels, ne satisfont pas en général les identités de puissance et de logarithme non modifiées, en particulier lorsqu’ils sont naïvement traités comme des fonctions à valeur unique ; voir échec des identités de puissance et de logarithme . Par exemple, ils ne satisfont pas

a b c = ( a b ) c . {displaystyle a^{bc}=left(a^{b}right)^{c}.} Les deux côtés de l’équation sont multivalués par la définition de l’exponentiation complexe donnée ici, et les valeurs de gauche sont un sous-ensemble de celles de droite.

Fonctions holomorphes

Une fonction f : C {displaystyle mathbb {C} } → C {displaystyle mathbb {C} } est dit holomorphe s’il satisfait les équations de Cauchy-Riemann . Par exemple, n’importe quel R {displaystyle mathbb {R} } -carte linéaire C {displaystyle mathbb {C} } → C {displaystyle mathbb {C} } peut s’écrire sous la forme

f ( z ) = a z + b z ̄ {displaystyle f(z)=az+b{overline {z}}} avec des coefficients complexes a et b . Cette application est holomorphe si et seulement si b = 0 . Le deuxième somme b z ̄ {displaystyle b{overline {z}}} est réel différentiable, mais ne satisfait pas les équations de Cauchy-Riemann .

L’analyse complexe montre certaines caractéristiques qui ne sont pas apparentes dans une analyse réelle. Par exemple, deux fonctions holomorphes f et g qui s’accordent sur un sous- ensemble ouvert arbitrairement petit de C {displaystyle mathbb {C} } forcément d’accord partout. Les fonctions méromorphes , fonctions qui peuvent localement être écrites comme f ( z )/( z − z ₀ ) ⁿ avec une fonction holomorphe f , partagent encore certaines des caractéristiques des fonctions holomorphes. D’autres fonctions ont des singularités essentielles , telles que sin(1/ z ) à z = 0 .

Applications

Les nombres complexes ont des applications dans de nombreux domaines scientifiques, notamment le traitement du signal , la théorie du contrôle , l ‘ électromagnétisme , la dynamique des fluides , la mécanique quantique , la cartographie et l’analyse des vibrations . Certaines de ces applications sont décrites ci-dessous.

Géométrie

Formes

Trois points non colinéaires u , v , w {displaystyle u,v,w} dans le plan déterminer la forme du triangle { u , v , w } {style d’affichage {u,v,w}} . En localisant les points dans le plan complexe, cette forme de triangle peut être exprimée par l’arithmétique complexe comme

S ( u , v , w ) = u − w u − v . {displaystyle S(u,v,w)={frac {uw}{uv}}.} La forme S {displaystyle S} d’un triangle restera le même, lorsque le plan complexe est transformé par translation ou dilatation (par une transformation affine ), correspondant à la notion intuitive de forme, et décrivant la similarité . Ainsi chaque triangle { u , v , w } {style d’affichage {u,v,w}} est dans une classe de similarité de triangles de même forme. ^[52] Géométrie fractale L’ensemble Mandelbrot avec les axes réels et imaginaires étiquetés.

L’ ensemble de Mandelbrot est un exemple populaire de fractale formée sur le plan complexe. Il est défini en traçant chaque emplacement c {displaystyle c} où l’itération de la séquence f c ( z ) = z 2 + c {displaystyle f_{c}(z)=z^{2}+c} ne diverge pas lorsqu’il est itéré à l’infini. De même, les ensembles de Julia ont les mêmes règles, sauf où c {displaystyle c} reste constant.

Triangles

Chaque triangle a une inellipse de Steiner unique – une ellipse à l’intérieur du triangle et tangente aux milieux des trois côtés du triangle. Les foyers de l’ellipse de Steiner d’un triangle peuvent être trouvés comme suit, selon le théorème de Marden : ^{[53] [54]} Notons les sommets du triangle dans le plan complexe comme a = x _A + y _A i , b = x _B + y _B i , et c = x _C + y _C je. Écrire l’ équation cubique ( x − a ) ( x − b ) ( x − c ) = 0 {displaystyle (xa)(xb)(xc)=0} , prenez sa dérivée, et égalisez la dérivée (quadratique) à zéro. Le théorème de Marden dit que les solutions de cette équation sont les nombres complexes indiquant les emplacements des deux foyers de l’ellipse de Steiner.

Théorie algébrique des nombres

Construction d’un pentagone régulier à la règle et au compas .

Comme mentionné ci-dessus, toute équation polynomiale non constante (en coefficients complexes) a une solution dans C {displaystyle mathbb {C} } . A fortiori , il en est de même si l’équation a des coefficients rationnels. Les racines de telles équations sont appelées nombres algébriques – elles sont un objet principal d’étude dans la théorie algébrique des nombres . Par rapport à Q ̄ {displaystyle {overline {mathbb {Q}}}} , la clôture algébrique de Q {displaystyle mathbb {Q}} , qui contient également tous les nombres algébriques, C {displaystyle mathbb {C} } a l’avantage d’être facilement compréhensible en termes géométriques. De cette façon, les méthodes algébriques peuvent être utilisées pour étudier des questions géométriques et vice versa. Avec des méthodes algébriques, appliquant plus spécifiquement la machinerie de la théorie des champs au corps de nombres contenant les racines de l’unité , on peut montrer qu’il n’est pas possible de construire un nonagone régulier en utilisant uniquement le compas et la règle – un problème purement géométrique.

Un autre exemple est les entiers gaussiens ; c’est-à-dire des nombres de la forme x + iy , où x et y sont des nombres entiers, qui peuvent être utilisés pour classer des sommes de carrés .

Théorie analytique des nombres

La théorie analytique des nombres étudie les nombres, souvent entiers ou rationnels, en tirant parti du fait qu’ils peuvent être considérés comme des nombres complexes, dans lesquels des méthodes analytiques peuvent être utilisées. Cela se fait en encodant des informations théoriques sur les nombres dans des fonctions à valeurs complexes. Par exemple, la fonction zêta de Riemann ζ( s ) est liée à la distribution des nombres premiers .

Intégrales incorrectes

Dans les domaines appliqués, les nombres complexes sont souvent utilisés pour calculer certaines intégrales impropres à valeurs réelles , au moyen de fonctions à valeurs complexes. Plusieurs méthodes existent pour ce faire; voir méthodes d’intégration des contours .

Équations dynamiques

Dans les équations différentielles , il est courant de trouver d’ abord toutes les racines complexes r de l ‘ équation caractéristique d’ une équation différentielle linéaire ou d’ un système d’ équations , puis de tenter de résoudre le système en termes de fonctions de base de la forme f ( t ) = e ^rt . De même, dans les équations aux différences , les racines complexes r de l’équation caractéristique du système d’équations aux différences sont utilisées pour tenter de résoudre le système en termes de fonctions de base de la forme f ( t ) = r ^t .

Algèbre linéaire

La décomposition propre est un outil utile pour calculer les puissances matricielles et les exponentielles matricielles . Cependant, il nécessite souvent l’utilisation de nombres complexes, même si la matrice est réelle (par exemple, une matrice de rotation ).

Les nombres complexes généralisent souvent des concepts conçus à l’origine dans les nombres réels. Par exemple, la transposée conjuguée généralise la transposée , les matrices hermitiennes généralisent les matrices symétriques et les matrices unitaires généralisent les matrices orthogonales .

En mathématiques appliquées

Théorie du contrôle

Dans la théorie du contrôle , les systèmes sont souvent transformés du domaine temporel au domaine fréquentiel complexe à l’aide de la transformée de Laplace . Les zéros et les pôles du système sont ensuite analysés dans le plan complexe . Les techniques du locus racine , du diagramme de Nyquist et du diagramme de Nichols utilisent toutes le plan complexe.

Dans la méthode du locus racine, il est important que les zéros et les pôles se trouvent dans les demi-plans gauche ou droit, c’est-à-dire qu’ils aient une partie réelle supérieure ou inférieure à zéro. Si un système linéaire invariant dans le temps (LTI) a des pôles qui sont

• dans le demi-plan droit, il sera instable ,
• le tout dans le demi-plan gauche, ce sera stable ,
• sur l’axe imaginaire, il aura une stabilité marginale .

Si un système a des zéros dans le demi-plan droit, il s’agit d’un système à phase non minimale .

Analyse des signaux

Les nombres complexes sont utilisés dans l’analyse des signaux et dans d’autres domaines pour une description pratique des signaux variant périodiquement. Pour des fonctions réelles données représentant des quantités physiques réelles, souvent en termes de sinus et de cosinus, on considère des fonctions complexes correspondantes dont les parties réelles sont les quantités d’origine. Pour une onde sinusoïdale d’une fréquence donnée , la valeur absolue | z | du z correspondant est l’ amplitude et l’ argument arg z est la phase .

Si l’analyse de Fourier est utilisée pour écrire un signal à valeur réelle donné comme une somme de fonctions périodiques, ces fonctions périodiques sont souvent écrites comme des fonctions à valeurs complexes de la forme

x ( t ) = Re ⁡ { X ( t ) } {displaystyle x(t)=operatorname {Re} {X(t)}}

et

X ( t ) = A e i ω t = a e i φ e i ω t = a e i ( ω t + φ ) {displaystyle X(t)=Ae^{iomega t}=ae^{iphi }e^{iomega t}=ae^{i(omega t+phi )}}

où ω représente la fréquence angulaire et le nombre complexe A code la phase et l’amplitude comme expliqué ci-dessus.

Cette utilisation est également étendue au traitement numérique du signal et au traitement numérique des images , qui utilisent des versions numériques de l’analyse de Fourier (et de l’analyse par ondelettes ) pour transmettre, compresser , restaurer et autrement traiter les signaux audio numériques , les images fixes et les signaux vidéo .

Un autre exemple, pertinent pour les deux bandes latérales de modulation d’amplitude de la radio AM, est :

cos ⁡ ( ( ω + α ) t ) + cos ⁡ ( ( ω − α ) t ) = Re ⁡ ( e i ( ω + α ) t + e i ( ω − α ) t ) = Re ⁡ ( ( e i α t + e − i α t ) ⋅ e i ω t ) = Re ⁡ ( 2 cos ⁡ ( α t ) ⋅ e i ω t ) = 2 cos ⁡ ( α t ) ⋅ Re ⁡ ( e i ω t ) = 2 cos ⁡ ( α t ) ⋅ cos ⁡ ( ω t ) . {displaystyle {begin{aligned}cos((omega +alpha )t)+cos left((omega -alpha )tright)&=operatorname {Re} left(e^ {i(omega +alpha )t}+e^{i(omega -alpha )t}right)\&=operatorname {Re} left(left(e^{ialpha t }+e^{-ialpha t}right)cdot e^{iomega t}right)\&=operatorname {Re} left(2cos(alpha t)cdot e ^{iomega t}right)\&=2cos(alpha t)cdot operatorname {Re} left(e^{iomega t}right)\&=2cos (alpha t)cdot cos left(omega tright).end{aligned}}}

En physique

Électromagnétisme et génie électrique

En génie électrique , la transformée de Fourier est utilisée pour analyser des tensions et des courants variables . Le traitement des résistances , des condensateurs et des inducteurs peut alors être unifié en introduisant des résistances imaginaires dépendant de la fréquence pour les deux derniers et en combinant les trois en un seul nombre complexe appelé l’ impédance . Cette approche est appelée calcul de phaseur .

En génie électrique, l’unité imaginaire est notée j , pour éviter toute confusion avec I , qui est généralement utilisé pour désigner le courant électrique , ou, plus particulièrement, i , qui est généralement utilisé pour désigner le courant électrique instantané.

Étant donné que la tension dans un circuit alternatif oscille, elle peut être représentée comme

V ( t ) = V 0 e j ω t = V 0 ( cos ⁡ ω t + j sin ⁡ ω t ) , {displaystyle V(t)=V_{0}e^{jomega t}=V_{0}left(cos omega t+jsin omega tright),}

Pour obtenir la grandeur mesurable, on prend la partie réelle :

v ( t ) = Re ⁡ ( V ) = Re ⁡ [ V 0 e j ω t ] = V 0 cos ⁡ ω t . {displaystyle v(t)=operatorname {Re} (V)=operatorname {Re} left[V_{0}e^{jomega t}right]=V_{0}cos omega t .}

Le signal à valeur complexe V ( t ) est appelé la représentation analytique du signal mesurable à valeur réelle v ( t ) . ^[55]

Dynamique des fluides

En dynamique des fluides , des fonctions complexes sont utilisées pour décrire l’ écoulement potentiel en deux dimensions .

Mécanique quantique

Le champ des nombres complexes est intrinsèque aux formulations mathématiques de la mécanique quantique , où les espaces de Hilbert complexes fournissent le contexte d’une telle formulation qui est pratique et peut-être la plus standard. Les formules de base originales de la mécanique quantique – l’ équation de Schrödinger et la mécanique matricielle de Heisenberg – utilisent des nombres complexes.

Relativité

En relativité restreinte et générale , certaines formules de la métrique sur l’ espace-temps deviennent plus simples si l’on considère que la composante temporelle du continuum de l’espace-temps est imaginaire. (Cette approche n’est plus standard en relativité classique, mais est utilisée de manière essentielle dans la théorie quantique des champs .) Les nombres complexes sont essentiels aux spineurs , qui sont une généralisation des tenseurs utilisés en relativité.

Généralisations et notions associées

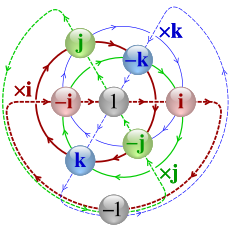
Graphique de quaternion de Cayley Q8 montrant des cycles de multiplication par i , j et k

Le processus d’extension du champ R {displaystyle mathbb {R} } de réels à C {displaystyle mathbb {C} } est connue sous le nom de construction de Cayley-Dickson . Il peut être porté plus loin à des dimensions plus élevées, donnant les quaternions H {displaystyle mathbb {H} } et octonions O {displaystyle mathbb {O}} qui (en tant qu’espace vectoriel réel) sont respectivement de dimension 4 et 8. Dans ce contexte, les nombres complexes ont été appelés les binarions . ^[56]

Tout comme en appliquant la construction aux réels, la propriété d’ ordonner est perdue, les propriétés familières des nombres réels et complexes disparaissent avec chaque extension. Les quaternions perdent la commutativité, c’est-à-dire x · y ≠ y · x pour certains quaternions x , y , et la multiplication des octonions , en plus de ne pas être commutative, n’est pas associative : ( x · y )· z ≠ x ·( y · z ) pour certains octonions x , y, z .

Les réels, les nombres complexes, les quaternions et les octonions sont tous des algèbres de division normées sur R {displaystyle mathbb {R} } . D’ après le théorème de Hurwitz, ils sont les seuls ; les sedenions , la prochaine étape de la construction Cayley-Dickson, n’ont pas cette structure.

La construction de Cayley-Dickson est étroitement liée à la représentation régulière de C , {displaystyle mathbb{C} ,} pensé comme un R {displaystyle mathbb {R} } – l’algèbre (un R {displaystyle mathbb {R} } -espace vectoriel avec une multiplication), par rapport à la base (1, i ) . Cela signifie ce qui suit : le R {displaystyle mathbb {R} } -carte linéaire

C → C z ↦ w z {displaystyle {begin{aligned}mathbb {C} &rightarrow mathbb {C} \z&mapsto wzend{aligned}}} pour un certain nombre complexe fixe, w peut être représenté par une matrice 2 × 2 (une fois qu’une base a été choisie). Par rapport à la base (1, i ) , cette matrice est ( Re ⁡ ( w ) − Im ⁡ ( w ) Im ⁡ ( w ) Re ⁡ ( w ) ) , {displaystyle {begin{pmatrix}operatorname {Re} (w)&-operatorname {Im} (w)\operatorname {Im} (w)&operatorname {Re} (w)end{pmatrix }},} c’est-à-dire celui mentionné dans la section sur la représentation matricielle des nombres complexes ci-dessus. Bien qu’il s’agisse d’une représentation linéaire de C {displaystyle mathbb {C} } dans les matrices réelles 2 × 2, ce n’est pas la seule. N’importe quelle matrice J = ( p q r − p ) , p 2 + q r + 1 = 0 {displaystyle J={begin{pmatrix}p&q\r&-pend{pmatrix}},quad p^{2}+qr+1=0} a la propriété que son carré est le négatif de la matrice identité : J ² = − I . Puis { z = a I + b J : a , b ∈ R } {displaystyle {z=aI+bJ:a,bin mathbb {R} }} est aussi isomorphe au champ C , {displaystyle mathbb{C} ,} et donne une structure complexe alternative sur R 2 . {displaystyle mathbb{R} ^{2}.} Ceci est généralisé par la notion de structure complexe linéaire .

Les nombres hypercomplexes se généralisent aussi R , { displaystyle mathbb {R} ,} C , {displaystyle mathbb{C} ,} H , {displaystyle mathbb{H} ,} et O . {displaystyle mathbb{O} .} Par exemple, cette notion contient les nombres complexes scindés , qui sont des éléments de l’anneau R [ x ] / ( x 2 − 1 ) {displaystyle mathbb {R} [x]/(x^{2}-1)} (par opposition à R [ x ] / ( x 2 + 1 ) {displaystyle mathbb {R} [x]/(x^{2}+1)} pour les nombres complexes). Dans cet anneau, l’équation a ² = 1 a quatre solutions.

Le champ R {displaystyle mathbb {R} } est l’achèvement de Q , {displaystyle mathbb {Q} ,} le corps des nombres rationnels , par rapport à la métrique usuelle des valeurs absolues . Autres choix de métriques sur Q {displaystyle mathbb {Q}} conduire aux champs Q p {displaystyle mathbb {Q} _{p}} de nombres p -adiques (pour tout nombre premier p ), qui sont ainsi analogues à R {displaystyle mathbb {R} } . Il n’y a pas d’autres façons non triviales de compléter Q {displaystyle mathbb {Q}} que R {displaystyle mathbb {R} } et Q p , {displaystyle mathbb {Q} _{p},} par le théorème d’Ostrowski . Les fermetures algébriques Q p ̄ {displaystyle {overline {mathbb {Q} _{p}}}} de Q p {displaystyle mathbb {Q} _{p}} portent toujours une norme, mais (contrairement C {displaystyle mathbb {C} } ) ne sont pas complètes à son égard. L’achèvement C p {displaystyle mathbb {C} _{p}} de Q p ̄ {displaystyle {overline {mathbb {Q} _{p}}}} se révèle algébriquement clos. Par analogie, le champ est appelé nombres complexes p -adiques.

Les champs R , { displaystyle mathbb {R} ,} Q p , {displaystyle mathbb {Q} _{p},} et leurs extensions de champ fini, y compris C , {displaystyle mathbb{C} ,} sont appelés champs locaux .

Voir également

Wikimedia Commons a des médias liés aux nombres complexes .

• Surface algébrique
• Mouvement circulaire utilisant des nombres complexes
• Système à base complexe
• Géométrie complexe
• Numéro à double complexe
• Entier d’Eisenstein
• L’identité d’Euler
• Algèbre géométrique (qui inclut le plan complexe comme sous-espace spineur bidimensionnel G 2 + {displaystyle {mathcal{G}}_{2}^{+}} )
• Numéro complexe d’unité

Systèmes de numération Complexe : C {displaystyle :;mathbb {C} } Real : R {displaystyle :;mathbb {R} } Rational : Q {displaystyle :;mathbb {Q} } Integer : Z {displaystyle :;mathbb {Z} } Natural : N {displaystyle :;mathbb {N} } Zero: 0 One: 1 Prime numbers Composite numbers Negative integers Fraction Finite decimal Dyadic (finite binary) Repeating decimal Irrational Algebraic irrational Transcendental Imaginary

Notes

1. ^ “Complex numbers, as much as reals, and perhaps even more, find a unity with nature that is truly remarkable. It is as though Nature herself is as impressed by the scope and consistency of the complex-Number system as we are ourselves, and has entrusted to these numbers the precise operations of her world at its minutest scales.” — R. Penrose (2016, p. 73)^[2]
2. ^ Solomentsev 2001: “The plane R 2 {displaystyle mathbb {R} ^{2}} whose points are identified with the elements of C {displaystyle mathbb {C} } is called the complex plane … The complete geometric interpretation of complex numbers and operations on them appeared first in the work of C. Wessel (1799). The geometric representation of complex numbers, sometimes called the ‘Argand diagram‘, came into use after the publication in 1806 and 1814 of papers by J.R. Argand, who rediscovered, largely independently, the findings of Wessel”.
3. ^ In modern notation, Tartaglia’s solution is based on expanding the cube of the sum of two cube roots: ( u 3 + v 3 ) 3 = 3 u v 3 ( u 3 + v 3 ) + u + v {displaystyle left({sqrt[{3}]{u}}+{sqrt[{3}]{v}}right)^{3}=3{sqrt[{3}]{uv}}left({sqrt[{3}]{u}}+{sqrt[{3}]{v}}right)+u+v} With x = u 3 + v 3 {displaystyle x={sqrt[{3}]{u}}+{sqrt[{3}]{v}}} , p = 3 u v 3 {displaystyle p=3{sqrt[{3}]{uv}}} , q = u + v {displaystyle q=u+v} , u and v can be expressed in terms of p and q as u = q / 2 + ( q / 2 ) 2 − ( p / 3 ) 3 {displaystyle u=q/2+{sqrt {(q/2)^{2}-(p/3)^{3}}}} and v = q / 2 − ( q / 2 ) 2 − ( p / 3 ) 3 {displaystyle v=q/2-{sqrt {(q/2)^{2}-(p/3)^{3}}}} , respectively. Therefore, x = q / 2 + ( q / 2 ) 2 − ( p / 3 ) 3 3 + q / 2 − ( q / 2 ) 2 − ( p / 3 ) 3 3 {displaystyle x={sqrt[{3}]{q/2+{sqrt {(q/2)^{2}-(p/3)^{3}}}}}+{sqrt[{3}]{q/2-{sqrt {(q/2)^{2}-(p/3)^{3}}}}}} . When ( q / 2 ) 2 − ( p / 3 ) 3 {displaystyle (q/2)^{2}-(p/3)^{3}} is negative (casus irreducibilis), the second cube root should be regarded as the complex conjugate of the first one.
4. ^ It has been proved that imaginary numbers have necessarily to appear in the cubic formula when the equation has three real, different roots by Pierre Laurent Wantzel in 1843, Vincenzo Mollame in 1890, Otto Hölder in 1891 and Adolf Kneser in 1892. Paolo Ruffini also provided an incomplete proof in 1799. — S. Confalonieri (2015)^[19]
5. ^ Argand 1814, p. 204 defines the modulus of a complex number but he doesn’t name it:
   “Dans ce qui suit, les accens, indifféremment placés, seront employés pour indiquer la grandeur absolue des quantités qu’ils affectent; ainsi, si a = m + n − 1 {displaystyle a=m+n{sqrt {-1}}} , m {displaystyle m} et n {displaystyle n} étant réels, on devra entendre que a ′ {displaystyle a_{‘}} ou a ′ = m 2 + n 2 {displaystyle a’={sqrt {m^{2}+n^{2}}}} .”
   [In what follows, accent marks, wherever they’re placed, will be used to indicate the absolute size of the quantities to which they’re assigned; thus if a = m + n − 1 {displaystyle a=m+n{sqrt {-1}}} , m {displaystyle m} and n {displaystyle n} being real, one should understand that a ′ {displaystyle a_{‘}} or a ′ = m 2 + n 2 {displaystyle a’={sqrt {m^{2}+n^{2}}}} .]
   Argand 1814, p. 208 defines and names the module and the direction factor of a complex number: “… a = m 2 + n 2 {displaystyle a={sqrt {m^{2}+n^{2}}}} pourrait être appelé le module de a + b − 1 {displaystyle a+b{sqrt {-1}}} , et représenterait la grandeur absolue de la ligne a + b − 1 {displaystyle a+b{sqrt {-1}}} , tandis que l’autre facteur, dont le module est l’unité, en représenterait la direction.”
   [… a = m 2 + n 2 {displaystyle a={sqrt {m^{2}+n^{2}}}} could be called the module of a + b − 1 {displaystyle a+b{sqrt {-1}}} and would represent the absolute size of the line a + b − 1 , {displaystyle a+b{sqrt {-1}},,} (Note that Argand represented complex numbers as vectors.) whereas the other factor [namely, a a 2 + b 2 + b a 2 + b 2 − 1 {displaystyle {tfrac {a}{sqrt {a^{2}+b^{2}}}}+{tfrac {b}{sqrt {a^{2}+b^{2}}}}{sqrt {-1}}} ], whose module is unity [1], would represent its direction.]
6. ^ Gauss writes:^[39]“Quemadmodum scilicet arithmetica sublimior in quaestionibus hactenus pertractatis inter solos numeros integros reales versatur, ita theoremata circa residua biquadratica tunc tantum in summa simplicitate ac genuina venustate resplendent, quando campus arithmeticae ad quantitates imaginarias extenditur, ita ut absque restrictione ipsius obiectum constituant numeri formae a + bi, denotantibus i, pro more quantitatem imaginariam − 1 {displaystyle {sqrt {-1}}} , atque a, b indefinite omnes numeros reales integros inter – ∞ {displaystyle infty } et + ∞ {displaystyle infty } .” [Of course just as the higher arithmetic has been investigated so far in problems only among real integer numbers, so theorems regarding biquadratic residues then shine in greatest simplicity and genuine beauty, when the field of arithmetic is extended to imaginary quantities, so that, without restrictions on it, numbers of the form a + bi — i denoting by convention the imaginary quantity − 1 {displaystyle {sqrt {-1}}} , and the variables a, b [denoting] all real integer numbers between − ∞ {displaystyle -infty } and + ∞ {displaystyle +infty } — constitute an object.]
7. ^ Gauss:^[40]“Tales numeros vocabimus numeros integros complexos, ita quidem, ut reales complexis non opponantur, sed tamquam species sub his contineri censeantur.” [We will call such numbers [namely, numbers of the form a + bi ] “complex integer numbers”, so that real [numbers] are regarded not as the opposite of complex [numbers] but [as] a type [of number that] is, so to speak, contained within them.]
8. ^ Gauss:^[41] “Productum numeri complexi per numerum ipsi conjunctum utriusque normam vocamus. Pro norma itaque numeri realis, ipsius quadratum habendum est.” [We call a “norm” the product of a complex number [e.g,. a + ib ] with its conjugate [a – ib ]. Therefore the square of a real number should be regarded as its norm.]
9. ^ However for another inverse function of the complex exponential function (and not the above defined principal value), the branch cut could be taken at any other ray thru the origin.

References

1. ^ For an extensive account of the history of “imaginary” numbers, from initial skepticism to ultimate acceptance, see Bourbaki, Nicolas (1998). “Foundations of Mathematics § Logic: Set theory”. Elements of the History of Mathematics. Springer. pp. 18–24.
2. ^ Penrose, Roger (2016). The Road to Reality: A complete guide to the laws of the universe (reprint ed.). Random House. pp. 72–73. ISBN 978-1-4464-1820-8.
3. ^ Axler, Sheldon (2010). College algebra. Wiley. p. 262. ISBN 9780470470770.
4. ^ Spiegel, M.R.; Lipschutz, S.; Schiller, J.J.; Spellman, D. (14 April 2009). Complex Variables. Schaum’s Outline Series (2nd ed.). McGraw Hill. ISBN 978-0-07-161569-3.
5. ^ Aufmann, Richard N.; Barker, Vernon C.; Nation, Richard D. (2007). “Chapter P”. College Algebra and Trigonometry (6 ed.). Cengage Learning. p. 66. ISBN 978-0-618-82515-8.
6. ^ ^{a b c} Bourbaki 1998, §VIII.1
7. ^ Ahlfors 1979.
8. ^ Brown, James Ward; Churchill, Ruel V. (1996). Complex variables and applications (6th ed.). New York: McGraw-Hill. p. 2. ISBN 978-0-07-912147-9. In electrical engineering, the letter j is used instead of i.
9. ^ Pedoe, Dan (1988). Geometry: A comprehensive course. Dover. ISBN 978-0-486-65812-4.
10. ^ ^{a b} Weisstein, Eric W. “Complex Number”. mathworld.wolfram.com. Retrieved 12 August 2020.
11. ^ Apostol 1981, p. 18.
12. ^ Kasana, H.S. (2005). “Chapter 1”. Complex Variables: Theory And Applications (2nd ed.). PHI Learning Pvt. Ltd. p. 14. ISBN 978-81-203-2641-5.
13. ^ Nilsson, James William; Riedel, Susan A. (2008). “Chapter 9”. Electric circuits (8th ed.). Prentice Hall. p. 338. ISBN 978-0-13-198925-2.
14. ^ Kline, Morris. A history of mathematical thought, volume 1. p. 253.
15. ^ Jurij., Kovič. Tristan Needham, Visual Complex Analysis, Oxford University Press Inc., New York, 1998, 592 strani. OCLC 1080410598.
16. ^ Katz, Victor J. (2004). “9.1.4”. A History of Mathematics, Brief Version. Addison-Wesley. ISBN 978-0-321-16193-2.
17. ^ Hamilton, Wm. (1844). “On a new species of imaginary quantities connected with a theory of quaternions”. Proceedings of the Royal Irish Academy. 2: 424–434.
18. ^ Nahin, Paul J. (2007). An Imaginary Tale: The Story of √-1. Princeton University Press. ISBN 978-0-691-12798-9. Archived from the original on 12 October 2012. Retrieved 20 April 2011.
19. ^ ^{a b} Confalonieri, Sara (2015). The Unattainable Attempt to Avoid the Casus Irreducibilis for Cubic Equations: Gerolamo Cardano’s De Regula Aliza. Springer. pp. 15–16 (note 26). ISBN 978-3658092757.
20. ^ Descartes, René (1954) [1637]. La Géométrie | The Geometry of René Descartes with a facsimile of the first edition. Dover Publications. ISBN 978-0-486-60068-0. Retrieved 20 April 2011.
21. ^ Euler, Leonard (1748). Introductio in Analysin Infinitorum [Introduction to the Analysis of the Infinite] (in Latin). Vol. 1. Lucerne, Switzerland: Marc Michel Bosquet & Co. p. 104.
22. ^ Wessel, Caspar (1799). “Om Directionens analytiske Betegning, et Forsog, anvendt fornemmelig til plane og sphæriske Polygoners Oplosning” [On the analytic representation of direction, an effort applied in particular to the determination of plane and spherical polygons]. Nye Samling af det Kongelige Danske Videnskabernes Selskabs Skrifter [New Collection of the Writings of the Royal Danish Science Society] (in Danish). 5: 469–518.
23. ^ Wallis, John (1685). A Treatise of Algebra, Both Historical and Practical … London, England: printed by John Playford, for Richard Davis. pp. 264–273.
24. ^ Argand (1806). Essai sur une manière de représenter les quantités imaginaires dans les constructions géométriques [Essay on a way to represent complex quantities by geometric constructions] (in French). Paris, France: Madame Veuve Blanc.
25. ^ Gauss, Carl Friedrich (1799) “Demonstratio nova theorematis omnem functionem algebraicam rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse.” [New proof of the theorem that any rational integral algebraic function of a single variable can be resolved into real factors of the first or second degree.] Ph.D. thesis, University of Helmstedt, (Germany). (in Latin)
26. ^ Ewald, William B. (1996). From Kant to Hilbert: A Source Book in the Foundations of Mathematics. Vol. 1. Oxford University Press. p. 313. ISBN 9780198505358. Retrieved 18 March 2020.
27. ^ Gauss 1831, p. 638.
28. ^ “Adrien Quentin Buée (1745–1845): MacTutor”.
29. ^ Buée (1806). “Mémoire sur les quantités imaginaires” [Memoir on imaginary quantities]. Philosophical Transactions of the Royal Society of London (in French). 96: 23–88. doi:10.1098/rstl.1806.0003. S2CID 110394048.
30. ^ Mourey, C.V. (1861). La vraies théore des quantités négatives et des quantités prétendues imaginaires [The true theory of negative quantities and of alleged imaginary quantities] (in French). Paris, France: Mallet-Bachelier. 1861 reprint of 1828 original.
31. ^ Warren, John (1828). A Treatise on the Geometrical Representation of the Square Roots of Negative Quantities. Cambridge, England: Cambridge University Press.
32. ^ Warren, John (1829). “Consideration of the objections raised against the geometrical representation of the square roots of negative quantities”. Philosophical Transactions of the Royal Society of London. 119: 241–254. doi:10.1098/rstl.1829.0022. S2CID 186211638.
33. ^ Warren, John (1829). “On the geometrical representation of the powers of quantities, whose indices involve the square roots of Negative numbers“. Philosophical Transactions of the Royal Society of London. 119: 339–359. doi:10.1098/rstl.1829.0031. S2CID 125699726.
34. ^ Français, J.F. (1813). “Nouveaux principes de géométrie de position, et interprétation géométrique des symboles imaginaires” [New principles of the geometry of position, and geometric interpretation of complex [number] symbols]. Annales des mathématiques pures et appliquées (in French). 4: 61–71.
35. ^ Caparrini, Sandro (2000). “On the Common Origin of Some of the Works on the Geometrical Interpretation of Complex Numbers”. In Kim Williams (ed.). Two Cultures. Birkhäuser. p. 139. ISBN 978-3-7643-7186-9.
36. ^ Hardy, G.H.; Wright, E.M. (2000) [1938]. An Introduction to the Theory of Numbers. OUP Oxford. p. 189 (fourth edition). ISBN 978-0-19-921986-5.
37. ^ Jeff Miller (21 September 1999). “MODULUS”. Earliest Known Uses of Some of the Words of Mathematics (M). Archived from the original on 3 October 1999.{{cite web}}: CS1 maint: unfit URL (link)
38. ^ Cauchy, Augustin Louis (1821). Cours d’analyse de l’École royale polytechnique (in French). Vol. 1. Paris, France: L’Imprimerie Royale. p. 183.
39. ^ Gauss 1831, p. 96
40. ^ Gauss 1831, p. 96
41. ^ Gauss 1831, p. 98
42. ^ Hankel, Hermann (1867). Vorlesungen über die complexen Zahlen und ihre Functionen [Lectures About the Complex Numbers and Their Functions] (in German). Vol. 1. Leipzig, [Germany]: Leopold Voss. p. 71. From p. 71: “Wir werden den Factor (cos φ + i sin φ) haüfig den Richtungscoefficienten nennen.” (We will often call the factor (cos φ + i sin φ) the “coefficient of direction”.)
43. ^ For the former notation, see Apostol 1981, pp. 15–16
44. ^ Abramowitz, Milton; Stegun, Irene A. (1964). Handbook of mathematical functions with formulas, graphs, and mathematical tables. Courier Dover Publications. p. 17. ISBN 978-0-486-61272-0. Archived from the original on 23 April 2016. Retrieved 16 February 2016., Section 3.7.26, p. 17 Archived 10 September 2009 at the Wayback Machine
45. ^ Cooke, Roger (2008). Classical Algebra: its nature, origins, and uses. John Wiley and Sons. p. 59. ISBN 978-0-470-25952-8. Archived from the original on 24 April 2016. Retrieved 16 February 2016., Extract: page 59 Archived 23 April 2016 at the Wayback Machine
46. ^ Ahlfors 1979, p. 3.
47. ^ ^{a b} Apostol 1981, pp. 15–16.
48. ^ Apostol 1981, p. 25.
49. ^ Marker, David (1996). “Introduction to the Model Theory of Fields”. In Marker, D.; Messmer, M.; Pillay, A. (eds.). Model theory of fields. Lecture Notes in Logic. Vol. 5. Berlin: Springer-Verlag. pp. 1–37. ISBN 978-3-540-60741-0. MR 1477154.
50. ^ Bourbaki 1998, §VIII.4.
51. ^ Corry, Leo (2015). A Brief History of Numbers. Oxford University Press. pp. 215–16.
52. ^ Lester, J.A. (1994). “Triangles I: Shapes”. Aequationes Mathematicae. 52: 30–54. doi:10.1007/BF01818325. S2CID 121095307.
53. ^ Kalman, Dan (2008a). “An Elementary Proof of Marden’s Theorem”. American Mathematical Monthly. 115 (4): 330–38. doi:10.1080/00029890.2008.11920532. ISSN 0002-9890. S2CID 13222698. Archived from the original on 8 March 2012. Retrieved 1 January 2012.
54. ^ Kalman, Dan (2008b). “The Most Marvelous Theorem in Mathematics”. Journal of Online Mathematics and Its Applications. Archived from the original on 8 February 2012. Retrieved 1 January 2012.
55. ^ Grant, I.S.; Phillips, W.R. (2008). Electromagnetism (2 ed.). Manchester Physics Series. ISBN 978-0-471-92712-9.
56. ^ McCrimmon, Kevin (2004). A Taste of Jordan Algebras. Universitext. Springer. p. 64. ISBN 0-387-95447-3. MR 2014924

Works cited

• Ahlfors, Lars (1979). Complex analysis (3rd ed.). McGraw-Hill. ISBN 978-0-07-000657-7.
• Apostol, Tom (1981). Mathematical analysis. Addison-Wesley.
• Argand (1814). “Reflexions sur la nouvelle théorie des imaginaires, suives d’une application à la demonstration d’un theorème d’analise” [Reflections on the new theory of complex numbers, followed by an application to the proof of a theorem of analysis]. Annales de mathématiques pures et appliquées (in French). 5: 197–209.
• Gauss, C. F. (1831). “Theoria residuorum biquadraticorum. Commentatio secunda” [Theory of biquadratic residues. Second memoir.]. Commentationes Societatis Regiae Scientiarum Gottingensis Recentiores (in Latin). 7: 89–148.
• Solomentsev, E.D. (2001) [1994], “Complex number”, Encyclopedia of Mathematics, EMS Press

Further reading

Wikiversity has learning resources about Complex Numbers

Wikibooks has a book on the topic of: Calculus/Complex numbers

Wikisource has the text of the 1911 Encyclopædia Britannica article “Number/Complex Numbers“.

• Penrose, Roger (2005). The Road to Reality: A complete guide to the laws of the universe. Alfred A. Knopf. ISBN 978-0-679-45443-4.
• Derbyshire, John (2006). Unknown Quantity: A real and imaginary history of algebra. Joseph Henry Press. ISBN 978-0-309-09657-7.
• Needham, Tristan (1997). Visual Complex Analysis. Clarendon Press. ISBN 978-0-19-853447-1.

Mathematical

• Ahlfors, Lars (1979). Complex analysis (3rd ed.). McGraw-Hill. ISBN 978-0-07-000657-7.
• Conway, John B. (1986). Functions of One Complex Variable I. Springer. ISBN 978-0-387-90328-6.
• Joshi, Kapil D. (1989). Foundations of Discrete Mathematics. New York: John Wiley & Sons. ISBN 978-0-470-21152-6.
• Pedoe, Dan (1988). Geometry: A comprehensive course. Dover. ISBN 978-0-486-65812-4.
• Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. (2007). “Section 5.5 Complex Arithmetic”. Numerical Recipes: The art of scientific computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8.
• Solomentsev, E.D. (2001) [1994], “Complex number”, Encyclopedia of Mathematics, EMS Press

Historical

• Bourbaki, Nicolas (1998). “Foundations of mathematics § logic: set theory”. Elements of the history of mathematics. Springer.
• Burton, David M. (1995). The History of Mathematics (3rd ed.). New York: McGraw-Hill. ISBN 978-0-07-009465-9.
• Katz, Victor J. (2004). A History of Mathematics, Brief Version. Addison-Wesley. ISBN 978-0-321-16193-2.
• Nahin, Paul J. (1998). An Imaginary Tale: The Story of − 1 {displaystyle scriptstyle {sqrt {-1}}} . Princeton University Press. ISBN 978-0-691-02795-1. — A gentle introduction to the history of complex numbers and the beginnings of complex analysis.
• Ebbinghaus, H. D.; Hermes, H.; Hirzebruch, F.; Koecher, M.; Mainzer, K.; Neukirch, J.; Prestel, A.; Remmert, R. (1991). Numbers (hardcover ed.). Springer. ISBN 978-0-387-97497-2. — An advanced perspective on the historical development of the concept of number.