Trou noir
Un trou noir est une région de l’espace -temps où la gravité est si forte que rien – aucune particule ou même un rayonnement électromagnétique tel que la lumière – ne peut s’en échapper. [2] La théorie de la relativité générale prédit qu’une masse suffisamment compacte peut déformer l’espace-temps pour former un trou noir. [3] [4] La limite d’aucune évasion s’appelle l’ horizon d’événement . Bien qu’il ait un effet énorme sur le sort et les circonstances d’un objet qui le traverse, il n’a pas de caractéristiques détectables localement selon la relativité générale. [5]À bien des égards, un trou noir agit comme un corps noir idéal , car il ne réfléchit aucune lumière. [6] [7] De plus, la théorie quantique des champs dans l’espace-temps courbe prédit que les horizons des événements émettent un rayonnement de Hawking , avec le même spectre qu’un corps noir d’une température inversement proportionnelle à sa masse. Cette température est de l’ordre du milliardième de kelvin pour les trous noirs stellaires , ce qui rend pratiquement impossible leur observation directe.
 Image directe d’un trou noir supermassif au cœur de Messier 87 [1]
Image directe d’un trou noir supermassif au cœur de Messier 87 [1]  Simulation animée d’un Trou noir de Schwarzschild avec une galaxie passant derrière. Au moment de l’alignement, une lentille gravitationnelle extrême de la galaxie est observée.
Simulation animée d’un Trou noir de Schwarzschild avec une galaxie passant derrière. Au moment de l’alignement, une lentille gravitationnelle extrême de la galaxie est observée.
Les objets dont les champs gravitationnels sont trop forts pour que la lumière puisse s’échapper ont été envisagés pour la première fois au XVIIIe siècle par John Michell et Pierre-Simon Laplace . [8] En 1916, Karl Schwarzschild a trouvé la première solution moderne de la relativité générale qui caractériserait un trou noir. David Finkelstein , en 1958, a publié pour la première fois l’interprétation du “trou noir” comme une région de l’espace d’où rien ne peut s’échapper. Les trous noirs ont longtemps été considérés comme une curiosité mathématique ; ce n’est que dans les années 1960 que les travaux théoriques ont montré qu’il s’agissait d’une prédiction générique de la relativité générale. La découverte des étoiles à neutrons par Jocelyn Bell Burnellen 1967 a suscité l’intérêt pour les objets compacts effondrés par gravité en tant que réalité astrophysique possible. Le premier trou noir connu était Cygnus X-1 , identifié par plusieurs chercheurs indépendamment en 1971. [9] [10]
Les trous noirs de masse stellaire se forment lorsque des étoiles massives s’effondrent à la fin de leur cycle de vie. Une fois qu’un trou noir s’est formé, il peut se développer en absorbant la masse de son environnement. Des trous noirs supermassifs de millions de masses solaires ( M ☉ ) peuvent se former en absorbant d’autres étoiles et en fusionnant avec d’autres trous noirs. Il existe un consensus sur l’existence de trous noirs supermassifs au centre de la plupart des galaxies .
La présence d’un trou noir peut être déduite de son interaction avec une autre matière et avec un rayonnement électromagnétique tel que la lumière visible. Toute matière qui tombe sur un trou noir peut former un disque d’accrétion externe chauffé par frottement, formant des quasars , certains des objets les plus brillants de l’univers. Les étoiles qui passent trop près d’un trou noir supermassif peuvent être déchiquetées en banderoles qui brillent très fort avant d’être “avalées”. [11] Si d’autres étoiles sont en orbite autour d’un trou noir, leurs orbites peuvent déterminer la masse et l’emplacement du trou noir. De telles observations peuvent être utilisées pour exclure d’éventuelles alternatives telles que les étoiles à neutrons. De cette façon, les astronomes ont identifié de nombreux candidats trous noirs stellaires danssystèmes binaires et a établi que la source radio connue sous le nom de Sagittarius A* , au cœur de la galaxie de la Voie lactée , contient un trou noir supermassif d’environ 4,3 millions de masses solaires.
Le 11 février 2016, la collaboration scientifique LIGO et la collaboration Virgo ont annoncé la première détection directe d’ ondes gravitationnelles , représentant la première observation d’une fusion de trous noirs. [12] Le 10 avril 2019, la première image directe d’un trou noir et de son voisinage a été publiée, suite aux observations faites par l’ Event Horizon Telescope (EHT) en 2017 du trou noir supermassif au centre galactique de Messier 87 . [13] [14] [15] En 2021 , le corps connu le plus proche considéré comme un trou noir se situe à environ 1 500 années-lumière (460 parsecs[update]) loin (voir Liste des trous noirs les plus proches ). Bien que seulement quelques douzaines de trous noirs aient été trouvés jusqu’à présent dans la Voie lactée , on pense qu’il y en a des centaines de millions, dont la plupart sont solitaires et ne provoquent pas d’émission de rayonnement. [16] Par conséquent, ils ne seraient détectables que par lentille gravitationnelle .
Histoire

 Vue simulée d’un trou noir devant le Grand Nuage de Magellan . Notez l’effet de lentille gravitationnelle, qui produit deux vues agrandies mais très déformées du nuage. En haut, le disque de la Voie lactée apparaît déformé en un arc. Publié en 2019. [17]
Vue simulée d’un trou noir devant le Grand Nuage de Magellan . Notez l’effet de lentille gravitationnelle, qui produit deux vues agrandies mais très déformées du nuage. En haut, le disque de la Voie lactée apparaît déformé en un arc. Publié en 2019. [17]
L’idée d’un corps si massif que même la lumière ne pourrait pas s’échapper a été brièvement proposée par le pionnier astronomique et membre du clergé anglais John Michell dans une lettre publiée en novembre 1784. Les calculs simplistes de Michell supposaient qu’un tel corps pourrait avoir la même densité que le Soleil, et concluaient que l’on formerait lorsque le diamètre d’une étoile dépasse celui du Soleil d’un facteur 500 et que sa vitesse d’ échappement en surface dépasse la vitesse habituelle de la lumière. Michell a qualifié ces corps d’ étoiles noires . [18] Il a correctement noté que de tels corps supermassifs mais non rayonnants pourraient être détectables par leurs effets gravitationnels sur les corps visibles proches. [8] [19] [20]Les érudits de l’époque étaient initialement enthousiasmés par la proposition selon laquelle des «étoiles noires» géantes mais invisibles pourraient se cacher à la vue de tous, mais l’enthousiasme s’est atténué lorsque la nature ondulatoire de la lumière est devenue apparente au début du XIXe siècle, [21] comme si la lumière était un onde plutôt qu’une particule, on ne savait pas quelle influence, le cas échéant, la gravité aurait sur les ondes lumineuses qui s’échappent. [8] [20]
La physique moderne discrédite la notion de Michell d’un rayon lumineux tirant directement de la surface d’une étoile supermassive, ralenti par la gravité de l’étoile, s’arrêtant puis retombant librement à la surface de l’étoile. [22]
Relativité générale
En 1915, Albert Einstein a développé sa théorie de la relativité générale , après avoir montré plus tôt que la gravité influence le mouvement de la lumière. Quelques mois plus tard seulement, Karl Schwarzschild a trouvé une solution aux équations de champ d’Einstein qui décrit le champ gravitationnel d’une masse ponctuelle et d’une masse sphérique. [23] [24] Quelques mois après Schwarzschild, Johannes Droste, un élève de Hendrik Lorentz , a indépendamment donné la même solution pour la masse ponctuelle et a écrit plus longuement sur ses propriétés. [25] [26]Cette solution avait un comportement particulier à ce qu’on appelle maintenant le rayon de Schwarzschild , où il est devenu singulier , ce qui signifie que certains des termes des équations d’Einstein sont devenus infinis. La nature de cette surface n’était pas tout à fait comprise à l’époque. En 1924, Arthur Eddington a montré que la singularité disparaissait après un changement de coordonnées (voir Coordonnées d’ Eddington-Finkelstein ), bien qu’il ait fallu attendre 1933 pour que Georges Lemaître se rende compte que cela signifiait que la singularité au rayon de Schwarzschild était une singularité de coordonnées non physiques . [27]Arthur Eddington a cependant commenté la possibilité d’une étoile avec une masse comprimée au rayon de Schwarzschild dans un livre de 1926, notant que la théorie d’Einstein nous permet d’exclure des densités trop importantes pour les étoiles visibles comme Bételgeuse car “une étoile de 250 millions de km de rayon pourrait n’aurait peut-être pas une densité aussi élevée que le Soleil. Premièrement, la force de Gravitation serait si grande que la lumière ne pourrait pas s’en échapper, les rayons retombant sur l’étoile comme une pierre sur la terre. Deuxièmement, le décalage vers le rouge des raies spectrales serait si grande que le spectre serait déplacé hors de l’existence. Troisièmement, la masse produirait tellement de courbure de la métrique de l’espace-temps que l’espace se refermerait autour de l’étoile, nous laissant à l’extérieur (c’est-à-dire nulle part). [28] [29]
En 1931, Subrahmanyan Chandrasekhar a calculé, en utilisant la relativité restreinte, qu’un corps non rotatif de matière dégénérée aux électrons au- dessus d’une certaine masse limite (maintenant appelée la limite de Chandrasekhar à 1,4 M ☉ ) n’a pas de solutions stables. [30] Ses arguments ont été opposés par beaucoup de ses contemporains comme Eddington et Lev Landau , qui ont soutenu qu’un mécanisme encore inconnu arrêterait l’effondrement. [31] Ils avaient en partie raison : une naine blanche légèrement plus massive que la limite de Chandrasekhar s’effondrera en une étoile à neutrons , [32] qui est elle-même stable. Mais en 1939,Robert Oppenheimer et d’autres ont prédit que les étoiles à neutrons au-dessus d’une autre limite (la limite de Tolman-Oppenheimer-Volkoff ) s’effondreraient davantage pour les raisons présentées par Chandrasekhar, et ont conclu qu’aucune loi de la physique n’était susceptible d’intervenir et d’empêcher au moins certaines étoiles de s’effondrer en trous noirs. [33] Leurs calculs originaux, basés sur le principe d’exclusion de Pauli , l’ont donné comme 0,7 M ☉ ; la prise en compte ultérieure de la répulsion neutron-neutron médiée par la force forte a porté l’estimation à environ 1,5 M ☉ à 3,0 M ☉ . [34] Observations de la fusion d’étoiles à neutrons GW170817, qui aurait généré un trou noir peu de temps après, ont affiné l’estimation de la limite TOV à ~ 2,17 M ☉ . [35] [36] [37] [38] [39]
Oppenheimer et ses co-auteurs ont interprété la singularité à la limite du rayon de Schwarzschild comme indiquant qu’il s’agissait de la limite d’une bulle dans laquelle le temps s’est arrêté. C’est un point de vue valable pour les observateurs externes, mais pas pour les observateurs internes. En raison de cette propriété, les étoiles effondrées étaient appelées “étoiles figées”, car un observateur extérieur verrait la surface de l’étoile figée dans le temps à l’instant où son effondrement l’amène au rayon de Schwarzschild. [40]
âge d’or
En 1958, David Finkelstein identifia la surface de Schwarzschild comme un horizon des événements , “une membrane unidirectionnelle parfaite : les influences causales ne peuvent la traverser que dans une seule direction”. [41] Cela n’a pas strictement contredit les résultats d’Oppenheimer, mais les a étendus pour inclure le point de vue d’observateurs infaillibles. La solution de Finkelstein a étendu la solution de Schwarzschild pour l’avenir des observateurs tombant dans un trou noir. Une extension complète avait déjà été trouvée par Martin Kruskal , qui fut invité à la publier. [42]
Ces résultats sont arrivés au début de l’ âge d’or de la relativité générale , qui a été marqué par la relativité générale et les trous noirs devenant des sujets de recherche courants. Ce processus a été aidé par la découverte de pulsars par Jocelyn Bell Burnell en 1967, [43] [44] qui, en 1969, se sont avérés être des étoiles à neutrons en rotation rapide. [45] Jusqu’à cette époque, les étoiles à neutrons, comme les trous noirs, étaient considérées comme de simples curiosités théoriques ; mais la découverte des pulsars a montré leur pertinence physique et a stimulé un intérêt supplémentaire pour tous les types d’objets compacts qui pourraient être formés par effondrement gravitationnel. [ citation nécessaire ]
Au cours de cette période, des solutions de trous noirs plus générales ont été trouvées. En 1963, Roy Kerr a trouvé la solution exacte pour un trou noir en rotation . Deux ans plus tard, Ezra Newman a trouvé la solution axisymétrique pour un trou noir à la fois rotatif et chargé électriquement . [46] Grâce aux travaux de Werner Israel , [47] Brandon Carter , [48] [49] et David Robinson [50] le théorème sans cheveux a émergé, déclarant qu’une solution de trou noir stationnaire est complètement décrite par les trois paramètres de la métrique de Kerr-Newman: masse , moment cinétique et charge électrique. [51]
Au début, on soupçonnait que les caractéristiques étranges des solutions de trous noirs étaient des artefacts pathologiques des conditions de symétrie imposées, et que les singularités n’apparaîtraient pas dans des situations génériques. Ce point de vue était notamment partagé par Vladimir Belinsky , Isaak Khalatnikov et Evgeny Lifshitz , qui ont tenté de prouver qu’aucune singularité n’apparaît dans les solutions génériques. Cependant, à la fin des années 1960, Roger Penrose [52] et Stephen Hawking ont utilisé des techniques globales pour prouver que les singularités apparaissent de manière générique. [53] Pour ces travaux, Penrose a reçu la moitié du prix Nobel de physique 2020 , Hawking étant décédé en 2018. [54]Basé sur des observations à Greenwich et à Toronto au début des années 1970, Cygnus X-1 , une source de rayons X galactique découverte en 1964, est devenu le premier objet astronomique communément accepté comme un trou noir. [55] [56]
Les travaux de James Bardeen , Jacob Bekenstein , Carter et Hawking au début des années 1970 ont conduit à la formulation de la thermodynamique des trous noirs . [57] Ces lois décrivent le comportement d’un trou noir en étroite analogie avec les lois de la thermodynamique en reliant la masse à l’énergie, la surface à l’ entropie et la gravité de surface à la température . L’analogie a été complétée lorsque Hawking, en 1974, a montré que la théorie quantique des champs implique que les trous noirs devraient rayonner comme un corps noir avec une température proportionnelle à la gravité de surface du trou noir, prédisant l’effet maintenant connu sous le nom deRayonnement de Hawking . [58]
Étymologie
John Michell a utilisé le terme “étoile noire”, [59] et au début du 20e siècle, les physiciens ont utilisé le terme “objet effondré par gravité”. L’écrivain scientifique Marcia Bartusiak fait remonter le terme “trou noir” au physicien Robert H. Dicke , qui au début des années 1960 aurait comparé le phénomène au trou noir de Calcutta , connu comme une prison où les gens entraient mais n’en sortaient jamais vivants. [60]
Le terme “trou noir” a été utilisé dans la presse écrite par les magazines Life and Science News en 1963, [60] et par la journaliste scientifique Ann Ewing dans son article ” ‘Black Holes’ in Space”, daté du 18 janvier 1964, qui était un rapport sur une réunion de l’ Association américaine pour l’avancement des sciences tenue à Cleveland, Ohio. [61] [62]
En décembre 1967, un étudiant aurait suggéré l’expression “trou noir” lors d’une conférence de John Wheeler ; [61] Wheeler a adopté le terme pour sa brièveté et sa “valeur publicitaire”, et il s’est rapidement répandu, [63] ce qui a conduit certains à créditer Wheeler d’avoir inventé l’expression. [64]
Propriétés et structure

 Illustration simple d’un trou noir sans rotation
Illustration simple d’un trou noir sans rotation
Le théorème sans cheveux postule qu’une fois qu’il atteint un état stable après sa formation, un trou noir n’a que trois propriétés physiques indépendantes : la masse, la charge électrique et le moment cinétique ; le trou noir est autrement sans relief. Si la conjecture est vraie, deux trous noirs qui partagent les mêmes valeurs pour ces propriétés, ou paramètres, sont indiscernables l’un de l’autre. La mesure dans laquelle la conjecture est vraie pour de vrais trous noirs selon les lois de la physique moderne est actuellement un problème non résolu. [51]
Ces propriétés sont particulières car elles sont visibles de l’extérieur d’un trou noir. Par exemple, un trou noir chargé repousse d’autres charges similaires comme n’importe quel autre objet chargé. De même, la masse totale à l’intérieur d’une sphère contenant un trou noir peut être trouvée en utilisant l’analogue gravitationnel de la loi de Gauss (à travers la masse ADM ), loin du trou noir. [65] De même, le moment cinétique (ou spin) peut être mesuré de loin en utilisant le glissement de cadre par le champ gravitomagnétique , par exemple l’ effet Lense-Thirring . [66]
Lorsqu’un objet tombe dans un trou noir, toute information sur la forme de l’objet ou la répartition de la charge sur celui-ci est uniformément répartie le long de l’horizon du trou noir et est perdue pour les observateurs extérieurs. Le comportement de l’horizon dans cette situation est un système dissipatif très analogue à celui d’une membrane conductrice extensible avec frottement et résistance électrique – le paradigme de la membrane . [67] Ceci est différent des autres théories des champs telles que l’électromagnétisme, qui n’ont pas de frottement ou de résistivité au niveau microscopique, car elles sont réversibles dans le temps. Parce qu’un trou noir finit par atteindre un état stable avec seulement trois paramètres, il n’y a aucun moyen d’éviter de perdre des informations sur les conditions initiales : les champs gravitationnel et électrique d’un trou noir donnent très peu d’informations sur ce qui est entré. L’information qui est perdue comprend toutes les quantités qui ne peuvent pas être mesurées loin de l’horizon du trou noir, y compris les nombres quantiques approximativement conservés tels que le nombre total de baryons et le nombre de leptons . Ce comportement est si déroutant qu’il a été appelé le paradoxe de la perte d’information du trou noir . [68] [69]

 Dilatation gravitationnelle du temps autour d’un trou noir
Dilatation gravitationnelle du temps autour d’un trou noir
Propriétés physiques
Les trous noirs statiques les plus simples ont une masse mais ni charge électrique ni moment cinétique. Ces trous noirs sont souvent appelés trous noirs de Schwarzschild d’après Karl Schwarzschild qui a découvert cette solution en 1916. [24] Selon le théorème de Birkhoff , c’est la seule solution de vide à symétrie sphérique . [70]Cela signifie qu’il n’y a pas de différence observable à distance entre le champ gravitationnel d’un tel trou noir et celui de tout autre objet sphérique de même masse. La notion populaire d’un trou noir “aspirant tout” dans son environnement n’est donc correcte qu’à proximité de l’horizon d’un trou noir; de loin, le champ gravitationnel externe est identique à celui de tout autre corps de même masse. [71]
Des solutions décrivant des trous noirs plus généraux existent également. Les trous noirs chargés non rotatifs sont décrits par la métrique de Reissner-Nordström , tandis que la métrique de Kerr décrit un trou noir rotatif non chargé. La solution de trou noir stationnaire la plus générale connue est la métrique de Kerr-Newman, qui décrit un trou noir avec à la fois une charge et un moment cinétique. [72]
Alors que la masse d’un trou noir peut prendre n’importe quelle valeur positive, la charge et le moment cinétique sont contraints par la masse. La charge électrique totale Q et le moment cinétique total J devraient satisfaire
Q 2 4 π ε 0 + c 2 J 2 G M 2 ≤ G M 2 {displaystyle {frac {Q^{2}}{4pi epsilon _{0}}}+{frac {c^{2}J^{2}}{GM^{2}}} leq GM^{2}} 
pour un trou noir de masse M . Les trous noirs avec la masse minimale possible satisfaisant cette inégalité sont appelés extrémaux . Les solutions des équations d’Einstein qui violent cette inégalité existent, mais elles ne possèdent pas d’horizon des événements. Ces solutions ont des singularités dites nues qui peuvent être observées de l’extérieur, et sont donc considérées comme non physiques . L’ hypothèse de la censure cosmique exclut la formation de telles singularités, lorsqu’elles sont créées par l’effondrement gravitationnel de la matière réaliste . [3] Ceci est étayé par des simulations numériques. [73]
En raison de la force relativement importante de la force électromagnétique , les trous noirs formés à partir de l’effondrement des étoiles devraient conserver la charge presque neutre de l’étoile. La rotation, cependant, devrait être une caractéristique universelle des objets astrophysiques compacts. La source de rayons X binaire candidate au trou noir GRS 1915+105 [74] semble avoir un moment cinétique proche de la valeur maximale autorisée. Cette limite non facturée est [75]
J ≤ G M 2 c , {displaystyle Jleq {frac {GM^{2}}{c}},} 
permettant de définir un paramètre de spin sans dimension tel que [75]
0 ≤ c J G M 2 ≤ 1. {displaystyle 0leq {frac {cJ}{GM^{2}}}leq 1.} 
[75] [Remarque 1]
| Classe | Environ. Masse |
Environ. rayon |
|---|---|---|
| Un trou noir supermassif | dix5 –1010 M ☉ | 0,001–400 UA |
| Trou noir de masse intermédiaire | dix3 M ☉ | 10 3 km ≈ R Terre |
| Trou noir stellaire | 10 M ☉ | 30 kilomètres |
| Micro-trou noir | jusqu’à M Lune | jusqu’à 0,1mm |
Les trous noirs sont généralement classés en fonction de leur masse, indépendante du moment cinétique, J . La taille d’un trou noir, déterminée par le rayon de l’horizon des événements, ou rayon de Schwarzschild, est proportionnelle à la masse, M , à travers
r s = 2 G M c 2 ≈ 2.95 M M ⊙ k m , {displaystyle r_{mathrm {s} }={frac {2GM}{c^{2}}}approx 2.95,{frac {M}{M_{odot }}}~mathrm {km ,} } 
où r s est le rayon de Schwarzschild et M ☉ est la masse du Soleil . [77] Pour un trou noir avec un spin et/ou une charge électrique non nuls, le rayon est plus petit, [Note 2] jusqu’à ce qu’un trou noir extrémal puisse avoir un horizon des événements proche de [78]
r + = G M c 2 . {displaystyle r_{mathrm {+} }={frac {GM}{c^{2}}}.} 
Horizon des événements

 Loin du trou noir, une particule peut se déplacer dans n’importe quelle direction, comme l’illustre le jeu de flèches. Elle n’est limitée que par la vitesse de la lumière.
Loin du trou noir, une particule peut se déplacer dans n’importe quelle direction, comme l’illustre le jeu de flèches. Elle n’est limitée que par la vitesse de la lumière. 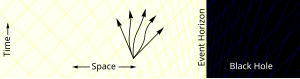
 Plus près du trou noir, l’espace-temps commence à se déformer. Il y a plus de chemins vers le trou noir que de chemins qui s’en éloignent. [Note 3]
Plus près du trou noir, l’espace-temps commence à se déformer. Il y a plus de chemins vers le trou noir que de chemins qui s’en éloignent. [Note 3] 
 À l’intérieur de l’horizon des événements, tous les chemins rapprochent la particule du centre du trou noir. Il n’est plus possible pour la particule de s’échapper.
À l’intérieur de l’horizon des événements, tous les chemins rapprochent la particule du centre du trou noir. Il n’est plus possible pour la particule de s’échapper.
La caractéristique déterminante d’un trou noir est l’apparition d’un horizon des événements – une limite dans l’ espace -temps à travers laquelle la matière et la lumière ne peuvent passer que vers l’intérieur vers la masse du trou noir. Rien, pas même la lumière, ne peut s’échapper de l’intérieur de l’horizon des événements. [80] [81] L’horizon des événements est appelé comme tel parce que si un événement se produit à l’intérieur de la frontière, les informations de cet événement ne peuvent pas atteindre un observateur extérieur, ce qui rend impossible de déterminer si un tel événement s’est produit. [82]
Comme prédit par la relativité générale, la présence d’une masse déforme l’espace-temps de telle manière que les chemins empruntés par les particules se courbent vers la masse. [83] À l’horizon des événements d’un trou noir, cette déformation devient si forte qu’il n’y a pas de chemin qui s’éloigne du trou noir. [84]
Pour un observateur distant, les horloges proches d’un trou noir sembleraient tourner plus lentement que celles plus éloignées du trou noir. [85] En raison de cet effet, connu sous le nom de dilatation gravitationnelle du temps , un objet tombant dans un trou noir semble ralentir à mesure qu’il s’approche de l’horizon des événements, prenant un temps infini pour l’atteindre. [86] En même temps, tous les processus sur cet objet ralentissent, du point de vue d’un observateur extérieur fixe, faisant apparaître toute lumière émise par l’objet plus rouge et plus sombre, un effet connu sous le nom de redshift gravitationnel . [87]Finalement, l’objet qui tombe s’estompe jusqu’à ce qu’il ne soit plus visible. En règle générale, ce processus se produit très rapidement, un objet disparaissant de la vue en moins d’une seconde. [88]
D’autre part, les observateurs indestructibles tombant dans un trou noir ne remarquent aucun de ces effets lorsqu’ils traversent l’horizon des événements. Selon leurs propres horloges, qui leur paraissent fonctionner normalement, ils traversent l’horizon des événements après un temps fini sans constater de comportement singulier ; en relativité générale classique, il est impossible de déterminer l’emplacement de l’horizon des événements à partir d’observations locales, en raison du principe d’équivalence d’Einstein . [89] [90]
La topologie de l’horizon des événements d’un trou noir à l’équilibre est toujours sphérique. [Note 4] [93] Pour les trous noirs non rotatifs (statiques), la géométrie de l’horizon des événements est précisément sphérique, tandis que pour les trous noirs rotatifs, l’horizon des événements est aplati. [94] [95] [96]
Singularité
Au centre d’un trou noir, tel que décrit par la relativité générale, peut se trouver une singularité gravitationnelle , une région où la courbure de l’espace-temps devient infinie. [97] Pour un trou noir non rotatif, cette région prend la forme d’un seul point ; pour un trou noir en rotation, il est étalé pour former une singularité annulaire qui se trouve dans le plan de rotation. [98] Dans les deux cas, la région singulière a un volume nul. On peut également montrer que la région singulière contient toute la masse de la solution du trou noir. [99] La région singulière peut donc être considérée comme ayant une densité infinie . [100]
Les observateurs tombant dans un Trou noir de Schwarzschild (c’est-à-dire non rotatif et non chargé) ne peuvent éviter d’être entraînés dans la singularité une fois qu’ils ont traversé l’horizon des événements. Ils peuvent prolonger l’expérience en accélérant pour ralentir leur descente, mais seulement jusqu’à une certaine limite. [101] Lorsqu’ils atteignent la singularité, ils sont écrasés à une densité infinie et leur masse s’ajoute au total du trou noir. Avant que cela ne se produise, ils auront été déchirés par les forces de marée croissantes dans un processus parfois appelé spaghettification ou “effet nouille”. [102]
Dans le cas d’un trou noir chargé (Reissner-Nordström) ou tournant (Kerr), il est possible d’éviter la singularité. Étendre ces solutions aussi loin que possible révèle la possibilité hypothétique de sortir du trou noir dans un espace-temps différent, le trou noir agissant comme un trou de ver . [103] La possibilité de voyager dans un autre univers n’est cependant que théorique puisque toute perturbation détruirait cette possibilité. [104] Il semble également possible de suivre des courbes temporelles fermées (retour à son propre passé) autour de la singularité de Kerr, ce qui conduit à des problèmes de causalité comme le paradoxe du grand -père . [105]On s’attend à ce qu’aucun de ces effets particuliers ne survive dans un traitement quantique approprié des trous noirs en rotation et chargés. [106]
L’apparition de singularités en relativité générale est communément perçue comme signalant l’effondrement de la théorie. [107] Cette répartition est toutefois attendue ; il se produit dans une situation où des effets quantiques devraient décrire ces actions, en raison de la densité extrêmement élevée et donc des interactions des particules. À ce jour, il n’a pas été possible de combiner les effets quantiques et gravitationnels en une seule théorie, bien qu’il existe des tentatives pour formuler une telle théorie de la gravité quantique . On s’attend généralement à ce qu’une telle théorie ne comporte aucune singularité. [108] [109]
Sphère de photons
La sphère de photons est une limite sphérique d’épaisseur nulle dans laquelle les photons qui se déplacent sur des tangentes à cette sphère seraient piégés sur une orbite circulaire autour du trou noir. Pour les trous noirs non rotatifs, la sphère de photons a un rayon 1,5 fois le rayon de Schwarzschild. Leurs orbites seraient dynamiquement instables , donc toute petite perturbation, telle qu’une particule de matière en chute, provoquerait une instabilité qui augmenterait avec le temps, soit en plaçant le photon sur une trajectoire vers l’extérieur le faisant s’échapper du trou noir, soit sur une trajectoire vers l’intérieur. spirale où il finirait par traverser l’horizon des événements. [110]
Alors que la lumière peut encore s’échapper de la sphère de photons, toute lumière qui traverse la sphère de photons sur une trajectoire entrante sera capturée par le trou noir. Par conséquent, toute lumière qui atteint un observateur extérieur depuis la sphère de photons doit avoir été émise par des objets situés entre la sphère de photons et l’horizon des événements. [110] Pour un trou noir de Kerr, le rayon de la sphère du photon dépend du paramètre de spin et des détails de l’orbite du photon, qui peut être prograde (le photon tourne dans le même sens que le spin du trou noir) ou rétrograde. [111] [112]
Ergosphère
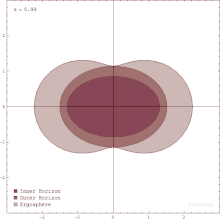
 L’ergosphère est une région en dehors de l’horizon des événements, où les objets ne peuvent pas rester en place. [113]
L’ergosphère est une région en dehors de l’horizon des événements, où les objets ne peuvent pas rester en place. [113]
Les trous noirs en rotation sont entourés d’une région de l’espace-temps dans laquelle il est impossible de rester immobile, appelée l’ergosphère. C’est le résultat d’un processus connu sous le nom de frame-dragging ; la relativité générale prédit que toute masse en rotation aura tendance à “traîner” légèrement le long de l’espace-temps qui l’entoure immédiatement. Tout objet à proximité de la masse en rotation aura tendance à commencer à se déplacer dans le sens de la rotation. Pour un trou noir en rotation, cet effet est si fort près de l’horizon des événements qu’un objet devrait se déplacer plus vite que la vitesse de la lumière dans la direction opposée pour rester immobile. [114]
L’ergosphère d’un trou noir est un volume délimité par l’horizon des événements du trou noir et l’ ergosurface , qui coïncide avec l’horizon des événements aux pôles mais est à une distance beaucoup plus grande autour de l’équateur. [113]
Les objets et les rayonnements peuvent s’échapper normalement de l’ergosphère. Grâce au processus de Penrose , les objets peuvent émerger de l’ergosphère avec plus d’énergie qu’ils n’y sont entrés. L’énergie supplémentaire provient de l’énergie de rotation du trou noir. Ainsi la rotation du trou noir ralentit. [115] Une variante du processus de Penrose en présence de champs magnétiques puissants, le processus de Blandford-Znajek est considéré comme un mécanisme probable pour l’énorme luminosité et les jets relativistes des quasars et autres noyaux galactiques actifs .
Orbite circulaire stable la plus interne (ISCO)
Dans la gravité newtonienne , les particules de test peuvent orbiter de manière stable à des distances arbitraires d’un objet central. En relativité générale, cependant, il existe une orbite circulaire stable la plus interne (souvent appelée ISCO), à l’intérieur de laquelle, toute perturbation infinitésimale d’une orbite circulaire conduira à une inspiration dans le trou noir. [116] La localisation de l’ISCO dépend du spin du trou noir, dans le cas d’un Trou noir de Schwarzschild (spin zéro) soit :
r I S C O = 3 r s = 6 G M c 2 , {displaystyle r_{rm {ISCO}}=3,r_{s}={frac {6,GM}{c^{2}}},} 
et diminue avec l’augmentation du spin du trou noir pour les particules en orbite dans la même direction que le spin. [117]
Formation et évolution
Compte tenu du caractère bizarre des trous noirs, on s’est longtemps demandé si de tels objets pouvaient réellement exister dans la nature ou s’ils n’étaient que des solutions pathologiques aux équations d’Einstein. Einstein lui-même pensait à tort que les trous noirs ne se formeraient pas, car il soutenait que le moment cinétique des particules qui s’effondrent stabiliserait leur mouvement à un certain rayon. [118] Cela a conduit la communauté de la relativité générale à rejeter tous les résultats contraires pendant de nombreuses années. Cependant, une minorité de relativistes a continué à soutenir que les trous noirs étaient des objets physiques, [119] et à la fin des années 1960, ils avaient persuadé la majorité des chercheurs dans le domaine qu’il n’y avait aucun obstacle à la formation d’un horizon des événements. [ citation nécessaire ]
Simulation de la collision de deux trous noirs
Penrose a démontré qu’une fois qu’un horizon d’événements se forme, la relativité générale sans mécanique quantique exige qu’une singularité se forme à l’intérieur. [52] Peu de temps après, Hawking a montré que de nombreuses solutions cosmologiques qui décrivent le Big Bang ont des singularités sans champs scalaires ou autre matière exotique (voir ” Théorèmes de singularité de Penrose-Hawking “). [ clarification nécessaire ] La solution de Kerr , le théorème sans cheveux et les lois de la thermodynamique des trous noirs ont montré que les propriétés physiques des trous noirs étaient simples et compréhensibles, ce qui en faisait des sujets de recherche respectables. [120]Les trous noirs conventionnels sont formés par l’effondrement gravitationnel d’objets lourds tels que des étoiles, mais ils peuvent aussi en théorie être formés par d’autres processus. [121] [122]
Effondrement gravitationnel

 Nuage de gaz déchiré par un trou noir au centre de la Voie lactée (les observations de 2006, 2010 et 2013 sont indiquées respectivement en bleu, vert et rouge). [123]
Nuage de gaz déchiré par un trou noir au centre de la Voie lactée (les observations de 2006, 2010 et 2013 sont indiquées respectivement en bleu, vert et rouge). [123]
L’effondrement gravitationnel se produit lorsque la pression interne d’un objet est insuffisante pour résister à la propre gravité de l’objet. Pour les étoiles, cela se produit généralement soit parce qu’une étoile a trop peu de “carburant” pour maintenir sa température par nucléosynthèse stellaire , soit parce qu’une étoile qui aurait été stable reçoit de la matière supplémentaire d’une manière qui n’augmente pas sa température centrale. Dans les deux cas, la température de l’étoile n’est plus assez élevée pour l’empêcher de s’effondrer sous son propre poids. [124] L’effondrement peut être arrêté par la pression de dégénérescence des constituants de l’étoile, permettant la condensation de la matière dans un état exotique plus dense . Le résultat est l’un des différents types d’ étoiles compactes. Le type de forme dépend de la masse du reste de l’étoile d’origine laissée si les couches externes ont été soufflées (par exemple, dans une supernova de type II ). La masse du reste, l’objet effondré qui survit à l’explosion, peut être sensiblement inférieure à celle de l’étoile d’origine. Les restes dépassant 5 M ☉ sont produits par des étoiles qui avaient plus de 20 M ☉ avant l’effondrement. [124]
Si la masse du résidu dépasse environ 3–4 M ☉ (la limite Tolman–Oppenheimer–Volkoff [33] ), soit parce que l’étoile d’origine était très lourde, soit parce que le résidu a collecté une masse supplémentaire par accrétion de matière, même la pression de dégénérescence de neutrons est insuffisante pour arrêter l’effondrement. Aucun mécanisme connu (hormis éventuellement la pression de dégénérescence des quarks, voir quark star ) n’est assez puissant pour arrêter l’implosion et l’objet s’effondrera inévitablement pour former un trou noir. [124]

 Vue d’artiste d’une graine de trou noir supermassif [125]
Vue d’artiste d’une graine de trou noir supermassif [125]
L’effondrement gravitationnel des étoiles lourdes est supposé être responsable de la formation de trous noirs de masse stellaire . La formation d’étoiles dans l’univers primitif peut avoir donné lieu à des étoiles très massives qui, lors de leur effondrement, auraient produit des trous noirs allant jusqu’à 103 M ☉ . Ces trous noirs pourraient être les germes des trous noirs supermassifs trouvés au centre de la plupart des galaxies. [126] Il a en outre été suggéré que des trous noirs massifs avec des masses typiques d’environ 105 M ☉ aurait pu se former à partir de l’effondrement direct de nuages de gaz dans le jeune univers. [121] Ces objets massifs ont été proposés comme les graines qui ont finalement formé les premiers quasars déjà observés au redshift z ∼ 7 {displaystyle zsim 7} 
. [127] Certains candidats pour de tels objets ont été trouvés dans les observations du jeune univers. [121]
Alors que la majeure partie de l’énergie libérée lors de l’effondrement gravitationnel est émise très rapidement, un observateur extérieur ne voit pas réellement la fin de ce processus. Même si l’effondrement prend un temps fini par rapport au cadre de référence de la matière qui tombe, un observateur distant verrait la matière qui tombe ralentir et s’arrêter juste au-dessus de l’horizon des événements, en raison de la dilatation gravitationnelle du temps. La lumière du matériau qui s’effondre prend de plus en plus de temps pour atteindre l’observateur, la lumière émise juste avant la formation de l’horizon des événements étant retardée d’une durée infinie. Ainsi, l’observateur extérieur ne voit jamais la formation de l’horizon des événements ; au lieu de cela, le matériau qui s’effondre semble devenir plus sombre et de plus en plus décalé vers le rouge, pour finalement disparaître. [128]
Les trous noirs primordiaux et le Big Bang
L’effondrement gravitationnel nécessite une grande densité. À l’époque actuelle de l’univers, ces densités élevées ne se trouvent que dans les étoiles, mais dans l’univers primitif peu de temps après le Big Bang, les densités étaient beaucoup plus importantes, permettant peut-être la création de trous noirs. La haute densité seule ne suffit pas pour permettre la formation de trous noirs car une distribution de masse uniforme ne permettra pas à la masse de se regrouper. Pour que des trous noirs primordiaux se soient formés dans un milieu aussi dense, il doit y avoir eu des perturbations de densité initiales qui pourraient ensuite se développer sous leur propre gravité. Différents modèles pour l’univers primitif varient considérablement dans leurs prédictions de l’ampleur de ces fluctuations. Divers modèles prédisent la création de trous noirs primordiaux dont la taille varie d’une masse de Planck ( mP = √ ħ c / G ≈1,2 × 10 19 GeV/ c 2 ≈2,2 × 10 −8 kg ) à des centaines de milliers de masses solaires. [122]
Bien que l’univers primitif soit extrêmement dense – beaucoup plus dense que ce qui est généralement nécessaire pour former un trou noir – il ne s’est pas re-effondré en trou noir pendant le Big Bang. Les modèles d’effondrement gravitationnel d’objets de taille relativement constante, comme les étoiles , ne s’appliquent pas nécessairement de la même manière à un espace en expansion rapide comme le Big Bang. [129]
Collisions à haute énergie

 Événement simulé dans le détecteur CMS : une collision dans laquelle un micro trou noir peut être créé
Événement simulé dans le détecteur CMS : une collision dans laquelle un micro trou noir peut être créé
L’effondrement gravitationnel n’est pas le seul processus qui pourrait créer des trous noirs. En principe, des trous noirs pourraient se former lors de collisions à haute énergie atteignant une densité suffisante. Depuis 2002, aucun événement de ce type n’a été détecté, que ce soit directement ou indirectement en tant que déficience du bilan de masse dans les expériences d’ accélérateur de particules. [130] Cela suggère qu’il doit y avoir une limite inférieure pour la masse des trous noirs. Théoriquement, cette frontière devrait se situer autour de la masse de Planck, où les effets quantiques devraient invalider les prédictions de la relativité générale. [131]Cela mettrait la création de trous noirs hors de portée de tout processus à haute énergie se produisant sur ou à proximité de la Terre. Cependant, certains développements de la gravité quantique suggèrent que la masse minimale du trou noir pourrait être beaucoup plus faible : certains scénarios braneworld par exemple placent la frontière aussi bas que1 TeV/ c 2 . [132] Cela rendrait concevable la création de micro trous noirs dans les collisions à haute énergie qui se produisent lorsque les rayons cosmiques frappent l’atmosphère terrestre, ou peut-être dans le Large Hadron Collider au CERN . Ces théories sont très spéculatives, et la création de trous noirs dans ces processus est jugée peu probable par de nombreux spécialistes. [133] Même si des micro trous noirs pouvaient se former, on s’attend à ce qu’ils s’évaporent en environ 10 à 25 secondes, ne posant aucune menace pour la Terre. [134]
Croissance
Une fois qu’un trou noir s’est formé, il peut continuer à se développer en absorbant de la matière supplémentaire . Tout trou noir absorbera continuellement le gaz et la poussière interstellaire de son environnement. Ce processus de croissance est une voie possible par laquelle certains trous noirs supermassifs ont pu se former, bien que la formation de trous noirs supermassifs soit encore un domaine de recherche ouvert. [126] Un processus similaire a été suggéré pour la formation de trous noirs de masse intermédiaire trouvés dans les amas globulaires . [135]Les trous noirs peuvent également fusionner avec d’autres objets tels que des étoiles ou même d’autres trous noirs. On pense que cela a été important, en particulier au début de la croissance des trous noirs supermassifs, qui auraient pu se former à partir de l’agrégation de nombreux objets plus petits. [126] Le processus a également été proposé comme l’origine de certains trous noirs de masse intermédiaire. [136] [137]
Évaporation
En 1974, Hawking a prédit que les trous noirs ne sont pas entièrement noirs mais émettent de petites quantités de rayonnement thermique à une température ħ c 3 /(8π GM k B ); [58] cet effet est devenu connu sous le nom de rayonnement de Hawking. En appliquant la théorie quantique des champs à un fond de trou noir statique, il a déterminé qu’un trou noir devrait émettre des particules qui affichent un spectre de corps noir parfait . Depuis la publication de Hawking, beaucoup d’autres ont vérifié le résultat par diverses approches. [138] Si la théorie de Hawking sur le rayonnement des trous noirs est correcte, on s’attend à ce que les trous noirs rétrécissent et s’évaporent avec le temps à mesure qu’ils perdent de la masse par l’émission de photons et d’autres particules. [58]La température de ce spectre thermique ( température de Hawking ) est proportionnelle à la gravité de surface du trou noir, qui, pour un Trou noir de Schwarzschild, est inversement proportionnelle à la masse. Par conséquent, les grands trous noirs émettent moins de rayonnement que les petits trous noirs. [139]
Un trou noir stellaire de 1 M ☉ a une température de Hawking de 62 nanokelvins . [140] C’est bien moins que la température de 2,7 K du rayonnement de fond cosmique des micro-ondes . Les trous noirs de masse stellaire ou plus grands reçoivent plus de masse du fond cosmique micro-ondes qu’ils n’en émettent par le rayonnement de Hawking et vont donc croître au lieu de rétrécir. [141] Pour avoir une température de Hawking supérieure à 2,7 K (et pouvoir s’évaporer), un trou noir aurait besoin d’une masse inférieure à la Lune . Un tel trou noir aurait un diamètre inférieur à un dixième de millimètre. [142]
Si un trou noir est très petit, les effets du rayonnement devraient devenir très forts. Un trou noir de la masse d’une voiture aurait un diamètre d’environ 10 −24 m et mettrait une nanoseconde à s’évaporer, période pendant laquelle il aurait brièvement une luminosité de plus de 200 fois celle du Soleil. On s’attend à ce que les trous noirs de masse inférieure s’évaporent encore plus rapidement; par exemple, un trou noir de masse 1 TeV/ c 2 mettrait moins de 10 −88 secondes à s’évaporer complètement. Pour un si petit trou noir, les effets de la gravité quantique devraient jouer un rôle important et pourraient hypothétiquement rendre un si petit trou noir stable, bien que les développements actuels de la gravité quantique n’indiquent pas que ce soit le cas. [143] [144]
Le rayonnement de Hawking pour un trou noir astrophysique devrait être très faible et serait donc extrêmement difficile à détecter depuis la Terre. Une exception possible, cependant, est la bouffée de rayons gamma émise lors de la dernière étape de l’évaporation des trous noirs primordiaux. Les recherches de tels éclairs se sont avérées infructueuses et fournissent des limites strictes à la possibilité d’existence de trous noirs primordiaux de faible masse. [145] Le télescope spatial à rayons gamma Fermi de la NASA lancé en 2008 poursuivra la recherche de ces éclairs. [146]
Si les trous noirs s’évaporent via le rayonnement de Hawking, un trou noir de masse solaire s’évaporera (commençant une fois que la température du fond diffus cosmologique descend en dessous de celle du trou noir) sur une période de 10 64 ans. [147] Un trou noir supermassif de masse 1011 M ☉ s’évaporera en environ 2×10 100 ans. [148] Certains trous noirs monstres dans l’univers devraient continuer à croître jusqu’à peut-être 1014 M ☉ lors de l’effondrement des superamas de galaxies. Même ceux-ci s’évaporeraient sur une échelle de temps allant jusqu’à 10 106 ans. [147]
Preuve observationnelle
La galaxie Messier 87 – la maison du premier trou noir imagé 
 le contexte
le contexte 
 fermer
fermer 
 un trou noir supermassif
un trou noir supermassif
Par nature, les trous noirs n’émettent eux-mêmes aucun rayonnement électromagnétique autre que l’hypothétique rayonnement de Hawking , de sorte que les astrophysiciens à la recherche de trous noirs doivent généralement s’appuyer sur des observations indirectes. Par exemple, l’existence d’un trou noir peut parfois être déduite en observant son influence gravitationnelle sur son environnement. [149]
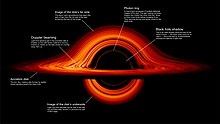
Le 10 avril 2019, une image d’un trou noir a été publiée, qui est agrandie car les trajets lumineux près de l’horizon des événements sont fortement courbés. L’ombre noire au milieu résulte des trajets lumineux absorbés par le trou noir. [150] L’image est en fausses couleurs , car le halo lumineux détecté dans cette image n’est pas dans le spectre visible, mais dans les ondes radio.

 Cette vue d’artiste représente les trajectoires des photons au voisinage d’un trou noir. La flexion gravitationnelle et la capture de la lumière par l’horizon des événements sont la cause de l’ombre capturée par le télescope Event Horizon.
Cette vue d’artiste représente les trajectoires des photons au voisinage d’un trou noir. La flexion gravitationnelle et la capture de la lumière par l’horizon des événements sont la cause de l’ombre capturée par le télescope Event Horizon.
L’ Event Horizon Telescope (EHT) est un programme actif qui observe directement l’environnement immédiat des horizons d’événements des trous noirs, comme le trou noir au centre de la Voie lactée. En avril 2017, EHT a commencé à observer le trou noir au centre de Messier 87 . [151] “En tout, huit observatoires radio sur six montagnes et quatre continents ont observé la galaxie dans la Vierge pendant 10 jours en avril 2017” pour fournir les données donnant l’image en avril 2019. [152] Après deux ans de données traitement, EHT a publié la première image directe d’un trou noir; plus précisément, le trou noir supermassif qui se trouve au centre de la galaxie susmentionnée. [153] [154]Ce qui est visible n’est pas le trou noir, qui apparaît comme noir en raison de la perte de toute lumière dans cette région sombre. Au lieu de cela, ce sont les gaz au bord de l’horizon des événements (affichés en orange ou en rouge) qui définissent le trou noir. [155]
On pense que l’éclaircissement de ce matériau dans la moitié «inférieure» de l’image EHT traitée est causé par le rayonnement Doppler , dans lequel le matériau s’approchant du spectateur à des vitesses relativistes est perçu comme plus brillant que le matériau s’éloignant. Dans le cas d’un trou noir, ce phénomène implique que la matière visible tourne à des vitesses relativistes (>1 000 km/s [2 200 000 mph]), les seules vitesses auxquelles il est possible d’équilibrer par centrifugation l’immense attraction gravitationnelle de la singularité , et ainsi rester en orbite au-dessus de l’horizon des événements. Cette configuration de matériau brillant implique que l’EHT a observé M87 * d’un point de vue capturant le disque d’accrétion du trou noir presque par la tranche, alors que l’ensemble du système tournait dans le sens des aiguilles d’une montre. [156] [157]Cependant, la lentille gravitationnelle extrême associée aux trous noirs produit l’illusion d’une perspective qui voit le disque d’accrétion d’en haut. En réalité, la majeure partie de l’anneau dans l’image EHT a été créée lorsque la lumière émise par la face cachée du disque d’accrétion s’est pliée autour du puits de gravité du trou noir et s’est échappée, ce qui signifie que la plupart des perspectives possibles sur M87* peuvent voir le disque entier. , même que directement derrière “l’ombre”.
En 2015, l’EHT a détecté des champs magnétiques juste à l’extérieur de l’horizon des événements du Sagittaire A* et a même discerné certaines de leurs propriétés. Les lignes de champ qui traversent le disque d’accrétion étaient un mélange complexe d’ordre et d’enchevêtrement. Les études théoriques des trous noirs avaient prédit l’existence de champs magnétiques. [158] [159]

 Apparition prédite d’un trou noir non rotatif avec un anneau toroïdal de matière ionisée, tel qu’il a été proposé [160] comme modèle pour Sagittarius A* . L’asymétrie est due à l’ effet Doppler résultant de l’énorme vitesse orbitale nécessaire à l’équilibre centrifuge de la puissante attraction gravitationnelle du trou.
Apparition prédite d’un trou noir non rotatif avec un anneau toroïdal de matière ionisée, tel qu’il a été proposé [160] comme modèle pour Sagittarius A* . L’asymétrie est due à l’ effet Doppler résultant de l’énorme vitesse orbitale nécessaire à l’équilibre centrifuge de la puissante attraction gravitationnelle du trou.
Détection des ondes gravitationnelles issues de la fusion de trous noirs
Le 14 septembre 2015, l’ observatoire d’ondes gravitationnelles LIGO a réalisé la toute première observation directe réussie d’ondes gravitationnelles . [12] [161] Le signal était cohérent avec les prédictions théoriques pour les ondes gravitationnelles produites par la fusion de deux trous noirs : l’un avec environ 36 masses solaires et l’autre autour de 29 masses solaires. [12] [162]Cette observation fournit la preuve la plus concrète de l’existence de trous noirs à ce jour. Par exemple, le signal d’onde gravitationnelle suggère que la séparation des deux objets avant la fusion n’était que de 350 km (soit environ quatre fois le rayon de Schwarzschild correspondant aux masses déduites). Les objets devaient donc être extrêmement compacts, laissant les trous noirs comme l’interprétation la plus plausible. [12]
Plus important encore, le signal observé par LIGO comprenait également le début du ringdown post-fusion , le signal produit lorsque l’objet compact nouvellement formé s’installe dans un état stationnaire. On peut dire que le ringdown est le moyen le plus direct d’observer un trou noir. [163] A partir du signal LIGO, il est possible d’extraire la fréquence et le temps d’amortissement du mode dominant du ringdown. À partir de ceux-ci, il est possible de déduire la masse et le moment cinétique de l’objet final, qui correspondent aux prédictions indépendantes des simulations numériques de la fusion. [164]La fréquence et le temps de décroissance du mode dominant sont déterminés par la géométrie de la sphère photonique. Ainsi, l’observation de ce mode confirme la présence d’une sphère de photons ; cependant, cela ne peut pas exclure d’éventuelles alternatives exotiques aux trous noirs suffisamment compacts pour avoir une sphère de photons. [163]
L’observation fournit également la première preuve observationnelle de l’existence de binaires de trous noirs de masse stellaire. De plus, il s’agit de la première preuve d’observation de trous noirs de masse stellaire pesant 25 masses solaires ou plus. [165]
Depuis lors, de nombreux autres événements d’ondes gravitationnelles ont été observés. [166]
Mouvements propres des étoiles en orbite autour du Sagittaire A*
Les mouvements propres des étoiles près du centre de notre propre Voie lactée fournissent des preuves observationnelles solides que ces étoiles sont en orbite autour d’un trou noir supermassif. [167] Depuis 1995, les astronomes ont suivi les mouvements de 90 étoiles en orbite autour d’un objet invisible coïncidant avec la source radio Sagittarius A*. En ajustant leurs mouvements aux orbites képlériennes , les astronomes ont pu déduire, en 1998, qu’unUn objet de 2,6 × 10 6 M ☉ doit être contenu dans un volume d’un rayon de 0,02 années-lumière pour provoquer les mouvements de ces étoiles. [168] Depuis lors, l’une des étoiles, appelée S2 , a effectué une orbite complète. A partir des données orbitales, les astronomes ont pu affiner les calculs de la masse pour4,3 × 10 6 M ☉ et un rayon inférieur à 0,002 années-lumière pour l’objet provoquant le mouvement orbital de ces étoiles. [167] La limite supérieure de la taille de l’objet est encore trop grande pour tester s’il est plus petit que son rayon de Schwarzschild ; néanmoins, ces observations suggèrent fortement que l’objet central est un trou noir supermassif car il n’y a pas d’autres scénarios plausibles pour confiner autant de masse invisible dans un si petit volume. [168] De plus, il existe des preuves d’observation que cet objet pourrait posséder un horizon des événements, une caractéristique unique aux trous noirs. [169]
Accrétion de matière

 Trou noir avec couronne, source de rayons X (concept d’artiste) [170]
Trou noir avec couronne, source de rayons X (concept d’artiste) [170]
En raison de la conservation du moment cinétique , [171] le gaz tombant dans le puits gravitationnel créé par un objet massif formera généralement une structure en forme de disque autour de l’objet. Les impressions d’artistes telles que la représentation d’accompagnement d’un trou noir avec couronne dépeignent généralement le trou noir comme s’il s’agissait d’un corps plat cachant la partie du disque juste derrière lui, mais en réalité, la lentille gravitationnelle déformerait considérablement l’image du disque d’accrétion. [172]
 La NASA a simulé la vue depuis l’extérieur de l’horizon d’un Trou noir de Schwarzschild éclairé par un mince disque d’accrétion.
La NASA a simulé la vue depuis l’extérieur de l’horizon d’un Trou noir de Schwarzschild éclairé par un mince disque d’accrétion.
Dans un tel disque, le frottement entraînerait le transport du moment cinétique vers l’extérieur, permettant à la matière de tomber plus loin vers l’intérieur, libérant ainsi de l’énergie potentielle et augmentant la température du gaz. [173]
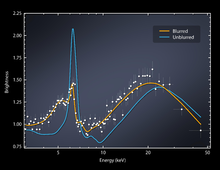
 Flou des rayons X près du trou noir ( NuSTAR ; 12 août 2014) [170]
Flou des rayons X près du trou noir ( NuSTAR ; 12 août 2014) [170]
Lorsque l’objet en accrétion est une étoile à neutrons ou un trou noir, le gaz du disque d’accrétion interne orbite à des vitesses très élevées en raison de sa proximité avec l’ objet compact . Le frottement qui en résulte est si important qu’il chauffe le disque interne à des températures auxquelles il émet de grandes quantités de rayonnement électromagnétique (principalement des rayons X). Ces sources lumineuses de rayons X peuvent être détectées par des télescopes. Ce processus d’accrétion est l’un des processus de production d’énergie les plus efficaces connus ; jusqu’à 40 % de la masse au repos du matériau accrété peuvent être émis sous forme de rayonnement. [173] (Dans la fusion nucléaire, environ 0,7 % seulement de la masse au repos sera émise sous forme d’énergie.) Dans de nombreux cas, les disques d’accrétion sont accompagnés de jets relativistesqui sont émis le long des pôles, qui emportent une grande partie de l’énergie. Le mécanisme de création de ces jets n’est actuellement pas bien compris, en partie à cause de données insuffisantes. [174]
Ainsi, bon nombre des phénomènes les plus énergétiques de l’univers ont été attribués à l’accrétion de matière sur les trous noirs. En particulier, les noyaux galactiques actifs et les quasars seraient les disques d’accrétion des trous noirs supermassifs. [175] De même, les binaires à rayons X sont généralement acceptés comme étant des systèmes d’ étoiles binaires dans lesquels l’une des deux étoiles est un objet compact accrétant la matière de son compagnon. [175] Il a également été suggéré que certaines sources de rayons X ultralumineuses pourraient être les disques d’accrétion de trous noirs de masse intermédiaire. [176]
En novembre 2011, la première observation directe d’un disque d’accrétion de quasars autour d’un trou noir supermassif a été signalée. [177] [178]
Binaires radiographiques Simulation informatique d’une étoile consommée par un trou noir. Le point bleu indique l’emplacement du trou noir. Cette animation compare les « battements de cœur » des rayons X de GRS 1915 et IGR J17091, deux trous noirs qui ingèrent le gaz des étoiles compagnes. 
 Une image de l’ observatoire Chandra X-Ray de Cygnus X-1 , qui a été le premier candidat trou noir puissant découvert
Une image de l’ observatoire Chandra X-Ray de Cygnus X-1 , qui a été le premier candidat trou noir puissant découvert
Les binaires à rayons X sont des systèmes d’étoiles binaires qui émettent la majorité de leur rayonnement dans la partie rayons X du spectre. On pense généralement que ces émissions de rayons X se produisent lorsqu’une des étoiles (objet compact) accrète la matière d’une autre étoile (régulière). La présence d’une étoile ordinaire dans un tel système permet d’étudier l’objet central et de déterminer s’il s’agit d’un trou noir. [175]
Si un tel système émet des signaux qui peuvent être directement retracés jusqu’à l’objet compact, il ne peut pas s’agir d’un trou noir. L’absence d’un tel signal n’exclut cependant pas la possibilité que l’objet compact soit une étoile à neutrons. En étudiant l’étoile compagne, il est souvent possible d’obtenir les paramètres orbitaux du système et d’obtenir une estimation de la masse de l’objet compact. Si celle-ci est beaucoup plus grande que la limite de Tolman – Oppenheimer – Volkoff (la masse maximale qu’une étoile peut avoir sans s’effondrer), alors l’objet ne peut pas être une étoile à neutrons et on s’attend généralement à ce qu’il soit un trou noir. [175]
Le premier candidat solide pour un trou noir, Cygnus X-1 , a été découvert de cette manière par Charles Thomas Bolton , [179] Louise Webster , et Paul Murdin [180] en 1972. [181] [182]Un doute subsistait cependant en raison des incertitudes qui résultent du fait que l’étoile compagne est beaucoup plus lourde que le trou noir candidat. Actuellement, de meilleurs candidats pour les trous noirs se trouvent dans une classe de binaires de rayons X appelés transitoires de rayons X mous. Dans cette classe de système, l’étoile compagne a une masse relativement faible permettant des estimations plus précises de la masse du trou noir. De plus, ces systèmes n’émettent activement des rayons X que pendant plusieurs mois une fois tous les 10 à 50 ans. Pendant la période de faible émission de rayons X (appelée quiescence), le disque d’accrétion est extrêmement faible permettant une observation détaillée de l’étoile compagne pendant cette période. L’un des meilleurs candidats de ce type est le V404 Cygni . [175]
Oscillations quasi-périodiques
Les émissions de rayons X des disques d’accrétion scintillent parfois à certaines fréquences. Ces signaux sont appelés oscillations quasi-périodiques et on pense qu’ils sont causés par des matériaux se déplaçant le long du bord intérieur du disque d’accrétion (l’orbite circulaire stable la plus à l’intérieur). Ainsi leur fréquence est liée à la masse de l’objet compact. Ils peuvent ainsi être utilisés comme un moyen alternatif pour déterminer la masse des trous noirs candidats. [183]
Noyaux galactiques 
 Les ondes magnétiques, appelées ondes S d’Alfvén , proviennent de la base des jets de trous noirs.
Les ondes magnétiques, appelées ondes S d’Alfvén , proviennent de la base des jets de trous noirs.
Les astronomes utilisent le terme “galaxie active” pour décrire les galaxies avec des caractéristiques inhabituelles, telles qu’une émission de raies spectrales inhabituelle et une très forte émission radio. Des études théoriques et observationnelles ont montré que l’activité de ces noyaux actifs galactiques (AGN) peut s’expliquer par la présence de trous noirs supermassifs, qui peuvent être des millions de fois plus massifs que les trous stellaires. Les modèles de ces AGN consistent en un trou noir central qui peut être des millions ou des milliards de fois plus massif que le Soleil ; un disque de gaz et de poussière interstellaire appelé disque d’accrétion ; et deux jets perpendiculaires au disque d’accrétion. [184] [185]

 Détection d’une éruption de rayons X inhabituellement brillante de Sagittarius A *, un trou noir au centre de la galaxie de la Voie lactée le 5 janvier 2015 [186]
Détection d’une éruption de rayons X inhabituellement brillante de Sagittarius A *, un trou noir au centre de la galaxie de la Voie lactée le 5 janvier 2015 [186]
Bien que l’on s’attende à ce que des trous noirs supermassifs soient trouvés dans la plupart des AGN, seuls les noyaux de certaines galaxies ont été étudiés plus attentivement dans le but d’identifier et de mesurer les masses réelles des candidats trous noirs supermassifs centraux. Certaines des galaxies les plus remarquables avec des candidats trous noirs supermassifs incluent la galaxie d’Andromède , M32 , M87 , NGC 3115 , NGC 3377 , NGC 4258 , NGC 4889 , NGC 1277 , OJ 287 , APM 08279+5255 et la galaxie du Sombrero . [187]
Il est maintenant largement admis que le centre de presque toutes les galaxies, pas seulement celles qui sont actives, contient un trou noir supermassif. [188] L’étroite corrélation observationnelle entre la masse de ce trou et la dispersion de la vitesse du renflement de la galaxie hôte , connue sous le nom de relation M-sigma , suggère fortement un lien entre la formation du trou noir et celle de la galaxie elle-même. [189]

 Simulation d’un nuage de gaz après une approche rapprochée du trou noir au centre de la Voie lactée. [190]
Simulation d’un nuage de gaz après une approche rapprochée du trou noir au centre de la Voie lactée. [190]
Microlentille
Une autre façon de tester la nature de trou noir d’un objet consiste à observer les effets causés par un fort champ gravitationnel à proximité. L’un de ces effets est la lentille gravitationnelle : la déformation de l’espace-temps autour d’un objet massif provoque la déviation des rayons lumineux, comme la lumière passant à travers une lentille optique . Des observations ont été faites de lentilles gravitationnelles faibles, dans lesquelles les rayons lumineux ne sont déviés que de quelques secondes d’ arc . La microlentille se produit lorsque les sources ne sont pas résolues et que l’observateur voit un petit éclaircissement. En janvier 2022, des astronomes ont signalé la première détection possible d’un événement de microlentille à partir d’un trou noir isolé. [191]
Une autre possibilité pour observer la lentille gravitationnelle d’un trou noir serait d’observer des étoiles en orbite autour du trou noir. Il existe plusieurs candidats à une telle observation en orbite autour de Sagittarius A* . [192]
Alternatives
La preuve des trous noirs stellaires repose fortement sur l’existence d’une limite supérieure pour la masse d’une étoile à neutrons. La taille de cette limite dépend fortement des hypothèses faites sur les propriétés de la matière dense. De nouvelles phases exotiques de la matière pourraient repousser cette limite. [175] Une phase de quarks libres à haute densité pourrait permettre l’existence d’étoiles à quarks denses, [193] et certains modèles supersymétriques prédisent l’existence d’ étoiles Q . [194] Certaines extensions du modèle standard postulent l’existence de préons comme éléments constitutifs fondamentaux des quarks et des leptons, qui pourraient hypothétiquement former des étoiles à préons . [195] Ces modèles hypothétiques pourraient potentiellement expliquer un certain nombre d’observations de candidats trous noirs stellaires. Cependant, il peut être démontré à partir d’arguments de la relativité générale que tout objet de ce type aura une masse maximale. [175]
Puisque la densité moyenne d’un trou noir à l’intérieur de son rayon de Schwarzschild est inversement proportionnelle au carré de sa masse, les trous noirs supermassifs sont beaucoup moins denses que les trous noirs stellaires (la densité moyenne d’un 108 M ☉ trou noir est comparable à celui de l’eau). [175] Par conséquent, la physique de la matière formant un trou noir supermassif est bien mieux comprise et les explications alternatives possibles pour les observations de trous noirs supermassifs sont beaucoup plus banales. Par exemple, un trou noir supermassif pourrait être modélisé par un grand groupe d’objets très sombres. Cependant, ces alternatives ne sont généralement pas suffisamment stables pour expliquer les candidats trous noirs supermassifs. [175]
La preuve de l’existence de trous noirs stellaires et supermassifs implique que pour que les trous noirs ne se forment pas, la relativité générale doit échouer en tant que théorie de la gravité, peut-être en raison de l’apparition de corrections mécaniques quantiques . Une caractéristique très attendue d’une théorie de la gravité quantique est qu’elle ne comportera pas de singularités ou d’horizons d’événements et que les trous noirs ne seraient donc pas de véritables artefacts. [196] Par exemple, dans le modèle fuzzball basé sur la théorie des cordes , les états individuels d’une solution de trou noir n’ont généralement pas d’horizon des événements ou de singularité, mais pour un observateur classique/semi-classique, la moyenne statistique de ces états apparaît juste comme un trou noir ordinaire déduit de la relativité générale.[197]
Quelques objets théoriques ont été conjecturés pour correspondre à des observations de candidats trous noirs astronomiques de manière identique ou quasi identique, mais qui fonctionnent via un mécanisme différent. Ceux-ci incluent le gravastar , l’ étoile noire , [198] et l’ étoile à énergie noire . [199]
Questions ouvertes
Entropie et thermodynamique
S =1/4 c 3 k/Għ UN La formule de l’entropie de Bekenstein-Hawking ( S ) d’un trou noir, qui dépend de la surface du trou noir ( A ). Les constantes sont la vitesse de la lumière ( c ), la constante de Boltzmann ( k ), la constante de Newton ( G ) et la constante de Planck réduite ( ħ ). En unités de Planck, cela se réduit à S = UN/4.
En 1971, Hawking a montré dans des conditions générales [Note 5] que la surface totale des horizons des événements de toute collection de trous noirs classiques ne peut jamais diminuer, même s’ils entrent en collision et fusionnent. [200] Ce résultat, maintenant connu sous le nom de deuxième loi de la mécanique des trous noirs , est remarquablement similaire à la deuxième loi de la thermodynamique , qui stipule que l’entropie totale d’un système isolé ne peut jamais diminuer. Comme pour les objets classiques au zéro absolutempérature, on a supposé que les trous noirs avaient une entropie nulle. Si tel était le cas, la deuxième loi de la thermodynamique serait violée par l’entrée de matière chargée d’entropie dans un trou noir, entraînant une diminution de l’entropie totale de l’univers. Par conséquent, Bekenstein a proposé qu’un trou noir ait une entropie et qu’elle soit proportionnelle à sa surface d’horizon. [201]
Le lien avec les lois de la thermodynamique a été encore renforcé par la découverte de Hawking en 1974 selon laquelle la théorie quantique des champs prédit qu’un trou noir émet un rayonnement de corps noir à une température constante. Cela provoque apparemment une violation de la deuxième loi de la mécanique des trous noirs, puisque le rayonnement emportera l’énergie du trou noir, le faisant rétrécir. Le rayonnement, cependant, emporte également de l’entropie, et il peut être prouvé sous des hypothèses générales que la somme de l’entropie de la matière entourant un trou noir et un quart de la surface de l’horizon mesurée en unités de Planck est en fait toujours croissante. Cela permet la formulation de la première loi de la mécanique des trous noirs comme un analogue de la première loi de la thermodynamique, avec la masse agissant comme énergie, la gravité de surface comme température et la surface comme entropie. [201]
Une caractéristique déroutante est que l’entropie d’un trou noir évolue avec sa surface plutôt qu’avec son volume, puisque l’entropie est normalement une quantité extensive qui évolue linéairement avec le volume du système. Cette propriété étrange a conduit Gerard ‘t Hooft et Leonard Susskind à proposer le principe holographique , qui suggère que tout ce qui se passe dans un volume d’espace-temps peut être décrit par des données à la limite de ce volume. [202]
Bien que la relativité générale puisse être utilisée pour effectuer un calcul semi-classique de l’entropie des trous noirs, cette situation est théoriquement insatisfaisante. En mécanique statistique , l’entropie est comprise comme le décompte du nombre de configurations microscopiques d’un système qui ont les mêmes qualités macroscopiques (comme la masse, la charge, la pression, etc.). Sans une théorie satisfaisante de la gravité quantique, on ne peut pas effectuer un tel calcul pour les trous noirs. Des progrès ont été réalisés dans diverses approches de la gravité quantique. En 1995, Andrew Strominger et Cumrun Vafa ont montré que le comptage des micro-états d’un trou noir supersymétrique spécifique dans la théorie des cordes reproduisait l’entropie de Bekenstein-Hawking. [203]Depuis lors, des résultats similaires ont été rapportés pour différents trous noirs à la fois dans la théorie des cordes et dans d’autres approches de la gravité quantique comme la gravité quantique en boucle . [204]
Une autre approche prometteuse consiste à traiter la gravité comme une théorie effective des champs . On calcule d’abord les corrections gravitationnelles quantiques au rayon de l’horizon des événements du trou noir, puis on les intègre pour trouver les corrections gravitationnelles quantiques à l’entropie telles que données par la formule de Wald . La méthode a été appliquée pour les trous noirs de Schwarzschild par Calmet et Kuipers, puis généralisée avec succès pour les trous noirs chargés par Campos Delgado. [206]
Paradoxe de la perte d’informations
Problème non résolu en physique :
L’information physique est-elle perdue dans les trous noirs ?
(plus de problèmes non résolus en physique)
Parce qu’un trou noir n’a que quelques paramètres internes, la plupart des informations sur la matière qui a formé le trou noir sont perdues. Quel que soit le type de matière qui entre dans un trou noir, il apparaît que seules les informations concernant la masse totale, la charge et le moment cinétique sont conservées. Tant que l’on pensait que les trous noirs persisteraient éternellement, cette perte d’information n’est pas si problématique, car l’information peut être considérée comme existant à l’intérieur du trou noir, inaccessible de l’extérieur, mais représentée sur l’horizon des événements conformément au principe holographique. Cependant, les trous noirs s’évaporent lentement en émettant un rayonnement de Hawking. Ce rayonnement ne semble pas contenir d’informations supplémentaires sur la matière qui a formé le trou noir, ce qui signifie que ces informations semblent avoir disparu à jamais.[207]
La question de savoir si l’information est vraiment perdue dans les trous noirs (le paradoxe de l’information du trou noir ) a divisé la communauté de la physique théorique (voir le pari Thorne-Hawking-Preskill ). En mécanique quantique, la perte d’information correspond à la violation d’une propriété appelée unitarité , et il a été soutenu que la perte d’unitarité impliquerait également une violation de la conservation de l’énergie, [208] bien que cela ait également été contesté. [209] Au cours des dernières années, des preuves se sont accumulées selon lesquelles l’information et l’unitarité sont effectivement préservées dans un traitement gravitationnel quantique complet du problème. [210]
Une tentative pour résoudre le paradoxe de l’information du trou noir est connue sous le nom de complémentarité du trou noir . En 2012, le « paradoxe du pare-feu » a été introduit dans le but de démontrer que la complémentarité des trous noirs ne résout pas le paradoxe de l’information. Selon la théorie quantique des champs dans l’espace-temps courbe , une seule émission de rayonnement de Hawking implique deux enchevêtrements mutuels.particules. La particule sortante s’échappe et est émise sous la forme d’un quantum de rayonnement de Hawking ; la particule qui tombe est avalée par le trou noir. Supposons qu’un trou noir s’est formé un temps fini dans le passé et s’évaporera complètement dans un temps fini dans le futur. Ensuite, il n’émettra qu’une quantité finie d’informations codées dans son rayonnement Hawking. Selon les recherches de physiciens comme Don Page [211] [212] et Leonard Susskind, il y aura finalement un moment où une particule sortante devra être intriquée avec tout le rayonnement de Hawking que le trou noir a précédemment émis. Cela crée apparemment un paradoxe : un principe appelé ” la monogamie de l’enchevêtrement” exige que, comme tout système quantique, la particule sortante ne puisse pas être complètement intriquée avec deux autres systèmes en même temps ; pourtant, ici, la particule sortante semble être intriquée à la fois avec la particule entrante et, indépendamment, avec le rayonnement de Hawking passé. [213 ] Afin de résoudre cette contradiction, les physiciens pourraient éventuellement être contraints d’abandonner l’un des trois principes éprouvés : le principe d’équivalence d’Einstein, l’unitarité ou la théorie des champs quantiques locaux. Une solution possible, qui viole le principe d’équivalence, est qu’un ” pare-feu “détruit les particules entrantes à l’horizon des événements. [214] En général, laquelle – le cas échéant – de ces hypothèses devrait être abandonnée reste un sujet de débat. [209]
Voir également
- Trou noir binaire
- Boîte noire
- Brane noire ou ficelle noire
- Initiative du trou noir
- Vaisseau trou noir
- Trous noirs dans la fiction
- Blanet
- Trou noir BTZ
- Trou noir à effondrement direct
- Singularité gravitationnelle
- Trou noir hypothétique (homonymie)
- Kugelblitz (astrophysique)
- Liste des trous noirs
- Liste des trous noirs les plus proches
- Aperçu des trous noirs
- Trou noir sonique
- Bataille Susskind-Hawking
- Chronologie de la physique des trous noirs
- Trou blanc
Remarques
- ^ La valeur de cJ/GM 2 peut dépasser 1 pour les objets autres que les trous noirs. La plus grande valeur connue pour une étoile à neutrons est ≤ 0,4, et les équations d’état couramment utilisées limiteraient cette valeur à < 0,7. [76]
- ^ Le rayon (extérieur) de l’horizon des événements est égal à : M + M 2 − ( J / M ) 2 − Q 2 . {displaystyle M+{sqrt {M^{2}-{(J/M)}^{2}-Q^{2}}}.}
- ↑ L’ensemble des chemins possibles, ou plus précisément le futur cône de lumière contenant toutes les lignes d’univers possibles (dans ce schéma le cône de lumière est représenté par la région en forme de V délimitée par des flèches représentant les lignes d’univers des rayons lumineux), est incliné de cette manière dans Coordonnées d’Eddington – Finkelstein (le diagramme est une version “dessin animé” d’un diagramme de coordonnées d’Eddington – Finkelstein), mais dans d’autres coordonnées, les cônes de lumière ne sont pas inclinés de cette manière, par exemple dans les coordonnées de Schwarzschild, ils se rétrécissent simplement sans s’incliner à l’approche duhorizon des événements, et dans les coordonnées de Kruskal – Szekeres, les cônes de lumière ne changent pas du tout de forme ou d’orientation. [79]
- ^ Ceci n’est vrai que pour les espaces-temps à quatre dimensions. Dans des dimensions plus élevées, des topologies d’horizon plus compliquées comme un anneau noir sont possibles. [91] [92]
- ↑ En particulier, il suppose que toute matière satisfait à la condition d’énergie faible .
Références
- ^ Oldham, LJ; Auger, MW (mars 2016). “Structure de galaxie à partir de plusieurs traceurs – II. M87 du parsec aux échelles de mégaparsec”. Avis mensuels de la Royal Astronomical Society . 457 (1): 421–439. arXiv : 1601.01323 . Bibcode : 2016MNRAS.457..421O . doi : 10.1093/mnras/stv2982 . S2CID 119166670 .
- ^ Wald 1984 , pp. 299-300
- ^ un b Wald, RM (1997). “Effondrement gravitationnel et censure cosmique”. À Iyer, BR ; Bhawal, B. (éd.). Trous noirs, rayonnement gravitationnel et univers . Dordrecht : Springer. p. 69–86. arXiv : gr-qc/9710068 . doi : 10.1007/978-94-017-0934-7 . ISBN 978-9401709347.
- ^ Au revoir, Dennis (8 juin 2015). “Chasseurs de trous noirs” . NASA . Archivé de l’original le 9 juin 2015 . Récupéré le 8 juin 2015 .
- ^ Hamilton, A. “Voyage dans un Trou noir de Schwarzschild” . jila.colorado.edu . Archivé de l’original le 3 septembre 2019 . Récupéré le 28 juin 2020 .
- ^ Schutz, Bernard F. (2003). Gravité du sol vers le haut . La presse de l’Universite de Cambridge. p. 110. ISBN 978-0-521-45506-0. Archivé de l’original le 2 décembre 2016.
- ^ Davies, PCW (1978). “Thermodynamique des trous noirs” (PDF) . Rapports sur les progrès de la physique . 41 (8) : 1313-1355. Code Bib : 1978RPPh …41.1313D . doi : 10.1088/0034-4885/41/8/004 . Archivé de l’original (PDF) le 10 mai 2013.
- ^ un bc Montgomery , Colin; Orchiston, Wayne; Whittingham, Ian (2009). “Michell, Laplace et l’origine du concept de trou noir”. Journal d’histoire et de patrimoine astronomiques . 12 (2): 90–96. Bibcode : 2009JAHH…12…90M .
- ^ Webster, B. Louise; Murdin, Paul (1972), “Cygnus X-1 – un binaire spectroscopique avec un compagnon lourd?”, Nature , 235 (5332): 37–38, Bibcode : 1972Natur.235…37W , doi : 10.1038/235037a0 , S2CID 4195462
- ^ Bolton, CT (1972), “Identification de Cygnus X-1 avec HDE 226868”, Nature , 235 (5336): 271–273, Bibcode : 1972Natur.235..271B , doi : 10.1038/235271b0 , S2CID 4222070
- ^ Cléry D (2020). “Des trous noirs pris en flagrant délit d’avaler des étoiles”. Sciences . 367 (6477): 495. Bibcode : 2020Sci…367..495C . doi : 10.1126/science.367.6477.495 . PMID 32001633 . S2CID 210984462 .
- ^ un bcd Abbott , BP ; et coll. (2016). “Observation des ondes gravitationnelles à partir d’une fusion de trous noirs binaires”. Phys. Rév. Lett. 116 (6) : 061102. arXiv : 1602.03837 . Bibcode : 2016PhRvL.116f1102A . doi : 10.1103/PhysRevLett.116.061102 . PMID 26918975 . S2CID 124959784 .
- ^ Télescope Event Horizon, Le (2019). “Résultats des premiers télescopes M87 Event Horizon. I. L’ombre du trou noir supermassif”. Le Journal d’Astrophysique . 875 (1) : L1. arXiv : 1906.11238 . Bibcode : 2019ApJ…875L…1E . doi : 10.3847/2041-8213/ab0ec7 . S2CID 145906806 .
- ^ Bouman, Katherine L. ; Johnson, Michael D.; Zoran, Daniel; Fish, Vincent L.; Doeleman, Sheperd S.; Freeman, William T. (2016). “Imagerie computationnelle pour la reconstruction d’images VLBI”. Conférence IEEE 2016 sur la vision par ordinateur et la reconnaissance de formes (CVPR) . pp. 913–922. arXiv : 1512.01413 . doi : 10.1109/CVPR.2016.105 . hdl : 1721.1/103077 . ISBN 978-1-4673-8851-1. S2CID 9085016 .
- ^ Gardiner, Aidan (12 avril 2018). “Quand un trou noir se révèle enfin, il est utile d’avoir notre propre journaliste cosmique – Les astronomes ont annoncé mercredi qu’ils avaient capturé la première image d’un trou noir. Dennis Overbye du Times répond aux questions des lecteurs” . Le New York Times . Archivé de l’original le 1er janvier 2022 . Récupéré le 15 avril 2019 .
- ^ “L’instrument ESO trouve le trou noir le plus proche de la Terre” . Observatoire européen austral . 6 mai 2020. Archivé de l’original le 6 mai 2020 . Récupéré le 2 avril 2021 .
- ^ Riazuelo, Alain (2019). “Voir la relativité – I. Ray tracing dans une métrique de Schwarzschild pour explorer l’extension analytique maximale de la métrique et faire un rendu correct des étoiles”. Journal international de physique moderne D . 28 (2) : 1950042. arXiv : 1511.06025 . Bibcode : 2019IJMPD..2850042R . doi : 10.1142/S0218271819500421 . S2CID 54548877 .
- ^ Schaffer, Simon (1979). “John Michell et les trous noirs” . Journal pour l’histoire de l’astronomie . 10 : 42–43. Bibcode : 1979JHA….10…42S . doi : 10.1177/002182867901000104 . S2CID 123958527 . Archivé de l’original le 22 mai 2020 . Récupéré le 27 août 2021 .
- ^ Michell, J. (1784). “Sur les moyens de découvrir la distance, la magnitude, etc. des étoiles fixes, en conséquence de la diminution de la vitesse de leur lumière, au cas où une telle diminution se produirait dans l’une d’elles, et de telles autres données devrait être obtenu à partir d’observations, comme cela serait encore plus nécessaire à cette fin” . Transactions philosophiques de la Royal Society . 74 : 35–57. Bibcode : 1784RSPT…74…35M . doi : 10.1098/rstl.1784.0008 . JSTOR 106576 .
- ^ un b Thorne 1994 , pp. 123–124
- ^ Tueur, Elizabeth M.; Tueur, Henry S. (1992). Microscopie optique et électronique . La presse de l’Universite de Cambridge. ISBN 978-0-521-33948-3. Archivé de l’original le 30 novembre 2017.
- ^ Crass, Institut d’astronomie – Conception par DR Wilkins et SJ “La lumière s’échappant des trous noirs” . www.ast.cam.ac.uk . Archivé de l’original le 6 juillet 2019 . Récupéré le 10 mars 2018 .
- ^ Levy, Adam (11 janvier 2021). “Comment les trous noirs sont passés de la théorie à la réalité” . Magazine connaissable . doi : 10.1146/connaissable-010921-1 . Récupéré le 25 mars 2022 .
- ^ un b Schwarzschild, K. (1916). “Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie” . Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften . 7 : 189–196. Bibcode : 1916SPAW…….189S .
- Traduction : Antoci, S. ; En ligneLoinger, A. (1999). “Sur le champ gravitationnel d’un point de masse selon la théorie d’Einstein”. arXiv : physique/9905030 .et Schwarzschild, K. (1916). “Über das Gravitationsfeld einer Kugel aus inkompressibler Flüssigkeit nach der Einsteinschen Theorie” . Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften . 18 : 424–434. Bibcode : 1916skpa.conf..424S .
- Traduction : Antoci, S. (1999). “Sur le champ gravitationnel d’une sphère de fluide incompressible selon la théorie d’Einstein”. arXiv : physique/9912033 .
- ^ Droste, J. (1917). “Sur le champ d’un seul centre dans la théorie de la Gravitation d’Einstein, et le mouvement d’une particule dans ce champ” (PDF) . Actes de l’Académie Royale d’Amsterdam . 19 (1): 197–215. Archivé de l’original (PDF) le 18 mai 2013 . Récupéré le 16 septembre 2012 .
- ^ Kox, AJ (1992). “Relativité générale aux Pays-Bas: 1915–1920” . A Eisenstaedt, Jean; Kox, AJ (éd.). Etudes d’histoire de la relativité générale . Birkhauser. p. 41. ISBN 978-0-8176-3479-7. Archivé de l’original le 10 août 2016 . Récupéré le 23 février 2016 .
- ^ ‘t Hooft, G. (2009). “Introduction à la théorie des trous noirs” (PDF) . Institut de Physique Théorique / Institut Spinoza. p. 47–48. Archivé de l’original (PDF) le 21 mai 2009 . Récupéré le 24 juin 2010 .
- ^ Eddington, Arthur (1926). La Constitution Interne des Etoiles . Sciences . Vol. 52. Presse universitaire de Cambridge. p. 233–40. doi : 10.1126/science.52.1341.233 . ISBN 978-0-521-33708-3. PMID 17747682 . Archivé de l’original le 11 août 2016.
- ^ Thorne, Kip S.; Hawking, Stephen (1994). Trous noirs et distorsions temporelles : l’héritage scandaleux d’Einstein . WW Norton & Compagnie. p. 134-135 . ISBN 978-0-393-31276-8. Récupéré le 12 avril 2019 . La première conclusion était la version newtonienne de la lumière qui ne s’échappe pas ; la seconde était une description semi-exacte et relativiste ; et la troisième était une hyperbole eddingtonienne typique … lorsqu’une étoile est aussi petite que la circonférence critique, la courbure est forte mais pas infinie, et l’espace n’est certainement pas enroulé autour de l’étoile. Eddington le savait peut-être, mais sa description a fait une bonne histoire, et elle a capturé de manière fantaisiste l’esprit de la courbure de l’espace-temps de Schwarzschild.”
- ^ Venkataraman, G. (1992). Chandrasekhar et sa limite . Presse des universités. p. 89. ISBN 978-81-7371-035-3. Archivé de l’original le 11 août 2016.
- ^ Detweiler, S. (1981). “Lettre de ressource BH-1 : Trous noirs”. Journal américain de physique . 49 (5): 394–400. Bibcode : 1981AmJPh..49..394D . doi : 10.1119/1.12686 .
- ^ Harpaz, A. (1994). Évolution stellaire . AK Peters . p. 105. ISBN 978-1-56881-012-6. Archivé de l’original le 11 août 2016.
- ^ un b Oppenheimer, JR ; Volkoff, GM (1939). “Sur les noyaux de neutrons massifs”. Examen physique . 55 (4): 374–381. Bibcode : 1939PhRv…55..374O . doi : 10.1103/PhysRev.55.374 .
- ^ Bombaci, I. (1996). “La masse maximale d’une étoile à neutrons”. Astronomie et astrophysique . 305 : 871–877. Bibcode : 1996A&A…305..871B .
- ^ Cho, A. (16 février 2018). “Une limite de poids émerge pour les étoiles à neutrons”. Sciences . 359 (6377): 724–725. Bibcode : 2018Sci…359..724C . doi : 10.1126/science.359.6377.724 . PMID 29449468 .
- ^ Margalit, B.; Metzger, BD (1er décembre 2017). “Contraindre la masse maximale des étoiles à neutrons à partir des observations multi-messagers de GW170817”. Le Journal d’Astrophysique . 850 (2) : L19. arXiv : 1710.05938 . Bibcode : 2017ApJ…850L..19M . doi : 10.3847/2041-8213/aa991c . S2CID 119342447 .
- ^ Shibata, M.; Fujibayashi, S.; Hotokezaka, K.; Kiuchi, K.; Kyutoku, K.; Sekiguchi, Y.; Tanaka, M. (22 décembre 2017). “Modélisation GW170817 basée sur la relativité numérique et ses implications”. Examen physique D . 96 (12) : 123012. arXiv : 1710.07579 . Bibcode : 2017PhRvD..96l3012S . doi : 10.1103/PhysRevD.96.123012 . S2CID 119206732 .
- ^ Ruiz, M.; Shapiro, SL; Tsokaros, A. (11 janvier 2018). “GW170817, simulations magnétohydrodynamiques relativistes générales et masse maximale de l’étoile à neutrons” . Examen physique D . 97 (2) : 021501. arXiv : 1711.00473 . Bibcode : 2018PhRvD..97b1501R . doi : 10.1103/PhysRevD.97.021501 . PMC 6036631 . PMID 30003183 .
- ^ Rezzolla, L.; La plupart, ER ; Weih, LR (9 janvier 2018). “Utilisation des observations d’ondes gravitationnelles et des relations quasi universelles pour contraindre la masse maximale des étoiles à neutrons”. Revue d’Astrophysique . 852 (2) : L25. arXiv : 1711.00314 . Bibcode : 2018ApJ…852L..25R . doi : 10.3847/2041-8213/aaa401 . S2CID 119359694 .
- ^ Ruffini, R. ; Wheeler, JA (1971). “Présentation du trou noir” (PDF) . La physique aujourd’hui . 24 (1): 30–41. Bibcode : 1971PhT….24a..30R . doi : 10.1063/1.3022513 . Archivé de l’original (PDF) le 25 juillet 2011 . Récupéré le 5 décembre 2009 .
- ^ Finkelstein, D. (1958). “Asymétrie passé-futur du champ gravitationnel d’une particule ponctuelle”. Examen physique . 110 (4): 965–967. Bibcode : 1958PhRv..110..965F . doi : 10.1103/PhysRev.110.965 .
- ^ Kruskal, M. (1960). “Extension maximale de Schwarzschild Metric”. Examen physique . 119 (5): 1743. Bibcode : 1960PhRv..119.1743K . doi : 10.1103/PhysRev.119.1743 .
- ^ Hewish, A. ; et coll. (1968). “Observation d’une source radio à pulsations rapides”. Nature . 217 (5130): 709–713. Bibcode : 1968Natur.217..709H . doi : 10.1038/217709a0 . S2CID 4277613 .
- ^ Pilkington, JDH; et coll. (1968). “Observations de quelques autres sources radio pulsées”. Nature . 218 (5137): 126–129. Bibcode : 1968Natur.218..126P . doi : 10.1038/218126a0 . S2CID 4253103 .
- ^ Hewish, A. (1970). “Pulsars”. Revue annuelle d’astronomie et d’astrophysique . 8 (1): 265–296. Bibcode : 1970ARA&A…8..265H . doi : 10.1146/annurev.aa.08.090170.001405 .
- ^ Newman, ET ; et coll. (1965). “Métrique d’une masse rotative et chargée”. Journal de physique mathématique . 6 (6): 918. Bibcode : 1965JMP…..6..918N . doi : 10.1063/1.1704351 .
- ^ Israël, W. (1967). “Event Horizons in Static Vacuum Space-Times”. Examen physique . 164 (5): 1776. Bibcode : 1967PhRv..164.1776I . doi : 10.1103/PhysRev.164.1776 .
- ^ Carter, B. (1971). “Le trou noir axisymétrique n’a que deux degrés de liberté”. Lettres d’examen physique . 26 (6): 331. Bibcode : 1971PhRvL..26..331C . doi : 10.1103/PhysRevLett.26.331 .
- ^ Carter, B. (1977). “Le théorème d’unicité du trou noir sous vide et ses généralisations concevables”. Actes de la 1ère rencontre Marcel Grossmann sur la relativité générale . p. 243–254.
- ^ Robinson, D. (1975). “Unicité du trou noir de Kerr”. Lettres d’examen physique . 34 (14): 905. Bibcode : 1975PhRvL..34..905R . doi : 10.1103/PhysRevLett.34.905 .
- ^ un b Heusler, M. (2012). “Trous noirs stationnaires : unicité et au-delà” . Revues vivantes en relativité . 15 (7) : 7. arXiv : 1205.6112 . Bibcode : 2012LRR….15….7C . doi : 10.12942/lrr-2012-7 . PMC 5255892 . PMID 28179837 .
- ^ un b Penrose, R. (1965). “Effondrement gravitationnel et singularités spatio-temporelles” (PDF) . Lettres d’examen physique . 14 (3): 57. Bibcode : 1965PhRvL..14…57P . doi : 10.1103/PhysRevLett.14.57 . S2CID 116755736 . Archivé de l’original (PDF) le 11 octobre 2020.
- ^ Ford, LH (2003). “Les Théorèmes de Singularité Classiques et Leurs Échappatoires Quantiques”. Journal international de physique théorique . 42 (6): 1219-1227. arXiv : gr-qc/0301045 . Bibcode : 2003gr.qc…..1045F . doi : 10.1023/A:1025754515197 . S2CID 14404560 .
- ^ “Le prix Nobel de physique 2020” . PrixNobel.org . Archivé de l’original le 24 avril 2021 . Récupéré le 8 octobre 2020 .
- ^ Rolston, Bruce (10 novembre 1997), The First Black Hole , Université de Toronto, archivé de l’original le 7 mars 2008 , récupéré le 11 mars 2008
- ^ Shipman, HL; Yu, Z; Du, YW (1975), “L’histoire invraisemblable des modèles d’étoiles triples pour Cygnus X-1 Preuve d’un trou noir”, Astrophysical Letters , 16 (1): 9–12, Bibcode : 1975ApL….16… .9S , doi : 10.1016/S0304-8853(99)00384-4
- ^ Bardeen, JM ; Carter, B. ; Hawking, SW (1973). “Les quatre lois de la mécanique des trous noirs” . Communications en Physique Mathématique . 31 (2): 161–170. Bibcode : 1973CMaPh..31..161B . doi : 10.1007/BF01645742 . MR 0334798 . S2CID 54690354 . Zbl 1125.83309 . Archivé de l’original le 16 mai 2020 . Récupéré le 4 juin 2021 .
- ^ un bc Hawking , SW (1974). “Explosions de trous noirs?”. Nature . 248 (5443): 30–31. Bibcode : 1974Natur.248…30H . doi : 10.1038/248030a0 . S2CID 4290107 .
- ^ Popova, Maria (27 juin 2016). « Cartographier les cieux : comment la cosmologie a façonné notre compréhension de l’univers et l’étrange histoire de la naissance du terme « trou noir » » . brainpickings.org . Archivé de l’original le 19 avril 2019 . Récupéré le 12 avril 2019 .
- ^ un b “Marcia Bartusiak du MIT sur la compréhension de notre place dans l’univers” . www.wbur.org . Archivé de l’original le 12 avril 2019 . Récupéré le 12 avril 2019 .
- ^ un b Siegfried, Tom (23 décembre 2013). “50 ans plus tard, il est difficile de dire qui a nommé les trous noirs” . Actualités scientifiques . Archivé de l’original le 9 mars 2017 . Récupéré le 24 septembre 2017 . Il semble que l’étiquette “trou noir” ait également été évoquée en janvier 1964 à Cleveland lors d’une réunion de l’Association américaine pour l’avancement des sciences. La journaliste de Science News Letter, Ann Ewing, a rendu compte de cette réunion, décrivant comment un champ gravitationnel intense pouvait provoquer l’effondrement d’une étoile sur elle-même. “Une telle étoile forme alors un ‘trou noir’ dans l’univers”, a écrit Ewing.
- ^ Brown, Emma (3 août 2010). “Ann E. Ewing, journaliste a d’abord signalé des trous noirs” . Boston.com . Archivé de l’original le 24 septembre 2017 . Récupéré le 24 septembre 2017 .
- ^ “Le physicien pionnier John Wheeler meurt à 96 ans” . Scientifique américain . Archivé de l’original le 28 novembre 2016 . Récupéré le 27 novembre 2016 .
- ^ Au revoir, Dennis (14 avril 2008). “John A. Wheeler, physicien qui a inventé le terme” trou noir “, est mort à 96 ans” . Le New York Times . Archivé de l’original le 22 novembre 2016 . Récupéré le 27 novembre 2016 .
- ^ Carroll 2004 , p. 253
- ^ Reynolds, Christopher S. (janvier 2019). “Observer la rotation des trous noirs” . Astronomie naturelle . 3 (1): 41–47. arXiv : 1903.11704 . Bib code : 2019NatAs …3…41R . doi : 10.1038/s41550-018-0665-z . ISSN 2397-3366 . S2CID 85543351 . Archivé de l’original le 18 novembre 2020 . Récupéré le 21 août 2020 .
- ^ Thorne, KS ; Prix, RH (1986). Trous noirs : le paradigme de la membrane . Presse universitaire de Yale. ISBN 978-0-300-03770-8.
- ^ Anderson, Warren G. (1996). “Le problème de la perte d’informations sur les trous noirs” . FAQ sur la physique Usenet . Archivé de l’original le 22 janvier 2009 . Récupéré le 24 mars 2009 .
- ^ Preskill, J. (21 octobre 1994). Trous noirs et information : une crise de la physique quantique (PDF) . Séminaire de théorie Caltech. Archivé de l’original (PDF) le 18 mai 2008 . Récupéré le 17 mai 2009 .
- ^ Hawking & Ellis 1973 , Annexe B
- ^ Graines, Michael A.; En ligneBackman, Dana E. (2007). Perspectives sur l’astronomie . Cengage Apprentissage. p. 167. ISBN 978-0-495-11352-2. Archivé de l’original le 10 août 2016.
- ^ Shapiro, SL; Teukolsky, SA (1983). Trous noirs, naines blanches et étoiles à neutrons : la physique des objets compacts . John Wiley et fils. p. 357.ISBN _ 978-0-471-87316-7.
- ^ Berger, BK (2002). “Approches numériques des singularités de l’espace-temps” . Revues vivantes en relativité . 5 (1): 2002–1. arXiv : gr-qc/0201056 . Bibcode : 2002LRR…..5….1B . doi : 10.12942/lrr-2002-1 . PMC 5256073 . PMID 28179859 .
- ^ McClintock, JE; Shafee, R.; Narayan, R.; Rémillard, RA; Davis, SW; Li, L.-X. (2006). “La rotation du trou noir de Kerr proche de l’extrême GRS 1915 + 105”. Revue d’Astrophysique . 652 (1): 518–539. arXiv : astro-ph/0606076 . Bibcode : 2006ApJ…652..518M . doi : 10.1086/508457 . S2CID 1762307 .
- ^ un bc Abbott , BP; et coll. ( Collaboration Scientifique LIGO et Collaboration Virgo ) (1 juin 2017). “GW170104: Observation d’une coalescence de trous noirs binaires de 50 masses solaires à Redshift 0,2”. Lettres d’examen physique . 118 (22) : 221101. arXiv : 1706.01812 . Bibcode : 2017PhRvL.118v1101A . doi : 10.1103/PhysRevLett.118.221101 . PMID 28621973 . S2CID 206291714 .
- ^ Abbott, BP; et coll. ( Collaboration scientifique LIGO et collaboration Virgo ) (16 octobre 2017). “GW170817: Observation des ondes gravitationnelles d’une étoile à neutrons binaire Inspiral”. Lettres d’examen physique . 119 (16) : 161101. arXiv : 1710.05832 . Bibcode : 2017PhRvL.119p1101A . doi : 10.1103/PhysRevLett.119.161101 . PMID 29099225 .
- ^ Wald 1984 , pp. 124–125
- ^ Saa, Alberto; Santarelli, Raphaël (18 juillet 2011). “Détruire un trou noir Kerr-Newman quasi extrême”. Examen physique D . 84 (2) : 027501. arXiv : 1105.3950 . Bibcode : 2011PhRvD..84b7501S . doi : 10.1103/PhysRevD.84.027501 . S2CID 118487989 .
- ^ Misner, Thorne & Wheeler 1973 , p. 848
- ^ Davies, Paul (1992). The New Physics (éd. illustré). La presse de l’Universite de Cambridge. p. 26. ISBN 978-0-521-43831-5. Archivé de l’original le 17 août 2021 . Récupéré le 25 septembre 2020 . Extrait de la page 26 Archivé le 15 août 2021 à la Wayback Machine
- ^ Fleisch, Daniel; En ligneKregenow, Julia (2013). Un guide de l’étudiant sur les mathématiques de l’astronomie (éd. illustré). La presse de l’Universite de Cambridge. p. 168. ISBN 978-1-107-03494-5. Archivé de l’original le 17 août 2021 . Récupéré le 25 septembre 2020 . Extrait de la page 168 Archivé le 17 août 2021 à la Wayback Machine
- ^ Wheeler 2007 , p. 179
- ^ Carroll 2004 , ch. 5.4 et 7.3
- ^ “Singularités et trous noirs> Lightcones et structure causale” . plato.stanford.edu . Encyclopédie de philosophie de Stanford . Archivé de l’original le 17 mai 2019 . Récupéré le 11 mars 2018 .
- ^ Carroll 2004 , p. 217
- ^ Carroll 2004 , p. 218
- ^ “À l’intérieur d’un trou noir” . Connaître l’univers et ses secrets . Archivé de l’original le 23 avril 2009 . Récupéré le 26 mars 2009 .
- ^ “Que vous arrive-t-il si vous tombez dans un trou noir” . math.ucr.edu . Jean Baez . Archivé de l’original le 13 février 2019 . Récupéré le 11 mars 2018 .
- ^ Carroll 2004 , p. 222
- ^ “Regardez: Trois façons dont un astronaute pourrait tomber dans un trou noir” . 1er février 2014. Archivé de l’original le 15 avril 2019 . Récupéré le 13 mars 2018 .
- ^ Emparan, R.; Reall, HS (2008). “Trous noirs dans des dimensions supérieures” . Revues vivantes en relativité . 11 (6): 6. arXiv : 0801.3471 . Bibcode : 2008LRR….11….6E . doi : 10.12942/lrr-2008-6 . PMC 5253845 . PMID 28163607 .
- ^ Obers, NA (2009). Papantonopoulos, Eleftherios (éd.). Trous noirs en gravité dimensionnelle supérieure (PDF) . Physique des trous noirs . Notes de cours en physique. Vol. 769. Berlin, Heidelberg. p. 211–258. arXiv : 0802.0519 . Bibcode : 2009LNP…769…..P . doi : 10.1007/978-3-540-88460-6 . ISBN 978-3-540-88459-0. Archivé (PDF) de l’original le 26 juillet 2018 . Récupéré le 27 juillet 2018 .
- ^ Hawking & Ellis 1973 , ch. 9.3
- ^ Smarr, L. (1973). “Géométrie de surface des trous noirs rotatifs chargés”. Examen physique D . 7 (2): 289–295. Bibcode : 1973PhRvD…7..289S . doi : 10.1103/PhysRevD.7.289 .
- ^ Visser, M. (22 janvier 2009). “L’espace-temps Kerr: Une brève introduction”. Dans le Wiltshire, DL; Visser, M.; Scott, SM (éd.). L’espace-temps de Kerr : rotation des trous noirs en relativité générale . La presse de l’Universite de Cambridge. arXiv : 0706.0622 . ISBN 978-052188512-6. Archivé de l’original le 20 mai 2020 . Récupéré le 12 janvier 2020 .
- ^ Delgado, JFM; Herdeiro, RCA ; Radu, E. (2018). “Géométrie horizontale pour les trous noirs de Kerr avec des cheveux synchronisés”. Examen physique D . 97 (12) : 124012. arXiv : 1804.04910 . Bibcode : 2018PhRvD..97l4012D . doi : 10.1103/PhysRevD.97.124012 . manche : 10773/24121 . S2CID 55732213 .
- ^ Carroll 2004 , p. 205
- ^ Carroll 2004 , pp. 264–265
- ^ Carroll 2004 , p. 252
- ^ “Tailles des trous noirs? Quelle est la taille d’un trou noir?” . Ciel et télescope . 22 juillet 2014. Archivé de l’original le 3 avril 2019 . Récupéré le 9 octobre 2018 .
- ^ Lewis, GF; En ligneKwan, J. (2007). “Pas de retour: maximisation du temps de survie sous l’horizon des événements de Schwarzschild”. Publications de la Société astronomique d’Australie . 24 (2): 46–52. arXiv : 0705.1029 . Code Bib : 2007PASA …24…46L . doi : 10.1071/AS07012 . S2CID 17261076 .
- ^ Wheeler 2007 , p. 182
- ^ Carroll 2004 , pp. 257–259 et 265–266
- ^ Droz, S.; Israël, W. ; Morsink, SM (1996). “Trous noirs: l’histoire intérieure”. Monde de la Physique . 9 (1): 34–37. Bibcode : 1996PhyW….9…34D . doi : 10.1088/2058-7058/9/1/26 .
- ^ Carroll 2004 , p. 266
- ^ Poisson, E.; Israël, W. (1990). “Structure interne des trous noirs”. Examen physique D . 41 (6): 1796-1809. Bibcode : 1990PhRvD..41.1796P . doi : 10.1103/PhysRevD.41.1796 . PMID 10012548 .
- ^ Wald 1984 , p. 212
- ^ Hamade, R. (1996). “Trous noirs et gravité quantique” . Relativité et cosmologie de Cambridge . Université de Cambridge. Archivé de l’original le 7 avril 2009 . Récupéré le 26 mars 2009 .
- ^ Palmer, D. “Demandez à un astrophysicien : Gravité quantique et trous noirs” . NASA. Archivé de l’original le 28 mars 2009 . Récupéré le 26 mars 2009 .
- ^ un b Nitta, Daisuke; Chiba, Takeshi; Sugiyama, Naoshi (septembre 2011). “Ombres de trous noirs en collision”. Examen physique D . 84 (6) : 063008. arXiv : 1106.2425 . Bibcode : 2011PhRvD..84f3008N . doi : 10.1103/PhysRevD.84.063008 . S2CID 119264596 .
- ^ Bardeen, James M.; Presse, William H. ; Teukolsky, Saul A. (1er décembre 1972). “Trous noirs rotatifs: cadres localement non rotatifs, extraction d’énergie et rayonnement synchrotron scalaire”. Le Journal d’Astrophysique . 178 : 347–370. Bibcode : 1972ApJ…178..347B . doi : 10.1086/151796 .
- ^ “Calculatrice de trou noir” . Fabio Pacucci . Archivé de l’original le 21 octobre 2020 . Récupéré le 29 septembre 2020 .
- ^ un b Visser, Matt (2007). “L’espace-temps Kerr: Une brève introduction”. page 35, Fig. 3. arXiv : 0706.0622 [ gr-qc ].
- ^ Carroll 2004 , ch. 6.6
- ^ Carroll 2004 , ch. 6.7
- ^ Misner, Thorne & Wheeler 1973
- ^ Bardeen, JM (1972). “Trous noirs rotatifs: cadres localement non rotatifs, extraction d’énergie et rayonnement synchrotron scalaire”. Le Journal d’Astrophysique . 178 : 347–370. Bibcode : 1972ApJ…178..347B . doi : 10.1086/151796 .
- ^ Einstein, A. (1939). “Sur un système stationnaire à symétrie sphérique composé de nombreuses masses gravitationnelles” (PDF) . Annales de Mathématiques . 40 (4): 922–936. Bibcode : 1939AnMat..40..922E . doi : 10.2307/1968902 . JSTOR 1968902 . S2CID 55495712 . Archivé de l’original (PDF) le 28 février 2019.
- ^ Kerr, RP (2009). “Les métriques Kerr et Kerr-Schild”. Dans le Wiltshire, DL; Visser, M.; Scott, SM (éd.). L’espace-temps de Kerr . La presse de l’Universite de Cambridge. arXiv : 0706.1109 . Bibcode : 2007arXiv0706.1109K . ISBN 978-0-521-88512-6.
- ^ Hawking, SW ; Penrose, R. (janvier 1970). “Les singularités de l’effondrement gravitationnel et de la cosmologie” . Actes de la Royal Society A . 314 (1519): 529–548. Bibcode : 1970RSPSA.314..529H . doi : 10.1098/rspa.1970.0021 . JSTOR 2416467 .
- ^ un bc Pacucci , F.; Ferrara, A.; Grazian, A.; Fiore, F.; En ligneGiallongo, E. (2016). “Première identification des candidats de trou noir à effondrement direct dans l’univers primordial dans CANDELS / GOODS-S”. Lun. Pas. R.Astron. Soc . 459 (2) : 1432. arXiv : 1603.08522 . Bibcode : 2016MNRAS.459.1432P . doi : 10.1093/mnras/stw725 . S2CID 118578313 .
- ^ un Carr b , BJ (2005). “Trous noirs primordiaux : existent-ils et sont-ils utiles ?”. Dans Suzuki, H.; Yokoyama, J.; Suto, Y.; Sato, K. (éd.). Gonflement de l’horizon de l’astrophysique des particules et de la cosmologie . Presse de l’Académie universelle. pp. astro–ph/0511743. arXiv : astro-ph/0511743 . Bib code : 2005astro.ph.11743C . ISBN 978-4-946443-94-7.
- ^ “Déchiré par un trou noir” . Communiqué de presse de l’ESO . Archivé de l’original le 21 juillet 2013 . Récupéré le 19 juillet 2013 .
- ^ un bc Carroll 2004 , Section 5.8
- ^ “L’impression d’artiste de la graine de trou noir supermassif” . Archivé de l’original le 30 mai 2016 . Récupéré le 27 mai 2016 .
- ^ un bc Rees , MJ; En ligneVolonteri, M. (2007). Karas, V.; Matt, G. (éd.). Trous noirs massifs : formation et évolution . Actes de l’Union astronomique internationale . Vol. 238. p. 51–58. arXiv : astro-ph/0701512 . Bibcode : 2007IAUS..238…51R . doi : 10.1017/S1743921307004681 . ISBN 978-0-521-86347-6. S2CID 14844338 .
- ^ Bañados, Eduardo; Venemans, Bram P.; Mazzucchelli, Chiara; Farina, Emanuele P.; Walter, Fabien ; Wang, Feige ; Decarli, Roberto; Stern, Daniel; ventilateur, Xiaohui; Davies, Frederick B.; Hennawi, Joseph F. (1er janvier 2018). “Un trou noir de 800 millions de masse solaire dans un univers significativement neutre à un décalage vers le rouge de 7,5”. Nature . 553 (7689): 473–476. arXiv : 1712.01860 . Bibcode : 2018Natur.553..473B . doi : 10.1038/nature25180 . PMID 29211709 . S2CID 205263326 .
- ^ Penrose, R. (2002). “Effondrement gravitationnel : le rôle de la relativité générale” (PDF) . Relativité générale et Gravitation . 34 (7): 1141. Bibcode : 2002GReGr..34.1141P . doi : 10.1023/A:1016578408204 . S2CID 117459073 . Archivé de l’original (PDF) le 26 mai 2013.
- ^ Philippe Gibbs. « Le Big Bang est-il un trou noir ? . Jean Baez . Archivé de l’original le 31 décembre 2018 . Récupéré le 16 mars 2018 .
- ^ Giddings, SB; En ligneThomas, S. (2002). “Les collisionneurs à haute énergie comme usines à trous noirs: la fin de la physique à courte distance”. Examen physique D . 65 (5) : 056010. arXiv : hep-ph/0106219 . Code Bib : 2002PhRvD..65e6010G . doi : 10.1103/PhysRevD.65.056010 . S2CID 1203487 .
- ^ Harada, T. (2006). “Existe-t-il une masse minimale de trou noir ?”. Examen physique D . 74 (8) : 084004. arXiv : gr-qc/0609055 . Bibcode : 2006PhRvD..74h4004H . doi : 10.1103/PhysRevD.74.084004 . S2CID 119375284 .
- ^ Arkani-Hamed, N.; Dimopoulos, S.; En ligneDvali, G. (1998). “Le problème de la hiérarchie et les nouvelles dimensions au millimètre”. Lettres de physique B . 429 (3–4): 263–272. arXiv : hep-ph/9803315 . Bibcode : 1998PhLB..429..263A . doi : 10.1016/S0370-2693(98)00466-3 . S2CID 15903444 .
- ^ Groupe d’évaluation de la sécurité du LHC (2008). “Examen de la sécurité des collisions du LHC” (PDF) . Tourillon de Physique G : Physique Nucléaire . 35 (11) : 115004. arXiv : 0806.3414 . Bib code : 2008JPhG …35k5004E . doi : 10.1088/0954-3899/35/11/115004 . S2CID 53370175 . Archivé (PDF) de l’original le 14 avril 2010.
- ^ Cavaglia, M. (2010). “Les accélérateurs de particules comme usines à trous noirs ?” . Einstein-Online . 4 : 1010. Archivé de l’original le 8 mai 2013 . Récupéré le 8 mai 2013 .
- ^ Vesperini, E.; McMillan, SLW ; d’Ercole, A.; et coll. (2010). “Trous noirs de masse intermédiaire dans les premiers amas globulaires”. Les lettres du journal astrophysique . 713 (1) : L41–L44. arXiv : 1003.3470 . Bibcode : 2010ApJ…713L..41V . doi : 10.1088/2041-8205/713/1/L41 . S2CID 119120429 .
- ^ Zwart, SFP; Baumgardt, H.; Hutte, P. ; et coll. (2004). “Formation de trous noirs massifs par des collisions incontrôlables dans de jeunes amas d’étoiles denses”. Nature . 428 (6984): 724–726. arXiv : astro-ph/0402622 . Bibcode : 2004Natur.428..724P . doi : 10.1038/nature02448 . PMID 15085124 . S2CID 4408378 .
- ^ O’Leary, RM; Rasio, FA; Frégeau, JM; et coll. (2006). “Fusions binaires et croissance des trous noirs dans les amas d’étoiles denses”. Le Journal d’Astrophysique . 637 (2): 937–951. arXiv : astro-ph/0508224 . Bibcode : 2006ApJ…637..937O . doi : 10.1086/498446 . S2CID 1509957 .
- ^ Page, DN (2005). “Le rayonnement de Hawking et la thermodynamique des trous noirs”. Nouveau Journal de Physique . 7 (1): 203. arXiv : hep-th/0409024 . Bibcode : 2005NJPh….7..203P . doi : 10.1088/1367-2630/7/1/203 . S2CID 119047329 .
- ^ Carroll 2004 , ch. 9.6
- ^ Siegel, Ethan (2017). « Demandez à Ethan : les trous noirs grandissent-ils plus vite qu’ils ne s’évaporent ? » . Forbes (blog “Starts With A Bang”) . Archivé de l’original le 22 novembre 2018 . Récupéré le 17 mars 2018 .
- ^ Sivaram, C. (2001). “Le rayonnement de Hawking du trou noir peut ne jamais être observé!”. Relativité générale et Gravitation . 33 (2): 175–181. Bibcode : 2001GReGr..33..175S . doi : 10.1023/A:1002753400430 . S2CID 118913634 .
- ^ “Evaporation des trous noirs?” . Einstein en ligne . Institut Max Planck de physique gravitationnelle. 2010. Archivé de l’original le 22 juillet 2011 . Récupéré le 12 décembre 2010 .
- ^ Giddings, SB; Mangano, ML (2008). “Implications astrophysiques d’hypothétiques trous noirs stables à l’échelle du TeV”. Examen physique D . 78 (3) : 035009. arXiv : 0806.3381 . Bibcode : 2008PhRvD..78c5009G . doi : 10.1103/PhysRevD.78.035009 . S2CID 17240525 .
- ^ Peskin, ME (2008). « La fin du monde au grand collisionneur de hadrons ? » . Physique . 1 : 14. Bibcode : 2008PhyOJ…1…14P . doi : 10.1103/Physique.1.14 .
- ^ Fichtel, CE; Bertsch, DL; Dingus, BL ; et coll. (1994). “Recherche des données du télescope d’expérimentation de rayons gamma énergétiques (EGRET) pour les sursauts de microsecondes de rayons gamma à haute énergie”. Revue d’Astrophysique . 434 (2): 557-559. Bibcode : 1994ApJ…434..557F . doi : 10.1086/174758 .
- ^ Naeye, R. “Tester la physique fondamentale” . NASA. Archivé de l’original le 31 août 2008 . Récupéré le 16 septembre 2008 .
- ^ un b Frautschi, S. (1982). “Entropie dans un univers en expansion”. Sciences . 217 (4560): 593–599. Bib code : 1982Sci …217..593F . doi : 10.1126/science.217.4560.593 . PMID 17817517 . S2CID 27717447 .Voir page 596 : tableau 1 et section « désintégration du trou noir » et phrase précédente sur cette page.
- ^ Page, Don N. (1976). “Taux d’émission de particules d’un trou noir: particules sans masse d’un trou non chargé et non rotatif”. Examen physique D . 13 (2): 198-206. Bibcode : 1976PhRvD..13..198P . doi : 10.1103/PhysRevD.13.198 . . Voir en particulier l’équation (27).
- ^ “Trous noirs | Direction de la mission scientifique” . NASA. Archivé de l’original le 17 novembre 2017 . Récupéré le 17 mars 2018 .
- ^ Falcke, Heino; Mélia, Fulvio ; Agol, Eric (1er janvier 2000). “Affichage de l’Ombre du Trou Noir au Centre Galactique” . Le Journal d’Astrophysique . 528 (1) : L13–L16. arXiv : astro-ph/9912263 . Bibcode : 2000ApJ…528L..13F . doi : 10.1086/312423 . PMID 10587484 . S2CID 119433133 . Archivé de l’original le 23 octobre 2020 . Récupéré 22 octobre 2020 .
- ^ “Observations d’avril 2017” . Télescope d’horizon d’événement . Archivé de l’original le 10 avril 2019 . Récupéré 11 avril 2019 .
- ^ Au revoir, Dennis (10 avril 2019). “Obscurité visible, enfin : les astronomes capturent la toute première image d’un trou noir” . Le New York Times . Archivé de l’original le 21 mai 2019 . Récupéré 11 avril 2019 .
- ^ AP (10 avril 2019). “Les astronomes révèlent la première image d’un trou noir” . Le New York Times (vidéo). Archivé de l’original le 22 mai 2019 . Récupéré 11 avril 2019 .
- ^ Doeleman, Shep (4 avril 2016). “Le télescope Event Horizon : Imagerie et résolution temporelle d’un trou noir” . Physique @ Berkeley . L’événement se produit à 46:50. Archivé de l’original le 1er décembre 2016 . Récupéré le 8 juillet 2016 .
- ^ Grossman, Lisa; Conover, Emily (10 avril 2019). “La première image d’un trou noir ouvre une nouvelle ère de l’astrophysique” . Actualités scientifiques . Archivé de l’original le 27 avril 2019 . Récupéré 11 avril 2019 .
- ^ Collaboration avec le télescope Event Horizon (2021). “Premiers résultats du télescope M87 Event Horizon. VII. Polarisation de l’anneau” . Le Journal d’Astrophysique . 910 (1) : L12. arXiv : 2105.01169 . Bibcode : 2021ApJ…910L..12E . doi : 10.3847/2041-8213/abe71d . S2CID 233851995 . Archivé de l’original le 20 avril 2021 . Récupéré le 18 avril 2021 .
- ^ “La première image d’un trou noir ouvre une nouvelle ère de l’astrophysique” . Actualités scientifiques . 10 avril 2019. Archivé de l’original le 27 avril 2019 . Récupéré le 30 septembre 2019 .
- ^ Johnson, MD; Poisson, VL ; Doeleman, SS; Marrone, DP ; Plambeck, RL; Wardle, JFC; Akiyama, K.; Asada, K.; Beaudoin, C. (4 décembre 2015). “Structure et variabilité du champ magnétique résolues près de l’horizon des événements du Sagittaire A *”. Sciences . 350 (6265): 1242–1245. arXiv : 1512.01220 . Bib code : 2015Sci …350.1242J . doi : 10.1126/science.aac7087 . PMID 26785487 . S2CID 21730194 .
- ^ “Le télescope Event Horizon révèle des champs magnétiques au trou noir central de la Voie lactée” . cfa.harvard.edu . 3 décembre 2015. Archivé de l’original le 31 décembre 2015 . Récupéré le 12 janvier 2016 .
- ^ O. Straub, FH Vincent, MA Abramowicz, E. Gourgoulhon, T. Paumard, “Modélisation de la silhouette du trou noir dans Sgr A * avec des tores ioniques”, Astron. Astroph 543 (2012) A8
- ^ Au revoir, Dennis (11 février 2016). “Les physiciens détectent les ondes gravitationnelles, prouvant qu’Einstein a raison” . Le New York Times . Archivé de l’original le 11 février 2016 . Récupéré le 11 février 2016 .
- ^ Abbott, Benjamin P.; et coll. ( Collaboration scientifique LIGO et collaboration Virgo ) (11 février 2016). “Propriétés de la fusion de trous noirs binaires GW150914”. Lettres d’examen physique . 116 (24) : 241102. arXiv : 1602.03840 . Bibcode : 2016PhRvL.116x1102A . doi : 10.1103/PhysRevLett.116.241102 . PMID 27367378 . S2CID 217406416 .
- ^ un b Cardoso, V.; Franzin, E.; En lignePani, P. (2016). “Le ringdown des ondes gravitationnelles est-il une sonde de l’horizon des événements?”. Lettres d’examen physique . 116 (17) : 171101. arXiv : 1602.07309 . Bibcode : 2016PhRvL.116q1101C . doi : 10.1103/PhysRevLett.116.171101 . PMID 27176511 . S2CID 206273829 .
- ^ Abbott, Benjamin P.; et coll. ( Collaboration scientifique LIGO et collaboration Virgo ) (11 février 2016). “Tests de relativité générale avec GW150914” . Lettres d’examen physique . 116 (22) : 221101. arXiv : 1602.03841 . Bibcode : 2016PhRvL.116v1101A . doi : 10.1103/PhysRevLett.116.221101 . PMID 27314708 . S2CID 217275338 . Archivé de l’original le 15 février 2016 . Récupéré le 12 février 2016 .
- ^ Abbott, BP; et coll. ( Collaboration scientifique LIGO et collaboration Virgo ) (2016). “Implications astrophysiques de la fusion de trous noirs binaires GW150914” . Astrophyse. J. Lett . 818 (2) : L22. arXiv : 1602.03846 . Bibcode : 2016ApJ…818L..22A . doi : 10.3847/2041-8205/818/2/L22 . manche : 1826/11732 . Archivé de l’original le 16 mars 2016.
- ^ “Détection des ondes gravitationnelles” . LIGO . Archivé de l’original le 20 mai 2020 . Récupéré le 9 avril 2018 .
- ^ un b Gillessen, S.; Eisenhauer, F.; Trippe, S.; et coll. (2009). “Surveillance des orbites stellaires autour du trou noir massif dans le centre galactique”. Le Journal d’Astrophysique . 692 (2): 1075-1109. arXiv : 0810.4674 . Bibcode : 2009ApJ…692.1075G . doi : 10.1088/0004-637X/692/2/1075 . S2CID 1431308 .
- ^ un b Ghez, SUIS; Klein, BL; Morris, M.; et coll. (1998). “Etoiles à mouvement propre élevé dans le voisinage du Sagittaire A *: Preuve d’un trou noir supermassif au centre de notre galaxie”. Le Journal d’Astrophysique . 509 (2): 678–686. arXiv : astro-ph/9807210 . Bibcode : 1998ApJ…509..678G . doi : 10.1086/306528 . S2CID 18243528 .
- ^ Broderick, Avery; Loeb, Abraham; Narayan, Ramesh (août 2009). “L’Horizon d’Événement du Sagittaire A*”. Le Journal d’Astrophysique . 701 (2) : 1357-1366. arXiv : 0903.1105 . Bibcode : 2009ApJ…701.1357B . doi : 10.1088/0004-637X/701/2/1357 . S2CID 12991878 .
- ^ un b “Le NuSTAR de la NASA voit le flou rare de la lumière du trou noir” . NASA . 12 août 2014. Archivé de l’original le 13 août 2014 . Récupéré le 12 août 2014 .
- ^ “Les chercheurs clarifient la dynamique de l’énergie de rotation du trou noir” . Archivé de l’original le 17 septembre 2018 . Récupéré le 17 septembre 2018 .
- ^ Marck, Jean-Alain (1er mars 1996). “Méthode raccourcie de solution des équations géodésiques pour le trou noir de Schwarzchild”. Gravité classique et quantique . 13 (3): 393–402. arXiv : gr-qc/9505010 . Bibcode : 1996CQGra..13..393M . doi : 10.1088/0264-9381/13/3/007 . ISSN 0264-9381 . S2CID 119508131 .
- ^ un McClintock b , JE; Rémillard, RA (2006). “Binaires de trou noir”. Dans Lewin, W.; van der Klis, M. (éd.). Sources de rayons X stellaires compactes . p. 157. arXiv : astro-ph/0306213 . Bibcode : 2006csxs.book..157M . ISBN 978-0-521-82659-4.paragraphe 4.1.5.
- ^ “Qu’est-ce qui alimente les puissants jets d’un trou noir?” . Sciences | AAAA . 19 novembre 2014. Archivé de l’original le 5 mai 2019 . Récupéré le 19 mars 2018 .
- ^ un bcdefghi Celotti , A .; _ _ _ _ Miller, JC; Sciama, DW (1999). “Preuve astrophysique de l’existence de trous noirs” (PDF) . Gravité classique et quantique . 16 (12A) : A3–A21. arXiv : astro-ph/9912186 . Bibcode : 1999CQGra..16A…3C . doi : 10.1088/0264-9381/16/12A/301 . S2CID 17677758 . Archivé (PDF) de l’original le 27 juillet 2018 . Récupéré le 27 juillet 2018 .
- ^ Hiver, LM; Mushotzky, RF; Reynolds, CS (2006). “Étude d’archives XMM-Newton de la population de rayons X ultralumineux dans les galaxies voisines”. Le Journal d’Astrophysique . 649 (2): 730–752. arXiv : astro-ph/0512480 . Bibcode : 2006ApJ…649..730W . doi : 10.1086/506579 . S2CID 118445260 .
- ^ information@eso.org. “Hubble observe directement le disque autour d’un trou noir” . www.spacetelescope.org . Archivé de l’original le 8 mars 2016 . Récupéré le 7 mars 2016 .
- ^ Muñoz, José A.; Médiavilla, Evencio; Kochanek, Christopher S.; Falco, Emilio; Mosquera, Ana María (1er décembre 2011). “Une étude de la chromaticité de la lentille gravitationnelle avec le télescope spatial Hubble”. Le Journal d’Astrophysique . 742 (2) : 67. arXiv : 1107.5932 . Bib code : 2011ApJ …742…67M . doi : 10.1088/0004-637X/742/2/67 . S2CID 119119359 .
- ^ Bolton, CT (1972). “Identification de Cygnus X-1 avec HDE 226868”. Nature . 235 (5336): 271–273. Bibcode : 1972Natur.235..271B . doi : 10.1038/235271b0 . S2CID 4222070 .
- ^ Webster, BL; En ligneMurdin, P. (1972). “Cygnus X-1 – un binaire spectroscopique avec un compagnon lourd?”. Nature . 235 (5332): 37–38. Bibcode : 1972Natur.235…37W . doi : 10.1038/235037a0 . S2CID 4195462 .
- ^ Rolston, B. (10 novembre 1997). “Le premier trou noir” . Le bulletin . Université de Toronto. Archivé de l’original le 2 mai 2008 . Récupéré le 11 mars 2008 .
- ^ Shipman, HL (1er janvier 1975). “L’histoire invraisemblable des modèles d’étoiles triples pour Cygnus X-1 Preuve d’un trou noir”. Lettres astrophysiques . 16 (1): 9–12. Code bib : 1975ApL ….16….9S .
- ^ “Les scientifiques de la NASA identifient le plus petit trou noir connu” (Communiqué de presse). Centre de vol spatial Goddard . 1er avril 2008. Archivé de l’original le 27 décembre 2008 . Récupéré le 14 mars 2009 .
- ^ Krolik, JH (1999). Noyaux galactiques actifs . Presse universitaire de Princeton. Ch. 1.2. ISBN 978-0-691-01151-6. Archivé de l’original le 14 août 2021 . Récupéré le 16 octobre 2020 .
- ^ Étincelle, LS ; Gallagher, JS (2000). Galaxies dans l’univers : une introduction . La presse de l’Universite de Cambridge. Ch. 9.1. ISBN 978-0-521-59740-1. Archivé de l’original le 22 mars 2022 . Récupéré le 16 octobre 2020 .
- ^ Chou, Félicia; Anderson, Janet; Watzke, Megan (5 janvier 2015). “LIBÉRATION 15-001 – Chandra de la NASA détecte une explosion record du trou noir de la Voie lactée” . NASA . Archivé de l’original le 6 janvier 2015 . Récupéré le 6 janvier 2015 .
- ^ Kormendy, J.; En ligneRichstone, D. (1995). “Inward Bound – La recherche de trous noirs supermassifs dans les noyaux galactiques”. Revue annuelle d’astronomie et d’astrophysique . 33 (1): 581–624. Bibcode : 1995ARA&A..33..581K . doi : 10.1146/annurev.aa.33.090195.003053 .
- ^ Roi, A. (2003). “Les trous noirs, la formation de galaxies et la relation MBH-σ”. Les lettres du journal astrophysique . 596 (1): 27-29. arXiv : astro-ph/0308342 . Bibcode : 2003ApJ…596L..27K . doi : 10.1086/379143 . S2CID 9507887 .
- ^ Ferrarese, L.; Merritt, D. (2000). “Une relation fondamentale entre les trous noirs supermassifs et leurs galaxies hôtes”. Les lettres du journal astrophysique . 539 (1): 9–12. arXiv : astro-ph/0006053 . Bibcode : 2000ApJ…539L…9F . doi : 10.1086/312838 . S2CID 6508110 .
- ^ “Le dîner d’un trou noir approche rapidement” . Communiqué de presse de l’ESO . Archivé de l’original le 13 février 2012 . Récupéré le 6 février 2012 .
- ^ Sahu, KC (2022). “Un trou noir de masse stellaire isolé détecté par microlentille astrométrique”. Revue d’Astrophysique . arXiv : 2201.13296 .
- ^ Bozza, V. (2010). “Lentille gravitationnelle par les trous noirs”. Relativité générale et Gravitation . 42 (9): 2269–2300. arXiv : 0911.2187 . Bib code : 2010GReGr..42.2269B . doi : 10.1007/s10714-010-0988-2 . S2CID 118635353 .
- ^ Kovacs, Z.; Cheng, KS ; En ligneHarko, T. (2009). “Les trous noirs de masse stellaire peuvent-ils être des quarks ?”. Avis mensuels de la Royal Astronomical Society . 400 (3) : 1632–1642. arXiv : 0908.2672 . Bibcode : 2009MNRAS.400.1632K . doi : 10.1111/j.1365-2966.2009.15571.x . S2CID 18263809 .
- ^ Kusenko, A. (2006). “Propriétés et signatures des Q-balls supersymétriques”. arXiv : hep-ph/0612159 .
- ^ Hansson, J.; Sandin, F. (2005). « Étoiles Preon : une nouvelle classe d’objets compacts cosmiques ». Lettres de physique B . 616 (1–2) : 1–7. arXiv : astro-ph/0410417 . Bibcode : 2005PhLB..616….1H . doi : 10.1016/j.physletb.2005.04.034 . S2CID 119063004 .
- ^ Kiefer, C. (2006). « Gravité quantique : introduction générale et développements récents ». Annalen der Physik . 15 (1–2): 129–148. arXiv : gr-qc/0508120 . Bibcode : 2006AnP…518..129K . doi : 10.1002/andp.200510175 . S2CID 12984346 .
- ^ Skenderis, K.; En ligneTaylor, M. (2008). “La proposition fuzzball pour les trous noirs”. Rapports de physique . 467 (4–5) : 117. arXiv : 0804.0552 . Bibcode : 2008PhR…467..117S . doi : 10.1016/j.physrep.2008.08.001 . S2CID 118403957 .
- ^ Choi, Charles Q. (2018). “Les prétendants au trou noir pourraient vraiment être des étoiles quantiques bizarres” . Scientifique américain . Archivé de l’original le 17 juin 2019 . Récupéré le 17 mars 2018 .
- ^ Boule, Philip (31 mars 2005). “Les trous noirs “n’existent pas” “. Nature . doi : 10.1038/news050328-8 .
- ^ Hawking, SW (1971). “Le rayonnement gravitationnel des trous noirs en collision”. Lettres d’examen physique . 26 (21): 1344-1346. Bibcode : 1971PhRvL..26.1344H . doi : 10.1103/PhysRevLett.26.1344 .
- ^ un b Wald, RM (2001). “La thermodynamique des trous noirs” . Revues vivantes en relativité . 4 (1): 6. arXiv : gr-qc/9912119 . Bibcode : 2001LRR…..4….6W . doi : 10.12942/lrr-2001-6 . PMC 5253844 . PMID 28163633 .
- ^ ‘t Hooft, G. (2001). “Le principe holographique”. Dans Zichichi, A. (éd.). Bases et faits saillants en physique fondamentale . Actes de l’École internationale de physique subnucléaire . Série subnucléaire. Vol. 37. Édition scientifique mondiale . p. 72–100. arXiv : hep-th/0003004 . Bibcode : 2001bhfp.conf…72T . doi : 10.1142/9789812811585_0005 . ISBN 978-981-02-4536-8. S2CID 119383028 .{{cite book}}: CS1 maint: date and year (link)
- ^ Strominger, A.; Vafa, C. (1996). “Origine microscopique de l’entropie de Bekenstein-Hawking”. Lettres de physique B . 379 (1–4) : 99–104. arXiv : hep-th/9601029 . Bibcode : 1996PhLB..379…99S . doi : 10.1016/0370-2693(96)00345-0 . S2CID 1041890 .
- ^ Carlip, S. (2009). “Thermodynamique des trous noirs et mécanique statistique”. Physique des trous noirs . Physique des trous noirs . Notes de cours en physique. Vol. 769. Berlin, Heidelberg. p. 89–123. arXiv : 0807.4520 . Bibcode : 2009LNP…769…89C . doi : 10.1007/978-3-540-88460-6_3 . ISBN 978-3-540-88459-0. S2CID 15877702 .
- ^ Calmet, Kuipers, Xavier, Folkert (2021). “Quantum gravitational corrections to the entropy of a Schwarzschild black hole”. Phys. Rev. D. 104 (6): 6. arXiv:2108.06824. Bibcode:2021PhRvD.104f6012C. doi:10.1103/PhysRevD.104.066012. S2CID 237091145.
- ^ Campos Delgado, Ruben (2022). “Quantum gravitational corrections to the entropy of a Reissner-Nordström black hole”. Eur. Phys. J. C. 82 (3): 272. Bibcode:2022EPJC…82..272C. doi:10.1140/epjc/s10052-022-10232-0. S2CID 247824137.
- ^ Hawking, S. W. “Does God Play Dice?”. www.hawking.org.uk. Archived from the original on 11 January 2012. Retrieved 14 March 2009.
- ^ Giddings, S. B. (1995). “The black hole information paradox”. Particles, Strings and Cosmology. Johns Hopkins Workshop on Current Problems in Particle Theory 19 and the PASCOS Interdisciplinary Symposium 5. arXiv:hep-th/9508151. Bibcode:1995hep.th….8151G.
- ^ a b Unruh, William G.; Wald, Robert M. (2017). “Information loss”. Reports on Progress in Physics. 80 (9): 092002. arXiv:1703.02140. Bibcode:2017RPPh…80i2002U. doi:10.1088/1361-6633/aa778e. PMID 28585922. S2CID 39957660.
- ^ Mathur, S. D. (2011). The information paradox: conflicts and resolutions. XXV International Symposium on Lepton Photon Interactions at High Energies. arXiv:1201.2079. Bibcode:2012Prama..79.1059M. doi:10.1007/s12043-012-0417-z.
- ^ Page, Don N. (1993). “Information in black hole radiation”. Phys. Rev. Lett. 71 (23): 3743–3746. arXiv:hep-th/9306083. Bibcode:1993PhRvL..71.3743P. CiteSeerX 10.1.1.267.174. doi:10.1103/PhysRevLett.71.3743. PMID 10055062. S2CID 9363821.
- ^ Page, Don N. (1993). “Average entropy of a subsystem”. Phys. Rev. Lett. 71 (9): 1291–1294. arXiv:gr-qc/9305007. Bibcode:1993PhRvL..71.1291P. CiteSeerX 10.1.1.339.7694. doi:10.1103/PhysRevLett.71.1291. PMID 10055503. S2CID 17058654.
- ^ Merali, Zeeya (3 April 2013). “Astrophysics: Fire in the hole!”. Nature. 496 (7443): 20–23. Bibcode:2013Natur.496…20M. doi:10.1038/496020a. PMID 23552926.
- ^ Amheiri, Ahmed; Marolf, Donald; Polchinski, Joseph; Sully, James (2013). “Black holes: Complementarity or Firewalls?”. Journal of High Energy Physics. 2013 (2): 62. arXiv:1207.3123. Bibcode:2013JHEP…02..062A. doi:10.1007/JHEP02(2013)062. S2CID 55581818.
Further reading
Popular reading
- Begelman, Mitchell; Rees, Martin (2021). Gravity’s Fatal Attraction: Black Holes in the Universe (Third ed.). New York: Cambridge University Press. ISBN 9781108819053. Archived from the original on 2 January 2022. Retrieved 6 November 2021.
- Ferguson, Kitty (1991). Black Holes in Space-Time. Watts Franklin. ISBN 978-0-531-12524-3.
- Hawking, Stephen (1988). A Brief History of Time. Bantam Books, Inc. ISBN 978-0-553-38016-3.
- Hawking, Stephen; Penrose, Roger (1996). The Nature of Space and Time. Princeton University Press. ISBN 978-0-691-03791-2. Archived from the original on 18 October 2021. Retrieved 16 May 2020.
- Levin, Janna (2020). Black hole survival guide. New York: Alfred A. Knopf. ISBN 9780525658221. Archived from the original on 22 March 2022. Retrieved 6 November 2021.
- Melia, Fulvio (2003). The Black Hole at the Center of Our Galaxy. Princeton U Press. ISBN 978-0-691-09505-9.
- Melia, Fulvio (2003). The Edge of Infinity. Supermassive Black Holes in the Universe. Cambridge U Press. ISBN 978-0-521-81405-8.
- Pickover, Clifford (1998). Black Holes: A Traveler’s Guide. Wiley, John & Sons, Inc. ISBN 978-0-471-19704-1.
- Thorne, Kip S. (1994). Black Holes and Time Warps. Norton, W. W. & Company, Inc. ISBN 978-0-393-31276-8.
- Susskind, Leonard (2008). The Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics. Little, Brown and Company. ISBN 978-0316016407.
- Wheeler, J. Craig (2007). Cosmic Catastrophes (2nd ed.). Cambridge University Press. ISBN 978-0-521-85714-7.
University textbooks and monographs
- Carroll, Sean M. (2004). Spacetime and Geometry. Addison Wesley. ISBN 978-0-8053-8732-2., the lecture notes on which the book was based are available for free from Sean Carroll’s website Archived 23 March 2017 at the Wayback Machine.
- Carter, B. (1973). “Black hole equilibrium states”. In DeWitt, B. S.; DeWitt, C. (eds.). Black Holes.
- Chandrasekhar, Subrahmanyan (1999). Mathematical Theory of Black Holes. Oxford University Press. ISBN 978-0-19-850370-5.
- Frolov, Valeri P.; Novikov, Igor D. (1998). Black Hole Physics. Fundamental Theories of Physics. Vol. 96. doi:10.1007/978-94-011-5139-9. ISBN 978-0-7923-5146-7.
- Frolov, Valeri P.; Zelnikov, Andrei (2011). Introduction to Black Hole Physics. Oxford: Oxford University Press. ISBN 978-0-19-969229-3. Zbl 1234.83001. Archived from the original on 22 March 2022. Retrieved 2 January 2022.
- Hawking, S. W.; Ellis, G. F. R. (1973). Large Scale Structure of space time. Cambridge University Press. ISBN 978-0-521-09906-6. Archived from the original on 21 July 2020. Retrieved 16 May 2020.
- Melia, Fulvio (2007). The Galactic Supermassive Black Hole. Princeton U Press. ISBN 978-0-691-13129-0.
- Misner, Charles; Thorne, Kip S.; Wheeler, John (1973). Gravitation. W. H. Freeman and Company. ISBN 978-0-7167-0344-0.
- Taylor, Edwin F.; Wheeler, John Archibald (2000). Exploring Black Holes. Addison Wesley Longman. ISBN 978-0-201-38423-9.
- Wald, Robert M. (1984). General Relativity. University of Chicago Press. ISBN 978-0-226-87033-5. Archived from the original on 11 August 2016. Retrieved 23 February 2016.
- Wald, Robert M. (1992). Space, Time, and Gravity: The Theory of the Big Bang and Black Holes. University of Chicago Press. ISBN 978-0-226-87029-8.
- Price, Richard; Creighton, Teviet (2008). “Black holes”. Scholarpedia. 3 (1): 4277. Bibcode:2008SchpJ…3.4277C. doi:10.4249/scholarpedia.4277.
Review papers
- Gallo, Elena; Marolf, Donald (2009). “Resource Letter BH-2: Black Holes”. American Journal of Physics. 77 (4): 294–307. arXiv:0806.2316. Bibcode:2009AmJPh..77..294G. doi:10.1119/1.3056569. S2CID 118494056.
- Hughes, Scott A. (2005). “Trust but verify: The case for astrophysical black holes”. arXiv:hep-ph/0511217. Lecture notes from 2005 SLAC Summer Institute.
External links
Black holeat Wikipedia’s sister projects
-
![]() Definitions from Wiktionary
Definitions from Wiktionary -
![]() Media from Commons
Media from Commons -
![]() News from Wikinews
News from Wikinews -
![]() Quotations from Wikiquote
Quotations from Wikiquote -
![]() Textbooks from Wikibooks
Textbooks from Wikibooks -
![]() Resources from Wikiversity
Resources from Wikiversity -
![]() Data from Wikidata
Data from Wikidata
| Scholia has a profile for black hole (Q589). |
- Black Holes on In Our Time at the BBC
- Stanford Encyclopedia of Philosophy: “Singularities and Black Holes” by Erik Curiel and Peter Bokulich.
- Black Holes: Gravity’s Relentless Pull – Interactive multimedia Web site about the physics and astronomy of black holes from the Space Telescope Science Institute (HubbleSite)
- ESA’s Black Hole Visualization
- Frequently Asked Questions (FAQs) on Black Holes
- Schwarzschild Geometry
- Black holes – basic (NYT; April 2021)
Videos
- 16-year-long study tracks stars orbiting Sagittarius A*
- Movie of Black Hole Candidate from Max Planck Institute
- Cowen, Ron (20 April 2015). “3D simulations of colliding black holes hailed as most realistic yet”. Nature. doi:10.1038/nature.2015.17360.
- Computer visualisation of the signal detected by LIGO
- Two Black Holes Merge into One (based upon the signal GW150914)
Portals: ![]() Astronomy
Astronomy ![]() History of science
History of science ![]() Mathematics
Mathematics ![]() Physics
Physics ![]() Stars
Stars

